-
-
May 8 2015, 14:46
Абсолютные ,относительные и приведенные погрешности измерений
Абсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины.
Действительное значение Хд измеряемой величины это найденное экспериментально значение измеряемой величины максимально близкое к ее истинному значению. Говоря простым языком действительное значение Хд это значение, измеренное эталонным прибором, или сгенерированное калибратором или задатчиком высокого класса точности. Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает).
См.Абсолютная погрешность микрокомпьютерного расходомера скоростемера МКРС
Относительная погрешность – это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины.
Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
См.Относительная погрешность ультразвукового уровнемера ЭХО-АС-01
Приведенная погрешность – это отношение абсолютной погрешности измерения Δ к нормирующему значению Хn, постоянному во всем диапазоне измерения или его части.
Нормирующее значение Хn зависит от типа шкалы датчика КИП:
- Если шкала датчика односторонняя и нижний предел измерения равен нулю (например, шкала датчика от 0 до 150 м3/ч), то Хn принимается равным верхнему пределу измерения (в нашем случае Хn = 150 м3/ч).
- Если шкала датчика односторонняя, но нижний предел измерения не равен нулю (например, шкала датчика от 30 до 150 м3/ч), то Хn принимается равным разности верхнего и нижнего пределов измерения (в нашем случае Хn = 150-30 = 120 м3/ч).
- Если шкала датчика двухсторонняя (например, от -50 до +150 ˚С), то Хn равно ширине диапазона измерения датчика (в нашем случае Хn = 50+150 = 200 ˚С).
Приведенная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
Довольно часто в описании на тот или иной датчик указывается не только диапазон измерения, например, от 0 до 50 мг/м3, но и диапазон показаний, например, от 0 до 100 мг/м3. Приведенная погрешность в этом случае нормируется к концу диапазона измерения, то есть к 50 мг/м3, а в диапазоне показаний от 50 до 100 мг/м3 погрешность измерения датчика не определена вовсе – фактически датчик может показать все что угодно и иметь любую погрешность измерения. Диапазон измерения датчика может быть разбит на несколько измерительных поддиапазонов, для каждого из которых может быть определена своя погрешность как по величине, так и по форме представления. При этом при поверке таких датчиков для каждого поддиапазона могут применяться свои образцовые средства измерения, перечень которых указан в методике поверки на данный прибор.
ВИДЕО УРОК
Абсолютная погрешность.
Разность между истинным значением измеряемой величины
и её приближённым значением называется абсолютной погрешностью.
Для подсчёта
абсолютной погрешности необходимо из большего числа вычесть меньшее число.
Существует формула
абсолютной погрешности. Обозначим точное число буквой А, а буквой а –
приближение к точному числу. Приближённое число – это число, которое
незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда
формула будет выглядеть следующим образом:
∆а = А – а.
ПРИМЕР:
В школе учится 374 ученика. Если округлить это число до 400,
то абсолютная погрешность измерения равна:
400 – 374 = 26.
ПРИМЕР:
На предприятии 1284 рабочих и
служащих. При округлении этого числа до 1300 абсолютная
погрешность составляет
1300 – 1284 = 16.
При округлении до 1280 абсолютная
погрешность составляет
1284 – 1280 = 4.
Редко когда можно
точно знать значение измеряемой величины, чтобы рассчитать абсолютную
погрешность. Но при выполнении различных измерений мы обычно представляем себе
границы абсолютной погрешности и всегда можем сказать, какого определённого
числа она не превосходит.
ПРИМЕР:
Торговые весы могут дать абсолютную погрешность, не
превышающую 5 г, а аптекарские – не превышающую одной сотой грамма.
Записывают
абсолютную погрешность числа, используя знак
±.
ПРИМЕР:
Длина рулона обоев составляет.
30 м ± 3
см.
Границу абсолютной
погрешности называют предельной абсолютной погрешностью.
Но абсолютная
погрешность не даёт нам представление о качестве измерения, то есть о том,
насколько тщательно это измерение выполнено. Чтобы понять эту мысль, достаточно
разобраться в таком примере.
ПРИМЕР:
Допустим, что при измерении коридора длиной в 20
м мы допустили абсолютную погрешность
всего только в 1 см. Теперь представим себе, что, измеряя корешок книги,
имеющий 18
см длины, мы тоже допустили абсолютную
погрешность в 1 см. Тогда понятно, что первое измерение нужно признать
превосходным, но зато второе – совершенно неудовлетворительным. Это значит, что
на 20
м ошибка в 1
см вполне допустима и неизбежна, но
на 18
см такая ошибка является очень грубой.
Отсюда ясно, что для оценки качества измерения
существенна не сама абсолютная погрешность, а та доля, какую она составляет от
измеряемой величины. При измерении коридора длиной в 20 м погрешность в 1 см
составляет
долю
измеряемой величины, а при измерении корешка книги погрешность в 1 см составляет
долю
измеряемой величины.
Делаем вывод, что измеряя корешок книги, имеющий 18
см длины и допустив погрешность в 1
см, можно считать измерение с большой ошибкой. Но если погрешность в 1
см была допущена при измерении коридора
длиной в 20
м, то это измерение можно считать максимально точным.
Если ошибка,
возникающая при измерении линейкой или каким либо другим измерительным
инструментом, значительно меньше, чем деления шкалы этой линейки, то в качестве
абсолютной погрешности измерения обычно берут половину деления. Если деления на
линейке нанесены достаточно точно, то ошибка при измерении близка к нулю.
Тогда
значение измеряемой длины предмета будет значение ближайшей метки линейки.
Поэтому, если измерение выполнено аккуратно, то истинная длина предмета может
отличаться от измеренной длины не более чем на половину деления шкалы, то есть 0,5 мм.
ПРИМЕР:
Для измерения длины болта использованы метровая линейка с
делениями 0,5 см и линейка с
делениями 1 мм. В обоих случаях получен результат 3,5
см. Ясно, что в первом случае отклонение найденной длины 3,5
см от истинной, не
должно по модулю превышать 0,5 см, во втором случае
0,1 см.
Если этот же результат получится при измерении
штангенциркулем, то
p(l; 3,5) = |l – 3,5 ≤ 0,01|.
Данный пример показывает зависимость абсолютной
погрешности и границ, в которых находится точный результат, от точности
измерительных приборов. В одном случае ∆l = 0,5 и, следовательно,
3
≤ l ≤ 4,
в другом – ∆l = 0,1 и
3,4
≤ l ≤ 3,6.
ПРИМЕР:
Длина листа бумаги формата А4 равна (29,7 ± 0,1)
см. А расстояние от Санкт-Петербурга до Москвы равно (650 ± 1) км. Абсолютная погрешность в первом случае
не превосходит одного миллиметра, а во втором – одного километра. Необходимо
сравнить точность этих измерений.
РЕШЕНИЕ:
Если вы думаете, что длина листа измерена точнее потому,
что величина абсолютной погрешности не
превышает 1 мм, то вы ошибаетесь.
Напрямую сравнить эти величины нельзя. Проведём некоторые рассуждения.
При измерении длины листа абсолютная погрешность не
превышает 0,1 см на 29,7 см, то есть в процентном отношении это составляет
0,1
: 29,7 ∙ 100% ≈ 0,33%
измеряемой величины.
Когда мы измеряем расстояние от Санкт-Петербурга до
Москвы, то абсолютная погрешность не превышает
1 км
на 650 км, что в процентном соотношении составляет
1
: 650 ∙ 100% ≈ 0,15%
измеряемой величины.
Видим, что расстояние между городами измерено точнее, чем
длинна листа формата А4.
Истинное значение
измеряемой величины известно бывает лишь в очень редких случаях, а поэтому и
действительная величина абсолютной погрешности почти никогда не может быть вычислена.
На практике абсолютной погрешности недостаточно для точной оценки измерения.
Поэтому на практике более важное значение имеет определение относительной
погрешности измерения.
Относительная погрешность.
Абсолютная
погрешность, как мы убедились, не даёт возможности судить о качестве измерения.
Поэтому для оценки качества приближения вводится новое понятие – относительная
погрешность. Относительная погрешность позволяет судить о качестве измерения.
Относительная погрешность –
это частное от деления абсолютной погрешности на модуль приближённого значения
измеряемой величины, выраженная в долях или процентах.
Относительная
погрешность величина всегда положительная. Это следует из того, что абсолютная погрешность
всегда положительная величина, и мы делим её на модуль приближённого значения
измеряемой величины, а модуль тоже всегда положителен.
ПРИМЕР:
Округлим дробь 14,7 до целых и найдём относительную погрешность приближённого
значения:
14,7 ≈ 15,
Для вычисления
относительной погрешности, кроме приближённого значения, нужно знать ещё и
абсолютную погрешность. Обычно абсолютная погрешность неизвестна, поэтому
вычислить относительную погрешность нельзя. В таких случаях ограничиваются
оценкой относительной погрешности.
ПРИМЕР:
При измерении в (сантиметрах) толщины
b
стекла и длины l книжной полки
получили следующие результаты:
b ≈ 0,4 с
точностью до 0,1,
l ≈ 100 с
точностью до 0,1.
Абсолютная погрешность каждого из этих измерений не
превосходит 0,1. Однако 0,1 составляет
существенную часть числа 0,4 и
ничтожную часть числа 100. Это показывает, что качество второго
измерения намного выше, чем первого.
В результате измерения нашли,
что b ≈ 0,4 с точностью до 0,1, то
есть абсолютная погрешность измерения не превосходит 0,1.
Значит, отношение абсолютной погрешности к приближённому значению меньше или равно
то есть относительная погрешность приближения не превосходит 25%.
Аналогично найдём, что
относительная погрешность приближения, полученного при измерении длины полки,
не превосходит
Говорят, что в первом случае измерение выполнено с
относительной точностью до 25%,
а во втором – с относительной точностью до 0,1%.
ПРИМЕР:
Если взять абсолютную погрешность в 1
см, при измерении длины отрезков 10
см и 10
м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для
отрезка длиной в 10 см погрешность
в 1
см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, эта ошибка всего в 0,1%.
Чем меньше относительная погрешность
измерения, тем оно точнее.
Различают
систематические и случайные погрешности.
Систематической погрешностью называют ту погрешность, которая остаётся неизменной при
повторных измерениях.
Случайной погрешностью называют ту погрешность, которая возникает в результате
воздействия на процесс измерения внешних факторов и может изменять своё
значение.
В большинстве
случаев невозможно узнать точное значение приближённого числа, а значит, и
точную величину погрешности. Однако почти всегда можно установить, что
погрешность (абсолютная или относительная) не превосходит некоторого числа.
ПРИМЕР:
Продавец взвешивает арбуз на чашечных весах. В наборе
наименьшая гиря – 50
г. Взвешивание показало 3600 г. Это число – приближённое. Точный вес арбуза
неизвестен. Но абсолютная погрешность не превышает 50
г. Относительная погрешность не превосходит
50/3600 ≈
1,4%.
Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной
погрешностью.
Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной
погрешностью.
В предыдущем примере
за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность 1,4%.
Величина предельной
погрешности не является вполне определённой. Так в предыдущем примере можно
принять за предельную абсолютную погрешность
100 г, 150 г и вообще всякое
число, большее чем 50 г.
На практике берётся по возможности меньшее значение предельной погрешности. В
тех случаях, когда известна точная величина погрешности, эта величина служит
одновременно предельной погрешностью. Для каждого приближённого числа должна
быть известна его предельная погрешность (абсолютная или относительная). Когда
она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено
приближённое число 4,78 без указания предельной погрешности, то подразумевается,
что предельная абсолютная погрешность составляет 0,005. В следствии этого соглашения всегда можно обойтись без указания
предельной погрешности числа.
Предельная
абсолютная погрешность обозначается греческой буквой ∆ (<<дельта>>),
предельная относительная погрешность – греческой буквой δ
(<<дельта малая>>). Если приближённое число обозначить буквой а,
Правила округления.
На практике
относительную погрешность округляют до двух значащих цифр, выполняя округление
с избытком, то есть, всегда увеличивая последнюю значащую цифру на единицу.
ПРИМЕР:
Для х = 1,7 ± 0,2 относительная погрешность измерений равна:
ПРИМЕР:
Длина карандаша измерена линейкой с миллиметровым
делением. Измерение показало 17,9 см. Какова предельная относительная погрешность этого
измерения ?
РЕШЕНИЕ:
Здесь а =
17,9 см. Можно принять ∆ = 0,1 см, так как с точностью
до 1 мм
измерить карандаш нетрудно, а значительно уменьшить предельную
погрешность не удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но
у самого карандаша рёбра могут отличаться на большую величину). Относительная погрешность равна
Округляя, находим
ПРИМЕР:
Цилиндрический поршень имеет около 35
мм в диаметре. С какой точностью нужно
его измерить микрометром, чтобы предельная относительная погрешность составляла 0,05% ?
РЕШЕНИЕ:
По условию, предельная относительная
погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная абсолютная
погрешность равна
или, усиливая, 0,02
мм.
Можно воспользоваться
формулой
Подставляя в формулу
а = 35,
𝛿 = 0,0005,
имеем
Значит,
∆
= 35 × 0,0005 = 0,0175 мм.
Действия над приближёнными числами.
Сложение и вычитание приближённых чисел.
Абсолютная погрешность суммы двух величин равна сумме
абсолютных погрешностей отдельных слагаемых.
ПРИМЕР:
Складываются приближённые числа
265 и 32.
РЕШЕНИЕ:
Пусть предельная погрешность первого есть 5,
а второго 1. Тогда предельная погрешность суммы равна
5
+ 1 = 6.
Так, если истинное значение первого есть 270,
а второго 33, то приближённая сумма
265
+ 32 = 297
на 6 меньше истинной
270
+ 33 = 303.
ПРИМЕР:
Найти сумму приближённых чисел:
0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667
+ 0,0625 + 0,0588 + 0,0556 + 0,0526.
РЕШЕНИЕ:
Сложение даёт следующий результат – 0,6187.
Предельная погрешность каждого слагаемого
0,00005.
Предельная погрешность суммы:
0,00005
∙ 9 = 0,00045.
Значит, в последнем (четвёртом) знаке суммы возможна ошибка до 5
единиц. Поэтому округляем сумму до третьего знака, то есть до тысячных.
Получаем 0,619,
здесь все знаки верные.
При значительном
числе слагаемых обычно происходит взаимная компенсация погрешностей, поэтому
истинная погрешность суммы лишь в исключительных случаях совпадает с предельной
погрешностью или близка к ней. Насколько редки эти случаи, видно из предыдущего
примера, где 9 слагаемых. Истинная величина каждого из них может
отличаться в пятом знаке от взятого приближённого значения на 1, 2, 3, 4 или даже на 5 единиц в ту и в другую сторону.
Например, первое
слагаемое может быть больше своего истинного значения на 4 единицы пятого знака, второе – на две, третье – меньше
истинного на одну единицу и так далее.
Расчёт показывает,
что число всех возможных случаев распределения погрешностей составляет около
одного миллиарда. Между тем лишь в двух случаях погрешность суммы может
достигнуть предельной погрешности 0,00045,
это произойдёт:
– когда истинная величина каждого слагаемого больше
приближённой величины на 0,00005;
– когда истинная величина каждого слагаемого меньше
приближённой величины на 0,00005.
Значит, случаи,
когда погрешность суммы совпадает с предельной, составляют только 0,0000002% всех возможных случаев.
Дальнейший расчёт
показывает, что случаи, когда погрешность суммы девяти слагаемых может
превысить три единицы последнего знака, тоже очень редки. Они составляют
лишь 0,07%
из числа всех
возможных. Две единицы последнего знака погрешность может превысить 2% всех возможных случаев, а одну единицу –
примерно в 25%.
В остальных 75% случаев погрешность девяти слагаемых не
превышает одной единицы последнего знака.
ПРИМЕР:
Найти сумму точных чисел:
0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667
+ 0,0625 + 0,0588 + 0,0556 + 0,0526.
РЕШЕНИЕ:
Сложение даёт следующий результат – 0,6187.
Округлим их до тысячных и сложим:
0,091
+ 0,083 + 0,077 + 0,071 + 0,067
+ 0,062 + 0,059 + 0,056 + 0,053 = 0,619.
Предельная погрешность суммы:
0,0005
∙ 9 = 0,0045.
Приближённая сумма отличается от истинной на 0,0003,
то есть на треть единицы последнего знака приближённых чисел. Все три знака
приближённой суммы верны, хотя теоретически последняя цифра могла быть грубо
неверной.
Произведём в наших слагаемых округление до сотых. Теперь
предельная погрешность суммы будет:
0,005
∙ 9 = 0,045.
Между тем получим:
0,09
+ 0,08 + 0,08 + 0,07 + 0,07
+ 0,06 + 0,06 + 0,06 + 0,05 = 0,62.
Истинная погрешность составляет только 0,0013.
Предельная абсолютная погрешность разности двух величин
равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.
ПРИМЕР:
Пусть предельная погрешность приближённого
уменьшаемого 85 равна 2,
а предельная погрешность вычитаемого 32 равна 3.
Предельная погрешность разности
85
– 32 = 53
есть
2
+ 3 = 5.
В самом деле, истинное значение уменьшаемого и
вычитаемого могут равняться
85
+ 2 = 87 и
32
– 3 = 29.
Тогда истинная разность есть
87
– 29 = 58.
Она на 5 отличается от
приближённой разности 53.
Относительная погрешность суммы и разности.
Предельную
относительную погрешность суммы и разности легко найти, вычислив сначала
предельную абсолютную погрешность.
Предельная
относительная погрешность суммы (но не разности!) лежит между наименьшей и
наибольшей из относительных погрешностей слагаемых. Если все слагаемые имеют
одну и ту же (или примерно одну и ту же) предельную относительную погрешность,
то и сумма имеет ту же (или примерно ту же) предельную относительную
погрешность. Другими словами, в этом случае точность суммы (в процентном
выражении) не уступает точности слагаемых. При значительном же числе слагаемых
сумма, как правило, гораздо точнее слагаемых.
ПРИМЕР:
Найти предельную абсолютную и предельную относительную
погрешность суммы чисел:
24,4
+ 25,2 + 24,7.
РЕШЕНИЕ:
В каждом слагаемом суммы
24,4
+ 25,2 + 24,7 = 74,3
предельная относительная погрешность примерно одна и та
же, а именно:
0,05
: 25 = 0,2%.
Такова же она и для суммы.
Здесь предельная абсолютная погрешность равна 0,15,
а относительная
0,15
: 74,3 ≈ 0,15 : 75 = 0,2%.
В противоположность
сумме разность приближённых чисел может быть менее точной, чем уменьшаемое и
вычитаемое. <<Потеря точности>> особенно велика в том случае, когда
уменьшаемое и вычитаемое мало отличаются друг от друга.
Относительные погрешности при сложении и вычитании
складывать нельзя.
Умножение и деление приближённых чисел.
При делении и умножении чисел требуется сложить
относительные погрешности.
ПРИМЕР:
Пусть перемножаются приближённые числа 50 и 20, и пусть предельная относительная погрешность первого
сомножителя есть 0,4%, а второго
0,5%.
Тогда предельная относительная погрешность произведения
50
× 20 = 1000
приближённо равна 0,9%.
В самом деле предельная абсолютная погрешность первого сомножителя есть
50
× 0,004 = 0,2,
а второго
20
× 0,005 = 0,1.
Поэтому истинная величина произведения не больше чем
(50
+ 0,2)(20 + 0,1) = 1009,02,
и не меньше, чем
(50
– 0,2)(20 – 0,1) = 991,022.
Если истинная величина произведения есть 1009,2,
то погрешность произведения равна
1009,2
– 1000 = 9,02,
а если 991,02, то погрешность произведения равна
1000
– 991,02 = 8,98.
Рассмотренные два случая – самые неблагоприятные. Значит,
предельная абсолютная погрешность произведения есть 9,02.
Предельная относительная погрешность равна
9,02
: 1000 = 0,902%,
то есть приближённо 0,9%.
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
- Урок 1. Числовые неравенства
- Урок 2. Свойства числовых неравенств
- Урок 3. Сложение и умножение числовых неравенств
- Урок 4. Числовые промежутки
- Урок 5. Линейные неравенства
- Урок 6. Системы линейных неравенств
- Урок 7. Нелинейные неравенства
- Урок 8. Системы нелинейных неравенств
- Урок 9. Дробно-рациональные неравенства
- Урок 10. Решение неравенств с помощью графиков
- Урок 11. Неравенства с модулем
- Урок 12. Иррациональные неравенства
- Урок 13. Неравенства с двумя переменными
- Урок 14. Системы неравенств с двумя переменными
- Урок 15. Приближённые вычисления
Отметим, что погрешности измерений
определяются, главным образом,
погрешностями средств измерений, но
они не тождественны им.
В общем случае погрешность средства
измерений(меры измерительного
преобразователя, измерительного прибора)
– это отклонение его реальной функции
преобразования от номинальной.
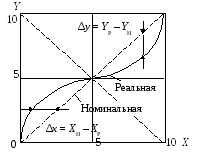
Отклонения реальной характеристики от
номинальной, отсчитанные вдоль оси
Х или оси У, т. е. разности вида y
= Ур– Унилиx
= Хр– Хн, естьабсолютные
погрешности преобразования, выраженные
в единицах величин Х или У (рис. 1).
Мерой точности абсолютная погрешность
быть не может, т. к., например, Х
= 0.5 мм при измерении высоты пенного слоя
пульпы, равной Х = 200 мм, достаточно мала,
а при измерении толщины листа стали,
при Х = 1 мм, эта погрешность очень велика.
Абсолютная погрешность измерительного
прибора XП– это разность между показанием прибора
ХПи истинным (действительным) ХДзначением измеряемой величины:
XП= ХП– ХД.
Рис. 1. К пояснению понятия абсолютной
погрешности
При этом за действительное значение
физической величины при оценке погрешности
рабочего средства измерений принимают
показания образцового средства
измерений, при оценке погрешности
образцового средства – показания,
полученные с помощью эталонного средства
измерений.
Абсолютная погрешность измерительного
преобразователя по входу– это
разность между значением величины на
входе преобразователя ХВи истинным
(действительным) значением этой величины
на входе ХВД. При этом значение
величины на входе ХВопределяется
по истинному (действительному)
значению величины на выходе преобразователя
с помощью градуировочной характеристики,
приписанной преобразователю. Таким
образом,
ХВ=Х*ВД – ХВД,
где ХВ–
погрешность измерительного преобразователя
по входу;
Х*ВД – истинное (действительное)
значение величины на выходе, найденное
по градировочной характеристике
преобразователя;
ХВД– истинное (действительное)
значение преобразуемой величины на
входе.
Абсолютная погрешность измерительного
преобразователя по выходу– это
разность между истинным (действительным)
значением величины преобразователя
на выходеDХВЫХ.Д
и значением величины на выходе
Х*ВЫХ.Д, определяемым по истинному
(действительному) значению величины
на входе с помощью градуировочной
характеристики, приписанной преобразователю.
Таким образом,
DХВЫХ.П = ХВЫХ.Д
– Х*ВЫХ.Д ,
где DХВЫХ.П–
погрешность измерительного преобразователя
по выходу;
ХВЫХ.Д – действительное значение
преобразуемой величины на выходе
преобразователя;
Х*ВЫХ.Д – действительное значение
преобразуемой величины на выходе,
определяемое по действительному значению
ее на входе с помощью градуировочной
характеристики.
Абсолютная погрешность– это разность
между номинальным значением меры ХН и
истинным (действительным) ХД воспроизводимой
ею величины, т. е.
ХМ= ХН– ХД,
где ХМ–
абсолютная погрешность мepы;
ХН– номинальное значение
мepы;
ХД– действительное значение
воспроизводимой мерой величины.
Пример. Погрешность меры длины (линейки)
с номинальным значением 100 мм и
действительным значением 100,0006 мм равна
0,6 мкм; погрешность меры сопротивления
с номинальным значением 1 Ом и действительным
значением 1,0001 Ом равна 0,0001 Ом.
Относительная погрешность меры или
измерительного прибора(П)
– это отношение абсолютной погрешности
меры или измерительного прибора к
истинному (действительному) значению
воспроизводимой или измеряемой
величины.
Относительная погрешность меры или
измерительного прибора, в процентах,
может быть выражена как:
.
Относительная погрешность измерительного
преобразователя по входу (выходу) –
это отношение абсолютной погрешности
измерительного преобразователя по
входу (выходу) к истинному
(действительному) значению величины на
входе (выходе), определяемому по истинному
значению величины на входе (выходе) с
помощью номинальной характеристики,
приписанной преобразователю.
Итак, относительная погрешность средства
измерений, выражаемая в процентах или
в относительных единицах, не остается
постоянной вследствие изменения величин
Х или Y по шкале измерительного
устройства.
С учетом того, что относительная
погрешность средства измерений не
остается постоянной, то вводится понятие
приведенной погрешности, в общем
виде определяемой:
,
где - приведенная
погрешность средства измерений;
XN– нормирующее значение
измеряемой величины.
Приведенная погрешность
измерительного прибора– это отношение
абсолютной погрешности измерительного
прибораХПк
нормирующему значению.Нормирующее
значение XN– это условно
принятое значение, равное или верхнему
пределу измерений,
или диапазону измерений**, или длине
шкалы***.
Приведенную погрешность обычно выражают
в процентах:
.
Приведенная погрешность позволяет
сравнивать по точности приборы,
имеющие разные пределы точности.
Пример. Определить абсолютную,
относительную и приведенную погрешности
амперметра с диапазоном измерения 0
-15 А при показании его ХП= 12 А и
действительном значении измеряемой
силы тока ХД= 12,6 А. За нормирующее
значение примем верхний предел измерения
Xv = 15 А.
Абсолютная погрешность амперметра
ХП= ХП– ХД= 12 – 12,6
= -0,6 А.
Относительная погрешность амперметра
Приведенная погрешность
При характеристике погрешностей средств
измерений часто пользуются понятием
предела допускаемой погрешности
измерений.
Предел допускаемой погрешности
средства измерений– это наибольшая,
без учета знака, погрешность средства
измерений, при котором оно может быть
признано и допущено к применению.
Определение применимо к основной и
дополнительной погрешности средств
измерений.
Пример. Одинаков ли предел допускаемой
относительной погрешности измерения
во всех точках шкалы автоматического
потенциометра?
Для всех точек шкалы одинаков предел
допускаемой абсолютной погрешности,
определяемой классом точности средства
измерений и диапазоном измерений, а
предел допускаемой относительной
погрешности измерения зависит от
конкретной отметки шкалы, т. е. чем
меньше показания прибора по шкале, тем
больше относительная погрешность.
Вследствие этого верхний предел показаний
прибора нужно выбирать таким образом,
чтобы значение измеряемой величины
находилось в конце шкалы.
По происхождению различают инструментальные
и методические погрешности средств
измерений.
Инструментальные погрешности– это
погрешности, вызываемые особенностями
свойств средств измерений. Они возникают
вследствие недостаточно высокого
качества элементов средств измерений,
К этим погрешностям можно отнести
изготовление и сборку элементов средств
измерений; погрешности из-за трения в
механизме прибора, недостаточной
жесткости его элементов и деталей и др.
Подчеркнем, что инструментальная
погрешность индивидуальна для каждого
средства измерений
Методическая погрешность– это
погрешность средства измерения,
возникающая из-за несовершенства метода
измерения, неточности соотношения,
используемого для оценки измеряемой
величины.
Основная и дополнительная погрешности.Деление это чисто условно. Погрешность
средств измерений, определяемую для
работающих в нормальных условиях,
называютосновной погрешностью.
Нормальными условиями принято считать
условия, когда температура окружающего
воздуха t = (20 ± 5) 0C, относительная влажность
W = 30 – 80 %, атмосферное давление Р = 630 –
795 мм рт. ст., напряжение питающей сети
(U = (220 ± 4,4) В, частота питающей сети f =
(50 ± 0,5) Гц. Такие условия выдерживаются
в лабораторных условиях при градуировке
средств измерений.
В реальных условиях производства эти
параметры отличаются от лабораторных.
Средства измерения помимо чувствительности
к измеряемой величине обладают и
некоторой чувствительностью к изменяющимся
величинам окружающей среды, что приводит
к искажению результатов измерения.
Погрешность, появляющуюся у средств
измерений, работающих в реальных
производственных условиях, называют
дополнительной погрешностью. Так
же, как основная, дополнительная
погрешность нормируется путем указания
коэффициентов влияния изменения
отдельных влияющих величин на изменение
показаний в виде
α =
,
α =·
Uпит.
Систематические и прогрессирующие
погрешности средств измерений
вызываются: первые – погрешностью
градуировки шкалы или ее небольшим
сдвигом, вторые – старением элементов
средства измерения. Систематическая
погрешность остается постоянной или
закономерно изменяющейся при многократных
измерениях одной и той же величины.
Особенность систематической погрешности
состоит в том, что она может быть полностью
устранена введением поправок. Особенностью
прогрессирующих погрешностей является
то, что они могут быть скорректированы
только в данный момент времени. Они
требуют непрерывной коррекции.
Аддитивные и мультипликативные
погрешности. Аддитивная погрешность
не зависит от чувствительности прибора
и является постоянной для всех значений
входной (измеряемой) величины в пределах
диапазона измерений (рис.2).
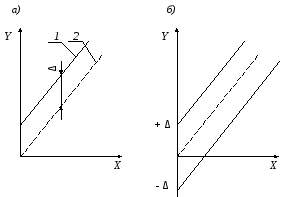
Если реальная характеристика 1 средства
измерения смещена относительно
номинальной 2 (см. рис. 2) так, что при всех
значениях преобразуемой величины Х
выходная величина У оказывается больше
(или меньше) на одну и ту же величину Δ,
то такая погрешность называется
аддитивной погрешностью нуля.
Рис. 2. К пояснению понятия аддитивной
погрешности средства измерения
К аддитивным погрешностям средств
измерений можно отнести погрешности,
вызванные трением в опорах
электроизмерительных приборов,
погрешность дискретности (квантования)
в цифровых приборах. Аддитивная
погрешность может носить систематический
характер. В этом случае она может быть
скорректирована смещением шкалы или
нулевого положения указателя.
В случае же, если аддитивная погрешность
является случайной, то она не может быть
скорректирована, и реальная характеристика
средства измерения, смещаясь произвольным
образом, но, оставаясь параллельной
самой себе, образует полосу погрешностей,
ширина которой остается постоянной для
любых значений измеряемой величины Х
(см. рис. 4.2, б).
Мультипликативная погрешность–
это погрешность чувствительности
средства измерения. Она может иметь
систематическую и случайную составляющие.
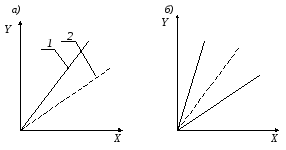
Сущность мультипликативной погрешности
заключается в том, что если абсолютная
погрешность возникает от некоторого
независимого от Х изменения чувствительности
преобразователя (изменение коэффициента
деления делителя, добавочного сопротивления
вольтметра и т. д.), то реальная
характеристика 1 преобразователя
отклоняется от номинальной 2 так, как
это показано на рис. 4.3, а, или образует
полосу погрешностей (рис. 4.3, б), если это
отклонение является случайным.
Рис. 4.3. К пояснению понятия мультипликативной
погрешности измерений
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нам нужно на некоторое время оторваться от рассмотрения методов измерений и вернуться с погрешностям. Я знаю, погрешности любят не многие, но уметь работать с ними необходимо. Большинство современных измерительных приборов состоят из нескольких компонентов (узлов), которые объединены в единое целое. Мы не раз говорили, что итоговая погрешность измерения равна сумме погрешностей метода, методики, измерительных преобразователей, приборов, методов обработки результата. Но не разбирались, а как именно эта сумма вычисляется? Сегодня этим и займемся.
В статье не получится избежать математики, но она будет довольно простой.
Еще раз, кратко, о погрешностях
Давайте вспомним, что мы уже знаем о погрешностях из того, что нам сегодня потребуется. Прежде всего, погрешности можно разделить на абсолютную, относительную, приведенную
Приведенная погрешность отличается от относительной тем, что знаменателем является не истинное, а нормирующее значение величины. Чаще всего, в качестве нормирующего значения выступает верхний предел соответствующего поддиапазона измерительного прибора.
Я уже рассказывал, зачем потребовалась приведенная погрешность. Дело в том, что мы не можем по результату измерения и параметрам погрешности прибора определить истинное значение величины. Не смотря на то, что приведенные выше формулы позволяют, на первый взгляд, усомниться в этом утверждении. Однако, погрешности это случайные величины, работать с которыми нужно по правилам математической статистики. И это очень важно.
Вы можете даже возмутиться “Как так, мы же знаем, что погрешность может быть систематической и случайной! Получается, что и систематическая погрешность случайна? Автор ничего не перепутал?”. Нет, автор ничего не перепутал. Давайте разберемся и вы сами все увидите.
Действительно, погрешность измерительного прибора, да и собственно измерения, можно представить как сумму систематической и случайной погрешностей. Причем для систематическая погрешность может быть как неизменной, так и изменяющейся. Примером неизменной систематической погрешности является “смещение нуля”, например, смещение начального положения стрелки прибора относительно нулевого деления. Примером изменяющейся систематической погрешности может быть “смещение нуля” в цифровом приборе, например, зависящее от температуры.
Систематическая погрешность конкретного экземпляра прибора прогнозируема в конкретных условиях измерения. И мы можем провести процедуру калибровки (не путать с регулировкой!) для определения систематической погрешности. Проблема в том, что это будет касаться лишь конкретного экземпляра прибора в условиях метрологической лаборатории. Для другого экземпляра прибора, других условий, или через некоторое время, погрешность может измениться. Причем не только по величине, но и по знаку. Но он останется прогнозируемой. В отличии от погрешности случайной.
То есть, для измерительных приборов в целом, а не конкретного экземпляра в конкретных условиях, даже систематическая погрешность будет величиной случайной, задающей границы возможных погрешностей для каждого конкретного экземпляра. И в паспортах измерительных приборов погрешность указывается именно как максимальная, определяющая границы, а не точное значение погрешности.
Систематическая погрешность может быть уменьшена с помощью различных ухищрений. Точно так же, как случайная погрешность может быть снижена с помощью вычисления среднего арифметического. Но сегодня мы этих вопросов касаться не будем.
Погрешности узлов измерительных приборов
Все сказанное выше применимо не только к измерительным приборам в целом, но и к отдельным компонентам приборов. За исключением приведенной погрешности, конечно. Давайте рассмотрим самый простой пример – постоянный резистор. Например, металлопленочный резистор MBB0207 сопротивлением 100 кОм. Вот документация на него
Эти резисторы обладают точностью сопротивления 1%. То есть, для нашего резистора реальное сопротивление будет лежать в диапазоне от 99 кОм до 101 кОм. Но это еще не все. Любой резистор имеет ненулевое значение ТКС (температурный коэффициент сопротивления). В данном случае – 5 Ом на каждый градус Цельсия (для сопротивления 100 кОм). Но и это еще не все. Резисторы подвержены старению, причем скорость старения зависит от рассеиваемой резистором мощности. Для нашего резистора сопротивление может измениться а пределах 0.25% за 1000 часов работы при рассеивании номинальной мощности. И на 0.5% за 8000 часов. В документации все указано.
Таким образом, не только реальное сопротивление может отличаться от номинала, но оно зависит и от температуры, и от времени наработки. Давайте посмотрим, что это для нас означает. Пусть рабочая температура резистора достигает 50 градусов. Номинальное сопротивление указывается для 25 градусов, так что при 50 градусах сопротивление изменится на
5 * 25 = 125 Ом
что составляет 0.125%. С одной стороны, это мало, по сравнению с точностью сопротивления. Но, с другой стороны, это может потребоваться учитывать. 1000 часов это примерно 1 квартал (3 месяца) ежедневной работы по 8 часов в день. Не много, но изменение сопротивления может достигать 0.25%. Итого, для заданных рабочих условий через примерно 3 месяца работы точность сопротивления резистора будет не 1%, а 1.375%!
Несколько неожиданный результат для части читателей. Но совершенно закономерный. Прецизионные резисторы не только имеют более высокую начальную точность, но и меньший ТКС. Например, С2-29В группы С имеет ТКС 10ppm, что в 5 раз ниже. Прецизионные резисторы и меньше изменяют сопротивление при старении. Но и это еще не все. На сопротивление влияет и атмосферное давление. И влажность воздуха, что наиболее значимо для высокоомных резисторов. Сопротивление резистора зависит и от приложения механической нагрузки.
Но давайте не будем слишком углубляться. Все эти тонкости нужны профессионалам, которые разрабатывают высокоточные устройства. Большинству читателей достаточно иметь представление, что оказывает влияние на сопротивление резистора, которое указано его маркировкой.
Давайте теперь рассмотрим простейший делитель напряжения, например, 1:10. Верхнее плечо будет иметь сопротивление 900 кОм, а нижнее 100 кОм. Да, я знаю, что 900 кОм не входит в стандартный ряд, нам сейчас это не важно. Точность 1%, резисторы новые, температура 25 градусов. То есть, сопротивление резистора верхнего плеча будет лежать в диапазоне от 891 кОм до 909 кОм. А нижнего плеча, как мы уже считали, в диапазоне от 99 кОм до 101 кОм.
Пусть на делитель подано напряжение 10 В, какое напряжение мы можем получить на выходе? Расчетное, исходя из номинальных сопротивлений резисторов, 1 В. А с учетом погрешностей? Мы не можем точно сказать. Мы можем лишь определить границы диапазона, когда отклонения сопротивлений резисторов максимальны и имеют разные знаки. Выходное напряжение будет лежать в диапазоне от 0.98 В до 1.02 В.
Давайте оценим относительную погрешность выходного напряжения. В обоих случаях отклонение составляет 0.02 В. То есть, относительная погрешность (модуль относительной погрешности) 2%. Все точно так, как и говорил в статье про учет тепла про расходомеры. И все верно, но с одним небольшим нюансом – это предельные границы, максимальная погрешность, самый плохой случай.
Суммирование арифметическое и геометрическое
Приведенный выше пример определения погрешности делителя напряжения является пессимистичным. Такой пессимизм действительно бывает нужен для задач требующих максимальной точности. Но во многих случаях достаточной будет оценка “типового случая”. Что же это за случай такой?
Давайте вспомним, что даже систематическая погрешность для каждого отдельного экземпляра будет случайной величиной для большой выборки (например, партии измерительных приборов или резисторов)
Если измерить сопротивления резисторов в большой партии и построить график плотности вероятности (гистограмму), то мы увидим хорошо знакомое нам нормальное распределение. Часть резисторов будет иметь сопротивление выше номинала (отклонение положительное), часть ниже (отклонение отрицательное). Для большинства резисторов отклонения будут малы, значительно меньше предельно допустимой погрешности. Резисторы, отклонение сопротивления которых превышает установленные границы (в нашем примере 1%) являются браком.
Эти границы, которые заданы как предельная величина отклонения, являются одновременно и доверительным интервалом. Мы видим, что вероятность рассмотренных ранее предельных случаев меньше, чем вероятность малых отклонений. Поэтому и отклонение выходного напряжения, ожидаемое, вероятно будет меньше, чем предельные случаи. И это действительно так.
Давайте вспомним, что в теории вероятности суммирование статистически независимых (некоррелированных) случайных величин осуществляется путем сложения их дисперсий. Отклонения сопротивлений наших резисторов действительно независимы и, как мы уже видели, являются случайными в большой партии. А значит, мы можем выполнять суммирование отклонений, погрешностей, как суммирование дисперсий.
На практике более привычным является среднеквадратичное отклонение, которое равняется квадратному корню из дисперсии. И мы получаем классическую формулу геометрической суммы. Поскольку для резисторов погрешность указана как относительная, то как сумму относительных погрешностей. Вот так это выглядит в общем виде
Да, корень квадратный из суммы квадратов. И мы можем сказать, для нашего делителя напряжения итоговая погрешность равна 1.41%, а не 2%. Это более оптимистичный вариант оценки погрешности, который можно назвать тем самым “типовым случаем”. Повторю, что такое определение суммарной погрешности возможно только для независимых погрешностей, причем с нормальным законом распределения плотности вероятности. Иначе формула будет иной. Кроме того, вспомним, что доверительный интервал суммы не равен сумме доверительных интервалов.
А теперь подумаем, являются ли отклонения сопротивлений резисторов вызванные изменением температуры независимыми? Это не такой простой вопрос. Но во многих случаях их нельзя считать независимыми. А значит, для суммирования нам придется использовать обычное арифметическое суммирование. Другими словами, мы должны по разному учитывать влияние различных составляющих погрешности каждого компонента на итоговую погрешность. Неверно просто взять суммарную погрешность отдельного компонента и рассчитать итоговую погрешность прибора через геометрическую сумму.
Это верно не только для вычисления погрешности измерительного прибора, но и для оценки погрешности всего измерительного эксперимента. То есть, погрешность измерения некоторой величины (прямая или косвенная) будет вычисляться как сумма всех погрешностей. Причем сумма геометрическая. Но некоторые составляющие этой погрешности могут суммировать и арифметически.
Коротко о записи результатов измерений с погрешностью
Существует старый спор между сторонниками “много знаков лучше” и сторонниками “без лишних знаков”. Метрология на стороне последних.
Как вы помните, результат измерений может быть весьма “точным” по виду, но весьма посредственным по своему содержанию. Магия большого количества отображаемых на дисплее цифрового прибора цифр совратила не мало неокрепших умов. Разрешающая способность может быть большой, но вот точность не обязательно соответствует разрядности. А о том, что погрешность прибора определяется суммой погрешностей, забывают многие.
Запись результата измерения, если говорить строго, должна включать в себя и указание погрешности. Причем запись не должна вызывать ложного чувства повышенной точности. Например,
12.5 В ± 1 В
неправильно, так как десятые доли вольта указанная погрешность делает недостоверными. Правильно будет
12 В ± 1 В
Другой пример,
134 В ± 1%
правильный, так как 1% равняется 1.34 В, что делает последнюю цифру результата достоверной. Но
134 В ± 10%
будет неверно, так как абсолютное значение погрешности составит 13.4 В, а значит, последняя цифра результата недостоверна. Правильно будет
130 В ± 10%
Это кажется мелочами и излишним педантизмом, но это не так. При этом результаты измерений, которые используются в дальнейших расчетах для получения итогового результата, не должны округляться. Округляется только собственно итоговый результат. Дело в том, что округление промежуточных результатов вычислений и измерений вносит дополнительную погрешность. А ошибки имеют свойство накапливаться.
О погрешности равной половине цены деления шкалы
Весьма распространенным заблуждением является утверждение, что погрешность измерительного прибора всегда равна половине деления шкалы, половине цены деления. Это верно лишь для случаев, когда в паспорте прибора нет указания погрешности в явном виде. Если погрешность указана явно, следует руководствоваться именно ей, а не вглядываться деления шкалы!
Заключение
Да, как всегда кратко и довольно упрощенно. Но затронутые сегодня вопросы являются важными. Причем именно с практической точки зрения.
До новых встреч!
Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.
- При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
- Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,
Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.
- Отсчет по шкале прибора указывает непосредственно измеряемое значение.
- Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
- При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).
Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
- Различают абсолютную (∆ X) и относительную (δ) погрешности измерений.
- Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,
Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),
Как вычислить погрешность измерений?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.
У нас есть два варианта определения длины этого бруска. (1). Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2). Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
В чем измеряется погрешность?
Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
- Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
- Инструментальные и методические погрешности.
- Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях.
- Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.
Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.
Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.
Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Как найти абсолютную погрешность измерительного прибора?
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ и x + Δ о x при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Что такое погрешность метода измерений?
По источнику возникновения — Инструментальная погрешность Эта погрешность определяется несовершенством прибора, возникающим, например, из-за неточной калибровки, Методическая погрешность Методической называют погрешность, обусловленную несовершенством метода измерений.
Что такое погрешность измерительного прибора?
Определение — Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.
Как определить погрешность деления?
Как определить погрешность и объем жидкости — Погрешность равна половине цены деления мензурки. В нашем случае погрешность составляет 2,5 мл. Чтобы определить объем, берем ближайшее число от верхней границы жидкости (на рисунке — это значение 40 мл) и прибавляем количество штрихов (на рисунке — 2 штриха) по 5 мл: V = 40 + 2 × 5 = 50 мл.
Как рассчитывается приведенная погрешность?
Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений.
- Общие требования» и им подобных.
- Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия.
- Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п.
Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.
- Абсолютная погрешность: Δ = X д — X изм, выражается в единицах измеряемой величины, например в килограммах (кг), при измерении массы. где X д – действительное значение измеряемой величины, принимаются обычно показания эталона, образцового средства измерений; X изм – измеренное значение.
- Относительная погрешность: δ = (Δ ⁄ X д ) · 100, выражается в % от действительного значения измеренной величины.
- Приведённая погрешность: γ = (Δ ⁄ X н ) · 100, выражается в % от нормирующего значения. где X н – нормирующее значение, выраженное в тех же единицах, что и Δ, обычно принимается диапазон измерения СИ (шкала).
По характеру проявления:
- систематические (могут быть исключены из результатов);
- случайные;
- грубые или промахи (как правило не включаются в результаты измерений).
В зависимости от эксплуатации приборов:
- основная – это погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
- дополнительная погрешность – это составляющая погрешности средства измерения, дополнительно возникающая из-за отклонения какой-либо из влияющих величин от нормативного значения или выход за пределы нормальной области значений. Например: измерение избыточного давления в рабочих условиях цеха, при температуре окружающего воздуха 40 ºС, относительной влажности воздуха 18% и атмосферном давлении 735 мм рт. ст., что не соответствует номинальным значениям влияющих величин при проведении поверки.
| Наимено вание погреш ности | Формула | Форма выражения, записи | Обозначение класса точности | |||||||||||||||
| В докумен тации | На сред стве изме рений | |||||||||||||||||
| Абсолют ная | Δ = X д — X изм | Δ = ±50 мг Примеры: Номинальная масса гири 1 кг ±50 мг Диапазон измерения весов среднего III класса точности от 20 г до 15 кг ±10 г | Класс точности: М 1 Класс точности: средний III Примечание: на многие виды измерений есть свои НД по выражению погрешностей, здесь для примера взято для гирь и весов. | М 1 | ||||||||||||||
| Относи тельная | δ = (Δ ⁄ X д ) · 100 | δ = ±0,5 Пример: Измеренное значение изб.
Как вычислить абсолютную погрешность формула?Поиск: Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ). Чему равна абсолютная погрешность?При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения. Для чего нужна погрешность измерений?Каждое физическое измерение в исследованиях и промышленности сопровождается определенной погрешностью. Даже незначительные колебания в условиях окружающей среды могут влиять на измерение и вызывать отклонения, которые делают результат измерения ненадежным. Для получения правильных результатов измерений необходимо учитывать связанную с результатами погрешность. Погрешность измерений указывает на недостающую информацию о настоящем значении измеряемой величины. Она определяется параметром, выраженным в процентах и относящимся к результату измерения, который обозначает отклонение значений, которое обоснованно можно присвоить измеряемой величине на основе имеющейся информации. Другими словами, это диапазон, в пределах которого с определенной вероятностью находится истинное значение измеряемой величины. Как найти абсолютную погрешность пример?Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26. Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.
Границу абсолютной погрешности называют предельной абсолютной погрешностью. Как определить цену деления и погрешность?Найти две соседних отметки шкалы, возле которых написаны величины, соответствующие этим отметкам шкалы; найти разность этих величин; сосчитать количество промежутков между величинами отметок шкалы; полученную разность величин разделить на количество промежутков. Что такое максимальная погрешность измерений?Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи. Как рассчитывается приведенная погрешность?Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования» и им подобных. Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия. Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п. Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.
По характеру проявления:
В зависимости от эксплуатации приборов:
|