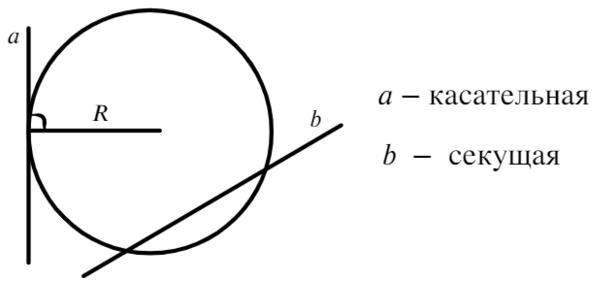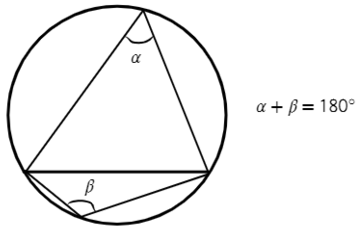Какие точки лежат на окружности как найти - Сайт, где вы сможете решить свои вопросы

Координаты точек на окружности

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

2π радиан = 360°
1 радиан = (360/2π) градусов
1 радиан = (180/π) градусов
360° = 2π радиан
1° = (2π/360) радиан
1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0).
Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0.
Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°.
Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr.
Длина дуги AB: (l_=frac =frac =frac .)
Тогда радианная мера угла: $$ angle AOB=frac =frac =frac $$

30°	45°	60°	90°	120°	135°	150°	180°	270°	360°
(frac )	(frac )	(frac )	(frac )	(frac )	(frac )	(frac )	(pi)	(frac )	(2pi)

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t).
При t=0, M(0)=A.
При t>0 двигаемся по окружности против часовой стрелки, описывая дугу
⌒ AM=t. Точка M — искомая.
При t Например:

Отметим на числовой окружности точки, соответствующие (frac , frac , frac , frac , pi), а также (-frac , -frac , -frac , -frac , -pi)
Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac , frac , frac ), и (-frac ).
Все четыре точки совпадают, т.к. begin Mleft(frac right)=Mleft(frac +2pi kright)\ frac -2pi=-frac \ frac +2pi=frac \ frac +4pi=frac end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac lt t lt frac $$ а также, с учетом периода $$ -frac +2pi klt tltfrac +2pi k $$
Интервал
$$ -frac leq t leq frac $$ а также, с учетом периода $$ -frac +2pi kleq tleqfrac +2pi k $$
Полуинтервал
$$ -frac leq t ltfrac $$ а также, с учетом периода $$ -frac +2pi kleq tltfrac +2pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^ =frac .\ EC=60^ =frac .\ AE=EC+CD=90^ +30^ =120^ =frac .\ ED=EC+CD=60^ +90^ =150^ =frac . end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; frac ; frac ; frac ).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac =-90^ , frac =135^ \ frac =210^ , frac =315^ end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; 5pi; frac ; frac ).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π.
Далее – действуем, как в примере 2. begin -frac =frac cdotpi=-6pi+frac rightarrow frac =90^ \ 5pi=4pi+pirightarrow pi=180^ \ frac =frac pi=3pi-frac rightarrow pi-frac =frac \ frac =frac pi=7pi-frac rightarrow pi-frac =frac end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac =1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac approx frac =4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb )), запишите количество полученных базовых точек.

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0).
Начало координат — точка O. Ее координаты равны нулю: O (0,0).
Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус.
Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x – 2 ) 2 + (y – ( -3 )) 2 = 4 2
или
(x – 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x – 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x – 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x – 2) 2 + ( y + 3) 2 = 16
( 2 – 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/kak-najti-koordinaty-tochki

http://www.profmeter.com.ua/communication/learning/course/course7/chapter0552/?LESSON_PATH=456.552

[/spoiler]

Источник

Уравнение окружности.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.

В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Прямоугольная декартова система координат на плоскости

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Точки принадлежащие кругу и окружности

Вводятся координаты (x;y) точки и радиус круга ( r ). Определить принадлежит ли данная точка кругу, если его центр находится в начале координат.

Будем считать, что точка принадлежит кругу, если находится внутри его или на его окружности.

Из любой точки координатной плоскости можно провести отрезок к началу координат. Если длина этого отрезка больше радиуса круга, то точка лежит за пределами круга и, следовательно, не принадлежит ему. Если же отрезок, соединяющий точку и начало координат, меньше радиуса круга с центром в начале координат или равен ему, то точка будет принадлежать кругу.

Отрезок между любой точкой и нулевой точкой (началом координат) является гипотенузой прямоугольного треугольника, катеты которого равны значениям x и y координаты данной точки.

Таким образом задача сводится по-сути к двум действия:

Нахождение длины отрезка между точкой и началом координат по теореме Пифагора (квадрат длины гипотенузы равен сумме квадратов длин катетов).
Сравнению полученного значения с радиусом круга.

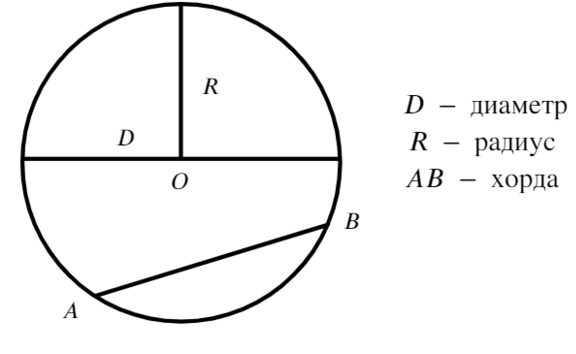
Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R .
Центр окружности обозначают буквой O.

Окружность разделяет плоскость на две части, внутреннюю и внешнюю. Внутренняя часть, включающая саму окружность, называется кругом. (Наведите курсор на рисунок.)

Точка O — это центр и круга и окружности.

Отрезки OA, OB, и OC — это радиусы, их длины равны. Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой D. Диаметр разделяет круг на два полукруга, а окружность на две полуокружности.

Диаметр равен двум радиусам, это хорошо видно на рисунке.

BC = OC + OB , так как BC = D а OC = OB = R , то

Точки A и B делят окружность на две части, которые называются дугами, а точки A и B концами этих дуг.

Дуга окружности — это часть окружности ограниченная двумя точками.

На рисунке точки B и C разделили окружность на две дуги, голубую и зеленую.

Записать их названия мы можем так:

BC (дуга BC) — в данном случае речь может идти как о голубой так и о зеленой;

BAC (дуга BAC) — в данном случае речь идет именно о зеленой дуге.

Выберите верные утверждения, исходя из рисунка:

1) Точки C, B и E не принадлежат кругу.

2) Точки D, B и O принадлежат окружности.

3) Точки A, B и O принадлежат кругу. Неверно. Точка B принадлежат кругу, так как окружность часть круга. Неверно. Точка O центр окружности, но не лежит на ней. 1) Точка О является центром и окружности, и круга.

2) Точка О является центром окружности, но не центром круга.

3) Точки D и B не принадлежат окружности. 1) Точки B и D не принадлежат кругу.

2) Точки A, B, D и O принадлежат кругу.

3) Точки B, D и E принадлежат кругу. Неверно. Точка О является центром и окружности, и круга. Неверно. Точки D и B принадлежат окружности. Неверно. Точки B и D принадлежат кругу, так как лежат на окружности, а она часть круга. 1) Точки B и D разделяют окружность на 4 дуги.

2) Точки B и D разделяют окружность на 3 дуги.

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке дается определение окружности и круга, а также определение дуги, радиуса, хорды и диаметра окружности, рассматривается взаимное расположение точек и окружности, а также двух окружностей, решаются различные задачи по этой теме.

Окружность и круг

Окружность можно построить с помощью циркуля (рис. 1). Ножку с иголкой устанавливают в точку, а ножка с грифелем опишет замкнутую линию, которую называют окружностью.

Окружность – это множество точек, равноудаленных от заданной точки (точки О), которую называют центром окружности. Окружность разделит плоскость на 2 части. Ту часть плоскости, которая лежит внутри окружности вместе с самой окружностью, называют кругом. Точка О является как центром окружности, так и центром круга (рис. 2).

Рис. 2. Окружность и круг

Взаимное расположение окружности и точки

Точки могут лежать на окружности, т. е. принадлежать окружности. Точки А и В принадлежат окружности с центром в точке О (Рис. 3); точки О, Е и D не принадлежат окружности с центром в точке О; точки О, Е, А, В принадлежат кругу с центром в точке О, а точка D не принадлежит этому кругу.

Рис. 3. Окружность и круг с центром в точке О

Точки А и В делят окружность на две части (рис. 4), каждую из которых называют дугой окружности; точки А и В – концами дуг.

Рис. 4. Окружность

Дуга, радиус, хорда, диаметр окружности

Дуга окружности – это часть окружности, ограниченная двумя точками. Пример. На окружности с центром в точке О отмечены точки А, В и С. Назовите дуги, на которые эти дуги делят окружность. Дуги с концами в точках А и В: дуга АВ, дуга АСВ. Дуги с концами в точках В и С: дуга ВС, дуга ВАС. Дуги с концами в точках А и С: дуга АС, дуга АВС. Отрезки ОА, ОВ соединяют центр окружности с точками, лежащими на окружности. Их называют радиусами (рис. 5).

Рис. 5. Радиусы окружности

Радиус – это расстояние от центра окружности до любой точки окружности. Радиусы одной окружности равны. Обозначают радиусы R или r. Отрезок, соединяющий две точки окружности, называют хордой. Хорду, проходящую через центр окружности, называют диаметром. Обозначают: d или D. Свойства диаметра: 1. диаметр – самая большая хорда. 2. d = 2R. Диаметр делит круг на два полукруга, а окружность – на две полуокружности

Задача 1

Постройте окружность с центром в точке О и радиусом 4 см. Постройте прямую а так, чтобы она пересекла окружность в двух точках А и В (рис. 6). На каком расстоянии от центра окружности находятся точки А и В?

Рис. 6. Окружность с центром в точке О и радиусом 4 см

Так как расстояние между двумя точками – это длина отрезка с концами в этих точках, то нам необходимо найти длины отрезков ОА и ОВ. По определению отрезки ОА и ОВ – радиусы одной и той же окружности. Тогда ОА = ОВ = R= 4 см. Значит, на расстоянии 4 см находятся точки А и В от центра окружности.

Задача 2

Постройте отрезок АВ, равный 4 см. Постройте первую окружность с центром в точке А радиусом 3 см, и другую окружность с центром в точке В радиусом 2 см. Назовите точки пересечения окружностей точками Е и С (рис. 7). Чему равны длины отрезков АЕ, АС, ЕВ и ВС?

Рис. 7. Отрезок АВ

По определению, отрезок АЕ, АС – это радиусы первой окружности. АЕ = АС = = 2 см.

Задача 3

Начертите отрезок СМ, равный 5 см. Постройте точку, удаленную от концов отрезка на 3 см. Сколько таких точек можно построить? Таких точек можно построить 2. Они будут лежать на пересечении двух окружностей с центром в точке С и с центром в точке М радиусом 3 см (рис. 8).

Рис. 8. Точки, удаленные от концов отрезка на 3 см

Список литературы

Н.Я. Виленкин. Учебник для 5 кл. общеобразовательных учреждений/ 17-е изд. – М.: Мнемозина, 2005.
Шевкин А.В. Текстовые задачи по математике: 5–6. – М.: Илекса, 2011. – 106 с.
Ершева А.П., Голобородько В.В. Вся школьная математика в самостоятельных и контрольных работах. Математика 5–6. – М.: Илекса, 2006. – 432 с.
Н.Н. Хлевнюк, М.В. Иванова. Формирование вычислительных навыков на уроках математики. 5–9 классы. – М.: Илекса, 2011. – 248 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Учебник математики. 5 класс. Н.Я. Виленкин. № 850–856.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

источники:

http://www.resolventa.ru/demo/him/diagege.htm

http://4apple.org/tochki-prinadlezhashhie-krugu-i-okruzhnosti/

Источник

Признак принадлежности четырёх точек одной окружности

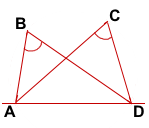
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

∠ABD=∠ACD

Доказать: точки A, B, C, D лежат на одной окружности

Доказательство:

Обозначим ∠ABD=∠ACD=α.

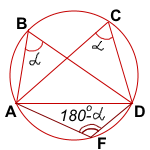
Опишем около треугольника ABD окружность.

Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.

Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:

∠ABD+∠AFD=180°.

Отсюда ∠AFD=180°-∠ABD=180°-α.

Рассмотрим четырехугольник ACDF.

∠ACD+∠AFD=α+180°-α=180°.

Отсюда следует, что четырёхугольник ABDF — вписанный.

Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.

Что и требовалось доказать.

Источник

Сегодня поговорим об единичной окружности 🧑‍🏫

Можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?🤔

Ну, конечно, можно! Записывай и запоминай общую формулу для нахождения координат точки:

x=x0+r⋅cos δ

y=y0+r⋅sin δ

x0,y0 — координаты центра окружности;

r — радиус окружности;

δ —угол поворота радиуса вектора.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Источник

Определение принадлежности точки кругу с центром в начале координат

Будем считать, что точка принадлежит кругу, если находится внутри его или на его окружности.

Таким образом задача сводится по-сути к двум действия:

Нахождение длины отрезка между точкой и началом координат по теореме Пифагора (квадрат длины гипотенузы равен сумме квадратов длин катетов).
Сравнению полученного значения с радиусом круга.

Pascal

Определение принадлежности точки кругу с центром в начале координат паскаль

Язык Си

Для gcc компилировать с ключом -lm.

Python

Определение принадлежности точки кругу с центром в начале координат Python

Уравнение окружности.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.

В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

Теория и практика окружности

Свойство касательных.

Свойства касательных и секущих.

Площадь, сектор, длина окружности.

Задачи на окружности.

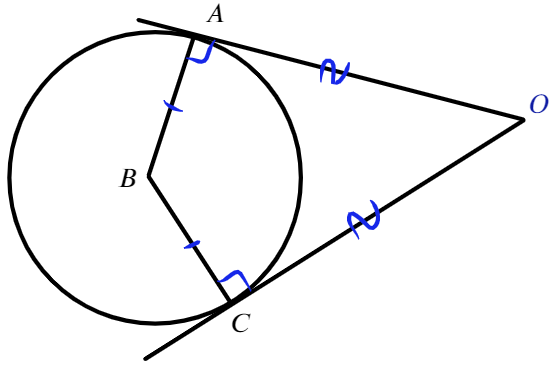
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!

Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.

В окружности может быть проведено 3 типа отрезка:

Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).

Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).

Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).

А также две прямые снаружи от окружности:

Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.

Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.

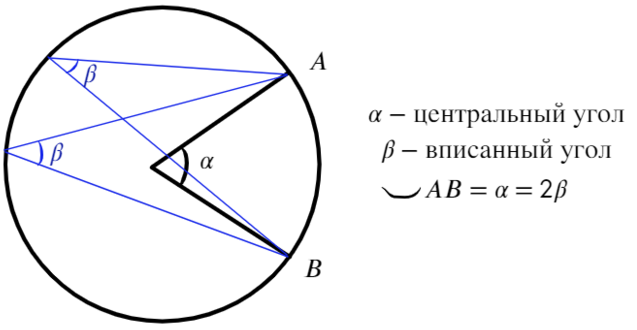
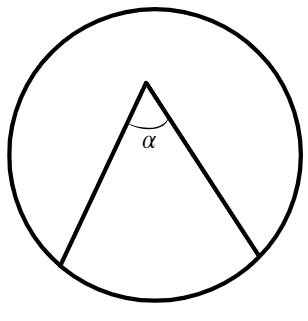
Теперь чуть-чуть об углах и дугах:

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.

Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.

Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.

Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.

А вот такой угол НЕвписанный, такой угол «никто и звать никак».

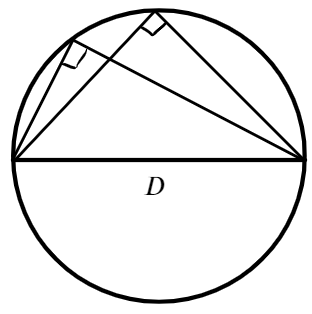
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:

Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.

Запишем основные свойства углов в окружности:

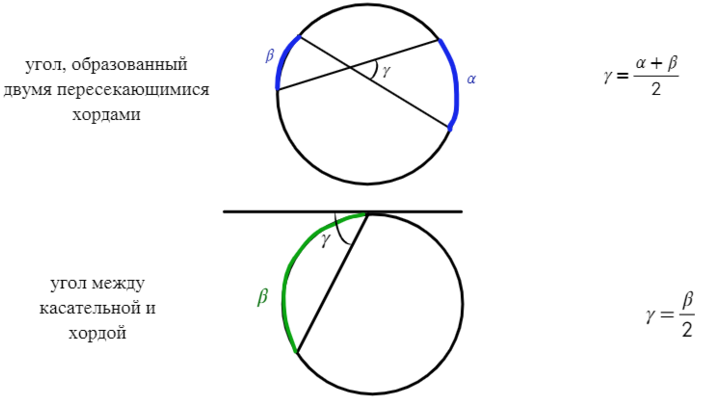
Нашел что-то общее?

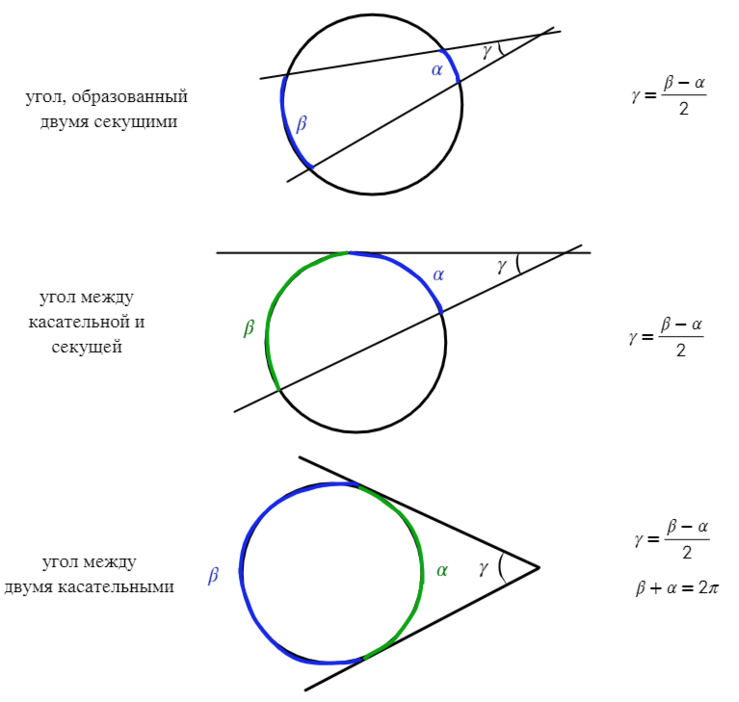
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.

Если угол находится внутри окружности, то находим его через полусумму дуг.

Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.

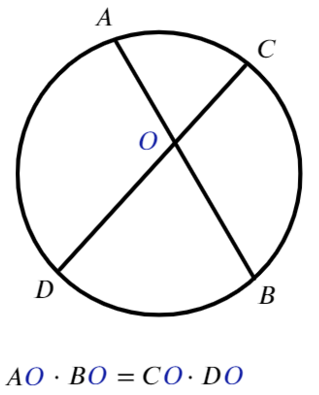
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:

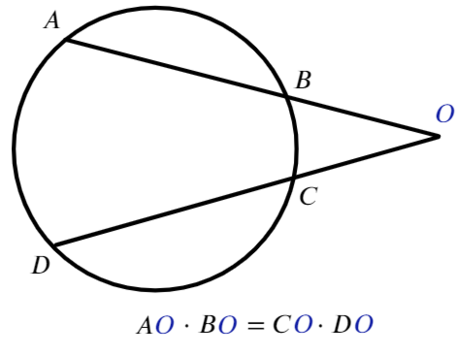
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:

Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).

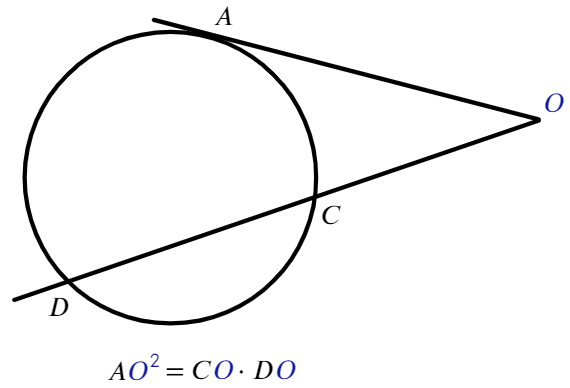
Если из точки, лежащей вне окружности, проведены касательная и секущая:

Аналогично в каждом отрезке присутствует точка, вне окружности (О).

Если теперь провести две касательные из точки O, то получим такие равные отрезки:

Касательные равны, как, сообственно, и радиусы!

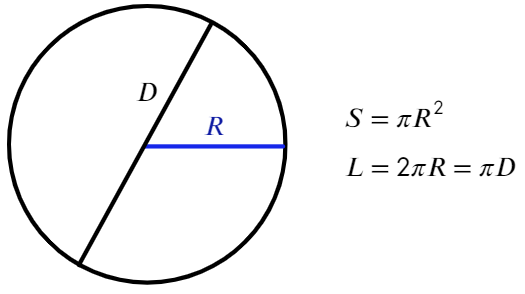
Площадь и длина окружности находятся по формуле:

По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD

Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!

Источник

Координаты точек на окружности

Единичная окружность

Единичная окружность в тригонометрии

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

п.2. Числовая окружность

п.3. Градусная и радианная мера угла

п.4. Свойства точки на числовой окружности

п.5. Интервалы и отрезки на числовой окружности

п.6. Примеры

Как найти координаты точки?

Понятие системы координат

Определение координат точки

Особые случаи расположения точек

Способы нахождения точки по её координатам

Уравнение окружности.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Задача. Принадлежит ли точка уравнению окружности

Уравнение окружности.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Задача. Принадлежит ли точка уравнению окружности

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Точки принадлежащие кругу и окружности

Этот видеоурок доступен по абонементу

Окружность и круг

Взаимное расположение окружности и точки

Дуга, радиус, хорда, диаметр окружности

Задача 1

Задача 2

Задача 3

Определение принадлежности точки кругу с центром в начале координат

Pascal

Язык Си

Python

Уравнение окружности.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Задача. Принадлежит ли точка уравнению окружности

Теория и практика окружности

Аналогично в каждом отрезке присутствует точка, вне окружности (О).

Вам также может понравиться

Как найти работу если я творческий человек

Как верно составить имена файлов

Как в ворде найти интервал между строками

Добавить комментарий Отменить ответ