Калькулятор как найти гипотенузу в прямоугольном треугольнике

Калькулятор как найти гипотенузу в прямоугольном треугольнике

Расчет гипотенузы

Заполните размеры в мм:

Ширина: Y

Длина: X

Инструкция к онлайн расчету гипотенузы прямоугольного треугольника

Укажите известные размеры в миллиметрах:

Y – длина стороны прилегающей к прямому углу слева.

X – размер стороны справа от угла 90°.

Отметив пункт «Черно-белый чертеж» Вы получите приближенный к требованиям ГОСТ чертеж и сможете его распечатать, не расходуя зря цветную краску или тонер.

Нажмите «Рассчитать».

Результаты расчета:

Иногда возникает необходимость (например, при строительстве, производстве мебели, планировании участка) найти гипотенузу, зная две стороны и имея прямой угол между ними. Не вдаваясь в подробности школьного курса геометрии это легко решить с помощью данного калькулятора. Возможности программы позволяют рассчитать длину диагонали (гипотенузы) прямоугольного треугольника и проверить, таким образом, действительно ли угол равен 90°. Необходимо только ввести известные данные и сравнить натурный размер диагонали с расчетным значением.

Источник

Как найти стороны прямоугольного треугольника

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Как найти стороны прямоугольного треугольника

Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Прямоугольный треугольник

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

  • для гипотенузы (с):
    • длины катетов a и b
    • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
    • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
  • для катета:
    • длину гипотенузы (с) и длину одного из катетов
    • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
    • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
    • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
    • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Катет a =
Катет b =
Гипотенуза c =

0

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =

0

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

c = a/cos(β) = b/cos(α)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =

0

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

c = a/sin(α) = b/sin(β)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Гипотенуза c =
Катет (известный) =
Катет (искомый) =

0

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

a = √c² – b²

b = √c² – a²

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √5² – 4² = √25 – 16 = √9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Гипотенуза c =
Угол (прилежащий катету) = °
Катет =

0

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

a = c ⋅ cos(β)

b = c ⋅ cos(α)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Гипотенуза c =
Угол (противолежащий катету) = °
Катет =

0

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

a = c ⋅ sin(α)

b = c ⋅ sin(β)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =

0

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

a = b ⋅ tg(α)

b = a ⋅ tg(β)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =

0

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

a = b / tg(β)

b = a / tg(α)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см

См. также

Источник

Гипотенуза прямоугольного треугольника в см по катетам (сторонам)

Как найти гипотенузу прямоугольного треугольника, если известны его катеты?

Гипотенуза — это сторона противоположная прямому углу (90 градусов) прямоугольного треугольника, является самой длинной стороной.

Катеты — это стороны прилегающие к прямому углу (90 градусов) прямоугольного треугольника.

Гипотенузу прямоугольного треугольника можно найти по теореме Пифагора: длина гипотенузы в квадрате равна сумме длин катетов в квадрате.

Формула теоремы Пифагора для поиска длины гипотенузы прямоугольного треугольника:

c2 = a2 + b2 ⇒

c = √(a2 + b2)

a — известная длина первого катета прямоугольного треугольника в см (сантиметрах);

b — известная длина второго катета прямоугольного треугольника в см (сантиметрах);

c — длина гипотенузы прямоугольного треугольника в см (сантиметрах).

Например:

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 5 см и 12 см.

Краткое решение: c = √(a2 + b2) = √(52 + 122) = 13 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 3 см и 4 см.

Краткое решение: c = √(a2 + b2) = √(32 + 42) = 5 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 6 см и 8 см.

Краткое решение: c = √(a2 + b2) = √(62 + 82) = 10 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 9 см и 12 см.

Краткое решение: c = √(a2 + b2) = √(92 + 122) = 15 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 25 см и 60 см.

Краткое решение: c = √(a2 + b2) = √(252 + 602) = 65 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 12 см и 16 см.

Краткое решение: c = √(a2 + b2) = √(122 + 162) = 20 см

Источник

Calculate the length of the hypotenuse in a right triangle using two sides or one side and one angle with the calculator below.

How to Find the Hypotenuse of a Right Triangle

The hypotenuse is the longest side of a right triangle and is always opposite the 90° right angle.

The illustration below is a right triangle. The hypotenuse is labeled as c, and the opposite 90° angle is typically symbolized with the square drawn at the vertex.

The two shorter side lengths (often called the legs of a right triangle), are labeled as a & b, and are opposite the interior angles labeled α & β.

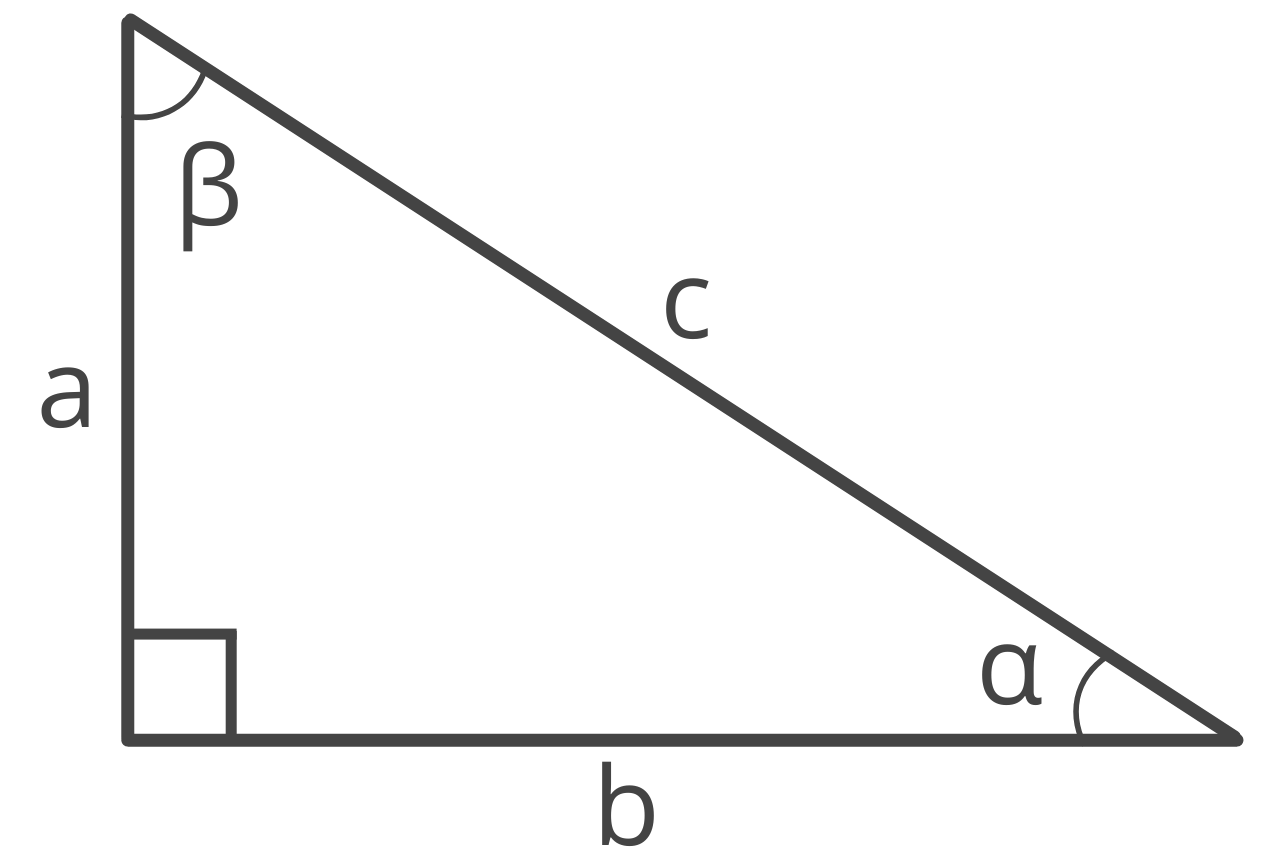
diagram of a right triangle showing hypotenuse c, sides a and b, angles alpha and beta, and the right angle

You can solve the hypotenuse using a little trigonometry and one of the following formulas.

Formula One: Given Two Legs

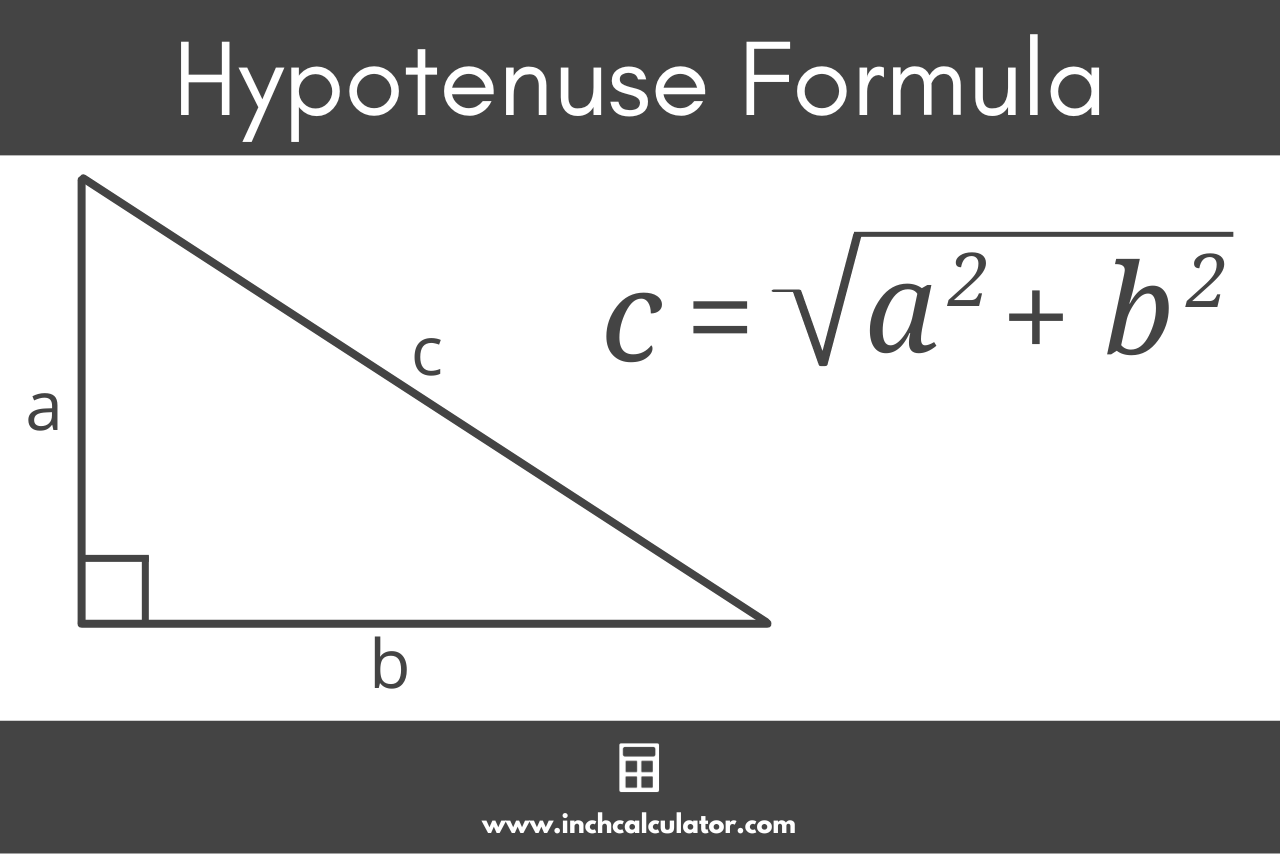
The Pythagorean theorem can be used to find the hypotenuse using the length of the two legs. The Pythagorean theorem states a² + b² = c².

This formula can be rewritten to solve for the hypotenuse c:

c = a² + b²

Thus, the hypotenuse c is equal to the square root of the quantity leg a squared plus leg b squared.

Graphic showing the hypotenuse formula, where c is equal to the square root of a squared plus b squared

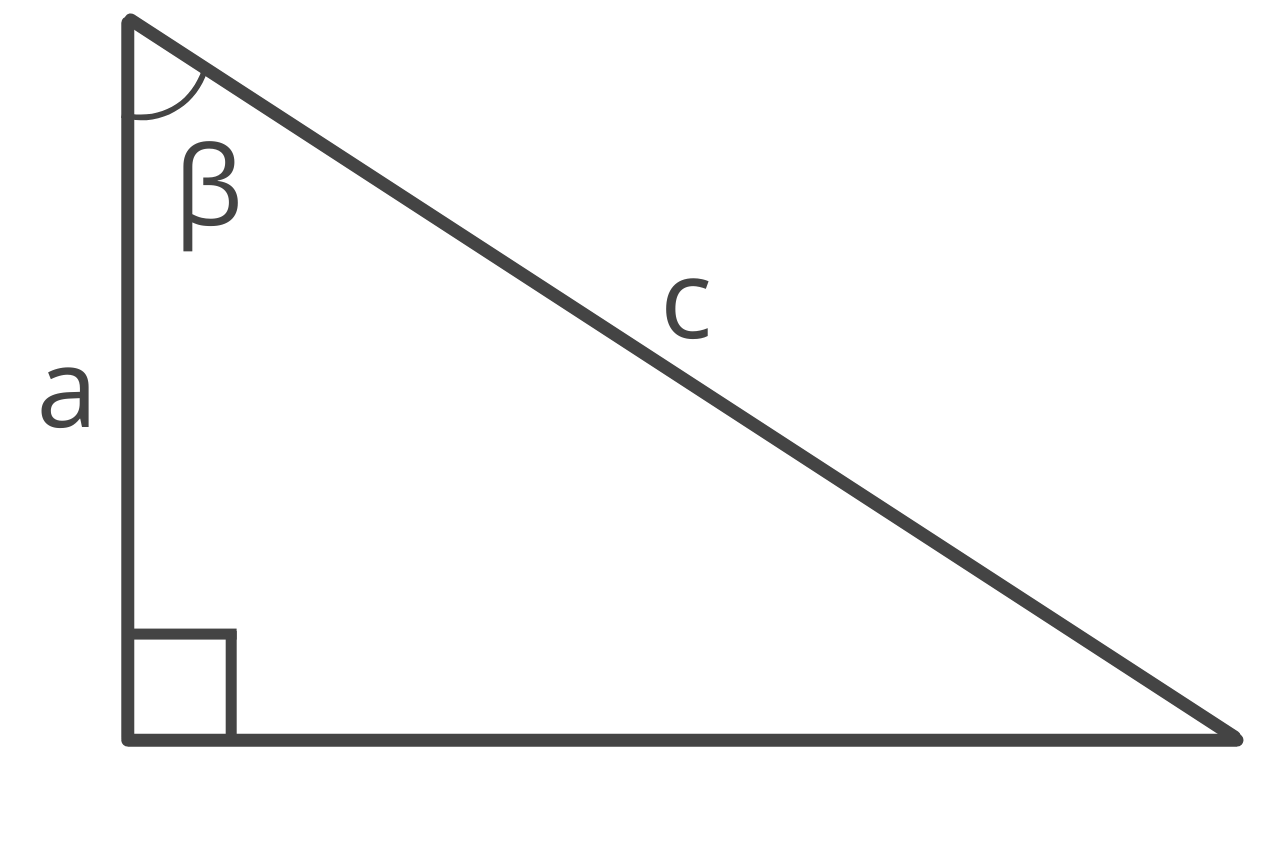
Formula Two: Given One Leg and the Adjacent Angle

Given the length of one leg and the adjacent angle, you can find the hypotenuse using the formula:

c = a / cos(β)

The hypotenuse c is equal to side a divided by the cosine of the adjacent angle β.

diagram of a triangle showing side a and adjacent angle b

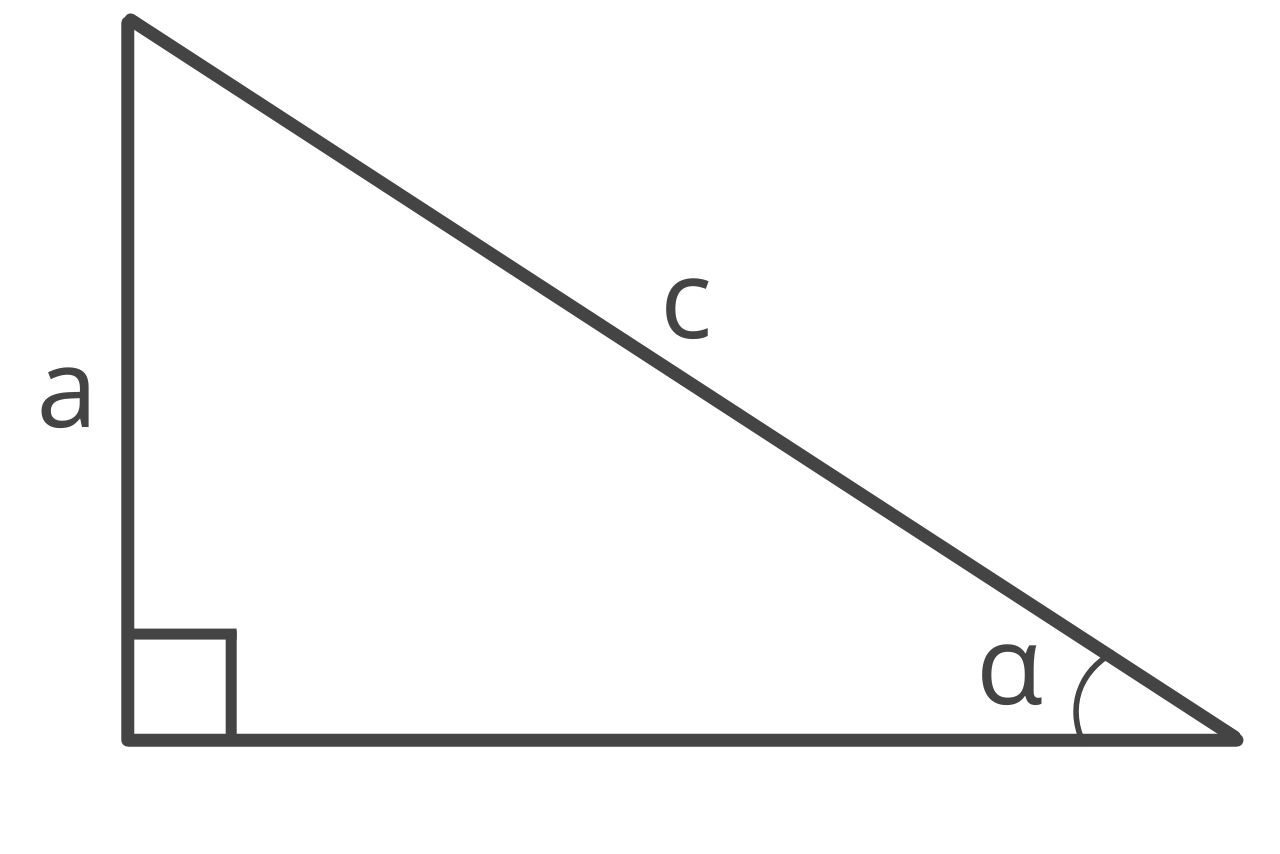
Formula Three: Given One Leg and the Opposite Angle

Given the length of one leg and the opposite angle, you can find the hypotenuse using the Law of Sines with the formula:

c = a / sin(α)

The hypotenuse c is equal to side a divided by the sine of the opposite angle α.

diagram of a triangle showing side a and opposite angle a

Formula Four: Given One Leg and the Area

If you know the length of one of the legs and the triangle area, you can find the length of the hypotenuse by using the area formula to solve for the length of the other leg, then using the Pythagorean theorem.

Given the formula to find the area of a right triangle, start by finding the length of the other leg:

A = 1 / 2ab

You can rearrange this formula to solve for the length of leg b like this:

b = 2A / a

The length of leg b is equal to 2 times the area A divided by the length of leg a.

Then, you can use the length of legs a and b to find the hypotenuse using the first formula above:

c = a² + b²

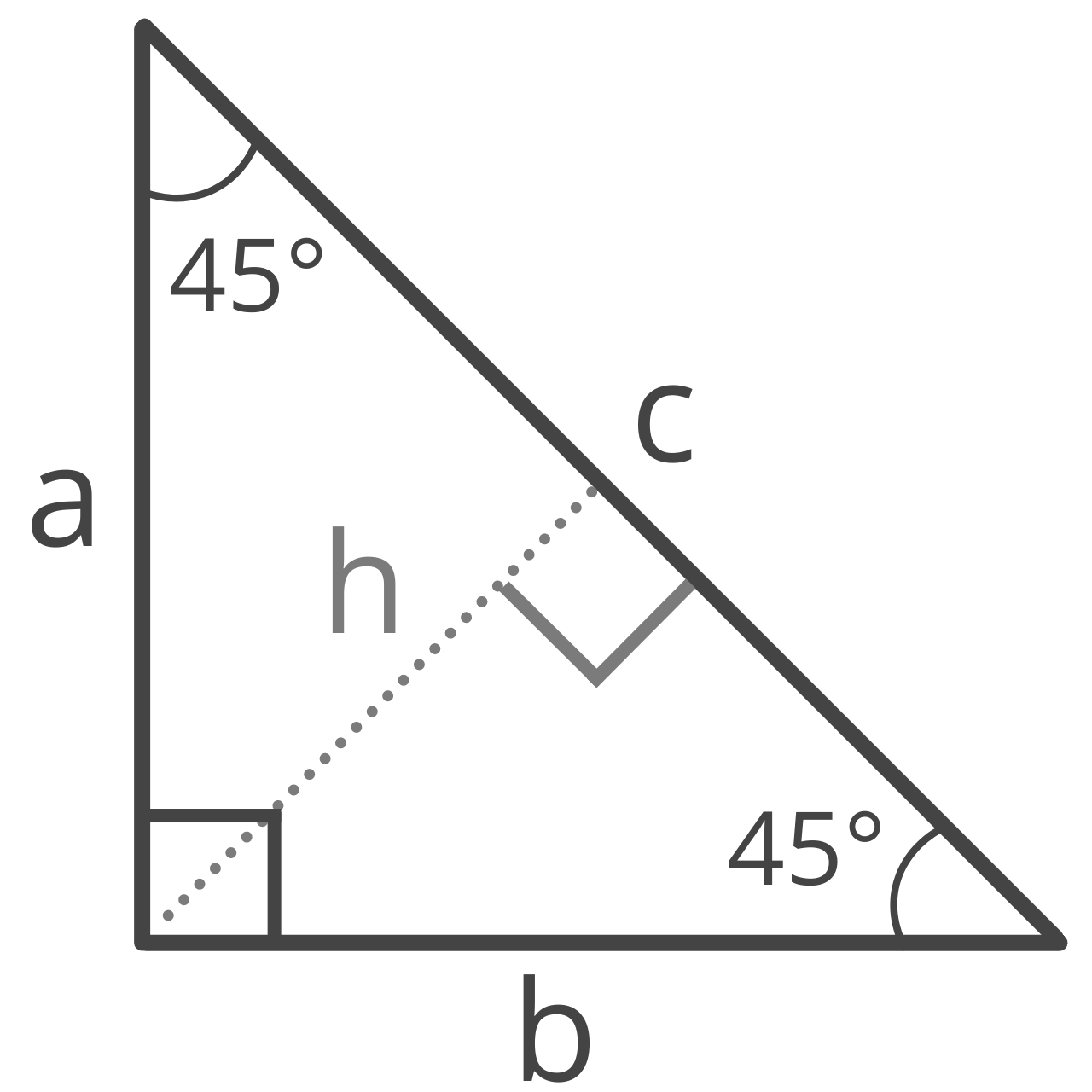
How to Find the Hypotenuse for a 45 45 90 Right Triangle

A 45 45 90 triangle is a special right triangle that is also an isosceles triangle. As the name implies, a 45 45 90 has two 45° interior angles and one right interior angle.

Since this is an isosceles triangle, both legs are equal in length, so you can find the length of the hypotenuse of a 45 45 90 right triangle using a simplified formula derived from the Pythagorean theorem.

c = a√2

The length of hypotenuse c is equal to the length of leg a times the square root of 2.

diagram of a special right 45 45 90 triangle showing legs a and b, hypotenuse c, 45 degree angles, and height h

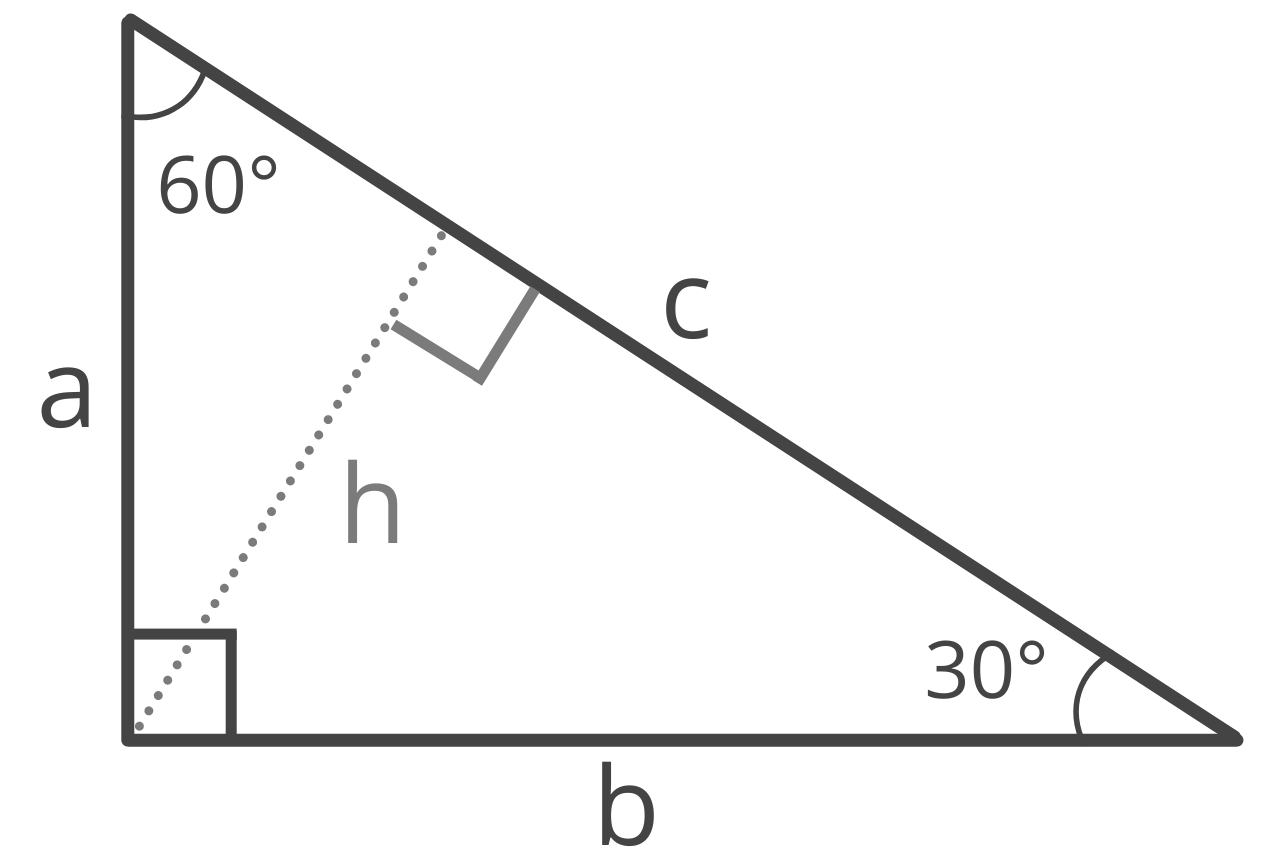
How to Find the Hypotenuse for a 30 60 90 Right Triangle

A 30 60 90 triangle is a special right triangle that has one 30° interior angle, one 60° interior angle, and one right interior angle.

In this special case, the length of the hypotenuse is always equal to two times the length of the shortest leg a of the triangle. Note, the shortest leg will always be opposite the 30° interior angle.

So, given the length of the shortest leg a, the formula to find the hypotenuse is:

c = 2a

The length of hypotenuse c is equal to 2 times the length of leg a.

diagram of a special right 30 60 90 triangle showing legs a and b, hypotenuse c, 30 & 60 degree angles, and height h

Источник

Недавно поступил запрос пользователя – длинна гипотенузы.
Я подумал, что в самом деле — калькуляторов про треугольники на сайте уже довольно много, а вот про прямоугольный треугольник еще нет. Отчасти видимо потому, что там все просто — теорема Пифагора. Но раз надо кому-то лень считать, то можно и сделать.

Калькулятор ниже — вводим длины двух сторон и выбираем их тип.
Если это два катета, то длина гипотенузы
c=sqrt{a^2+b^2}
Если это катет и гипотенуза, то длина оставшегося катета
a=sqrt{c^2-b^2}

PLANETCALC, Длина стороны прямоугольного треугольника

Длина стороны прямоугольного треугольника

Точность вычисления

Знаков после запятой: 2

На закуску — в (Википедии можно прочитать, что существует 367 доказательств теоремы Пифагора.

Источник

Добавить комментарий