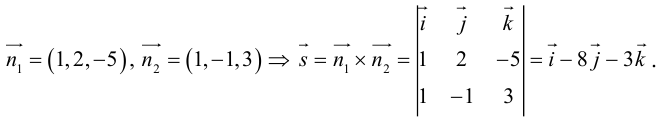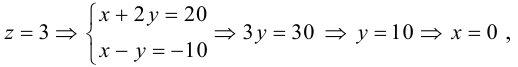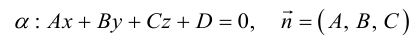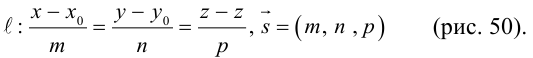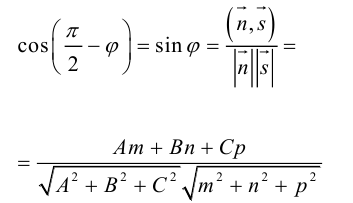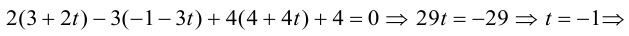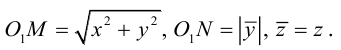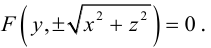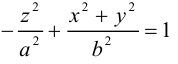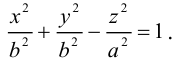Определение
1. Кривая
второго порядка на плоскости
– это линия, уравнение которой в заданной
системе координат имеет вид:
|
|
(7.5) |
где
,
,
,
,
,
– числовые коэффициенты, причем хотя бы
одно из чисел,
или
не
равно нулю.
Уравнение
(7.5) содержит две части:
линейная
часть
=
квадратичная
форма
=
Будем
предполагать, что система координат, в
которой рассматриваем кривую, это
декартова прямоугольная система, то
есть репер с ортонормированным базисом
.
В общем случае построить кривую по
уравнению (7. ) довольно трудно. Но всегда
можно перейти к другому ортонормированному
реперу, в котором легко установить вид
кривой, а затем и построить ее. Процедура
перехода к другому реперу выполняется
за 2 шага:
Шаг
1. Привести
квадратичную форму
=
к главным осям.
-
Матрица
квадратичной формы:
.
-
Характеристическое
уравнение:
.
-
Собственные
значения матрицы
:
.
-
Собственные
направления матрицы
:

Последнее
равенство требует, чтобы
,
то есть.
Последнее условие нарушено, если
=
.
Таким
образом, если
,
то квадратичная форма приведена к
главным осям и дальнейших ее преобразований
не требуется.
-
Ортонормированный
базис собственных векторов: ().
-
Матрица
перехода от базиса ()
к базису ():
.
-
Преобразование
координат «старого» базиса:
.
-
Матрица
квадратичной формы в базисе ():
.
-
Вид
квадратичной формы в базисе ():
.
-
Вид
линейной формы в базисе ():
=
=
=
=
-
Вид
уравнения кривой второго порядка в
базисе ():
Шаг
2. Не меняя
базиса (),
перейдем к новому началу координат,
координаты которого в «старом» репере
().
Целью этого перехода является получение
уравнения кривой, в котором коэффициенты
при линейных слагаемых равны нулю. Сразу
оговоримся, что такую процедуру можно
выполнить не всегда. Пользуясь формулами
(7. стр. ), имеем:
.
Раскрывая скобки
и группируя линейные и квадратичные
слагаемые, получаем:
+
.
Приравняем
коэффициенты при линейных слагаемых к
нулю и из полученных равенств найдем
:

Последние
равенства выполнимы, если
и
.
При выполнении этих условий, уравнение
кривой принимает вид:
,
(7. )
где
.
Если
же
или
,
то уравнение кривой в базисе ()
имеет вид:
|
|
(7.6) |
Преобразуем
первое из уравнений (7. ).
выберем так, чтобы свободный член
уравнения и коэффициент пристали равными нулю:
|
|
(7.7) |

После
этих преобразований уравнение (7.6)
принимает вид:
,
где
.
Второе
уравнение (7.6) аналогичными преобразованиями
приводим к виду:
,
где
.
Вывод.
Существует
система координат с ортонормированным
базисом, в котором уравнение кривой
второго порядка имеет одну из следующих
форм:
,
где
,
,
,
– любые действительные числа. Такую
систему координат называютканонической
системой координат кривой второго
порядка,
а ее уравнение в этой системе –
каноническим
уравнением кривой второго порядка.
Геометрическими
образами уравнения
являются следующие линии:
-
Пустая
линия.
.
Если,
то равенствоневыполнимо при любых значениях
и
.
-
Точка.
,
и
имеют одинаковые знаки, например,
.
Равенствовыполнимо
лишь в точке.
-
Пара
пресекающихся прямых.
,
и
имеют разные знаки, например,
.
Равенствораспадается на два равенства:
,
каждое из которых определяет прямую,
проходящую через начало координат. -
Пара
параллельных прямых и пара совпадающих
прямых.
,
–
уравнение двух прямых, параллельных
вектору,
если,
– уравнение пары совпадающих прямых.
-
Эллипс.
,
,
.
-
Гипербола.
,
,
.
Аналогично.
-
Уравнения
,
,
определяютпараболу.
Пример.
Определить
тип линии, заданной уравнением:
.
Решение
Задание
будем выполнять по действиям.
Выделим
в уравнении линии линейную часть и
квадратичную форму:
.
Приведем квадратичную
форму к главным осям:
-
Матрица
квадратичной формы:
.
-
Составим
и решим характеристическое уравнение:
,
.
-
Найдем
собственные направления матрицы:
|
|
|
|
|
|
|
|
|
-
Проверим
ортогональность векторов
и
:
=

-
Нормируем
векторы
и
:
;

;

-
Матрица
перехода от базиса
к базису
и
преобразование координат:

Вид
квадратичной формы в базисе
:
.
Вид
линейной части в базисе
:
=
.
Вид
уравнения кривой в базисе
:
+
=0.
2.
Перенесем начало координат в точку
так,
чтобы исчезли линейные слагаемые:
+
=0
=0
.
Ответ:
В репере
уравнение имеет вид:
Уравнение
определяет пару пересекающихся прямых:и
.
Рассмотрим
наиболее важные кривые второго порядка
– эллипс, гиперболу и параболу.
|
–
– |
Эллипсом
Характеристики
|
-
Эксцентриситет
.
Эксцентриситет
характеризует степень вытянутости
эллипса:
,
чем больше,
тем «уже» эллипс. В предельных случаях:
(а)эллипс становится окружностью, (б)
эллипс вырождается в двойной отрезок.
Каноническая
система координат – система, оси которой
совпадают с осями симметрии эллипса.
Уравнения эллипса в канонической системе
координат: (а)
– большая ось совпадает с осью
,
(б)– большая ось совпадает с осью
.
|
– |
Гиперболой
Характеристики
|
-
Эксцентриситет
.
-
Асимптоты
гиперболы: прямые
,
к которым приближается гипербола на
бесконечности.
Эксцентриситет
характеризует степень «раскрытости»
гиперболы:
,
чем больше,
тем более раскрыта гипербола.
Каноническая
система координат – система, оси которой
совпадают с осями симметрии гиперболы.
Уравнения эллипса в канонической системе
координат: (а)
– действительная ось совпадает с осью
,
(б)– действительная ось совпадает с осью
.
|
|
Параболой
Парабола
Одна |
.
Канонические
уравнения параболы:
-
,
.
Ось симметрии совпадает с осью
,
ветви параболы направлены вправо. -
,
.
Ось симметрии совпадает с осью
,
ветви параболы направлены влево. -
,
.
Ось симметрии совпадает с осью
,
ветви параболы направлены вверх. -
,
.
Ось симметрии совпадает с осью
,
ветви параболы направлены вниз.
Соседние файлы в папке Математика
- #
- #
- #
- #
- #
- #
Канонические координаты — независимые параметры в гамильтоновом формализме классической механики. Обозначают их обычно как 

Канонические координаты удовлетворяют фундаментальным соотношениям, выраженным через скобки Пуассона:
Канонические координаты можно получить из обобщённых координат лагранжевой механики с помощью преобразований Лежандра или из другого множества канонических координат с помощью канонических преобразований. Если гамильтониан определён на кокасательном расслоении, то обобщённые координаты связаны с каноническими координатами с помощью уравнений Гамильтона — Якоби.
Хотя может существовать много вариантов выбора канонических координат физической системы, обычно выбираются параметры, которые удобны для описания конфигурации системы и которые упрощают решение уравнений Гамильтона.
Близкие понятия используются также в квантовой механике, см. теорема Стоуна — фон Неймана[en] и канонические коммутационные соотношения.
Обобщение[править | править код]
Поскольку гамильтонова механика по математической структуре представляет собой симплектическую геометрию, то канонические преобразования являются частным случаем контактных преобразований.
Канонические координаты определяются как специальное множество координат на кокасательном расслоении многообразия. Они обычно записываются как множество 

Обычное определение канонических координат — это система координат на кокасательном расслоении, в которых каноническая 1-форма[en] записывается в виде
с точностью до прибавления полного дифференциала. Изменение координат, сохраняющее этот вид, является каноническим преобразованием. Это является специальным случаем симплектоморфизма[en]*, который, по существу, является изменением координат на симплектическом многообразии.
Формальное исследование[править | править код]
Если задано действительное многообразие Q, то векторное поле X на Q (или, эквивалентно, сечение касательного расслоения TQ) можно рассматривать как функцию, действующую на кокасательное расслоение[en]*, ввиду двойственности касательного и кокасательного пространств. То есть функция
такая, что
сохраняет все кокасательные вектора p в 



В локальных координатах векторное поле X в точке q может быть записано как
,
где 
,
где 




Литература[править | править код]
- Herbert Goldstein, Charles P. Poole, Jr., John L. Safko. Classical Mechanics. — 3rd. — San Francisco: Addison Wesley, 2002. — С. 347–349. — ISBN 0-201-65702-3.
- Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.
Приведение кривой второго порядка к каноническому виду
Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.
Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы 
Характеристическое уравнение: 

Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x1 2 -2y1 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. 
Собственный вектор, отвечающий числу λ=-2 при x1=1: x 1=(1,-1).
В качестве единичного собственного вектора принимаем вектор 

Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы 
x 2=(1,1); 
Итак, имеем новый ортонормированный базис ( i 1, j 1).
По формулам (5) пункта 4.3.3. переходим к новому базису:

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 – 20 = 0.
Решение.Пример 2
Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение
Задание. Привести уравнение к каноническому виду: 16x 2 – 9y 2 -64x – 8y +199 = 0.
Решение.Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Аналитическая геометрия
- Общее уравнение кривой второго порядка. Приведение общего уравнения кривой второго порядка к каноническому виду.
Общее уравнение кривой второго порядка. Каноническое уравнение кривой второго порядка.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Множество точек плоскости $R^2,$ удовлетворяющих условию $$sumlimits_^2a_x_ix_j+2sumlimits_^nb_kx_k+c=0,$$ называется кривой второго порядка. Каноническое уравнение кривой второго порядка может принимать один из следующих видов:
$$1),, lambda_1x^2+lambda_2y^2+c=0,,, (lambda_1lambda_2neq 0);$$
$$2),, lambda_1x^2+by=0qquad(lambda_1neq 0);$$
$$3),, lambda_1x^2+c=0qquad(lambda_1neq 0).$$
Пример.
4.226. Написать каноническое уравнение кривой второго порядка, определить ее тип и найти каноническую систему координат.
Решение.
Матрица квадратичной части многочлена второй степени имеет вид $$begin9&-2\-2&6end.$$
Найдем ее собственные числа:
$$det(A-lambda E)=begin9-lambda&-2\-2&6-lambdaend=(9-lambda)(6-lambda)-(-2)cdot(-2)=$$ $$=lambda^2-15lambda+40=0.$$
Далее находим собственные вектора:
Собственный вектор для собственного числа $lambda_1=10$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A-10E)X=0, Xneq 0$$
Решим однородную систему уравнений:
Вычислим ранг матрицы коэффициентов $A=begin-1&-2\-2&-4end$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=begin-1&-2\-2&-4end=4-4=0.$
Таким образом ранг матрицы $A$ равен одному.
Выберем в качестве базисного минор $M=begin-1end=-1neq 0.$ Тогда, полагая $x_2=c,$ получаем: $$-x_1-2c=0Rightarrow x_1=-2c.$$
Таким образом, общее решение системы $X(c)=begin-2c\cend.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=begin-2\1end.$
Соответствующий ортонормированный собственный вектор: $$e_1’=left(frac<-2><sqrt<4+1>>,frac<1><sqrt<4+1>>right)=left(frac<-2><sqrt 5>,frac<1><sqrt 5>right).$$
Собственный вектор для собственного числа $lambda_2=5$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A-5E)X=0, Xneq 0$$
Решим однородную систему уравнений:
Вычислим ранг матрицы коэффициентов $A=begin4&-2\-2&1end$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=begin4&-2\-2&1end=4-4=0.$
Таким образом ранг матрицы $A$ равен одному.
Выберем в качестве базисного минор $M=begin4end=4neq 0.$ Тогда, полагая $x_2=c,$ получаем: $$4x_1-2c=0Rightarrow x_1=c/2$$
Таким образом, общее решение системы $X(c)=beginc/2\cend.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=begin1/2\1end.$
Соответсвующий ортонормированный собственный вектор: $$e_1’=left(frac<1><sqrt<4+1>>,frac<2><sqrt<4+1>>right)=left(frac<1><sqrt 5>,frac<2><sqrt 5>right).$$
Таким образом, мы нашли вектора
Выделим по переменной $x’$ полный квадрат: $$10^2-frac<40><sqrt 5>x’=10left(^2-frac<4><sqrt 5>+frac<4><5>right)-8=10left(x’-frac<2><sqrt 5>right)^2-8.$$
Делаем замену переменных:
$$x”=x’-frac<2><sqrt 5>, qquadquad y”=y’$$ (замена переменных соответствует сдвигу по оси $Ox.$ ) Получаем: $$10^2+5^2-10=0Rightarrow ^2+frac<^2><2>=1.$$ Это уравнение эллипса.
Результирующее преобрзование координат имеет вид
Ответ: Эллипс $^2+frac<^2><2>=1.$ $O=left(-frac<4><5>, frac<2><5>right),$
Домашнее задание:
Написать каноническое уравнение кривой второго порядка, определить ее тип и найти каноническую систему координат.
4.227. $x^2-2xy+y^2-10x-6y+25=0.$
Ответ: Парабола $^2=4sqrt 2 x.$ $O’=left(2, 1right),$
4.228.$5x^2+12xy-22x-12y-19=0.$
Ответ: Гипербола $ frac<^2><4>-frac<^2><9>=1.$ $O’=left(1, 1right),$
Кривые и поверхности второго порядка в математике с примерами решения и образцами выполнения
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.
Кривые второго порядка используются при решении задач по аналитической геометрии, кривые других порядков используются при решении задач математического анализа в разделе вычисления кратных, криволинейных и поверхностных интегралов.
Кривые и поверхности второго порядка
Преобразование координат на плоскости
Пусть на плоскости заданы две прямоугольные декартовы системы координат, Оху и О’х’у’ (рис. 1). Произвольная точка М относительно одной из этих координатных систем определяется парой чисел х и у, а относительно другой — парой чисел x’ и у’. Ясно, что между парами (х,у) и (x’, у’) имеется связь. Найдем ее.
Параллельный перенос
Предположим, что соответствующие координатные оси параллельны и сонаправлены, а точки начала отсчета различны. Это означает, что орты координатных осей соответственно равны (рис. 2).
Пусть г и г’ — радиусы-векторы точки М, т.е.
и а, β — координаты точки О’ относительно системы координат Оху, т. е.
Поворот
Предположим, что координатные оси одной системы координат получаются из координатных осей другой системы поворотом на угол φ, а начальные точки совпадают (рис.4). Координатами единичного вектора i’ являются косинусы углов φ и , образованных этим вектором с осями Ох и Оу:
а координатами единичного вектора j’ служат косинусы углов и φ:
(рис. 5). Так как радиус-векторы
произвольной точки М в рассматриваемом случае равны,
то, заменяя векторы i’ и j’ их выражениями, получаем, что
Зеркальное отражение
В случае, когда оси абсцисс Ох и Ох’ координатных систем совпадают, а оси ординат Оу и Оу’ направлены противоположно, координаты (х, у) и (х’,у’) произвольной точки М связаны равенствами
Справедливо следующее утверждение.
Любое преобразование прямоугольных декартовых координат (с сохранением масштаба) можно представить в виде последовательного выполнения переноса, поворота и <если необходимо) зеркального отражения.
Кривые второго порядка
Пусть на плоскости задана прямоугольная декартова система координат Оху. Множество точек плоскости, координаты х и у которых удовлетворяют равенству
F(x, у) = 0,
где F(x, у) — некоторая функция двух переменных, называется плоской кривой, или плоской линией само равенство называется уравнением данной линии (кривой).
Например, равенство х — у = 0 есть уравнение прямой — биссектрисы первого и третьего координатных углов (рис. 7). Равенство x 2 + y 2 — 1 = 0 — уравнение окружности единичного радиуса с центром в начале координат (рис. 8).
Рассмотрим многочлен второй степени от двух переменных х и у:
F(x,y) = 0
будем называть уравнением линии (кривой) второго порядка.
Если линиями первого порядка являются именно прямые и только они, то множество кривых второго порядка заметно разнообразней. Поэтому исследованию общего уравнения кривой второго порядка естественно предпослать изучение некоторых частных, но важных случаев.
Эллипс
Эллипсом называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение эллипса имеет вид (1), называется канонической (для данного эллипса); само уравнение (!) называется каноническим уравнением эллипса. Окружность
является частным случаем эллипса (при а = b). Это позволяет несложным способом определить форму эллипса: эллипс (1) получается из окружности (2) путем ее равномерного сжатия» к оси Ох (с коэффициентом), т.е. заменой в уравнении x 2 + y 2 = a 2 координаты у на (рис.9).
Свойства эллипса
- Эллипс (I) содержится в прямоугольнике
В этом легко убедиться, заметив, что, если точка М(х, у) принадлежит эллипсу (1), то (рис. 10)
Точки (±а, 0), (0, ±b) называются вершинами эллипса.
2. Координатные оси Ох и Оу канонической системы являются осями симметрии эллипса, а начало координат О — его центром симметрии. Это означает, что если точка Мо(хo, yо) принадлежит эллипсу, то точки (-хо, yо), (-xо, -yо) и (хо, -yо) также ему принадлежат (рис. 11).
3. Если эллипс не является окружностью, то координатные оси канонической системы — единственные оси симметрии.
Положим с = . Ясно, что с 0 называется преобразование, переводящее произвольную точку М(х, у) окружности в точку М’ ().
Пусть сначала М(х, у) — произвольная точка эллипса
Вычислим ее расстояния от фокусов эллипса (рис. 12). Имеем
Заменяя y 2 его выражением
после несложных преобразований получаем, что
Последнее равенство вытекает из того, что
Легко убедиться в том, что
Доказательство того, что точки, обладающие указанным свойством, принадлежат эллипсу, было проведено ранее (см. раздел «Простейшие задачи аналитической геометрии» Введения, задача 2).
называется эксцентриситетом эллипса (I). Ясно, что 0
называются директрисами эллипса. У каждого эллипса две директрисы — левая и правая (рис. 13).
5. Эллипс есть множество точек плоскости, отношение расстояний от которых до данной точки (фокуса эллипса) и доданной прямой (одноименной с фокусом директрисы эллипса) постоянно (равно эксцентриситету эллипса).
Пусть сначала М(х,у) — произвольная точка эллипса (1). Вычислим расстояния от нее до правого фокуса и до правой директрисы (рис. 14). Имеем соответственно
Откуда легко получаем требуемое
Аналогично проверяется, что
Рассмотрим теперь на плоскости точку (с, 0) и прямую х =(с = ае). Возьмем произвольную точку М(х, у) и вычислим расстояния от нее до выбранной точки (с, 0) —
— и до выбранной прямой —
Возведем обе части последнего соотношения в квадрат и, положив и учтя равенство с = ае, после простых преобразований получим
Тем самым, точка М(х,у) лежит на эллипсе (1).
Гипербола
Гиперболой называется кривая, уравнение которой в некоторой прямоугольной системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение гиперболы имеет вид (1), называется канонической (для данной гиперболы); само уравнение (1) называется каноническим уравнением гиперболы.
Свойства гиперболы
- Гипербола (1) лежит вне полосы |x|
и, значит, |x| ≥ а (рис. 15).
Точки (±а, 0) называются вершинами гиперболы.
2. Гипербола (1) лежит в вертикальных углах, образованных прямыми у = ±х и содержащих точки оси Ох (рис. 16).
вытекает, что если точка М(х, у) лежит на гиперболе (1), то
Таким образом, гипербола состоит из двух частей — ветвей гиперболы, левой и правой. Прямые
называются асимптотами гиперболы.
3, На гиперболе лежат точки, сколь угодно далекие от начала координат O(0, 0).
Пусть, например, точка М(х, у) лежит на гиперболе (1) и у = n, где n — произвольное положительное число (рис. 17).
Возьмем в первой четверти две точки: точку гиперболы (1) и точку ее асимптоты = 0 с одинаковой абсциссой х > а —
соответственно — и вычислим расстояние между ними. Имеем
Умножив и разделив полученное выражение на сумму х +и перейдя затем к пределу при получим
Тем самым, установлен следующий факт.
4. Если текущая точка асимптоты неограниченно удаляется от начала координат, т.е. х —» + ∞, то на гиперболе можно указать соответствующую ей точку так, чтобы расстояние между ними стремилось к нулю (рис. 18).
Верно и обратное.
стремится к нулю.
6. Оси канонической координатной системы являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис. 19).
Координатные оси канонической системы — единственные оси симметрии гиперболы.
Положим с = . Ясно, что с > 0. .Точки (-с, 0) и (с, 0) называются фокусами гиперболы, 2с — фокусное расстояние.
Гипербола есть множество точек, абсолютная величина разности расстояний от которых до двух данных точек (фокусов гиперболы) постоянна (равна заданному числу).
Доказательство этого свойства проводится так же, как и доказательство свойства 4 эллипса. Покажем, например, что каждая точка гиперболы обладает указанным свойством. Если М(х, у) — точка гиперболы (1), то расстояния от нее до фокусов соответственно равны
(рис. 20). Так как > 1, то
Отсюда нетрудно вычислить, что
называется эксцентриситетом гиперболы (1). Ясно, что е > 1. Прямые
называются директрисами гиперболы (рис. 21). У каждой гиперболы две директрисы — левая и правая.
Практически также, как и для эллипса, доказывается следующий факт.
8. Гипербола есть множество точек, отношение расстояний от которых до данной точки (фокуса гиперболы) и доданной прямой (одноименной с фокусом директрисы) постоянно (равно эксцентриситету гиперболы) (рис. 22).
Гипербола (2)
называется сопряженной гиперболе (1). Взаимное расположение гипербол (1) и (2) указано на рис. 23.
Парабола
Параболой называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение параболы имеет вид (1), называется канонической (для данной параболы); уравнение (]) называется каноническим уравнением параболы.
Свойства параболы
- Все точки параболы лежат в правой полуплоскости: х ≥ 0 (рис. 25). Точка 0(0, 0) лежит на параболе и называется ее вершиной.
- На параболе лежат точки, сколь угодно далеко расположенные от начала координат О(0, 0).
- Ось абсцисс канонической координатной системы является (единственной) осью симметрии параболы (рис. 26).
Ось симметрии параболы называется осью параболы. Число р называется фокальным параметром параболы; точка (; 0) — фокус параболы; прямая х = — директриса параболы.
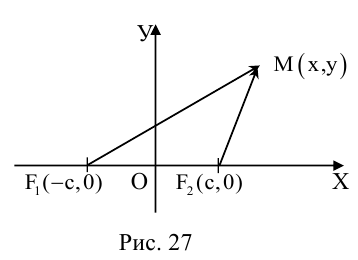
4. Парабола есть множество точек, равноудаленных отданной точки (фокуса параболы) и от данной прямой (директрисы параболы) (рис. 27).
Пусть точка М(х, у) лежит на параболе (1). Вычислим расстояния от нее до фокуса (;0)
и до директрисы х = —
Заменяя у 2 его выражением 2рх, легко убеждаемся в том, что
Верно и обратное. Если для некоторой точки М(х, у) расстояния от нее до точки (; 0) и до прямой х = — равны —
то, возводя в квадрат, после простых преобразований получаем, что эта точка лежит на параболе:
Оптическое свойство кривых второго порядка
Касательные к эллипсу и гиперболе
Если кривая задана уравнением
y = f(x)
то уравнение касательной к ней, проходящей через точку (хо,у0)> где Уо = f(xо), можно записать в следующем виде
Пусть Мо(хо, yо) — точка эллипса
Предположим для определенности, что точка М0 лежит в первой четверти, т. е. хо > 0, yо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением
Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо
а так как точка (х0, у о) лежит на эллипсе, то
Полученное соотношение после несложных преобразований можно записать так:
Отсюда с учетом тождества
приходим к уравнению
(рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (х0, yо), и в общем случае ее произвольного расположения, т. е. при любых знаках хо и уо.
Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид
Подчеркнем, что точка (хо, yо) лежит на гиперболе.
Касательные к параболе
Если кривая задана уравнением
х = g(у),
то уравнение касательной к ней, проходящей через точку (хo,уo), где х0 = g (уо), можно записать в следующем виде
Пусть М0(х0, у0) — точка параболы. Пользуясь формулой (I), получаем уравнение касательной к параболе
Отсюда в силу равенства приходим к уравнению касательной вида
Замечание:
Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, что для получения последних не требуется специальных вычислений. В самом деле, заменяя у 2 на уу 0 , а х 2 на хх 0 (в случае параболы 2х нужно заменить на x + х 0 ). приходим к уравнению соответствующей касательной. Еще раз отметим, что сказанное справедливо лишь в том случае, когда точка (x 0 . y 0 ) лежит на кривой.
Оптическое свойство эллипса
Пусть М 0 — произвольная точка эллипса
Как уже отмечалось, расстояния от нее до фокусов Fл и F n — фокальные радиусы — равны соответственно
Проведем через точку М 0 касательную к эллипсу,
и вычислим, на каком расстоянии от этой касательной лежат фокусы Fл (-c, 0) и Fn (c; 0) (напомним, что для этого следует воспользоваться формулой (10).
— нормирующий множитель (рис. 29). Нетрудно проверить, что
Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания. Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания.
Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).
Оптическое свойство гиперболы
Устанавливается аналогичными выкладками и заключается в следующем.
Если поместить в один из фокусов гиперболы точечный источник света, то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31).
Оптическое свойство параболы
Если в фокус параболы помещен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис. 32).
Классификация кривых второго порядка
Многочлены второй степени на плоскости
Теорема:
Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть
— многочлен второй степени от переменных х и у.
Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X и Y исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов:
1-й шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль.
Пусть b ≠ 0 (при 6 = 0 этот шаг не нужен). Повернем оси координат вокруг точки О. Эта операция описывается следующими формулами
При этом координатные оси исходной системы Оху поворачиваются на угол φ (рис.33).
Заменим переменные х и у в формуле (1) их выражениями (2) через x’ и у’ и вычислим коэффициент 2b’ при произведении х’у’. Он равен
и обращается в нуль, если
Так как полученное уравнение разрешимо относительно φ, то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.
Приступая ко второму этапу преобразования, будем считать, что исходный многочлен f(x,у) уже имеет вид
где а 2 + с 2 >0. Для определенности положим с ≠ 0 (это не ограничивает общности наших рассуждений, так как заменой х, у в случае необходимости этого всегда можно добиться).
2-й шаг. Переносом начала координат можно достичь дальнейшего упрощения вида многочлена f(x,y). Эта операция описывается следующими формулами:
координатные оси новой системы O’XY получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, — β) (рис. 34).
Укажем конкретные значения а и β. Возможны три случая
I. а ≠ 0, с ≠ 0. Тогда, полагая
где А = а, В = с, С = g —
II. а = 0, d ≠ 0. Тогда, полагая
III. а = d = 0. Тогда, полагая
где В = с, Е = g —
Канонические уравнения кривых второго порядка
Если многочлен второй степени F(X, У) приравнять к нулю, то получим уравнение линии второго порядка
F(X, У) = 0.
Рассмотрим каждый из трех полученных выше случаев I, II, III отдельно.
I.
Э. А • В > 0. Домножением обеих частей уравнения на — 1 и заменой X на У, а У на X (в случае необходимости) всегда можно добиться того, чтобы В ≥ А > 0.
-
С
(мнимый эллипс)2). На действительной плоскости нет ни одной точки (X, Y), координаты которой обращали бы это уравнение в тождество.
Точка (0, 0) является единственной точкой плоскости, координаты которой удовлетворяют этому уравнению; точку (0,0) можно мыслить как действительную точку пересечения двух мнимых пересекающихся прямых 3).
Г. А • В 0, В
— пару пересекающихся прямых:
2) Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса.
3) Название можно объяснить некоторым сходством этого уравнения с уравнением пары пересекающихся
прямых.
II. BY 2 + 2DX = О, В • D ≠ 0.
Всегда можно добиться того, чтобы В • D
III. BY 2 + Е = 0, В ≠ 0. Можно считать, что В > 0.
1. Е
Y 2 — с 2 = 0, с > 0
— пару параллельных прямых.
Y 2 — с 2 = 0, с 2 = 0
— пара совпадающих прямых.
Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.
— уравнение линии второго порядка. Введем следующие обозначения
Числа D и ∆ не зависят от выбора системы координат на плоскости и называются инвариантами. Из приводимой таблицы видно, какому сочетанию знаков определителей D и ∆ соответствует та или иная линия второго порядка.
Задача:
Убедитесь в том, что D и ∆ при рассмотренных преобразованиях системы координат действительно остаются неизменными.
4) Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных прямых.
Поверхности второго порядка
Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Множество точек пространства, координаты х, у и z которых удовлетворяют равенству
F(x, у, z) = О,
называется поверхностью; равенство (*) называется уравнением этой поверхности.
Пример:
— уравнение сферы радиуса о с центром в точке (0,0,0) (рис. 35).
Рассмотрим многочлен второй степени от трех переменных х, у и z
Уравнение
F(x, y, z) = 0
будем называть уравнением поверхности второго порядка.
Исследование общего уравнения поверхностей второго порядка оказывается зна-чительноболее сложным, чем исследование общего уравнения кривых второго порядка, требует разработки соответствующего математического аппарата и будет проведено в конце главы VI.
В оставшихся параграфах этой главы мы сначала остановимся на изучении геометрических свойств некоторых важных классов общих поверхностей; затем используем их для рассмотрения канонических уравнений основных поверхностей второго порядка и исследования структуры этих поверхностей.
Некоторые классы поверхностей
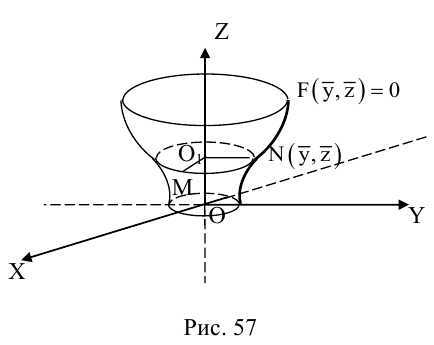
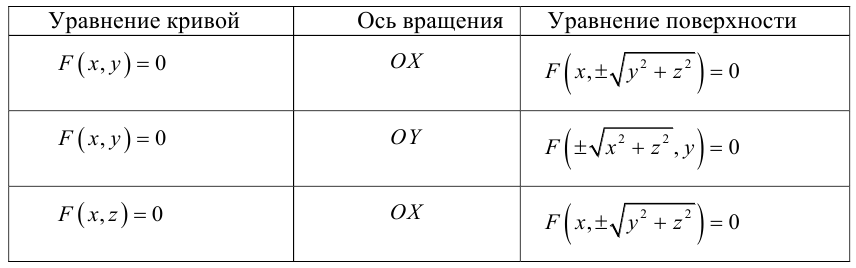
Поверхности вращения
Рассмотрим на плоскости Oxz кривую γ, заданную уравнением
г = f(x), х ≥ 0
(рис. 36). При вращении кривой γ вокруг оси Oz она будет заметать некоторую поверхность, называемую поверхностью вращения (рис. 37). Найдем уравнение этой поверхности, т. е. равенство, которому должны удовлетворять координаты точек построенной поверхности и только они.
Тем самым, координаты х, у и z0 любой точки М этой окружности связаны следующим равенством
В силу произвольности выбора точки М0 на кривой γ искомое уравнение полученной поверхности вращения имеет вид
Цилиндрические поверхности
Через каждую точку некоторой заданной кривой γ проведем прямую l параллельно заданной прямой l0. Множество точек, лежащих на так построенных прямых, назовем цилиндрической поверхностью (рис. 39); кривая γ называется направляющей цилиндрической поверхности, а прямая l — ее образующей.
Найдем уравнение, описывающее цилиндрическую поверхность.
Возьмем произвольную точку О и проведем через нее плоскость П, перпендикулярную образующей I. Построим в пространстве прямоугольную координатную систему Oxyz, взяв за ось Oz прямую, перпендикулярную плоскости П. Тогда плоскость П будет координатной плоскостью Оху (рис.40). Плоскость П пересекает цилиндрическую поверхность по направляющей γ0.
F(x,y) = 0
— уравнение этой направляющей. Убедимся в том, что последнее соотношение можно считать уравнением искомой цилиндрической поверхности.
самом деле, пусть (х, у, z) — точка цилиндрической поверхности (рис. 41). Тогда точка (х, у, 0) лежит на γ0 и, значит, удовлетворяет уравнению
F(x,y)=0.
Но координаты точки (х, у, z) также обращают это уравнение в тождество. Последнее обстоятельство и позволяет считать соотношение F(x,y) = 0 искомым уравнением.
Пример:
Введем в пространстве прямоугольные декартовы координаты Охуz. Соотношение
является уравнением цилиндрической поверхности (эллиптического цилиндра) (рис. 42).
Замечание:
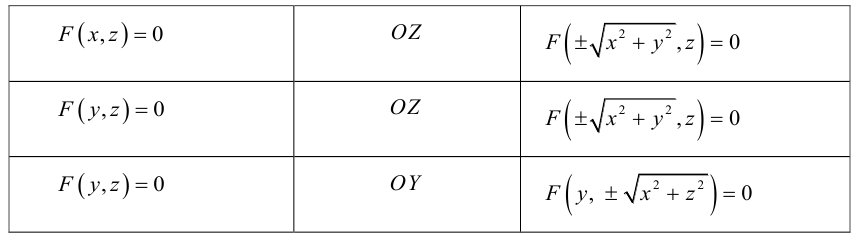
F(y, z) = 0
описывает цилиндрическую поверхность с образующей, параллельной координатной оси Оx, а уравнение
F(x,z) = 0
— цилиндрическую поверхность с образующей, параллельной оси Oy.
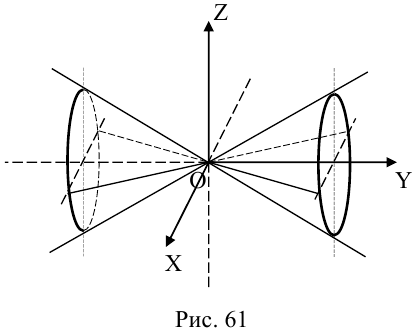
Конические поверхности
Пусть γ — произвольная кривая и О — точка вне eе. Через каждую точку кривой γ и точку О проведем прямую l. Множество точек, лежащих на построенных таким образом прямых, называется конической поверхностью (рис.43); кривая γ — направляющая конической поверхности, l — ее образующая, точка О — вершина. Рассмотрим функцию
F (x, у, z)
переменных х, у и z. Функция F(x, у, z) называется однородной функцией степени q, если для любого t > 0 выполняется равенство
Покажем, что если F(x, у, z) однородная функция, то F
является уравнением конической поверхности.
В самом деле, пусть
т.е. точка М0(xo, уо, zо) лежит на этой поверхности. Будем считать, что . Проведем через эту точку и точку 0(0,0, 0) (считая, что F(0,0, 0) = 0) прямую I (рис. 44). Ее параметрические уравнения имеют вид
Подставляя полученные выражения для х, у и z в функцию F(x, у, z), видим, что
Это означает, что вся прямая l лежит на поверхности, определяемой уравнением F(x,y,z) = 0, которое, следовательно, и описывает коническую поверхность.
Пример:
является однородной функцией второй степени:
— уравнение конической поверхности (конуса второго порядка) (рис.45).
Воспользуемся теперь полученными выше результатами для исследования геометрической формы поверхностей второго порядка.
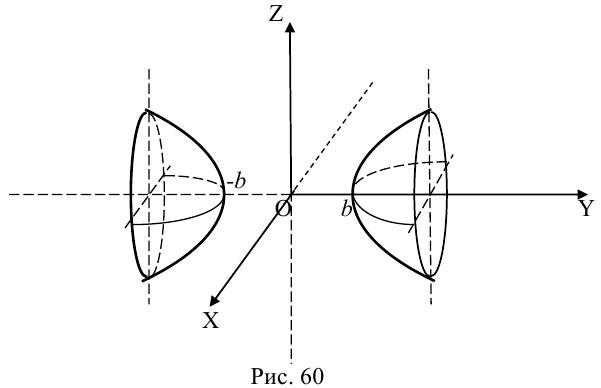
Эллипсоид. Гиперболоиды. Параболоиды. Цилиндры и конус второго порядка
Эллипсоид
Эллипсоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид
где а ≥ b ≥ с > 0. Для того, чтобы выяснить, как выглядит эллипсоид, поступим следующим образом. Возьмем на плоскости Oxz эллипс
и будем вращать его вокруг оси Oz (рис. 46).
— эллипсоид вращения — уже дает представление о том, как устроен эллипсоид общего вида. Чтобы получить его уравнение, достаточно равномерно сжать эллипсоид вращения . вдоль оси Оу с коэффициентом — ≤ 1, т. с. заменить в его уравнении у на y 5).
Гиперболоиды
вокруг оси Oz (рис. 47), получим поверхность, называемую однополостным гиперболоидом вращения. Его уравнение имеет вид
получается тем же способом, что и в случае эллипсоида вращения.
5) Эллипсоид вращения («) можно получить равномерным сжатием сферы х 2 + у 2 + z 2 = а 2 вдоль оси Оz с коэффициентом — ≤ 1.
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом ≤ 1 получим однополостный гиперболоид общего вида. Его уравнение
получается тем же способом, что и в разобранном выше случае эллипсоида. Путем вращения вокруг оси Oz сопряженной гиперболы
получим двуполостный гиперболоид вращения (рис.48). Его уравнение
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом ≤ 1 приходим к двуполостному гиперболоиду общего вида. Заменой у на у получаем его уравнение
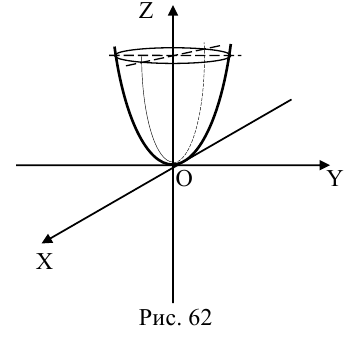
Эллиптический параболоид
вокруг оси Oz (рис.49), получаем параболоид вращения. Его уравнение имеет вид
Путем сжатия параболоида вращения вдоль оси Оу с коэффициентом получаем эллиптический параболоид. Его уравнение
получается из уравнения параболоида вращения
путем замены у на . Если р Гиперболический параболоид
Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид
где р > 0, q > 0. Вид этой поверхности определим, применив так называемый метод сечений, который заключается в следующем: параллельно координатным плоскостям проводятся плоскости, пересекающие исследуемую поверхность, и по изменению конфигурации возникающих в результате плоских кривых делается вывод о структуре самой поверхности.
Начнем с сечений плоскостями z = h = const, параллельными координатной плоскости Оху. При h > 0 получаем гиперболы
при h
при h = 0 — пару пересекающихся прямых
Заметим, что эти прямые являются асимптотами для всех гипербол (т. е. при любом h ≠ 0). Спроектируем получаемые кривые на плоскость Ох у. Получим следующую картину (рис. 51). Уже это рассмотрение позволяет сделать заключение о седлообразном строении рассматриваемой поверхности (рис. 52).
Рассмотрим теперь сечения плоскостями
у = h.
Заменяя в уравнении поверхности у на h, получаем уравнения парабол (рис.53).
Аналогичная картина возникает при рассечении заданной поверхности плоскостями
х = h.
В этом случае также получаются параболы
ветви которых направлены вниз (а не вверх, как для сечения плоскостями у = h) (рис. 54).
Используя последние два типа сечений, приходим к заключению, что гиперболический параболоид можно получить путем параллельного переноса параболы х2 = 2pz вдоль параболы у2 = -2qz, или наоборот (рис. 55).
Замечание:
Методом сeчeний можно разобраться в строении и всех ранее рассмотренных поверхностей второго порядка. Однако путем вращения кривых второго порядка и последующего равномерного сжатия к пониманию их структуры можно прийти проще и значительно быстрее.
Оставшиеся поверхности второго порядка по существу уже рассмотрены ранее. Это цилиндры:
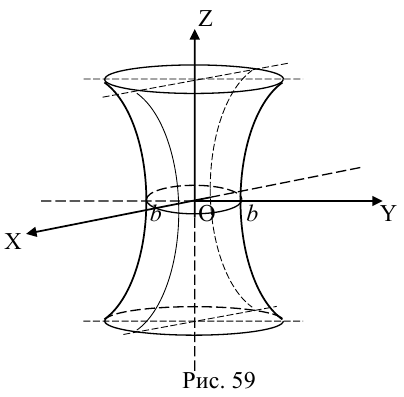
представление о котором можно получить либо путем вращения пары пересекающихся прямых
вокруг оси Oz и последующего сжатия, либо методом сечений. Конечно, в обоих случаях получим, что исследуемая поверхность имеет вид, указанный на рис. 59.
Дополнение к поверхностям второго порядка
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://mathportal.net/index.php/analiticheskaya-geometriya/obshchee-uravnenie-krivoj-vtorogo-poryadka-privedenie-obshchego-uravneniya-krivoj-vtorogo-poryadka-k-kanonicheskomu-vidu
http://lfirmal.com/poverhnosti-vtorogo-poryadka/
[/spoiler]
Содержание:
Аналитическая геометрия
В этой главе все геометрические объекты мы будем определять и изучать с помощью соответствующих уравнений этих объектов и, следовательно, в принципе геометрия может быть изложена без единого чертежа. И, действительно, все чертежи, которые мы будем использовать, будут служить лишь для визуальной иллюстрации наших рассуждений.
Уравнение поверхности в выбранной декартовой системе координат
т. е. в виде связи или зависимости между координатами х, у, z произвольной точки поверхно-аналогично, уравнение
определяет некоторую линию (кривую) в системе координат 
Кривая в пространстве может быть задана как пересечение двух поверхностей и, следовательно, она определяется системой из уравнений этих поверхностей:
Кроме того, кривую на плоскости или в пространстве можно также задать с помощью зависимостей координат произвольной то’жи этой кривой от некоторого параметра, т. е. с помощью параметрических уравнений:
где t – действительный параметр.
Плоскость в пространстве. Различные виды уравнения плоскости
Найдем уравнение плоскости в пространстве с выбранной в нем декартовой системой координат 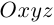
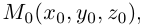
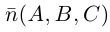
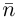
Пусть 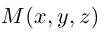
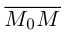
или, учитывая, что 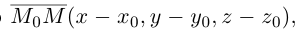
Преобразовав полученное уравнение к виду
мы получим тем самым общее уравнение плоскости.
Рассмотрим теперь некоторые частные случаи общего уравнения плоскости. Если в общем уравнении плоскости отсутствует, одна из координат, то нормальный вектор 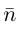
Аналогично, если в общем уравнении плоскости отсутствуют две координаты, то нормальный вектор данной плоскости перпендикулярен соответствующей координатной плоскости и, значит, плоскость расположена параллельно этой координатной плоскости.
Научимся теперь находить уравнение плоскости по трем элементам.
1) Плоскость, проходящая через точку, параллельно двум векторам.
Пусть плоскость 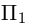
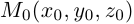
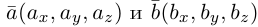
Обозначим через 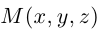
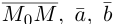
Раскрыв определитель (проще всего, разлагая его по первой строке), получим общее уравнение плоскости
2)Плоскость, проходящая через две точки, параллельно вектору.
Найдем уравнение плоскости 
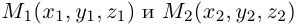
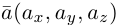
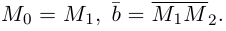
– искомое уравнение плоскости
3)Плоскость, проходящая через три точки.
Если плоскость 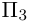
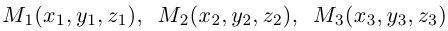
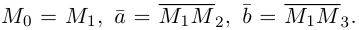
Замечание. Во всех трех случаях уравнение плоскости можно найти, вычислив предварительно ее нормальный вектор. Например, в первом случае в качестве нормального вектора можно взять векторное произведение 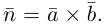
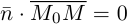
Пример №1
Найти уравнение плоскости 11 ^ – перпендикулярной плоскости
параллельной вектору 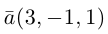
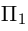
Решение. Из уравнения плоскости 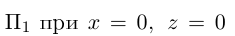
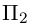
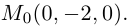
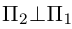
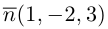
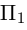
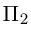
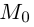
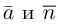
Таким образом, общее уравнение плоскости 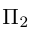
Пусть плоскость 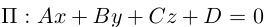
Разделив обе части уравнения плоскости на число D. мы можем записать его в виде:
Числа а, b, с представляют собой величины отрезков, которые плоскость П отсекает на координатных осях. Полученное уравнение называется уравнением плоскости в отрезках.
Найдем теперь формулу для вычисления расстояния от точки 
Обозначим искомое расстояние через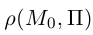
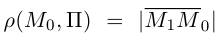
С другой,
так как 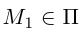
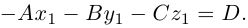
В заключение этого параграфа выясним характер взаимного расположения двух плоскостей. Пусть плоскости заданы своими общими уравнениями:
Очевидно, что угол 
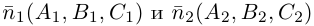
В частности,
Пример №2
Убедиться в том, что плоскость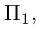
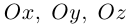
параллельны и найти расстояние между ними.
Решение. Запишем уравнение плоскости II| в отрезках:
Преобразовав его к общему виду, получим:
Так как нормальные векторы 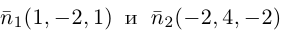
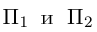
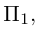
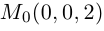
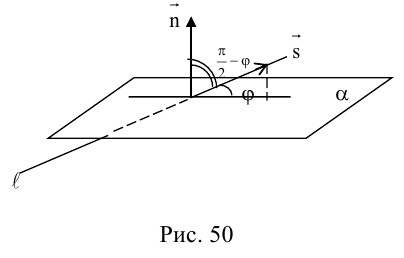
Уравнения прямой в пространстве
Пусть прямая L в пространстве с декартовой системой координат 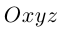
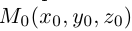
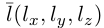
Обозначим через 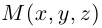
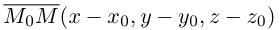
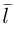
Эта двойная пропорция представляет собой канонические уравнения прямой в пространстве.
Заметим, что в канонических уравнениях прямой формально допускается запись нулей в знаменателях, это означает лишь то, что прямая перпендикулярна соответствующей координатной оси или координатной плоскости.
Если прямая проходит через две точки 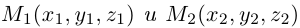
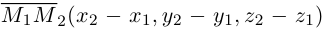
Коллинеарные векторы 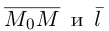
Если точка М перемещается вдоль прямой, параметр t изменяется в пределах от 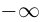
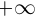
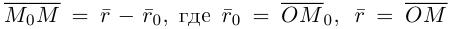
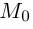
Это уравнение называется векторным уравнением прямой.
Переходя в полученном векторном уравнении к координатам, запишем параметрические уравнения прямой:
Прямую в пространстве можно задать также как пересечение двух плоскостей.
Система
составленная из уравнений этих плоскостей, дает нам общие уравнения прямой в пространстве. Для перехода от общих к каноническим уравнениям прямой, достаточно найти какую-нибудь точку на ней, решив при фиксированном значении одной из координат систему уравнений плоскостей, а также определить направляющий вектор прямой, которым может служить векторное произведение нормальных векторов 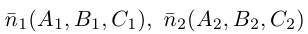
Пример №3
Найти канонические уравнения прямой
Решение. Полагая в данной системе z = 0, получим
Решив эту систему, найдем х = 1, у = —2. Таким образом, мы получили точку 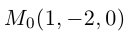
Осталось записать канонические уравнения данной прямой:
Научимся теперь вычислять расстояние от точки до прямой в пространстве. Пусть задана точка 
Искомое расстояние 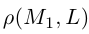
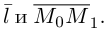
Пусть нам известны канонические уравнения двух прямых в пространстве:
Очевидно,
Один из углов между этими прямыми равен углу между их направляющими векторами 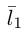
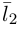
Изучим взаимное расположение прямых 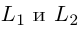
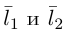
В случае, когда 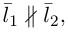
Прямые пересекаются, очевидно, тогда и только тогда, когда векторы 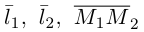
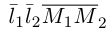
Расстояние 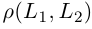
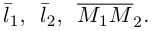
Пример №4
Убедиться в том, что прямые
являются скрещивающимися. Найти расстояние между ними и уравнение общего перпендикуляра к ним.
Решение. Первая прямая проходит через точку 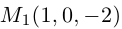
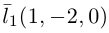
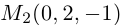
следовательно, прямые 
Осталось найти уравнение общего перпендикуляра к данным прямым. Заметим, прежде всего, что его направляющим вектором является уже вычисленный нами вектор 
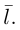
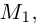
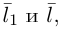
Таким образом, плоскость 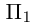
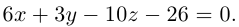
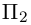
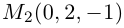
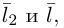
и, стало быть, 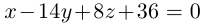
В заключение этого параграфа вычислим угол между прямой L, заданной каноническими уравнениями
и плоскостью П, для которой известно ее общее уравнение
Очевидно, искомый угол 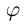
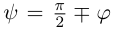
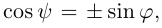
В частности, если
Прямая на плоскости
Для прямой на плоскости наблюдается большее разнообразие ее уравнений, так как на плоскости прямая фиксируется точкой, через которую она проходит и, либо вектором ей перпендикулярным (нормальным вектором), либо вектором ей параллельным (направляющим вектором) и, следовательно, для прямой на плоскости можно записывать как уравнения, характерные для плоскости в пространстве (§1), так и аналоги уравнений прямой в пространстве (§2). Перечислим, не повторяя деталей, изложенных в предыдущих двух параграфах, основные уравнения прямой на плоскости и связанные с ними формулы.
Пусть прямая L на плоскости с выбранной в ней системой координат 
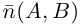
Уравнение такой прямой имеет вид:
откуда после очевидных преобразований получим уравнение
которое представляет собой общее уравнение прямой на плоскости.
Пусть прямая L отсекает на координатных осях 
Тогда, как и для плоскости, мы можем записать уравнение прямой в отрезках:
Если прямая L содержит точку 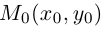
то ее каноническое уравнение имеет вид:
По аналогии с прямой в пространстве, прямая на плоскости может быть задана также векторным уравнением
и параметрическими уравнениями
Расстояние от точки 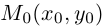
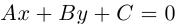
Найдем еще одно уравнение прямой на плоскости, характерное для этого геометрического объекта. Пусть прямая L, заданная своим каноническим уравнением 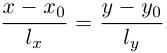
Тогда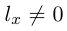
где 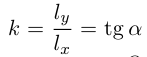
представляет собой уравнение прямой с угловым коэффициентом, которая проходит через точку
Если две прямые на плоскости заданы общими или каноническими уравнениями, то их взаимное расположение исследуется по аналогии с плоскостями или прямыми, заданными такими же уравнениями (§1 или §2). Изучим поэтому взаимное расположение двух прямых, которые заданы уравнениями с угловым коэффициентом. Итак, рассмотрим две прямые
Предположим сначала, что прямые не являются перпендикулярными, обозначим через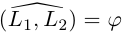
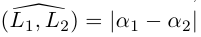
Если же
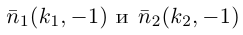
Таким образом, для перпендикулярности прямых 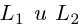
Очевидно. прямые 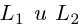
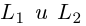
Пример №5
Даны прямая 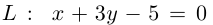
Решение. Прямые
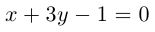
Так как 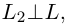
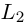
Из уравнения прямой L находим 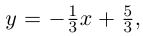
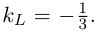
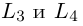
откуда, 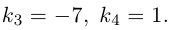
Кривые второго порядка на плоскости
В предыдущих трех параграфах нами были изучены линейные геометрические объекты -плоскость и прямая в пространстве и на плоскости. Мы показали, что в декартовой системе координат они определяются алгебраическими уравнениями первой степени, т. е. линейными уравнениями. Предметом нашего исследования в этом параграфе будут являться кривые второго порядка, т. е. линии на плоскости, уравнения которых в декартовой системе координат Оху имеют вид:
где А, В, С, D, Е, F – действительные числа. Мы убедимся в том, что, за исключением случаев вырождения данное уравнение определяет одну из трех замечательных линий — эллипс, гиперболу или параболу. Приведем сначала геометрическое определение каждой из этих линий и найдем их канонические уравнения.
Эллипс
Определение: Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух фиксированных точек (фокусов эллипса) есть величина постоянная.
Найдем каноническое уравнение эллипса. Обозначим через 2с фокусное расстояние, т. е. расстояние между фокусами, а через 2а — постоянную сумму расстояний от точек эллипса до фокусов. Из неравенства треугольника следует, что 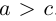
Пусть М(х, у) — произвольная точка эллипса. По определению этой линии,
Упростим последнее уравнение:
откуда, использовав обозначение 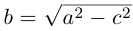
Построим эту линию. Для этого прежде всего заметим, что она симметрична относительно координатных осей и начала координат, так как переменные x и у входят в каноническое уравнение в квадратах. Отсюда следует, что эллипс достаточно построить в первой координатной четверти и затем отразить его относительно координатных осей. Из канонического уравнения эллипса находим:
Очевидно, эта функция определена и убывает при 
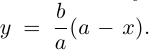
Числа а и b называются соответственно большой и малой полуосями эллипса. Точка O(0,0) -центр эллипса, точки 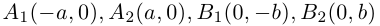
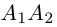
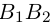
Форму эллипса характеризует величина 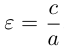
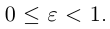
то при 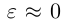
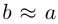
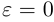
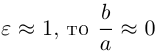
Замечание. В уравнении эллипса может оказаться, что 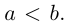
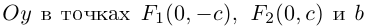
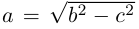
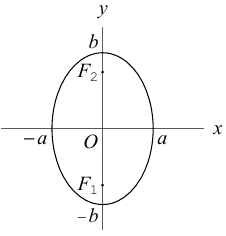
Гипербола
Определение: Гипербола представляет собой линию на плоскости, для каждой точки которой абсолютная величина разности расстояний до двух фиксированных точек (фокусов гиперболы) есть величина постоянная.
Обозначим и здесь фокусное расстояние через 2с. а через 2а — постоянную абсолютную величину разности расстояний от точек гиперболы до фокусов. Для гиперболы а < с, что следует из неравенства треугольника. Выберем декартову систему координат на плоскости точно также, как и при выводе канонического уравнения эллипса.
По определению гиперболы для произвольной точки М(х, у) этой линии
Избавляясь от корней в этом уравнении, получим:
Обозначая здесь 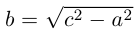
Как видно из ее уравнения, гипербола симметрична относительно координатных осей и начала координат. Из канонического уравнения гиперболы следует, что в первой четверти
Эта функция возрастает, 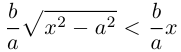
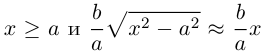
а а а а
Это означает, что в первой четверти гипербола, выходя из точки (а, 0) на оси Ох, приближается
затем при больших значениях х к прямой 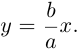
Прямые 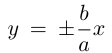
Как и для эллипса, определим эксцентриситет гиперболы как отношение половины фокусного расстояния к действительной полуоси:
Так как
то эксцентриситет гиперболы характеризует величину угла, в котором она располагается. При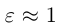
Замечание. В каноническом уравнении гиперболы знаки перед квадратами могут располагаться и в обратном порядке:
В этом случае фокусы и вершины находятся на оси
Парабола
Определение: Параболой называется множество точек плоскости, равноудаленных от. фиксированной точки (фокуса параболы) и фиксированной прямой (директрисы параболы).
Обозначим расстояние от фокуса до директрисы через р. Число р > 0 называется параметром параболы. Выберем удобную систему координат на плоскости: ось Ох направим через фокус F перпендикулярно директрисе D, а начало координат возьмем посередине между директрисой и фокусом.
Если М(х,у) – произвольная точка параболы, то по определению этой кривой
После возведения в квадрат и очевидных преобразований, получим каноническое уравнение параболы:
Очевидно, парабола проходит через начало координат и симметрична относительно оси Ох. Точка O(0,0) называется вершиной параболы, ось Ох – осью параболы.
Замечание. Если бы при выборе системы координат мы направили ее оси в противоположные стороны, то каноническое уравнение параболы приняло бы вид:
Аналогично, уравнения
также определяют параболы, фокусы которых расположены на оси Оу. а директрисы параллельны оси Ох.
Приведение уравнения кривой второго порядка к каноническому виду
Покажем, что общее уравнение кривой второго порядка на плоскости, кроме случаев вырождения, определяет одну из линий — эллипс, гиперболу или параболу.
Выясним сначала, как преобразуются координаты точки на плоскости при параллельном переносе системы координат. Предположим, что осуществлен параллельный перенос системы координат Оху в точку 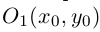
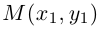
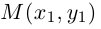
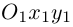
Так как 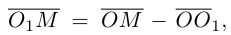
Рассмотрим теперь уравнение второго порядка на плоскости в частном случае, когда оно не содержит произведения координат ху :
причем коэффициенты А и С не равны одновременно нулю. Здесь возможны три случая.
а) АС > 0. Очевидно, всегда можно считать, тгго А > 0, С > 0. Выделяя в уравнении второго порядка полные квадраты по переменным х и у, получим:
где 
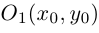
и, следовательно, в смещенной с помощью параллельного переноса в точку 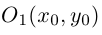
b) АС < 0. Будем считать для определенности, что А > 0. С < 0.
В этом случае исходное уравнение второго порядка также приводится к виду (1). При F = 0 оно определяет пару прямых, проходящих, через точку 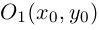
Если же 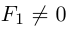
и, стало быть, после параллельного переноса системы координат в точку 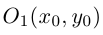
c) АС = 0. Предположим, например, что
Выделяя в данном уравнении второго порядка полный квадрат по переменной у, получим:
С {у ~ Уо)2 + Dx + F1=0.
Если в этом уравнении D = 0, то при 
Если же 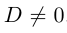
т.е. после параллельного переноса системы координат в точку 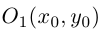
Аналогично. если в исходном уравнении второго порядка 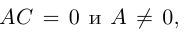
Пример №6
Привести уравнение второго порядка к каноническому виду, назвать и построить кривую:
Решение. Выделяя полные квадраты по обеим переменным, получим:
что представляет собой каноническое уравнение эллипса в смещенной в точку 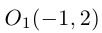
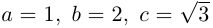
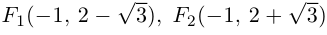
Пример №7
Найти каноническое уравнение параболы с вершиной в точке 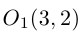
Решение. Фокус параболы находится в точке F(0 , 2), следовательно, уравнение параболы с учетом смещения имеет вид:
Здесь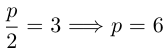
каноническое уравнение параболы.
Замечание. Для приведения к каноническому виду уравнения второго порядка, содержащего произведение координат ху, необходимо кроме параллельного переноса выполнить еще и поворот системы координат на определенный угол. Например, для равносторонней гиперболы ху = 1 следует повернуть систему координат Оху вокруг ее начала на угол 45° против часовой стрелки. Поскольку вершины гиперболы находятся на расстоянии 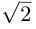
Поверхности второго порядка в пространстве
В заключение этой главы мы изучим поверхности в пространстве, которые в декартовой системе координат задаются алгебраическими уравнениями второй степени. Существуют пять видов таких поверхностей: эллипсоид, гиперболоиды, параболоиды, цилиндры второго порядка и конус второго порядка.
Поверхность вращения
Найдем уравнение поверхности, которая получается вращением некоторой линии вокруг одной из координатных осей. Пусть линия L, которая в координатной плоскости Oyz задается уравнением F(y, z) = 0. вращается вокруг оси Oz.
Пусть M(x,y,z) – произвольная точка на поверхности вращения. Перегоним ее по окружности, расположенной в сечении поверхности плоскостью, проходящей через данную точку перпендикулярно оси Oz, в точку N на линии L. Поскольку расстояние от точки М до оси Oz равно 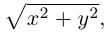
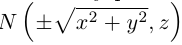
Найдем теперь уравнения поверхностей, которые получаются вращением кривых второго порядка с последующей линейной деформацией этих поверхностей.
Эллипсоид
Возьмем в плоскости Oyz эллипс
и будем вращать его вокруг оси Oz. В результате, как следует из предыдущего пункта, мы получим поверхность с уравнением
которая называется эллипсоидом вращения. Заменив в найденном уравнении координату х на —
Положительные числа а, b, с называются полуосями эллипсоида.
Очевидно, сечениями эллипсоида плоскостями параллельными координатным, являются эллипсы.
Замечание. В частном случае, когда а = b = с = R эллипсоид превращается в сферу
радиуса R с центром в начале координат.
Гиперболоиды
а) Однополостный гиперболоид.
Вращая гиперболу
вокруг оси Oz, получим однополостный гиперболоид вращения с уравнением
После линейной деформации вдоль оси Ох эта поверхность превращается в однополостный гиперболоид общего вида с осью Oz :
Аналогично, уравнения однополостных гиперболоидов с осями Ох и Оу имеют, соответственно, вид:
Сечениями однополостного гиперболоида плоскостями, перпендикулярными его оси, являются эллипсы, а в сечениях плоскостями, перпендикулярными другим координатным осям, располагаются гиперболы.
Двухполостный гиперболоид
Поверхность, полученная вращением вокруг оси Оz гиперболы
вершины которой расположены на оси вращения, называется двухполостным гиперболоидом вращения. Запишем уравнение двухполостного гиперболоида:
Линейная деформация двухполостного гиперболоида вращения вдоль оси Ох прообразует его в двухполостный гиперболоид общего вида с осью Oz. Уравнение этой поверхности имеет вид:
Двухполостные гиперболоиды с осями Ох и Оу имеют, соответственно, уравнения:
Как и в случае однополостного гиперболоида, сечениями двухполостного гиперболоида плоскостями, параллельными координатным, являются эллипсы и гиперболы.
Параболоиды
а) Эллиптический параболоид
Вращение параболы вокруг ее оси приводит к поверхности, которая называется параболоидом вращения. В частности, если параболу с каноническим уравнением 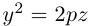
Линейная деформация параболоида вращения вдоль оси Оу превращает его в эллиптический параболоид с уравнением:
Положительные числа p, q называются параметрами параболоида, точка O(0,0) – вершина, ось Oz – ось эллиптического параболоида.
Уравнения эллиптических параболоидов с осями Ох и Оу имеют, соответственно, вид:
Как следует из уравнения эллиптического параболоида, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, а в сечениях плоскостями, параллельными другим координатным, находятся параболы.
Замечание. Изменение знака в правой части уравнения эллиптического параболоида приводит к отражению этой поверхности относительно координатной плоскости, перпендикулярной оси параболоида.
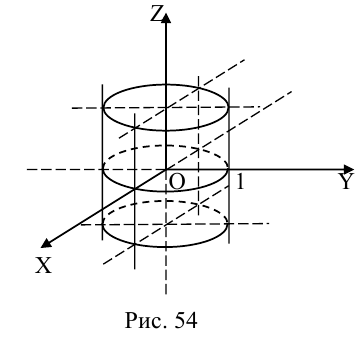
b) Гиперболический параболоид.
Будем поступательно перемещать образующую параболу
расположенную в плоскости Oyz, параллельно самой себе вдоль направляющей параболы
находящейся в плоскости Oxz. Полученная таким образом поверхность называется гиперболическим параболоидом или седловидной поверхностью.
Найдем уравнение этой поверхности. Пусть М(х. у, z) – произвольная точка гиперболического параболоида. По его построению точка М принадлежит параболе с вершиной в точке 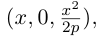
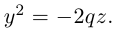
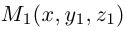
то, подставив в него координаты точки М, мы и получим после несложных преобразований уравнение гиперболического параболоида:
Здесь, как и для эллиптического параболоида, числа р, q – параметры гиперболического параболоида, точка O(0,0) и ось Oz – соответственно вершина и ось гиперболического параболоида.
Замечание 1. Седловидная поверхность может быть также получена перемещением параболы 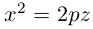
Судя по уравнению гиперболического параболоида, в сечениях этой поверхности плоскостями z = h > 0 находятся гиперболы, действительные оси которых параллельны координатной оси Ох. Аналогично, плоскости z = h < 0 пересекают данную поверхность по гиперболам с действительными осями, параллельными оси Оу. Наконец, плоскость Оху пересекает гиперболический параболоид по двум прямым
Гиперболические параболоиды, осями которых служат координатные оси Ох и Оу, имеют, соответственно, уравнения:
Замечание 2. Отразив седловидную поверхность относительно координатной плоскости, перпендикулярной ее оси, получим гиперболический параболоид, уравнение которого отличается знаком правой части от уравнения исходной поверхности.
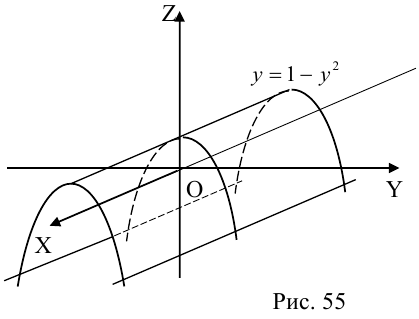
Цилиндры второго порядка
Цилиндром второго порядка называется поверхность, полученная перемещением некоторой прямой (образующей) вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей образующую, параллельно фиксированному ненулевому вектору в пространстве.
Ограничимся случаем, когда направляющая расположена в одной из координатных плоскостей, а образующая перпендикулярна этой плоскости. Возьмем для определенности в плоскости Оху кривую второго порядка и будем перемещать прямую, параллельную оси Oz, вдоль этой кривой. Так как проекцией любой точки M(x,y,z) полученного таким образом цилиндра на плоскость Оху является точка N(x,y), принадлежащая кривой второго порядка, то координаты точки М удовлетворяют уравнению этой кривой. Следовательно, уравнением построенного цилиндра является уравнение его направляющей.
Перечислим теперь цилиндры второго порядка.
1) 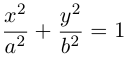
В частности, при а = b мы получим круговой цилиндр.
2 2 X у
2) 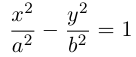
3) 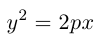
Аналогичные уравнения имеют цилиндры второго порядка, образующие которых параллельны осям Ох и Оу, а направляющие расположены в координатных плоскостях Oyz и Oxz, соответственно.
Конус второго порядка
Конус второго порядка представляет собой поверхность, которая может быть получена перемещением прямой (образующей), имеющей неподвижную точку, которая называется вершиной конуса, вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей вершину.
Найдем уравнение конуса, вершина которого совпадает с началом координат, а направляющей служит эллипс с уравнением
расположенный в плоскости z = с, с > 0.
Пусть M(x,y,z) – произвольная точка конуса. Обозначим через 
а точки M – уравнениям
Из последних уравнений мы находим:
Подставив найденные выражения для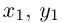
Координатная ось Oz называется осью конуса. Если а = b, то конус является круговым.
Конусы второго порядка с осями Ох и Оу имеют, соответственно, уравнения:
Покажем, что вид конуса второго порядка не зависит от выбора направляющей. Действительно, если в качестве направляющей взять гиперболу
находящегося в плоскости 2 = с, то после рассуждений, аналогичных предыдущим, получим поверхность с уравнением
т. е. конус с осью Ох. Если же за направляющую мы выберем в плоскости z = с параболу с уравнением
то построенный таким образом конус имеет уравнение
Наблюдая со стороны положительной полуоси Оу, повернем систему координат Oxz вокруг оси Оу на угол 45° против часовой стрелки. Тогда произведение xz в системе координат
запишется как 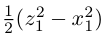
и, стало быть, эта поверхность является конусом с осью
Как следует из уравнения конуса и его построения, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, сечениями конуса плоскостями, параллельными его оси, являются гиперболы, и, наконец, в сечениях конуса плоскостями, параллельными образующей, располагаются параболы.
Приведение уравнения поверхности второго порядка к каноническому виду
По аналогии с уравнением кривой второго порядка (§4, пункт 4), уравнение поверхности второго порядка, не содержащее произведений координат, мы можем за счет выделения полных квадратов привести к уравнению одной из рассмотренных в пунктах 1—5 поверхностей. Следовательно, мы получим одну из поверхностей второго порядка в смещенной с помощью параллельного переноса системе координат. Исключение, правда, составляет случай, когда уравнение поверхности содержит полный квадрат и два линейных слагаемых относительно других координат. Такая поверхность представляет собой параболический цилиндр в смещенной с помощью параллельного переноса и повернутой затем вокруг одной из координатных осей системе координат.
Пример №8
Привести уравнение второго порядка
к каноническому виду, назвать и построить поверхность.
Решение. После выделения полных квадратов по переменным у, z получим:
Переписав это уравнение в виде
мы замечаем, что в смещенной с помощью параллельного переноса в точку 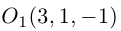
Прямая на плоскости. Общее уравнение прямой на плоскости
Докажем, что всякая прямая на плоскости задается в любой пдск уравнением первой степени относительно двух переменных.
Если A – некоторая точка на прямой 
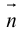
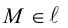
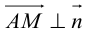
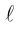
Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY .
В этой системе координат
Пусть M (x, y) – произвольная точка
на 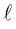
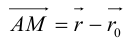
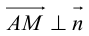
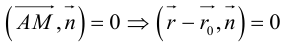
Координаты точек, лежащих на прямой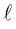
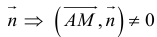
Определение: Любой ненулевой вектор 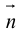
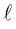
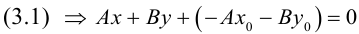
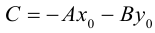
(3.2) – общее уравнение прямой на плоскости,
Уравнение прямой с направляющим вектором
Определение: Любой ненулевой вектор 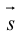
Если A – некоторая точка на прямой 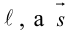
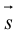
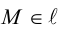
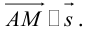
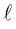
Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY . В этой системе координат
Пусть M (x, y) – произвольная точка на . Тогда 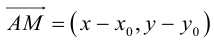
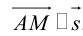
(3.3) – уравнение прямой на плоскости с направляющим вектором.
Если 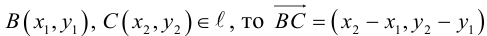
Уравнение прямой с угловым коэффициентом
Пусть 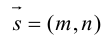
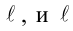
Определение: Угловым коэффициентом прямой 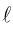
Очевидно, что если 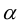
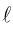
Рассмотрим уравнение (3.3) прямой с направляющим вектором
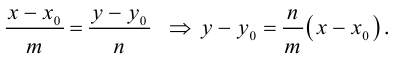
Отсюда следует (3.5) – уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку
Из (3.5) получим 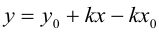
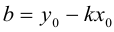
(3.6) – уравнение прямой с угловым коэффициентом.
Угол между прямыми на плоскости
Определение: Углом между двумя прямыми на плоскости называется любой из двух смежных углов, образованных ими при пересечении. Если прямые параллельны, то угол между ними равен 0 или
Пусть прямые заданы общими уравнениями.
Условие параллельности прямых:
Условие перпендикулярности прямых:
Рассмотрим случай, когда прямые заданы уравнениями с угловым коэффициентом.
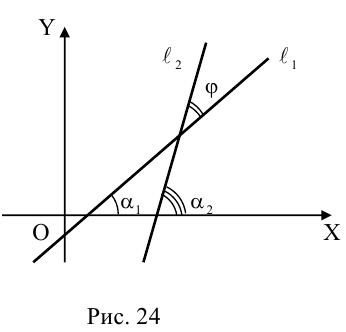
Так как 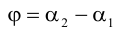
Условие параллельности прямых:
Условие перпендикулярности:
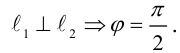
не существует, то
Пример №9
Даны вершины треугольника:
Написать:
а) уравнение медианы AM , б) высоты AH , в) найти угол между AM и AH
(рис. 25).

Перепишем уравнение медианы в общем виде:
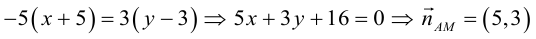
б)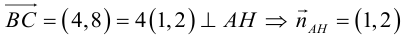
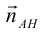
в)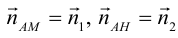
Расстояние от точки до прямой на плоскости
Пусть в некоторой пдск XOY задана прямая 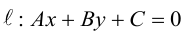
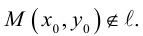
Пусть 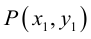
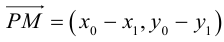
Нормаль
где d – искомое расстояние, 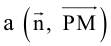
Следовательно,
Так как 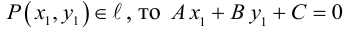
Отсюда
(3.8) – формула для вычисления расстояния от точки до прямой на плоскости.
Пример №10
Найти длину высоты
Уравнение 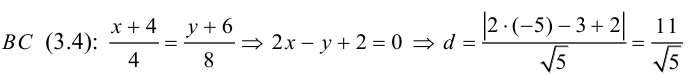
искомая длина высоты АН.
Кривые второго порядка
Окружность
Определение: Кривые второго порядка – плоские линии, которые в пдск XOY задаются уравнениями второй степени относительно двух переменных x,y.
Определение: Окружностью называется совокупность точек плоскости, равноудаленных от фиксированной точки, называемой ее центром.
Выведем уравнение окружности. Зададим пдск XOY . Пусть 
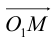
Если точка M (x, y) не лежит на окружности, то 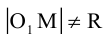
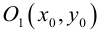
Если 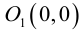
(3.10) – каноническое уравнение окружности.
Пример №11
Показать, что уравнение 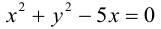
Приведем данное уравнение к виду (3.9), выделив полный квадрат по переменной x :
Пример №12
Написать уравнение линии центров окружностей
Найдем центр второй окружности:
Уравнение прямой (3.4), проходящей через две точки:
Эллипс
Определение: Эллипс – совокупность точек плоскости, сумма расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Чтобы вывести уравнение эллипса, выберем пдск следующим образом: ось абсцисс проведем через фокусы 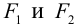
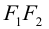
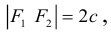
2a>2c определению эллипса.
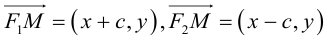
Запишем в виде уравнения свойство точек, принадлежащих эллипсу, сформулированное в определении:
(3.11) – уравнение эллипса в выбранной системе координат. Преобразуем его к
более простому (каноническому) виду. Для этого умножим (3.11) на сопряженное выражение:
Сложим (3.11) и (3.12) и результат возведем в квадрат:
Так как по определению a>c, то есть 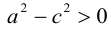
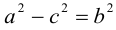
Тогда из (3.13) получим:
(3.14) – каноническое уравнение эллипса.
Исследуем форму эллипса по его каноническому уравнению. Найдем точки пересечения с осями координат:
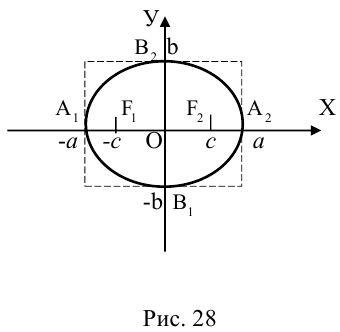
Из (3.14) следует, что
Значит, эллипс расположен в прямоугольнике со сторонами 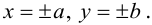
Кроме того, из уравнения следует, что он симметричен относительно OX и OY . O(0,0) – точка пересечения осей симметрии – центр симметрии эллипса.
Ось, на которой лежат фокусы, называется фокальной осью эллипса. Точки пересечения эллипса с осями симметрии называются его вершинами.
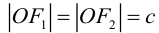
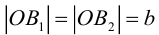
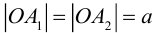
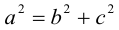
Отношение полуфокусного расстояния к длине большой полуоси 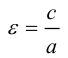
Так как 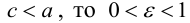
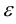
ЗАМЕЧАНИЕ 1. Уравнение эллипса, центр которого 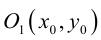
ЗАМЕЧАНИЕ 2. К кривым второго порядка эллиптического типа относятся также мнимый эллипс
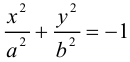
Пример №13
Найти эксцентриситет эллипса 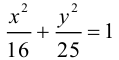
Так как 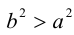
Гипербола
Определение: Гипербола – совокупность точек плоскости, модуль разности расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
Чтобы вывести уравнение гиперболы, выберем пдск следующим образом:
ось абсцисс проведем через фокусы 
ка 
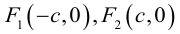
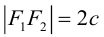
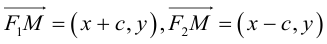
Запишем свойство точек, принадлежащих гиперболе, сформулированное в определении:
(3.16) – уравнение гиперболы в выбранной системе координат ( «+» – если разность расстояний положительна, и «–» – если отрицательна). Чтобы привести это уравнение к более простому виду, умножим (3.16) на сопряженное выражение и выполним такие же действия, как при упрощении уравнения эллипса, после чего получим:
По определению 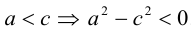
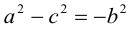
(3.18) – каноническое уравнение гиперболы.
Исследуем форму гиперболы по ее каноническому уравнению.
Из (3.18) следует, что гипербола симметрична относительно осей координат. Если x=0, 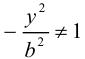
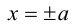
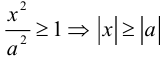
c – полуфокусное расстояние, a – действительная полуось, b – мнимая полуось. Отношение полуфокусного расстояния к длине действительной полуоси называется эксцентриситетом гиперболы: 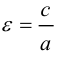
Считая, что 
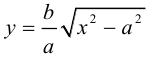
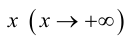
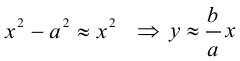
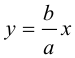
причем ординаты точек на ней меньше соответствующих ординат точек на этой
прямой: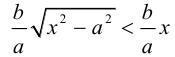
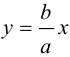
Из симметрии гиперболы следует, что то же самое происходит во второй, третьей и четвертой четвертях. Поэтому 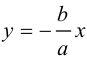
Итак, прямые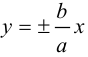
Если фокусы гиперболы лежат на OY , то ее уравнение имеет вид:
Гиперболы (3.18) и (3.19) называются сопряженными (рис. 31). Уравнения асимптот (3.19) такие же, как и для (3.18), но действительной является ось OY .
Если a = b, то гипербола называется равносторонней: 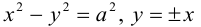
Очевидно, в этом случае асимптоты перпендикулярны. После поворота осей координат на 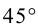
ЗАМЕЧАНИЕ 1. Если центр гиперболы в точке 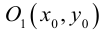
ЗАМЕЧАНИЕ 2. К кривым второго порядка гиперболического типа относится также пара пересекающихся прямых:
Пример №14
Найти координаты центра и написать уравнения асимптот гиперболы
Приведем данное уравнение к виду (3.20):
Таким образом, 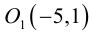
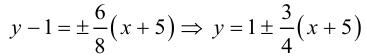
Парабола
Определение: Парабола – совокупность точек плоскости, равноудаленных от фиксированной точки этой плоскости, называемой фокусом, и фиксированной прямой, не проходящей через эту точку, называемой директрисой. Чтобы вывести уравнение параболы, выберем пдск следующим образом: ось абсцисс проведем через фокус перпендикулярно директрисе, а ось ординат посередине между фокусом и директрисой (рис. 33).
Пусть расстояние между фокусом F и директрисой DK равно p . Тогда 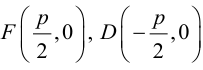
(3.21) – уравнение параболы в выбранной системе координат.
Упростим его:
(3.22) – каноническое уравнение параболы; p называется ее параметром.
Из уравнения следует, что парабола симметрична относительно OX и проходит через начало координат. Кроме того, если 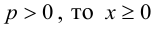
Если фокус параболы на оси ОУ (рис. 35), то ее каноническое уравнение имеет вид
ЗАМЕЧАНИЕ 1. Если вершина параболы в точке 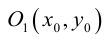
ЗАМЕЧАНИЕ 2. К кривым второго порядка параболического типа относятся также 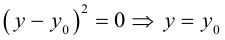
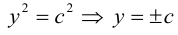
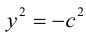
Пример №15
Написать уравнение геометрического места точек, равноудаленных от прямой x + y – 1 = 0 и точки F(-3,2).
По определению множество точек, равноудаленных от данных точки и прямой, является параболой. Пусть M (x, y) – произвольная точка искомой параболы, тогда 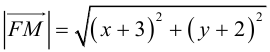
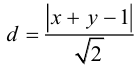
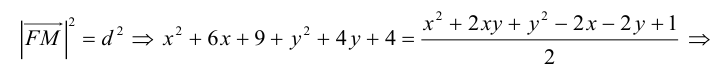
Если оси координат системы XOY повернуть на угол 
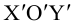
ЗАМЕЧАНИЕ. Можно показать, что, кроме окружности, эллипса, гиперболы, параболы и вырожденных случаев, указанных в замечаниях, других кривых второго порядка не существует.
Преобразования координат на плоскости
Преобразование координат — замена системы координат на плоскости, в пространстве или, в самом общем случае, на заданном n-мерном многообразии.
Параллельный перенос координатных осей
Пусть на плоскости задана пдск ХОУ. Будем называть ее “старой”. “Новая” система координат 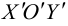
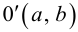
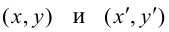
Пусть 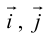
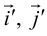
Тогда
так как 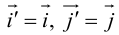
Так как 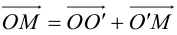
или
(3.23) – формулы параллельного переноса осей пдск.
Поворот координатных осей на угол α
Поворот координатных осей на угол 
Пусть “новая” пдск 
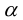
Из рис. 38 очевидно, что
Так как 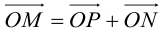
(3.24) – формулы поворота координатных осей на угол , выражающие старые координаты точки через новые.
Если обозначить 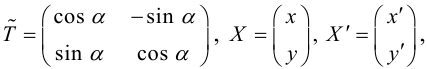
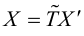
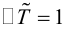
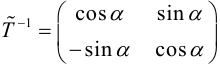
(3.25) – формулы поворота координатных осей на угол 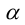
Пример №16
Каким будет уравнение прямой x + y – 1 = 0 после поворота координатных осей на угол
новое уравнение прямой (рис. 39).
Линейные преобразования на плоскости
Рассмотрим систему линейных уравнений:
Каждой точке плоскости M(x, y) по формулам (3.26) можно поставить в соответствие единственную точку 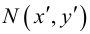
Преобразование (3.26) определяется матрицей 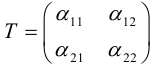
(3.26) можно переписать в виде 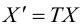
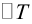
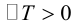
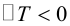
Пример №17
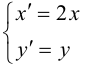
оси OX в 2 раза.
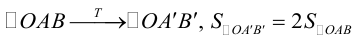
Пример №18
при этом направление обхода 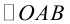
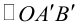
Определение: Линейное преобразование (3.26) называется невырожденным, если
В этом случае существует обратная матрица 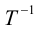
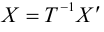
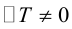
Можно показать, что невырожденное линейное преобразование переводит прямую в прямую, а кривую второго порядка – в кривую второго порядка.
Пример №19
Пусть 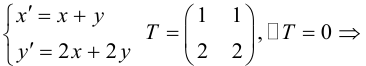
Какими будут образы точек, лежащих, например, на прямой x + y – 1 = 0
(рис. 42)?
Очевидно, что если 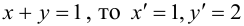
Пример №20
Рассмотрим формулы (3.25):
Очевидно, что поворот осей пдск на угол 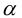
Так как это линейное преобразование невырожденное, то существует
Заметим, что в этом случае
Определение: Матрица A называется ортогональной, если 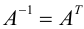
Линейное преобразование, матрица которого ортогональна, называется ортогональным.
Таким образом, поворот координатных осей – ортогональное линейное преобразование.
Можно показать, что если A – ортогональная матрица, то 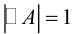
Произведение линейных преобразований
Рассмотрим матрицы 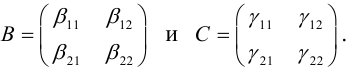
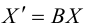
В свою очередь точка N под действием линейного преобразования 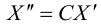
Такое последовательное выполнение линейных преобразований называется их произведением:
Покажем, что произведение линейных преобразований также линейное преобразование, и найдем его матрицу. Подставим (3.27) в (3.28):
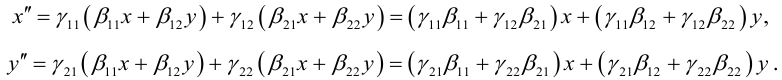
То есть
(3.29) – система линейных уравнений, а потому произведение линейных преобразований линейно. Матрица (3.29) имеет вид:
Таким образом, матрица произведения линейных преобразований равна произведению их матриц. Само же правило умножения матриц, сформулированное в гл.1, находит объяснение в этом выводе.
Приведение квадратичной формы к каноническому виду
Определение: Квадратичной формой относительно двух переменных x и y называется однородный многочлен второй степени:
Уравнение 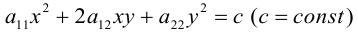
начала координат, то есть является центральной кривой (эллиптического или гиперболического типа).
Предположим, что уравнение 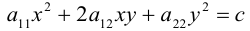
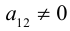
угол 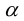
Матрица 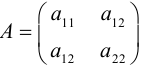
Пусть
Вычислим
Таким образом, квадратичная форма может быть записана в матричном виде:
Пусть x, y – координаты точек плоскости в системе XOY , а 
(3.32) – ортогональное линейное преобразование с матрицей
По определению ортогональной матрицы
(В результате ортогонального преобразования не происходит изменение площадей фигур, то есть фигуры не деформируются.)
Чтобы узнать, как изменится матрица квадратичной формы в результате линейного преобразования (3.32), подставим (3.32) в (3.31): 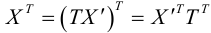
(свойство 2 умножения матриц и равенство (3.33)) – матрица новой квадратичной формы.
Так как в “новой” системе координат кривая должна задаваться каноническим уравнением, то есть в нем должно отсутствовать произведение координат xy, то 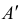
, где 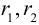
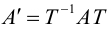
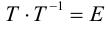
По определению равных матриц имеем:
Системы уравнений (3.34), (3.35) – линейные и однородные. Они имеют нетривиальное решение, если их определители равны 0.
Это означает, что 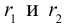
Уравнение (3.36) называется характеристическим уравнением матрицы A (характеристическим уравнением квадратичной формы). Его решения 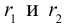
Покажем, что дискриминант квадратного уравнения (3.36) положителен, то есть любая квадратичная форма двух переменных имеет 2 различных собственных значения.
Вычислим определитель (3.36):
Дискриминант
так как 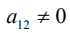
Таким образом, коэффициентами при 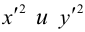
Решим (3.36) и подставим 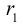
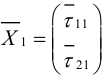
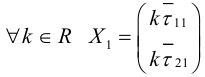
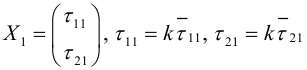
Векторы 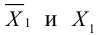
Аналогично подставим 
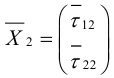
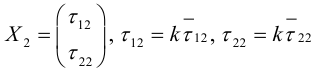
Можно показать, что 
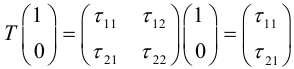
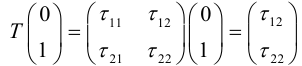
вектор, поэтому ортами “новой” системы координат 
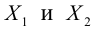
ВЫВОД.
Чтобы привести квадратичную форму к каноническому виду, надо:
- Составить и решить характеристическое уравнение (3.36); его решения – собственные значения – являются коэффициентами при
в каноническом виде квадратичной формы.
- Найти единичные собственные векторы, решив (3.34) и (3.35); они будут ортами новой системы координат
.При этом если ось
сонаправлена с
– канонический вид, который квадратичная форма имеет в системе
.
Приведение общего уравнения кривой второго порядка к каноническому виду
Общее уравнение кривой второго порядка имеет вид:
В результате невырожденного линейного преобразования с матрицей T квадратичная форма перейдет в квадратичную форму, линейная – в линейную, а свободный член 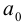
После поворота осей подберем параллельный перенос новой системы 
Пример №21
Привести к каноническому виду ранее полученное уравнение параболы (стр. 58) и построить ее:
1) Составим матрицу квадратичной формы:
2) Составим и решим характеристическое уравнение (3.36):
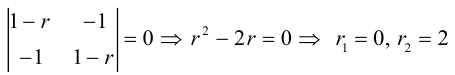
3) Найдем первый единичный собственный вектор, то есть решим систему (3.34):
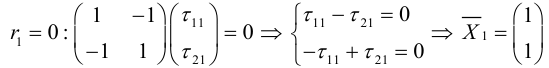
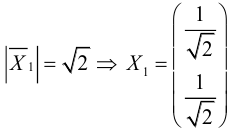
4) Найдем второй единичный собственный вектор, то есть решим (3.35):
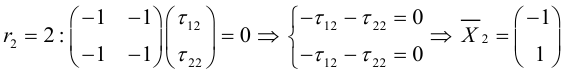
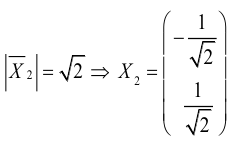
Заметим, что 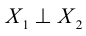
В полученной таким образом системе координат 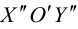
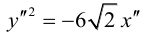
Сравните эскиз (рис. 36) и данный рисунок, являющийся результатом точных расчетов.
Плоскость
Покажем, что плоскость в пространстве задается в любой пдск линейным уравнением относительно трех переменных x, y, z.
Если A – некоторая точка на плоскости 
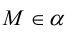
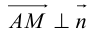
Чтобы вывести уравнение плоскости, зададим в пространстве пдск OXYZ . В этой системе координат
Пусть M(x,y,z) – произвольная точка на плоскости 
Тогда 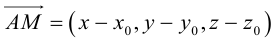
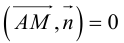
Вычислив скалярное произведение, получим:
Координаты точек, лежащих в плоскости 
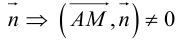
Раскрыв скобки в (3.38), получим 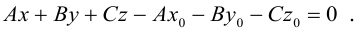
Обозначим 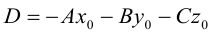
(3.39) – общее уравнение плоскости в пространстве,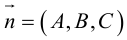
Определение: Любой ненулевой вектор 
Особые случаи расположения плоскости
Выясним, какие особенности в расположении плоскости влечет за собой равенство нулю одного или нескольких коэффициентов в уравнении (3.39).
координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.
, так как
, значит, плоскость
.
, так как
.Значит, плоскость
.
так как
. Значит, плоскость
.
проходит через OX .
проходит через OY .
проходит через OZ .
-
или
.
или
.
-
или
.
– плоскость YOZ .
– плоскость XOZ .
– плоскость XOY .
Уравнение плоскости в отрезках
Пусть плоскость 
Рассмотрим 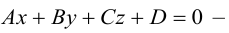
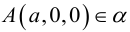
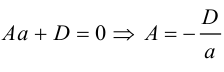
Аналогично 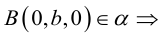
Подставив А, В, С в общее уравнение, получим
(3.40) – уравнение плоскости в отрезках.
Пример №22
Вычислить объем тетраэдра, образованного плоскостями
Перепишем уравнение плоскости в виде (3.40):
уравнение данной плоскости в отрезках. Поэтому (рис. 47)
Уравнение плоскости, проходящей через три точки
Пусть в некоторой пдск заданы три точки, не лежащие на одной прямой:
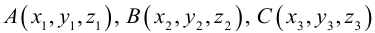
Чтобы вывести ее уравнение, рассмотрим произвольную точку этой плоскости M(x,y,z) . Тогда 
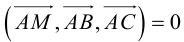
(3.41) – уравнение плоскости, проходящей через три точки.
ЗАМЕЧАНИЕ. Если точки лежат на одной прямой, то векторы 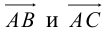
Пример №23
Написать уравнение плоскости, проходящей через точки
Угол между плоскостями
Определение: Углом между плоскостями называется любой из двух смежных двугранных углов, образованных плоскостями при их пересечении.
Если плоскости параллельны, то угол между ними равен 0 или 
Рассмотрим плоскости 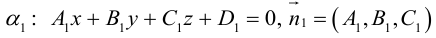
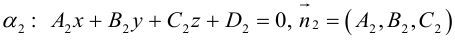
Очевидно,
или
Если 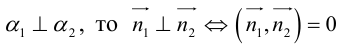
Если 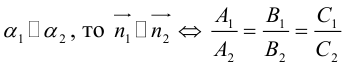
Пример №24
Найти угол между плоскостями
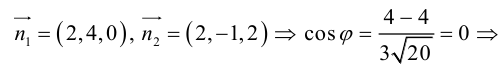
Прямая линия в пространстве
Всякая линия в пространстве есть результат пересечения двух поверхностей. В частности прямую линию можно рассматривать как результат пересечения двух плоскостей
и
Если 
определяет прямую линию в пространстве.
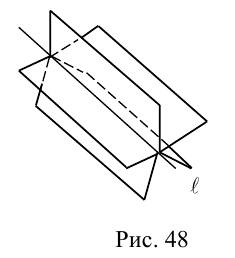
Уравнения (3.42) называются общими уравнениями прямой в пространстве.
Очевидно, одна и та же прямая может быть результатом пересечения разных пар плоскостей (рис. 48), поэтому прямую в пространстве можно задать различными способами.
Уравнения (3.42) неудобны в использовании, так как не дают представления о расположении прямой относительно выбранной системы координат.
Поэтому выведем более удобные уравнения, эквивалентные (3.42), то есть из бесконечного множества плоскостей, проходящих через данную прямую, выберем в некотором смысле более заметную пару.
Канонические уравнения прямой в пространстве
Пусть в некоторой пдск задана прямая 
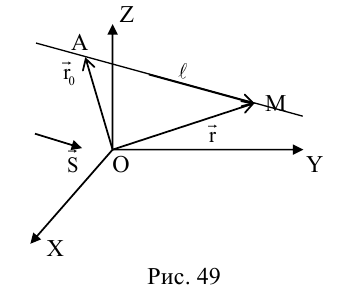
Для произвольной точки 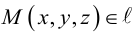
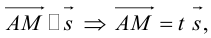
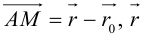
(рис. 49).
Отсюда 
(3.43) – векторное уравнение прямой в пространстве. Из (3.43) получаем:
(3.44) – параметрические уравнения прямой в пространстве, 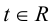
Выразим из каждого уравнения (3.44) параметр:
Тогда
(3.45) – канонические уравнения прямой в пространстве, то есть уравнения прямой, проходящей через точку 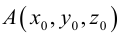
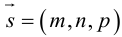
Заметим, что уравнения (3.45) задают прямую как результат пересечения плоскостей
одна из которых параллельна OZ , а вторая – OY или как
где первая плоскость параллельна OZ , а вторая – OX .
Если прямая 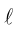
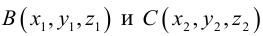
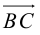
(3.46) – уравнения пространственной прямой, проходящей через две заданные точки.
Угол между прямыми в пространстве
Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:
и
Определение: Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.
Из определения следует, что 
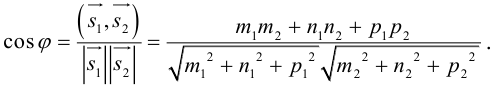
1)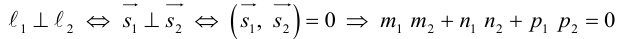
2)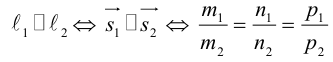
Пример №25
Найти угол между прямой 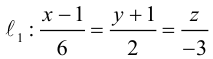
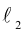
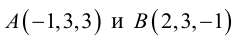
Заметим, что уравнение прямой 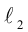
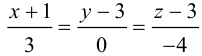
Приведение общих уравнений прямой в пространстве к каноническому виду
Рассмотрим прямую 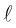
Привести эти уравнения к каноническому виду можно двумя способами:
- найти координаты какой-либо точки
, лежащей на
, ее направляющий вектор s и написать уравнения (3.45);
- найти координаты двух точек, лежащих на
, и воспользоваться уравнениями (3.46).
1 способ.
Координаты точки A – любое частное решение системы линейных уравнений (3.42). Эта система имеет бесконечное множество решений, так как ранги основной и расширенной матриц 
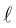
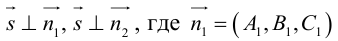
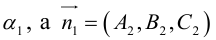
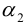
Пример №26
Привести уравнения прямой 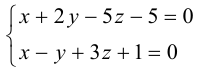
Найдем какое-нибудь частное решение этой системы: пусть, например,
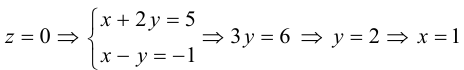
Таким образом, 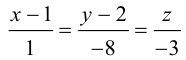
2 способ.
Найдем два произвольных частных решения системы уравнений, задающей прямую.
В рассмотренном примере 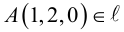
тогда 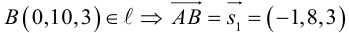
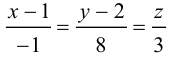
Угол между прямой и плоскостью
Определение: Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Пусть в некоторой пдск заданы плоскость
и прямая
Определение общих точек прямой и плоскости
Чтобы найти общие точки прямой : 
Решение этой системы будет наименее трудоемким, если перейти к параметрическим уравнениям прямой (3.44):
1) Пусть 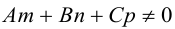
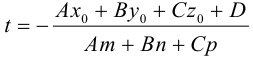
и по формулам (3.44) M(x,y,z) – их точку пересечения.
2) Пусть 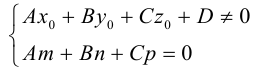
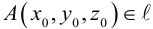
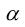
3) Пусть 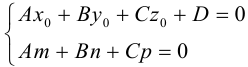
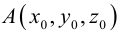
Пример №27
Найти проекцию точки 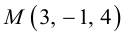
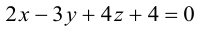
Пусть прямая 
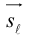
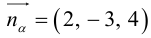
Напишем канонические уравнения прямой (3.45):
Цилиндрические поверхности
Уравнение F(x, y, z)=0 задает в пространстве некоторую поверхность.
Пусть уравнение содержит только две переменные, например, F(x,y)=0.Рассмотренное в плоскости XOY , оно задает некоторую кривую. Но ему будут удовлетворять и все точки пространства, которые проецируются в точки этой кривой, так как в уравнении отсутствует z , то есть все точки M(x,y,z) у которых х и у связаны соотношением 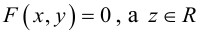
Пример №28
Построить поверхность 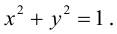
На плоскости это уравнение задает окружность с центром О(0, 0) и R=1.
В пространстве ему удовлетворяют координаты всех точек, проекция которых на плоскость ХОУ лежит на этой окружности. Очевидно, что эта поверхность – круговой цилиндр
(рис. 54).
Цилиндрические поверхности бывают не только круговыми.
Определение: Цилиндрической называется поверхность, полученная движением прямой, параллельной некоторому вектору, и пересекающей при движении некоторую кривую. При этом движущаяся прямая называется образующей, а кривая, которую она пересекает, называется направляющей цилиндрической поверхности.
Для поверхности 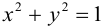
ВЫВОД. Если уравнение поверхности содержит только две переменные, то оно задает цилиндрическую поверхность. У поверхности F(y,z) ,образующая параллельна OX , а направляющая лежит в плоскости YOZ . Для поверхности F(x,z) ,образующая параллельна OY , направляющая в плоскости XOZ .
Пример №29
Построить и назвать поверхности 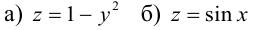
Поверхности вращения
Определение: Поверхностью вращения называется поверхность, полученная в результате вращения плоской кривой вокруг оси, лежащей в ее
плоскости.
Из определения следует, что сечением такой поверхности любой плоскостью, перпендикулярной оси вращения, является окружность.
Пусть в плоскости YOZ задана кривая 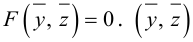
Пусть M(x,y,z) – произвольная точка на поверхности, 
Тогда 
Но
Таким образом, уравнение поверхности вращения получим, если в уравнении кривой 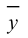
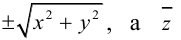
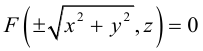
Очевидно, что если кривая F(y,z)=0 вращается вокруг OY , то уравнение
поверхности вращения имеет вид:
Некоторые поверхности второго порядка
1. Пусть эллипс 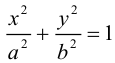
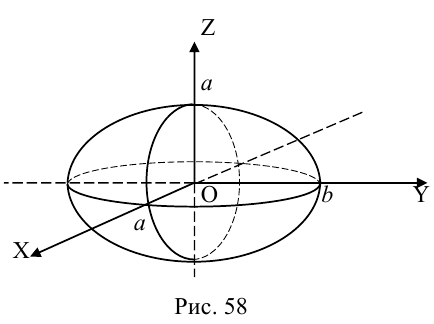
Полученная поверхность является поверхностью второго порядка, так ее уравнение 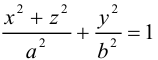
Поверхность, задаваемая уравнением 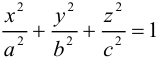
2. Если гипербола 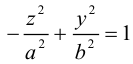
поверхности вращения имеет вид
или
Такая поверхность называется однополостным гиперболоидом вращения (рис. 59).
3. Если гипербола 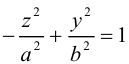
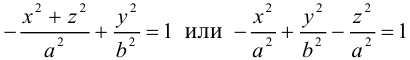
4. Если пара пересекающихся прямых 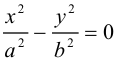
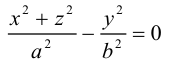
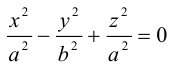
5. При вращении параболы 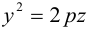
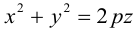
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Векторная алгебра
- Геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
From Wikipedia, the free encyclopedia
In mathematics and classical mechanics, canonical coordinates are sets of coordinates on phase space which can be used to describe a physical system at any given point in time. Canonical coordinates are used in the Hamiltonian formulation of classical mechanics. A closely related concept also appears in quantum mechanics; see the Stone–von Neumann theorem and canonical commutation relations for details.
As Hamiltonian mechanics are generalized by symplectic geometry and canonical transformations are generalized by contact transformations, so the 19th century definition of canonical coordinates in classical mechanics may be generalized to a more abstract 20th century definition of coordinates on the cotangent bundle of a manifold (the mathematical notion of phase space).
Definition in classical mechanics[edit]
In classical mechanics, canonical coordinates are coordinates 

A typical example of canonical coordinates is for 


Canonical coordinates can be obtained from the generalized coordinates of the Lagrangian formalism by a Legendre transformation, or from another set of canonical coordinates by a canonical transformation.
Definition on cotangent bundles[edit]
Canonical coordinates are defined as a special set of coordinates on the cotangent bundle of a manifold. They are usually written as a set of 

A common definition of canonical coordinates is any set of coordinates on the cotangent bundle that allow the canonical one-form to be written in the form
up to a total differential. A change of coordinates that preserves this form is a canonical transformation; these are a special case of a symplectomorphism, which are essentially a change of coordinates on a symplectic manifold.
In the following exposition, we assume that the manifolds are real manifolds, so that cotangent vectors acting on tangent vectors produce real numbers.
Formal development[edit]
Given a manifold Q, a vector field X on Q (a section of the tangent bundle TQ) can be thought of as a function acting on the cotangent bundle, by the duality between the tangent and cotangent spaces. That is, define a function
such that
holds for all cotangent vectors p in 



In local coordinates, the vector field X at point q may be written as
where the 
where the 

The 


Generalized coordinates[edit]
In Lagrangian mechanics, a different set of coordinates are used, called the generalized coordinates. These are commonly denoted as 


See also[edit]
- Linear discriminant analysis
- Symplectic manifold
- Symplectic vector field
- Symplectomorphism
- Kinetic momentum
- Complementarity (physics)
- Canonical quantization
- Canonical quantum gravity
References[edit]
- Goldstein, Herbert; Poole, Charles P., Jr.; Safko, John L. (2002). Classical Mechanics (3rd ed.). San Francisco: Addison Wesley. pp. 347–349. ISBN 0-201-65702-3.
- Ralph Abraham and Jerrold E. Marsden, Foundations of Mechanics, (1978) Benjamin-Cummings, London ISBN 0-8053-0102-X See section 3.2.
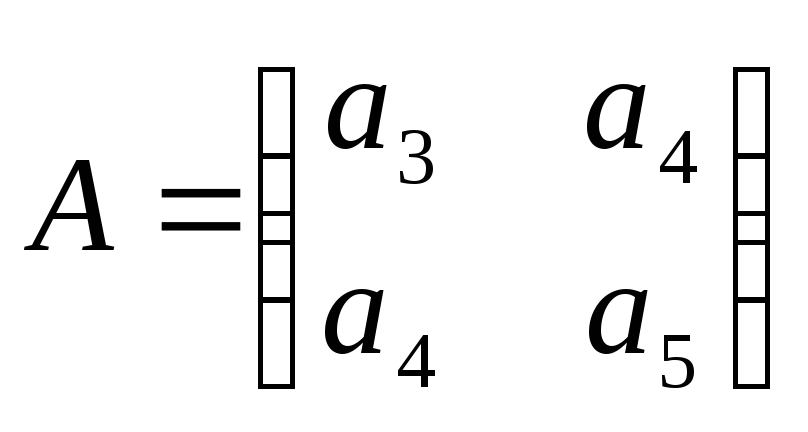 .
. .
. .
. .
.

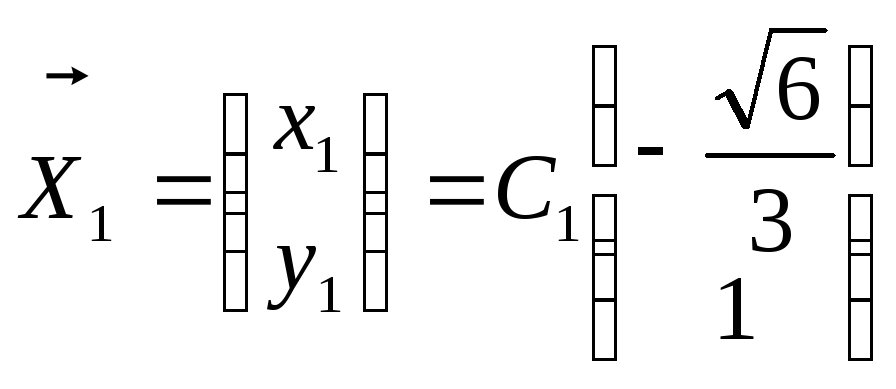





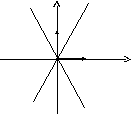









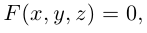
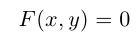
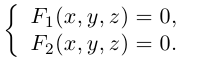

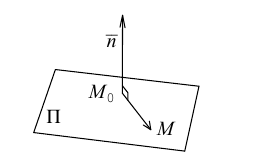
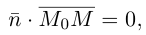
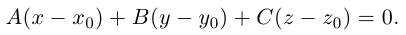
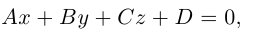
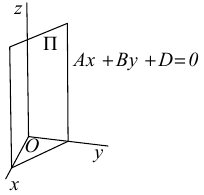
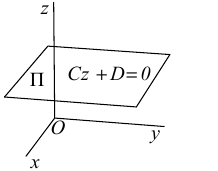
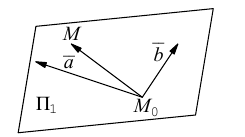
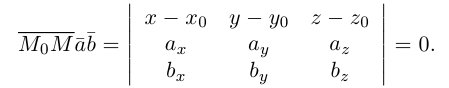
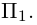
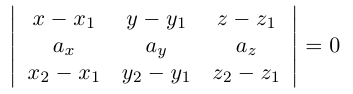
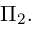
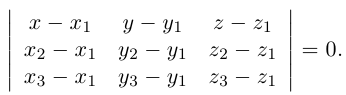
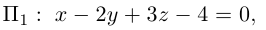
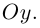
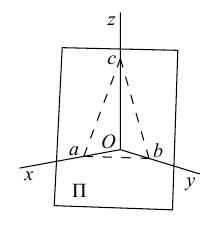
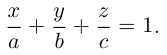
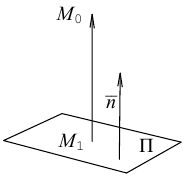
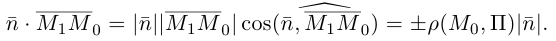
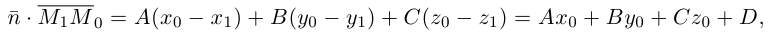
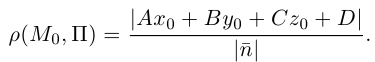
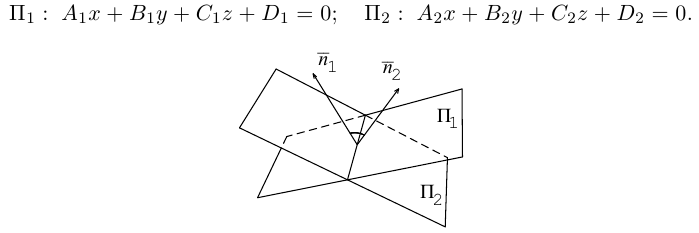
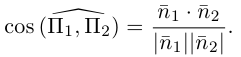
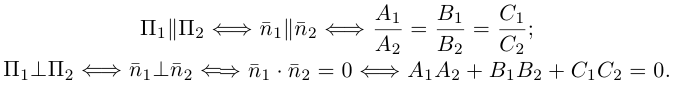
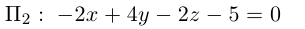
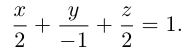
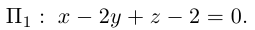
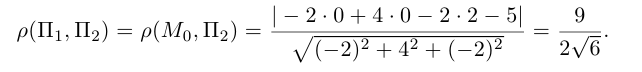
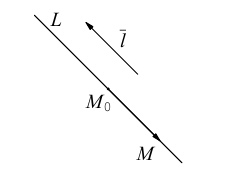
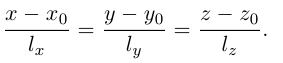
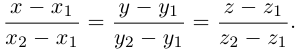
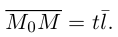
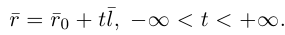
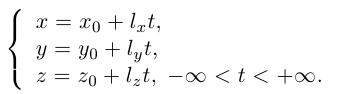
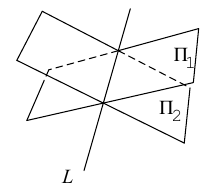
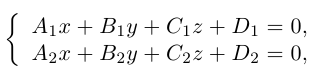
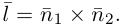
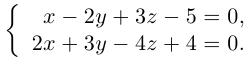
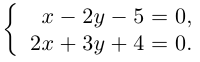
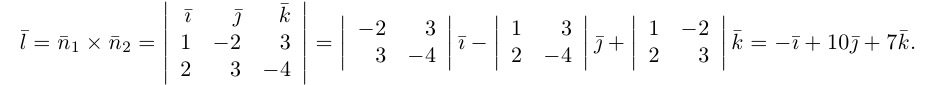
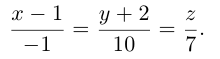
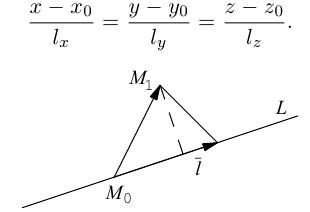
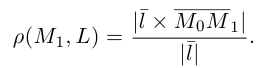
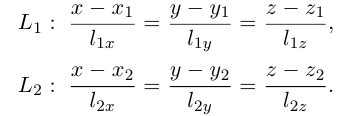
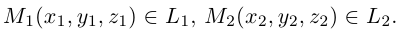
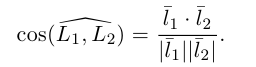
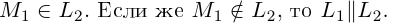
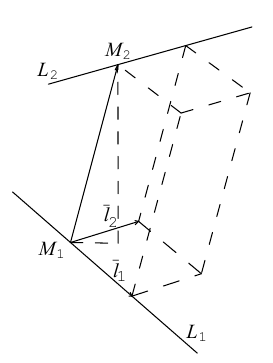
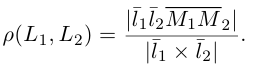
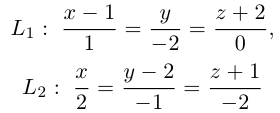
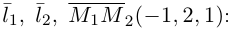
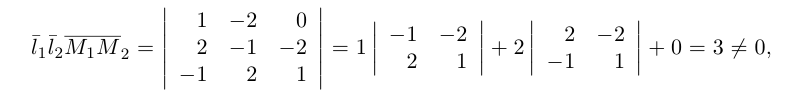
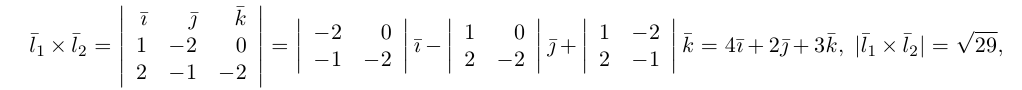
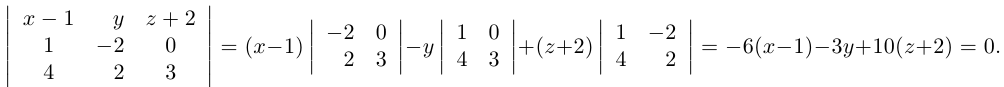
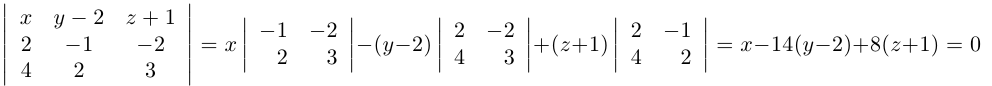
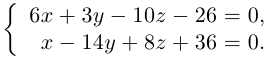
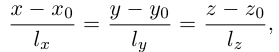
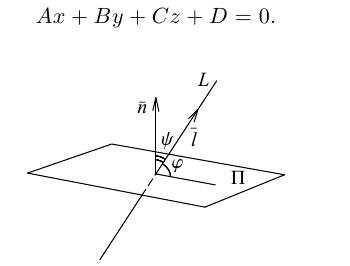
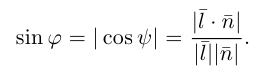
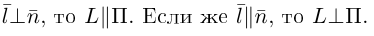
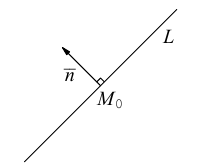
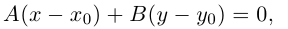
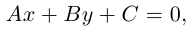
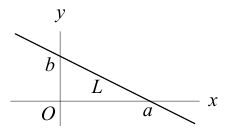
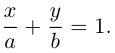
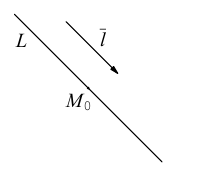
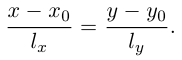
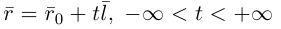
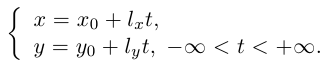
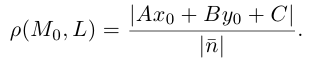
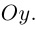
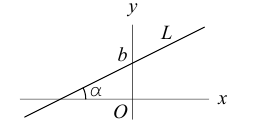
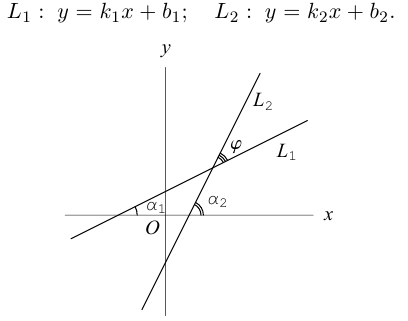
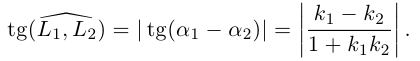
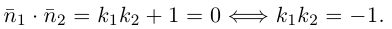
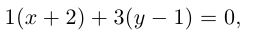
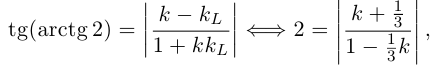
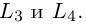
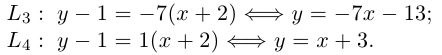
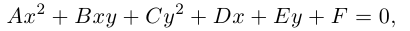
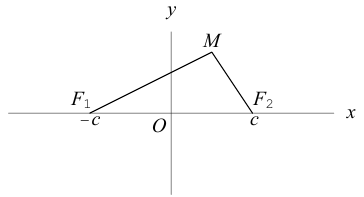
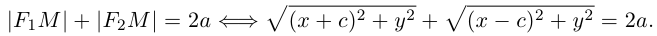
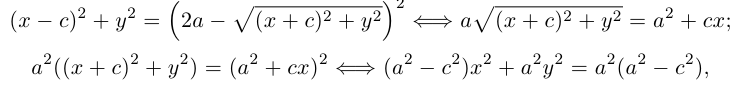
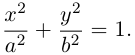
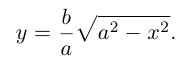
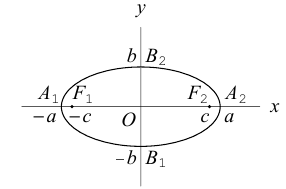
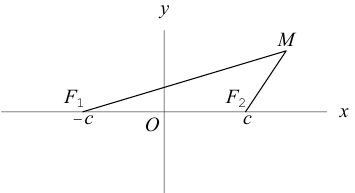
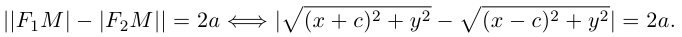
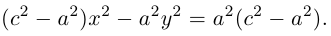
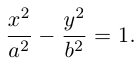
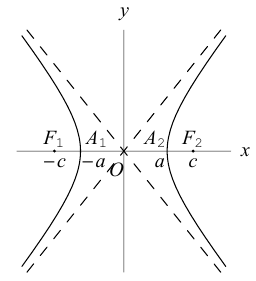
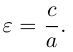
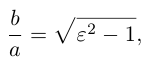
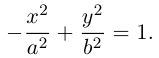
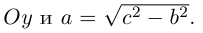
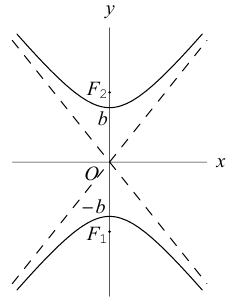
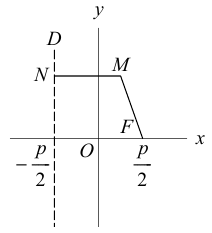
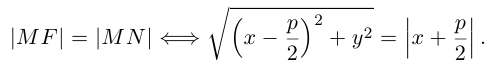
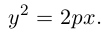
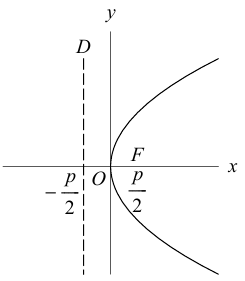
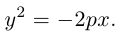
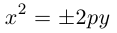
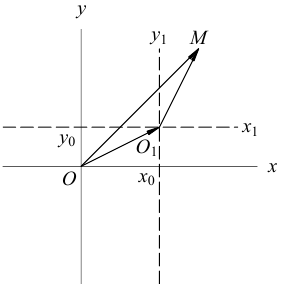
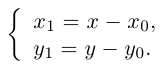
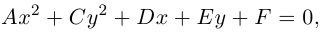
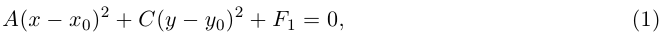
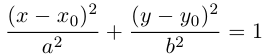
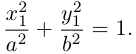
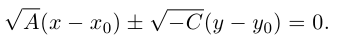
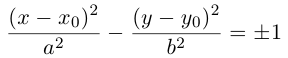
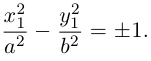
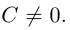
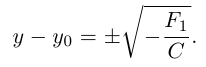
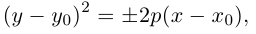
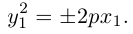
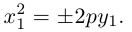
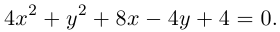
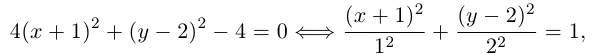
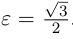
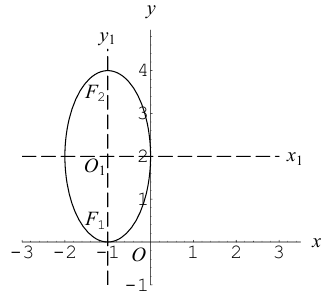
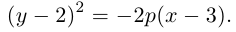
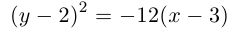
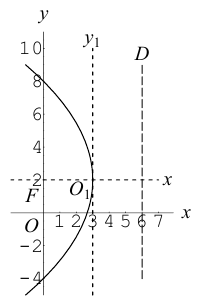
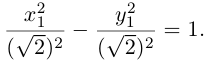
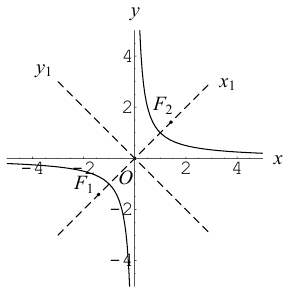
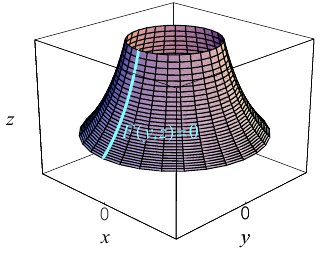
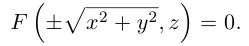
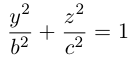
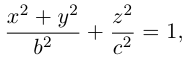
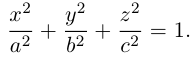
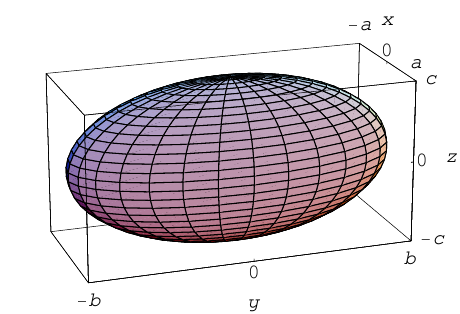
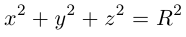
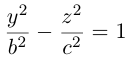
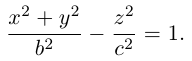
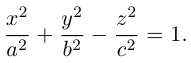
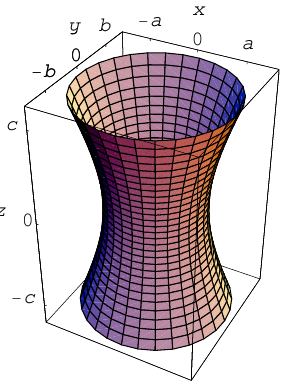
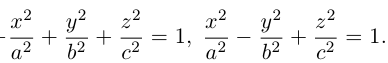
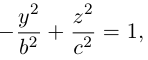
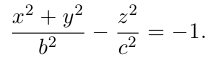
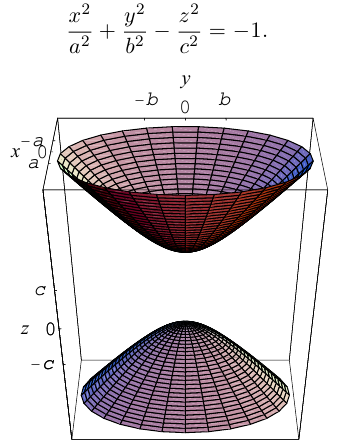
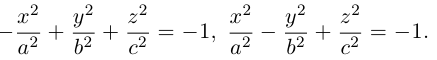
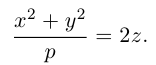
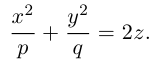
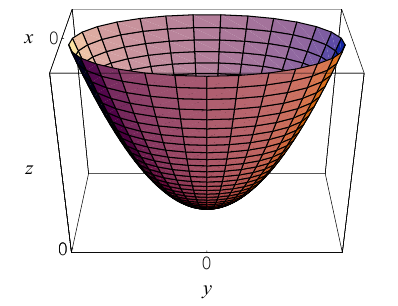
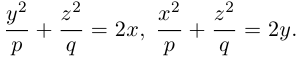
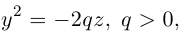
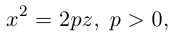
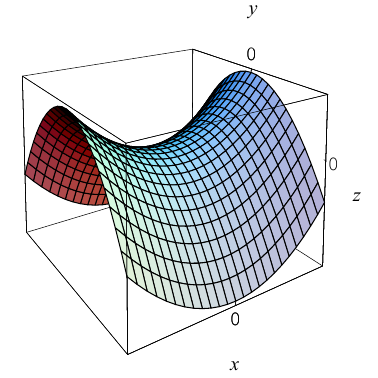
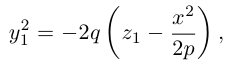
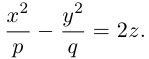
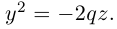
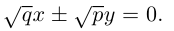
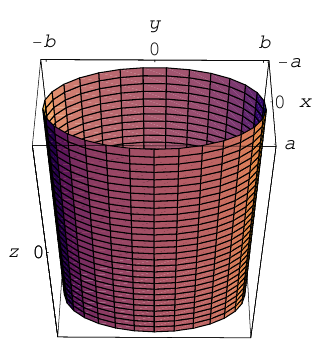
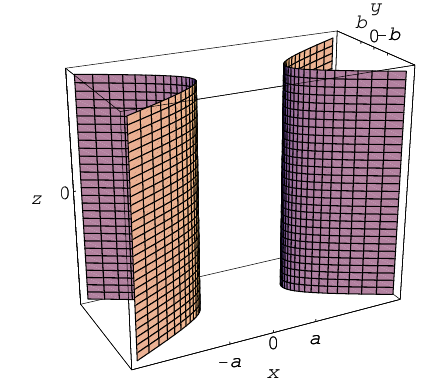
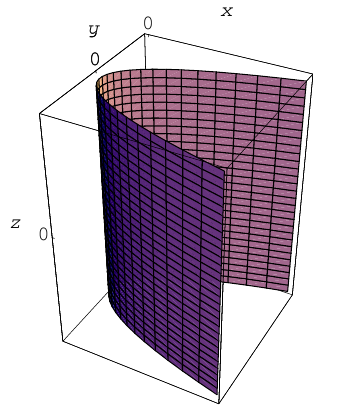
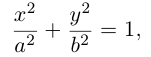
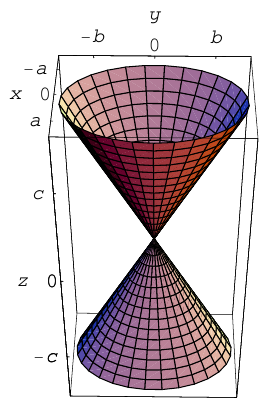
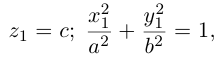
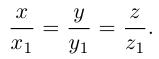
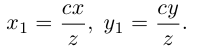
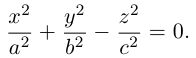
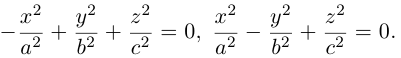
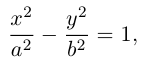
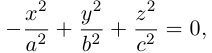
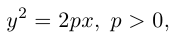
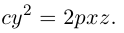
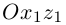
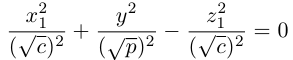
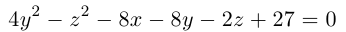
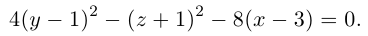
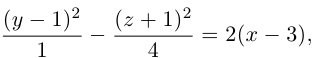
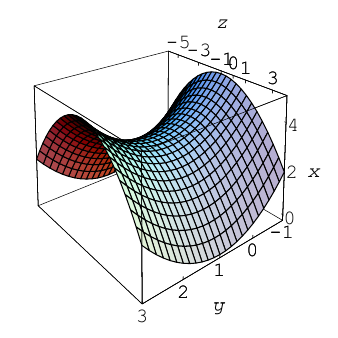
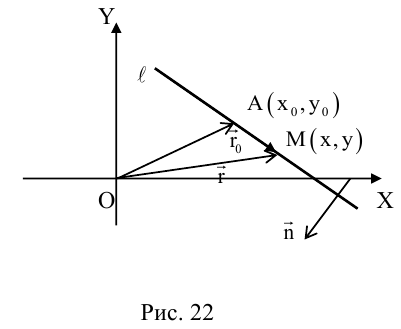
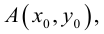
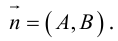


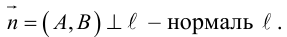
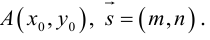


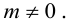
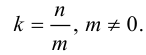
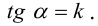
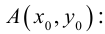


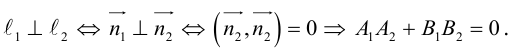
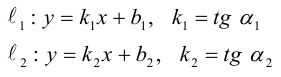
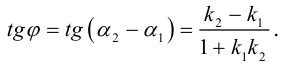
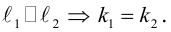
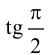
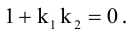
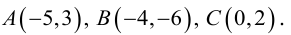
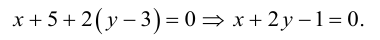
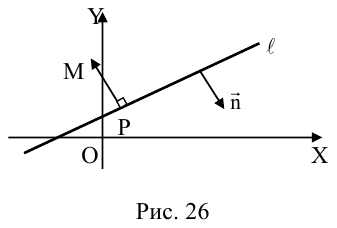
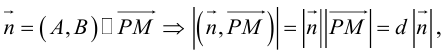
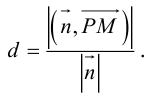
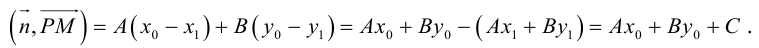

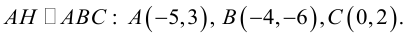
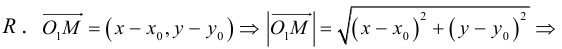


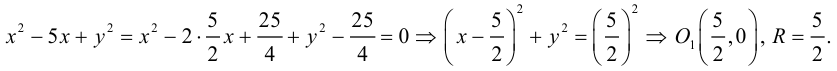
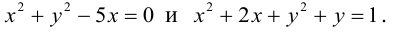
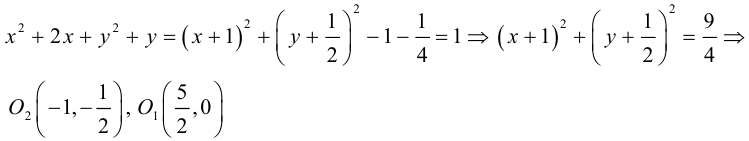
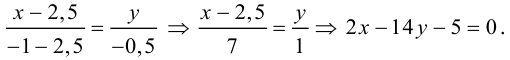
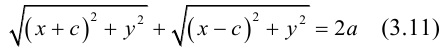
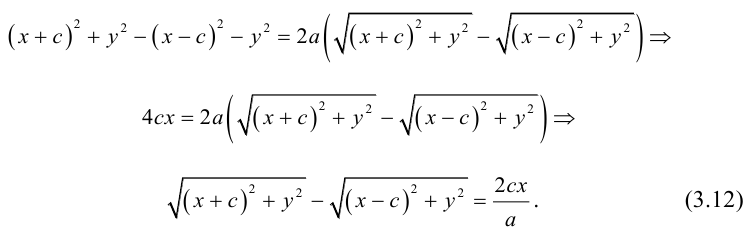
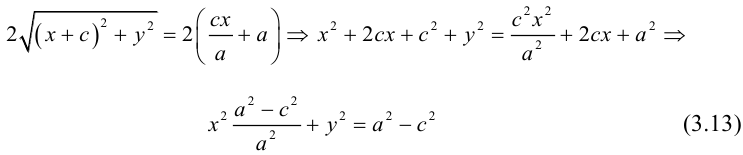

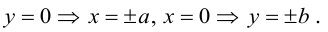
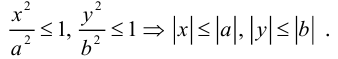

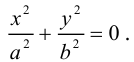
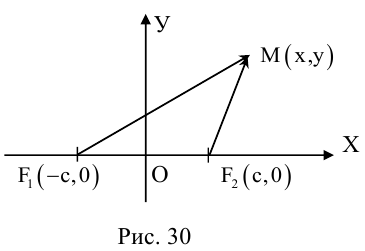


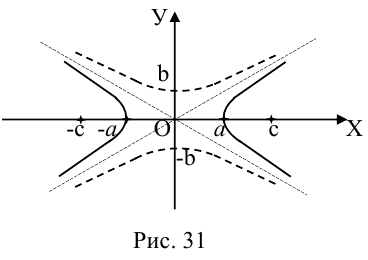

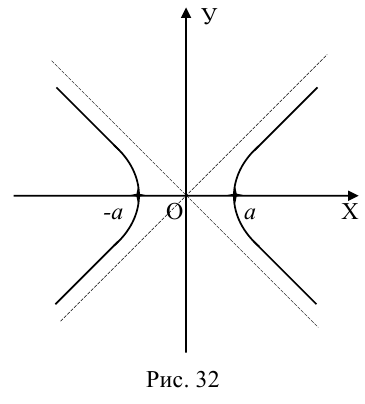
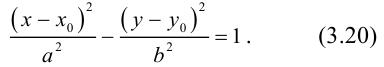
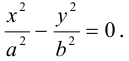
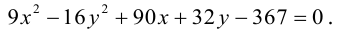
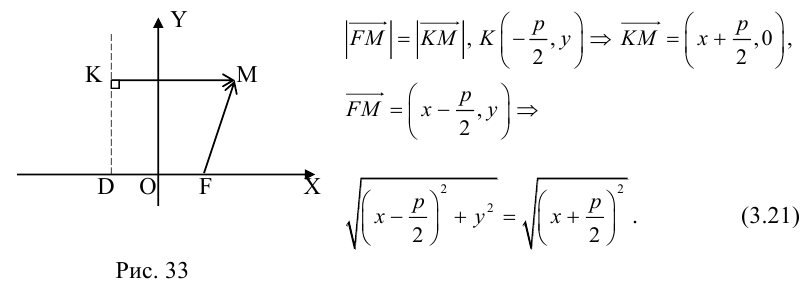
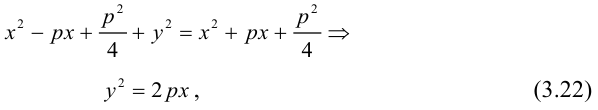
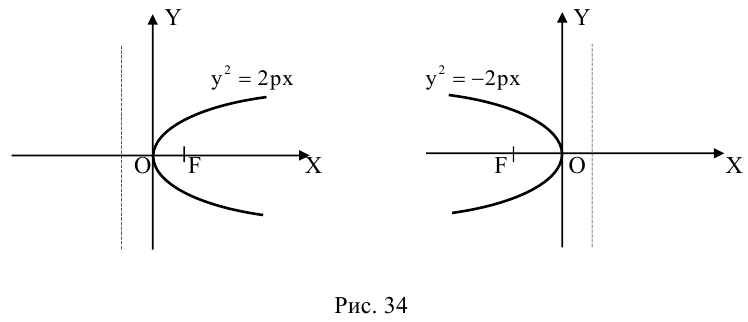
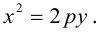
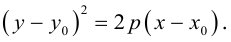
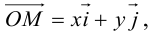
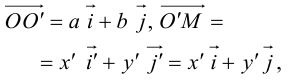
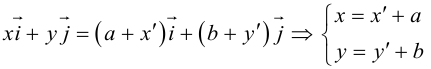

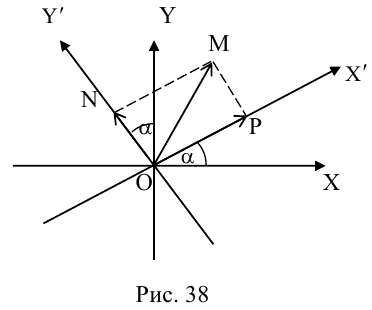

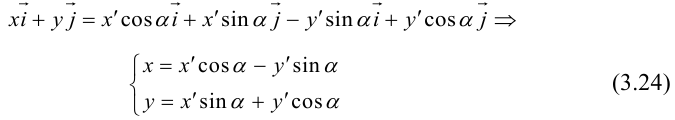
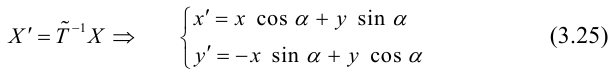
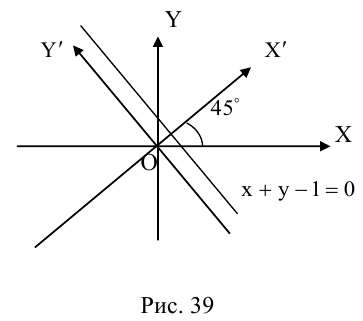
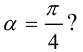
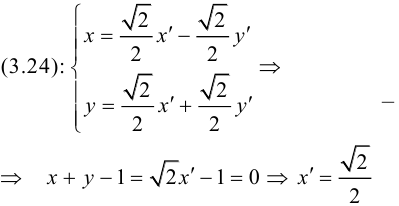

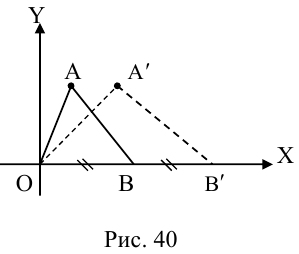
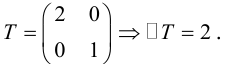
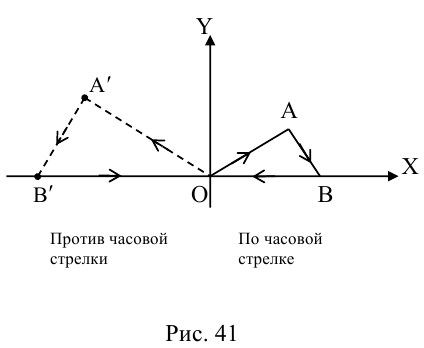
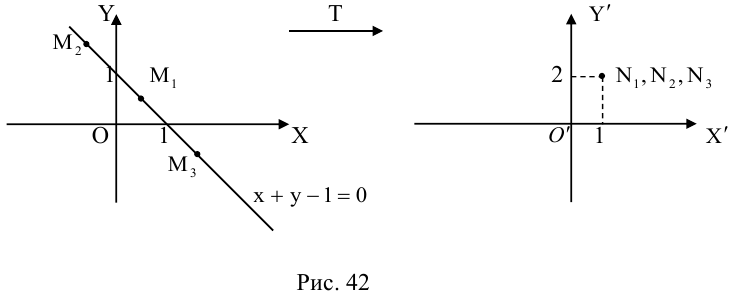
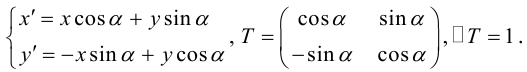
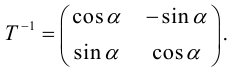
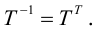
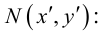

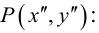

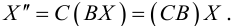
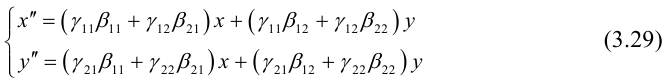
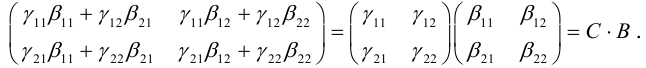
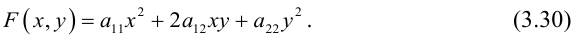
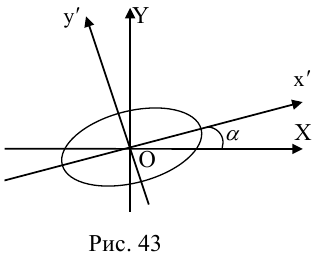
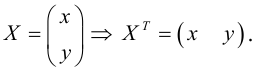
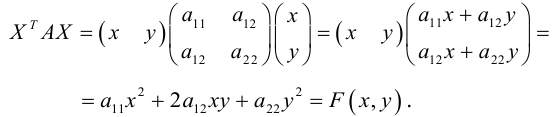

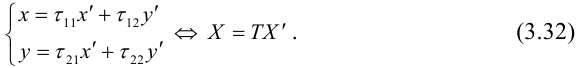
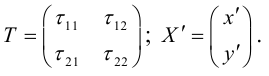

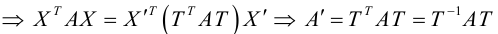
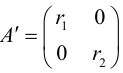
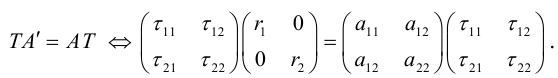
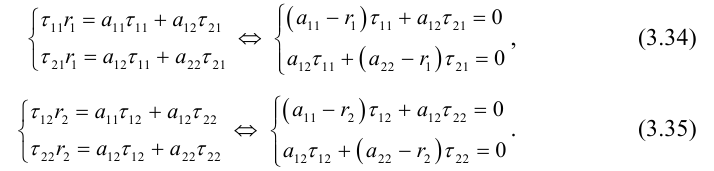
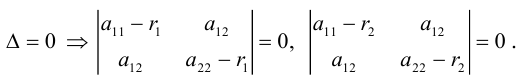
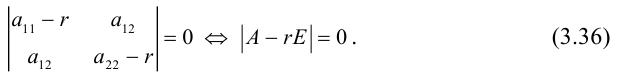
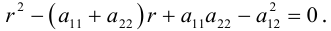
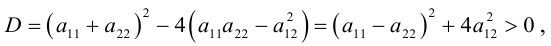
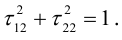
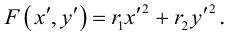
 в каноническом виде квадратичной формы.
в каноническом виде квадратичной формы.  .При этом если ось
.При этом если ось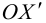 сонаправлена с
сонаправлена с 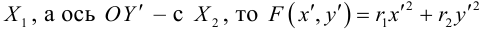 – канонический вид, который квадратичная форма имеет в системе
– канонический вид, который квадратичная форма имеет в системе 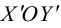 .
.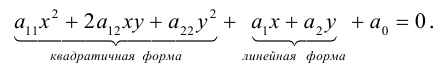
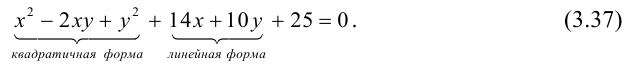
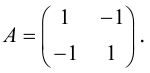
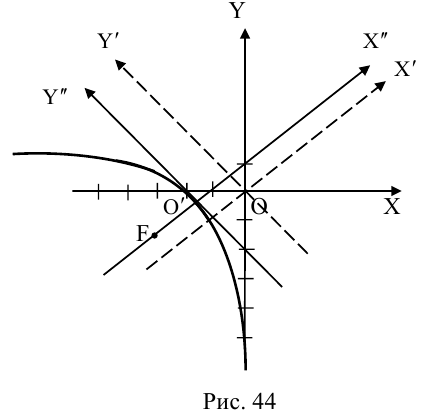
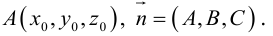

 координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.
координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат. 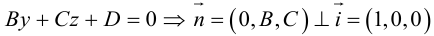 , так как
, так как 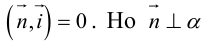 , значит, плоскость
, значит, плоскость  .
. 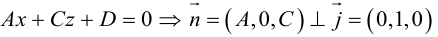 , так как
, так как 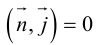 .Значит, плоскость
.Значит, плоскость  .
.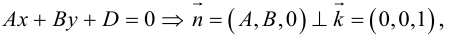 так как
так как  . Значит, плоскость
. Значит, плоскость  .
. 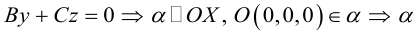 проходит через OX .
проходит через OX . 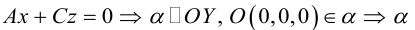 проходит через OY .
проходит через OY . 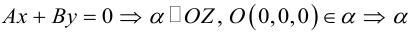 проходит через OZ .
проходит через OZ . 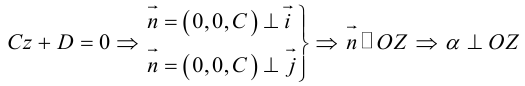 или
или  .
. 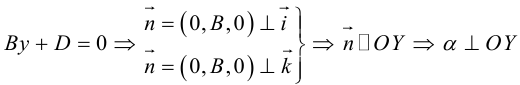 или
или 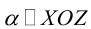 .
. 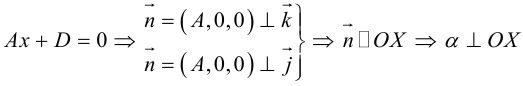 или
или 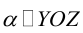 .
. 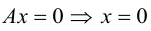 – плоскость YOZ .
– плоскость YOZ . 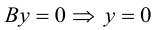 – плоскость XOZ .
– плоскость XOZ . 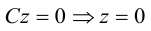 – плоскость XOY .
– плоскость XOY . 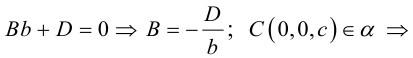
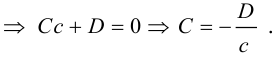
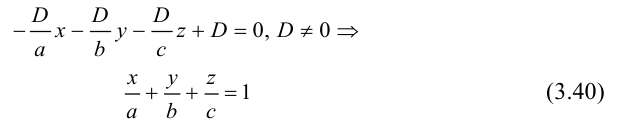
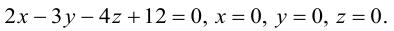
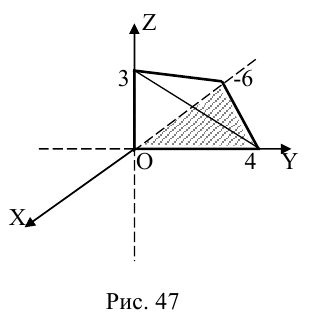
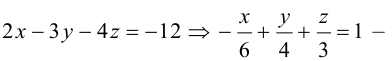
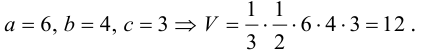
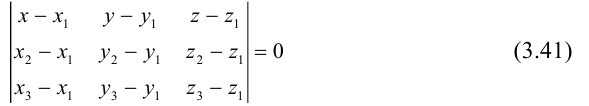
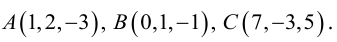
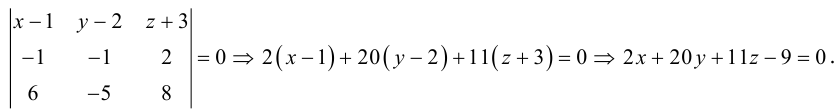
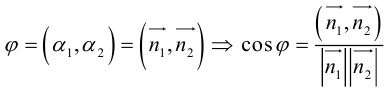
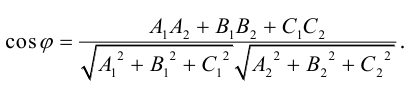
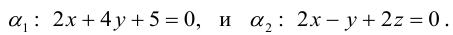
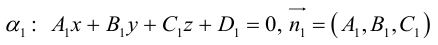
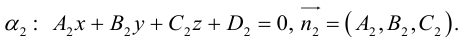
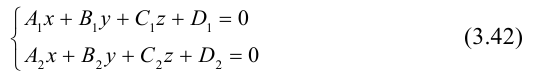

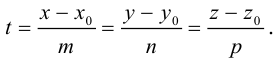

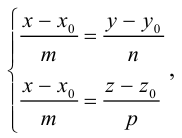
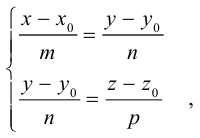

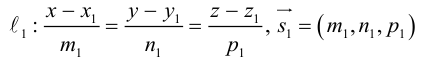
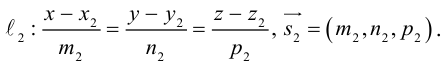
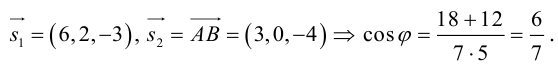
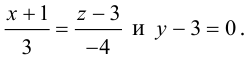
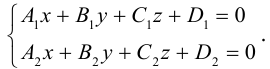
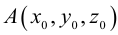 , лежащей на
, лежащей на