Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.
На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
- Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.
Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α – красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) – это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y=2x сливается с прямой у=х+1.
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.
Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу – kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.
Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
- Касательная параллельна ох, когда угловой коэффициент равняется нулю. Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.
Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1–192-13 или y0=3·-1–192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.
Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter
Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.
Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.
Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter
В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:
Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания – 234; -5+34.
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
Уравнение касательной к графику функции
Чтобы закрепить
предыдущий параграф, рассмотрим задачу
нахождения касательной к графику функции
в данной точке. Это задание встречалось
нам в школе, и оно же встречается в курсе
высшей математики.
Рассмотрим
«демонстрационный» простейший пример.
Составить
уравнение касательной к графику
функции 
в
точке с абсциссой 
.
Я сразу приведу готовое графическое
решение задачи (на практике этого делать
в большинстве случаев не надо):
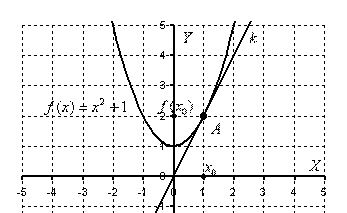
Строгое
определение касательной дается с помощью
определения самой производной функции,
и с этим пока повременим. Наверняка
практически всем интуитивно понятно,
что такое касательная. Если объяснять
«на пальцах», то касательная к графику
функции – этопрямая,
которая касается графика функции
в единственной точке.
При этом все близлежащие точки прямой
расположены максимально близко к графику
функции.
Применительно
к нашему случаю: при
касательная 
(стандартное
обозначение) касается графика функции
в единственной точке 
.
И наша
задача состоит в том, чтобы найти
уравнение прямой
.
Как
составить уравнение касательной в точке
с абсциссой 
?
Общая формула
знакома нам еще со школы:
Значение
нам
уже дано в условии.
Теперь
нужно вычислить, чему равна сама
функция в
точке
:
На
следующем этапе находим производную:
Находим
производную в точке (задание, которое
мы недавно рассмотрели):
Подставляем
значения
, 
и 
в
формулу
:
Таким
образом, уравнение касательной:
Это
«школьный» вид уравнения прямой с
угловым коэффициентом. В высшей математике
уравнение прямой принято записывать в
так называемой общей
форме 
,
поэтому перепишем найденное уравнение
касательной в соответствии с традицией:
Очевидно,
что точка 
должна
удовлетворять данному уравнению:
–
верное равенство.
Следует
отметить, что такая проверка является
лишь частичной. Если мы неправильно
вычислили производную в точке 
,
то выполненная подстановка нам ничем
не поможет.
Рассмотрим еще
два примера.
Пример 5
Составить
уравнение касательной к графику
функции 
в
точке с абсциссой 
Уравнение
касательной составим по формуле
1)
Вычислим значение функции в точке
:
2)
Найдем производную. Дважды используем
правило дифференцирования сложной
функции:
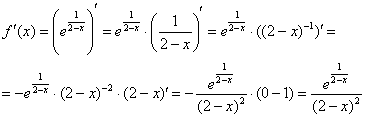
3)
Вычислим значение производной в
точке
:
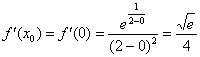
4)
Подставим значения
, 
и 
в
формулу
:
Готово.
Выполним
частичную проверку:
Подставим
точку 
в
найденное уравнение:
–
верное равенство.
Пример 6
Составить
уравнение касательной к графику
функции 
в
точке с абсциссой 
Полное решение и
образец оформления в конце урока.
В задаче на
нахождение уравнения касательной очень
важно ВНИМАТЕЛЬНО и аккуратно выполнить
вычисления, привести уравнение прямой
к общему виду.
Дифференциал функции одной переменной
Коль скоро я не
объяснил (на данный момент), что такое
производная функции, то не имеет смысла
объяснять, и что такое дифференциал
функции. В самой примитивной формулировке
дифференциал – это «почти то же самое,
что и производная».
Производная
функции чаще всего обозначается через
.
Дифференциал
функции стандартно обозначается
через 
(так
и читается – «дэ игрек»)
Дифференциал
функции одной переменной записывается
в следующем виде:
Другой
вариант записи: 
Простейшая
задача: Найти дифференциал функции 
1) Первый этап.
Найдем производную:
2) Второй этап.
Запишем дифференциал:
Готово.
Дифференциал
функции одной или нескольких переменных
чаще всего используют дляприближенных
вычислений.
Помимо других
задач с дифференциалом время от времени
встречается и «чистое» задание на
нахождение дифференциала функции. Кроме
того, как и для производной, для
дифференциала существует понятие
дифференциала в точке. И такие примеры
мы тоже рассмотрим.
Пример 7
Найти
дифференциал функции 
Перед
тем, как находить производную или
дифференциал, всегда целесообразно
посмотреть, а нельзя ли как-нибудь
упростить функцию (или запись функции)
ещё додифференцирования?
Смотрим на наш пример. Во-первых, можно
преобразовать корень:
(корень
пятой степени относится именно к синусу).
Во-вторых, замечаем,
что под синусом у нас дробь, которую,
очевидно, предстоит дифференцировать.
Формула дифференцирования дроби очень
громоздка. Нельзя ли избавиться от
дроби? В данном случае – можно, почленно
разделим числитель на знаменатель:
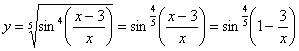
Функция
сложная. В ней два вложения: под степень
вложен синус, а под синус вложено
выражение 
.
Найдем производную, используя правило
дифференцирования сложной функции
два
раза:
Запишем
дифференциал, при этом снова представим
в
первоначальном «красивом» виде:
Готово.
Когда
производная представляет собой дробь,
значок 
обычно
«прилепляют» в самом конце числителя
(можно и справа на уровне дробной черты).
Пример 8
Найти
дифференциал функции 
Это пример для
самостоятельного решения.
Следующие два
примера на нахождение дифференциала в
точке.
Пример 9
Вычислить
дифференциал функции 
в
точке
Найдем
производную:
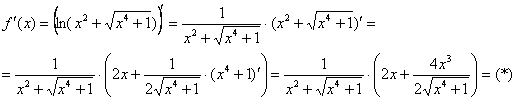
Опять, производная
вроде бы найдена. Но в эту бодягу еще
предстоит подставлять число, поэтому
результат максимально упрощаем:
Труды
были не напрасны, записываем дифференциал:
Теперь
вычислим дифференциал в точке
:
В
значок дифференциала
единицу
подставлять не нужно, он немного из
другой оперы.
Ну и
хорошим тоном в математике считается
устранение иррациональности в знаменателе.
Для этого домножим числитель и знаменатель
на 
.
Окончательно:
Пример 10
Вычислить
дифференциал функции 
в
точке 
.
В ходе решения производную максимально
упростить.
Это пример для
самостоятельного решения. Примерный
образец оформления и ответ в конце
урока.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
08.02.20157.31 Mб91.rtf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Число (e) — иррациональное, т. е. представляет собой бесконечную десятичную непериодическую дробь: (e = 2,7182818284590…); на практике обычно полагают, что e≈2,7.
График функции y=ex (называется экспонентой) изображён на рисунке:
Угол между касательной к экспоненте в точке (x = 0) и осью абсцисс равен 45°. Этим график функции y=ex отличается от других графиков экспоненциального вида (показательных функций с другими основаниями).
Свойства функции y=ex:
1) D(f)=(−∞;+∞)′;
2) ни чётная, ни нечётная;
3) возрастающая;
4) ограниченная снизу;
5) у функции нет наибольшего и наименьшего значений;
6) непрерывная;
7) E(f)=(0;+∞);
8) выпукла вниз;
9) дифференцируема.
Формула для отыскания производной функции y=ex: ex′=ex.
Пример:
вычислить значение производной функции y=e4x−12 в точке (x = 3).
Решение. Воспользуемся правилом дифференцирования функции y=f(kx+m), согласно которому y′=kf(kx+m), и тем, что ex′=ex. Получим:
y′=e4x−12′=4e4x−12;y′(3)=4e4⋅3−12=4e12−12=4e0=4.
Ответ: (4).
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 августа 2022 года; проверки требуют 5 правок.
Запрос «EXP» перенаправляется сюда; о классе сложности см. Класс EXPTIME.
Экспоне́нта — показательная функция 
, где 
— число Эйлера.
Определение[править | править код]
Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:
или через предел:
.
Здесь 
— любое комплексное число.
Происхождение понятия[править | править код]
Слово экспонента происходит от лат. “exponere”, что переводится как “выставить вперёд; показать“, которое в свою очередь произошло от лат. приставки “ex-“ (“впереди”) и лат. слова “ponere” (“ставить, расположить”);[1] Смысл использования такого слова для показателя степени заключается в том, что знак экспоненты “ставят вне” привычной линии письма 
(немного выше и правее места, где обычно должна быть поставлена цифра).
Свойства[править | править код]
Комплексная экспонента[править | править код]
График экспоненты в комплексной плоскости.
Легенда
Комплексная экспонента — математическая функция, задаваемая соотношением 
, где 
есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты 
вещественного переменного :
Определим формальное выражение
- .
Определённое таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции 
, то есть показать, что разлагается в некоторый сходящийся к данной функции ряд. Покажем это:
- .
Сходимость данного ряда легко доказывается:
- .
Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции . Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция всюду определена и аналитична.
Свойства[править | править код]
Вариации и обобщения[править | править код]
Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры.
В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента[править | править код]
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора 
с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы 
Следовательно, экспонента от матрицы 
всегда определена и сама является матрицей.
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение 
с начальным условием 
имеет своим решением 
h-экспонента[править | править код]
Введение 
-экспоненты основано на втором замечательном пределе:
При 
получается обычная экспонента[2].
Обратная функция[править | править код]
Обратная функция к экспоненциальной функции — натуральный логарифм.
Обозначается 
:
См. также[править | править код]
- Показательная функция
- Список интегралов от экспоненциальных функций
- Экспоненциальный рост
Примечания[править | править код]
- ↑ exponent (n.) (англ.).
- ↑ A.I. Olemskoi, S.S. Borysov, a, and I.A. Shuda. Statistical field theories deformed within different calculi
Литература[править | править код]
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
- Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.
Ссылки[править | править код]
- An Intuitive Guide To Exponential Functions & e | BetterExplained (англ.)
В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.
- Определение и формула экспоненты
- График экспоненты
- Свойства экспоненциальной функции
Определение и формула экспоненты
Экспонента – это показательная функция, формула которой выглядит следующим образом:
f (x) = exp(x) = e x
где e – число Эйлера.
Экспоненциальная функция (так часто называют экспоненту) может быть определена:
Через предел (lim):
Через степенной ряд Тейлора:
График экспоненты
Ниже представлен график экспоненциальной функции y = e x.
Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y.
Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox, но никогда не пересечет и не коснется ее.
Пересечение с осью ординат Oy – в точке (0, 1), так как e0 = 1.
Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.
Свойства экспоненциальной функции
- Экспонента определена для всех x, причем функция везде возрастает, и ее значение всегда больше нуля. То есть:
- область определения: – ∞ < x + ∞;
- область значений: 0 < y < + ∞.
- Обратная к экспоненте функция – это натуральный логарифм (ln x).
- ln e x = x;
- e ln x = x, где x > 0.
- Для экспоненты применимы правила операций с показателями, например: e (a + b) = e a ⋅ e b.
- Производная экспоненты:
- (e x)‘ = e x.
- если вместо x – сложная функция u: (e u)‘ = e u + u‘.
- Интеграл экспоненты: ∫ e x dx = e x + C, где C – константа интегрирования.
