Касательная к окружности как найти сторону

Касательная к окружности

О чем эта статья:

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

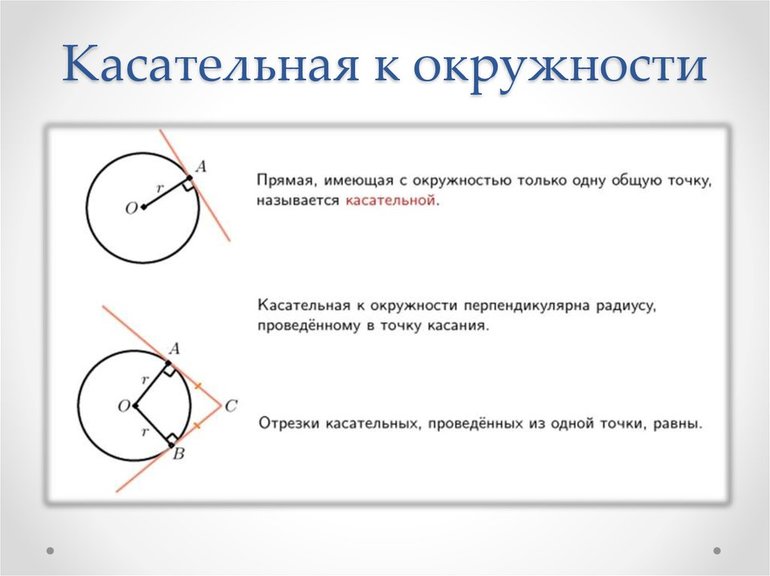
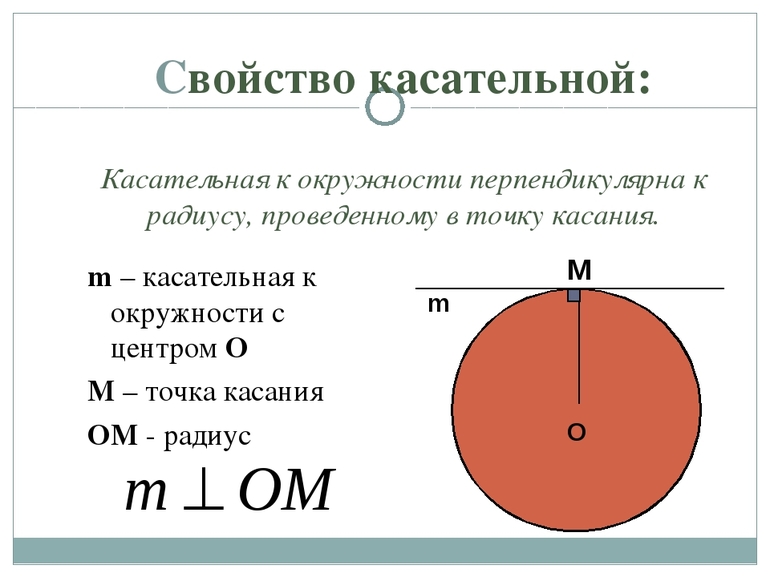
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° – ∠САО – ∠АСО = 180° – 90° – 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

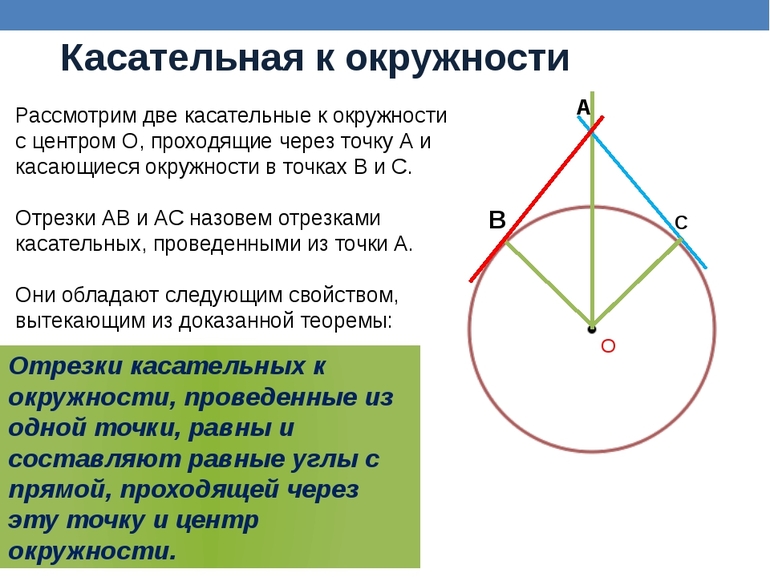
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° – ∠МКN) : 2 = (180° – 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ – ВС = 16 – 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у – R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° – ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° – ∠КОМ) : 2 = (180° – 168°) : 2 = 6°

Об отрезках касательной к окружности

Разделы: Математика

Чаще всего именно геометрические задачи вызывают затруднения у абитуриентов, выпускников, участников математических олимпиад. Если посмотреть статистику ЕГЭ 2010 года, то видно, что к геометрической задаче С4 приступило около 12% участников, а получило полный балл только 0,2% участников, а в целом задача оказалась самой сложной из всех предложенных.

Очевидно, что чем раньше мы предложим школьникам красивые или неожиданные по способу решения задачи, тем больше вероятность заинтересовать и увлечь всерьёз и надолго. Но, как же трудно найти интересные и сложные задачи на уровне 7 класса, когда только начинается систематическое изучение геометрии. Что можно предложить интересующемуся математикой школьнику, знающему только признаки равенства треугольников, свойства смежных и вертикальных углов? Однако, можно ввести понятие касательной к окружности, как прямой, имеющей с окружностью одну общую точку; принять, что радиус, проведённый в точку касания, перпендикулярен касательной. Конечно, стоит рассмотреть все возможные случаи расположения двух окружностей и общих касательных к ним, которых можно провести от нуля до четырёх. Доказав ниже предложенные теоремы, можно значительно расширить набор задач для семиклассников. При этом попутно доказать важные или просто интересные и занимательные факты. Причём, поскольку многие утверждения не входят в школьный учебник, то обсуждать их можно и на занятиях кружка и с выпускниками при повторении планиметрии. Актуальными эти факты оказались в прошлом учебном году. Так как многие диагностические работы и сама работа ЕГЭ содержали задачу, для решения которой необходимо было использовать доказываемое ниже свойство отрезка касательной.

Т₁ Отрезки касательных к окружности, проведённые из
одной точки равны (рис. 1)

Вот именно с теоремой можно сначала познакомить семиклассников.
В процессе доказательства использовали признак равенства прямоугольных треугольников, сделали вывод о том, что центр окружности лежит на биссектрисе угла ВСА.
Попутно вспомнили, что биссектриса угла есть геометрическое место точек внутренней области угла, равноудалённых от его сторон. На этих доступных даже только начинающим изучать геометрию фактах основывается решение уже далеко нетривиальной задачи.

1. Биссектрисы углов А, В и С выпуклого четырёхугольника АВСD пересекаются в одной точке. Лучи АВ и DC пересекаются в точке Е, а лучи
ВС и АD в точке F. Докажите, что у невыпуклого четырёхугольника AECF суммы длин противоположных сторон равны.

Решение (рис. 2). Пусть О – точка пересечения данных биссектрис. Тогда О равноудалена от всех сторон четырёхугольника АВСD, то есть
является центром окружности вписанной в четырёхугольник. По теореме 1 верны равенства: AR = AK, ER = EP, FT = FK. Почленно сложим левые и правые части, получим верное равенство:

Рассмотрим необычную по формулировке задачу, для решения которой достаточно знание теоремы 1.

2. Существует ли n-угольник, стороны которого последовательно 1, 2, 3, …, n, в который можно вписать окружность?

Решение. Допустим, такой n-угольник существует. А₁А₂ =1, …, А_n-1А_n = n – 1, А_nА₁ = n. B₁, …, B_n – соответствующие точки касания. Тогда по теореме 1 A₁B₁ = A₁B_n Можно обобщить этот факт – суммы сторон описанного чётноугольника, взятых через одну, равны. Например, для шестиугольника ABCDEF верно: AB + CD + EF = BC + DE + FА.

3. МГУ. В четырёхугольнике ABCD расположены две окружности: первая окружность касается сторон AB, BC и AD, а вторая – сторон BC, CD и AD. На сторонах BC и AD взяты точки E и F соответственно так, отрезок EF касается обеих окружностей, а периметр четырёхугольника ABEF на 2p больше периметра четырёхугольника ECDF. Найти AB, если CD = a.

Решение (рис. 1). Так как четырёхугольники ABEF и ECDF вписанные, то по теореме 2 Р_ABEF = 2(AB + EF) и Р_ECDF = 2(CD + EF), по условию

Р_ABEF – Р_ECDF = 2(AB + EF) – 2(CD + EF) = 2p. AB – CD = p. АВ = а + р.

Опорная задача 1. Прямые АВ и АС – касательные в точках В и С к окружности с центром в точке О. Через произвольную точку Х дуги ВС
проведена касательная к окружности, пересекающая отрезки АВ и АС в точках М и Р соответственно. Докажите, что периметр треугольника АМР и величина угла МОР не зависят от выбора точки Х.

Решение (рис. 5). По теореме 1 МВ = МХ и РС = РХ. Поэтому периметр треугольника АМР равен сумме отрезков АВ и АС. Или удвоенной касательной, проведённой к вневписанной окружности для треугольника АМР. Величина угла МОР измеряется половиной величины угла ВОС, который не зависит от выбора точки Х.

Опорная задача 2а. В треугольник со сторонами а, b и c вписана окружность, касающаяся стороны АВ и точке К. Найти длину отрезка АК.

Решение (рис. 6). Способ первый (алгебраический). Пусть АК = АN = x, тогда BK = BM = c – x, CM = CN = a – c + x. АС = АN + NC, тогда можем составить уравнение относительно х: b = x + (a – c + x). Откуда .

Способ второй (геометрический). Обратимся к схеме. Отрезки равных касательных, взятые по одному, в сумме дают полупериметр
треугольника. Красный и зелёный составляют сторону а. Тогда интересующий нас отрезок х = р – а. Безусловно, полученные результаты совпадают.

Опорная задача 2б. Найти длину отрезка касательной АК, если К – точка касания вневписанной окружности со стороной АВ. Решение (рис. 7). АК = АM = x, тогда BK = BN = c – x, CM = CN. Имеем уравнение b + x = a + (c – x). Откуда . Заметим, что из опорной задачи 1 следует, что СМ = р _{Δ АВС}. b + x = p; х = р – b. Полученные формулы имеют применение в следующих задачах.

4. Найдите радиус окружности, вписанной в прямоугольный треугольник с катетами а, b и гипотенузой с. Решение (рис. 8). Так как OMCN – квадрат, то радиус вписанной окружности равен отрезку касательной CN. .

5. Докажите, что точки касания вписанной и вневписанной окружности со стороной треугольника симметричны относительно середины этой стороны.

Решение (рис. 9). Заметим, АК – отрезок касательной вневписанной окружности для треугольника АВС. По формуле (2) . ВМ – отрезок касательной вписанной окружности для треугольника АВС. По формуле (1) . АК = ВМ, а это и означает, что точки К и М равноудалены от середины стороны АВ, что и требовалось доказать.

6. К двум окружностям проведены две общие внешние касательные и одна внутренняя. Внутренняя касательная пересекает внешние в точках А, В и касается окружностей в точках А₁ и В₁. Докажите, что АА₁ = ВВ₁.

Решение (рис. 10). Стоп… Да что тут решать? Это же просто другая формулировка предыдущей задачи. Очевидно, что одна из окружностей является вписанной, а другая вневписанной для некоего треугольника АВС. А отрезки АА₁ и ВВ₁ соответствуют отрезкам АК и ВМ задачи 5. Примечательно, что задача, предлагавшаяся на Всероссийской олимпиаде школьников по математике, решается столь очевидным образом.

7. Стороны пятиугольника в порядке обхода равны 5, 6, 10, 7, 8. Доказать, что в этот пятиугольник нельзя вписать окружность.

Решение (рис. 11). Предположим, что в пятиугольник АВСDE можно вписать окружность. Причём стороны AB, BC, CD, DE и ЕA равны соответственно 5, 6, 10, 7 и 8. Отметим последовательно точки касания – F, G, H, M и N. Пусть длина отрезка AF равна х.

Но, AF = AN. То есть 10 – х = х; х = 5. Однако, отрезок касательной AF не может равняться стороне АВ. Полученное противоречие и доказывает, что в данный пятиугольник нельзя вписать окружность.

8. В шестиугольник вписана окружность, его стороны в порядке обхода равны 1, 2, 3, 4, 5. Найти длину шестой стороны.

Решение. Конечно, можно отрезок касательной обозначить за х, как и в предыдущей задаче, составить уравнение и получить ответ. Но, гораздо эффективнее и эффектнее использовать примечание к теореме 2: суммы сторон описанного шестиугольника, взятых через одну, равны.

Тогда 1 + 3 + 5 = 2 + 4 + х, где х – неизвестная шестая сторона, х = 3.

9. МГУ, 2003 г. химический факультет, № 6(6). В пятиугольник АВСDE вписана окружность, Р – точка касания этой окружности со стороной ВС. Найдите длину отрезка ВР, если известно, что длины всех сторон пятиугольника есть целые числа, АВ = 1, СD = 3.

Решение (рис.12). Так как длины всех сторон являются целыми числами, то равны дробные части длин отрезков BT, BP, DM, DN, AK и AT. Имеем, АТ + ТВ = 1, и дробные части длин отрезков AT и TB равны. Это возможно только тогда, когда АТ + ТВ = 0,5. По теореме 1 ВТ + ВР.
Значит, ВР = 0,5. Заметим, что условие СD = 3 оказалось невостребованным. Очевидно, авторы задачи предполагали какое-то другое решение. Ответ: 0,5.

10. В четырёхугольнике ABCD AD = DC, AB = 3, BC = 5. Окружности, вписанные в треугольники ABD и CBD касаются отрезка BD в точках M и N соответственно. Найти длину отрезка MN.

Решение (рис. 13). MN = DN – DM. По формуле (1) для треугольников DBA и DBС соответственно, имеем:

11. В четырёхугольник ABCD можно вписать окружность. Окружности, вписанные в треугольники ABD и CBD имеют радиусы R и r соответственно. Найти расстояние между центрами этих окружностей.

Решение (рис. 13). Так как по условию четырёхугольник ABCD вписанный, по теореме 2 имеем: AB + DC = AD + BC. Воспользуемся идеей решения предыдущей задачи. . Это означает, что точки касания окружностей с отрезком DM совпадают. Расстояние между центрами окружностей равно сумме радиусов. Ответ: R + r.

Фактически доказано, что условие – в четырёхугольник ABCD можно вписать окружность, равносильно условию – в выпуклом четырехугольнике ABCD окружности, вписанные в треугольники ABC и ADC касаются друг друга. Верно обратное.

Доказать эти два взаимно-обратных утверждения предлагается в следующей задаче, которую можно считать обобщением данной.

12. В выпуклом четырехугольнике ABCD (рис. 14) окружности, вписанные в треугольники ABC и ADC касаются друг друга. Докажите, что окружности, вписанные в треугольники ABD и BDC также касаются друг друга.

13. В треугольнике АВС со сторонами а, b и c на стороне ВС отмечена точка D так, что окружности, вписанные в треугольники АВD и ACD касаются отрезка AD в одной точке. Найти длину отрезка BD.

Решение (рис. 15). Применим формулу (1) для треугольников ADC и ADB, вычислив DM двумя

Оказывается, D – точка касания со стороной ВС окружности, вписанной в треугольник АВС. Верно обратное: если вершину треугольника соединить с точкой касания вписанной окружности на противоположной стороне, то окружности, вписанные в получившиеся треугольники, касаются друг друга.

14. Центры О₁, О₂ и О₃ трёх непересекающихся окружностей одинакового радиуса расположены в вершинах треугольника. Из точек О₁, О₂, О₃ проведены касательные к данным окружностям так, как показано на рисунке.

Известно, что эти касательные, пересекаясь, образовали выпуклый шестиугольник, стороны которого через одну покрашены в красный и синий цвета. Докажите, что сумма длин красных отрезков равна сумме длин синих.

Решение (рис. 16). Важно понять, как использовать тот факт, что заданные окружности имеют одинаковые радиусы. Заметим, что отрезки ВR и DМ равны, что следует из равенства прямоугольных треугольников О₁ВR и O₂BM. Аналогично DL = DP, FN = FK. Почленно складываем равенства, затем вычитаем из полученных сумм одинаковые отрезки касательных, проведенных из вершин А, С, и Е шестиугольника ABCDEF: АR и AK, CL и CM, EN и EP. Получаем требуемое.

Вот пример задачи по стереометрии, предлагавшейся на XII Международном математическом турнире старшеклассников “Кубок памяти А. Н. Колмогорова”.

16. Дана пятиугольная пирамида SA₁A₂A₃A₄A₅. Существует сфера w , которая касается всех ребер пирамиды и другая сфера w ₁, которая касается всех сторон основания A₁A₂A₃A₄A₅ и продолжений боковых рёбер SA₁, SA₂, SA₃, SA₄, SA₅ за вершины основания. Докажите, что вершина пирамиды равноудалена от вершин основания. (Берлов С. Л., Карпов Д. В.)

Решение. Пересечение сферы w с плоскостью любой из граней сферы – это вписанная окружность грани. Пересечение сферы w ₁ с каждой из граней SA_iA_i+1 – вневписанная окружность, касающаяся стороны A_iA_i+1 треугольника SA_iA_i+1 и продолжений двух других сторон. Обозначим точку касания w ₁ с продолжением стороны SA_i через B_i. По опорной задаче 1 имеем, что SB_i = SB_i+1 = p_SAiAi+1 , следовательно, периметры всех боковых граней пирамиды равны. Обозначим точку касания w со стороной SA_i через С_i. Тогда SC₁ = SC₂ = SC₃ = SC₄ = SC₅= s,
так как отрезки касательных равны. Пусть C_iA_i = a_i. Тогда p_SAiAi+1 = s+a_i+a_i+1, и из равенства периметров следует, что a₁ = a₃ = a₅ = a₂ = a₄, откуда SA₁ = SA₂ = SA₃ = SA₄ = SA₅.

17. ЕГЭ. Диагностическая работа 8.12.2009 г, С–4. Дана трапеция ABCD, основания которой BC = 44, AD = 100, AB = CD = 35. Окружность, касающаяся прямых AD и AC, касается стороны CD в точке K. Найдите длину отрезка CK.

Найдем диагональ AC. Опустим из вершин B и C на сторону AD перпендикуляры BE и CF соответственно. AE = FD, так как трапеция равнобедренная. BCFE – прямоугольник.

Возможны две геометрические конфигурации.

Первый случай (рис. 18): окружность вписана в треугольник ACD.

По формуле (1)

Второй вариант (рис.19): окружность касается продолжений сторон AC и AD за точками C и D соответственно и отрезка CD.

По формуле (2)

18. ЕГЭ. 4.6. 2010 г. В треугольнике АВС АВ = 13, ВС = 11, СА = 9. Точка D лежит на прямой АС, причём АD : DС = 1 : 9. Окружности, вписанные в каждый из треугольников ВDС и ВDА, касаются стороны ВD в точках Е и F. Найдите длину отрезка EF.

Решение. Возможны два случая (рис. 20 и рис. 21). По формуле (1) найдём длины отрезков DE и DF.

В первом случае AD = 0,1АС, СD = 0,9AC. Во втором – AD = 0,125АС, СD = 1,125AC. Подставляем данные и получаем ответ: 4,6 или 5,5.

Задачи для самостоятельного решения/

1. Периметр равнобедренной трапеции, описанной около окружности равен 2р. Найдите проекцию диагонали трапеции на большее основание. (1/2р)

2. Открытый банк задач ЕГЭ по математике. В4. К окружности, вписанной в треугольник ABC (рис. 22), проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника. (24)

3. В треугольник АВС вписана окружность. MN – касательная к окружности, M Î АС, N Î ВС, ВС = 13, АС = 14, АВ = 15. Найдите периметр треугольника MNC. (12)

4. К окружности, вписанной в квадрат со стороной а, проведена касательная, пересекающая две его стороны. Найдите периметр отсечённого треугольника. (а)

5. Окружность вписана в пятиугольник со сторонами а, d, c, d и e. Найдите отрезки, на которые точка касания делит сторону, равную а.

Ответ:

6. В треугольник со сторонами 6, 10 и 12 вписана окружность. К окружности проведена касательная так, что она пересекает две большие стороны. Найдите периметр отсечённого треугольника. (16)

7. CD – медиана треугольника ABC. Окружности, вписанные в треугольники ACD и BCD, касаются отрезка CD в точках M и N. Найдите MN, если АС – ВС = 2. (1)

8. В треугольнике АВС со сторонами а, b и c на стороне ВС отмечена точка D. К окружностям, вписанным в треугольники АВD и ACD, проведена общая касательная, пересекающая AD в точке М. Найти длину отрезка АМ. (Длина АМ не зависит от положения точки D и
равна ½ (c + b – a))

9. В прямоугольный треугольник вписана окружность радиуса а. Радиус окружности, касающейся гипотенузы и продолжений катетов, равен R. Найдите длину гипотенузы. (R – a)

10. В треугольнике АВС известны длины сторон: АВ = с, АС = b, ВС = а. Вписанная в треугольник окружность касается стороны АВ в точке С₁. Вневписанная окружность касается продолжения стороны АВ за точку А в точке С₂. Определите длину отрезка С₁С₂. (b)

11. Найдите длины сторон треугольника, разделённых точкой касания вписанной окружности радиуса 3 см на отрезки 4 см и 3 см. (7, 24 и 25 см в прямоугольном треугольнике)

12. Соросовская олимпиада 1996 г, 2 тур, 11 класс. Дан треугольник АВС, на сторонах которого отмечены точки А₁, В₁, С₁. Радиусы окружностей вписанных в треугольники АС₁В₁, ВС₁А₁, СА₁В₁ равны по r. Радиус окружности, вписанной в треугольник А₁В₁С₁ равен R. Найти радиус окружности, вписанной в треугольник АВС. (R + r).

Задачи 4–8 взяты из задачника Гордина Р. К. “Геометрия. Планиметрия.” Москва. Издательство МЦНМО. 2004.

Касательная к окружности – свойства, теорема и уравнение

Общие сведения

Важно знать терминологию, соотношения и теоремы для решения задач этого класса. Касательной к окружности называется прямая, которая имеет с ней только одну точку соприкосновения. Прямая — это линия, не имеющая границ, т. е. она ничем не ограничена. Окружностью называется геометрическое место точек, удаленных от центра на одинаковые расстояния.

Следует отметить, что касательные бывают внешними и внутренними. Внешней называет прямая линия, проходящая с внешней стороны окружности. Внутренние касательные пересекают отрезок, который соединяет центры двух окружностей. Последний тип прямых не существует, когда два круга пересекаются. Касательные нужно уметь правильно строить, поскольку от этого зависит правильность решения задачи.

Построение касательных

Для построения касательной к окружности следует на последней отметить произвольную точку. Затем необходимо через нее провести прямую. Нужно отметить, что у круга может быть несколько таких прямых. Когда даны две окружности, тогда можно проводить не только внешние, но и внутренние. Существует определенный алгоритм, по которому можно построить первый тип:

1. Начертить 2 окружности с центрами в точках О1 и О2. При этом должно соблюдаться условие r1 > r2, где r1 и r2 — радиусы I и II соответственно.
2. Нарисовать III окружность с центром в О1 и радиусом r3 = r1 — r2.
3. Провести 2 касательные из точки О2 к III. Они параллельны искомым, поскольку радиусы I и II уменьшаются на r2.

Существует более простая модель построения таких прямых. Для этого следует начертить один круг, а затем отметить две произвольные точки на его противоположных сторонах. Далее начертить II круг, превышающий I по радиусу. Отметить на нем точки, воспользовавшись подобием, т. е. они должны быть в тех же местах, что и на I. Затем провести прямые, которые должны соприкасаться с I и II кругами только в одной точке.

Для построения внутренних касательных существует определенная методика. В интернете можно найти много информации. В одних источниках алгоритм построения является сложным, а в других — простым. Однако есть один метод, позволяющий осуществить данную операцию. Специалисты описали его на «понятном» языке для новичков. Суть методики заключается в следующем:

1. Необходимо построить два круга, которые не пересекаются, с радиусами r1 и r2. Расстояния между ними должно составлять r1 + r2.
2. Соединить их центры (середины) отрезком.
3. Отметить на нем среднюю точку, которая делит его на две равные части.
4. Через точку, полученную на третьем шаге методики, провести прямую. Она должна иметь только одну точку соприкосновения с I и II окружностями.
5. Аналогично провести еще одну прямую.
6. Искомые прямые являются внутренними касательными.

Далее нужно рассмотреть некоторые свойства, на основании которых можно решать задачи и доказывать геометрические тождества.

Основные свойства

Свойства — утверждения, полученные в результате доказательства теорем о касательной к окружности. Первые нет необходимости доказывать, поскольку об этом уже позаботились математики. Они выделяют всего 4 свойства касательных к окружности:

1. Если провести из одной точки две касательные к некоторой окружности, то отрезки, лежащие на них, будут равны. Искомый угол будет делиться радиусом пополам.
2. Любая касательная и радиус, проведенный к ее точке, образуют прямой угол. Справедливо и обратное утверждение: радиус, который проведен в точку касания, перпендикулярен данной прямой.
3. Вся секущая, умноженная на свою внешнюю часть, равна квадрату расстояния касательной, которая проведена из общей с ней точки.
4. Образованный угол между касательной и секущей, эквивалентен градусной мере угла, который опирается на образованную хорду.

Для рассмотрения I свойства необходимо начертить окружность с центром О1. Затем нужно отметить точку М вне окружности. Из М провести одну прямую, которая соприкасается с кругом в точке А. Такую же операцию следует проделать и для другой касательной. Точку соприкосновения назвать В. Отрезки АМ и ВМ равны между собой.

Если провести радиусы к точкам А и В, то можно сделать вывод, что углы являются прямыми. Чтобы понять третье свойство, необходимо начертить окружность и отметить некоторую точку М за ее пределами. После этого следует из искомой точки провести секущую и касательную. Первой называется прямая, проходящая через окружность и пересекающая ее в двух точках. Для касательной точку соприкосновения необходимо обозначить А. Тогда секущая пересекает круг в точках В (ближняя) и С (дальняя). В результате этого получается такое соотношение: АМ 2 = АВ * МС.

Когда для произвольной окружности существуют касательная и секущая, тогда между ними образуется некоторый угол.

Хорда, полученная в результате прохождения через окружность, образует также угол. Он опирается на искомую хорду и является вписанным. Следовательно, по свойству градусные меры углов равны между собой. Далее нужно разобрать частные случаи, на основании которых можно сделать вывод о количестве касательных.

Когда окружность вписана в ромб, тогда их точки касания нужно рассматривать по первому свойству. Радиус окружности можно найти по следующим формулам:

1. Через диагонали (d1, d2) и сторону (a): r = (d1 * d2) / 4а.
2. Только по диагоналям: r = (d1 * d2) / [(d1)^2 + (d2)^2]^(½).

Следует отметить, что у ромба две диагонали. Они различаются по размеру. Одна из них больше другой (d1 > d2).

Частные случаи

В некоторых задачах нужно определить количество касательных у двух окружностей. Можно выполнить ряд сложных и трудоемких доказательств. В результате этого будет потрачено много времени, а можно воспользоваться уже готовыми дополнительными свойствами:

1. Четыре касательных: круги не соприкасаются, т. е. d > r1 + r2 (значение диаметра больше суммы радиусов r1 и r2).
2. Две общие внешние и одна внутренняя: окружности соприкасаются только в одной точке (d = r1 + r2).
3. Только две внешние: пересечение окружностей в двух точках (|r1 — r2| d > – r1 — r2).
4. Внутренняя общая (одна): соприкасаются внутри (d = |r2 — r1|).
5. Четыре: при d > |r1 — r2|.

Когда заданы окружности, радиус одной из которых равен 0, тогда «нулевой» круг эквивалентен двойной точке. Прямая является двойной и проходит через эту точку. В этом случае математики определяют всего две внешних. Если r1 = r2 = 0, то всего 4 внешних общих касательных. Далее для решения задач нужно разобрать доказательства некоторых свойств.

Доказательства утверждений

Очень важно знать доказательства некоторых свойств и теорем, поскольку одним из типов задач считаются упражнения повышенной сложности, требующие логических расчетов в общем виде. Например, нужно доказать, что касательная образует с радиусом, проведенным к точке касания, прямой угол. Существует тип доказательства от противного.

Для этого следует предположить, что искомый угол не равен 90 градусам. Пусть дана некоторая касательная р. Она имеет с кругом общую точку А. Нужно провести к ней перпендикуляр (радиус). Далее нужно провести из центра О отрезок ОВ на р. Образуется прямоугольный треугольник АВО с гипотенузой ОВ. Если опираться на утверждение от противного, то гипотенуза будет меньше катета (d 2 + y 2 = 2x + 6y + 19), проходящих через координаты х =0 у= -14. Для решения задачи следует действовать по такому алгоритму:

1. Перенести все слагаемые, кроме 19, в левую сторону: х 2 + y 2 — 2x — 6y = 19.
2. Выделить полный квадрат для окончательной записи уравнения окружности: х 2 — 2x + 1 — 1 + y 2 — 6y +9 — 9 = (х — 1)^2 + (y — 3)^2 = 29.
3. Уравнение прямой, проходящей через (0;-14) в общем виде: y — (-14) = k * (x — 0) или у = кх — 14.
4. Составить систему уравнений: (х — 1)^2 + (y — 3)^2 = 29 и у = кх — 14.
5. Подставить второе в первое: (х — 1)^2 + (кх — 14 — 3)^2 = 29.
6. Упростить выражение: (х — 1)^2 + (кх — 14 — 3)^2 — 29 = х 2 — 2x + 1 +k 2 * x 2 — 34kx + 289 — 29 = (1 + k 2 ) * x 2 — 2 * (17k + 1) + 261.
7. Решением уравнения должен быть один корень: D/4 = 0.
8. Упростить тождество: D/4 = (-(17k + 1))^2 — 261 (1 + k 2 ) = 289k 2 + 34k + 1 — 261 — 261k 2 = 28k 2 + 34k — 260 = 0.
9. Найти значение D: 17 2 — 28 * (-260) = 289 + 7280 = 7569.
10. Первый коэффициент к1 = (-17 — 87) / 28 = -26/7.
11. Коэффициент к2 = (-17 + 87) / 28 = 5/2.
12. Записать уравнения прямых с учетом к1 и к2: у1 = (-26/7) * х — 14 (26х + 7у + 98 = 0) и у2 = (5/2) * х — 14 (5х — 2у — 28 = 0).

Следует отметить, что уравнение окружности с радиусом, равным единице, описывается функцией x 2 + y 2 = 1. Эта запись применяется для решения задач в общем виде. Прямая — функция, описанная прямой пропорциональностью у = кх + b. Чтобы связать окружность и касательные, нужно составить систему уравнений. Этот математический ход объясняется тем, что у функций должны быть общие решения (точка на окружности). После решения можно выполнить проверочные вычисления, подставив корни в систему.

Таким образом, для решения задач об окружности и касательной следует знать общие понятия, а также основные свойства и теоремы.

[spoiler title=”источники:”]

http://urok.1sept.ru/articles/590193

http://nauka.club/matematika/geometriya/kasateln%D0%B0y%D0%B0-k-okruzhnosti.html

[/spoiler]

Касательная к окружности

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Расскажем подробнее, что такое касательная и секущая.

Напомним, что расстояние от точки до прямой — это длина перпендикуляра, опущенного из точки на прямую.

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности. В этом случае она имеет с окружностью ровно одну общую точку. Такую прямую называют касательной к окружности.

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность в двух точках. Такую прямую называют секущей.

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая не имеет с окружностью общих точек.

Запишем основные теоремы о касательных. Они помогут нам при решении задач ЕГЭ и ОГЭ.

Теорема 1.

Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

На рисунке радиус OA перпендикулярен прямой m.

Теорема 2. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Доказательство:

Дана окружность с центром O.

Прямые AB и AC — касательные, точки B и C — точки касания. Докажем, что
AB = AC и

Проведем радиусы OB и OC в точки касания.

По свойству касательной, и .

В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC и

Теорема 3. Отрезки касательных, проведенных к окружности из одной точки, равны.

Доказательство:

Пусть из точки A к окружности проведены касательные AB и AC. Соединим точку A с центром окружности точкой O. Треугольники AOB и AOC равны по гипотенузе и катету, следовательно, AB = AC.

Теорема 4. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

Угол ACМ на рисунке равен половине угловой величины дуги AC.

Доказательство теоремы здесь.

Теорема 5, о секущей и касательной.

Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.

Доказательство теоремы смотрите здесь.

Разберем задачи ЕГЭ и ОГЭ по теме: Касательная к окружности.

Задача 1.

Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Решение:

Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол CAO — прямой. Из треугольника ACO получим, что угол AOC равен 62 градуса. Bеличина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги AB— тоже 62 градуса.

Ответ: 62.

Задача 2.

Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.

Решение:

Это чуть более сложная задача. Центральный угол AOD опирается на дугу AD, следовательно, он равен 116 градусов. Тогда угол AOC равен Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол OAC — прямой. Тогда угол ACO равен

Ответ: 26.

Задача 3.

Хорда AB стягивает дугу окружности в Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Решение:

Проведем радиус OB в точку касания, а также радиус OA. Угол OBC равен Треугольник BOA — равнобедренный. Нетрудно найти, что угол OBA равен 44 градуса, и тогда угол CBA равен 46 градусов, то есть половине угловой величины дуги AB.

Мы могли также воспользоваться теоремой: Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

Задача 4.

К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

Решение:

Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника ABC складывается из периметров отсеченных треугольников.

Ответ: 24.

Вот более сложная задача из вариантов ЕГЭ:

Задача 5.

Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.

Решение:

Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку O — и проведите перпендикулярные сторонам радиусы в точки касания.

Соедините точку O с вершинами A, B, C, D, E. Получились треугольники AOB, BOC, COD, DOE и EOA.

Очевидно, что площадь многоугольника

Треугольники АОВ, ВОС, COD, DOE и ЕОА имеют равные высоты, причем все эти высоты равны радиусу окружности.

где p — полупериметр многоугольника.

По условию, P = 10, S = 5, тогда

Ответ: 1

Задачи ЕГЭ

1. Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B . Найдите величину меньшей дуги AB окружности. Ответ дайте в градусах.

Решение:

По условию, CA — касательная, A — точка касания.

. Треугольник ACO — прямоугольный, .

Угол — центральный, и он равен угловой величине дуги AB, на которую опирается. Значит, градусная мера дуги AB равна . Это меньшая дуга AB, а большая — с другой стороны от точек A и B, и она больше 180 градусов.

Ответ: 63.

2. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна . Найдите угол ACB. Ответ дайте в градусах.

Решение:

Центральный угол AOB равен угловой величине дуги, на которую он опирается, то есть

AC и BC — касательные, поэтому , поскольку касательная перпендикулярна радиусу, проведенному в точку касания.

Сумма углов четырехугольника ACBO равна

Ответ: 122.

3. Хорда AB стягивает дугу окружности в . Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Решение:

Применим теорему об угле между касательной и хордой.

Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.

Значит, угол ABC равен .

Ответ: 46.

4. Через концы A и B дуги окружности с центром О проведены касательные AC и BC. Угол CAB равен . Найдите угол AOB. Ответ дайте в градусах.

Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.

Поэтому меньшая дуга AB окружности равна . Центральный угол равен угловой величине дуги, на которую он опирается, значит, угол AOB равен .

Мы могли бы решить задачу и по-другому, рассматривая четырехугольник ACBO, как в задаче 2.

Ответ: 64.

5. Через концы A, B дуги окружности в проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Решение:

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними. В треугольнике ABC:

Ответ: 118.

6. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, сторона CO пересекает окружность в точках B и D, а дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.

Решение:

По условию, DB — диаметр окружности, поэтому дуга AВ, не содержащая точки D, равна . На эту дугу опирается центральный угол AOB, он равен . Треугольник AOC прямоугольный, так как касательная CA перпендикулярна радиусу ОA, проведенному в точку касания.

Ответ: 26.

Задачи ОГЭ по теме: Касательная к окружности

1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Решение:

Отрезок OB — радиус, проведённый в точку касания, поэтому AB и OB перпендикулярны, треугольник AOB — прямоугольный. По теореме Пифагора:

Ответ: 5.

2. Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный . Найдите величину угла OMK. Ответ дайте в градусах.

Решение:

Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому угол OКD — прямой. Тогда Треугольник OMK — равнобедренный, его стороны OК и OМ являются радиусами окружности, поэтому

Ответ: 7.

3. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Решение:

Касательная перпендикулярна радиусу, проведенному в точку касания, значит, треугольник AOB — прямоугольный. Из прямоугольного треугольника AOB по теореме Пифагора найдём AO:

Ответ: 10.

4. На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

Решение:

Проведём радиус AH в точку касания. Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому треугольник ABН — прямоугольный. Из прямоугольного треугольника ABH по теореме Пифагора найдём BH:

Ответ: 40.

5. Касательные в точках A и B к окружности с центром O пересекаются под углом . Найдите угол ABO. Ответ дайте в градусах.

Решение:

Касательные, проведённые к окружности из одной точки, равны, поэтому AC=BC и треугольник ABC — равнобедренный.

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними, значит, дуга AB равна . Угол AOB — центральный, он равен дуге, на которую опирается, то есть . Треугольник AOB равнобедренный,

Ответ: 36.

6. Из точки A проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен , а расстояние от точки A до точки O равно 8.

Решение:

Проведём радиусы OB и OC в точки касания. Треугольники AOB и AOC — прямоугольные. Эти треугольники равны по катету и гипотенузе.

OB — OC как радиусы окружности, гипотенуза общая. Значит,

Из треугольника AOB найдём OB, то есть радиус окружности.

Ответ: 4.

7. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK.

Решение:

По теореме о секущей и касательной,

Ответ: 4.

8. На окружности отмечены точки A и B так, что меньшая дуга AB равна . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Решение:

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.

Ответ: 36.

Касательная прямая к окружности в евклидовой геометрии на плоскости — прямая, которая имеет с окружностью ровно одну общую точку. Также можно определить касательную как предельное положение секущей, когда точки пересечения её с окружностью бесконечно сближаются. Касательные прямые к окружностям служат предметом рассмотрения ряда теорем и играют важную роль во многих геометрических построениях и доказательствах.

Касательные прямые к одной окружности[править | править код]

Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических преобразованиях^[en], таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.

Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).

Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.

Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.

Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.

Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.

Геометрическое построение[править | править код]

Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.

Для построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.

Теорема об описанном четырёхугольнике и вписанные окружности[править | править код]

Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть

Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a.
Но каждая сторона четырёхугольника состоит из двух таких отрезков

,

что и доказывает утверждение.

Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.^[1]

Эта теорема и обратная к ней имеют различные применения. Например, из теоремы немедленно следует, что ни в какой прямоугольник не может быть вписана окружность, если только это не квадрат, а также что можно вписать окружность в любой ромб, хотя в общем случае вписать в параллелограмм окружность нельзя.

Касательные прямые к двум окружностям[править | править код]

Для двух окружностей в общем случае имеется четыре различные прямые, касательные к обеим окружностям, если одна окружность не лежит в другой, но в вырожденных случаях может быть любое число касательных от нуля до четырёх. Эти случаи описаны ниже. Из четырёх касательных прямых две являются внешними касательными, когда окружности оказываются лежащими по одну сторону от касательной прямой. Для двух других прямых, внутренних касательных, окружности оказываются лежащими по разные стороны от касательной прямой. Внешние касательные пересекаются в центре внешней гомотетии^[en], в то время как внутренние касательные пересекаются в центре внутренней гомотетии. И внутренний, и внешний центры гомотетии лежат на прямой, проходящей через центры окружностей, ближе к центру меньшей окружности. Если две окружности имеют одинаковые радиусы, остаются те же четыре касательных, но внешние касательные прямые параллельны и внешнего центра гомотетии на аффинной плоскости не существует. На проективной плоскости внешний центр гомотетии лежит в бесконечно удалённой точке, соответствующей пересечению прямых.^[2]

Внешняя касательная[править | править код]

Красные прямые, соединяющие точки T₁ и T₃, T₂ и T₄, являются внешними касательными двух окружностей.

Внутренняя касательная[править | править код]

Внутренние касательные — это касательные, которые пересекают отрезок, соединяющий центры окружностей. Заметим, что внутренние касательные не существуют в случае пересекающихся окружностей.

Построение[править | править код]

Касательные к двум окружностям могут быть построены с помощью нахождения центров гомотетии, как описано выше, а затем построения касательных, проходящих через эти центры. Можно также построить касательные прямые и касательные точки прямо, как описано ниже.

Элементарная геометрия[править | править код]

Пусть O₁ и O₂ — два центра двух окружностей C₁ и C₂ и пусть r₁ и r₂ — их радиусы, при этом r₁ > r₂. Другими словами, окружность C₁ будем считать большей из двух окружностей. Два различных способа можно использовать для построения внешних и внутренних касательных прямых.

Внешние касательные

Рисуем новую окружность C₃ с радиусом r₁ − r₂ с центром в O₁. Используя метод, описанный выше, проводим две касательные прямые из точки O₂ к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиусов обеих окружностей C₁ и C₂ на одно и то же число r₂, в результате чего окружность C₂ превращается в точку. Через две точки касания на окружности C₃ можно провести два луча из центра O₁. Эти лучи пересекают C₁ в искомых точках касания. Искомые касательные перпендикулярны этим радиальным лучам и могут быть построены, как показывалось выше.

Внутренние касательные

Рисуем новую окружность C₃ с радиусом r₁ + r₂ с центром в O₁. Используя метод, описанный выше, проводим две касательные прямые из точки O₂ к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиуса окружности C₂ до нуля с одновременным увеличением радиуса C₁ на ту же константу r₂. Два радиальных луча можно провести из центра O₁ через точки касания на C₃. Эти лучи пересекают C₁ в искомых точках касания. Искомые внутренние касательные перпендикулярны радиальным лучам и пересекают лучи в найденных точках, так что их можно построить вышеуказанным методом.

Фактически это то же самое построение, что и для внешних касательных, если принять, что радиус меньшей окружности отрицателен.

Аналитическая геометрия[править | править код]

Пусть окружности имеют центры c₁ = (x₁,y₁) и c₂ = (x₂,y₂) и радиусы r₁ и r₂ соответственно. Пусть касательная прямая имеет уравнение с нормализацией a² + b² = 1, тогда расстояние от центров окружностей до прямой вычисляется по формулам:

ax₁ + by₁ + c = r₁ и

ax₂ + by₂ + c = r₂.

Вычтем первое уравнение из второго, получим

aΔx + bΔy = Δr

где Δx = x₂ − x₁, Δy = y₂ − y₁ и Δr = r₂ − r₁.

Если  — расстояние от c₁ до c₂, мы можем нормализовать, сделав замену X = Δx/d, Y = Δy/d и R = Δr/d для упрощения уравнений, что даёт уравнения aX + bY = R и a² + b² = 1. Решаем их и получаем два решения (k = ±1) для двух внешних касательных линий:

a = RX − kY√(1 − R²)

b = RY + kX√(1 − R²)

c = r₁ − (ax₁ + by₁)

Геометрически это соответствует вычислению угла, образованного касательной и прямой, проведённой через центры, а затем линия центов поворачивается для получения уравнения касательной. Угол можно вычислить с помощью тригонометрии из прямоугольного треугольника, вершинами которого являются (внешний) центр гомотетии, центр окружности и точка касания. Гипотенуза лежит на прямой центров, радиус является катетом, противоположным углу, а прилегающий к углу катет лежит на касательной прямой.

(X, Y) — это единичный вектор, направленный от c₁ в c₂, в то время как R равен , где  — угол между линией центров и касательной. тогда равен (в зависимости от знака , что эквивалентно направлению вращения), и приведённые выше уравнения являются вращением (X, Y) на с помощью матрицы вращения

k = 1 — это касательная прямая справа от окружностей, если смотреть из c₁ в направлении c₂.

k = −1 — это касательная прямая справа от окружностей, если смотреть из c₂ в направлении c₁.

Все рассуждения выше предполагают, что радиусы окружностей положительны. Если r₁ положителен, а r₂ отрицателен, то c₁ будет лежать слева от каждой прямой, а c₂ — справа, и две касательные прямые пересекутся. Таким путём можно получить все четыре решения. Смена знака обоих радиусов приводит к обмену вариантов k = 1 и k = −1.

Векторы[править | править код]

В общем случае точки касания t₁ и t₂ для любой из четырёх касательных прямых к окружностям с центрами в v₁ и v₂ и с радиусами r₁ и r₂ получаются путём решения четырёх уравнений:

Эти уравнения выражают тот факт, что касательная прямая перпендикулярна радиусам, а точки касания лежат на соответствующих окружностях.

Эти четыре квадратных уравнения с двумерными векторными переменными в общем случае дают четыре пары решений.

Вырожденные случаи[править | править код]

Две различные окружности могут иметь, в зависимости от взаимного расположения, от нуля до четырёх прямых, касающихся обеих окружностей. Варианты можно классифицировать по расстоянию между центрами и радиусам.

И наконец, если окружности совпадают, любая касательная прямая к одной окружности будет общей касательной.

Далее понятие общей касательной прямой можно расширить на случай окружностей отрицательного радиуса (которые образованы теми же самыми точками но «наизнанку»). В этом случае, если радиусы имеют противоположные знаки (одна окружность имеет положительный радиус, другая — отрицательный) внешний и внутренний центры гомотетии меняются местами и внешние и внутренние общие касательные меняются местами. Если же радиусы имеют один и тот же знак (оба радиуса положительны или оба отрицательны), то понятия «внешний» и «внутренний» имеют обычный смысл.

Общие касательные можно определить для окружностей с нулевым радиусом. В этом случае окружность с нулевым радиусом трактуется как двойная точка, а потому любая прямая, проходящая через эту точку, пересекает её с кратностью^[en] два. Если окружность имеет радиус ноль, общая касательная прямая — это просто касательная прямая к окружности, проходящая через точку, но считается эта прямая дважды. Если обе окружности имеют нулевой радиус, то общая касательная прямая — это прямая, проходящая через две точки, и эта прямая имеет кратность четыре.

Заметим, что в этих вырожденных случаях внешний и внутренний центры гомотетии остаются (внешний центр уходит в бесконечность, если радиусы равны), за исключением случая, когда окружности совпадают (в этом случае внешний центр не определён), или когда обе окружности имеют нулевой радиус (в этом случае отсутствует внутренний центр).

Приложения[править | править код]

Задача о ремённой передаче[править | править код]

Внутренние и внешние касательные полезны при решении задачи о ремённой передаче^[en], которая заключается в вычислении длины ремня, который плотно бы прилегал к колёсам передачи. Если считать ремень математической кривой с пренебрежительно малой толщиной и если колёса передачи находятся точно в одной плоскости, задача сводится к суммированию отрезков касательных с соответствующими длинами дуг. Если ремень натянут на колёса с пересечением, необходимо рассматривать внутренние касательные. Если же ремень натянут без пересечения, необходимо рассматривать внешние касательные. Последний случай иногда называется задачей шкивов.

Касательные прямые к трём окружностям: теорема Монжа[править | править код]

Для трёх окружностей C₁, C₂ и C₃ существует три пары окружностей (C₁C₂, C₂C₃ и C₁C₃). Поскольку каждая пара окружностей имеет два центра гомотетии, всего получим шесть центров гомотетии^[en]. Гаспар Монж показал в начале 19-го века, что эти шесть точек лежат на четырёх прямых, и на каждой прямой лежат три точки.

Касательные прямые и бильярд[править | править код]

Система касательных прямых прицеливания битка использует прямую, проходящую через середину кия, для создания двух касательных прямых от битка в направлении прицельного шара. Две касательные прямые и прямая через середину битка пересекают прямую, проходящую через середину прицельного шара и центр лузы. Необходимо направить удар так, чтобы конечное положение битка (воображаемый шар на рисунке) касалось прицельного шара в точке касания прямой, перпендикулярной направлению на лузу (на рисунке эта касательная выделена зелёным цветом).

Задача Аполлония[править | править код]

Много частных случаев задачи Аполлония используют нахождение окружностей, касающихся одной или нескольких прямых. В простейшем из этих случаев строится окружность, касающаяся трёх заданных прямых (задача LLL). Центр любой такой окружности должен лежать на биссектрисе угла в точке пересечения любой пары этих прямых. В каждой точке пересечения прямых есть две биссектрисы. Пересечения этих биссектрис дают центры окружностей, являющихся решением. В общем случае существует четыре таких окружностей для треугольника, образованного пересечением трёх прямых — вписанная окружность и три вневписанных.

В общем случае задачу Аполлония можно свести к более простой задаче построения окружности, касающейся одной окружности и двух параллельных прямых (это сам по себе частный случай LLC). Чтобы это сделать, увеличиваем пропорционально^[en] две из этих трёх заданных окружностей вплоть до их касания. Инверсия относительно окружности подходящего радиуса с центром в точке касания переводит эти две окружности в две параллельные прямые, а третью окружность — в другую окружность. Таким образом, решение может быть найдено путём перемещения окружности постоянного радиуса между двумя параллельными прямыми, пока не получим касание с преобразованной третьей окружностью. Обратная инверсия даст решения исходной задачи.

Обобщения[править | править код]

Понятие касательной прямой к одной и более окружностям можно обобщить несколькими путями. В первую очередь, свойство парности касательных прямых и точек касания можно обобщить до полюса и полярной прямой, когда полюс может находиться в любом месте, не обязательно на окружности. Во-вторых, объединение двух окружностей является особым (приводимым^[en]) случаем плоской кривой четвёртой степени, а внешние и внутренние касательные прямые являются касательными к двум точкам^[en] этой кривой. В общем случае плоская кривая четвёртой степени имеет 28 прямых, касающихся её дважды.

Третье обобщение относится скорее к касательным окружностям, а не к касательным прямым. Касательную прямую можно рассматривать как касательную окружность с бесконечным радиусом. В частности, внешние касательные прямые к двум окружностям можно рассматривать как частные случаи из семейства окружностей, касающихся с внутренней или внешней стороны обеих окружности, в то время как внутренние касательные прямые можно рассматривать как частные случаи семейства окружностей, касающихся с внутренней стороны одной окружности и с внешней стороны другой) ^[3].

В геометрии Мёбиуса или инверсной геометрии прямые рассматриваются как окружности с центром «в бесконечности» и для любой прямой и для любой окружности существует преобразование Мёбиуса, которое переводит одну фигуру в другую. В геометрии Мёбиуса касание прямой и окружности становится особым случаем касания двух окружностей. Эта эквивалентность развивается далее в сферической геометрии Ли^[en].

Примечания[править | править код]

Литература[править | править код]

• Paul Kunkel. The tangency problem of Apollonius: three looks // BSHM Bulletin: Journal of the British Society for the History of Mathematics. — 2007. — Т. 22, вып. 1. — doi:10.1080/17498430601148911.
• David Fraivert. Properties of the tangents to a circle that forms Pascal points on the sides of a convex quadrilateral // Forum Geometricorum. — 2017. — Vol. 17. — P. 223–243.
• Shlomo Libeskind. Euclidean and Transformational Geometry: A Deductive Inquiry. — 2007.

См. также[править | править код]

• Степень точки относительно окружности
• окружность
• Радикальная ось
• Радикальный центр

Ссылки[править | править код]

• Weisstein, Eric W. Tangent lines to one circle (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Tangent lines to two circles (англ.) на сайте Wolfram MathWorld.

Угол между касательной и хордой

Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла.

Прежде всего: как это понимать? Подробнее о том, что такое «градусная мера дуги», написано в теме «Окружность. Вписанный угол».

Здесь напомним только, что в дуге столько же градусов, сколько в центральном угле, заключающем эту дугу. 

То есть «градусная мера дуги» – это «сколько градусов в центральном угле» – и всё!

Ну вот, как говорит Карлсон, продолжаем разговор. Рисуем ещё раз теорему об угле между касательной и хордой.

Смотри, хорда ( displaystyle AB) разбила окружность на две дуги. Одна дуга находится ВНУТРИ угла ( displaystyle BAC), а другая дуга – внутри угла ( displaystyle BAD).

И теорема об угле между касательной и хордой говорит, что ( displaystyle angle CAB) равен ПОЛОВИНЕ угла ( displaystyle AOB), ( displaystyle angle DAB) равен ПОЛОВИНЕ большего (на рисунке — зеленого) угла ( displaystyle AOB).

При чем же тут тот факт, что радиус, проведенный в точку касания, перпендикулярен касательной?

Сейчас и увидим. ( displaystyle OA) – радиус, ( displaystyle AC) – касательная.

Значит, ( displaystyle angle OAC=90{}^circ ).

Поэтому:( displaystyle angle 1=90{}^circ -angle 4).

Но ( displaystyle angle 2=angle 1) (( displaystyle OA) и ( displaystyle OB) – радиусы)( displaystyle angle 2=90{}^circ -angle 4).

И осталось вспомнить, что сумма углов треугольника ( displaystyle AOB) равна ( displaystyle 180{}^circ ).

Пишем:

Короче:

Здорово, правда? И самым главным оказалось то, что ( displaystyle angle OAC=90{}^circ ).

Равенство отрезков касательных

Задумывался ли ты над вопросом «а сколько касательных можно провести из одной точки к одной окружности»? Вот, представь себе, ровно две! Вот так:

А ещё более удивительный факт состоит в том, что:

Отрезки касательных, проведённых из одной точки к одной окружности, равны.

То есть, на нашем рисунке, ( displaystyle AB=AC).

И для этого факта тоже самым главным является то, что радиус, проведённый в точку касания, перпендикулярен касательной.

Вот, убедись.

Проведём радиусы ( displaystyle OB) и ( displaystyle OC) и соединим ( displaystyle O) и ( displaystyle A).

( displaystyle OB) – радиус.

( displaystyle AB) – касательная, значит, ( displaystyle OBbot AB).
Ну, и так же ( displaystyle OCbot AC).

Получилось два прямоугольных треугольника ( displaystyle AOB) и ( displaystyle AOC), у которых:

( displaystyle Rightarrow Delta AOB = Delta AOC)

(заглядываем в тему «Прямоугольный треугольник«, если не помним, когда бывают равны прямоугольные треугольники).

Но раз ( displaystyle Delta AOB=Delta AOC,) то( displaystyle AB=AC). УРА!

И ещё раз повторим – этот факт тоже очень важный:

Отрезки касательных, проведённых из одной точки, – равны.

И есть ещё один факт, который мы здесь не будем доказывать, но он может оказаться тебе полезен при решении задач.

Для любой прямой ( displaystyle AD), пересекающей окружность,( displaystyle ADcdot AC=A{{B}^{2}}), где ( displaystyle AB) – отрезок касательной.

Хитроумными словами об этом говорят так:

«Квадрат длины отрезка касательной равен произведению секущей на её внешнюю часть».

Страшно? Не бойся, помни только, что в буквах это:

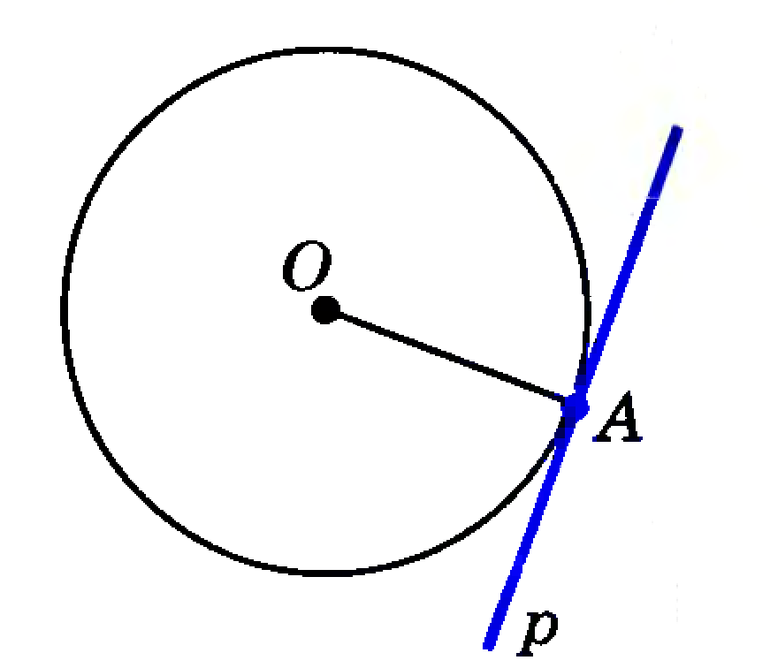
Общие сведения

Важно знать терминологию, соотношения и теоремы для решения задач этого класса. Касательной к окружности называется прямая, которая имеет с ней только одну точку соприкосновения. Прямая — это линия, не имеющая границ, т. е. она ничем не ограничена. Окружностью называется геометрическое место точек, удаленных от центра на одинаковые расстояния.

Следует отметить, что касательные бывают внешними и внутренними. Внешней называет прямая линия, проходящая с внешней стороны окружности. Внутренние касательные пересекают отрезок, который соединяет центры двух окружностей. Последний тип прямых не существует, когда два круга пересекаются. Касательные нужно уметь правильно строить, поскольку от этого зависит правильность решения задачи.

Построение касательных

Для построения касательной к окружности следует на последней отметить произвольную точку. Затем необходимо через нее провести прямую. Нужно отметить, что у круга может быть несколько таких прямых. Когда даны две окружности, тогда можно проводить не только внешние, но и внутренние. Существует определенный алгоритм, по которому можно построить первый тип:

1. Начертить 2 окружности с центрами в точках О1 и О2. При этом должно соблюдаться условие r1 > r2, где r1 и r2 — радиусы I и II соответственно.
2. Нарисовать III окружность с центром в О1 и радиусом r3 = r1 — r2.
3. Провести 2 касательные из точки О2 к III. Они параллельны искомым, поскольку радиусы I и II уменьшаются на r2.

Существует более простая модель построения таких прямых. Для этого следует начертить один круг, а затем отметить две произвольные точки на его противоположных сторонах. Далее начертить II круг, превышающий I по радиусу. Отметить на нем точки, воспользовавшись подобием, т. е. они должны быть в тех же местах, что и на I. Затем провести прямые, которые должны соприкасаться с I и II кругами только в одной точке.

Для построения внутренних касательных существует определенная методика. В интернете можно найти много информации. В одних источниках алгоритм построения является сложным, а в других — простым. Однако есть один метод, позволяющий осуществить данную операцию. Специалисты описали его на «понятном» языке для новичков. Суть методики заключается в следующем:

1. Необходимо построить два круга, которые не пересекаются, с радиусами r1 и r2. Расстояния между ними должно составлять r1 + r2.
2. Соединить их центры (середины) отрезком.
3. Отметить на нем среднюю точку, которая делит его на две равные части.
4. Через точку, полученную на третьем шаге методики, провести прямую. Она должна иметь только одну точку соприкосновения с I и II окружностями.
5. Аналогично провести еще одну прямую.
6. Искомые прямые являются внутренними касательными.

Далее нужно рассмотреть некоторые свойства, на основании которых можно решать задачи и доказывать геометрические тождества.

Основные свойства

Свойства — утверждения, полученные в результате доказательства теорем о касательной к окружности. Первые нет необходимости доказывать, поскольку об этом уже позаботились математики. Они выделяют всего 4 свойства касательных к окружности:

1. Если провести из одной точки две касательные к некоторой окружности, то отрезки, лежащие на них, будут равны. Искомый угол будет делиться радиусом пополам.
2. Любая касательная и радиус, проведенный к ее точке, образуют прямой угол. Справедливо и обратное утверждение: радиус, который проведен в точку касания, перпендикулярен данной прямой.
3. Вся секущая, умноженная на свою внешнюю часть, равна квадрату расстояния касательной, которая проведена из общей с ней точки.
4. Образованный угол между касательной и секущей, эквивалентен градусной мере угла, который опирается на образованную хорду.

Для рассмотрения I свойства необходимо начертить окружность с центром О1. Затем нужно отметить точку М вне окружности. Из М провести одну прямую, которая соприкасается с кругом в точке А. Такую же операцию следует проделать и для другой касательной. Точку соприкосновения назвать В. Отрезки АМ и ВМ равны между собой.

Если провести радиусы к точкам А и В, то можно сделать вывод, что углы являются прямыми. Чтобы понять третье свойство, необходимо начертить окружность и отметить некоторую точку М за ее пределами. После этого следует из искомой точки провести секущую и касательную. Первой называется прямая, проходящая через окружность и пересекающая ее в двух точках. Для касательной точку соприкосновения необходимо обозначить А. Тогда секущая пересекает круг в точках В (ближняя) и С (дальняя). В результате этого получается такое соотношение: АМ ² = АВ * МС.

Когда для произвольной окружности существуют касательная и секущая, тогда между ними образуется некоторый угол.

Хорда, полученная в результате прохождения через окружность, образует также угол. Он опирается на искомую хорду и является вписанным. Следовательно, по свойству градусные меры углов равны между собой. Далее нужно разобрать частные случаи, на основании которых можно сделать вывод о количестве касательных.

Когда окружность вписана в ромб, тогда их точки касания нужно рассматривать по первому свойству. Радиус окружности можно найти по следующим формулам:

1. Через диагонали (d1, d2) и сторону (a): r = (d1 * d2) / 4а.
2. Только по диагоналям: r = (d1 * d2) / [(d1)^2 + (d2)^2]^(½).

Следует отметить, что у ромба две диагонали. Они различаются по размеру. Одна из них больше другой (d1 > d2).

Частные случаи

В некоторых задачах нужно определить количество касательных у двух окружностей. Можно выполнить ряд сложных и трудоемких доказательств. В результате этого будет потрачено много времени, а можно воспользоваться уже готовыми дополнительными свойствами:

1. Четыре касательных: круги не соприкасаются, т. е. d > r1 + r2 (значение диаметра больше суммы радиусов r1 и r2).
2. Две общие внешние и одна внутренняя: окружности соприкасаются только в одной точке (d = r1 + r2).
3. Только две внешние: пересечение окружностей в двух точках (|r1 — r2| < d < r1 + r2).
4. Одна общая внешняя: окружности касаются внутри друг друга (d = |r1 — r2|).
5. Отсутствуют: один круг находится внутри другого (d < |r1 — r2|).

В последнем случае любая касательная будет являться секущей для другой окружности. Существует еще одно положение, когда окружности совпадают. Тогда любая касательная считается общей. В высшей математике разбирается также «отрицательный» радиус. Тогда вышеперечисленные свойства можно править следующим образом:

1. Нет касательных: окружности не соприкасаются, и для них выполняется условие d < – (r1 + r2).
2. Две внутренние (общие) и одна внешняя: круги соприкасаются в одной точке (d = -r1 — r2).
3. Одна пара внутренних: пересечение в 2 точках (|r1 — r2| > d > – r1 — r2).
4. Внутренняя общая (одна): соприкасаются внутри (d = |r2 — r1|).
5. Четыре: при d > |r1 — r2|.

Когда заданы окружности, радиус одной из которых равен 0, тогда «нулевой» круг эквивалентен двойной точке. Прямая является двойной и проходит через эту точку. В этом случае математики определяют всего две внешних. Если r1 = r2 = 0, то всего 4 внешних общих касательных. Далее для решения задач нужно разобрать доказательства некоторых свойств.

Доказательства утверждений

Очень важно знать доказательства некоторых свойств и теорем, поскольку одним из типов задач считаются упражнения повышенной сложности, требующие логических расчетов в общем виде. Например, нужно доказать, что касательная образует с радиусом, проведенным к точке касания, прямой угол. Существует тип доказательства от противного.

Для этого следует предположить, что искомый угол не равен 90 градусам. Пусть дана некоторая касательная р. Она имеет с кругом общую точку А. Нужно провести к ней перпендикуляр (радиус). Далее нужно провести из центра О отрезок ОВ на р. Образуется прямоугольный треугольник АВО с гипотенузой ОВ. Если опираться на утверждение от противного, то гипотенуза будет меньше катета (d < r). Однако радиус не может быть больше диаметра, поскольку он рассчитывается по следующей формуле: d = 2 * r. Следовательно, утверждение доказано.

Аналогично доказывается и обратное свойство. Его формулировка имеет такой вид: прямая, проходящая под прямым углом через точку, которая образована радиусом, является касательной. В этом случае можно доказывать не от противного. Расстояние от прямой до центра окружности эквивалентно некоторой величине и является радиусом. Из определения следует, что прямая и окружность имеют общую точку, и только одну. Следовательно, она и есть касательная.

Доказательство об отрезках, проведенных из одной точки, тоже нужно разобрать, поскольку такой прием применяется в решении сложных задач. Отрезки равны между собой и образуют с прямой, проведенной к центру круга, эквивалентные углы.

Следует выполнить построение окружности с центром Р. Далее нужно обозначить точку А за ее пределами и провести из нее лучи-касательные к искомой окружности. Они образуют на круге точки А и В. Кроме того, следует доказать равенство углов ОАВ и САО. При построении образовалось два треугольника ОВА и ОСА. Фигуры являются прямоугольными на основании свойства о касательной и радиусе.

Далее необходимо доказать равенство фигур ОВА и ОСА. Это сделать довольно просто: гипотенуза — общая, катеты ОВ и ОС равны (радиусы) и углы АВО = АСО = 90. Следовательно, они равны по первому признаку, а также эквивалентны друг другу стороны АВ и АС. Кроме того, угол ОАВ = САО. Утверждение доказано. Гипотенуза является также и биссектрисой. В некоторых источниках можно встретить доказательство равенства тангенсов углов.

Пример решения задачи

Нужно составить уравнения касательных к окружности (описанной графиком функции х ² + y ² = 2x + 6y + 19), проходящих через координаты х =0 у= -14. Для решения задачи следует действовать по такому алгоритму:

1. Перенести все слагаемые, кроме 19, в левую сторону: х ² + y ² — 2x — 6y = 19.
2. Выделить полный квадрат для окончательной записи уравнения окружности: х ² — 2x + 1 — 1 + y ² — 6y +9 — 9 = (х — 1)^2 + (y — 3)^2 = 29.
3. Уравнение прямой, проходящей через (0;-14) в общем виде: y — (-14) = k * (x — 0) или у = кх — 14.
4. Составить систему уравнений: (х — 1)^2 + (y — 3)^2 = 29 и у = кх — 14.
5. Подставить второе в первое: (х — 1)^2 + (кх — 14 — 3)^2 = 29.
6. Упростить выражение: (х — 1)^2 + (кх — 14 — 3)^2 — 29 = х ² — 2x + 1 +k ² * x ² — 34kx + 289 — 29 = (1 + k ² ) * x ² — 2 * (17k + 1) + 261.
7. Решением уравнения должен быть один корень: D/4 = 0.
8. Упростить тождество: D/4 = (-(17k + 1))^2 — 261 (1 + k ² ) = 289k ² + 34k + 1 — 261 — 261k ² = 28k ² + 34k — 260 = 0.
9. Найти значение D: 17 ² — 28 * (-260) = 289 + 7280 = 7569.
10. Первый коэффициент к1 = (-17 — 87) / 28 = -26/7.
11. Коэффициент к2 = (-17 + 87) / 28 = 5/2.
12. Записать уравнения прямых с учетом к1 и к2: у1 = (-26/7) * х — 14 (26х + 7у + 98 = 0) и у2 = (5/2) * х — 14 (5х — 2у — 28 = 0).

Следует отметить, что уравнение окружности с радиусом, равным единице, описывается функцией x² + y ² = 1. Эта запись применяется для решения задач в общем виде. Прямая — функция, описанная прямой пропорциональностью у = кх + b. Чтобы связать окружность и касательные, нужно составить систему уравнений. Этот математический ход объясняется тем, что у функций должны быть общие решения (точка на окружности). После решения можно выполнить проверочные вычисления, подставив корни в систему.

Таким образом, для решения задач об окружности и касательной следует знать общие понятия, а также основные свойства и теоремы.