Кинематическая вязкость как найти

Кинематическая вязкость как найти

Вязкость жидкости

Вязкость жидкости

Вязкость жидкости – это свойство реальных жидкостей оказывать сопротивление касательным усилиям (внутреннему трению) в потоке. Вязкость жидкости не может быть обнаружена при покое жидкости, так как она проявляется только при её движении. Для правильной оценки таких гидравлических сопротивлений, возникающих при движении жидкости, необходимо прежде всего установить законы внутреннего трения жидкости и составить ясное представление о механизме самого движения.

Содержание статьи

  • Физический смысл вязкости
  • Вязкость кинематическая, динамическая и абсолютная
  • Коэффициент вязкости жидкости
  • Методы измерения вязкости. Метод Стокса
  • Видео о вязкости

Физический смысл вязкости

Для понятия физической сущности такого понятия как вязкость жидкости рассмотрим пример. Пусть есть две параллельные пластинки А и В. В пространство между ними заключена жидкость: нижняя пластинка неподвижна, а верхняя пластинка движется с некоторой постоянной скоростью υ1

Вязкость жидкости

Как при этом показывает опыт, слои жидкости, непосредственно прилегающие к пластинкам (так называемые прилипшие слои), будут иметь одинаковые с ним скорости, т.е. слой, прилегающий к нижней пластинке А, будет находиться в покое, а слой, примыкающий к верхней пластинке В, будет двигаться со скоростью υ1.

Промежуточные слои жидкости будут скользить друг по другу, причем их скорости будут пропорциональны расстояниям от нижней пластинки.

Ещё Ньютоном было высказано предположение, которое вскоре подтвердилось опытом, что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. Если взять площадь соприкосновения равной единице, это положение можно записать в виде

Вязкость жидкости

где τ – сила сопротивления, отнесенная к единице площади, или напряжение трения

μ – коэффициент пропорциональности, зависящий от рода жидкости и называемый коэффициентом абсолютной вязкости или просто абсолютной вязкостью жидкости.

Величину dυ/dy – изменение скорости в направлении, нормальном к направлению самой скорости, называют скоростью скольжения.

Таким образом вязкость жидкости – это физическое свойство жидкости, характеризующее их сопротивление скольжению или сдвигу

Вязкость кинематическая, динамическая и абсолютная

Теперь определимся с различными понятиям вязкости:

Динамическая вязкость. Единицей измерения этой вязкости является паскаль в секунду (Па*с). Физический смысл состоит в снижении давления в единицу времени. Динамическая вязкость характеризует сопротивление жидкости (или газа) смещению одного слоя относительно другого.

Динамическая вязкость зависит от температуры. Она уменьшается при повышении температуры и увеличивается при повышении давления.

Кинематическая вязкость. Единицей измерения является Стокс. Кинематическая вязкость получается как отношение динамической вязкости к плотности конкретного вещества.

Определение кинематической вязкости производится в классическом случае измерением времени вытекания определенного объема жидкости через калиброванное отверстие при воздействии силы тяжести

Абсолютная вязкость получается при умножении кинематической вязкости на плотность. В международной системе единиц абсолютная вязкость измеряется в Н*с/м2 – эту единицу называют Пуазейлем.

Коэффициент вязкости жидкости

В гидравлике часто используют величину, получаемую в результате деления абсолютной вязкости на плотность. Эту величину называют коэффициентом кинематической вязкости жидкости или просто кинематической вязкостью и обозначают буквой ν. Таким образом кинематическая вязкость жидкости

ν = μ / ρ,

где ρ – плотность жидкости.

Единицей измерения кинематической вязкости жидкости в международной и технической системах единиц служит величина м2/с.

В физической системе единиц кинематическая вязкость имеет единицу измерения см2/с и называется Стоксом(Ст).

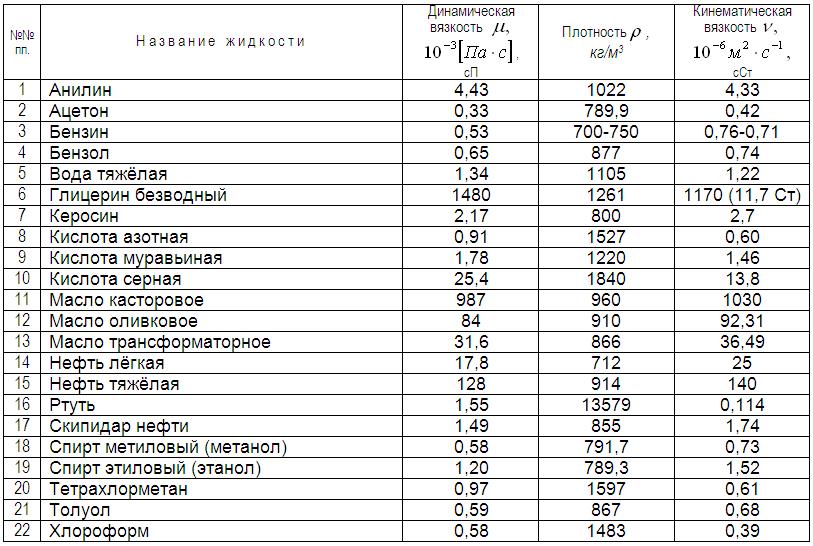
Вязкость некоторых жидкостей

Жидкость t, °С ν, Ст
Вода 0 0,0178
Вода 20 0,0101
Вода 100 0,0028
Бензин 18 0,0065
Спирт винный 18 0,0133
Керосин 18 0,0250
Глицерин 20 8,7
Ртуть 0 0,00125

Величину, обратную коэффициенту абсолютной вязкости жидкости, называют текучестью

ξ = 1/μ

Как показывают многочисленные эксперименты и наблюдения, вязкость жидкости уменьшается с увеличением температуры. Для различных жидкостей зависимость вязкости от температуры получается различной.

Поэтому, при практических расчетах к выбору значения коэффициента вязкости следует подходить очень осторожно. В каждом отдельном случае целесообразно брать за основу специальные лабораторные исследования.

Вязкость жидкостей, как установлено из опытов, зависит так же и от давления. Вязкость возрастает при увеличении давления. Исключение в этом случае является вода, для которой при температуре до 32 градусов Цельсия с увеличением давления вязкость уменьшается.

Что касается газов, то зависимость вязкости от давления, так же как и от температуры, очень существенна. С увеличением давления кинематическая вязкость газов уменьшается, а с увеличением температуры, наоборот, увеличивается.

Методы измерения вязкости. Метод Стокса.

Вязкость жидкости

Область, посвященная измерению вязкости жидкости, называется вискозиметрия, а прибор для измерения вязкости называется вискозиметр.

Современные вискозиметры изготавливаются из прочных материалов, а при их производстве используются самые современные технологии, для обеспечение работы с высокой температурой и давлением без вреда для оборудования.

Существует следующие методы определения вязкости жидкости.

Капиллярный метод.

Сущность этого метода заключается в использовании сообщающихся сосудов. Два сосуда соединяются стеклянной трубкой известного диаметра и длины. Жидкость помещается в стеклянный канал и за определенный промежуток времени перетекает из одного сосуда в другой. Далее зная давление в первом сосуде и воспользовавшись для расчетов формулой Пуазейля определяется коэффициент вязкости.

Метод по Гессе.

Этот метод несколько сложнее предыдущего. Для его выполнения необходимо иметь две идентичные капиллярные установки. В первую помещают среду с заранее известным значением внутреннего трения, а во вторую – исследуемую жидкость. Затем замеряют время по первому методу на каждой из установок и составляя пропорцию между опытами находят интересующую вязкость.

Ротационный метод.

Для выполнения этого метода необходимо иметь конструкцию из двух цилиндров, причем один из них должен быть расположен внутри другого. В промежуток между сосудами помещают исследуемую жидкость, а затем придают скорость внутреннему цилиндру.

Жидкость вращается вместе с цилиндром со своей угловой скоростью. Разница в силе момента цилиндра и жидкости позволяет определить вязкость последней.

Метод Стокса

вискозиметр Гепплера

Для выполнения этого опыта потребуется вискозиметр Гепплера, который представляет из себя цилиндр, заполненный жидкостью.

Вначале делаются две пометки по высоте цилиндра и замеряют расстояние между ними. Затем шарик определенного радиуса помещается в жидкость. Шарик начинает погружаться в жидкость и проходит расстояние от одной метки до другой. Это время фиксируется. Определив скорость движения шарика затем вычисляют вязкость жидкости.

Видео по теме вязкости

Определение вязкости играет большую роль в промышленности, поскольку определяет конструкцию оборудования для различных сред. Например, оборудование для добычи, переработки и транспортировки нефти.

Вместе со статьей “Вязкость жидкости” читают:

Источник
Механика сплошных сред
BernoullisLawDerivationDiagram.svg
Сплошная среда

Классическая механика

Закон сохранения массы · Закон сохранения импульса

Теория упругости

Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость

Гидродинамика

Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение

Основные уравнения

Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука

См. также: Портал:Физика

Поведение жидкости с малой (сверху) и с большой (снизу) вязкостью

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате макроскопическая работа, затрачиваемая на это перемещение, рассеивается в виде тепла. Твёрдые тела (стекло, металлы, полупроводники, диэлектрики, ферромагнетики)[1] также могут обладать вязкостью, но внутреннее трение в твёрдых телах в силу специфики явления обычно рассматривается отдельно в теории упругости и пластичности.

Механизм внутреннего трения в жидкостях и газах заключается в том, что движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Вязкость газов и жидкостей характеризуют динамическим коэффициентом вязкости (единица измерения в Международной системе единиц (СИ) — паскаль-секунда, Па·с, в системе СГС — пуаз, П; 1 Па·с = 10 П, 1 сП = 10−3 Па·с = 1 мПа·с) или кинематическим коэффициентом вязкости (единица измерения в СИ — м2/c, в СГС — стокс, Ст; 1 Ст = см2/с = 10−4 м2/с, 1 сСт = 1 мм2/с = 10−6 м2/с; внесистемная единица — градус Энглера). Кинематический коэффициент вязкости — отношение динамического коэффициента к плотности вещества. Классические методы измерения вязкости включают, например, измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 1011—1012 Па·с.

Сила вязкого трения[править | править код]

Если параллельные плоские тела площадью S каждое, находящиеся на малом расстоянии h, движутся в той же плоскости со скоростью vec{v} друг относительно друга, а пространство между телами заполнено жидкостью или газом, то на каждое из них действует сила, в простейшем случае пропорциональная относительной скорости vec{v} и площади S и обратно пропорциональная расстоянию между телами h:

{displaystyle {vec {F}}sim -{frac {{vec {v}}cdot S}{h}}.}

Коэффициент пропорциональности, зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости. Этот закон был предложен Исааком Ньютоном в 1687 году и носит его имя (закон вязкости Ньютона). Экспериментальное подтверждение закона было получено в начале XIX века в опытах Кулона с крутильными весами и в экспериментах Хагена и Пуазёйля с течением воды в капиллярах[2].

Эта сила называется силой вязкого трения. Её качественное отличие от сухого трения, кроме прочего, в том, что она пропорциональна скорости. Следовательно, при наличии только вязкого трения и сколь угодно малой внешней силы тело обязательно придёт в движение, то есть для вязкого трения не существует трения покоя.

Вторая вязкость[править | править код]

Вторая вязкость, или объёмная вязкость, — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и (или) при учёте неоднородности коэффициента второй вязкости по пространству.

Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.

Объёмная вязкость играет большую роль в затухании звука и ударных волн и экспериментально определяется путём измерения этого затухания.

Вязкость газов[править | править код]

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

{displaystyle eta ={frac {1}{3}}langle urangle langle lambda rangle rho ,}

где {displaystyle langle urangle } — средняя скорость теплового движения молекул, {displaystyle langle lambda rangle } − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность rho прямо пропорциональна давлению, а длина пробега {displaystyle langle lambda rangle } — обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа u, растущей с температурой как {sqrt {T}}.

Влияние температуры на вязкость газов[править | править код]

В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:[3]

{displaystyle mu =mu _{0}{frac {T_{0}+C}{T+C}}left({frac {T}{T_{0}}}right)^{3/2},}

где

mu  — динамическая вязкость (в Па·с) при заданной температуре T;
mu _{0} — контрольная вязкость (в Па·с) при некоторой контрольной температуре T_{0};
T — заданная температура в кельвинах;
T_{0} — контрольная температура в кельвинах;
C — постоянная Сазерленда для того газа, вязкость которого требуется определить.

Эту формулу можно применять для температур в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10 %, обусловленной зависимостью вязкости от давления.

Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже:

Газ C, K T_{0}, K mu _{0}, мкПа·с
Воздух 120 291,15 18,27
Азот 111 300,55 17,81
Кислород 127 292,25 20,18
Углекислый газ 240 293,15 14,8
Угарный газ 118 288,15 17,2
Водород 72 293,85 8,76
Аммиак 370 293,15 9,82
Оксид серы(IV) 416 293,65 12,54
Гелий 79,4[4] 273 19[5]

Вязкость жидкостей[править | править код]

Динамическая вязкость[править | править код]

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Для так называемых ньютоновских жидкостей (которых вокруг нас большинство) справедлив общий закон внутреннего трения — закон Ньютона:

{displaystyle tau =-eta {frac {partial v}{partial n}}.}

Коэффициент вязкости eta (коэффициент динамической вязкости, динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что eta будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля — Андраде:

{displaystyle eta =Ce^{w/kT}.}

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским[6]. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества {displaystyle V_{M}}. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

{displaystyle eta ={frac {c}{V_{M}-V_{C}}},}

где:

c — константа, характерная для определённой жидкости;
{displaystyle V_{C}} — собственный объём, занимаемый частицами жидкости.

Динамическая вязкость жидкостей уменьшается с увеличением температуры и растёт с увеличением давления.

Кинематическая вязкость[править | править код]

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной

nu ={frac {eta }{rho }},

и эта величина получила название кинематической вязкости[7].

Здесь rho  — плотность жидкости; eta  — коэффициент динамической вязкости.

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом: 1 сСт = 1 мм2/c = 10−6 м2/c.

Условная вязкость[править | править код]

Условная вязкость — величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма раствора через вертикальную трубку (определённого диаметра). Измеряют в градусах Энглера (по имени немецкого химика К. О. Энглера), обозначают — °ВУ. Определяется отношением времени истечения 200 мл испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 мл дистиллированной воды из того же прибора при 20 °С. Условную вязкость до 16 °ВУ переводят в кинематическую по таблице ГОСТ, а условную вязкость, превышающую 16 °ВУ, по формуле

{displaystyle nu =7,4cdot 10^{-6}E_{t},}

где nu  — кинематическая вязкость (в м2/с), а {displaystyle E_{t}} — условная вязкость (в °ВУ) при температуре t.

Ньютоновские и неньютоновские жидкости[править | править код]

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье — Стокса[8]):

{displaystyle sigma _{ij}=eta left({frac {partial v_{i}}{partial x_{j}}}+{frac {partial v_{j}}{partial x_{i}}}right),}

где sigma_{ij} — тензор вязких напряжений.

Среди неньютоновских жидкостей по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.[источник не указан 1007 дней]

Вязкость аморфных материалов[править | править код]

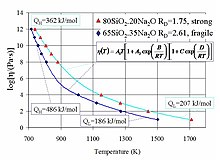
Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс[9]:

{displaystyle eta (T)=Aexp left({frac {Q}{RT}}right),}

где

Q — энергия активации вязкости (Дж/моль);
T — температура (К);
R — универсальная газовая постоянная (8,31 Дж/моль·К);
A — некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости Q изменяется от большой величины Q_{H} при низких температурах (в стеклообразном состоянии) на малую величину Q_{L} при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда {displaystyle (Q_{H}-Q_{L})<Q_{L}}, или ломкие, когда {displaystyle (Q_{H}-Q_{L})geqslant Q_{L}}. Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса {displaystyle R_{D}={frac {Q_{H}}{Q_{L}}}}: сильные материалы имеют {displaystyle R_{D}<2}, в то время как ломкие материалы имеют {displaystyle R_{D}geqslant 2}.

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением[10]

{displaystyle eta (T)=A_{1}Tleft(1+A_{2}exp {frac {B}{RT}}right)left(1+Cexp {frac {D}{RT}}right)}

с постоянными A_{1}, A_{2}, B, C и D, связанными с термодинамическими параметрами соединительных связей аморфных материалов.

В узких температурных интервалах недалеко от температуры стеклования T_{g} это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Если температура существенно ниже температуры стеклования, {displaystyle T<T_{g}}, двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

{displaystyle eta (T)=A_{L}Texp left({frac {Q_{H}}{RT}}right)}

с высокой энергией активации Q_{H}=H_{d}+H_{m}, где H_{d} — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а H_{m} — энтальпия их движения. Это связано с тем, что при {displaystyle T<T_{g}} аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При {displaystyle Tgg T_{g}} двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

{displaystyle eta (T)=A_{H}Texp left({frac {Q_{L}}{RT}}right),}

но с низкой энергией активации Q_{L}=H_{m}. Это связано с тем, что при {displaystyle Tgg T_{g}} аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Относительная вязкость[править | править код]

В технических науках часто пользуются понятием относительной вязкости, под которой понимают отношение коэффициента динамической вязкости (см. выше) раствора к коэффициенту динамической вязкости чистого растворителя:

{displaystyle mu _{r}={frac {mu }{mu _{0}}},}

где

μ — динамическая вязкость раствора;
μ0 — динамическая вязкость растворителя.

Вязкость некоторых веществ[править | править код]

Для авиастроения и судостроения наиболее важно знать вязкости воздуха и воды.

Вязкость воздуха[править | править код]

Зависимость вязкости сухого воздуха от давления при температурах 300, 400 и 500 K

Вязкость воздуха зависит в основном от температуры.
При 15,0 °C вязкость воздуха составляет 1,78⋅10−5 кг/(м·с) = 17,8 мкПа·с = 1,78⋅10−5 Па·с. Можно найти вязкость воздуха как функцию температуры с помощью программ расчёта вязкостей газов[11].

Вязкость воды[править | править код]

Зависимость динамической вязкости воды от температуры в жидком состоянии (Liquid Water) и в виде пара (Vapor)

Динамическая вязкость воды составляет 8,90·10−4 Па·с при температуре около 25 °C. Как функция температуры: T = A × 10B/(T−C), где A = 2,414·10−5 Па·с, B = 247,8 K, C = 140 K.

Значения динамической вязкости жидкой воды при разных температурах вплоть до точки кипения приведены в таблице:

Температура, °C Вязкость, мПа·с
10 1,308
20 1,002
30 0,7978
40 0,6531
50 0,5471
60 0,4668
70 0,4044
80 0,3550
90 0,3150
100 0,2822

Динамическая вязкость разных веществ[править | править код]

Ниже приведены значения коэффициента динамической вязкости некоторых ньютоновских жидкостей:

Вязкость отдельных видов газов

Газ при 0 °C (273 K), мкПа·с при 27 °C (300 K), мкПа·с
воздух 17,4 18,6
водород 8,4 9,0
гелий 20,0
аргон 22,9
ксенон 21,2 23,2
углекислый газ 15,0
метан 11,2
этан 9,5
Вязкость жидкостей при 25 °C

Жидкость Вязкость, Па·с Вязкость, мПа·с
ацетон 3,06·10−4 0,306
бензол 6,04·10−4 0,604
кровь (при 37 °C) (3—4)·10−3 3—4
касторовое масло 0,985 985
кукурузный сироп 1,3806 1380,6
этиловый спирт 1.074·10−3 1.074
этиленгликоль 1,61·10−2 16,1
глицерин (при 20 °C) 1,49 1490
мазут 2,022 2022
ртуть 1,526·10−3 1,526
метиловый спирт 5,44·10−4 0,544
моторное масло SAE 10 (при 20 °C) 0,065 65
моторное масло SAE 40 (при 20 °C) 0,319 319
нитробензол 1,863·10−3 1,863
жидкий азот (при 77K) 1,58·10−4 0,158
пропанол 1,945·10−3 1,945
оливковое масло 0,081 81
пек 2,3·108 2,3·1011
серная кислота 2,42·10−2 24,2
вода 8,94·10−4 0,894

Примечания[править | править код]

  1. ↑ Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках: Сб. статей / Под ред. Ф. Н. Тавадзе. — М.: Наука, 1978. — 235 с.
  2. ↑ О некоторых ошибках в курсах гидродинамики Архивная копия от 22 декабря 2015 на Wayback Machine, с. 3—4.
  3. ↑ Alexander J. Smits, Jean-Paul Dussauge Turbulent shear layers in supersonic flow Архивная копия от 17 июля 2017 на Wayback Machine. — Birkhäuser, 2006. — P. 46. — ISBN 0-387-26140-0.
  4. ↑ Data constants for Sutherland’s formula Архивная копия от 6 марта 2018 на Wayback Machine.
  5. ↑ Viscosity of liquids and gases Архивная копия от 3 октября 2017 на Wayback Machine.
  6. ↑ Хмельницкий Р. А. Физическая и коллоидная химия: Учебних для сельскохозяйственных спец. вузов. — М.: Высшая школа, 1988. — С. 40. — 400 с. — ISBN 5-06-001257-3.
  7. ↑ Попов Д. Н. Динамика и регулирование гидро- и превмосистем : Учеб. для машиностроительных вузов. — М. : Машиностроение, 176. — С. 175. — 424 с.
  8. ↑ Седов Л. И. Механика сплошной среды Архивная копия от 28 ноября 2014 на Wayback Machine. Т. 1. — М.: Наука, 1970. — С. 166.
  9. ↑ Френкель Я. И. Кинетическая теория жидкостей. — Ленинград, Наука, 1975. — с. 226.
  10. ↑ Ojovan M. Viscous flow and the viscosity of melts and glasses. Physics and Chemistry of Glasses, 53 (4) 143—150 (2012).
  11. ↑ Gas Viscosity Calculator Архивная копия от 21 июля 2011 на Wayback Machine.

Литература[править | править код]

  • R. H. Doremus. J. Appl. Phys., 92, 7619—7629 (2002).
  • M. I. Ojovan, W. E. Lee. J. Appl. Phys., 95, 3803—3810 (2004).
  • M. I. Ojovan, K. P. Travis, R. J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
  • Л. И. Седов. Механика сплошной среды. Т. 1. — М.: Наука, 1970. — 492 с.
  • П. Н. Гедык, М. И. Калашникова. Смазка металлургического оборудования. — М.: Металлургия, 1976. — 380 с.
  • И. Ф. Голубев. Вязкость газов и газовых смесей. — М.: Физматлит, 1959.
  • Ред. Ф. Н. Тавадзе Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках. — М., Наука, 1978. — 235 c.

Ссылки[править | править код]

  • Аринштейн А. Сравнительный вискозиметр Жуковского // Квант, № 9, 1983.
  • Измерение вязкости нефтепродуктов
  • Булкин П. С. Попова И. И., Общий физический практикум. Молекулярная физика
  • Градус условной вязкости // Большой энциклопедический политехнический словарь. — 2004.
  • Вязкость воды
Источник

В
гидравлических расчетах применяют
отношение коэффициента динамической
вязкости μ к плотности ρ жидкости,
которое называется коэффициентом
кинематической вязкости и обозначается
ν:

В
системе МКГСС коэффициент кинематической
вязкости выражается в м2/сек
и в системе СГС – в см2/сек.
Величина вязкости, равная 1 см2/сек,
называется стоксом (сm). В технической
практике получили распространение
сантистоксы (ссm), причем 1 ссm = 0,01 сm = 1
мм2/сек.

Указанные
единицы кинематической вязкости связаны
соотношением 1 м2/сек
= 10 000 сm = 1 000 000 ссm.

В
отечественных стандартах обычно дается
кинематическая вязкость, выраженная в
сантистоксах при 500
С.

В
гидросистемах машин, предназначенных
для работы в стабильных температурных
условиях при давлении менее 100 кГ/см2,
обычно применяют масла с вязкостью
20-40 ссm (при 500
С), а при давлении до 200 кГ/см2
вязкость жидкости достигает значений
110-150 ссm.

В
гидросистемах с быстроходными насосами
и в гидросистемах, предназначенных для
работы в широком температурном диапазоне
и при низких температурах, применяются
масла с меньшими значениями вязкости.

2.3.5.
Условные (относительные) единицы вязкости

Точных
методов непосредственного измерения
коэффициентов абсолютной или кинематической
вязкости не существует. Лишь в некоторых
случаях для определения коэффициентов
абсолютной или кинематической вязкости
пользуются тарированными приборами,
позволяющими с приемлемой точностью
определить вязкость прямым методом.

На
практике с помощью вискозиметров
определяют относительную вязкость,
единицы измерения которой непосредственно
не связаны с физической природой
вязкости. В отечественной промышленности
применяются единицы условной вязкости,
измеряемые в секундах или градусах.
Энглера с помощью вискозиметра,
основанного на методе истечения жидкости
через калиброванное отверстие
определенного диаметра (2,8 мм). В этом
приборе определяется время t истечения
под собственным весом 200 см3
испытываемой жидкости из цилиндрического
сосуда через заданное отверстие при
данной температуре, которое сравнивается
с временем tв
истечения из того же сосуда 200 см3
воды при 200
С. В соответствии с этим вязкость жидкости
в градусах Энглера выражается отношением

причем
время истечения воды в этом приборе
обычно равно tв
= 50 ÷ 52 сек. Вискозиметр Энглера применим
для жидкостей с вязкостью не меньше
1,10
Е.

Относительная
вязкость часто выражается также в
секундах Энглера, которые показывают
время истечения определенного объема
измеряемой жидкости из указанного
вискозиметра в секундах. Покольку
вискозиметр Энглера рассчитан на
истечение воды за 50 – 52 сек, единица
вязкости в секундах Энглера в 50 – 52 раза
меньше единицы вязкости в градусах
Энглера.

2.3.6.
Перевод условных единиц вязкости в
абсолютные

До
настоящего времени не существует метода
точного перевода условных (относительных)
единиц вязкости в абсолютные, пересчет
проводится по приближенным эмпирическим
формулам и таблицам. Для применяемых в
гидросистемах масел при среднем значении
γ = 900 кГ/м3
коэффициенты кинематической и условной
вязкости, выраженной в градусах Энглера,
выражаются соотношением

Пересчет
градусов Энглера в единицы абсолютной
вязкости может быть осуществлен для
распространенных в гидросистемах
жидкостей по упрощенной формуле μ =
0,000650
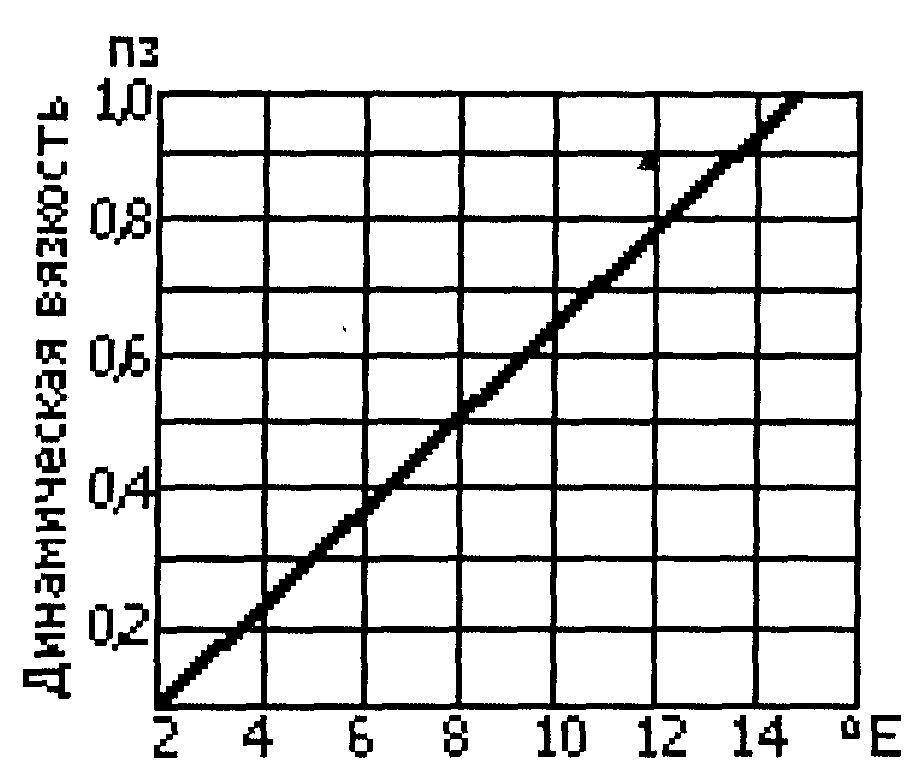
Е. Для пересчета коэффициента динамической
вязкости μ в единицы условной вязкости
можно также пользоваться графиком,
показанным на рис.1.

Рис.
1. График для пересчета динамической
вязкости

в
условную

Следует
отметить, что существующие вискозиметры
обеспечивают получение более или менее
достоверных результатов для жидкостей
с вязкостью от 2 до 30 ссm.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #

    30.04.2022606.21 Кб229.doc

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Вязкость жидкости


При подборе насосов мы задаем нашим клиентам ряд вопросов:

      1. Какую именно жидкость вы перекачиваете?
      2. Её температура?
      3. Плотность?
      4. Вязкость?

И если первые три пункта чаще всего не вызывают затруднений при ответе, то про вязкость нечасто услышишь конкретные цифры, например 100 сантипуаз или 235 сантистокс.

Обычно ответы в стиле:

  • как сметанка,
  • вроде жидкого мёда,
  • как масло машинное в Якутии,
  • я посмотрел в интернете похожее, думаю, что у меня глицерин вязкостью 10000 Ст.


И это нормально, потому что не все покупатели имеют под рукой вискозиметры или технологов,

паспорта на жидкости, или реальную таблицу зависимости вязкости перекачиваемой жидкости от температуры.

Что такое вязкость жидкости простыми словами

Вязкость (кинематическая или динамическая) — это свойство жидкости (или газа) оказывать сопротивление относительному движению (сдвигу) её частиц. Все жидкости обладают вязкостью, которая проявляется в виде внутреннего трения при смещении прилегающих друг к другу слоёв этой жидкости. Вследствие тормозящего влияния стенок/стенки, слои жидкости будут двигаться с разными скоростями, значения которых возрастают по мере отдаления от стенки.

Рис. 1. Пример перемещения слоёв жидкости при неподвижной нижней стенке.

Пример перемещения слоёв жидкости при неподвижной нижней стенке


Свойство, обратное вязкости (1/μ) – текучесть.

Динамическая вязкость жидкости

Динамическая вязкость – это свойства реальных жидкостей (в науке есть ещё понятие идеальной жидкости, это теоретическая упрощённая субстанция, придумана для облегчения решения задач гидромеханики) оказывать сопротивление сдвигающим касательным усилиям. Проявляется при движении жидкости. Динамическую вязкость (η) ещё называют абсолютной.

Физический смысл динамического коэффициента вязкости заключается в том, что он численно равен касательному напряжению, возникающему между слоями жидкости, движущимися друг относительно друга со скоростью, равной единице, при расстоянии между этими слоями, равном единице длины.

Размерность динамического коэффициента вязкости η в системе СИ есть Па*с:

1 Па*с = 1 кг*с/м2, чаще пользуемся мПа -1/1000 Па.

В системе СГС динамический коэффициент вязкости измеряется в Пуазах (по имени французского ученого Пуазейля)

1 Пуаз = 0,1 кг*с/м2.

Обычно пользуются в сто раз меньшей единицей – сантипуазом, которой соответствует динамическая вязкость воды при +20,5°С.

Кинематическая вязкость жидкости

Наряду с динамическим коэффициентом вязкости, широко применяется кинематический коэффициент вязкости ν, представляющий собой отношение первого к плотности ρ жидкости или газа:

ν= η/ρ.

Согласно системе СИ, обозначение кинематического коэффициента вязкости ν есть м2/с.

В системе СГС кинематический коэффициент вязкости измеряется в Стоксах (1 Ст = 1 см2/с = 10-4 м2/с) или в сантистоксах (1 сСт = 10-2 (0,01) Ст).

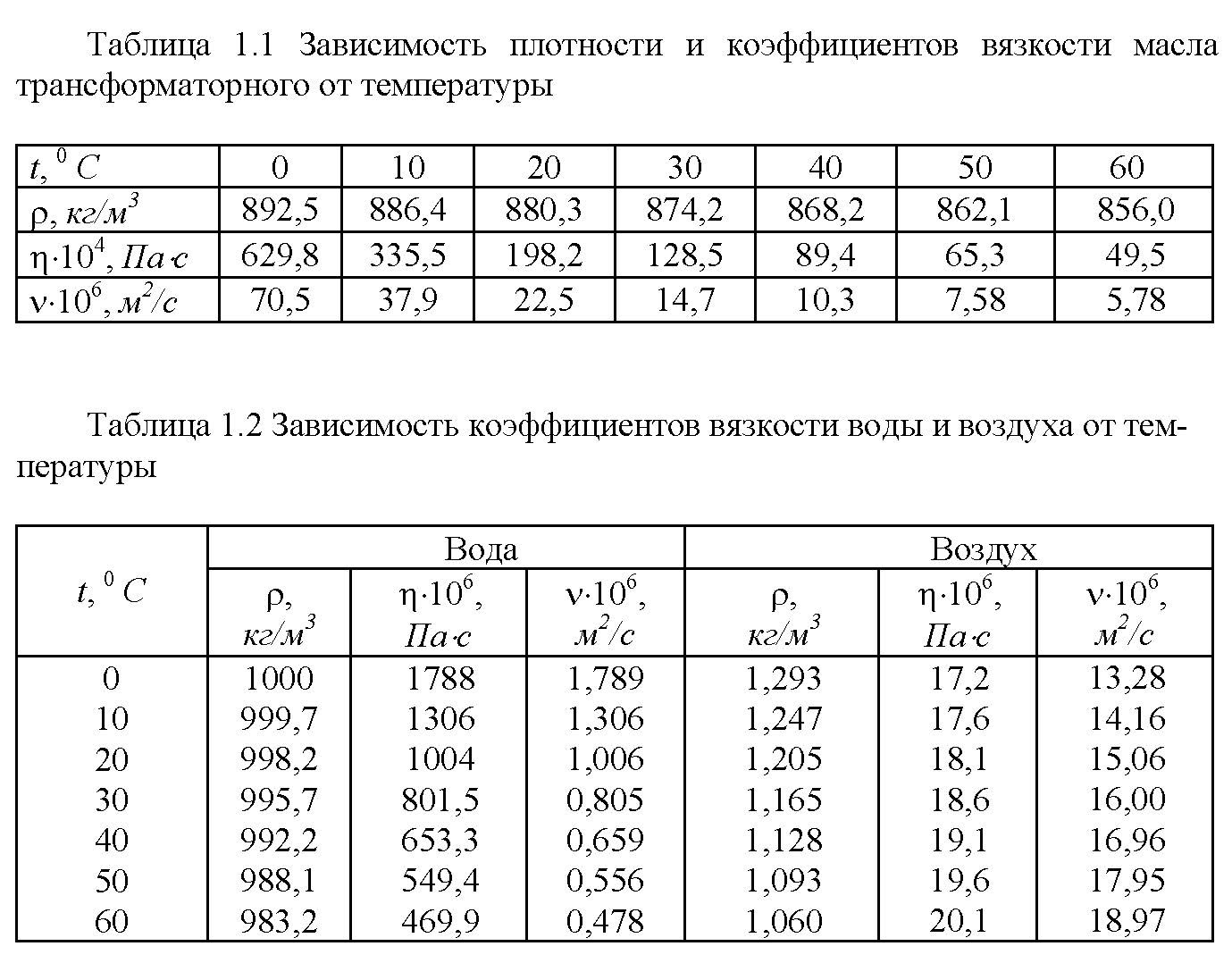
Ниже в таблицах приведены значения коэффициентов вязкости трансформаторного масла, воды и воздуха при различных температурах. Из данных таблиц следует, что с ростом температуры коэффициенты вязкости жидкостей уменьшаются, а газов увеличиваются.

коэффициенты вязкости при различных температурах

Вязкость довольно сильно зависит от температуры жидкости. Она уменьшается при повышении температуры и увеличивается при повышении давления.

Определение кинематической вязкости производится в классическом случае измерением времени вытекания под воздействием силы тяжести определённого объёма жидкости через калиброванное отверстие.

Как уже упоминалось выше, измерение кинематической и динамической вязкости возможно благодаря специализированным приборам – вискозиметрам, различным по принципу действия: ротационным, капиллярным, вибрационным, пузырьковым, с падающим шариком. Их существует много типов и разновидностей – Брукфилда, Стокса, по чашкам Форда, но нам это сейчас не столь первостепенно необходимо, и полученного общего понимания достаточно, чтобы двигаться дальше.

Рис. 2 Различные вискозиметры.

Различные вискозиметры. картинка 1Различные вискозиметры. картинка 2

Различные вискозиметры. картинка 3Различные вискозиметры. картинка 4

В практическо-бытовом понимании каждый знает, что есть разница, как течёт из половника бульон, кисель или мёд.

И, при подборе оборудования для перекачивания жидкости, в связи с этим возникает некая вариативность,

так как невозможно качать мёд насосами для воды, а битум – шестерёнными насосами без рубашки обогрева.

Часто бывает так, что при использовании различных типов вискозиметров для измерения вязкости, возникает необходимость перевода одних единиц измерения в другие, или в единицы измерения Метрической Системы.

Таблицы конверсии различных величин измерения вязкости и примерной вязкости всем знакомых жидкостей приведены ниже.

Таблица соответствия различных единиц измерения вязкости жидкости

Универсальные секунды Сейболта ssu

Кинематическая вязкость сантистоксы

Секунды Редвуда

Единицы Энглера

Секунды по чашке Партина № 10

Секунды по чашке Партина № 15

Секунды по чашкеПартина № 20

Секунды по чашке Форда № 3

Секунды по чашке Форда № 4

31

1.00

29

1

—

—

—

—

—

35

2.56

32.1

1.16

—

—

—

—

—

40

4.30

36.2

1.31

—

—

—

—

—

50

7.40

44.3

1.58

—

—

—

—

—

60

10.3

52.3

1.88

—

—

—

—

—

70

13.1

60.9

2.17

—

—

—

—

—

80

15.7

69.2

2.45

—

—

—

—

—

90

18.2

77.6

2.73

—

—

—

—

—

100

20.6

85.6

3.02

—

—

—

—

—

150

32.1

128

4.48

—

—

—

—

—

200

43.2

170

5.92

—

—

—

—

—

250

54.0

212

7.35

—

—

—

—

—

300

65.0

254

8.79

15

6.0

3.0

30

20

400

87.6

338

11.70

21

7.2

3.2

42

28

500

110

423

14.60

25

7.8

3.4

50

34

600

132

508

17.50

30

8.5

3.6

58

40

700

154

592

20.45

35

9.0

3.9

67

45

800

176

677

23.35

39

9.8

4.1

74

50

900

198

762

26.30

41

10.7

4.3

82

57

1000

220

896

29.20

43

11.5

4.5

90

62

1500

330

1270

43.80

65

15.2

63

132

90

2000

440

1690

58.40

86

19.5

7.5

172

118

2500

550

2120

73.0

108

24

9

218

147

3000

660

2540

87.60

129

28.5

11

258

172

4000

880

3380

117.0

172

37

14

337

230

5000

1100

4230

146

215

47

18

425

290

6000

1320

5080

175

258

57

22

520

350

7000

1540

5920

204.3

300

67

25

600

410

8000

1760

6770

233.5

344

76

29

680

465

9000

1980

7620

263

387

86

32

780

520

10000

2200

8460

292

430

96

35

850

575

15000

3300

13700

438

650

147

53

1280

860

20000

4400

18400

584

860

203

70

1715

1150

Таблица вязкости ряда распространенных жидкостей

Жидкость

t, 0С

ν, сСт
Бензин 15 0, 9
Воск жидкий 90 500
Глицерин 50%-ный водный раствор 20 6
Глицерин 80%-ный водный раствор 20 110
Глицерин безводный 20 1200
Дизельное топливо 20 8
Зубная паста 40 30000
Керосин 15 3
Концентрат фруктового сока 20 2500
Мазут 20 2000
Молоко цельное 20 1,8
Моторные масла 20 30-900
Нефть легкая 18 25
Нефть тяжелая 18 140
Оливковое масло 20 90
Патока 18 60000
Полиол (А) 10 85000
Скипидар 16 2
Спирт этиловый 20 1,5
Эфир 20 0,3

Принципы действия насосов под различные виды жидкости

Ампика – фирма насосная, поэтому нам вязкость интересна прежде всего с точки зрения правильного выбора принципа действия насосов под различные жидкости. Упрощая, подбор насосов, исходя из критерия вязкости, осуществляется по примерно такой градации:

Невязкие жидкости, 0-50 сСт

– Вода, ДТ, бензин – подходящие типы насосов: центробежные, вихревые, шиберные, многосекционные.

Жидкости с невысокой вязкостью, 50-300 сСт

– Масла – шиберные, шестерённые, винтовые.

Средней вязкости, 300-3000 сСт

– Мазут, лак – шиберные, шестерённые, винтовые, перистальтические, мембранные, ламинарные.

Высокой вязкости, до 70000 сСт

– Смазки, шпаклевки, пасты – винтовые, мембранные, шестерённые.

Видео 1. Образцы жидкостей с вязкостью 1/50/100/500/1000/5000/10000/50000/100000 CP.

При подборе насосов для вязких жидкостей очень важна информация о том, как жидкость будет попадать в насос:

самотёком, или необходимо всасывание, если да, то с какой глубины, по трубе какого диаметра?

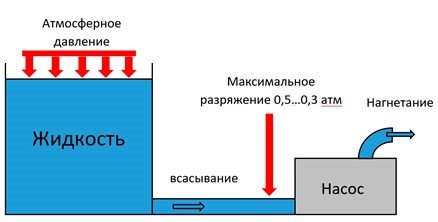
Довольно часто бывает ситуация, когда создаваемое насосом разряжение недостаточно для того, чтобы жидкость попала в насос (т.к. жидкость поддавливается во всасывающий трубопровод атмосферным давлением, которое на поверхности планеты Земля составляет всего 1 атм.). На практике разряжения больше чем 0,3…0,5 атм на входе в насос для вязких жидкостей получить не удаётся (из-за особенностей конструкций таких насосов) + есть ещё сопротивление перекачиванию самой жидкости = жидкость может просто не потечь по всасывающей трубе и насос будет молотить впустую.

Рис. 3 Схема поступления жидкости в насос самотеком

Схема поступления жидкости в насос самотеком

При перекачке вязких жидкостей следует устанавливать насос как можно ближе к ёмкости и, по возможности, ставить насос ниже уровня жидкости, чтобы она попадала в насос самотёком.

Обязательно нужно рассчитывать достаточный диаметр трубы на входе и выходе насоса, учитывать количество задвижек, клапанов и поворотов трубопровода. Всё это сильно влияет на сопротивление перекачиванию. Нельзя просто выбрать насос без привязки к гидравлической системе, т.к. в противном случае он может просто не качать, или не выдавать требуемые параметры.

В ряде случаев помогает уменьшение длины всасывающего шланга и увеличение его диаметра.

Либо можно использовать полупогружной насос, который не всасывает жидкость, а сразу толкает её (внизу заборной трубы находится насосная часть, погружённая в жидкость, а двигатель находится выше её уровня).

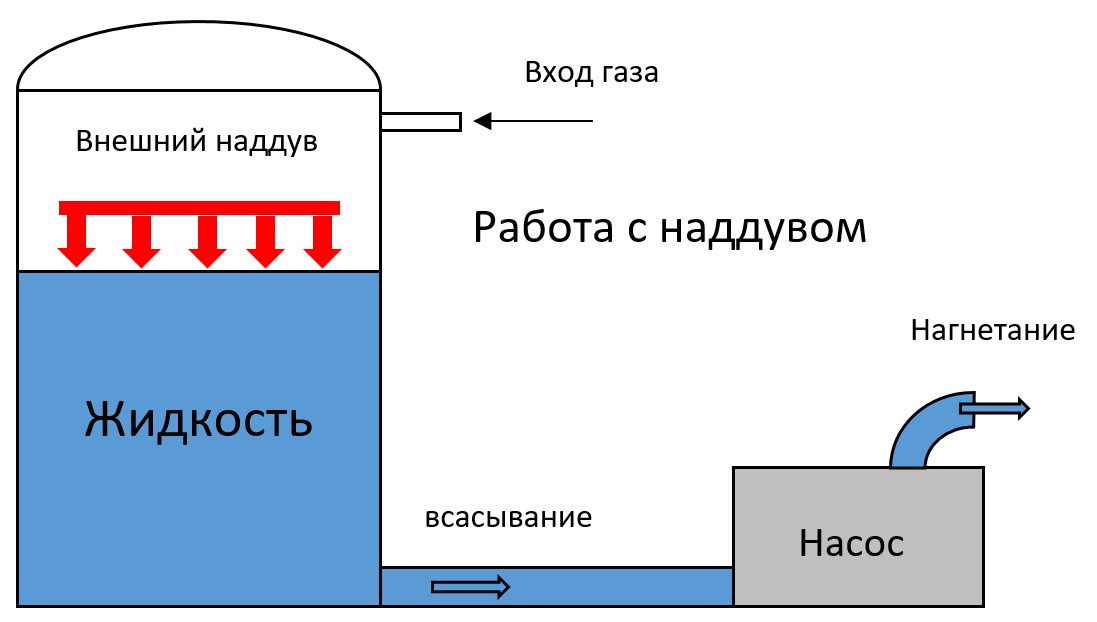
Но достаточно часто это не помогает, и жидкость отказывается затекать даже в погружной насос. Тогда нужно устраивать поддавливание жидкости (например, создавать наддув в закрытой ёмкости или использовать систему с прижимным диском).

Рис. 4 Схема поступления жидкости в насос с наддувом/доп. нагнетанием

Схема поступления жидкости в насос с наддувом/доп. нагнетанием

Существуют установки с прижимным диском (иногда его называют следящей плитой) двух видов:

1) когда диск опускается под действием атмосферного давления (а оно теоретически равно 1 кг/см2, хотя по факту несколько меньше).

Например, диск диаметром 600 мм (60 см), теоретически будет поджимать жидкость с таким давлением:

π*D2/4 (площадь диска) = 3,14*3600/4=2826 см2. То есть 2826 кг/см2 (~2,8 тонны).

2) когда диск механически прижимается с помощью пневморамы (или электроприводом).

Рис. 5 Система подачи вязких жидкостей с прижимным диском (прижим атмосферным давлением

Система подачи вязких жидкостей с прижимным диском (прижим атмосферным давлением)

Система подачи вязких жидкостей с прижимным диском (прижим атмосферным давлением).

Порой жидкость при рабочей температуре настолько высоковязкая, что для её перемещения проще либо использовать

механический способ (лопатой), или же нагревать её до приемлемого уровня вязкости.

Нельзя не учитывать возможность застывания (кристаллизации) жидкости в насосе, особенно это касается битумных насосов. Именно поэтому такие насосы снабжаются рубашкой обогрева (нагрев проточной части паром, горячим маслом или электричеством).

Также важно на какое расстояние/высоту и по какой трубе/шлангу требуется переместить жидкость. Очень большую важность приобретает подбор оборотов двигателя, ведь для высоковязких жидкостей с большой инерцией сдвига требуются двигатели с меньшим числом оборотов/минуту, нежели для жидкостей невязких.

Видео 2.

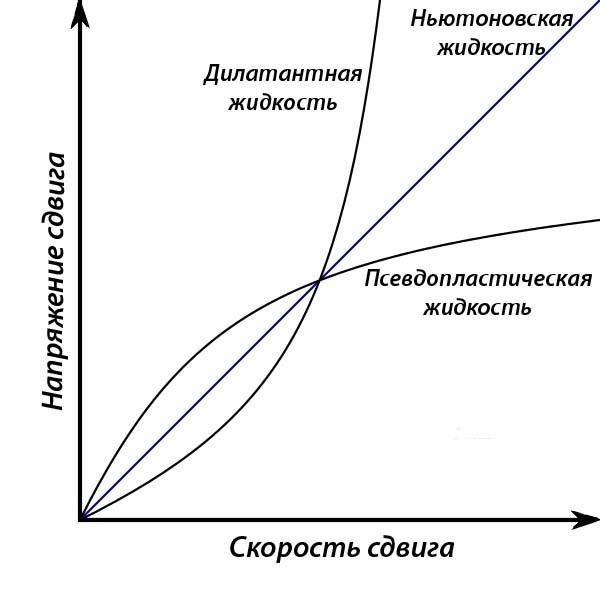
И это мы ещё не учитываем градацию жидкостей по типу – ньютоновская/неньютоновская. Если кратко,

вязкость ньютоновских жидкостей – константа при конкретной температуре, вязкость неньютоновских зависит от скорости и направления сдвига. Ярким примером таких являются, например, томатные пасты/кетчупы – у них вязкость уменьшается от приложенной силы сдвига, или крахмало-водяная смесь – у неё вязкость возрастает от приложенной силы, практически до состояния твёрдого вещества.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 1011—1012 Па·с.

Рис. 6 График зависимости напряжения/скорости сдвига для ньютовскихи неньютоновских жидкостей.

График зависимости напряжения/скорости сдвига для ньютовскихи неньютоновских жидкостей.

Советы экспертов компании Ампика


Подведём итог. Подбирая оборудование самостоятельно, старайтесь учесть все нюансы происходящего тех. процесса. Подробности очень важны. Если есть сомнения, лучше опишите вашу задачу нам.

Мы уточним всё, что нужно, и подберём насосы, которые реально будут работать. У нас есть для этого и опыт, и возможности расчёта и подбора самого подходящего насосного оборудования.

Источник

Физические величины. Вязкость жидкости

Вязкость – свойство жидкости, которое определяет сопротивление жидкости к внешнему воздействию. Вязкость можно представить как внутреннее трение между отдельными слоями жидкости при их смещении относительно друг друга.

Существуют два основных параметра для определения вязкости жидкости: динамическая (или абсолютная) вязкость и кинематическая вязкость. Динамическая вязкость представляется как отношение единицы силы, необходимой для смещения слоя жидкости на единицу расстояния, к единице площади слоя.

Определяющее уравнение для динамической вязкости

Вязкость 1.jpg

В международной системе единиц СИ при выражении единицы давления сдвига  F/S в паскалях, градиента скорости grad υ   (изменение скорости жидкости, отнесённого к расстоянию между слоями) в секундах в минус первой степени динамическая вязкость µ выразится в паскалях-секундах (П·с). В метрической системе единица вязкости представляется в грамм/сантиметр в секунду, называемой пуаз. Принятое обозначение пуаз – П

   1 П·с = 10 пуаз.

Единицы измерения динамической вязкости паскаль-секунда и пуаз значительны по своему размеру и применяют дольные единицы – миллипаскаль-секунда мПа и сантипуаз сП

 1 мПа·с = 1 сП.

Переводные множители для расчёта динамической вязкости приведены в таблице.

Вязкость 5.jpg

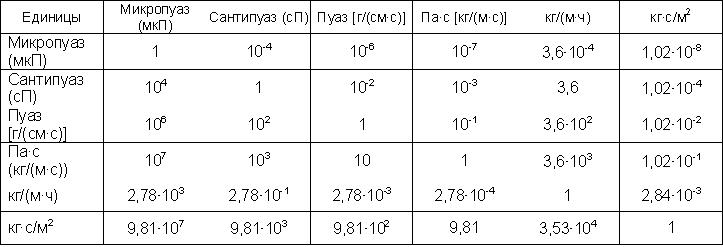
Величина обратная динамической вязкости жидкости определяется как текучесть жидкости и в международной системе единиц (СИ) выражается Па-1·С-1.

Формула для определения кинематической вязкости при заданной динамической вязкости выглядит так:

Вязкость 3.jpg

Единица измерения кинематической вязкости в системе СИ – квадратный метр на секунду, в метрической системе – квадратный сантиметр на секунду называемый стокс. Принятое обозначение стокса – Ст.

1 м2/с = 104 Ст

Единица измерения кинематической вязкости квадратный метр на секунду и стокс значительна по своему размеру и для практических применений используют дольные единицы – квадратный миллиметр на секунду и сантистокс сСт

1 мм2/с = 1 сСт.

Переводные множители для расчёта кинематической вязкости приведены в таблице:

Вязкость 6.jpg

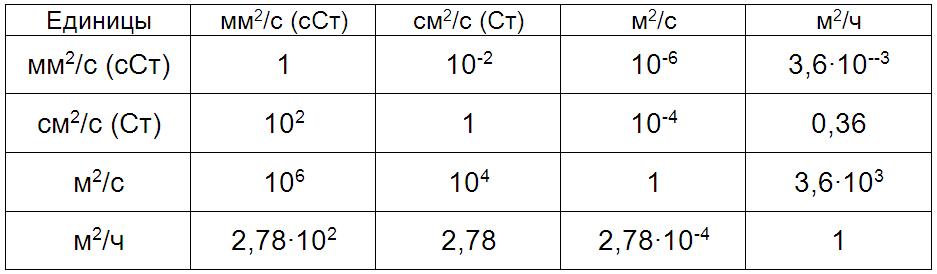
При необходимости пересчёта параметров вязкости можно воспользоваться соотношением  соблюдая размерности физических величин, например:

Вязкость 4.jpg

Вязкость и плотность жидкостей при 20°С:

Вязкость 8.jpg

Источник

Добавить комментарий