Загрузить PDF
Загрузить PDF
Существует два вида энергии: потенциальная и кинетическая. Потенциальная энергия — это энергия одного объекта по отношению к другому, которая зависит от их взаимного расположения.[1]
Например, если вы стоите на вершине холма, то ваша потенциальная энергия будет отличаться от той, которой вы обладали бы у подножия этого холма. Кинетическая энергия — это энергия движущегося объекта.[2]
Кинетическая энергия возникает при колебаниях, вращении и поступательном движении (перемещении тела из одного места в другое).[3]
Кинетическую энергию любого объекта легко вычислить, если известны его масса и скорость.[4]
-

1
Запомните формулу для вычисления кинетической энергии. Формула для нахождения кинетической энергии (КЕ) имеет следующий вид: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[5]
- Ответ должен быть выражен в стандартных единицах измерения кинетической энергии, джоулях (Дж). Один джоуль эквивалентен 1 кг * м2/с2.
-

2
Определите массу объекта. Если в исходном условии не дана масса, ее придется определить самостоятельно. Для этого можно взвесить предмет и найти массу в килограммах (кг).
- Настройте весы. Прежде чем взвешивать предмет, необходимо выставить на весах ноль. Это называется тарировкой весов.[6]
- Положите объект на весы. Осторожно положите предмет на весы и запишите его массу в килограммах.
- При необходимости переведите граммы в килограммы. В конечную формулу необходимо подставить значение массы в килограммах.
- Настройте весы. Прежде чем взвешивать предмет, необходимо выставить на весах ноль. Это называется тарировкой весов.[6]
-

3
Найдите скорость объекта. Часто в условии задачи дается скорость объекта. Если скорость не дана, ее можно найти по пройденному расстоянию и затраченному для этого времени.[7]
Скорость измеряется в метрах в секунду (м/с).- Чтобы определить скорость, необходимо расстояние поделить на время: V = d/t. Скорость является векторной величиной, то есть имеет абсолютное значение и направление. Абсолютное значение соответствует величине скорости, а направление указывает на то, куда движется объект.
- Например, скорость объекта может составлять 80 м/с или –80 м/с, в зависимости от направления движения.
- Чтобы вычислить скорость, просто поделите пройденное расстояние на затраченное время.
Реклама
-

1
Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[8]
- Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м2/с2.
-

2
Подставьте в формулу массу и скорость. Если в условии задачи не дана масса или скорость, необходимо найти их. Предположим, что заданы обе эти величины, и необходимо решить следующую задачу: Найдите кинетическую энергию женщины массой 55 кг, которая бежит со скоростью 3,87 м/с. В условии даны масса и скорость, поэтому их можно сразу подставить в формулу:[9]
- KE = 0,5 x mv2
- KE = 0,5 x 55 x (3,87)2
-

3
Проведите вычисления. После подстановки массы и скорости можно рассчитать кинетическую энергию (KE). Возведите скорость в квадрат и умножьте полученное значение на массу и на 0,5. Помните, что ответ должен получиться в джоулях (Дж).[10]
- KE = 0,5 x 55 x (3,87)2
- KE = 0,5 x 55 x 14,97
- KE = 411,675 Дж
Реклама
-

1
Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[11]
- Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м2/с2.
-

2
Подставьте в формулу известные значения. В некоторых задачах дается кинетическая энергия и масса, или кинетическая энергия и скорость. Сначала необходимо подставить в формулу все известные величины.
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
- KE = 0,5 x mv2
- 500 Дж = 0,5 x 30 x v2
- Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
- KE = 0,5 x mv2
- 100 Дж = 0,5 x m x 52
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
-

3
Преобразуйте уравнение, чтобы найти неизвестную величину. Путем алгебраических преобразований перенесите искомую величину по одну, а все известные величины — по другую сторону знака равенства.
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
- KE = 0,5 x mv2
- 500 Дж = 0,5 x 30 x v2
- Умножим массу на 0,5: 0,5 x 30 = 15
- Поделим кинетическую энергию на получившееся значение: 500/15 = 33,33
- Извлечем квадратный корень, чтобы найти скорость: 5,77 м/с
- Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
- KE = 0,5 x mv2
- 100 Дж = 0,5 x m x 52
- Возведем скорость в квадрат: 52 = 25
- Умножим полученное значение на 0,5: 0,5 x 25 = 12,5
- Поделим кинетическую энергию на эту величину: 100/12,5 = 8 кг
Реклама
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
Об этой статье
Эту страницу просматривали 29 428 раз.
Была ли эта статья полезной?
Download Article
Download Article
There are two basic forms of energy: potential and kinetic energy. Potential energy is the energy an object has relative to the position of another object.[1]
For example, if you are at the top of a hill, you have more potential energy than if you are at the bottom of the hill. Kinetic energy is the energy an object has when it is in motion.[2]
Kinetic energy can be due to vibration, rotation, or translation (movement from one place to another).[3]
The kinetic energy of an object can easily be determined by an equation using the mass and velocity of that object.[4]
-

1
Know the formula for calculating kinetic energy. The formula for calculating kinetic energy (KE) is KE = 0.5 x mv2. Here m stands for mass, the measure of how much matter is in an object, and v stands for the velocity of the object, or the rate at which the object changes its position.[5]
- Your answer should always be stated in joules (J), which is the standard unit of measurement for kinetic energy. It is equivalent to 1 kg * m2/s2.
-

2
Determine the mass of an object. If you are solving a problem where the mass isn’t given, you will have to determine the mass yourself. This can be done by weighing the object on a balance and obtaining the mass in kilograms (kg).
- Tare the balance. Before you weigh your object, you must set it to zero. Zeroing out the scale is called taring.[6]
- Place your object in the balance. Gently, place the object on the balance and record its mass in kilograms.
- If necessary, convert grams to kilograms. For the final calculation, the mass must be in kilograms.
Advertisement
- Tare the balance. Before you weigh your object, you must set it to zero. Zeroing out the scale is called taring.[6]
-

3
Calculate the velocity of the object. Oftentimes, the problem will give you the velocity of the object. If this is not the case, you can determine the velocity by using the distance an object travels and how long it takes to cover that distance.[7]
The units for velocity are meters per second (m/s).- Velocity is defined by the equation, displacement divided by time: V = d/t. Velocity is a vector quantity, meaning it has both a magnitude and a direction. Magnitude is the number value that quantifies the speed, while the direction is the direction in which the speed takes place during motion.
- For example, an object’s velocity can be 80 m/s or -80 m/s depending on the direction of travel.
- To calculate velocity, simply divide the distance the object traveled by the time it took to travel that distance.
Advertisement
-

1
Write the equation. The formula for calculating kinetic energy (KE) is KE = 0.5 x mv2. Here m stands for mass, the measure of how much matter is in an object, and v stands for velocity of the object, or the rate at which the object changes its position.[8]
- Your answer should always be stated in joules (J), which is the standard unit of measurement for kinetic energy. It is equivalent to 1 kg * m2/s2.
-

2
Plug the mass and velocity into the equation. If you don’t know the mass or velocity of the object, then you’ll have to calculate it. But let’s say that you do know both quantities and are working to solve the following problem: Determine the kinetic energy of a 55 kg woman running with a velocity of 3.87m/s. Since you know the mass and velocity of the woman, you can plug it into the equation:[9]
- KE = 0.5 x mv2
- KE = 0.5 x 55 x (3.87)2
-

3
Solve the equation. Once you’ve plugged in the mass and velocity, you can solve for kinetic energy (KE). Square the velocity and then multiply all of the variables together. Remember to state your answer in joules (J). [10]
- KE = 0.5 x 55 x (3.87)2
- KE = 0.5 x 55 x 14.97
- KE = 411.675 J
Advertisement
-

1
Write the equation. The formula for calculating kinetic energy (KE) is KE = 0.5 x mv2. Here m stands for mass, the measure of how much matter is in an object, and v stands for velocity of the object, or the rate at which the object changes its position.[11]
- Your answer should always be stated in joules (J), which is the standard unit of measurement for kinetic energy. It is equivalent to 1 kg * m2/s2.
-

2
Plug in the known variables. In some problems, you may know the kinetic energy and the mass or kinetic energy and velocity. The first step to solving this problem is to plug in all of the variables that are known.
- Example 1: What is the velocity of an object with a mass of 30 kg and a kinetic energy of 500 J?
- KE = 0.5 x mv2
- 500 J = 0.5 x 30 x v2
- Example 2: What is the mass of an object with a kinetic energy of 100 J and a velocity of 5 m/s?
- KE = 0.5 x mv2
- 100 J = 0.5 x m x 52
- Example 1: What is the velocity of an object with a mass of 30 kg and a kinetic energy of 500 J?
-

3
Rearrange the equation to solve for the unknown variable. Using algebra, you can solve for the unknown variable by rearranging all of the known variables to one side of the equation.
- Example 1: What is the velocity of an object with a mass of 30 kg and a kinetic energy of 500 J?
- KE = 0.5 x mv2
- 500 J = 0.5 x 30 x v2
- Multiply mass by 0.5: 0.5 x 30 = 15
- Divide kinetic energy by the product: 500/15 = 33.33
- Square root to find velocity: 5.77 m/s
- Example 2: What is the mass of an object with a kinetic energy of 100 J and a velocity of 5 m/s?
- KE = 0.5 x mv2
- 100 J = 0.5 x m x 52
- Square the velocity: 52 = 25
- Multiply by 0.5: 0.5 x 25 = 12.5
- Divide kinetic energy by product: 100/12.5 = 8 kg
- Example 1: What is the velocity of an object with a mass of 30 kg and a kinetic energy of 500 J?
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
What is the kinetic energy possessed by a car having a mass of 1500 kg and travelling at a velocity of 50 km/h?

Recalulate 50 km/h into m/s which is 13.889 m/s; then apply the formula:
KE = 0.5 * 1500kg * (13.889 m/s)^2 = 144678 J => appr. 145 kJ
-
Question
If mass and velocity of body is doubled how can I figure out the change in kinetic energy?

The formula given for K.E. is K.E. = 0.5m(v^2). Doubling mass gives m = 2m. Doubling velocity gives v^2 = (2v)^2 =4v^2. Which makes K.E. 4 x 2 = 8 times bigger in total.
-
Question
What if the amount is in grams?

Electric gears
Community Answer
If it’s in grams, you’ll have to convert it to kilograms by dividing it by 1000. For example, 100g becomes 0.1kg, and 3g becomes 0.003kg.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
About This Article
Article SummaryX
To calculate kinetic energy, write out a formula where kinetic energy is equal to 0.5 times mass times velocity squared. Add in the value for the mass of the object, then the velocity with which it is moving. Solve for the unknown variable. Your answer should be stated in joules, or J. If you want to learn how to solve velocity or mass using kinetic energy, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,061,556 times.
Did this article help you?
Содержание:
Кинетическая энергия:
Иногда значение работы можно найти, не используя понятия силы и перемещения, на основании характеристики изменения энергии тела.
Рассмотрим тело массой m, на которое действует сила F. Направление действия силы совпадает с направлением перемещения. Работа, которую выполняет эта сила,
A = Fs.
Согласно второму закону механики Ньютона значение силы 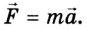
Как известно, модуль перемещения равен:
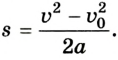
Поэтому 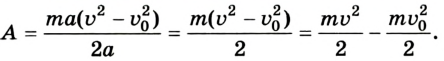
Как известно, выражение 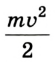 называется кинетической энергией. Следовательно, для расчета работы достаточно определить только массу тела и его начальную и конечную скорости, т. е. знать изменение кинетической энергии тела. Такой метод удобен, поскольку им можно пользоваться даже в случае переменной силы и произвольной траектории.
называется кинетической энергией. Следовательно, для расчета работы достаточно определить только массу тела и его начальную и конечную скорости, т. е. знать изменение кинетической энергии тела. Такой метод удобен, поскольку им можно пользоваться даже в случае переменной силы и произвольной траектории.
Физическая величина, описывающая состояние движущегося тела и изменение которой определяет работу, называется кинетической энергией.
Для измерения энергии, как и работы, используется единица джоуль (Дж), названная в честь английского ученого Д. Джоуля.
Кинетической энергией обладает тело, движущееся в данной системе отсчета с определенной скоростью: 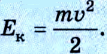
Скорость тела, измеренная в разных системах отсчета, будет иметь разное значение, т. е. она является относительной величиной. Поэтому кинетическая энергия тела постоянной массы тоже величина относительная и в разных системах отсчета имеет разное значение.
Рассмотрим, например, два железнодорожных вагона, массы которых составляют по 2 • 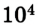 кг, движущиеся в одном направлении со скоростями 15 м/с и 10 м/с относительно железнодорожного полотна, причем первый догоняет второго. Их кинетическая энергия соответственно будет:
кг, движущиеся в одном направлении со скоростями 15 м/с и 10 м/с относительно железнодорожного полотна, причем первый догоняет второго. Их кинетическая энергия соответственно будет:
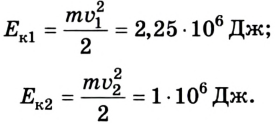
Если же систему отсчета связать со вторым вагоном, то первый будет двигаться со скоростью 5 м/с , а второй – со скоростью v = 0. В этом случае
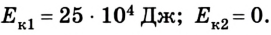
Следовательно, при расчетах в разных инерциальных системах отсчета следует учитывать, что кинетическая энергия в случае перехода из одной системы в другую будет изменяться.
Что такое кинетическая энергия
Кинетическая энергия (от греческого слова кинетикос – тот, что приводит в движение) – это энергия, которой тело обладает вследствие собственного движения.
Кинетической энергией обладает ветер, её используют для сообщения движения ветряным двигателям. Движущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их вращаться. На рисунке 175, а изображена ветряная мельница, в которой за счёт энергии ветра мелют зерно. Современные довольно мощные ветряные двигатели (рис. 175, б) используют для того, чтобы вырабатывать электроэнергию, качать из скважин воду и подавать её в водонапорные башни.
Движущаяся вода или нагретый пар, вращая турбины электростанции, теряет часть своей кинетической энергии и выполняет работу. Самолёт, летящий высоко в небе, кроме потенциальной обладает и кинетическуй энергией. Если тело находится в состоянии покоя, т. е. его скорость относительно Земли равна нулю, то и его кинетическая энергия относительно Земли будет равна нулю.
Опытами установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его кинетическая энергия. Выявленная зависимость математически выражается такой формулой: 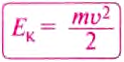
где 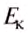 — кинетическая энергия тела;
— кинетическая энергия тела; 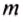 — масса тела;
— масса тела; 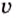 — скорость движения тела.
— скорость движения тела.
Определение кинетической энергии
Наблюдения явлений природы показывают, что работа может выполняться при движении тел. Так, движущийся тепловоз, стыкуясь с вагоном, перемещает его на некоторое расстояние. Выполняется работа и в том случае, когда брошенный камень разбивает лед. Выстреленная из ружья пуля пробивает доску и т. п. Если потенциальной энергией обладают тела, на которые действует сила, то в упомянутых выше случаях работа выполняется потому, что они осуществляли перемещение, двигались.
Какой энергией обладают движущиеся тела
Энергию движущегося тела называют кинетической энергией.
Кинетическая энергия является физической величиной ее значение можно рассчитывать. Для этого необходимо знать, от каких физических величин она зависит.
Как рассчитывают кинетическую энергию
Поставим желоб под некоторым углом к поверхности стола. На некотором расстоянии от его нижнего конца поставим брусок. На средней части желоба разместим маленький стальной шарик и отпустим его. Скатившись по желобу, шарик ударится о брусок и переместит его на некоторое расстояние. Отметим расстояние, на которое сместился брусок.
Поместим шарик в верхней части желоба и отпустим его. В этом случае, скатившись желобом к основе, шарик приобрел большую скорость, чем раньше. Ударившись в брусок, он переместит его на большее расстояние, чем в предыдущем опыте, соответственно выполнив большую работу.
Таким образом, кинетическая энергия тела зависит от его скорости. Эта зависимость нелинейная, что заметно на графике зависимости кинетической энергии тела от его скорости. График имеет вид кривой линии (рис. 126).
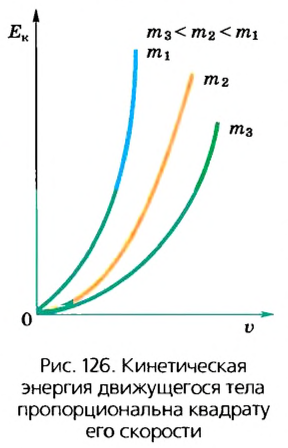
Кинетическая энергия тела относительна
Как известно, скорость тела является относительной величиной и зависит от выбора тела отсчета. Поэтому и кинетическая энергия является величиной относительной. Если артиллерийский снаряд, попав в стену, причиняет значительные разрушения, то снаряд, посланный вдогонку сверхзвуковому самолету, не причинит ему существенных повреждений, поскольку скорость снаряда относительно самолета будет небольшой.
Последствия столкновения автомобилей в случае их движения навстречу друг другу будут всегда более ощутимы, чем тогда, когда один автомобиль догоняет другой.
Кинетическая энергия зависит и от массы тела. Если повторим предыдущие опыты с шариком большей массы, то увидим, что перемещения бруска в этом случае будет большим. Эта зависимость линейная, поэтому можно сказать, что кинетическая энергия тела пропорциональна его массе (рис. 127).
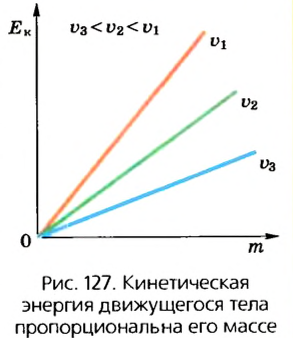
Как рассчитать кинетическую энергию
Чтобы рассчитать кинетическую энергию, используют формулу:

где 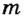 — масса тела;
— масса тела; 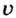 — скорость тела.
— скорость тела.
Кинетическая энергия разных физических тел используется для выполнения механической работы. Так, опытные водители автомобилей время от времени отсоединяют двигатель от колес, выключая сцепление, и этим экономят топливо. Работа по преодолению сил трения выполняется за счет кинетической энергии автомобиля. Конструкторы работают над моделью городского автобуса, который начинает движение за счет энергии раскрученного во время стоянки большого маховика. Это дает возможность существенно уменьшить выбросы вредных газов в атмосферу и экономить топливо.
В южных областях Украины, в частности на Крымском полуострове, используют ветряные электростанции, которые работают за счет кинетической энергии потоков воздуха — ветра (рис. 128).

- Заказать решение задач по физике
Кинетическая энергия тела
Рассмотрим движение тела массой т под действием нескольких сил, например движение санок (см. рис. 124). Предположим также, что сила натяжения веревок постоянна, а следовательно, постоянной будет и результирующая сила 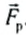 . Она совпадает по направлению с перемещением тела или противоположна ему. Эта сила, естественно, вызывает ускорение санок, т. е. изменяет их скорость. Кроме того, она совершает работу. Следовательно, между работой результирующей силы и изменением скорости санок должна существовать связь.
. Она совпадает по направлению с перемещением тела или противоположна ему. Эта сила, естественно, вызывает ускорение санок, т. е. изменяет их скорость. Кроме того, она совершает работу. Следовательно, между работой результирующей силы и изменением скорости санок должна существовать связь.
Рассмотрим случай, когда проекция результирующей силы на направление движения положительна, т. е. санки движутся равноускоренно с ускорением а, которое находится из второго закона Ньютона:
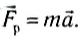 (1)
(1)
Работа результирующей силы:
A = Fp△r, (2)
где △r— модуль перемещения тела за некоторый промежуток времени. Подставим выражение (1) в (2). В результате получим:
A = ma△r. (3)
При равноускоренном одномерном движении модуль перемещения △r и изменение скорости связаны соотношением:
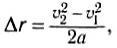 (4)
(4)
где 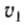 и
и 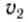 — начальная и конечная скорости тела, которое совершило перемещение △r с ускорением а.
— начальная и конечная скорости тела, которое совершило перемещение △r с ускорением а.
Соотношение (3) с учетом (4) примет вид:
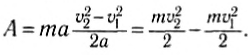 (5)
(5)
Полученная формула связывает работу результирующей силы, действующей на тело, с изменением величины 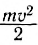 . Эта величина называется кинетической энергией тела и обычно обозначается К.
. Эта величина называется кинетической энергией тела и обычно обозначается К.
Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости:
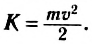 (6)
(6)
Тогда формула (5) примет вид:
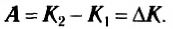 (7)
(7)
Итак, работа результирующей силы, действующей на тело, равна изменению кинетической энергии тела. Как вы уже знаете, изменение какой-то величины равно разности конечного значения и начального. Из формулы (7) очевидно следует, что кинетическая энергия выражается в тех же единицах, что и работа, т. е. в СИ в джоулях.
Когда результирующая сила действует по направлению движения тела и, следовательно, совершает положительную работу, то K2>K1. Это означает, что кинетическая энергия тела увеличивается. Понятно, что, если результирующая сила направлена в сторону, противоположную движению, она совершает отрицательную работу, и кинетическая энергия тела уменьшается. Следует отметить, что, хотя мы получили формулу (7) для частного случая равноускоренного и прямолинейного движения, она справедлива и в случае изменяющейся во времени результирующей силы. Поэтому формулу (7) часто называют теоремой о кинетической энергии.
Итак, любое движущееся тело (рис. 127, 128) обладает кинетической энергией. Поскольку скорость тела зависит от выбора инерциальной системы отсчета, то и кинетическая энергия также зависит от выбора системы отсчета. Очевидно, что, как и работа, кинетическая энергия является скалярной физической величиной. Она не зависит от направления движения тела, а определяется его массой и квадратом скорости.
Главные выводы:
- Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости и зависит от выбора системы отсчета.
- Изменение кинетической энергии равно работе всех сил, действующих на тело.
- Кинетическая энергия измеряется в тех же единицах, что и работа.
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия
- Движение и силы
- Давление в физике
- Взаимодействие тел
- Механическая энергия и работа
- Золотое правило механики
- Потенциальная энергия
Кинетическая энергия
Расчеты
Энергия, приобретенная телом только в результате движения, называется кинетической. Если тело не движется, находится в состоянии покоя, кинетическая энергия будет равняться 0. Разница между полной (всей) энергией и энергией покоя является энергией движения или кинетической энергией, она рассчитывается как произведение массы тела умноженной на квадрат скорости, поделенное на 2.
К. э. = mv2/2
m — масса тела, кг;
Y — его скорость, м/c.
За единицу измерения энергии принят джоуль (Дж) = кг м2/с2.
Кинетическая энергия тела массой m, совершающего движение со скоростью Y, равняется работе, которую производит сила, направленная на тело, находящееся в покое, чтобы сообщить ему Y скорость.
Обозначим: работу — А; кинетическую энергию — Ek.
А = mv2/2 = Ek
Работа, которая потребуется для полной остановки тела, совершающего движение со скоростью Y, будет равна:
А = — mv2/2 = — Ek
Правильно определить кинетическую энергию и другие величины вам поможет онлайн калькулятор, если вы введете исходные данные.
Расчет кинетической энергии тела онлайн
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая |
|
| ‹♦› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная |
|
| Химическая | ||
| Ядерная | ||
 |
Гравитационная | |
 |
Вакуума | |
| Гипотетические: | ||
 |
Тёмная | |
| См. также: Закон сохранения энергии |
Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек[1]. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии[2]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как
где индекс 



Упрощённо, кинетическая энергия — это работа, которую необходимо совершить, чтобы тело массой 



История и этимология понятия[править | править код]
Прилагательное «кинетический» происходит от греческого слова κίνησις (kinesis, «движение»). Дихотомия между кинетической энергией и потенциальной энергией восходит к аристотелевским концепциям потенциальности и актуальности[en][5] .
Принцип классической механики, согласно которому E ∝ mv2/2, был впервые разработан Готфридом Лейбницем и Иоганном Бернулли, описавшими кинетическую энергию как живую силу (лат. vis viva)[6]. Вильгельм Гравезанд из Нидерландов предоставил экспериментальные доказательства этой связи. Сбрасывая грузы с разной высоты на глиняный блок, он определил, что глубина их проникновения пропорциональна квадрату скорости удара. Эмили дю Шатле осознала значение данного эксперимента и опубликовала объяснение[7].
Понятия «кинетическая энергия» и «работа» в их нынешнем научном значении восходят к середине XIX века. В 1829 году Гаспар-Гюстав Кориолис опубликовал статью Du Calcul de l’Effet des Machines, в которой излагалась математика того, что по сути является кинетической энергией. Создание и введение в оборот самого термина «кинетическая энергия» приписывают Уильяму Томсону (лорду Кельвину) c 1849—1851 гг.[8][9]. Ренкин, который ввел термин «потенциальная энергия» в 1853 году[10], позже цитировал У. Томсона и П. Тэйта с заменой слова «кинетическая» на «фактическая»[11].
Кинетическая энергия в классической механике[править | править код]
Случай одной материальной точки[править | править код]
По определению, кинетической энергией материальной точки массой 
,
при этом предполагается, что скорость точки 


Если 





Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина 
Случай абсолютно твёрдого тела[править | править код]
При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:
Здесь 



Кинетическая энергия в гидродинамике[править | править код]
В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа 


где по повторяющемуся индексу 
Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса[13]. Если, в согласии с методом Рейнольдса, представить 

где 





Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.
Кинетическая энергия в квантовой механике[править | править код]
В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (

где 


Кинетическая энергия в релятивистской механике[править | править код]
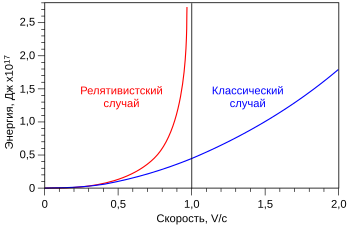
Зависимости кинетической энергии от скорости в классическом и релятивистском случаях для массы в 1 кг
Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как:
- где
— масса материальной точки,
— скорость движения в выбранной инерциальной системе отсчёта,
— скорость света в вакууме (
— энергия покоя).
Кинетическая энергия в этой формуле может быть разложена в ряд Маклорена по степеням 
При скоростях много меньших скорости света (


Как и в классическом случае, имеет место соотношение 


Релятивистское соотношение между кинетической энергией и импульсом p записывается в виде
Разложив это выражение по степеням 
первый член которого равен нерелятивистскому выражению кинетической энергии через импульс, а последующие члены — релятивистские поправки к этому выражению, которые малы при 
Свойства кинетической энергии[править | править код]
- Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему[1].
- Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки и направления её скорости, а зависит лишь от модуля скорости или от квадрата её скорости[1].
- Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
- Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии[15][16].
Физический смысл кинетической энергии[править | править код]
Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии[2]:
Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения 
Соотношение кинетической и внутренней энергии[править | править код]
Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.
То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.
См. также[править | править код]
- Теорема о кинетической энергии системы
- Потенциальная энергия
- Закон сохранения энергии
- Хаос
- Энтальпия
- Негэнтропия
- Термодинамика
- Парадокс кинетической энергии
Примечания[править | править код]
- ↑ 1 2 3 4 Айзерман, 1980, с. 49.
- ↑ 1 2 Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.
- ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва, Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
- ↑ Brenner, Joseph. Logic in Reality. — illustrated. — Springer Science & Business Media, 2008. — P. 93. — ISBN 978-1-4020-8375-4. Архивная копия от 25 января 2020 на Wayback Machine Extract of page 93 Архивировано 4 августа 2020 года.
- ↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
- ↑ Judith P. Zinsser. Emilie Du Châtelet : daring genius of the Enlightenment. — New York: Penguin Books, 2007. — viii, 376 pages, 16 unnumbered pages of plates с. — ISBN 0-14-311268-6, 978-0-14-311268-6.
- ↑ Crosbie Smith. Energy and empire : a biographical study of Lord Kelvin. — Cambridge [Cambridgeshire]: Cambridge University Press, 1989. — xxvi, 866 pages с. — ISBN 0-521-26173-2, 978-0-521-26173-9. Архивировано 25 января 2022 года.
- ↑ John Theodore Merz. A history of European thought in the nineteenth century. — Gloucester, Mass.: Peter Smith, 1976. — 4 volumes с. — ISBN 0-8446-2579-5, 978-0-8446-2579-9.
- ↑ William John Macquorn Rankine. XVIII. On the general law of the transformation of energy // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. — 1853-02. — Т. 5, вып. 30. — С. 106–117. — ISSN 1941-5990 1941-5982, 1941-5990. — doi:10.1080/14786445308647205.
- ↑ W.J. Macquorn Rankine. XIII. On the phrase “Potential energy,” and on the definitions of physical quantities // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. — 1867-02. — Т. 33, вып. 221. — С. 88–92. — ISSN 1941-5990 1941-5982, 1941-5990. — doi:10.1080/14786446708639753.
- ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245. Архивировано 23 августа 2017 года.
- ↑ 1 2 Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
- ↑ Блохинцев Д. И. Основы квантовой механики Архивная копия от 15 февраля 2022 на Wayback Machine, 5-е изд. Наука, 1976. — 664 с., см. § 26.
- ↑ Айзерман, 1980, с. 54.
- ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» Архивная копия от 1 января 2015 на Wayback Machine // УФН, 59, с. 325—362, (1956)
Литература[править | править код]
- Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.
- Фриш С. Э. Курс общей физики. В 3-х тт. Т.1. Физические основы механики. Молекулярная физика. Колебания и волны. 13-е изд. — СПб.: Лань, 2010. — 480 с. — ISBN 978-5-8114-0663-0.
- Сивухин Д. В. Общий курс физики. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2006. — 560 с. — ISBN 5-9221-0715-1.










