Класс как найти объем призмы цилиндра

Класс как найти объем призмы цилиндра

Теория

1. Объём и площадь поверхности цилиндра

Задания

1. Изменение объёма цилиндра

Сложность:
лёгкое

1

2. Объём цилиндра, полученного вращением квадрата

Сложность:
лёгкое

1

3. Угол между диагоналями осевого сечения

Сложность:
среднее

1

4. Объём цилиндра, описанного около куба

Сложность:
среднее

2

5. Объём цилиндра, описанного около призмы

Сложность:
среднее

1

6. Длина проводника цилиндрической формы

Сложность:
среднее

2

7. Сечение, проведённое параллельно оси цилиндра

Сложность:
среднее

1

8. Открытый цилиндрический бак

Сложность:
сложное

5

9. Mаксимальный объём цилиндра

Сложность:
сложное

5

Тесты

1. Тренировка по теме Как найти объём цилиндра

Сложность: среднее

12

Материалы для учителей

1. Методическое описание
Источник

Геометрия, 11 класс

Урок №12. Объемы прямой призмы и цилиндра

Перечень вопросов, рассматриваемых в теме

1) Доказательство теорем об объемах прямой призмы и цилиндра

2) Определение призмы, вписанной в цилиндр и призмы описанной около цилиндра

3) Решение задач на нахождение объемов прямой призмы и цилиндра

V=Sh объем прямой призмы и цилиндра

Основная литература:

Бутузов В. Ф., Кадомцев С. Б., Атанасян Л. С. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. Уровни – М.: Просвещение, 2014. – 255, сс. 121-126.

Дополнительная литература:

Шарыгин И.Ф. Геометрия. 10–11 кл.: учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Прямая призма — это призма, у которой боковые ребра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками

Объем всякого цилиндра равен произведению площади основания на высоту

Объем призмы — это произведение площади ее основания на высоту

Призма вписана в цилиндр, если ее основания вписаны в основания цилиндра.

Призма описана около цилиндра, если ее основания описаны около оснований цилиндра.

Высота любой призмы (вписанной в цилиндр или описанной около цилиндра), равна высоте самого цилиндра

Примеры и разбор решения заданий тренировочного модуля

№1. Найти объем прямой треугольной призмы высотой 6, в основании которой – прямоугольный треугольник с катетами 3 и 7.

Решение: Объем призмы вычисляется по формуле , т.к. в основании призмы – прямоугольный треугольник, то объем призмы будет вычисляться по формуле , где а и в – катеты треугольника. Подставляя все данные задачи в формулу, получаем ответ: .

№2. Найти объём правильной -угольной призмы, у которой каждое ребро равно а, если: а) n=3, б) n=4, в) n=6.

Решение: поскольку призма правильная, значит, это прямая призма и в основании лежит правильный многоугольник.

Формулу для вычисления объёма прямой призмы мы только что вывели . Поскольку, по условию все ребра призмы равны a, значит, высота призмы равна h=a. Осталось найти площадь основания.

Основанием правильной треугольной призмы является правильный, то есть равносторонний треугольник n=3. Площадь правильного треугольника со стороной f вычислить несложно, она равна .

Применяя формулу для вычисления объёма прямой призмы, получим, что объём правильной треугольной призмы равен .

Основанием правильной четырёхугольной призмы является квадрат n=4. Площадь квадрата со стороной a равна . Тогда объём правильной четырёхугольной призмы равен .

Основанием правильной шестиугольной призмы является правильный шестиугольник n=6. Своими большими диагоналями шестиугольник делится на 6 равносторонних треугольников. Площадь каждого из треугольников равна , значит, площадь правильного шестиугольника равна . Тогда объём правильной шестиугольной призмы равен .

Ответ 3/2 ед3

№3 Найди объём прямой призмы  если  =120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см2 .

Решение: боковая грань прямой призмы является прямоугольником.

Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.

То есть большая боковая грань содержит большую сторону основания.

По условию =120°,  – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.

Получим, что длина стороны АС=7см.

Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.

Получим, что длина высоты призмы равна .

Для нахождения объёма призмы, воспользуемся только что доказанной формулой . Площадь основания можно найти либо по формуле Герона , либо по формуле .

Мы воспользуемся второй формулой. Получим, что площадь основания равна .

Тогда объём прямой призмы равен .

Ответ 75/4 см3

Источник

Введение

Для решения задач потребуется вспомнить формулы для нахождения объемов куба, прямоугольного параллелепипеда и прямой треугольной призмы. (См. Рис. 1.)

Рис. 1. Объемы известных фигур

На этой базе мы сегодня выведем формулы для вычисления объемов еще двух фигур – произвольной прямой призмы и цилиндра.

Теорема 1. Объем прямой призмы

Объем прямой призмы равен произведению ее площади основания на высоту: .

Доказательство (для произвольной треугольной призмы (см. Рис. 2) и для любой призмы (см. Рис. 3)):

 

Рис. 2. Произвольная треугольная призма

Рис. 3. Произвольная призма

1. Рассмотрим треугольную призму  (см. Рис. 4).

Рис. 4. Треугольная призма

Проведем высоты  и  (см. Рис. 5).

Рис. 5. Высоты  и

Рис. 6. Две образовавшиеся призмы

Получается, что призма  разбилась на две призмы:  и . (См. Рис. 6.)

Тогда по свойству объемов объем исходной призмы будет равен сумме объемов призм разбиения .

Рис. 7. Прямоугольные треугольники в основаниях призм

Каждая из призм  и  является прямой призмой, в основании которой лежит прямоугольный треугольник. (См. Рис. 7.)

Рис. 8. Общая высота

Тогда  и . Так как высота у этих призм одинаковая , то, складывая объемы, эту высоту можно вынеси за скобки. (См. Рис. 8.)

Таким образом, .

Что и требовалось доказать.

Рис. 9. Разбиение оснований на треугольник

2. Рассмотрим произвольную призму, т.е. -угольную, но при этом прямую. Разбиваем ее основания на треугольники. (См. Рис. 9).  

Рис 10. Полученные прямоугольные призмы

Образовалось несколько треугольных призм. (См. Рис.10). Количество полученных призм не имеет значения.

Рис. 11. Площадь основания равна сумме площадей полученных треугольников

Тогда понятно, что объем исходной призмы будет равен сумме объемов полученных треугольных призм, т. е. . Поскольку каждая из полученных призм прямая и треугольная, то для данной формулы будет выполняться равенство из пункта 1 (см. Рис. 11):

 

(Высота у полученных призм одинаковая, т. к. эта высота является высотой исходной призмы (см. Рис. 12)).

Таким образом,  для любой призмы. Теорема доказана.

Рис. 12. Общая для всех призм (полученных и исходной) высота

Пример 1

Найти объем прямой призмы  (см. Рис. 13), если ; ;  (где  – высота ).

Рис. 13 Прямая призма

Решение. Рассмотрим . Он равнобедренный, значит, его высота  совпадает с биссектрисой, то есть  (см. Рис. 14).

Рис.14 Выносной рисунок

Тогда из треугольника :
 . Значит, .

А тогда .

Ответ: .

Формула для вычисления объема цилиндра

Теперь найдем формулу для вычисления объема цилиндра. Как обычно, речь пойдет о прямом круговом цилиндре.

Рис.15 Комбинации цилиндра и призмы

Напомним, что цилиндр называется вписанным в призму, если его основания вписаны в основания призмы, и наоборот, описанным – если основания описаны около оснований цилиндра. Также, напомним, что высоты у призмы и вписанного, равно как и описанного, цилиндров совпадут (см. Рис. 15).

Теорема. Объем цилиндра равен произведению площади основания на высоту. .

Формула схожа с формулой объема призмы, т. к., по сути, цилиндр – это предельный случай призмы, когда  угольник в основании призмы стремится к окружности.

Рис. 16 Вписанная в цилиндр призма

Впишем в данный цилиндр  радиуса  и высоты  правильную -угольную призму . Тогда логично, что в окружность основания цилиндра вписан правильный -угольник. Высота этой призмы будет также  (см. Рис. 16).

Найдем объем призмы . Пусть  – сторона основания призмы,  – центр основания (см. Рис. 17). Тогда 

Рис. 17 Треугольник в основании призмы

То есть 

Наряду с этим опишем около данного цилиндра правильную -угольную призму . Высота этой призмы будет также  (см. Рис. 18).


Рис. 18 Описанная около цилиндра призма

 

Рис. 19 Треугольник в основании )

Найдем объем призмы . Пусть – сторона основания призмы,  – центр основания (см. Рис. 19). Тогда 

То есть .

Таким образом, искомый объем цилиндра удовлетворяет неравенству , то есть он больше объема призмы, вписанной в него, и меньше объема призмы, описанной около него.

Устремим  к бесконечности. С помощью замечательного предела можно получить, что обе площади устремятся к площади круга . 

Первый замечательный предел

Вспомним замечательный предел: .

Тогда 

Аналогично .

Подставляя эти результаты в формулы, получаем требуемый результат.

Значит, получаем, что , что и требовалось доказать.

Пример 2

Площадь основания цилиндра равна , а площадь осевого сечения равна . Найти объем цилиндра (См. Рис. 20).


Рис. 20 Искомый цилиндр

Решение., значит, .

Далее, площадь осевого сечения равна ;

Окончательно, .

Ответ: .

Задача

В цилиндр вписана призма , основанием которой является прямоугольный треугольник (), в котором , , . Найти отношение объемов призмы и цилиндра (см. Рис. 1).

 

Рис.1 Иллюстрация задачи

Решение.

Рис. 2 Основание призмы

Высота цилиндра равна боковому ребру призмы, т. е.. Найдем площадь основания призмы. Рассмотрим прямоугольный  в основании призмы. Катет , а угол напротив этого катета , значит, гипотенуза

 (см. Рис. 2).

А радиус описанной около основания окружности – это и есть радиус основания цилиндра. Кроме того, катет (по определению синуса).

Подставим данные в формулы, учитывая, что высоты у фигур совпадают, .

.

 

Окончательно .

Ответ: .

Заключение

Были разобраны две теоремы: две новые формулы для нахождения объемов прямой призмы и цилиндра. Выяснили, что в обоих случаях .

Список литературы

1. Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.

2. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.

3. В.Ф. Бутузов, Ю.А. Глазков. Рабочая тетрадь по геометрии 11 класс.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «ЯКласс» (Источник)

2. Интернет-сайт «Математика? Легко!» (Источник)

3.Интернет-сайт «ЯКласс» (Источник)

Домашнее задание

1. В цилиндр вписана правильная треугольная призма, а в призму вписан цилиндр. Найдите отношение объемов цилиндров.

2. Основание прямой призмы – ромб с острым углом 3. Диагональ боковой грани образует с плоскостью основания угол . Найдите объем призмы, если ее высота равна  см.

3. Через одну образующую цилиндра проведены два сечения, угол между плоскостями которых равен , а площадь каждого из полученных сечений равна . Найдите объем цилиндра, если его высота равна  см.

Источник

Приложение 3.2.4

ПЛАН-КОНСПЕКТ УРОКА «Объем прямой призмы и цилиндра»

Школа: МОУ «Лицей №1», г. Воркуты.

Учитель: Курылева Светлана Сергеевна

Предмет: Геометрия

Класс: 11 (математический).

Тема: Объемы прямой призмы и цилиндра (задача 8 в ЕГЭ).

Тип урока: урок обучения умениям и навыкам.

Форма урока: урок-практикум.

Цель на урок: выработать умение применять формулы для вычисления объёма прямой призмы и цилиндра при решении задач.

Задачи на урок:

        • дидактические: повторить формулы для вычисления объема прямой призмы и цилиндра многоугольников; учиться применять формулы для вычисления объема прямой призмы и цилиндра при решении задач; рассмотреть задачи на вычисление объема призмы, вписанной в цилиндр и призмы, описанной около цилиндра; контроль уровня усвоения основных знаний, умений и навыков по данной теме.

  • развивающие: развивать познавательный интерес у учащихся, логическое мышление, интеллектуальные способности; формировать математическую речь; развивать умения применять знания в конкретной ситуации; развитие самостоятельной деятельности обучающихся.

  • воспитательные: воспитывать у учащихся потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог, формировать эстетические навыки при оформлении записей в тетради.

Оборудование: компьютер, мультимедийный проектор, экран, листы на каждого ученика с подбором заданий по теме урока, заданий для самостоятельной работы, домашней работы, дополнительная задача.

Средства обучения: мультимедийная презентация к уроку «Объем прямой призмы и цилиндра».

Ход урока.

I. Организационный момент.

Сегодня на уроке мы будем решать задачи по теме «Объемы прямой призмы и цилиндра» из открытого банка ЕГЭ, это группы В10, В13.

Французский государственный и военный деятель, инженер и ученый Лазар Карно сказал: «Первое условие, которое надлежит выполнять в математике, – это быть точным, второе – быть ясным и, насколько можно, простым».

Исходя из темы урока, какие задачи вы можете перед собой поставить?

Задачи, которые мы сегодня будем разбирать, может быть, кому-то покажутся легкими, но без знания соответствующего теоретического материала справиться с ними практически нельзя.

II. Устная работа.

На предыдущем уроке мы вывели формулы для вычисления объемов прямой призмы и цилиндра. Какова общая запись этих формул?

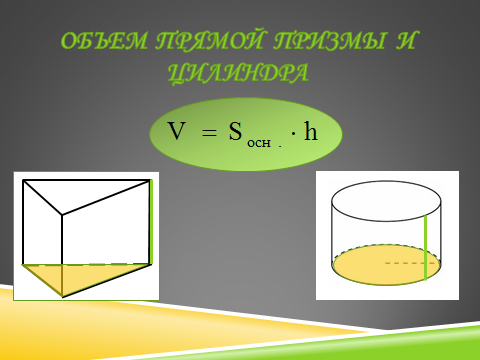
Какие фигуры наиболее часто встречаются в основании прямой призмы в задачах ЕГЭ?

Треугольник

Как найти площадь прямоугольного треугольника, правильного треугольника, произвольного треугольника? Какие еще формулы для вычисления площади произвольного треугольника вы знаете?

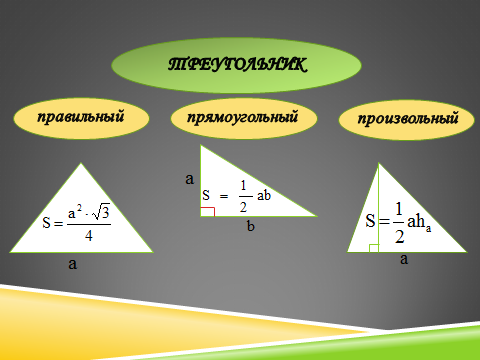
Четырехугольник

Как найти площадь квадрата, прямоугольника, параллелограмма, ромба? Какие еще формулы для вычисления площади параллелограмма вы знаете?

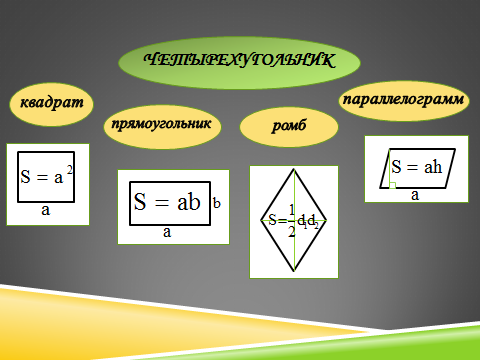
Правильный шестиугольник

Как найти площадь правильного шестиугольника?

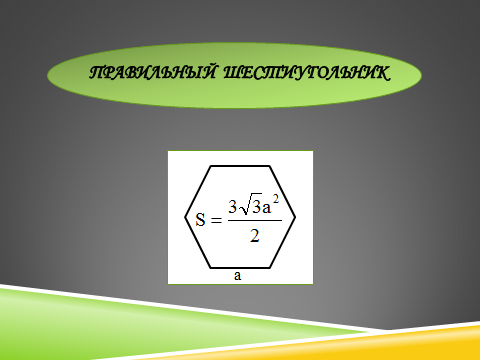
Давайте также вспомним еще ряд соотношений, необходимых для успешности как сегодняшнего урока, так и для решения задач по геометрии в целом.

С помощью каких формул можно вычислить радиусы описанной и вписанной окружностей для

  • правильного треугольника,

  • прямоугольного треугольника,

  • квадрата,

  • прямоугольника,

  • правильного шестиугольника?

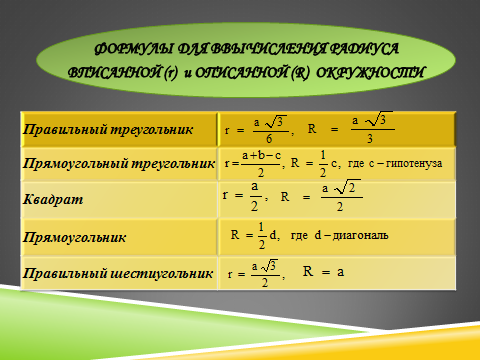
Для решения задач нам также потребуются некоторые отношения подобия.

Как найти коэффициент подобия для подобных многоугольников, для кругов?

Чему равно отношение периметров подобных многоугольников?

Чему равно отношение площадей подобных фигур?

Чему равно отношение объемов подобных тел?

Ответьте, пожалуйста, ещё на ряд вопросов.

  1. Во сколько раз увеличится площадь треугольника, если его стороны увеличить в 3 раза?

  2. Во сколько раз увеличится площадь прямоугольного треугольника, если один из катетов увеличить в 5 раз?

  3. Как изменится площадь квадрата, если его стороны уменьшить в 4 раза?

  4. Как изменится площадь прямоугольника, если одну из его сторон увеличить в 2 раза, обе стороны увеличить в 2 раза?

  5. Как изменится площадь правильного шестиугольника, если его стороны уменьшить в 1,5 раза?

  6. Как изменится объем призмы, если все ребра уменьшить в 3 раза; если стороны основания уменьшить в 3 раза, а высоту оставить неизменной?

  7. Как изменится объем цилиндра, если увеличить его высоту в 7 раз, а основание оставить прежним?

  8. Представьте себе ситуацию: воду из одного сосуда переливают во второй сосуд, дно которого с коэффициентом 2 подобно дну первого сосуда. Как изменится при этом уровень воды?

III. Решение тренировочных упражнений.

Итак, всю необходимую теорию мы повторили, приступаем к решению задач.

Одним из пунктов домашнего задания был выбор из прототипов открытого банка ЕГЭ заданий на вычисление объема прямой призмы и цилиндра и распределение их по группам. Какие группы вы получили, и какие задания отнесли к той или иной группе?

Призма

Цилиндр

Призма, описанная

около цилиндра

Призма, вписанная

в цилиндр

27047

27048

27082

27083

27084

245357

245335

245344

27045

27046

27053

27091

27118

27196

27199

27200

27201

27041

27042

27049

27050

Для удобства я выделила эти задачи в отдельный блок (задания для классной работы) (Приложение 1). При отборе задач кое-кто из вас, вероятно, уже «прикинул», как они решаются. Кто хочет проверить свои силы и решить несколько аналогичных задач самостоятельно? Раздать варианты задач для самостоятельного решения (решить не менее любых пяти из десяти предложенных). (Приложение 2)

Ну а с остальными поработаем вместе.

Прежде чем мы приступим к решению, три ученика пойдут к доске и оформят решение задач на вычисление объема части цилиндра на доске, это задачи 7 – 9.

Задача 1.

Дополнительный вопрос: с чем совпадает высота прямой призмы?

Задача 2.

Ученик комментирует решение с места, краткая запись появляется на экране.

Задача 3.

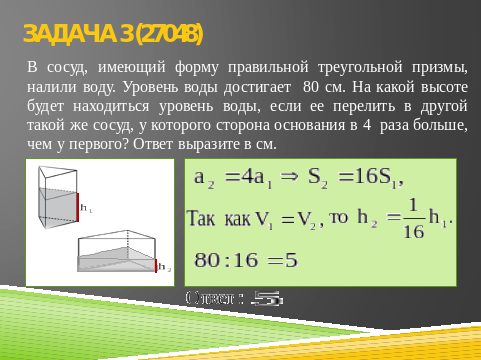
Задача 4.

(для определения объема тела лучше всего подходит способ, изобретенный еще Архимедом: будучи погруженным в жидкость, тело вытесняет ровно столько, сколько и составляет его объем).

Задача 5.

Задача 6.

(выразим измерения второго цилиндра через измерения первого и упростим получившееся выражение, отделим произведение, равное объёму первого цилиндра и вычислим объем второго)

Задачи 7 – 9

(прокомментировав решение, ученики садятся, все остальные записывают решение задач в тетради)

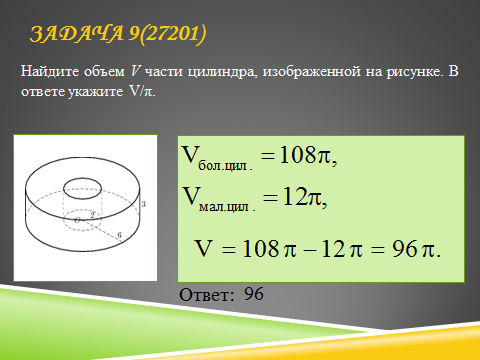
Прежде чем приступить к решению следующих задач, давайте вспомним, какая призма называется вписанной в цилиндр? Какую призму можно вписать в цилиндр?

Какие конфигурации тел чаще всего встречаются в задачах ЕГЭ?

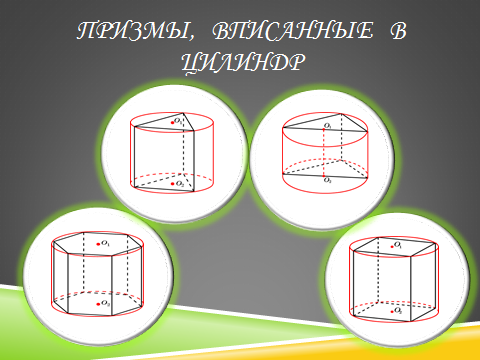
Задача 10.

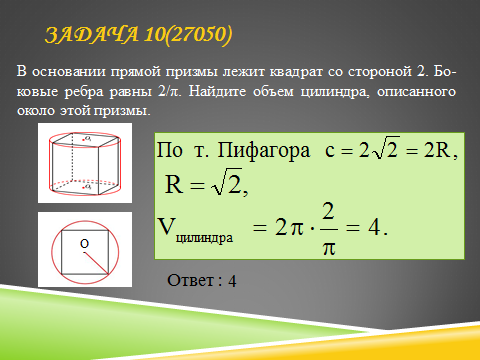
Какую призму называют описанной около цилиндра? Какую призму можно описать около цилиндра?

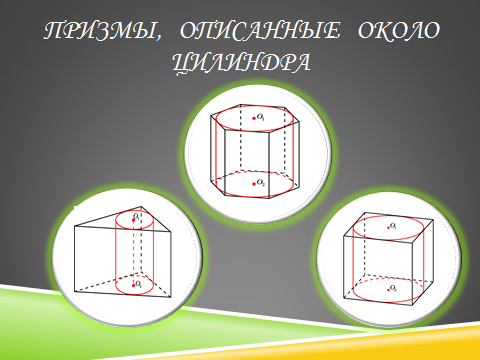
Задача 11.

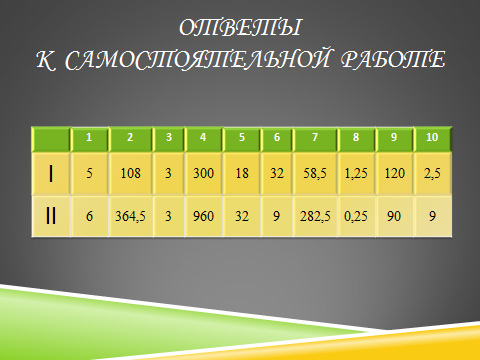
Ну а теперь поменяемся местами. Те учащиеся, кто работал самостоятельно, отложите работы, чуть позже мы их проверим, а те ребята, которые работали вместе со мной, проверят свои силы при выполнении самостоятельной работы. Перед вами лежат задания в двух вариантах, в каждом варианте по десять задач. Вам необходимо решить не менее трех из них. Какие задачи выполнить – выбирайте сами.

(более сильной группе ребят выдать тексты дополнительной задачи с изображением призмы) (Приложение 3)

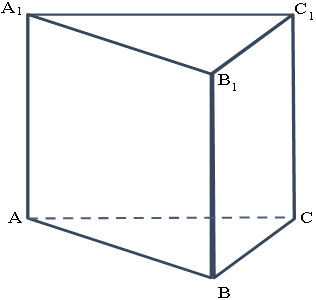
Дополнительная задача

Все ребра правильной треугольной призмы равны между собой. Найдите объем призмы, если площадь сечения плоскостью, проходящей через сторону BC нижнего основания и середину ребра верхнего основания, равна .

Итак, вы ознакомились с условием задачи, решать на уроке мы её не будем, но чтобы вы дома успешно с ней справились, давайте составим план решения.

Первый пункт лежит на поверхности и мы его выполним:

  1. Построить сечение призмы.

(Пусть К – середина ребра А1В1. Точки В и К лежат в одной плоскости, соединим их. Так как плоскости АВС и А1В1С1 параллельны, то секущая плоскость пересекает их по параллельным прямым. Через точку К проведем прямую, параллельную ВС, пусть она пересекает ребро А1С1 в точке М. Точки М и С лежат в одной плоскости, мы их соединяем).

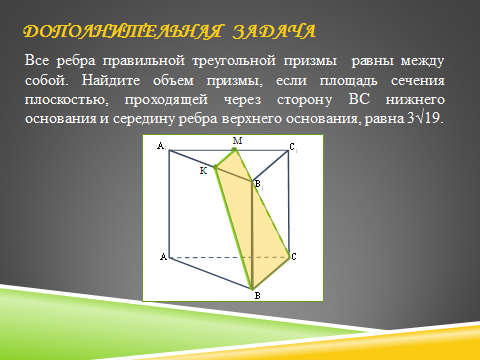
Учащиеся высказывают предположения о дальнейшем ходе решения, учитель производит корректировку.

IV. Подведение итогов. Рефлексия.

Итак, занятие подходит к концу. Давайте подведем итоги. Каждый из вас сегодня поработал самостоятельно. Возьмите ваши работы, поменяйтесь с рядом сидящим, оцените работы друг друга. Вспомните, отвечал ли ваш товарищ сегодня устно, сколько раз он отвечал, правильно ли. Добавьте по баллу за каждый правильный ответ.

Если ваш товарищ набрал 5 баллов и больше, поставьте ему «5» (отлично)

4 балла – «4» (хорошо)

3 балла – «3» (удовлетворительно)

Кто получил отметку отлично, хорошо? Есть такие, чья работа была неудовлетворительной?

Попробуйте дома разобраться в своих ошибках, выяснить причину, по которой вы их допустили.

Ну а сейчас мне хотелось бы, чтобы каждый из вас определил, на какой ступеньке изучения данной темы он находится?

Есть стоящие лишь на первой ступени? На последней ступени? Сделайте соответствующие выводы.

V. Информирование о домашнем задании. (Приложение 4)

Источник

ТЕМА УРОКА: «ВЫЧИСЛЕНИЕ ОБЪЁМОВ ПРЯМОЙ ПРИЗМЫ И ЦИЛИНДРА»

ЦЕЛИ УРОКА:

  1. Продолжить изучение темы «Объёмы геометрических тел».

  2. Актуализировать и закрепить знания учащимися формул для вычисления объёмов прямой призмы и цилиндра, для решения задач по материалам ЕГЭ.

  3. Актуализировать знания учащихся по некоторым разделам планиметрии, требующиеся для решения задач урока и тестов ЕГЭ по математике.

  4. Повторить ряд теорем: площадь прямоугольного треугольника и трапеции, площадь правильного треугольника и шестиугольника, площадь ромба.

  5. Обратить внимание учащихся на необходимость осознанного изучения материала и практическое его применение.

ОБОРУДОВАНИЕ: компьютер, проектор, экран.

ТИП ЗАНЯТИЯ: урок совершенствования знаний, умений и навыков

ФОРМА ЗАНЯТИЯ: фронтальная, индивидуальная, парная.

ХОД УРОКА

  1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

Сегодня мы продолжаем изучение темы «Вычисление объёмов призмы и цилиндра». Мы уже познакомились на предыдущих уроках с формулами для вычисления объёмов этих тел, и нам предстоит увидеть, как знания по этой теме необходимы при сдаче выпускного экзамена.

  1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

  1. Проверка домашнего задания

№728

1 ученик выполняет чертёж на доске и рассказывает план решения задачи.

План решения

  1. площадь основания S= 21

  2. диагональ ВД=5 (по т. косинусов)

  3. высота ВВ1= ВД

  4. объём V =105

Задача

В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.

  1. Повторение формул

Давайте вспомним формулы для вычисления объёма призмы и цилиндра.

– Итак, как же вычисляются объёмы призмы и цилиндра?

– Как же так, тела разные, а формула одна?

– В чём все же состоит отличие этих формул?

– Какие многоугольники могут лежать в основании призмы?

Итак, в основании призмы могут лежать разные многоугольники, но чаще всего это треугольники, четырехугольники, шестиугольники, поэтому в каждой конкретной задаче площадь основания призмы будет вычисляться по-разному. Назовите формулы, по которым можно найти площадь этих многоугольников. Наиболее часто применяемые в задачах запишем в тетрадь, используя записи на слайдах.

  1. РЕШЕНИЕ ЗАДАЧ

1) Решение задач на вычисление объёмов прямой призмы и цилиндра по готовым чертежам

  1. Найдите объём прямой призмы. Обсуждаем классом решение задач, затем три человека по две задачи выполняют вычисления на доске.

Ответы:

2. Найдите объём цилиндра

Ответы:

2) Решение задач по материалам открытого банка ЕГЭ

Сегодня большую часть урока мы посвятим решению различных задач по данной теме, которые есть в КИМах ЕГЭ по математике. Выполняем в парах.. Проверка решения задач с помощью показа слайдов презентации.

Задача №1

Найти объем прямой треугольной призмы высотой 5, в основании которой – прямоугольный треугольник с катетами 6 и 8.

Задача №2

Найдите объем правильной шестиугольной призмы, сторона основания которой равны 1, а боковые ребра равны √3.

Задача №3

В цилиндрический сосуд налили 1200 см3 воды, уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь, при этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? (в см3)

Задача №4

В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого? (в см)

Задача №5

В сосуд, имеющий форму правильной треугольной призмы, налили 1500 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 28 см. Найдите объем детали (в см3)

Задача №6

В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если ее перелить в сосуд такой же формы, но сторона основания в 4 раза больше, чем у первого? (в см)

  1. ПОВТОРЕНИЕ

1) Вычисление площадей фигур на клеточной бумаге по материалам открытого банка ЕГЭ

Вычислите площади фигур, изображённых на клеточной бумаге. Индивидуальная работа по карточкам.

Ответы: 8 14,5 13,5 24

2 человека сзади на доске вычисляют площади фигур, затем проверяем.

2) Вычисление площадей фигур на клеточной бумаге по формуле Пика

Для точности и проверки вычислений площадей фигур можно применять формулу Пика.

Пусть L − число целочисленных точек внутри многоугольника, B − количество целочисленных точек на его границе, S − его площадь. Тогда верна формула Пика: S = L + B/2 – 1

S = 15 + 4/2 – 1 = 16 S = 16 + 9/2 – 1 = 19,5

  1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА

Ребята, сегодня на уроке мы рассмотрели ряд задач на вычисление объёмов цилиндра и призмы. Вы увидели, что решение стереометрических задач базируется на формулах и теоремах из планиметрии, а также на умении сводить стереометрическую задачу к одной или нескольким плоскостным задачам. На следующем уроке мы рассмотрим ряд более сложных задач.

  1. ДОМАШНЕЕЕ ЗАДАНИЕ

1. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 18 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого? (в см)

2. Найдите объем правильной шестиугольной призмы, сторона основания 9 см, а боковые ребра см.

3. В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,9 раза. Чему равен объем детали? (в литрах)

4. Одна цилиндрическая кружка вдвое выше второй, зато вторая в 3 раза шире. Найдите отношение объема второй кружки к объему первой.

Список использованной литературы и Интернет-ресурсы

1. Открытый банк заданий по математике http://mathege.ru

2. Е.М. Рабинович Математика. Задачи и упражнения на готовых чертежах. Геометрия 10-11 классы

Источник

Добавить комментарий