Надежность результата многократных измерений. Коэффициент Стьюдента.
Доверительной
вероятностью или надежностью
P
серии измерений называется вероятность
попадания истинного значения измеряемой
величины в данный интервал (выражается
в долях единицы или в процентах).
Интервал
(<x>±-
∆x)
в который попадает истинное значение
искомой величины с заданной доверительной
вероятностью P(∆x)
, называют доверительным
интервалом или интервалом надежности
и для краткости обозначают как ∆x.
Чем
больше доверительный интервал, тем
больше доверительная вероятность того,
что результат измерения попадет в него.
Величина доверительного интервала,
рассчитывается методами теории
вероятностей и математической статистики
и определяется выбором вида функции
распределения случайных величин f(∆x).
Для
всех функций распределения, базовым
является распределение
Гаусса,
справедливое для большого количества
равноточных
измерений
:

где
величина
называется среднеквадратичным
или стандартным отклонением
от среднего
значения <x>
а,
дисперсией
распределения.
Распределение
Гаусса показывает, что вероятность
появления малых случайных погрешностей
больше вероятности появления больших
погрешностей, при этом случайные
погрешности равные по абсолютной
величине, но противоположные по знаку
встречаются одинаково часто.
При
лабораторных измерениях (n
< 20) для расчета интервала надежности
используется распределение
Стьюдента (при
распределение Стьюдента переходит в
распределение Гаусса),
которое
позволяет по заданной величине надежности
P(∆x)
найти величину доверительного интервала
∆x,
с помощью поправочных коэффициентов
Стьюдента:
[1.6]
где
– коэффициент
Стьюдента, зависящий от выбора
доверительной вероятности p
и числа измерений n,
S
– среднеквадратичное отклонение –
(СКО), вычисляемое по формуле:

Величина
интервала ∆x,
рассчитанная при помощи формулы [1.6]
стремится к нулю при увеличении числа
опытов.
Коэффициенты Стьюдента
|
Число измерений n |
Доверительная |
|||
|
0,90 |
0,95 |
0,99 |
0,999 |
|
|
2 |
6,314 |
12,706 |
63,657 |
636,619 |
|
3 |
2,920 |
4,303 |
9,925 |
31,598 |
|
4 |
2,353 |
3,182 |
5,841 |
12,941 |
|
5 |
2,132 |
2,776 |
4,604 |
8,610 |
|
6 |
2,015 |
2,571 |
4,032 |
6,859 |
|
7 |
1,943 |
2,447 |
3,707 |
5,959 |
|
8 |
1,895 |
2,365 |
3,499 |
5,405 |
|
9 |
1,860 |
2,306 |
3,355 |
5,041 |
|
10 |
1,833 |
2,262 |
3,250 |
4,781 |
Очевидно, что число
опытов имеет смысл выбрать таким, чтобы
случайная погрешность среднего сравнялась
с погрешностью прибора либо стала меньше
ее. Дальнейшее увеличение числа измерений
теряет смысл, так как не увеличит точность
получаемого результата
Расчет погрешности прямых измерений
Прежде,
чем приступить к измерениям, необходимо
предварительно определить пределы
точности данных приборов (инструментальные
погрешности
).
Равноточные
измерения любой физической величины
делаются не менее трех раз и заносятся
в таблицу, с учетом инструментальной
погрешности. В зависимости от поведения
значений результатов измерения, возникают
две различные схемы:
Случайная
погрешность много меньше инструментальной
Если
оказывается, что все время получается
один и тот же результат (нет разброса),
то в качестве интервала надежности
берется стандартная (инструментальная)
погрешность прибора ∆и,
рассчитанная по его классу точности
(или погрешность градуировки прибора)
и результат записывается в виде:
При
этом доверительная вероятность
(надежность) равна
и, как правило, не указывается.
Случайная
погрешность сравнима с инструментальной
Если
разброс значений физической величины
x
превышает погрешность градуировки, то
количество измерений n
увеличивают до тех пор, пока они не
окажутся величинами одного порядка.
Интервал надежности вычисляют в следующей
последовательности:
-
Находят
среднее значение:
-
Оценивают
среднеквадратичное отклонение – СКО:
-
По
заданному значению надежности p
и числу измерений n,
находят
случайную составляющую погрешности:
-
Полную
погрешность вычисляют как корень
квадратный из суммы квадратов случайной
∆хсл
и инструментальной ∆xи
составляющих:
-
Находят
относительную погрешность:
-
Результат
записывают в виде:
,
,
р
= …
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 декабря 2021 года; проверки требуют 3 правки.
Кванти́ли распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики, таких как построение доверительных интервалов и проверка статистических гипотез.
Определение[править | править код]
Пусть 


![alpha in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/daf3c62599ea71319c85f715c9e590d2bab2d036)


.
Замечания[править | править код]
.
- Функция
не имеет простого представления. Однако, возможно вычислить её значения численно.
- Распределение
симметрично. Следовательно,
.
Таблица квантилей[править | править код]
Нижеприведённая таблица получена с помощью функции tinv Архивная копия от 5 апреля 2010 на Wayback Machine пакета MATLAB. Чтобы получить значение 



Если необходимо использовать 



Квантили
| one-tailed test (односторонний) | 1-0,9/2 (55 %) | 1-0,8/2 (60 %) | 1-0,7/2 (65 %) | 1-0,6/2 (70 %) | 1-0,5/2 (75 %) | 1-0,4/2 (80 %) | 1-0,3/2 (85 %) | 1-0,2/2 (90 %) | 1-0,1/2 (95 %) | 1-0,05/2 (97,5 %) | 1-0,02/2 (99 %) | 1-0,01/2 (99,5 %) | 1-0,005/2 (99,75 %) | 1-0,002/2 (99,9 %) | 1-0,001/2 (99,95 %) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| two-tailed test (двухсторонний) | 1-0,9 ( =0,9, P=0,1 (10 %) =0,9, P=0,1 (10 %) |
1-0,8 ( =0,8, P=0,2 (20 %) =0,8, P=0,2 (20 %) |
1-0,7 ( =0,7, P=0,3 (30 %) =0,7, P=0,3 (30 %) |
1-0,6 ( =0,6, P=0,4 (40 %) =0,6, P=0,4 (40 %) |
1-0,5 ( =0,5, P=0,5 (50 %) =0,5, P=0,5 (50 %) |
1-0,4 ( =0,4, P=0,6 (60 %) =0,4, P=0,6 (60 %) |
1-0,3 ( =0,3, P=0,7 (70 %) =0,3, P=0,7 (70 %) |
1-0,2 ( =0,2, P=0,8 (80 %) =0,2, P=0,8 (80 %) |
1-0,1 ( =0,1, P=0,9 (90 %) =0,1, P=0,9 (90 %) |
1-0,05 ( =0,05, P=0,95 (95 %) =0,05, P=0,95 (95 %) |
1-0,02 ( =0,02, P=0,98 (98 %) =0,02, P=0,98 (98 %) |
1-0,01 ( =0,01, P=0,99 (99 %) =0,01, P=0,99 (99 %) |
1-0,005 ( =0,005, P=0,995 (99,5 %) =0,005, P=0,995 (99,5 %) |
1-0,002 ( =0,002, P=0,998 (99,8 %) =0,002, P=0,998 (99,8 %) |
1-0,001 ( =0,001, P=0,999 (99,9 %) =0,001, P=0,999 (99,9 %)
|
| 1 | 0,1584 | 0,3249 | 0,5095 | 0,7265 | 1,0000 | 1,3764 | 1,9626 | 3,0777 | 6,3138 | 12,7062 | 31,8205 | 63,657 | 127,32 | 318,31 | 636,62 |
| 2 | 0,1421 | 0,2887 | 0,4447 | 0,6172 | 0,8165 | 1,0607 | 1,3862 | 1,8856 | 2,9200 | 4,3027 | 6,9646 | 9,9248 | 14,089 | 22,327 | 31,599 |
| 3 | 0,1366 | 0,2767 | 0,4242 | 0,5844 | 0,7649 | 0,9785 | 1,2498 | 1,6377 | 2,3534 | 3,1824 | 4,5407 | 5,8409 | 7,4533 | 10,215 | 12,924 |
| 4 | 0,1338 | 0,2707 | 0,4142 | 0,5686 | 0,7407 | 0,9410 | 1,1896 | 1,5332 | 2,1318 | 2,7764 | 3,7469 | 4,6041 | 5,5976 | 7,1732 | 8,6103 |
| 5 | 0,1322 | 0,2672 | 0,4082 | 0,5594 | 0,7267 | 0,9195 | 1,1558 | 1,4759 | 2,0150 | 2,5706 | 3,3649 | 4,0321 | 4,7733 | 5,8934 | 6,8688 |
| 6 | 0,1311 | 0,2648 | 0,4043 | 0,5534 | 0,7176 | 0,9057 | 1,1342 | 1,4398 | 1,9432 | 2,4469 | 3,1427 | 3,7074 | 4,3168 | 5,2076 | 5,9588 |
| 7 | 0,1303 | 0,2632 | 0,4015 | 0,5491 | 0,7111 | 0,8960 | 1,1192 | 1,4149 | 1,8946 | 2,3646 | 2,9980 | 3,4995 | 4,0293 | 4,7853 | 5,4079 |
| 8 | 0,1297 | 0,2619 | 0,3995 | 0,5459 | 0,7064 | 0,8889 | 1,1081 | 1,3968 | 1,8595 | 2,3060 | 2,8965 | 3,3554 | 3,8325 | 4,5008 | 5,0413 |
| 9 | 0,1293 | 0,2610 | 0,3979 | 0,5435 | 0,7027 | 0,8834 | 1,0997 | 1,3830 | 1,8331 | 2,2622 | 2,8214 | 3,2498 | 3,6897 | 4,2968 | 4,7809 |
| 10 | 0,1289 | 0,2602 | 0,3966 | 0,5415 | 0,6998 | 0,8791 | 1,0931 | 1,3722 | 1,8125 | 2,2281 | 2,7638 | 3,1693 | 3,5814 | 4,1437 | 4,5869 |
| 11 | 0,1286 | 0,2596 | 0,3956 | 0,5399 | 0,6974 | 0,8755 | 1,0877 | 1,3634 | 1,7959 | 2,2010 | 2,7181 | 3,1058 | 3,4966 | 4,0247 | 4,437 |
| 12 | 0,1283 | 0,2590 | 0,3947 | 0,5386 | 0,6955 | 0,8726 | 1,0832 | 1,3562 | 1,7823 | 2,1788 | 2,6810 | 3,0545 | 3,4284 | 3,9296 | 4,3178 |
| 13 | 0,1281 | 0,2586 | 0,3940 | 0,5375 | 0,6938 | 0,8702 | 1,0795 | 1,3502 | 1,7709 | 2,1604 | 2,6503 | 3,0123 | 3,3725 | 3,852 | 4,2208 |
| 14 | 0,1280 | 0,2582 | 0,3933 | 0,5366 | 0,6924 | 0,8681 | 1,0763 | 1,3450 | 1,7613 | 2,1448 | 2,6245 | 2,9768 | 3,3257 | 3,7874 | 4,1405 |
| 15 | 0,1278 | 0,2579 | 0,3928 | 0,5357 | 0,6912 | 0,8662 | 1,0735 | 1,3406 | 1,7531 | 2,1314 | 2,6025 | 2,9467 | 3,286 | 3,7328 | 4,0728 |
| 16 | 0,1277 | 0,2576 | 0,3923 | 0,5350 | 0,6901 | 0,8647 | 1,0711 | 1,3368 | 1,7459 | 2,1199 | 2,5835 | 2,9208 | 3,252 | 3,6862 | 4,015 |
| 17 | 0,1276 | 0,2573 | 0,3919 | 0,5344 | 0,6892 | 0,8633 | 1,0690 | 1,3334 | 1,7396 | 2,1098 | 2,5669 | 2,8982 | 3,2224 | 3,6458 | 3,9651 |
| 18 | 0,1274 | 0,2571 | 0,3915 | 0,5338 | 0,6884 | 0,8620 | 1,0672 | 1,3304 | 1,7341 | 2,1009 | 2,5524 | 2,8784 | 3,1966 | 3,6105 | 3,9216 |
| 19 | 0,1274 | 0,2569 | 0,3912 | 0,5333 | 0,6876 | 0,8610 | 1,0655 | 1,3277 | 1,7291 | 2,0930 | 2,5395 | 2,8609 | 3,1737 | 3,5794 | 3,8834 |
| 20 | 0,1273 | 0,2567 | 0,3909 | 0,5329 | 0,6870 | 0,8600 | 1,0640 | 1,3253 | 1,7247 | 2,0860 | 2,5280 | 2,8453 | 3,1534 | 3,5518 | 3,8495 |
| 21 | 0,1272 | 0,2566 | 0,3906 | 0,5325 | 0,6864 | 0,8591 | 1,0627 | 1,3232 | 1,7207 | 2,0796 | 2,5176 | 2,8314 | 3,1352 | 3,5272 | 3,8193 |
| 22 | 0,1271 | 0,2564 | 0,3904 | 0,5321 | 0,6858 | 0,8583 | 1,0614 | 1,3212 | 1,7171 | 2,0739 | 2,5083 | 2,8188 | 3,1188 | 3,505 | 3,7921 |
| 23 | 0,1271 | 0,2563 | 0,3902 | 0,5317 | 0,6853 | 0,8575 | 1,0603 | 1,3195 | 1,7139 | 2,0687 | 2,4999 | 2,8073 | 3,104 | 3,485 | 3,7676 |
| 24 | 0,1270 | 0,2562 | 0,3900 | 0,5314 | 0,6848 | 0,8569 | 1,0593 | 1,3178 | 1,7109 | 2,0639 | 2,4922 | 2,7969 | 3,0905 | 3,4668 | 3,7454 |
| 25 | 0,1269 | 0,2561 | 0,3898 | 0,5312 | 0,6844 | 0,8562 | 1,0584 | 1,3163 | 1,7081 | 2,0595 | 2,4851 | 2,7874 | 3,0782 | 3,4502 | 3,7251 |
| 26 | 0,1269 | 0,2560 | 0,3896 | 0,5309 | 0,6840 | 0,8557 | 1,0575 | 1,3150 | 1,7056 | 2,0555 | 2,4786 | 2,7787 | 3,0669 | 3,435 | 3,7066 |
| 27 | 0,1268 | 0,2559 | 0,3894 | 0,5306 | 0,6837 | 0,8551 | 1,0567 | 1,3137 | 1,7033 | 2,0518 | 2,4727 | 2,7707 | 3,0565 | 3,421 | 3,6896 |
| 28 | 0,1268 | 0,2558 | 0,3893 | 0,5304 | 0,6834 | 0,8546 | 1,0560 | 1,3125 | 1,7011 | 2,0484 | 2,4671 | 2,7633 | 3,0469 | 3,4082 | 3,6739 |
| 29 | 0,1268 | 0,2557 | 0,3892 | 0,5302 | 0,6830 | 0,8542 | 1,0553 | 1,3114 | 1,6991 | 2,0452 | 2,4620 | 2,7564 | 3,038 | 3,3962 | 3,6594 |
| 30 | 0,1267 | 0,2556 | 0,3890 | 0,5300 | 0,6828 | 0,8538 | 1,0547 | 1,3104 | 1,6973 | 2,0423 | 2,4573 | 2,75 | 3,0298 | 3,3852 | 3,646 |
| 31 | 0,1267 | 0,2555 | 0,3889 | 0,5298 | 0,6825 | 0,8534 | 1,0541 | 1,3095 | 1,6955 | 2,0395 | 2,4528 | 2,744 | 3,0221 | 3,3749 | 3,6335 |
| 32 | 0,1267 | 0,2555 | 0,3888 | 0,5297 | 0,6822 | 0,8530 | 1,0535 | 1,3086 | 1,6939 | 2,0369 | 2,4487 | 2,7385 | 3,0149 | 3,3653 | 3,6218 |
| 33 | 0,1266 | 0,2554 | 0,3887 | 0,5295 | 0,6820 | 0,8526 | 1,0530 | 1,3077 | 1,6924 | 2,0345 | 2,4448 | 2,7333 | 3,0082 | 3,3563 | 3,6109 |
| 34 | 0,1266 | 0,2553 | 0,3886 | 0,5294 | 0,6818 | 0,8523 | 1,0525 | 1,3070 | 1,6909 | 2,0322 | 2,4411 | 2,7284 | 3,002 | 3,3479 | 3,6007 |
| 35 | 0,1266 | 0,2553 | 0,3885 | 0,5292 | 0,6816 | 0,8520 | 1,0520 | 1,3062 | 1,6896 | 2,0301 | 2,4377 | 2,7238 | 2,996 | 3,34 | 3,5911 |
| 36 | 0,1266 | 0,2552 | 0,3884 | 0,5291 | 0,6814 | 0,8517 | 1,0516 | 1,3055 | 1,6883 | 2,0281 | 2,4345 | 2,7195 | 2,9905 | 3,3326 | 3,5821 |
| 37 | 0,1265 | 0,2552 | 0,3883 | 0,5289 | 0,6812 | 0,8514 | 1,0512 | 1,3049 | 1,6871 | 2,0262 | 2,4314 | 2,7154 | 2,9852 | 3,3256 | 3,5737 |
| 38 | 0,1265 | 0,2551 | 0,3882 | 0,5288 | 0,6810 | 0,8512 | 1,0508 | 1,3042 | 1,6860 | 2,0244 | 2,4286 | 2,7116 | 2,9803 | 3,319 | 3,5657 |
| 39 | 0,1265 | 0,2551 | 0,3882 | 0,5287 | 0,6808 | 0,8509 | 1,0504 | 1,3036 | 1,6849 | 2,0227 | 2,4258 | 2,7079 | 2,9756 | 3,3128 | 3,5581 |
| 40 | 0,1265 | 0,2550 | 0,3881 | 0,5286 | 0,6807 | 0,8507 | 1,0500 | 1,3031 | 1,6839 | 2,0211 | 2,4233 | 2,7045 | 2,9712 | 3,3069 | 3,551 |
| 41 | 0,1264 | 0,2550 | 0,3880 | 0,5285 | 0,6805 | 0,8505 | 1,0497 | 1,3025 | 1,6829 | 2,0195 | 2,4208 | 2,7012 | 2,967 | 3,3013 | 3,5442 |
| 42 | 0,1264 | 0,2550 | 0,3880 | 0,5284 | 0,6804 | 0,8503 | 1,0494 | 1,3020 | 1,6820 | 2,0181 | 2,4185 | 2,6981 | 2,963 | 3,296 | 3,5377 |
| 43 | 0,1264 | 0,2549 | 0,3879 | 0,5283 | 0,6802 | 0,8501 | 1,0491 | 1,3016 | 1,6811 | 2,0167 | 2,4163 | 2,6951 | 2,9592 | 3,2909 | 3,5316 |
| 44 | 0,1264 | 0,2549 | 0,3878 | 0,5282 | 0,6801 | 0,8499 | 1,0488 | 1,3011 | 1,6802 | 2,0154 | 2,4141 | 2,6923 | 2,9555 | 3,2861 | 3,5258 |
| 45 | 0,1264 | 0,2549 | 0,3878 | 0,5281 | 0,6800 | 0,8497 | 1,0485 | 1,3006 | 1,6794 | 2,0141 | 2,4121 | 2,6896 | 2,9521 | 3,2815 | 3,5203 |
| 46 | 0,1264 | 0,2548 | 0,3877 | 0,5281 | 0,6799 | 0,8495 | 1,0483 | 1,3002 | 1,6787 | 2,0129 | 2,4102 | 2,687 | 2,9488 | 3,2771 | 3,515 |
| 47 | 0,1263 | 0,2548 | 0,3877 | 0,5280 | 0,6797 | 0,8493 | 1,0480 | 1,2998 | 1,6779 | 2,0117 | 2,4083 | 2,6846 | 2,9456 | 3,2729 | 3,5099 |
| 48 | 0,1263 | 0,2548 | 0,3876 | 0,5279 | 0,6796 | 0,8492 | 1,0478 | 1,2994 | 1,6772 | 2,0106 | 2,4066 | 2,6822 | 2,9426 | 3,2689 | 3,5051 |
| 49 | 0,1263 | 0,2547 | 0,3876 | 0,5278 | 0,6795 | 0,8490 | 1,0475 | 1,2991 | 1,6766 | 2,0096 | 2,4049 | 2,68 | 2,9397 | 3,2651 | 3,5004 |
| 50 | 0,1263 | 0,2547 | 0,3875 | 0,5278 | 0,6794 | 0,8489 | 1,0473 | 1,2987 | 1,6759 | 2,0086 | 2,4033 | 2,6778 | 2,937 | 3,2614 | 3,496 |
| 100 | 0,1260 | 0,2540 | 0,3864 | 0,5261 | 0,6770 | 0,8452 | 1,0418 | 1,2901 | 1,6602 | 1,9840 | 2,3642 | 2,6259 | 2,8707 | 3,1737 | 3,3905 |
| 1000 | 0,1257 | 0,2534 | 0,3854 | 0,5246 | 0,6747 | 0,8420 | 1,0370 | 1,2824 | 1,6464 | 1,9623 | 2,3301 | 2,5808 | 2,8133 | 3,0984 | 3,3003 |
| Inf | 0,1257 | 0,2534 | 0,3853 | 0,5244 | 0,6745 | 0,8416 | 1,0364 | 1,2816 | 1,6449 | 1,9600 | 2,3263 | 2,5758 | 2,8070 | 3,0902 | 3,2905 |
Пример[править | править код]
(
=0,2, k=4);
(
=0,8, k=4).
См. также[править | править код]
- Средняя квадратическая погрешность
- Доверительный интервал для математического ожидания нормальной выборки
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) – числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
Содержание
- 1 Определение
- 2 Замечания
- 3 Таблица квантилей
- 3.1 Пример
- 4 См. также
Определение
Пусть 


![{displaystyle alpha in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daf3c62599ea71319c85f715c9e590d2bab2d036)


.
Замечания
- Прямо из определения следует, что случайная величина, имеющая распределение Стьюдента с
степенями свободы, не превышает значение
с вероятностью
и превышает его с вероятностью
.
- Функция
строго возрастает для любого
. Следовательно, определена её обратная функция
, и
.
- Функция
не имеет простого представления. Однако, возможно вычислить её значения численно.
- Распределение
симметрично. Следовательно,
.
Таблица квантилей
Нижеприведённая таблица получена с помощью функции tinv пакета MATLAB. Чтобы получить значение 


Пример
;
.
См. также
- Распределение Стьюдента;
- Доверительный интервал для математического ожидания нормальной выборки.
Квантили
| 0.55 | 0.6 | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | 0.975 | 0.99 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.1584 | 0.3249 | 0.5095 | 0.7265 | 1.0000 | 1.3764 | 1.9626 | 3.0777 | 6.3138 | 12.7062 | 31.8205 |
| 2 | 0.1421 | 0.2887 | 0.4447 | 0.6172 | 0.8165 | 1.0607 | 1.3862 | 1.8856 | 2.9200 | 4.3027 | 6.9646 |
| 3 | 0.1366 | 0.2767 | 0.4242 | 0.5844 | 0.7649 | 0.9785 | 1.2498 | 1.6377 | 2.3534 | 3.1824 | 4.5407 |
| 4 | 0.1338 | 0.2707 | 0.4142 | 0.5686 | 0.7407 | 0.9410 | 1.1896 | 1.5332 | 2.1318 | 2.7764 | 3.7469 |
| 5 | 0.1322 | 0.2672 | 0.4082 | 0.5594 | 0.7267 | 0.9195 | 1.1558 | 1.4759 | 2.0150 | 2.5706 | 3.3649 |
| 6 | 0.1311 | 0.2648 | 0.4043 | 0.5534 | 0.7176 | 0.9057 | 1.1342 | 1.4398 | 1.9432 | 2.4469 | 3.1427 |
| 7 | 0.1303 | 0.2632 | 0.4015 | 0.5491 | 0.7111 | 0.8960 | 1.1192 | 1.4149 | 1.8946 | 2.3646 | 2.9980 |
| 8 | 0.1297 | 0.2619 | 0.3995 | 0.5459 | 0.7064 | 0.8889 | 1.1081 | 1.3968 | 1.8595 | 2.3060 | 2.8965 |
| 9 | 0.1293 | 0.2610 | 0.3979 | 0.5435 | 0.7027 | 0.8834 | 1.0997 | 1.3830 | 1.8331 | 2.2622 | 2.8214 |
| 10 | 0.1289 | 0.2602 | 0.3966 | 0.5415 | 0.6998 | 0.8791 | 1.0931 | 1.3722 | 1.8125 | 2.2281 | 2.7638 |
| 11 | 0.1286 | 0.2596 | 0.3956 | 0.5399 | 0.6974 | 0.8755 | 1.0877 | 1.3634 | 1.7959 | 2.2010 | 2.7181 |
| 12 | 0.1283 | 0.2590 | 0.3947 | 0.5386 | 0.6955 | 0.8726 | 1.0832 | 1.3562 | 1.7823 | 2.1788 | 2.6810 |
| 13 | 0.1281 | 0.2586 | 0.3940 | 0.5375 | 0.6938 | 0.8702 | 1.0795 | 1.3502 | 1.7709 | 2.1604 | 2.6503 |
| 14 | 0.1280 | 0.2582 | 0.3933 | 0.5366 | 0.6924 | 0.8681 | 1.0763 | 1.3450 | 1.7613 | 2.1448 | 2.6245 |
| 15 | 0.1278 | 0.2579 | 0.3928 | 0.5357 | 0.6912 | 0.8662 | 1.0735 | 1.3406 | 1.7531 | 2.1314 | 2.6025 |
| 16 | 0.1277 | 0.2576 | 0.3923 | 0.5350 | 0.6901 | 0.8647 | 1.0711 | 1.3368 | 1.7459 | 2.1199 | 2.5835 |
| 17 | 0.1276 | 0.2573 | 0.3919 | 0.5344 | 0.6892 | 0.8633 | 1.0690 | 1.3334 | 1.7396 | 2.1098 | 2.5669 |
| 18 | 0.1274 | 0.2571 | 0.3915 | 0.5338 | 0.6884 | 0.8620 | 1.0672 | 1.3304 | 1.7341 | 2.1009 | 2.5524 |
| 19 | 0.1274 | 0.2569 | 0.3912 | 0.5333 | 0.6876 | 0.8610 | 1.0655 | 1.3277 | 1.7291 | 2.0930 | 2.5395 |
| 20 | 0.1273 | 0.2567 | 0.3909 | 0.5329 | 0.6870 | 0.8600 | 1.0640 | 1.3253 | 1.7247 | 2.0860 | 2.5280 |
| 21 | 0.1272 | 0.2566 | 0.3906 | 0.5325 | 0.6864 | 0.8591 | 1.0627 | 1.3232 | 1.7207 | 2.0796 | 2.5176 |
| 22 | 0.1271 | 0.2564 | 0.3904 | 0.5321 | 0.6858 | 0.8583 | 1.0614 | 1.3212 | 1.7171 | 2.0739 | 2.5083 |
| 23 | 0.1271 | 0.2563 | 0.3902 | 0.5317 | 0.6853 | 0.8575 | 1.0603 | 1.3195 | 1.7139 | 2.0687 | 2.4999 |
| 24 | 0.1270 | 0.2562 | 0.3900 | 0.5314 | 0.6848 | 0.8569 | 1.0593 | 1.3178 | 1.7109 | 2.0639 | 2.4922 |
| 25 | 0.1269 | 0.2561 | 0.3898 | 0.5312 | 0.6844 | 0.8562 | 1.0584 | 1.3163 | 1.7081 | 2.0595 | 2.4851 |
| 26 | 0.1269 | 0.2560 | 0.3896 | 0.5309 | 0.6840 | 0.8557 | 1.0575 | 1.3150 | 1.7056 | 2.0555 | 2.4786 |
| 27 | 0.1268 | 0.2559 | 0.3894 | 0.5306 | 0.6837 | 0.8551 | 1.0567 | 1.3137 | 1.7033 | 2.0518 | 2.4727 |
| 28 | 0.1268 | 0.2558 | 0.3893 | 0.5304 | 0.6834 | 0.8546 | 1.0560 | 1.3125 | 1.7011 | 2.0484 | 2.4671 |
| 29 | 0.1268 | 0.2557 | 0.3892 | 0.5302 | 0.6830 | 0.8542 | 1.0553 | 1.3114 | 1.6991 | 2.0452 | 2.4620 |
| 30 | 0.1267 | 0.2556 | 0.3890 | 0.5300 | 0.6828 | 0.8538 | 1.0547 | 1.3104 | 1.6973 | 2.0423 | 2.4573 |
| 31 | 0.1267 | 0.2555 | 0.3889 | 0.5298 | 0.6825 | 0.8534 | 1.0541 | 1.3095 | 1.6955 | 2.0395 | 2.4528 |
| 32 | 0.1267 | 0.2555 | 0.3888 | 0.5297 | 0.6822 | 0.8530 | 1.0535 | 1.3086 | 1.6939 | 2.0369 | 2.4487 |
| 33 | 0.1266 | 0.2554 | 0.3887 | 0.5295 | 0.6820 | 0.8526 | 1.0530 | 1.3077 | 1.6924 | 2.0345 | 2.4448 |
| 34 | 0.1266 | 0.2553 | 0.3886 | 0.5294 | 0.6818 | 0.8523 | 1.0525 | 1.3070 | 1.6909 | 2.0322 | 2.4411 |
| 35 | 0.1266 | 0.2553 | 0.3885 | 0.5292 | 0.6816 | 0.8520 | 1.0520 | 1.3062 | 1.6896 | 2.0301 | 2.4377 |
| 36 | 0.1266 | 0.2552 | 0.3884 | 0.5291 | 0.6814 | 0.8517 | 1.0516 | 1.3055 | 1.6883 | 2.0281 | 2.4345 |
| 37 | 0.1265 | 0.2552 | 0.3883 | 0.5289 | 0.6812 | 0.8514 | 1.0512 | 1.3049 | 1.6871 | 2.0262 | 2.4314 |
| 38 | 0.1265 | 0.2551 | 0.3882 | 0.5288 | 0.6810 | 0.8512 | 1.0508 | 1.3042 | 1.6860 | 2.0244 | 2.4286 |
| 39 | 0.1265 | 0.2551 | 0.3882 | 0.5287 | 0.6808 | 0.8509 | 1.0504 | 1.3036 | 1.6849 | 2.0227 | 2.4258 |
| 40 | 0.1265 | 0.2550 | 0.3881 | 0.5286 | 0.6807 | 0.8507 | 1.0500 | 1.3031 | 1.6839 | 2.0211 | 2.4233 |
| 41 | 0.1264 | 0.2550 | 0.3880 | 0.5285 | 0.6805 | 0.8505 | 1.0497 | 1.3025 | 1.6829 | 2.0195 | 2.4208 |
| 42 | 0.1264 | 0.2550 | 0.3880 | 0.5284 | 0.6804 | 0.8503 | 1.0494 | 1.3020 | 1.6820 | 2.0181 | 2.4185 |
| 43 | 0.1264 | 0.2549 | 0.3879 | 0.5283 | 0.6802 | 0.8501 | 1.0491 | 1.3016 | 1.6811 | 2.0167 | 2.4163 |
| 44 | 0.1264 | 0.2549 | 0.3878 | 0.5282 | 0.6801 | 0.8499 | 1.0488 | 1.3011 | 1.6802 | 2.0154 | 2.4141 |
| 45 | 0.1264 | 0.2549 | 0.3878 | 0.5281 | 0.6800 | 0.8497 | 1.0485 | 1.3006 | 1.6794 | 2.0141 | 2.4121 |
| 46 | 0.1264 | 0.2548 | 0.3877 | 0.5281 | 0.6799 | 0.8495 | 1.0483 | 1.3002 | 1.6787 | 2.0129 | 2.4102 |
| 47 | 0.1263 | 0.2548 | 0.3877 | 0.5280 | 0.6797 | 0.8493 | 1.0480 | 1.2998 | 1.6779 | 2.0117 | 2.4083 |
| 48 | 0.1263 | 0.2548 | 0.3876 | 0.5279 | 0.6796 | 0.8492 | 1.0478 | 1.2994 | 1.6772 | 2.0106 | 2.4066 |
| 49 | 0.1263 | 0.2547 | 0.3876 | 0.5278 | 0.6795 | 0.8490 | 1.0475 | 1.2991 | 1.6766 | 2.0096 | 2.4049 |
| 50 | 0.1263 | 0.2547 | 0.3875 | 0.5278 | 0.6794 | 0.8489 | 1.0473 | 1.2987 | 1.6759 | 2.0086 | 2.4033 |
| 100 | 0.1260 | 0.2540 | 0.3864 | 0.5261 | 0.6770 | 0.8452 | 1.0418 | 1.2901 | 1.6602 | 1.9840 | 2.3642 |
| 1000 | 0.1257 | 0.2534 | 0.3854 | 0.5246 | 0.6747 | 0.8420 | 1.0370 | 1.2824 | 1.6464 | 1.9623 | 2.3301 |
Коэффициенты Стьюдента
- Коэффициенты Стьюдента
-
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
Содержание
- 1 Определение
- 2 Замечания
- 3 Таблица квантилей
- 3.1 Пример
- 4 См. также
Определение
Пусть Fn — функция распределения Стьюдента t(n) с n степенями свободы, и
. Тогда α-квантилью этого распределения называется число tα,n такое, что
.
Замечания
.
- Функция
не имеет простого представления. Однако, возможно вычислить её значения численно.
- Распределение t(n) симметрично. Следовательно,
- t1 − α,n = − tα,n.
Таблица квантилей
Нижеприведённая таблица получена с помощью функции tinv пакета tα,n, необходимо найти строку, соответствующую нужному n, и колонку, соответствующую нужному α. Искомое число находится в таблице на их пересечении.
Пример
- t0.2,4 = 0.2707;
- t0.8,4 = − t0.2,4 = − 0.2707.
См. также
- Распределение Стьюдента;
- Доверительный интервал для математического ожидания нормальной выборки.
Квантили tα,n
two-tailed test 1-0.9/2 1-0.8/2 1-0.7/2 1-0.6/2 1-0.5/2 1-0.4/2 1-0.3/2 1-0.2/2 1-0.1/2 1-0.05/2 1-0.02/2 one-tailed test 1-0.9 1-0.8 1-0.7 1-0.6 1-0.5 1-0.4 1-0.3 1-0.2 1-0.1 1-0.05 1-0.02 1 0.1584 0.3249 0.5095 0.7265 1.0000 1.3764 1.9626 3.0777 6.3138 12.7062 31.8205 2 0.1421 0.2887 0.4447 0.6172 0.8165 1.0607 1.3862 1.8856 2.9200 4.3027 6.9646 3 0.1366 0.2767 0.4242 0.5844 0.7649 0.9785 1.2498 1.6377 2.3534 3.1824 4.5407 4 0.1338 0.2707 0.4142 0.5686 0.7407 0.9410 1.1896 1.5332 2.1318 2.7764 3.7469 5 0.1322 0.2672 0.4082 0.5594 0.7267 0.9195 1.1558 1.4759 2.0150 2.5706 3.3649 6 0.1311 0.2648 0.4043 0.5534 0.7176 0.9057 1.1342 1.4398 1.9432 2.4469 3.1427 7 0.1303 0.2632 0.4015 0.5491 0.7111 0.8960 1.1192 1.4149 1.8946 2.3646 2.9980 8 0.1297 0.2619 0.3995 0.5459 0.7064 0.8889 1.1081 1.3968 1.8595 2.3060 2.8965 9 0.1293 0.2610 0.3979 0.5435 0.7027 0.8834 1.0997 1.3830 1.8331 2.2622 2.8214 10 0.1289 0.2602 0.3966 0.5415 0.6998 0.8791 1.0931 1.3722 1.8125 2.2281 2.7638 11 0.1286 0.2596 0.3956 0.5399 0.6974 0.8755 1.0877 1.3634 1.7959 2.2010 2.7181 12 0.1283 0.2590 0.3947 0.5386 0.6955 0.8726 1.0832 1.3562 1.7823 2.1788 2.6810 13 0.1281 0.2586 0.3940 0.5375 0.6938 0.8702 1.0795 1.3502 1.7709 2.1604 2.6503 14 0.1280 0.2582 0.3933 0.5366 0.6924 0.8681 1.0763 1.3450 1.7613 2.1448 2.6245 15 0.1278 0.2579 0.3928 0.5357 0.6912 0.8662 1.0735 1.3406 1.7531 2.1314 2.6025 16 0.1277 0.2576 0.3923 0.5350 0.6901 0.8647 1.0711 1.3368 1.7459 2.1199 2.5835 17 0.1276 0.2573 0.3919 0.5344 0.6892 0.8633 1.0690 1.3334 1.7396 2.1098 2.5669 18 0.1274 0.2571 0.3915 0.5338 0.6884 0.8620 1.0672 1.3304 1.7341 2.1009 2.5524 19 0.1274 0.2569 0.3912 0.5333 0.6876 0.8610 1.0655 1.3277 1.7291 2.0930 2.5395 20 0.1273 0.2567 0.3909 0.5329 0.6870 0.8600 1.0640 1.3253 1.7247 2.0860 2.5280 21 0.1272 0.2566 0.3906 0.5325 0.6864 0.8591 1.0627 1.3232 1.7207 2.0796 2.5176 22 0.1271 0.2564 0.3904 0.5321 0.6858 0.8583 1.0614 1.3212 1.7171 2.0739 2.5083 23 0.1271 0.2563 0.3902 0.5317 0.6853 0.8575 1.0603 1.3195 1.7139 2.0687 2.4999 24 0.1270 0.2562 0.3900 0.5314 0.6848 0.8569 1.0593 1.3178 1.7109 2.0639 2.4922 25 0.1269 0.2561 0.3898 0.5312 0.6844 0.8562 1.0584 1.3163 1.7081 2.0595 2.4851 26 0.1269 0.2560 0.3896 0.5309 0.6840 0.8557 1.0575 1.3150 1.7056 2.0555 2.4786 27 0.1268 0.2559 0.3894 0.5306 0.6837 0.8551 1.0567 1.3137 1.7033 2.0518 2.4727 28 0.1268 0.2558 0.3893 0.5304 0.6834 0.8546 1.0560 1.3125 1.7011 2.0484 2.4671 29 0.1268 0.2557 0.3892 0.5302 0.6830 0.8542 1.0553 1.3114 1.6991 2.0452 2.4620 30 0.1267 0.2556 0.3890 0.5300 0.6828 0.8538 1.0547 1.3104 1.6973 2.0423 2.4573 31 0.1267 0.2555 0.3889 0.5298 0.6825 0.8534 1.0541 1.3095 1.6955 2.0395 2.4528 32 0.1267 0.2555 0.3888 0.5297 0.6822 0.8530 1.0535 1.3086 1.6939 2.0369 2.4487 33 0.1266 0.2554 0.3887 0.5295 0.6820 0.8526 1.0530 1.3077 1.6924 2.0345 2.4448 34 0.1266 0.2553 0.3886 0.5294 0.6818 0.8523 1.0525 1.3070 1.6909 2.0322 2.4411 35 0.1266 0.2553 0.3885 0.5292 0.6816 0.8520 1.0520 1.3062 1.6896 2.0301 2.4377 36 0.1266 0.2552 0.3884 0.5291 0.6814 0.8517 1.0516 1.3055 1.6883 2.0281 2.4345 37 0.1265 0.2552 0.3883 0.5289 0.6812 0.8514 1.0512 1.3049 1.6871 2.0262 2.4314 38 0.1265 0.2551 0.3882 0.5288 0.6810 0.8512 1.0508 1.3042 1.6860 2.0244 2.4286 39 0.1265 0.2551 0.3882 0.5287 0.6808 0.8509 1.0504 1.3036 1.6849 2.0227 2.4258 40 0.1265 0.2550 0.3881 0.5286 0.6807 0.8507 1.0500 1.3031 1.6839 2.0211 2.4233 41 0.1264 0.2550 0.3880 0.5285 0.6805 0.8505 1.0497 1.3025 1.6829 2.0195 2.4208 42 0.1264 0.2550 0.3880 0.5284 0.6804 0.8503 1.0494 1.3020 1.6820 2.0181 2.4185 43 0.1264 0.2549 0.3879 0.5283 0.6802 0.8501 1.0491 1.3016 1.6811 2.0167 2.4163 44 0.1264 0.2549 0.3878 0.5282 0.6801 0.8499 1.0488 1.3011 1.6802 2.0154 2.4141 45 0.1264 0.2549 0.3878 0.5281 0.6800 0.8497 1.0485 1.3006 1.6794 2.0141 2.4121 46 0.1264 0.2548 0.3877 0.5281 0.6799 0.8495 1.0483 1.3002 1.6787 2.0129 2.4102 47 0.1263 0.2548 0.3877 0.5280 0.6797 0.8493 1.0480 1.2998 1.6779 2.0117 2.4083 48 0.1263 0.2548 0.3876 0.5279 0.6796 0.8492 1.0478 1.2994 1.6772 2.0106 2.4066 49 0.1263 0.2547 0.3876 0.5278 0.6795 0.8490 1.0475 1.2991 1.6766 2.0096 2.4049 50 0.1263 0.2547 0.3875 0.5278 0.6794 0.8489 1.0473 1.2987 1.6759 2.0086 2.4033 100 0.1260 0.2540 0.3864 0.5261 0.6770 0.8452 1.0418 1.2901 1.6602 1.9840 2.3642 1000 0.1257 0.2534 0.3854 0.5246 0.6747 0.8420 1.0370 1.2824 1.6464 1.9623 2.3301
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое “Коэффициенты Стьюдента” в других словарях:
-
Процентили распределения Стьюдента — Квантили (процентили) распределения Стьюдента (коэффициенты Стьюдента) числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез. Содержание 1 … Википедия
-
Квантили распределения Стьюдента — Квантили (процентили) распределения Стьюдента (коэффициенты Стьюдента) числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.… … Википедия
-
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
-
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
-
Наименьших квадратов метод — один из методов ошибок теории (См. Ошибок теория) для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближённого представления заданной функции другими (более простыми)… … Большая советская энциклопедия
-
Математи́ческие ме́тоды — в медицине совокупность методов количественного изучения и анализа состояния и (или) поведения объектов и систем, относящихся к медицине и здравоохранению. В биологии, медицине и здравоохранении в круг явлений, изучаемых с помощью М.м., входят… … Медицинская энциклопедия
-
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
-
РДМУ 109-77: Методические указания. Методика выбора и оптимизации контролируемых параметров технологических процессов — Терминология РДМУ 109 77: Методические указания. Методика выбора и оптимизации контролируемых параметров технологических процессов: 73. Адекватность модели Соответствие модели с экспериментальными данными по выбранному параметру оптимизации с… … Словарь-справочник терминов нормативно-технической документации
-
ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… … Словарь-справочник терминов нормативно-технической документации
-
Нахождение дисперсии ошибки определения коэффициента регрессии — 3.9.3. Нахождение дисперсии ошибки определения коэффициента регрессии При равном числе параллельных опытов (m0) во всех точках плана матрицы дисперсию ошибки определения коэффициента регрессии определяют по формуле… … Словарь-справочник терминов нормативно-технической документации
Уравнение множественной регрессии
Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:
- уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
- множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;
Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Отбор факторов обычно осуществляется в два этапа:
- теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
- количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа – однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
- Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
- Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
- Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность – тесная линейная связь между факторами.
Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X
| 1 | 5 | 14.5 |
| 1 | 12 | 18 |
| 1 | 6 | 12 |
| 1 | 7 | 13 |
| 1 | 8 | 14 |
Матрица Y
Транспонируем матрицу X, получаем X T :
| 1 | 1 | 1 | 1 | 1 |
| 5 | 12 | 6 | 7 | 8 |
| 14.5 | 18 | 12 | 13 | 14 |
| Умножаем матрицы, X T X = |
|
В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X
| Умножаем матрицы, X T Y = |
Находим обратную матрицу (X T X) -1
| 13.99 | 0.64 | -1.3 |
| 0.64 | 0.1 | -0.0988 |
| -1.3 | -0.0988 | 0.14 |
Вектор оценок коэффициентов регрессии равен
| (X T X) -1 X T Y = y(x) = |
|
* | = |
Получили оценку уравнения регрессии: Y = 34.66 + 1.97X1-2.45X2
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 – s 2 e/∑(yi – yср) 2 = 1 – 33.18/77.2 = 0.57
F = R 2 /(1 – R 2 )*(n – m -1)/m = 0.57/(1 – 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k1 = 2 и k2 = n-m-1 = 5 – 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X1 (%), а также по уровню инфляции X2 (%).
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| X1 | 3,5 | 2,8 | 6,3 | 4,5 | 3,1 | 1,5 | 7,6 | 6,7 | 4,2 | 2,7 | 4,5 | 3,5 | 5,0 | 2,3 | 2,8 |
| X2 | 4,5 | 3,0 | 3,1 | 3,8 | 3,8 | 1,1 | 2,3 | 3,6 | 7,5 | 8,0 | 3,9 | 4,7 | 6,1 | 6,9 | 3,5 |
| Y | 9,0 | 6,0 | 8,9 | 9,0 | 7,1 | 3,2 | 6,5 | 9,1 | 14,6 | 11,9 | 9,2 | 8,8 | 12,0 | 12,5 | 5,7 |
Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .
Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),
После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X1 + 1.4798X2
Скачать.
Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).
Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.
| ВВП | 16331,97 | 16763,35 | 17492,22 | 18473,83 | 19187,64 | 20066,25 | 21281,78 | 22326,86 | 23125,90 |
| Потребление в текущих ценах | 771,92 | 814,28 | 735,60 | 788,54 | 853,62 | 900,39 | 999,55 | 1076,37 | 1117,51 |
| Инвестиции в текущих ценах | 176,64 | 173,15 | 151,96 | 171,62 | 192,26 | 198,71 | 227,17 | 259,07 | 259,85 |
Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).
Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:
- Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
- Рассчитать частные коэффициенты эластичности. Сделать вывод.
- Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
- Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
- Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.
Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X
| 1 | 3.9 | 10 |
| 1 | 3.9 | 14 |
| 1 | 3.7 | 15 |
| 1 | 4 | 16 |
| 1 | 3.8 | 17 |
| 1 | 4.8 | 19 |
| 1 | 5.4 | 19 |
| 1 | 4.4 | 20 |
| 1 | 5.3 | 20 |
| 1 | 6.8 | 20 |
| 1 | 6 | 21 |
| 1 | 6.4 | 22 |
| 1 | 6.8 | 22 |
| 1 | 7.2 | 25 |
| 1 | 8 | 28 |
| 1 | 8.2 | 29 |
| 1 | 8.1 | 30 |
| 1 | 8.5 | 31 |
| 1 | 9.6 | 32 |
| 1 | 9 | 36 |
Матрица Y
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 8 |
| 8 |
| 8 |
| 10 |
| 9 |
| 11 |
| 9 |
| 11 |
| 12 |
| 12 |
| 12 |
| 12 |
| 14 |
| 14 |
Матрица X T
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3.9 | 3.9 | 3.7 | 4 | 3.8 | 4.8 | 5.4 | 4.4 | 5.3 | 6.8 | 6 | 6.4 | 6.8 | 7.2 | 8 | 8.2 | 8.1 | 8.5 | 9.6 | 9 |
| 10 | 14 | 15 | 16 | 17 | 19 | 19 | 20 | 20 | 20 | 21 | 22 | 22 | 25 | 28 | 29 | 30 | 31 | 32 | 36 |
Умножаем матрицы, (X T X)
Умножаем матрицы, (X T Y)
Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1
Уравнение регрессии
Y = 1.8353 + 0.9459X 1 + 0.0856X 2
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y – X*s
| 0.62 |
| 0.28 |
| 0.38 |
| 0.01 |
| 0.11 |
| -1 |
| -0.57 |
| 0.29 |
| -0.56 |
| 0.02 |
| -0.31 |
| 1.23 |
| -1.15 |
| 0.21 |
| 0.2 |
| -0.07 |
| -0.07 |
| -0.53 |
| 0.34 |
| 0.57 |
se 2 = (Y – X*s) T (Y – X*s)
Несмещенная оценка дисперсии равна
Оценка среднеквадратичного отклонения равна
Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1
| k(x) = 0.36 |
|
= |
|
Дисперсии параметров модели определяются соотношением S 2 i = Kii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)
Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора хi при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции – последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции
Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами – точность подбора уравнения регрессии – высокая
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл: Tтабл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
Построение парной регрессионной модели
Рекомендации к решению контрольной работы.
Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.
Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x1, дохода компании x2 и объема инвестиций в расширение и модернизацию производства x3. Исходные данные представлены выборкой объема n=50.
Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x1, x2, x3 взятых по отдельности. Для каждой объясняющей переменной:
- Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
- Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации
.
- Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
- Постройте на поле корреляции прямую линию выборочной регрессии по точкам
.
- Постройте диаграмму остатков.
- Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение Fтабл определите с помощью функции FРАСПОБР).
- Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
- Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
- Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
- Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.
Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации 
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.
Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
общая сумма квадратов отклонений (TSS)
сумма квадратов отклонений, обусловленная регрессией (RSS)
остаточная сумма квадратов отклонений (ESS)
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Использование критерия Стьюдента для проверки значимости параметров регрессионной модели
Проверка статистической значимости параметров регрессионного уравнения (коэффициентов регрессии) выполняется по t-критерию Стьюдента, который рассчитывается по формуле:
где P – значение параметра;
Sp – стандартное отклонение параметра.
Рассчитанное значение критерия Стьюдента сравнивают с его табличным значением при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы N–k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели Y=A*X+B подставляем k=1).
Если вычисленное значение tp выше, чем табличное, то коэффициент регрессии является значимым с данной доверительной вероятностью. В противном случае есть основания для исключения соответствующей переменной из регрессионной модели.
Величины параметров и их стандартные отклонения обычно рассчитываются в алгоритмах, реализующих метод наименьших квадратов.
[spoiler title=”источники:”]
http://www.chem-astu.ru/science/reference/student.html
[/spoiler]














![alpha in [0,1]](https://dic.academic.ru/pictures/wiki/files/55/74f725ac10fd07911d173c277b58814f.png) . Тогда
. Тогда 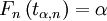 .
.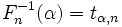 .
.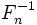 не имеет простого представления. Однако, возможно вычислить её значения численно.
не имеет простого представления. Однако, возможно вычислить её значения численно.