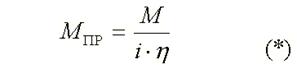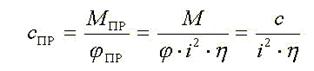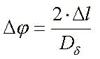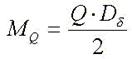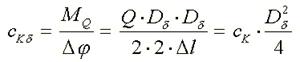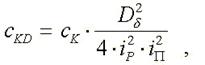Коэффициент жесткости каната как найти

Спрятать решение

Силы сопротивления делят на полезные сопротивления, для преодоления которых предназначен данный механизм и которые обусловлены технологическим процессом, и вредные сопротивления (силы трения в кинематических парах, сопротивление жесткости канатов и цепей, гидродинамическое и аэродинамическое сопротивления).  [c.56]

Решение. На клеть действуют две силы сила веса Р и сила упругости каната F = k, где с —жесткость каната, X — его удлинение. Пока клеть опускается равномерно, удлинение каната равно статическому удлинению и сила Р урав-  [c.310]

Efn Е i М Замечая, что жесткость каната с равна  [c.216]

А. Недостаточная прочность каната. Б. Недостаточная жесткость каната.  [c.64]

Слитковоз с канатным приводом (фиг. I, а), управляемый по системе генератор—двигатель (Г — Д), при анализе неустановившихся процессов может быть представлен расчетной схемой (рис. 1,6), полученной в результате таких допущений 1) жесткость звеньев лебедки, соединяющих электродвигатель с барабаном, велика по сравнению с жесткостью канатов, поэтому все вращающиеся массы можно заменить одной приведенной к барабану массой 2) влияние профиля пути на движение слитковоза незначительно, поэтому можно считать слитковоз перемещающимся по горизонтальному пути 3) жесткость канатов в процессе неустановившегося движения принимается переменной в зависимости от положения слитковоза и усилия в канате.  [c.106]

С целью выяснить влияние изменения длины канатов на динамические процессы на электронной модели производилось исследование (рис. 12) при постоянной А) и переменной Б) жесткостях ветвей канатов. В первом случае жесткость канатов принималась для крайнего дальнего положения  [c.117]

Подъемные сосуды, закрепленные на канатах, совершают линейные колебания. Жесткость канатов подсчитывается по формуле  [c.15]

При расчете на колебания обычно пользуются эквивалентной схемой, в которой совершаются либо одни крутильные, либо одни линейные колебания. Такое приведение выполняется несложно. Умно жая жесткость каната при растяжении и массу концевых грузов на квадрат радиуса барабана подъемной машины, получим жесткость  [c.15]

При рассмотрении динамических процессов, возникающих в линиях передач главного привода экскаватора вследствие действия технологических нагрузок, обычно пренебрегают массой стрелы из-за ее относительной малости. Так, например, в экскаваторах ЭГЛ-15 масса стрелы, приведенная к радиусу навивки барабана, примерно в 25 раз меньше приведенной массы редукторного привода. Кроме того, жесткость канатов подвески стрелы примерно в 4 раза больше, чем жесткость подъемных канатов.  [c.17]

Для этого случая, схема которого показана на рис. 1. 1, а, вследствие бесконечной жесткости каната массу поднимаемого груза следует просуммировать с приведенной к окружности навивки каната массе лебедки. Принимая за обобщенную координату угол (р поворота канатного барабана, получим следующее уравнение движения  [c.31]

Как видно, амплитуды этих колебаний невелики, к тому же если учесть затухание колебаний груза от сил трения и сопротивления воздуха, то ясно, что, принимая жесткость каната бесконечной, мы особой ошибки в расчет кинематики движения системы не внесем.  [c.33]

Приложим к точкам Л и Б обода блока по две равные и противоположные силы Р и —Р и Q и —Q, изображенные на рис. 256 штриховыми линиями. Мы видим, что благодаря запаздываниям в распрямлении каната у точки Л и изгибанию у точки В, к блоку будут приложены как бы две пары сил Р,. —Р и Q, —Q с плечами а, обе стремящиеся вращать блок против его угловой скорости (на рис. 256 составляющие этих пар перечеркнуты). Эти пары будут представлять собой сопротивление жесткости каната или вообще гибкой связи и носить название пар сопротивления жесткости. Присутствие этих пар вызовет снижение к. п. д. блока и потери в тяговом усилии.  [c.364]

Вычисляем коэффициент жесткости каната, беря среднее значение для коэффициента жесткости, приведенное выше,  [c.366]

Составим еще выражение для коэффициента потери барабана подъемной машины с учетом жесткости каната и трения в цапфах. Такой барабан изображен на рис. 259. Для того чтобы устранить влияние на искомый коэффициент потери окружного усилия зубчатого колеса, которое приводит в движение барабан и увеличивает нагрузку цапф оси барабана и потери от которого учитываются к. п. д. зубчатой пары, предположим, что вал барабана приводится в движение парой сил с моментом Мд .  [c.369]

Анализ этой формулы показывает, что чем больше угол обхвата блока канатом, а также чем больше жесткость каната и трение в опоре блока, тем меньше значение КПД блока и тем больше дополнительная сила, которую необходимо приложить к канату, чтобы обеспечить равномерное движение груза. На КПД блока наиболее существенное влияние оказывают потери на трение в опоре блока, зависящее от конструкции и состояния  [c.179]

При подъеме или опускании груза вследствие действия сил сопротивления от жесткости каната и от трения в опорах блоков натяжение отдельных ветвей каната различно. Обозначим  [c.180]

Г з — к. п, д. для барабана со стальным канатом, равен 0,95 (с учетом потерь на жесткость каната)  [c.542]

О коэффициенте е, характеризующем жесткость каната, в настоящее время нет достаточно надежных данных, определяющих его в зависимости от диаметров каната и блока, типа свивки, жесткости проволок, величины натяжения каната и срока его службы поэтому при точных расчетах исходят из экспериментальных данных. Выше мы рассматривали условия работы блока с учетом потерь на сопротивление жесткости, тогда как в действительности должно учитываться и сопротивление в опорах оси блока. Для приближенных расчетов в среднем принимают е = 1,02- 1,05.  [c.545]

Обозначив через k — коэффициент всех сопротивлений блока вращению, а через Р — тяговое усилие с учетом сопротивления от жесткости каната и трения в подшипниках, запишем равенство  [c.545]

С учетом жесткости каната и сопротивления в опорах оси блока  [c.547]

Расчет натяжения гибких элементов в полиспастах исходит из следующих положений. Груз Q, в величину которого обычно входит и вес подвижной обоймы с блоками, а также и грузозахватные детали в рассматриваемом нами случае (см. рис. 32, а) подвешен на 4 ветвях гибкого элемента. Пренебрегая жесткостью каната и сопротивлением трения, можно было бы написать, что натяжение каждой ветви So Q  [c.549]

Вращающий момент М(, на барабане по формуле (21а) с учетом потерь на преодоление жесткости каната т]з = 0,95 будет  [c.583]

Срок службы канатов зависит от их гибкости — способности огибать блоки и барабаны при наименьших усилиях изгиба. Свойство, обратное гибкости, называется жесткостью канатов. Чем жестче канат, тем он менее износостоек, и наоборот. Жесткость канатов обусловливается диаметром проволок, составляющих канат, материалом сердечника и взаимным направлением свивки проволок в пряди и прядей в канат.  [c.21]

Чем обусловливается жесткость канатов  [c.31]

Пример 26, Какой наибольший груз может быть поднят полиспастом (рис. 29), состоящим из четырех блоков, если стальной проволочный канат состоит из 160 проволок диаметром 0,8 мм каждая. Трением и жесткостью каната можно пренебречь. Допускаемое напряжение [ст]= 120 н1мм .  [c.53]

Благодаря жесткости каната, прилегание каната к барабану начинается не в точке А, а в точке А, так что на уровне точки А канат отходит от поверхности барабана на расстояние а — плеча жесткости. Прикладывая к точке А барабана две равные и противоположные силы Q и —Q, получим пару жесткости Q, —Q с плечом а (составляющие этой пары на рисунке перечеркнуты). Составим выражение для фбар  [c.370]

Пример 1. Требуется определить действительную нагрузку кранового останова подъемного механизма при следующих данных нормальная грузоподъемность Q = 100 000 н передаточное число редуктора i = 24,4 полиспаст двухкратный, сдвоенный с четырьмя ветвями радиус барабана Rg = 0,25 м] приведенная жесткость каната и валопроводов с = 4000 н-м1рад. Останов расположен на приводном валу.  [c.190]

II—коэффициент полезного действия полиспаста, учитывающий потерн на трепне роликов на осях и сопротивление от жесткости каната при огибании нм роликов определяется по табл. 17-5,  [c.447]

Коэффициент полезного действия блока – это отношение полезной работы 5набЛ при подъеме груза весом G p на высоту h к полной работе, совершенной при этом силой 5сбег на том же пути h с учетом преодоления потерь на трение и жесткости каната. Поэтому для неподвижного блока, у которого перемещение набегающей и сбегающей ветвей каната одинаково, КПД выражается формулой  [c.179]

Очевидно, что при работе (без учета трения в опорах) для преодоления вредного сопротивления жесткости каната необходимо увеличить силу Ро на некоторую величину W, откуда сила, действующая на сбегаюш,ую ветвь каната, будет равна сумме Ро + W (см. рис. 29).  [c.545]

Для окончательного выявления общего передаточного числа определяем общий к. п д. лебедки, без учета потерь на жесткость каната, которые уже учтены в предварительном расчете к. п. д. трех пар зубчатых обработанных колес принимаем т] =0,96 , к. п. д. в опорах трех валов, работающих в подшипниках качения, т] =0,98 (см. рекомендации в разделе Расчет лебедок , гл. XII Б) т1общ = = 0,963-0,983 = 0,83.  [c.583]

Динамическая модель грейферного крана (см. рис. V 1.2.25, б, в) [3, 28, 29 ] учитывает п.араметры металлической конструкции, грейфера и механизмов его замыкания и подъема. Для мостового перегружателя с подрессоренной тележкой trii и /Па — масса тележки и приведенная масса металлической конструкции и Са — коэффициенты жесткости рессор и конструкция для мостовых грейферных кранов j — со (рессор нет) для портальных j = со, mi = 0. Для лебедки с независимыми барабанами (см. рис. 1.2.19) Яд и Рд — движущие усилия приводов замыкания и подъема, определяемые в зависимости от их скоростей по формуле Клосса 10.51 и Ша — приведенные к канатам момешя инерции вращающихся частей приводов замыкания и подъема Сз и Сп — жесткости канатов,  [c.403]

Форма кулисы, вес передрижного груза, координаты и плечи рычагов подобраны 1 к, чтобы момент М. приложенный к рычагу 3 от натяжения канатов (от нагрузки на крюк), при опасной перегрузке в каждый данный момент положения стрелы превышал момент Мг от веса подвижного груза 6 относительно оси О, т. е. Mj— —М2>0, что заставит сработать выключатель 5. Например, если при данном весе груза крановщик станет увеличивать вылет стрелы сверх допустимого, то вследствие перемещения груза 6 влево момент уменьшится настолько, что момент М вызовет поворот рычага 3 по часовой стрелке и выключатель 5 сработает. К недостаткам описанной конструкции относится сравнительно малая точность работы (6—8%) при эксплуатации вследствие износа кулис, наличия зазоров, трудноучиты-ваемого трения, возможных перекосов. На точность оказывает влияние также жесткость канатов ввиду изменяющегося большого угла обхвата блока. Кроме того, ограничитель тяжел и громоздок.  [c.87]

Сопротивления шкивов и отдельных роликов определяют как султму сил сопротивлений от трения в цапфах и от жесткости каната  [c.422]

---

Условие задачи:

Каков коэффициент жесткости буксировочного троса, если при буксировке автомобиля массой 2 т трос удлинился на 0,01 м, причем автомобиль через 4 с после начала движения достиг скорости 2 м/с. Трением пренебречь. Движение считать равноускоренным.

Задача №2.6.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=2) т, (x=0,01) м, (t=4) с, (upsilon=2) м/с, (k-?)

Решение задачи:

На автомобиль вдоль оси (x) действует только сила упругости, поэтому второй закон Ньютона в проекции на эту ось запишется в следующем виде:

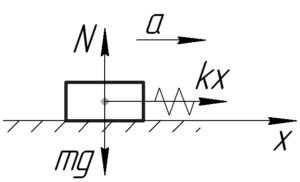
[kx = ma]

Запишем также формулу определения ускорения:

[a = frac{{upsilon  – {upsilon _0}}}{t}]

Так как начальная скорость автомобиля (upsilon_0) равна нулю, то:

[a = frac{upsilon }{t}]

Самое первое равенство в таком случае примет такой вид:

[kx = mfrac{upsilon }{t}]

[k = frac{{mupsilon }}{{xt}}]

Переведем массу машины в систему СИ и посчитаем ответ.

[2; т = 2000; кг]

[k = frac{{2000 cdot 2}}{{0,01 cdot 4}} = {10^5}; Н/м = 100; кН/м]

Ответ: 100 кН/м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.6.6 Груз массой 1 кг, прикрепленный к пружине, равномерно тянут по горизонтальной
2.6.8 Найти удлинение буксирного троса с жесткостью 100 кН/м при буксировке автомобиля
2.6.9 Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины

Жесткость – канат

Cтраница 1

Жесткость каната зависит от ею диаметра, конструкции, числа проволок в прядях и числа прядей, типа и конструкции сердечника, механических свойств материала проволок и трения между отдельными проволоками и между прядями. Жесткость цени определяется в основном сопротивлением сил трения в шарнирах пластинчатой цепи или сил трения между звеньями сварной цепи.
 [1]

Благодаря жесткости каната, прилегание каната к барабану начинается не в точке Л, а в точке Л, так что на уровне точки Л канат отходит от поверхности барабана на расстояние а – плеча жесткости.
 [2]

Пренебрегая жесткостью каната, рассматриваем несущий канат ( рис. 119) как абсолютно гибкую нить. Канат нагружен равномерно распределенной нагрузкой от силы тяжести собственной массы и сосредоточенной нагрузкой от силы тяжести масс тележки с грузом.
 [4]

Вопрос о жесткости каната при использовании его в качестве колонны насосных штанг возникает в связи с тем, что в настоящее время ШСНУ используются для откачки пластовой жидкости из глубоких ( до 3500 м) скважин со значительными величинами динамического уровня ( до 2000 м) и при дебитах до 80 м3 / сут, для чего используют насосы с диаметрами до 70 – 120 мм.
 [6]

Чем обусловливается жесткость канатов.
 [7]

Определению коэффициентов жесткости канатов посвящено много работ, дающих разнообразные и резко различающиеся значения. Здесь приведено значение коэффициента, наиболее часто применяемое в практике расчета канатных дорог.
 [8]

Некоторое уменьшение жесткости канатов достигается применением пеньковых ( органических) сердечников. Пропитываемые смазкой сердечники служат своеобразными масленками, смазывая постоянно канатные проволоки изнутри.
 [9]

Вследствие потерь от трения и жесткости каната натяжение в каждой струне талевого каната в процессе работы изменяется. Это объясняется тем, что натяжение в неподвижном и ходовом концах каната во время спуска и подъема бурового инструмента различно.
 [10]

О коэффициенте е, характеризующем жесткость каната, в настоящее время нет достаточно надежных данных, определяющих его в зависимости от диаметров каната и блока, типа свивки, жесткости проволок, величины натяжения каната и срока его службы; поэтому при точных расчетах исходят из экспериментальных данных. Выше мы рассматривали условия работы блока с учетом потерь на сопротивление жесткости, тогда как в действительности должно учитываться и сопротивление в опорах оси блока.
 [11]

Но вследствие потерь на трение и жесткости каната натяжение в каждой струне талевого блока изменяется, так как натяжение в сбегающем конце каната не равно натяжению в набегающем1 конце каната. Вследствие этого в зависимости от направления вращения роликов в талевом блоке будет изменяться и натяжение в канате; а так как направление вращения роликов зависит от того, происходит ли спуск или подъем инструмента, то и распределение усилий в канатах будет неодинаковым при спуске и при подъеме.
 [12]

Коэффициент сопротивления в блоках, помимо жесткости канатов, зависит также от типа подшипников и рода смазки осей блоков.
 [13]

Отсюда легко установить механический смысл коэффициентов жесткости каната, а именно: коэффициент А есть жесткость каната при чистом растяжении; В – жесткость при чистом кручении. Коэффициент С может быть назван коэффициентом взаимности деформаций растяжения и кручения в канате.
 [14]

Страницы:  

   1

   2

   3

   4

Жесткость – это способность упругого элемента сопротивляться образованию
деформаций.
      Численно она характеризуется коэффициентом
жесткости – отношением силового фактора к той деформации, которая вызывается
его действием:

·       
Линейная жесткость  

·       
Угловая крутильная жесткость

где Р – сила,
вызывающая линейную деформацию y ; М –
момент, вызывающий угловую деформацию .

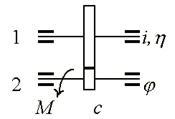
      На валу 2 в силовом режиме действует момент
М, который при жесткости вала с вызывает его деформацию

.

Приведем крутящий момент к валу 1.

Приведем деформацию вала 2 к валу 1

C учетом уравнений (*) и
(**) определим приведенную к валу 2 жесткость вала 1

      Жесткости
приводятся от одного вала к другому аналогично моментам инерции и массам.
      Если каждый упругий элемент воспринимает
весь силовой поток, то их соединение – последовательное. А если упругие
элементы системы воспринимают только часть силового потока, то их соединение
называется параллельным.
      При параллельном соединении упругих
элементов их коэффициенты жесткости складываются, а при последовательном –
складываются коэффициенты податливости ( величины,
обратные коэффициентам жесткости ).

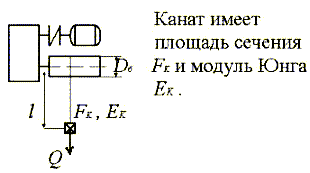
      Приведем линейную жесткость одинарного
полиспаста к крутильной (к валу барабана).

Деформация
каната (линейная)

где с – жесткость каната.
      Линейной деформации  будет соответствовать
угол поворота барабана

      Действие
веса груза Q на канат эквивалентно действию на окружность барабана крутящего
момента M_Q

      Жесткость
каната, приведенная к оси барабана

      Нетрудно
показать, что жесткость каната, приведенная к валу двигателя
определяется по формуле

где – передаточное отношение редуктора, – кратность полиспаста.