Колебательный контур
Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.
Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.
Работа колебательного контура
Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.
Что будет, если в цепь включить индуктивную катушку:
- При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
- Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
- Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;
Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком.
- После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.
Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.
Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.
Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.

Эквивалентная схема реальной катушки индуктивности
Каждый дроссель можно представить в виде эквивалентной схемы.
Данная схема состоит из элементов:
- Rw – сопротивление обмотки с выводами;
- L – индуктивность;
- Cw – паразитная ёмкость;
- Rl – сопротивление потерь.
Изготавливая индуктивный элемент, стремятся снизить величину сопротивления потерь, паразитную ёмкость. При работе катушки на низкой частоте учитывают сопротивление её обмотки Rw. На таких частотах действуют токи большой величины.

Правильно рассчитанная катушка индуктивности будет иметь высокую добротность (180-300) и стабильность работы при влиянии внешних условий (температуры и влажности). Зная способы различной намотки и манипуляции с шагом, можно уменьшить влияние паразитных факторов.
Собственные колебания
Определение 1
Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.
В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.
В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.
Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.
По характеру взаимодействия с окружающей средой колебания разделяют на:
- вынужденные;
- автоколебания;
- параметрические;
- собственные.
В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.
При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.
В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.
Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.
В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).
Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.
В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.
Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.
Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:
Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ
Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.
Что касается реальных систем, то в них собственные колебания затухают из-за потерь энергии, поэтому их следует считать лишь приближенно гармоническими в интервале времени, меньшем $1/δ$. Затухающие колебания могут быть представлены в виде нескольких гармонических колебаний, непрерывно заполняющих определенный интервал частот, тем меньшим, чем меньше $δ$. В таком случае следует говорить о расширении спектральной линии, характеризуемой добротностью $Q$ и равной отношению запасенной энергии $W$ к потерям $P$. Отсюда следует, что отношение сгущение спектра из-за потерь энергии может повлечь за собой превращение дискретного спектра в сплошной при приближении ширины линий к интервалу между ними.
Конструкция катушки
По конструктивному исполнению индуктивные элементы различаются:
- видом намотки: винтоспиральная, винтовая; кольцевая;
- количеством слоёв: однослойные или многослойные;
- типом изолированного провода: одножильный, многожильный;
- наличием каркаса: каркасные или бескаркасные (при небольшом количестве витков толстого провода);
- геометрией каркаса: прямоугольный, квадратный, тороидальный;
- наличием сердечника: ферритовый, из карбонильного железа, электротехнической стали, пермаллоевый (магнитомягкий сплав), металлический (латунный);
- геометрией сердечника: стержневой (разомкнутый), кольцо-образный или ш-образный (замкнутый);
- возможностью изменять L в узких интервалах (движение сердечника по отношению к обмотке).
Расчет падения напряжения в кабеле
Существуют плоские катушки, в печатном исполнении устанавливаемые на платах цифровых устройств.
К сведению. Намотка провода может быть как рядовой (витком к витку), так и в навал. Последний способ укладки провода снижает паразитную ёмкость.

Что такое колебательный контур
Колебательный контур это несколько элементов в любой электрической цепи, емкость и индуктивность, которых соединены параллельно или последовательно. Для нормального функционирования колебательного контура в цепи необходим источник энергии.

При параллельном или последовательном соединениях элементов, входящих в состав электрической цепи, та или иная замкнутая проводниковая система получает одноимённое название. Явление резонанса в обоих случаях, возникает аналогичным образом, только в случае параллельного колебательного контура этот показатель относится к силе тока, а в случае с последовательным – возникает предельная частотность мгновенного изменения напряжений.
Расчет колебательного контура:
В сети на разных сайтах можно найти, в основном, одну и ту же версию такого калькулятора. Здесь предлагается совершенно другой вариант… Справка по расчету здесь.
ВАРИАНТ РАСЧЕТА:
ВВЕСТИ ДАННЫЕ:
| L | = | – Индуктивность |
| C | = | – Емкость |
РЕЗУЛЬТАТ:
| f | = | – Частота |
| ρ | = Oм | – Характеристическое сопротивление |
Добавить комментарий Все посты предварительно модерируются. Посты, подписанные несуществующим E-mail опубликованы не будут.
Зачем нужен расчёт индуктивности
Индуктивность: формула
Расчет индуктивности нужен, потому что конструктивно это могут быть по-разному выполненные катушки. Применение дросселей в разных отраслях электрики и электроники, их работа под влиянием постоянного и переменного тока требуют тщательного подбора индуктивности, добротности и стабильности работы. При выполнении своими руками дросселей заданного параметра L нужно выполнить расчёт. Для каждого типа индуктивного двухполюсника используется своя формула.
Практическое применение[править | править код]
Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях, радиоприёмниках, а также в различных устройствах автоматики. Например, на самолётах Ил-62М, Ил-76 и Ту-154М установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от подвозбудителя генератора
(сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя[4].
Применение колебательного контура
Колебательный контур широко применяется на практике. На его основе строятся частотные фильтры, без него не обходится ни один радиоприемник или генератор сигналов определенной частоты.
Если вы не знаете, как подступиться к расчету LC-контура или на это совершенно нет времени, обратитесь в профессиональный студенческий сервис. Качественная и быстрая помощь в решении любых задач не заставит себя ждать!
Автор: Иван
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Резонанс токов
Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:
Чему будет равняться резонансный ток Iрез ? Считаем по закону Ома:
Iрез = Uген /Rрез , где Rрез = L/CR.
Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток Iкон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.
Расчет параметров катушки
Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.
Расчет L в зависимости от заданной конструкции
Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:
L = 0,01*D*w2/(l/D) + 0,46,
где:
- D – диаметр каркаса, см;
- w – число витков;
- l – длина намотки, см;
- L – индуктивность, мкГн.
Подставляя численные значения в формулу, получают значение L.
Расчет количества витков по индуктивности
Зная D каркаса и L, рассчитывают количество витков в катушке, формула имеет вид:
w = 32*√(L*D),
где:
- L – индуктивность, мкГн;
- D – диаметр каркаса, мм.
Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:
w = l/d,
где:
- l – длина намотки, мм;
- d – диаметр провода, мм.
Измерения диаметра провода проводят линейкой или штангенциркулем.
Расчёт индуктивности прямого провода
Собираясь найти L круглого прямого проводника, обращаются к приближённой формуле:
L = (μ0/2π)*l*( μe*ln(l/r) + 1/4* μi,
где:
- μ0 – магнитная постоянная;
- μe – относительная магнитная проницаемость (ОМП) среды (для вакуума – 1);
- μi – ОМП проводника;
- l – длина провода;
- r – радиус провода.
Формула справедлива для длинного проводника.
Расчёт однослойной намотки
Однослойные дроссели без сердечника легко и быстро можно рассчитать при помощи онлайн-калькулятора, в окно которого можно забить все известные характеристики, и программа выдаст значение L.
Вычисления проводятся и вручную, с использованием математического выражения. Оно имеет вид:
L = D2*n2/45D + 100*l,
где:
- D – диаметр катушки, см;
- l – длина намотанного провода, см;
- n – количество витков.
Формула подходит для вычислений L дросселей без ферритовых сердечников.

Дроссель с сердечником
При наличии сердечника следует учесть его размеры и форму. В случае одинаковых катушках индуктивность больше у той, которая располагается на сердечнике.

Многослойная намотка
Особенности расчёта при подобном способе наматывания провода заключаются в том, что нужно учитывать его толщину. Формула для дросселя без сердечника имеет вид:
N²=(L*(3Dk+9l+10t))/0.008Dk²,
где:
- Dk – общий диаметр (диаметр каркаса и намотки);
- t – толщина слоя;
- l – длина накрученного провода.
Все значения подставляют в мм, величину L – в мкГн.

Главная > Теория > Резонансная частота: формула
Для генерации высокочастотных волн часто применяются схемы на основе колебательного контура. Подобрав параметры элементов цепи, можно производить частоты свыше 500 МГц. Схемы используются в ВЧ-генераторах, высокочастотном нагреве, телевизионных и радиоприемниках.

Колебательный контур
Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.
Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.
Работа колебательного контура
Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.
Что будет, если в цепь включить индуктивную катушку:
- При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
- Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
- Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;
Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком.
- После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.
Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.
Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.
Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.

Как работает контур колебаний
Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.
Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.
Вам это будет интересно Средства защиты от статического электричества

Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников.
Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.

При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.
Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.

Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот.
Резонанс
Если схема с конденсатором, катушкой и резистором возбуждается напряжением, постоянно меняющимся во времени с определенной частотой, то также изменяются реактивные сопротивления: индуктивное и емкостное. Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.
Частота вращения: формула
Индуктивное сопротивление прямо пропорционально частоте:
X(L) = 2π x f x L,
а емкостное сопротивление обратно пропорционально этому показателю:
X(C) = 1/(2π x f x C).
Важно! На более низких частотах индуктивное сопротивление незначительное, а емкостное будет высоким и сможет создавать практически разомкнутый контур. На высоких частотах картина обратная.
При конкретной комбинации конденсатора и катушки схема становится резонансной, или настроенной, имеющей частоту колебаний, при которой индуктивное сопротивление идентично емкостному. И они компенсируют друг друга.
Следовательно, в цепи остается исключительно активное сопротивление, противостоящее протекающему току. Созданные условия получили наименование резонанса колебательного контура. Фазовый сдвиг между током и напряжением отсутствует.

Для расчета резонансной частоты колебательного контура учитывается следующее условие:
X(L) = X(C).
Следовательно, 2π x f x L = 1/(2πx f x C).
Отсюда получается формула резонансной частоты:
f = 1/(2π x √(L x C)).
Расчет резонансной частоты, индуктивности и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения.
Скорость, с которой рассеивается энергия от LC-схемы, должна быть такой же, как энергия, подаваемая на схему. Устойчивые, или незатухающие, колебания производятся электронными схемами генераторов.
LC-цепи используются либо для генерации сигналов на определенной частоте, либо для выделения частотного сигнала из более сложного. Они являются ключевыми компонентами многих электронных устройств, в частности радиооборудования, используемого в генераторах, фильтрах, тюнерах и частотных микшерах.
Формула индуктивности
Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:
- Количество и расположение витков обмотки;
- Наличие или отсутствие сердечника;
- Материал сердечника.
Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.
Вам это будет интересно Особенности активно-емкостной нагрузки

Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках.
Виды и особенности
Схемы колебательных контуров бывают двух видов: последовательными и параллельными. Они отличаются типом соединения элементов емкости и индуктивности. В первом случае они соединены последовательно, а во втором — параллельно. Для работы необходима постоянная электрическая энергия, в противном случае происходит ее затухание, поскольку часть уходит на генерацию электромагнитного поля и нагрев провода обмотки катушки индуктивности. Контур также может быть открытым и закрытым. Открытый выпускается без специальной защитной крышки.
При решении задач по физике можно встретить интересное понятие — идеальный колебательный контур. Если в задании встречается такой термин, то это говорит о том, что энергия остается в системе, а не уходит на описанные выше процессы.
Устройство постоянно генерирует электромагнитные колебания, то есть является подобием вечного двигателя, однако такого не может быть вообще. На практике при расчете параметров учитываются затухания — постепенные уменьшения амплитуды электромагнитной волны.
Последовательное соединение
Последовательный контур — простейшая резонансно-колебательная система. Он состоит из двух элементов, подсоединенных последовательно. Через них при подключении переменного напряжения будет протекать ток переменной составляющей. Его величина определяется по закону Ома: i = U / Zlc. В этой формуле Zlc является суммой реактивных сопротивлений катушки индуктивности (Xl) и конденсатора (Xc).

Величины определяются по формулам Xl = wL и Xc = 1 / (wC). Параметр w — угловая частота, которую можно найти по такому соотношению через частоту переменного тока и число Pi: w = 2 * Pi * f. Из соотношений можно сделать вывод, что реактивное сопротивление на индуктивности растет с увеличением f, а для емкости — уменьшается. В первом случае тип зависимости называется прямо пропорциональным, а во втором — обратно пропорциональным.
При определенном значении частоты сопротивления двух элементов равны по модулю друг другу. Следовательно, это явление называется резонансом колебательной системы. Частоту w при таком условии называют собственной резонансной частотой контура. Рассчитать ее довольно просто, поскольку следует приравнять две формулы для получения уравнения: wL = 1 / (wC). Далее нужно выразить значение f: f = [(1 / (L * C))^(½)] / 2Pi. Последнее соотношение называется формулой Томсона.

Когда контур подключается к цепи генератора (источника) переменного напряжения с активным сопротивлением R, полный импеданс цепи (Z) определяется с помощью соотношения Z = [R2 + Zlc2]^(½). Если происходит резонанс, то Z = R, а реактивная составляющая исчезает.
У контура существуют еще две важные характеристики: добротность (Q) и характеристическое сопротивление (р). Последней называется величина сопротивления реактивного типа при резонансе. Вычисляется она по формуле р = (L * C)^(½) и показывает количество энергии катушки и конденсатора, которое было запасено. Для емкости значение определяется по соотношению Wс = (C * U2) / 2, а для индуктивности — Wl = (L * I2) / 2.
Отношение величины энергии, которая была запасена конденсатором и катушкой, к показателю потерь называется добротностью колебательного контура (Q). Параметр определяет амплитуду и ширину АЧХ резонанса и показывает превышение энергии запаса над потерями за одно колебание. При этом учитывается реактивная нагрузка R. Характеристика определяется по формуле Q = (1 / R) * [(L / C)^(½)].
В некоторых случаях описывать добротность можно другим тождеством: Q = p / R. Современные устройства выполняются на дискретных катушках, а их Q колеблется от нескольких единиц до сотен. Системы, построенные на принципе пьезоэлектронных устройств (кварцевые резонаторы), имеют высокий показатель Q. Его значение может достигать 1 тыс. и больше. Затухание контура (d) — характеристика, которая является обратной добротности. Она определяется по такому соотношению: d = 1 / Q.
Параллельный контур
Контур параллельного типа состоит также из конденсатора и катушки. Отличие заключается в том, что эти два элемента соединены параллельно между собой. Этот тип устройства применяется чаще, чем последовательный контур. Чтобы найти общее сопротивление индуктивного характера, нельзя просто сложить значения Xl и Xc. Складываются только проводимости двух элементов.
Из курса физики известно, что проводимость — величина, обратная сопротивлению, то есть Xc = 1 / Gc и Xl = 1 / Gl. Следовательно, формулы для параллельного соединения имеют такой вид:

- Gl = 1 / wL.
- Gc = wC.
- Q = R * [(С / L)^(½)].
Для примера необходимо рассмотреть электрическую цепь, состоящую из генератора переменного тока и параллельного контура. В какой-то момент времени их частоты будут совпадать. Кроме того, проводимости двух элементов равны по модулю между собой. В результате этого происходит явление резонанса токов.
В цепи будет только активное сопротивление Rэкв, которое называют в радиотехнике эквивалентным. Оно вычисляется по формуле Rэкв = Q * p. Если частота не соответствует резонансной, то в устройстве происходят другие процессы: на низких наблюдается уменьшение индуктивного сопротивления, а на высоких — емкостного.
Во время работы контура за период колебаний два раза происходит обмен энергией между катушкой и конденсатором. В радиоэлементе протекает ток, по силе превосходящий внешний в Q раз.
- Категория: 9. Технический расчет контурных катушек переменной индуктивности коротковолновых передатчиков
Для расчёта плоских спиралей удобно пользоваться эмпирической формулой:
![]() , мкГн
, мкГн
откуда число витков n равно
n=10,5![]() , (9.4)
, (9.4)
где ![]() и
и ![]() – соответственно минимальный и максимальный диаметры спирали (рис.9.5); h – шаг намотки спирали в мм, выбор которого был рассмотрен выше; n – число витков. Формула (9.3) справедлива при 0,2<
– соответственно минимальный и максимальный диаметры спирали (рис.9.5); h – шаг намотки спирали в мм, выбор которого был рассмотрен выше; n – число витков. Формула (9.3) справедлива при 0,2<![]() <0,7. При
<0,7. При ![]() < 0,2 и
< 0,2 и ![]() > 0,7 можно воспользоваться формулой:
> 0,7 можно воспользоваться формулой:
L=6,28·10-3 ∙Dсрn2·[ln(4Dср/c )–0,5] , (9.5)
где с = h∙n, Dср=Dmin+(n – 1)·h.
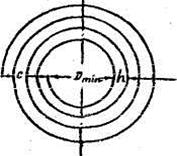
Рис. 9.5. Плоская спираль.
В формуле (9.5) индуктивность L – в мкГн, а все линейные размеры – в см.
Обычно отношение Dmin/Dmax выбирают от 0,3 до 0,6. После определения числа витков n можно вычислить ![]() и
и ![]() , воспользовавшись уже выбранным отношением
, воспользовавшись уже выбранным отношением ![]() и формулой
и формулой
Dmax=![]() ,
, ![]()
или (9.6)
Dmin= ![]() .
.
Не следует делать ![]()
![]() 50 мм. Обычно
50 мм. Обычно ![]() = (10 – 20)∙h при навивке спирали из ленты и
= (10 – 20)∙h при навивке спирали из ленты и ![]() = (5 – 8)∙h при навивке из трубки. Невыполнение этих условий затрудняет навивку спирали и приводит к неоправданному увеличению габаритов.
= (5 – 8)∙h при навивке из трубки. Невыполнение этих условий затрудняет навивку спирали и приводит к неоправданному увеличению габаритов.
Колебательный контур
Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.
Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.
Работа колебательного контура
Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.
Что будет, если в цепь включить индуктивную катушку:
- При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
- Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
- Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;
Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком.
- После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.
Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.
Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.
Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.

Колебательный контур LC
Колебательный контур
— электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C
– реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию. — Катушка индуктивности
L
– реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC
.
Основные свойства индуктивности
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией . — Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Природа электромагнитных колебаний в контуре
Период свободных колебаний контура LC
можно описать следующим образом:
Если конденсатор ёмкостью C
заряжен до напряжения
U
, потенциальная энергия его заряда составит. Если параллельно заряженному конденсатору подключить катушку индуктивности
L
, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.
Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t
1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта
t
1 = . По истечении времени
t
1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны. Накопленная катушкой магнитная энергия в этот момент составит. В идеальном рассмотрении, при полном отсутствии потерь в контуре,
EC
будет равна
EL
. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.
Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t
2 =
t
1, он перезарядит конденсатор от нулевого до максимального отрицательного значения (
-U
). Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t
1 и
t
2 составят половину периода полного колебания в контуре. Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени
t
3, сменив полярность полюсов.
В течении заключительного этапа колебания (t
4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения
U
(в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде. Время t
1 +
t
2 +
t
3 +
t
4 составит период колебаний . Частота свободных колебаний контура ƒ = 1 /
T
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL
равно реактивному сопротивлению ёмкости
XC=1/(2πfC)
.
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице. При переключении множителей автоматически происходит пересчёт результата.
Наверх
Расчёт частоты:
Частота резонанса колебательного контура LC. ƒ = 1/(2π√(LC))
Расчёт ёмкости:
Ёмкость для колебательного контура LC C = 1/(4𲃲L)
Расчёт индуктивности:
Индуктивность для колебательного контура LC L = 1/(4𲃲C)
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
Собственные колебания
Определение 1
Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.
В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.
В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.
Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.
По характеру взаимодействия с окружающей средой колебания разделяют на:
- вынужденные;
- автоколебания;
- параметрические;
- собственные.
В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.
При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.
В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.
Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.
В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).
Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.
В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.
Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.
Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:
Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ
Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.
Что касается реальных систем, то в них собственные колебания затухают из-за потерь энергии, поэтому их следует считать лишь приближенно гармоническими в интервале времени, меньшем $1/δ$. Затухающие колебания могут быть представлены в виде нескольких гармонических колебаний, непрерывно заполняющих определенный интервал частот, тем меньшим, чем меньше $δ$. В таком случае следует говорить о расширении спектральной линии, характеризуемой добротностью $Q$ и равной отношению запасенной энергии $W$ к потерям $P$. Отсюда следует, что отношение сгущение спектра из-за потерь энергии может повлечь за собой превращение дискретного спектра в сплошной при приближении ширины линий к интервалу между ними.
Что такое колебательный контур
Колебательный контур это несколько элементов в любой электрической цепи, емкость и индуктивность, которых соединены параллельно или последовательно. Для нормального функционирования колебательного контура в цепи необходим источник энергии.

При параллельном или последовательном соединениях элементов, входящих в состав электрической цепи, та или иная замкнутая проводниковая система получает одноимённое название. Явление резонанса в обоих случаях, возникает аналогичным образом, только в случае параллельного колебательного контура этот показатель относится к силе тока, а в случае с последовательным – возникает предельная частотность мгновенного изменения напряжений.
Радиолюбитель
Практический расчет последовательного или параллельного LC контура.
Доброго дня уважаемые радиолюбители! Сегодня мы с вами рассмотрим порядок расчета LC контура.
Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители (естественно, в основном молодые), увлекаются сборкой так называемых “жучков” – устройств позволяющих на расстоянии прослушивать что-нибудь. Конечно я уверен, что это делается без всяких нехороших (даже грязных) мыслей подслушать кого-нибудь, а в благих целях. Например устанавливают “жучок” в комнате с малышом, а на радиовещательный приемник прослушивают не проснулся ли он. Все схемы “радиожучков” работают на определенной частоте, но что делать, когда эта частота вас не устраивает. Вот тут вам придет на помощь знание нижеприведенной статьи.
LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах. Как известно из курса физики, колебательный контур состоит из катушки индуктивности и конденсатора (емкости), которые могут быть включены параллельно (параллельный контур) или последовательно (последовательный контур), как на рис.1:

Реактивные сопротивления индуктивности и емкости, как известно, зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости – падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. Таким образом, для каждого контура есть некоторая частота резонанса, на которой индуктивное и емкостное сопротивления оказываются равными. В момент резонанса резко увеличивается амплитуда переменного напряжения на параллельном контуре или резко увеличивается амплитуда тока на последовательном контуре. На рис.2 показан график зависимости напряжения на параллельном контуре или тока на последовательном контуре от частоты:

На частоте резонанса эти величины имеют максимальное значение. А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.
Теперь перейдем к практике. Предположим нам нужно сделать параллельный контур, имеющий резонанс на частоте 1 МГц. Прежде всего нужно сделать предварительный расчет такого контура. То есть, определить необходимую емкость конденсатора и индуктивность катушки. Для предварительного расчета есть упрощенная формула:
L=(159,1/F)2/C где: L – индуктивность катушки в мкГн; С – емкость конденсатора в пФ; F – частота в МГц
Зададимся частотой 1 МГц и емкостью, к примеру, 1000 пФ. Получим:
L=(159,1/1)2 /1000 = 25 мкГн
Таким образом, если мы захотим контур на частоту 1 МГц, то нужен конденсатор на 1000 пФ и индуктивность на 25 мкГн. Конденсатор можно подобрать,, а вот индуктивность нужно сделать самостоятельно.
Рассчитать число витков для катушки без сердечника можно по такой формуле:
N=32 *√(L/D) где: N – требуемое число витков; L – заданная индуктивность в мкГн; D – диаметр каркаса в мм, на котором предполагается намотать катушку.
Предположим, диаметр каркаса – 5 мм, тогда:
N=32*√(25/5) = 72 витка.
Данная формула является приближенной, она не учитывает собственную межвитковую емкость катушки. Формула служит для предварительного вычисления параметров катушки, которые затем настраиваются при настройке контура.
В радиолюбительской практике чаще используются катушки с подстроечными сердечниками из феррита, имеющими длину 12-14 мм и диаметр 2,5 – 3 мм. Такие сердечники, например, применяются в контурах телевизоров и приемников. Для предварительного расчета числа витков для такого сердечника есть другая приближенная формула:
N=8,5*√L , подставляем значения для нашего контура N=8,5*√25 = 43 витка. То есть, в таком случае на потребуется намотать на катушку 43 витка провода.
Расчет колебательного контура:
В сети на разных сайтах можно найти, в основном, одну и ту же версию такого калькулятора. Здесь предлагается совершенно другой вариант… Справка по расчету здесь.
ВАРИАНТ РАСЧЕТА:
ВВЕСТИ ДАННЫЕ:
| L | = | – Индуктивность |
| C | = | – Емкость |
РЕЗУЛЬТАТ:
| f | = | – Частота |
| ρ | = Oм | – Характеристическое сопротивление |
Добавить комментарий Все посты предварительно модерируются. Посты, подписанные несуществующим E-mail опубликованы не будут.
Практическое применение[править | править код]
Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях, радиоприёмниках, а также в различных устройствах автоматики. Например, на самолётах Ил-62М, Ил-76 и Ту-154М установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от подвозбудителя генератора
(сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя[4].
Применение колебательного контура
Колебательный контур широко применяется на практике. На его основе строятся частотные фильтры, без него не обходится ни один радиоприемник или генератор сигналов определенной частоты.
Если вы не знаете, как подступиться к расчету LC-контура или на это совершенно нет времени, обратитесь в профессиональный студенческий сервис. Качественная и быстрая помощь в решении любых задач не заставит себя ждать!
Автор: Иван
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Расчёт растягивающих конденсаторов контура настройки.
Как загнать пределы перестройки конденсатора переменной ёмкости (КПЕ) в колеба- тельном LC контуре в нужный диапазон изменения частоты. Онлайн калькулятор ёмкостей конденсаторов растяжки.
«В процессе конструирования генераторов сигналов и задающих генераторов передатчиков радиолюбители часто сталкиваются с трудностями приобретения конденсатора переменной ёмкости с нужными пределами изменения ёмкости. Я предлагаю читателям простой способ расчёта ёмкостей дополнительных конденсаторов С1 и С2 (см. рисунок), включение которых в колебательный контур генератора позволяет получить нужный диапазон перестройки».
Рис.1 Общая схема колебательного контура с растягивающими конденсаторами
Так начинается очень полезная статья, опубликованная в журнале Радио, 1992, №11, с.23, под авторством С. Бирюкова. Далее там приведены уравнения и довольно громоздкие итоговые формулы для расчёта величин растягивающих конденсаторов С1 и С2, а также практический пример расчёта контура с КПЕ. Для желающих освоить теоретическую часть процесса порекомендую обратиться к статье в журнале, а для практиков приведу простую таблицу, позволяющую без излишнего напряга, калькулятора и деревянных счёт в режиме онлайн рассчитать значения искомых конденсаторов. К тому же формулы уважаемого автора не учитывают ёмкости, обозначенной на Рис.1 — Сконт. Тем не менее, эта ёмкость в реальном устройстве всегда присутствует и численно равна сумме: собственной ёмкости катушки индуктивности, общей ёмкости подключённых к ней радиоэлементов, а также ёмкости проводников печатного или какого-либо иного монтажа. И надо сильно постараться, чтобы величина этой суммарной ёмкости уложилась в десяток пикофарад. Даже при довольно продуманном монтаже значение Сконт, как правило, составляет 15…20 пФ. Короче, для максимальной достоверности итогового результата — величину этой ёмкости учитывать необходимо!
КАЛЬКУЛЯТОР РАСЧЁТА РАСТЯГИВАЮЩИХ КОНДЕНСАТОРОВ LC-КОНТУРА.
Необходимо иметь в виду, что выбираемые значения исходных величин должны быть корректными. Например, это относится к частотам диапазона, который не должен быть чрезмерно широк для выбранного КПЕ. Важно следить за тем, чтобы посчитанный номинал ёмкости С1 был больше величины «максимальная ёмкость КПЕ с учётом С1, С2». Если это не так, то надо либо уменьшить индуктивность катушки, либо снизить ширину диапазона перестройки. Возможны иные варианты ограничений, в которых пользователь может разобраться самостоятельно, действуя методом проб и ошибок.
Ну а воспользовавшись простыми, как ситцевые трусы формулами для расчёта последовательно — параллельного соединения конденсаторов, можно решить обратную задачу и посмотреть, какой будет полоса перестройки контура при впаивании в схему конденсаторов из имеющегося у радиолюбителя ряда.
КАЛЬКУЛЯТОР ЧАСТОТ ПЕРЕСТРОЙКИ LC-КОНТУРА С РАСТЯГИВАЮЩИМИ КОНДЕНСАТОРАМИ.
Данный калькулятор не подвержен влиянию вводимых данных и покажет корректный результат при любых значениях исходных величин.
Резонанс токов
Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:
Чему будет равняться резонансный ток Iрез ? Считаем по закону Ома:
Iрез = Uген /Rрез , где Rрез = L/CR.
Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток Iкон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.
Принцип действия колебательного контура
Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора.
Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности.
Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе.
Это обусловлено тем, что контур состоит из реальных материалов (конденсатор, катушка, провода), обладающих таким свойством, как электрическое сопротивление, и потери энергии в реальном колебательном контуре неизбежны. В противном случае это нехитрое устройство могло бы стать вечным двигателем, существование которого, как известно, невозможно.

Еще одна важная характеристика LC-контура – добротность Q. Добротность определяет амплитуду резонанса и показывает, во сколько раз запасы энергии в контуре превышают потери энергии за один период колебаний. Чем выше добротность системы, тем медленнее будут затухать колебания.
Рассчитать число витков катушки
Рассчитать число витков катушки индуктивности
по формуле:
n = √((5*L(9*D+20*I))/D;
где:
L — индуктивность катушки, мкГн;
D — диаметр катушки, см;
I — длина намотки катушки, см;
n — число витков катушки.
Рассчитать число витков катушки – онлайн
Диаметр катушки, см:
Длина намотки катушки, см:
Индуктивность катушки :
Число витков катушки:
Диаметр провода:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:
