Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения: 
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) – результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | – |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Прежде
чем воспользоваться процедурой Excel
построения гистограммы необходимо
найти границы интервалов группировки
Вычислим
интервалы группировки.
В
рассматриваемом варианте n
= 53.
Число
интервалов группировки k
в Excel
вычисляется по формуле
,
где,
скобки
означают – округление до целой части
числа в меньшую сторону, следовательно.
=
8.
Величина
интервала группировки вычисляется по
формуле
Тогда,
так как
,
то
.
Строгого
научного обоснования для определения
числа интервалов группировки
и их величины
нет. Существует много эмпирических
формул для определения числаk.
Разброс
значений числа k
(числа интервалов группировки), который
дают эти формулы, позволяет исследователю
выбрать удобные для вычисления границы
частичных интервалов группировки. Так
в рассматриваемом варианте исходных
данных
99,5, а максимальное значение
117,88. Дробные величины неудобны для
восприятия.
Тогда,
пусть левая (нижняя) граница всего
интервала будет равной
= 98 (меньше
99,5), а величина интервала группировки
,
следовательно,
= 98+3 = 101,
= 101+3 = 104,
=107,
= 110
= 113
= 116
= 119
Пусть
верхняя граница последнего частичных
интервалов группировки будет
= 119, так как
117,88 входит в этот последний интервал.
Получили
границы интервалов группировки (карманы,
как их называют вExcel)
красивыми целыми числами. Занесите
полученные результаты в столбецExcel,рис.7.
Рис.
7. Массив границ (карманов) группировкиA57:A64
Теперь
можно приступить к построению гистограммы.
В
главном меню Excel
выбрать Данные
→ Анализ данных → Гистограмма → ОК.
Далее
необходимо заполнить поля ввода в
диалоговом окне Гистограмма.
Входной
интервал:
53 случайных чисел (вариант, значений
признака) в ячейках $B$2:
$B$54;
Интервал
карманов:
ввести массив границ интервалов
группировки (карманов) ис
2 A57:A64;
Выходной
интервал:
адрес ячейки, с которой начинается вывод
результатов процедуры Гистограмма;
Вывод
графика –
поставьте галочку. OK.
Рис.
8. Диалоговое окно Гистограмма
с заполненными полями.
Если
в диалоговом окне Гистограмма
поле ввода
Интервал
карманов не
заполняется, то процедура вычисляет
число интервалов группировки k
и границы интервалов автоматически.
В
результате выполнения процедуры
Гистограмма
появляется таблица, содержащая границы
интервалов группировки (столбец –Карман)
и частоту попадания признака выборки
в k–ый
интервал (столбец
–
Частота).
Справа
от таблицы – график гистограммы.
Рис.
9. Фрагмент листа Excel
с результатами процедуры Гистограмма
Принято
столбики гистограммы строить без зазора.
Приведите
гистограмму к виду как показано на рис.
10.
Для
этого щелкните правой кнопкой мыши на
столбике диаграммы и выберите Формат
ряда данных → Без зазора → Нет заливки.
Выберите
цвет границ, стили границ и толщину
линии границ.
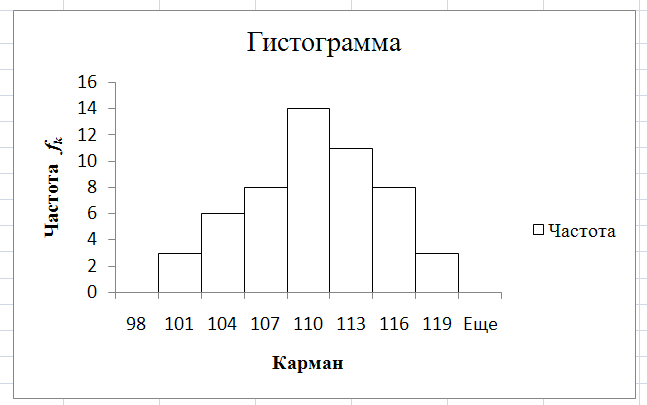
Рис.
10.
Гистограмма
частот
При
вычислении моды для интервального
вариационного ряда необходимо определить
модальный интервал (по максимальной
частоте), а затем – значение моды
по формуле
Модальный интервал
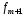
Рис
11. График гистограммы с модальным
интервалом, интервалом предшествующим
модальному и следующим за модальным
интервалам.
Для
рассматриваемого варианта:
= 107,
= 110 – это границы модального интервала
= 8– частота
интервала, предшествующего модальному
интервалу;
= 14– частота
модального интервала;
= 11 – частота
интервала, следующего за модальным
интервалом.
Среднее
= 108,9134, Мода
=109
, Медиана
= 109,5;
Медиану
можно найти графическим способом,
построив кумуляту.
Для
построения кумуляты в таблице
Карман-Частота
добавьте столбец накопленных эмпирических
частот
.
(
)
Рис
12. Таблица Карман-Частота,
полученная при построении гистограммы,
с добавленным столбцом накопленных
эмпирических частот.
Далее
постройте график кумуляты.
Медиана
соответствует варианте, стоящей в
середине ранжированного ряда. Положение
медианы определяется ее номером
.
На
оси
графика кумуляты отложите
.
Найдите соответствующее значение
варианты
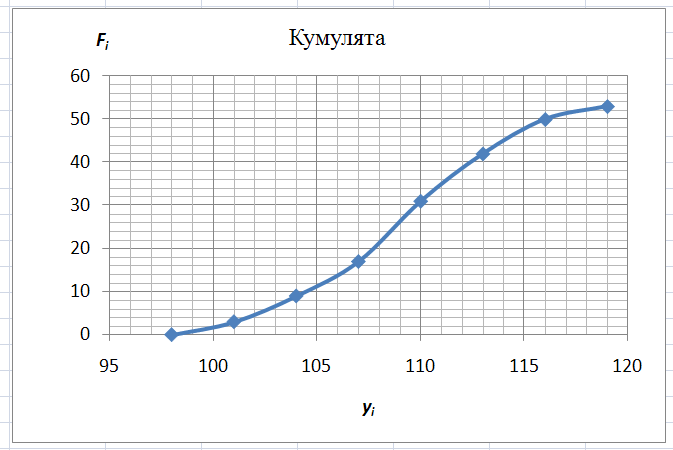
Рис
13. График кумуляты с определенным
графическим способом значением
.
Приблизительное
равенство оценок
=
108,9134,
= 109 и
= 109,5
позволяет предположить, что распределения
признаков генеральной совокупности
имеет нормальный
закон.
По
виду гистограммы можно принять гипотезу
о нормальном распределении признаков
(случайных чисел) выборки.
Далее,
для того чтобы убедиться в правильности
выбранной гипотезы (по крайней мере
визуально) надо, первое
– построить график гипотетического
нормального закона распределения,
выбрав в качестве параметров (среднее
и среднее квадратическое отклонение)
их оценки (оценки среднего и стандартного
отклонения), и совместить график
гипотетического распределения с графиком
гистограммы.
И,
второе
– используя критерий согласия Пирсона
установить справедливость выбранной
гипотезы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Все курсы > Анализ и обработка данных > Занятие 4 (часть 2)
Во второй части занятия рассмотрим нахождение различий в данных и выявление взаимосвязи.
Продолжим работать в том же ноутбуке⧉
Нахождение различий
Два категориальных признака
Вначале возьмем случай двух категориальных признаков. Например, мы хотим понять насколько выживаемость пассажира (целевая переменная) зависит от класса, которым он путешествовал.
countplot и barplot
В первую очередь стоит визуально оценить, есть ли такое различие или нет. Для этого подойдут столбчатые диаграммы, где мы либо располагаем два столбца целевого признака рядом друг с другом (grouped), либо делаем один столбец и разбиваем его на две части (stacked).
Библиотека Seaborn
Начнем с того, что построим несколько counplots/barplots в библиотеке Seaborn с помощью функции countplot() и параметра hue.
|
# создадим grouped countplot, где по оси x будет класс, а по оси y – количество пассажиров # в каждом классе данные разделены на погибших (0) и выживших (1) sns.countplot(x = ‘Pclass’, hue = ‘Survived’, data = titanic); |
|
# горизонтальный countplot получится, # если передать данные о классе пассажира в переменную y sns.countplot(y = ‘Pclass’, hue = ‘Survived’, data = titanic); |
Для создания таких графиков мы также можем использовать более универсальную функцию catplot(). Передадим ей все те же параметры, что и функции countplot(), а также параметр kind = ‘count’, который и сообщит, что мы хотим построить именно countplot.
|
sns.catplot(x = ‘Pclass’, hue = ‘Survived’, data = titanic, kind = ‘count’); |
|
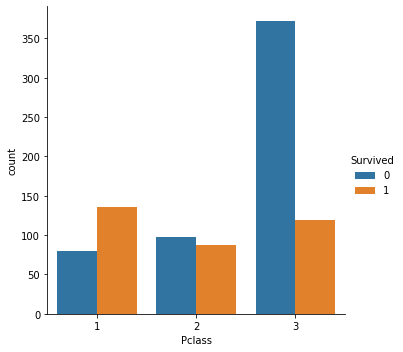
# добавим еще один признак (пол) через параметр col sns.catplot(x = ‘Pclass’, hue = ‘Survived’, col = ‘Sex’, kind = ‘count’, data = titanic); |
На основе графиков выше видно, что класс пассажира имеет большое значение для определения его виживаемости. При этом пол также оказал влияние. Например, в третьем классе большая часть мужчин погибла, в то время как среди женщин, количество выживших и не выживших примерно одинаковое.
Теперь посмотрим, как создать подобные графики в библиотеке Plotly.
Библиотека Plotly
Для построения графика countplot используем функцию px.histogram() (для barplot подойдет px.bar()). Начнем с варианта, когда разбитые по какому-либо признаку столбцы стоят рядом друг с другом (grouped).
|
px.histogram(titanic, # возьмем данные x = ‘Pclass’, # диаграмму будем строить по столбцу Pclass color = ‘Survived’, # с разбивкой на выживших и погибших barmode = ‘group’, # разделенные столбцы располагаются рядом друг с другом text_auto = True, # выведем количество наблюдений в каждом столбце title = ‘Survival by class’ # также добавим заголовок ) |
Теперь выведем вариант, когда каждый столбец диаграммы разделен на две части (stacked). Так как мы будем вручную корректировать подписи к графику и расстояние между столбцами, необходимо использовать объектно-ориентированный подход.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# создадим объект fig, в который поместим столбчатую диаграмму fig = px.histogram(titanic, x = ‘Pclass’, color = ‘Survived’, barmode = ‘stack’, # каждый столбец класса будет разделен по признаку Survived text_auto = True) # применим метод .update_layout к объекту fig fig.update_layout( title_text = ‘Survival by class’, # заголовок xaxis_title_text = ‘Pclass’, # подпись к оси x yaxis_title_text = ‘Count’, # подпись к оси y bargap = 0.2, # расстояние между столбцами # подписи классов пассажиров на оси x xaxis = dict( tickmode = ‘array’, tickvals = [1, 2, 3], ticktext = [‘Class 1’, ‘Class 2’, ‘Class 3’] ) ) fig.show() |
Теперь разобьем данные по трем категориальным переменным: полу, классу и выживаемости.
|
# для этого используем новый параметр facet_col = ‘Sex’ px.histogram(titanic, x = ‘Pclass’, color = ‘Survived’, facet_col = ‘Sex’, barmode = ‘group’, text_auto = True, title = ‘Survival by class and gender’) |
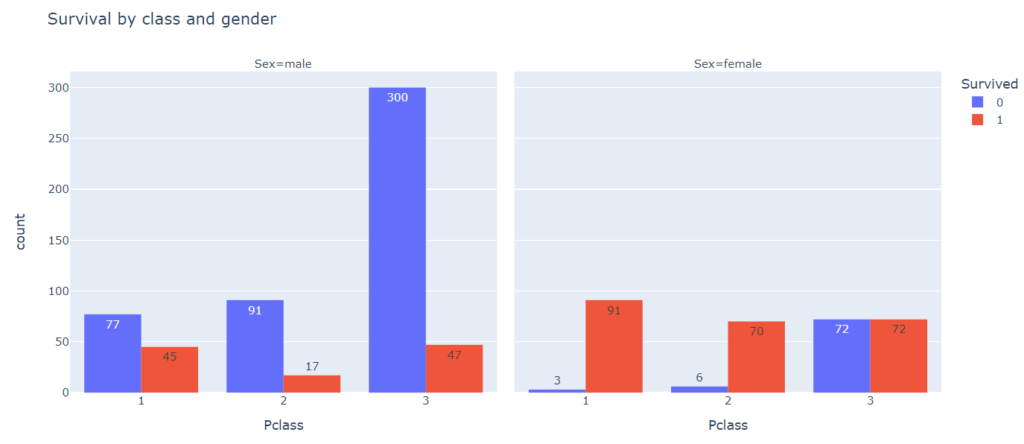
Более того, мы можем добавить еще один категориальный признак, порт посадки пассажира (Embarked).
|
# используем одновременно параметры facet_col и facet_row px.histogram(titanic, x = ‘Pclass’, color = ‘Survived’, facet_col = ‘Embarked’, facet_row = ‘Sex’, barmode = ‘group’, text_auto = True, title = ‘Survival by class, gender and port of embarkation’) |
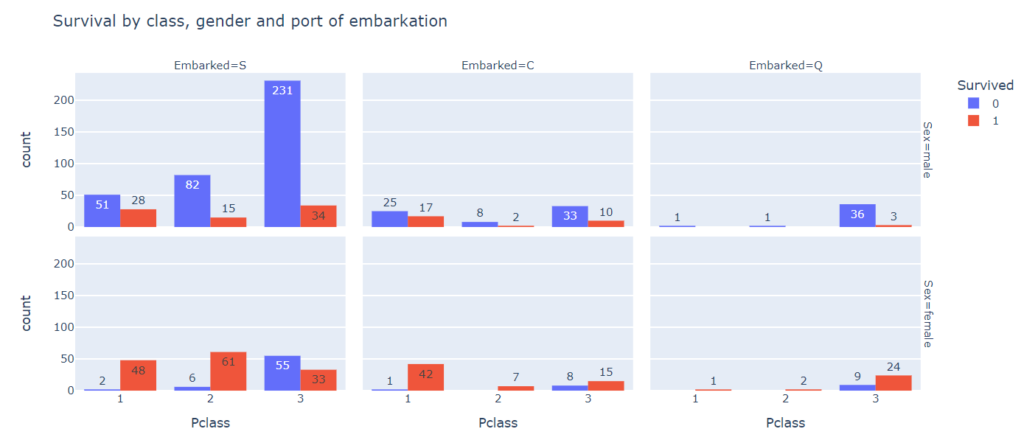
Здесь конечно, нужно следить за тем, чтобы объем предоставляемой информации не ухудшал информативности графиков.
Таблица сопряженности
Таблица сопряженности (contingency table) позволяет количественно измерить зависимость одной категориальной переменной от другой. Например, количественно оценим зависимость выживаемости от класса пассажира. Вначале оценим абсолютное количество наблюдений.
Абсолютное количество наблюдений
Для создания таблиц сопряженности в библиотеке Pandas используется функция pd.crosstab().
|
# создадим таблицу сопряженности # в параметр index мы передадим данные по классу, в columns – по выживаемости pclass_abs = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived) # создадим названия категорий класса и выживаемости pclass_abs.index = [‘Class 1’, ‘Class 2’, ‘Class 3’] pclass_abs.columns = [‘Not survived’, ‘Survived’] # выведем результат pclass_abs |
Теперь для каждого класса мы видим количество выживших и количество погибших. На основе таблицы сопряженности очень удобно строить столбчатую диаграмму (можно использовать график barplot, а не countplot, потому что количество значений в каждой категории уже посчитано).
Начнем с библиотеки Pandas.
|
# построим grouped barplot в библиотеке Pandas # rot = 0 делает подписи оси х вертикальными pclass_abs.plot.bar(rot = 0); |
|
# параметр stacked = True делит каждый столбец класса на выживших и погибших pclass_abs.plot.bar(rot = 0, stacked = True); |
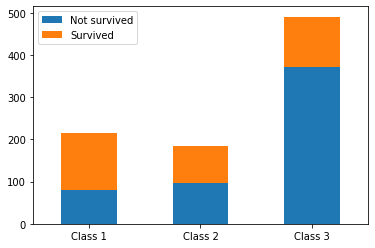
Теперь посмотрим, как построить stacked barplot в библиотеке Matplotlib.
|
# вначале создадим barplot для одной (нижней) категории plt.bar(pclass_abs.index, pclass_abs[‘Not survived’]) # затем еще один barplot для второй (верхней), указав нижнуюю в параметре bottom plt.bar(pclass_abs.index, pclass_abs[‘Survived’], bottom = pclass_abs[‘Not survived’]); |
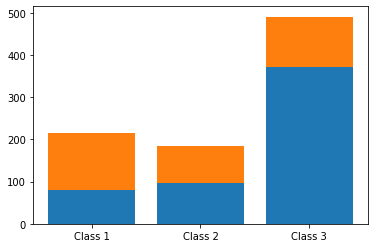
Таблица сопряженности вместе с суммой
С помощью параметра margins = True мы можем вывести сумму наблюдений по каждой строке и каждому столбцу (эти показатели еще называют маргинальными частотами, marginal frequencies).
|
# для подсчета суммы по строкам и столбцам используется параметр margins = True pclass_abs = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived, margins = True) # новой строке и новому столбцу с суммами необходимо дать название (например, Total) pclass_abs.index = [‘Class 1’, ‘Class 2’, ‘Class 3’, ‘Total’] pclass_abs.columns = [‘Not survived’, ‘Survived’, ‘Total’] pclass_abs |
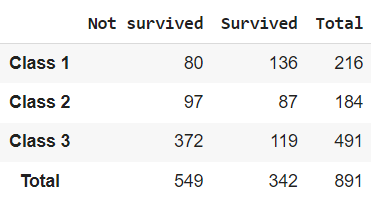
Относительное количество наблюдений
Для получения относительного количества наблюдений (относительных частот) следует использовать параметр normalize. Так как нам важно понимать долю выживших и долю погибших, укажем
normalize = ‘index’. В этом случае каждое значение будет разделено на общее количество наблюдений в строке.
|
# сумма по строкам в этом случае должна быть равна единице pclass_rel = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived, normalize = ‘index’) pclass_rel.index = [‘Class 1’, ‘Class 2’, ‘Class 3’] pclass_rel.columns = [‘Not survived’, ‘Survived’] pclass_rel |
Если бы в индексе (в строках) была выживаемость, а в столбцах — классы, то логично было бы использовать параметр
normalize = ‘columns’ для деления на сумму по столбцам.
|
pclass_rel_T = pd.crosstab(index = titanic.Survived, columns = titanic.Pclass, normalize = ‘columns’) pclass_rel_T.index = [‘Not survived’, ‘Survived’] pclass_rel_T.columns = [‘Class 1’, ‘Class 2’, ‘Class 3’] pclass_rel_T |
Теперь на stacked barplot мы видим доли выживших в каждом из классов.
|
pclass_rel.plot.bar(rot = 0, stacked = True).legend(loc = ‘lower left’); |
Количественный и категориальный признаки
rcParams
Прежде чем продолжить, давайте посмотрим, как мы можем задать размер для всех (или почти всех) последующих графиков в ноутбуке. Так нам не придется вручную менять размер каждой визуализации.
В библиотеке Matplotlib и связанных с ней библиотеках (например, Seaborn) есть так называемые параметры конфигурации среды (runtime configuration parameters), то есть параметры, которые используются по умолчанию при создании графиков.
Эти параметры и их значения содержатся в словаре, к которому можно получить доступ через атрибут rcParams библиотеки Matplotlib.
|
# импортируем всю библиотеку Matplotlib import matplotlib # и посмотрим, какой размер графиков (ключ figure.figsize) установлен по умолчанию matplotlib.rcParams[‘figure.figsize’] |
Изменить эти параметры можно, обновив значение словаря rcParams по соответствующему ключу. Передадим новое значение размера по ключу figure.figuresize.
|
# обновим этот параметр через прямое внесение изменений в значение словаря matplotlib.rcParams[‘figure.figsize’] = (7, 5) matplotlib.rcParams[‘figure.figsize’] |
Также можно воспользоваться функцией sns.set() или, что то же самое, sns.set_theme().
|
# изменим размер обновив словарь в параметре rc функции sns.set() sns.set(rc = {‘figure.figsize’ : (8, 5)}) # посмотрим на результат matplotlib.rcParams[‘figure.figsize’] |
Теперь все последующие графики в библиотеках Matplotlib, Seaborn и Pandas будут иметь размеры восемь на пять дюймов. Вернемся к исследованию переменных.
Гистограммы
Когда у нас есть одна количественная и одна категориальная переменные, для их визуализации проще всего построить две наложенные друг на друга гистограммы. Мы уже строили такие графики в рамках вводного курса.
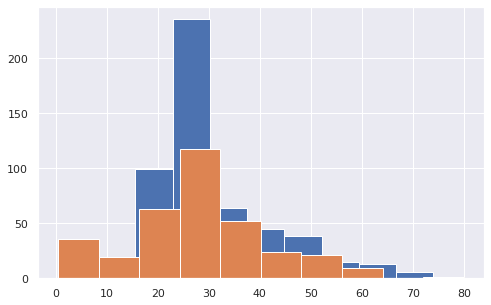
Посмотрим, различается ли распределение возраста выживших и погибших пассажиров Титаника.
|
# выведем две гистограммы на одном графике в библиотеке Matplotlib # отфильтруем данные по погибшим и выжившим и построим гистограммы по столбцу Age plt.hist(x = titanic[titanic[‘Survived’] == 0][‘Age’]) plt.hist(x = titanic[titanic[‘Survived’] == 1][‘Age’]); |
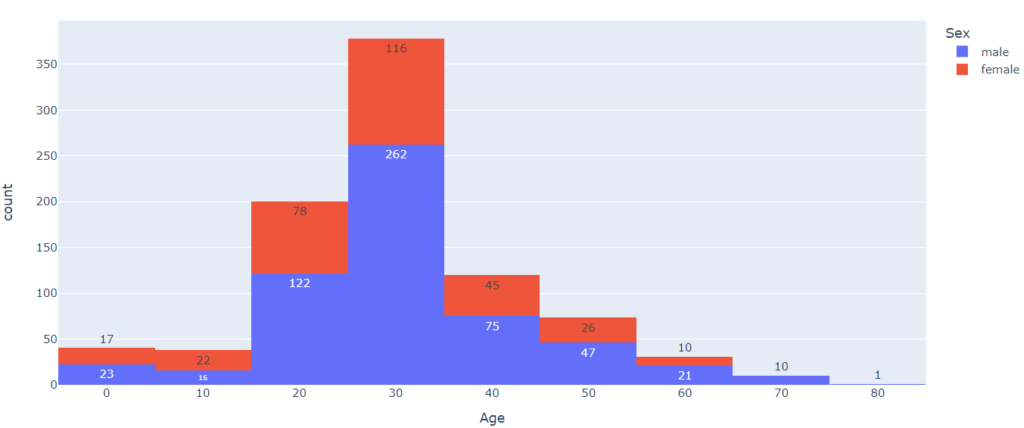
Теперь посмотрим, зависит ли распределение возраста от пола пассажира.
|
# в библиотеке Seaborn в x мы поместим количественный признак, в hue – категориальный sns.histplot(x = ‘Age’, hue = ‘Sex’, data = titanic, bins = 10); |
|
# в Plotly количественный признак помещается в x, категориальный – в color px.histogram(titanic, x = ‘Age’, color = ‘Sex’, nbins = 8, text_auto = True) |
Сравнение двух распределений может быть не вполне корректным, если размер выборок существенно различается. Например, в нашем случае количество мужчин и женщин на борту далеко не одинаково.
|
# сравним количество мужчин и женщин на борту titanic.Sex.value_counts() |
|
male 577 female 314 Name: Sex, dtype: int64 |
Исправить ситуацию может параметр density = True.
|
# параметр alpha отвечает за прозрачность каждой из гистограмм plt.hist(x = titanic[titanic[‘Sex’] == ‘male’][‘Age’], density = True, alpha = 0.5) plt.hist(x = titanic[titanic[‘Sex’] == ‘female’][‘Age’], density = True, alpha = 0.5); |
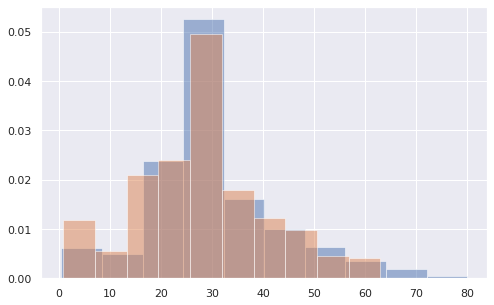
В этом случае гистограмма показывает плотность вероятности, а ее общая площадь всегда равна единице. Как следствие, мы можем адекватно сравнивать распределения между собой.
График плотности
С другой стороны, для плотности вероятности есть отдельный график, density plot. Площадь под кривой такого графика также всегда равна единице. Воспользуемся функцией .displot() с параметром kde = True.
|
# построим графики плотности распределений суммы чека в обеденное и вечернее время sns.displot(tips, x = ‘total_bill’, hue = ‘time’, kind = ‘kde’); |
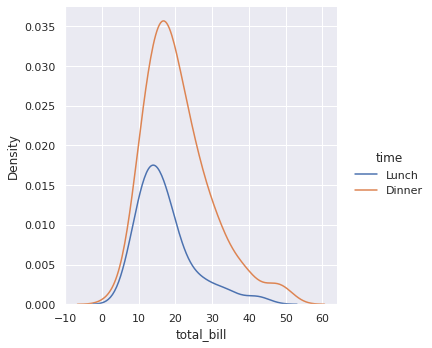
Из-за особенностей расчета графика kde мы можем получить «неестественные значения». Например, на диаграмме выше встречаются отрицательные значения чека. В реальности такого быть не может.
Избавиться от таких значений можно с помощью параметра clip, который задает диапазон значений.
|
# зададим границы диапазона от 0 до 70 долларов через clip = (0, 70) # дополнительно заполним цветом пространство под кривой с помощью fill = True sns.displot(tips, x = ‘total_bill’, hue = ‘time’, kind = ‘kde’, clip = (0, 70), fill = True); |
boxplots
Для сравнения распределений количественной переменной, разбитой по какому-либо категориальному признаку, также очень удобно использовать несколько графиков boxplot (side-by-side boxplots).
Построим такие графики в библиотеках Seaborn и Plotly. Вначале посмотрим, как различается сумма чека по дням недели.
|
sns.boxplot(x = ‘day’, y = ‘total_bill’, data = tips); |
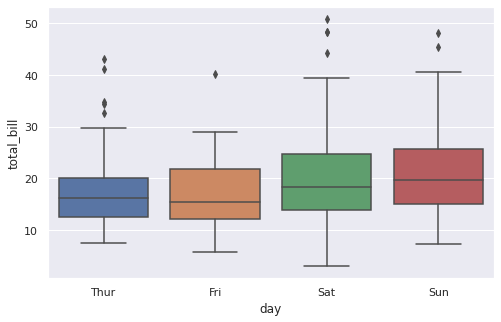
Что можно сказать про эти распределения?
- Медианный чек выше по воскресеньям
- Самый широкий диапазон суммы по чеку наблюдается в субботу, в пятницу же наоборот разброс наименьший
- Выбросы присутствуют только в верхних значениях распределения
Теперь посмотрим, как различается сумма чека в обеденное и вечернее время.
|
px.box(tips, x = ‘time’, y = ‘total_bill’, points = ‘all’) |
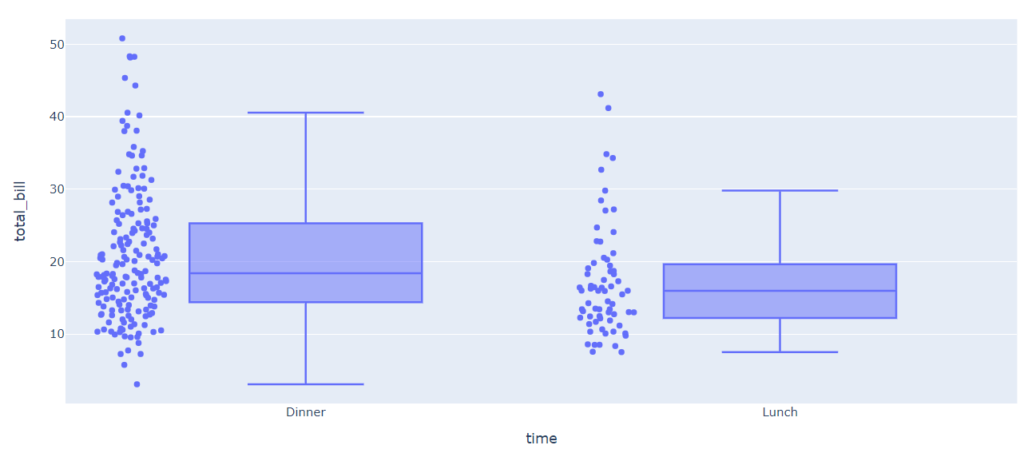
Ожидаемо, как разброс, так и медианное значение меньше в обеденное время.
Дополнительно замечу, что с помощью параметра points = ‘all’ в библиотеке Plotly для каждого распределения мы построили график, который называется stripplot. Он, в частности, показывает, что гостей за ужином бывает существенно больше. Об этом графике мы дополнительно поговорим чуть ниже.
Гистограммы и boxplots
Гистограммы и boxplots можно совместить. Сделать это проще всего в Plotly.
|
px.histogram(tips, x = ‘total_bill’, # количественный признак color = ‘sex’, # категориальный признак marginal = ‘box’) # дополнительный график: boxplot |
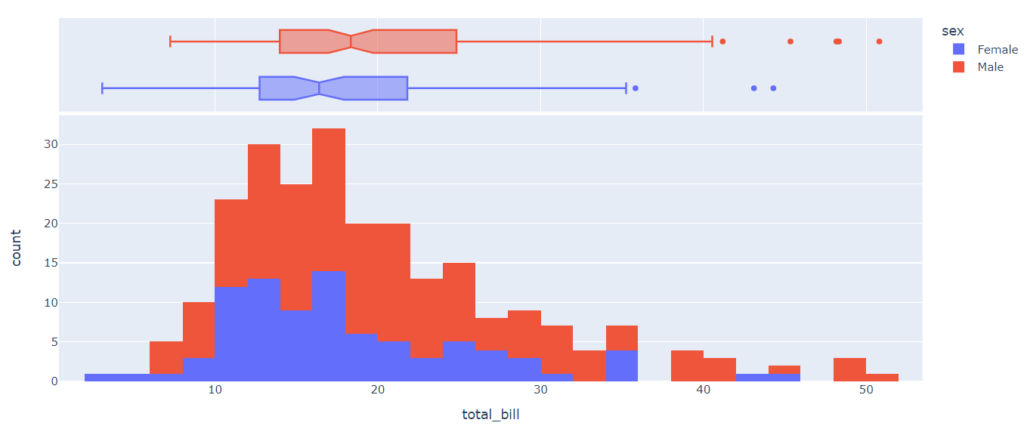
stripplot, violinplot
Более редкими типами графиков для визуализации количественных распределений являются stripplot и violinplot. Первый график, stripplot, как мы уже видели выше, визуализирует сами наблюдения.
|
# по сути, stripplot – это точечная диаграмма (scatterplot), # в которой одна из переменных категориальная sns.stripplot(x = ‘day’, y = ‘total_bill’, data = tips); |
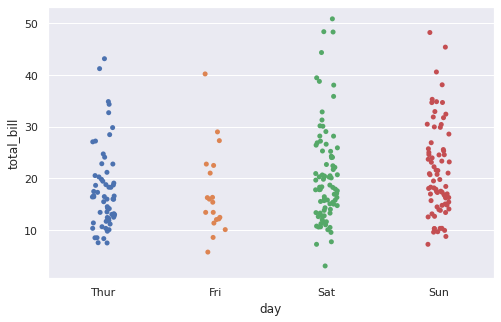
График stripplot можно построить как с помощью приведенной в примере выше функции sns.stripplot(), так и с помощью функции sns.catplot() с параметром kind = ‘strip’.
|
# с помощью sns.catplot() мы можем вывести распределение количественной переменной (total_bill) # в разрезе трех качественных: статуса курильщика, пола и времени приема пищи sns.catplot(x = ‘sex’, y = ‘total_bill’, hue = ‘smoker’, col = ‘time’, data = tips, kind = ‘strip’); |
Хотя stripplot достаточно информативен сам по себе, его очень удобно применять совместно с boxplot (как мы это делали выше).
График violinplot (от англ. violin, «скрипка») представляет собой комбинацию boxplot и графика плотности.
|
# построим violinplot для визуализации распределения суммы чека по дням недели sns.violinplot(x = ‘day’, y = ‘total_bill’, data = tips); |
Внутри каждого из violinplot находится миниатюрный boxplot, который помогает более точно оценить параметры распределения.
Преобразования данных
Иногда так бывает, что для повышения читаемости графика, данные сначала нужно преобразовать.
Логарифмическая шкала
Например, возьмем вот такие данные о продажах.
|
products = [‘Phone’, ‘TV’, ‘Laptop’, ‘Desktop’, ‘Tablet’] sales = [800, 4, 550, 500, 3] |
Предположим, что в этих данных нет ошибки и было действительно продано четыре телевизора и три планшета. На графике эти позиции из-за сильно различающегося масштаба будут нулевыми.
|
sns.barplot(x = products, y = sales) plt.title(‘Продажи в январе 2020 года’); |
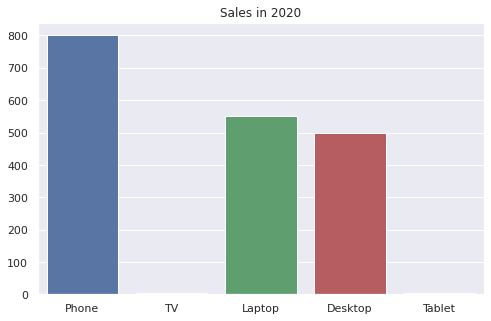
Для того чтобы эти продажи все-таки были видны, можно перевести ось y в логарифмическую шкалу.
|
sns.barplot(x = products, y = sales) plt.title(‘Продажи в январе 2020 года (log)’) plt.yscale(‘log’); |
Границы по оси y
В ноутбуке с моделью текучести кадров сотрудников⧉ (в разделе, посвященном практике), один из признаков — это баллы на последней аттестации. Для покинувших и продолжающих работать сотрудников различие не велико.
|
# код для получения этих значений вы найдете в ноутбуке по ссылке выше eval_left = [0.715473, 0.718113] # построим столбчатую диаграмму, # для оси x – выведем строковые категории, для y – доли покинувших компанию сотрудников sns.barplot(x = [‘0’, ‘1’], y = eval_left) plt.title(‘Last evaluation vs. left’); |
Иногда для наглядности бывает полезно ограничить диапазон значений по оси y.
|
sns.barplot(x = [‘0’, ‘1’], y = eval_left) plt.title(‘Last evaluation vs. left’) # для ограничения значений по оси y можно использовать функцию plt.ylim() plt.ylim(0.7, 0.73); |
Перейдем к выявлению взаимосвязи между переменными.
Выявление взаимосвязи
Выявление взаимосвязи предполагает анализ двух количественных переменных.
На сегодняшем занятии мы поговорим про графические способы ее выявления, а в следующем разделе разберем количественные показатели взаимосвязи переменных (то есть ковариацию и корреляцию).
Линейный график
Базовым способом визуализации двух количественных переменных является линейный график (linear plot). Построить его можно с помощью функции plt.plot() библиотеки Matplotlib.
|
# создадим последовательность от -2пи до 2пи # с интервалом 0,1 x = np.arange(–2*np.pi, 2*np.pi, 0.1) # сделаем эту последовательность значениями по оси x, # а по оси y выведем функцию косинуса plt.plot(x, np.cos(x)) plt.title(‘cos(x)’); |
Точечная диаграмма
Еще один базовый график — уже знакомая нам точечная диаграмма (scatter plot). Ее удобно использовать, когда одна переменная не имеет строгой зависимости от другой. Воспользуемся функцией plt.scatter() библиотеки Matplotlib.
|
plt.scatter(tips.total_bill, tips.tip) plt.xlabel(‘total_bill’) plt.ylabel(‘tip’) plt.title(‘total_bill vs. tip’); |
Такой же график можно построить в библиотеке Pandas.
|
# перед созданием этого графика в Pandas принудительно удалим # предупреждения и сообщения об ошибках # (в Colab появляется предупреждение, связанное с параметром c (color)) from matplotlib.axes._axes import _log as matplotlib_axes_logger matplotlib_axes_logger.setLevel(‘ERROR’) # воспользуемся методом .plot.scatter() tips.plot.scatter(‘total_bill’,‘tip’) plt.title(‘total_bill vs. tip’); |
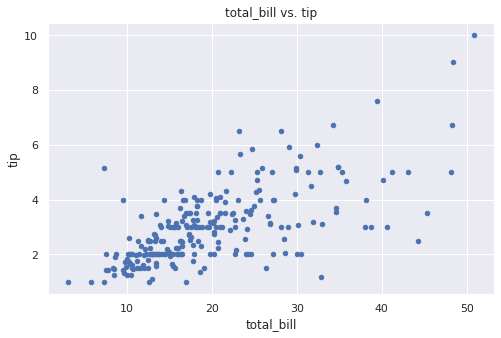
На графиках выше мы видим, что в среднем с ростом суммы чека растет и размер чаевых (другими словами, взаимосвязь прослеживается).
При этом мы видим гетероскедастичность (различную изменчивость) данных, когда при небольшом чеке диапазон чаевых меньше, чем когда сумма чека увеличивается.
Почему это влияет на качество модели и как с этим бороться, мы поговорим на следующем курсе.
В точечной диаграмме можно учесть и категориальный признак. Например, посмотрим, есть ли различие во взаимосвязи между суммой чека и размером чаевых в зависимости от времени дня.
|
# категориальный признак добавляется через параметр hue sns.scatterplot(data = tips, x = ‘total_bill’, y = ‘tip’, hue = ‘time’) plt.title(‘total_bill vs. tip by time’); |
Мы можем констатировать, что при сохранении взаимосвязи как в обеденное, так и в вечернее время, за ужином минимальная и максимальное сумма чека, а также разброс чаевых выше.
pairplot
График pairplot позволяет визуализировать взаимосвязи сразу нескольких количественных переменных. В библиотеке Pandas такой график строится с помощью функции pd.plotting.scatter_matrix().
|
# построим pairplot в библиотеке Pandas # в качестве данных возьмем столбцы total_bill и tip датасета tips pd.plotting.scatter_matrix(tips[[‘total_bill’, ‘tip’]]); |
Как вы видите, там, где перемекаются разные признаки, строится точечная диаграмма, на пересечении одного и того же признака по главной диагонали — его гистограмма.
Примерно такой же график можно построить с помощью функции sns.pairplot() библиотеки Pandas.
|
# параметр height функции pairplot() задает высоту каждого графика в дюймах sns.pairplot(titanic[[‘Age’, ‘Fare’]].sample(frac = 0.2, random_state = 42), height = 4); |
Обратите внимание на метод .sample() с параметром frac = 0,2, который мы применили к датафрейму titanic. Таким образом, мы сделали случайную выборку из 20% или $ 891 times 0,2 approx 178 $ наблюдений.
|
# параметр random_state обеспечивает воспроизводимость результата titanic[[‘Age’, ‘Fare’]].sample(frac = 0.2, random_state = 42) |
Метод .sample() в данном случае применяется для того, чтобы ускорить создание pairplot. Зачастую, при наличии большого числа наблюдений, график может строиться очень долго.
При добавлении параметра hue (разделение по категориальной переменной) гистограмма по умолчанию превращается в график плотности.
|
# обратите внимание, столбец Survived мы добавили и в параметр hue и в датафрейм с данными sns.pairplot(titanic[[‘Age’, ‘Fare’, ‘Survived’]].sample(frac = 0.2, random_state = 42), hue = ‘Survived’, height = 4); |
По большому счету с помощью такого графика мы пытаемся ответить на вопрос, есть ли взаимосвязь между возрастом пассажиров и стоимостью их билетов в разрезе выживаемости.
Функция sns.pairplot() является надстройкой (упрощенной версией) другой функции этой библиотеки, sns.PairGrid(). Ее стоит использовать, если требуются более продвинутые настройки графика pairplot.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим объект класса PairGrid, в качестве данных передадим ему # как количественные, так и категориальные переменные g = sns.PairGrid(tips[[‘total_bill’, ‘tip’, ‘time’, ‘smoker’]], # передадим в hue категориальный признак, который мы будем различать цветом hue = ‘time’, # зададим размер каждого графика height = 5) # метод .map_diag() с параметром sns.histplot выдаст гистограммы на диагонали g.map_diag(sns.histplot) # слева и снизу от диагонали мы выведем точечные диаграммы и зададим # дополнительный категориальный признак smoker с помощью размера точек графика g.map_lower(sns.scatterplot, size = tips[‘smoker’]) # справа и сверху будет график плотности сразу двух количественных признаков g.map_upper(sns.kdeplot) # добавим легенду, adjust_subtitles = True делает текст легенды более аккуратным g.add_legend(title = ”, adjust_subtitles = True); |
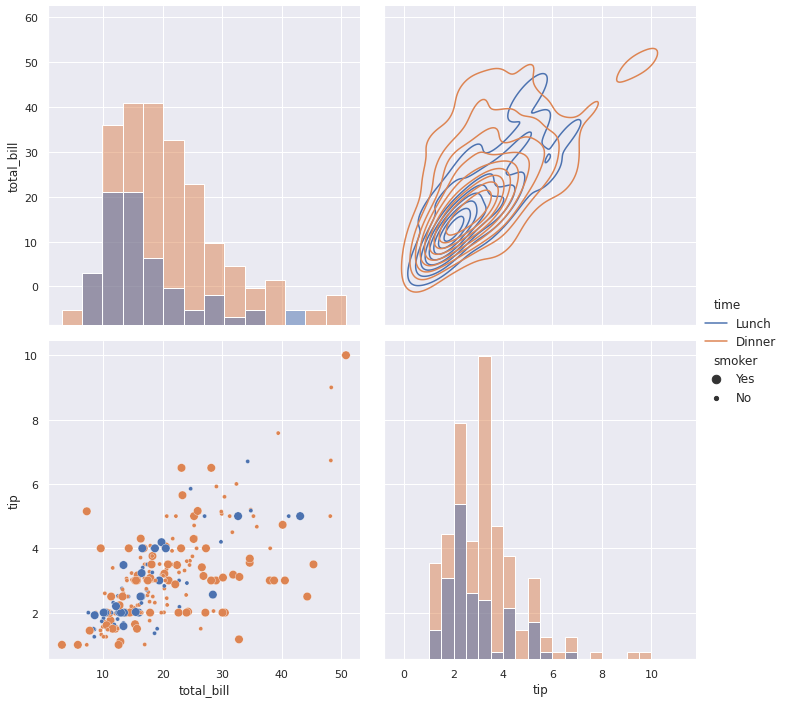
При построении таких сложных графиков важно помнить про их информативность. В примере выше некоторые графики (например, точечную диаграмму) уже достаточно сложно анализировать.
jointplot
Совместное распределение двух переменных
График плотности (kde plot) двух количественных признаков (верхний справа в примере выше) представляет собой визуализацию совместного распределения (joint distribution) двух количественных признаков (tip и total_bill) с разделением по категориальному признаку (time). Другими словами, мы смотрим на то, как изменяется распределение одного количественного признака под воздействием другого. И так для каждой из двух категорий.
В результате мы получаем графики изолиний (contour lines), которые показывают, что между суммой чека и чаевыми есть взаимосвязь (если бы ее не было, изолинии представляли бы собой круги). Теоретические основы совместных распределений мы рассмотрим на курсе по статистике вывода, а пока изучим инструмент их визуализации, который называется jointplot.
sns.jointplot()
Вначале построим точно такой же график плотности (kde plot) совместного распределения tip и total_bill с разделением по признаку time. Для этого функции sns.jointplot() передадим данные и укажем параметр kind = ‘kde’.
|
sns.jointplot(data = tips, # передадим данные x = ‘total_bill’, # пропишем количественные признаки, y = ‘tip’, hue = ‘time’, # категориальный признак, kind = ‘kde’, # тип графика height = 8); # и его размер |
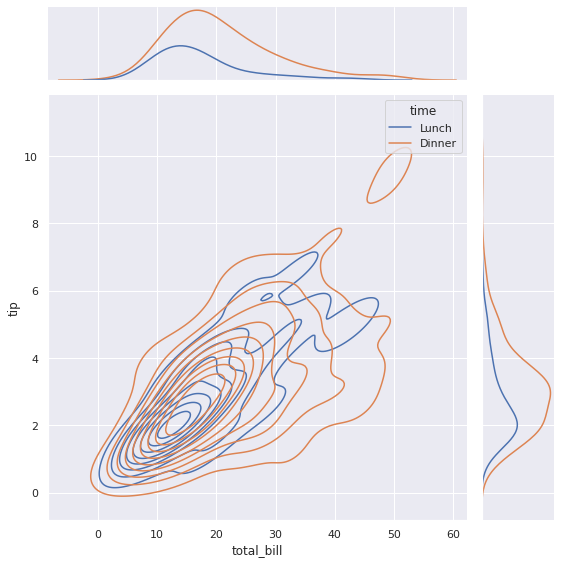
По краям мы видим графики плотности так называемого безусловного распределения (marginal distribution) каждого из признаков. Это одномерные распределения (univariate distribution). Основной график показывает совместное распределение (joint distribution) уже двух переменных. Это двумерное распределение (bivariate distribution).
Возможно более интуитивным покажется использование точечной диаграммы (kind = ‘scatter’) вместо графика плотности.
|
sns.jointplot(data = tips, x = ‘total_bill’, y = ‘tip’, hue = ‘time’, # построим точечную диаграмму kind = ‘scatter’, # дополнительно укажем размер точек s = 100, # и их прозрачность alpha = 0.7, height = 8); |
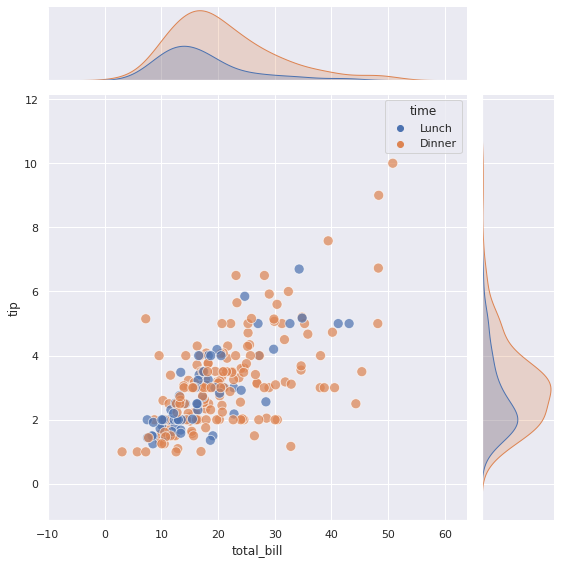
Кроме того, мы можем построить линию регрессии, проходящую через точки. Правда в этом случае придется отказаться от параметра hue, разделять данные на категории и одновременно строить линию регрессии sns.jointplot() не умеет.
|
# для построения линии регрессии на данных # используем параметр kind = ‘reg’ sns.jointplot(data = tips, x = ‘total_bill’, y = ‘tip’, kind = ‘reg’, height = 8); |
heatmap
Наконец, если мы хотим вывести какие-либо статистические показатели взаимосвязи двух количественных переменных (например, корреляцию), это можно сделать с помощью чисел. Выведем корреляционную матрицу между total_bill и tip с помощью метода .corr().
|
tips[[‘total_bill’, ‘tip’]].corr() |
В следующем разделе мы более подробно поговорим про взаимосвязь переменных в целом и корреляцию в частности.
Или с помощью цвета. Во втором случае мы будем строить то, что называется тепловой картой (heatmap). Поместим созданную выше корреляционную матрицу в функцию sns.heatmap().
|
sns.heatmap(tips[[‘total_bill’, ‘tip’]].corr(), # дополнительно пропишем цветовую гамму cmap= ‘coolwarm’, # и зададим диапазон от -1 до 1 vmin = –1, vmax = 1); |
Более насыщенный красный цвет (верхняя граница шкалы) демонстрирует корреляцию признака с самим собой, менее насыщенный — достаточно сильную положительную корреляцию признаков.
Сравнение датасетов
Рассмотрим еще одну библиотеку, которая позволяет не просто сравнивать количественные и качественные переменные в датасете, а сразу сравнивать два датасета. Зачастую, сравнение двух датасетов имеет смысл, когда перед нами обучающая и тестовая выборки.
Скачаем и подгрузим в сессионное хранилище тестовую часть датасета «Титаник».
Библиотека Sweetviz
Теперь установим и импортируем библиотеку sweetviz.
Импортируем обучающую и тестовую выборки.
|
train = pd.read_csv(‘/content/train.csv’) test = pd.read_csv(‘/content/test.csv’) |
Передадим оба датасета в функцию sv.compare(). Эта функция создаст объект DataframeReport, к которому мы сможем применить метод .show_notebook() для выведения результата.
|
comparison = sv.compare(train, test) |
|
# посмотрим на тип созданного объекта type(comparison) |
|
sweetviz.dataframe_report.DataframeReport |
|
# применим метод .show_notebook() comparison.show_notebook() |
Интерактивную версию этого отчета вы найдете в ноутбуке к занятию⧉.
Количественные переменные
По большому счету мы получаем информацию о каждой из переменных в разрезе двух датафреймов. Обратимся к столбцу Age.
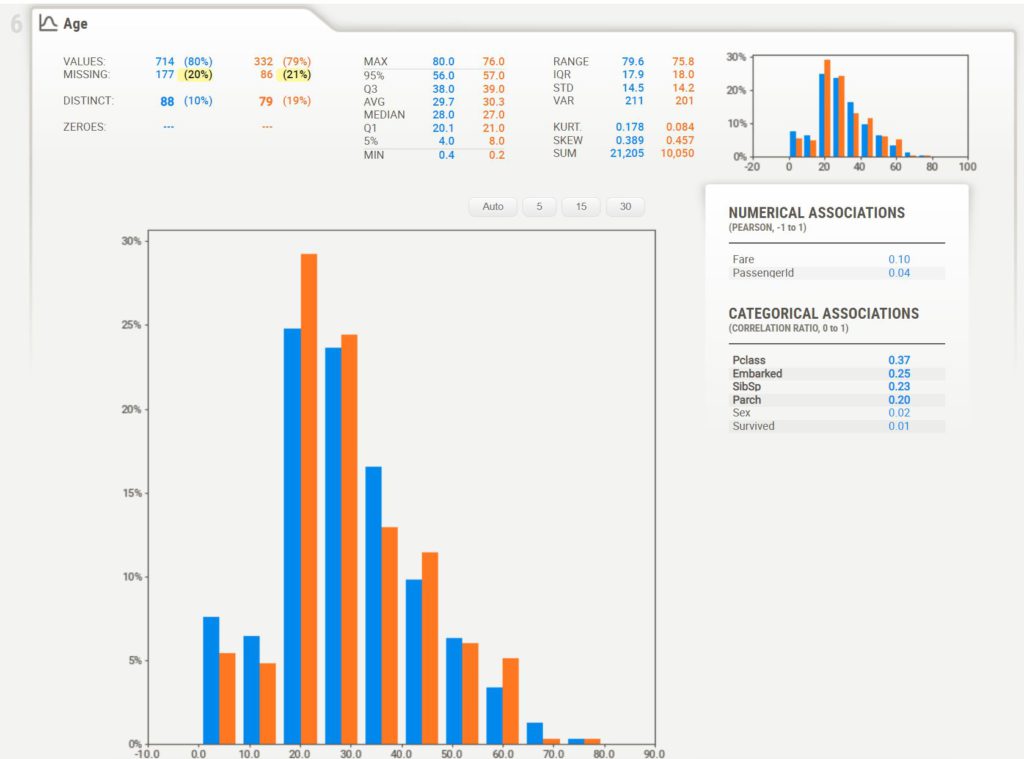
В отчете есть информация о присутствующих (values) и отсутствующих значениях (missing), количестве уникальных (distinct) и нулевых (zeroes) значений. Кроме того, мы видим базовые статистические показатели и гистограмму распределения переменной в каждом из датафреймов.
Отдельно стоит отметить выявление взаимосвязи:
- для двух количественных переменных используется коэффициент корреляции Пирсона (Pearson correlation coefficient); и здесь мы видим, что корреляция возраста со столбцами Fare и PassengerId ожидаемо близка к нулю
- для выявления взаимосвязи между количественной и качественной переменными используется корреляционное отношение (correlation ratio); например, мы видим, что возраст в некоторой степени связан с классом пассажира Pclass
Качественные переменные
Обратимся к столбцу Sex.
В первую очередь отметим, что программа самостоятельно определила, что речь идет именно о категориальном признаке. Для его визуализации была построена столбчатая диаграмма с разбивкой по обучающей и тестовой выборке. Кроме того, мы можем количественно оценить значения в каждой из категорий.
Для поиска же взаимосвязи между двумя категориальными переменными используется коэффициент неопределенности (uncertainty coefficient) или U Тиля, и мы видим некоторую связь с целевой переменной Survived. Для количественной и качественной переменных по-прежнему используется корреляционное отношение.
Более подробную информацию об этой библиотеке можно посмотреть на странице документации⧉.
Перейдем к третьей части занятия.
При обработке большого числа экспериментальных данных их предварительно группируют и оформляют в виде так называемого Интервального ряда.
Пример 1. Средняя месячная зарплата за год каждого из пятидесяти случайно отобранных работников хозяйства такова:
317 304 230 285 290 320 262 274 205 180 234 221 241 270 257 290 258 296 301 150 160 210 235 308 240 370 180 244 365 130 170 250 370 267 288 231 253 315 201 256 279 285 226 367 247 252 320 160 215 350.
Здесь переменной величиной X является средняя месячная зарплата. Как видно из приведенных данных, наименьшее значение величины Х равно 130, а наибольшее — 370. Таким образом, диапазон наблюдений представляет собой интервал 130 – 370, длина которого равна 370 – 130 = 240.
Разобьем диапазон наблюдений на части (разряды) Так, чтобы каждый разряд содержал несколько экспериментальных данных. Например, разделим интервал 130 – 370 на 6 равных частей, тогда длина каждого разряда будет 40. Границами разрядов будут числа 130, 170, 210, 250, 290, 330, 370 (рис. 3).
Подсчитаем число значений, попавших в каждый разряд. Например, в первый разряд попадают следующие числа: 150 (1 раз), 160 (2 раза), 130 (1 раз), 170 (1 раз). Поскольку число 170 находится на границе между первым и вторым разрядами, мы включим его и в первый и во второй разряды, но с кратностью 1/2. Сложив кратности, мы получим Абсолютную частоту первого разряда:
M1 = 1 + 2 + 1 + 0,5 = 4,5.
Разделив абсолютную частоту на число П всех наблюдений, получим Относительную частоту 
Попадания величины Х в первый разряд:
Проделав вычисления для всех разрядов, мы получим следующую таблицу.
Таблица 6
Здесь Mi — абсолютные частоты, 
— относительные частоты. Табл. 6 называется Интервальным рядом.
Сумма всех абсолютных частот равна числу всех приведенных в табл. 6 значений переменной величины:
4,5 + 5 + 12 + 14,5 + 9 + 5 = 50.
Это свойство используется для проверки правильности вычислений. Из него следует, что сумма всех относительных частот равна единице:
0,09 + 0,10 + 0,24 + 0,29 + 0,18 + 0,10 = 1.
Интервальный ряд изображают графически в виде Гистограммы, которая строится так. Сначала вычисляют плотности частот H1, H2, H3, … , разделив относительную частоту каждого разряда на его длину:
Затем выбирают на плоскости систему координат и откладывают на оси Х значения 40, 80, 120, … , соответствующие границам разрядов. На каждом из отрезков длины 40, как на основании, строят прямоугольник, высота которого равна плотности частоты соответствую щего разряда. Полученная фигура и называется Гистограммой. Она изображена на рис. 4.
Заметьте, что высоты H1, H2, … , H6 прямоугольников, образующих гистограмму, выбраны так, что их площади будут 
, т. е. равны соответствующим относительным частотам. Отсюда вытекает такое правило:
Для того, чтобы найти долю тех значений величины. X, которые попадают в некоторый интервал, нужно найти площадь той части гистограммы, основанием которой является данный интервал.
Определим, например, долю значений величины X, Принадлежащих интервалу 210 – 300. Для этого вычислим площадь фигуры с основанием 210 – 300 (на рисунке она выделена штриховкой). Площади первых двух прямоугольников, составляющих фигуру, равны соответственно 
= 0,24 и 
= 0,29; площадь третьего равна 10 • 0,0045 = 0,045. Сумма площадей 0,24 + 0,29 + 0,045 = 0,575 и дает нужное число. Иными словами, 57,5% значений величины Х находится в границах от 210 до 300.
Как мы заметили в начале параграфа, интервальный ряд составляют при обработке больших массивов информации. В таких случаях, как правило, отдельные значения величины Х не фиксируются, а подсчитывается количество ее значений, попавших в каждый разряд (т. е. абсолютные частоты). Поэтому исследователь не знает отдельных значений наблюдаемой величины Х и не может воспользоваться формулами (1), (5) и (7) для вычисления среднего арифметического, дисперсии и среднего квадратического отклонения. Но приближенное значение этих числовых характеристик можно найти с помощью интервального ряда. Для этого сначала находят середины разрядов: 
(здесь K — Число всех разрядов интервального ряда); затем проводят вычисления по следующим формулам:
Результаты расчетов по данным табл. 6 сведены в следующую таблицу:
Таблица 7
В первом столбце записаны номера разрядов, во втором — числа 
(середины разрядов), в третьем — произведения 
, и т. д. Таблица заполняется по столбцам. Середину разряда вычисляем как полусумму его границ:
Согласно формуле (8), сумма чисел третьего столбца дает среднее арифметическое 
= 256,8. Оно записано в последней строке этого столбца. Сумма чисел последнего столбца равна дисперсии D = 3113,75 [см. формулу (9)]. Наконец, по формуле (10) определяем среднее квадратическое отклонение S = 
= 55,80.
Интервальный ряд, гистограмма и числовые характеристики, найденные по формулам (8)—(10), составляют Математическую модель средней заработной платы. Она используется при проведении различных социологических исследований, например, при определении уровня жизни работников какой-либо отрасли.
ТИПОВЫЕ ЗАДАНИЯ
1. Для проведения демографических исследований выбрали 50 семей и получили следующие данные о количестве членов семьи:
2 5 3 4 1 3 6 2 4 3 4 1 3 5 2 3 4 4 3 3 2 5 3 4 4
3 3 4 4 3 2 5 3 1 4 3 4 2 6 3 2 3 1 6 4 3 3 2 1 7.
Укажите переменную величину; составьте табл. 5; найдите числовые характеристики — среднее арифметическое, дисперсию, среднее квадратическое отклонение.
2. Управление сельского хозяйства Дрюковского района представило сводку по пятидесяти хозяйствам. Согласно этой сводке, урожайность ржи в них составила (в центнерах с гектара):
17.5 17.8 18.6 18.3 19.1 19.9 20.6 20.1 22 21.4 17.5 18.5 19 20 22 20.6 19.1 18.6 17.9 19.1 22 19 17.5 22 22.6 21 21.4 19 17.8 18.3 19.9 20.1 21.4 18.5 20 20.6 18.6 21.4 21 20 20 18 18 18 17.5 18.6 19.1 20.6 17.5 18.6 .
Постройте интервальный ряд (табл. 6), гистограмму, составьте табл. 7 и по формулам (8)-(10) найдите числовые характеристики — среднее арифметическое, дисперсию, среднее квадратическое отклонение.
| < Предыдущая | Следующая > |
|---|
Гистограмма и ящик с усами на пальцах
Время на прочтение
4 мин
Количество просмотров 76K
В этой заметке я хочу описать два типа графиков для одномерных данных, а именно
- гистограмма
- ящик с усами
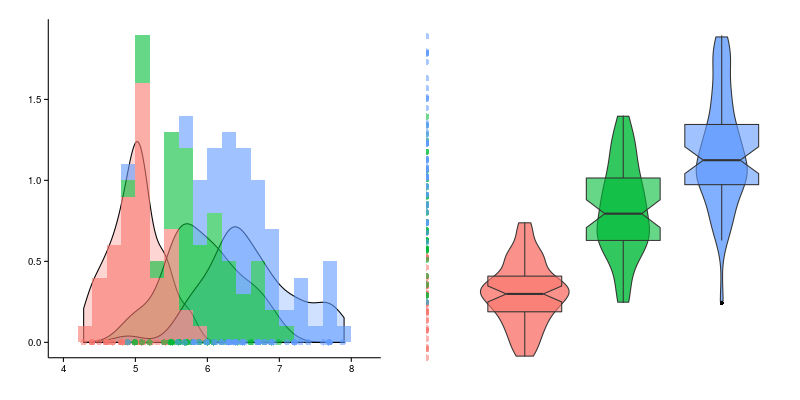
Рассмотрим произвольную выборку вещественных чисел 
, будем обозначать порядковую статистику , такую что .
Гистограмма
Скорее всего все поменять этот тип графика из школьной или университетской программы, который выглядит приблизительно так как на картинке.
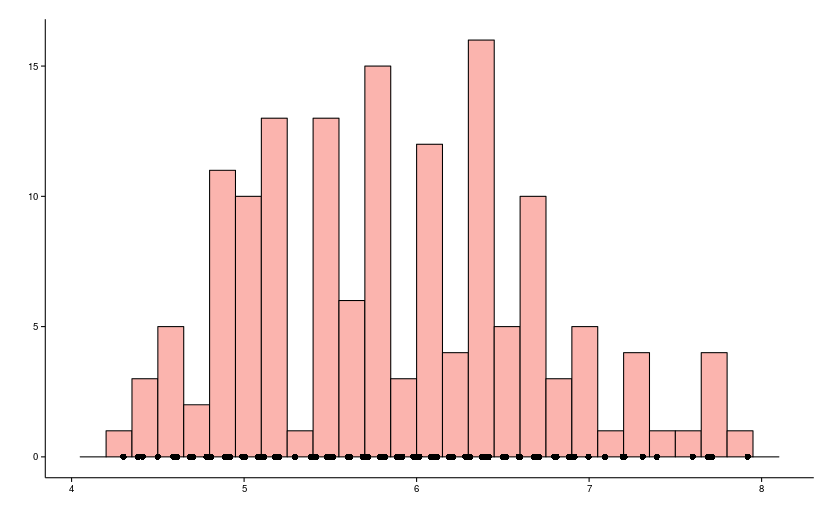
Прежде всего необходимо помнить, что значения входной выборки располагаются по оси x, а по оси y располагается число раз, которое данное значение встретилось (назовем их отсчеты). Гистограмма позволяет огрубить и сделать набор данных более компактным, при этом не умаляя его специфичность.
Важными характеристиками гистограммы являются следующие:
- число столбцов (которые называются bins или bars)
- абсолютные или плотностные отсчеты по оси y
- как сгруппированы данные
Столбцы
В подавляющем большинстве случаев гистограмма определена на отрезке , где — исходная выборка, вспомогательные константы, округляющие до ближайших “читаемых” чисел, которые в каждом случае зависят от масштаба и, обычно, это делители десятки в масштабе исходных данных. Если вдруг стало интересно, как ставить отсечки в данных, то можно посмотреть ссылку: R (pretty).
Так же обычно гистограммы делят отрезок I на подотрезки равной длины и, вот, выбор числа отрезков является искусством, хотя можно привести несколько формул:
- Правило Стёрджеса (Не фотограф).
- Правило Скотта.
- Правило Фридмана-Дьякониса.
где — число столбцов, — размер исходной выборки, — оценка стандартного отклонения, — интерквартильное расстояние, которое еще встретится ниже.
Так же можно отметить несколько правил здравого смысла:
- хорошо чтобы в большинстве столбцов было больше одного исходного значения
- каждый столбец гистограммы требует хотя бы одного пикселя по ширине, и в целом ограничение “не более 200” столбцов достаточно распространено
В противном случае, если число столбцов избыточно, а исходных данных мало, гистограмма будет напоминать штрих-код, как например на рисунке ниже.
Ось Y
Гистограммы бывают в абсолютных значениях, когда по оси y откладывается количество элементов исходной выборки попавших в каждый из интервалов, и в относительных, когда сумма столбцов нормируются на единицу, в этом случае гистограмма является оценкой плотности распределения и с точки зрения графика меняется лишь масштаб.
Так как обычная гистограмма является оценкой плотности, то мы можем суммировать столбцы и получить оценку функции вероятности следующим образом: . Два следующих графика построены по одним и тем же данным, слева не нормализованная гистограмма, справа аккумулированные значения нормализованной гистограммы.
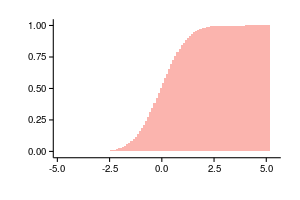
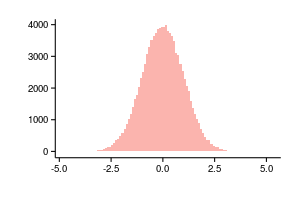
Группировка данных
До сих пор был рассмотрен случай, когда у нас есть характеристика, на которую мы просто хотим взглянуть, обычно намного более интересно сравнивать поведение одной и той же характеристики для различных подгрупп. В таком случае гистограмма будет иметь следующий вид.
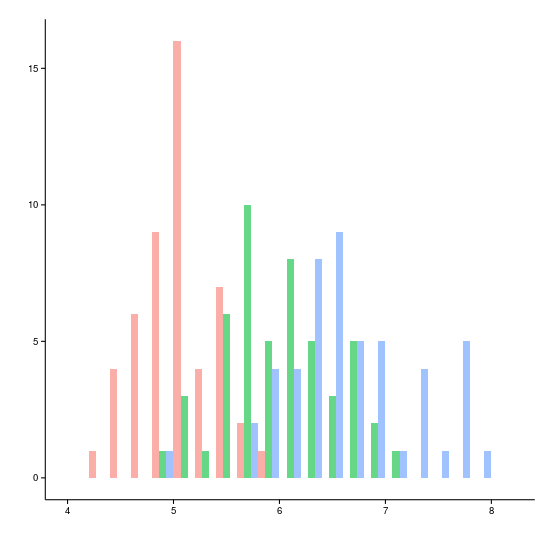
В данном случае, ширина каждого столбца для каждой группы уменьшается пропорционально числу групп и слегка сдвигаются друг относительно друга, в качестве альтернативы можно рассмотреть полупрозрачное перекрытие, которое будет выглядеть следующим образом для тех же данных.
В сухом остатке
Для отрисовки гистограммы необходимо определить
- Число столбцов
- Нужна ли нормализация и аккумулирование данных
- Способ отображения различных групп
Для отрисовки гистограммы для каждой группы требуется хранить следующие значения:
Диаграмма размаха
“Ящик с усами” не имеет официально устоявшегося названия, а называть его “ящиком с усами“ у меня язык не поворачивается, тем более когда ящиков несколько, а диаграмма размаха хоть и не очень частотное, но более благозвучное название. Приведем пример трех ящиков слева отображены соответствующие значения исходных данных (не являются частью диаграммы размаха). Прежде всего необходимо отметить, что в случае диаграмм размаха, исходная характеристика откладывается по оси Y, а ось X условна и представляет собой группирующую переменную.
Чтобы нарисовать ящик для одной группы про исходные данные необходимо знать всего три характеристики:
- Первый квартиль
- Медиану
- Третий квартиль
Иногда к “обязательному” набору добавляют следующие дополнительные:
Таким образом, ящик с усами в разрезе будет выглядеть следующим образом.
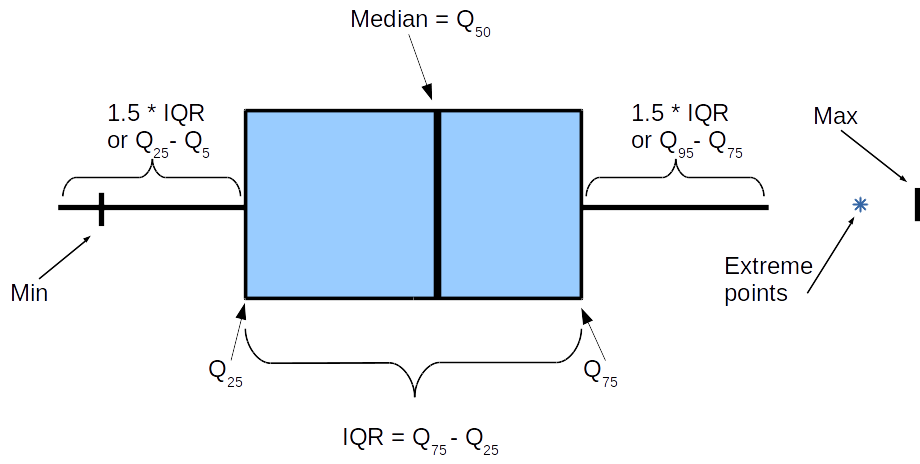
Некоторые моменты требуют пояснения. Ящик, то есть объект между и , практически везде ограничен этими значениями, а вот “усы” могут различаться и если вас действительно интересуют числа, необходимо уточнять, что имеется в виду в каждом отдельном случае. Самое важное это длина усов: исходим из того, что она .
Отметки минимума и максимума часто опускаются, экстремальные точки, то есть выходящие за пределы усов тоже опускаются либо рисуются точками или звездочками. В зависимости от структуры данных желание отрисовывать экстремальные значения может значительно увеличить объем данных для отрисовки диаграммы размаха.
Магическое число появилось в работе Тьюки Exploratory Data Analysis (1977) и причина его появления не очень ясна, но с тех времен ничего не менялось, многие инструменты предлагают его в качестве значения по умолчанию, но позволяют выставлять произвольное, вплоть до нуля, в этом случае, “усы” будут покрывать весь отрезок от минимального до максимального значений исходных данных.
Есть предположение, что возникло следующим образом. Ширина усов составляет , известно, что для симметричных распределений совпадает с абсолютным отклонением от медианы (MAD), которая в свою очередь, является оценкой дисперсии с коэффициентом . А значит, , мы получаем не безызвестные 3 сигмы влево, 3 сигмы вправо.
Иногда в качестве концов усов предлагается интервал , в таком случае очевидно, что всегда (если исходных данных больше 20) должны получаться точки, не попадающие внутрь интервала и поэтому их обычно игнорируют при таком подходе.
В сухом остатке
Для отрисовки “диаграммы размаха” необходимо определить:
- способ группировки данных
- длину усов
- нужно ли отмечать экстремальные значения
Для отрисовки “ящика с усами” для одной группы требуется всего 3 числа.
