Комплексно сопряженные корни как найти - Сайт, где вы сможете решить свои вопросы

From Wikipedia, the free encyclopedia

In mathematics, the complex conjugate root theorem states that if P is a polynomial in one variable with real coefficients, and a + bi is a root of P with a and b real numbers, then its complex conjugate a − bi is also a root of P.^[1]

It follows from this (and the fundamental theorem of algebra) that, if the degree of a real polynomial is odd, it must have at least one real root.^[2] That fact can also be proved by using the intermediate value theorem.

Examples and consequences[edit]

The polynomial x² + 1 = 0 has roots ± i.
Any real square matrix of odd degree has at least one real eigenvalue. For example, if the matrix is orthogonal, then 1 or −1 is an eigenvalue.
The polynomial

${displaystyle x^{3}-7x^{2}+41x-87}$

has roots

and thus can be factored as

In computing the product of the last two factors, the imaginary parts cancel, and we get

${displaystyle (x-3)(x^{2}-4x+29).}$

The non-real factors come in pairs which when multiplied give quadratic polynomials with real coefficients. Since every polynomial with complex coefficients can be factored into 1st-degree factors (that is one way of stating the fundamental theorem of algebra), it follows that every polynomial with real coefficients can be factored into factors of degree no higher than 2: just 1st-degree and quadratic factors.

If the roots are a+bi and a−bi, they form a quadratic

${displaystyle x^{2}-2ax+(a^{2}+b^{2})}$

If the third root is c, this becomes

${displaystyle (x^{2}-2ax+(a^{2}+b^{2}))(x-c)}$

${displaystyle =x^{3}+x^{2}(-2a-c)+x(2ac+a^{2}+b^{2})-c(a^{2}+b^{2})}$

Corollary on odd-degree polynomials[edit]

It follows from the present theorem and the fundamental theorem of algebra that if the degree of a real polynomial is odd, it must have at least one real root.^[2]

This can be proved as follows.

Since non-real complex roots come in conjugate pairs, there are an even number of them;
But a polynomial of odd degree has an odd number of roots;
Therefore some of them must be real.

This requires some care in the presence of multiple roots; but a complex root and its conjugate do have the same multiplicity (and this lemma is not hard to prove). It can also be worked around by considering only irreducible polynomials; any real polynomial of odd degree must have an irreducible factor of odd degree, which (having no multiple roots) must have a real root by the reasoning above.

This corollary can also be proved directly by using the intermediate value theorem.

Proof[edit]

One proof of the theorem is as follows:^[2]

Consider the polynomial

P(z) = a_0 + a_1z + a_2z^2 + cdots + a_nz^n

where all a_r are real. Suppose some complex number ζ is a root of P, that is . It needs to be shown that

{displaystyle P{big (},{overline {zeta }},{big )}=0}

as well.

If P(ζ ) = 0, then

${displaystyle a_{0}+a_{1}zeta +a_{2}zeta ^{2}+cdots +a_{n}zeta ^{n}=0}$

which can be put as

$sum_{r=0}^n a_rzeta^r = 0.$

Now

${displaystyle P{big (},{overline {zeta }},{big )}=sum _{r=0}^{n}a_{r}{big (},{overline {zeta }},{big )}^{r}}$

and given the properties of complex conjugation,

${displaystyle sum _{r=0}^{n}a_{r}{big (},{overline {zeta }},{big )}^{r}=sum _{r=0}^{n}a_{r}{overline {zeta ^{r}}}=sum _{r=0}^{n}{overline {a_{r}zeta ^{r}}}={overline {sum _{r=0}^{n}a_{r}zeta ^{r}}}.}$

Since

${displaystyle {overline {sum _{r=0}^{n}a_{r}zeta ^{r}}}={overline {0}},}$

it follows that

${displaystyle sum _{r=0}^{n}a_{r}{big (},{overline {zeta }},{big )}^{r}={overline {0}}=0.}$

That is,

${displaystyle P{big (},{overline {zeta }},{big )}=a_{0}+a_{1}{overline {zeta }}+a_{2}{big (},{overline {zeta }},{big )}^{2}+cdots +a_{n}{big (},{overline {zeta }},{big )}^{n}=0.}$

Note that this works only because the a_r are real, that is, ${displaystyle {overline {a_{r}}}=a_{r}}$ . If any of the coefficients were non-real, the roots would not necessarily come in conjugate pairs.

Notes[edit]

^ Anthony G. O’Farell and Gary McGuire (2002). “Complex numbers, 8.4.2 Complex roots of real polynomials”. Maynooth Mathematical Olympiad Manual. Logic Press. p. 104. ISBN 0954426908. Preview available at Google books
^ ^a ^b ^c Alan Jeffrey (2005). “Analytic Functions”. Complex Analysis and Applications. CRC Press. pp. 22–23. ISBN 158488553X.

Источник

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Определение 1

Двучленным называется уравнение вида $x^{n} =A$.

Рассмотрим три случая:

В случае если $A$ – это положительное действительное число, то корни уравнения находятся по формуле

[x_{k} =sqrt[{n}]{A} cdot left(cos frac{2kpi }{n} +icdot sin frac{2kpi }{n} right),, , , k=0,..,n-1.]

В случае если $A$ – это отрицательное действительное число, то корни уравнения находятся по формуле

[x_{k} =sqrt[{n}]{|A|} cdot left(cos frac{pi +2kpi }{n} +icdot sin frac{pi +2kpi }{n} right),, , , k=0,..,n-1.]

В случае если $A$ – это комплексное число, то корни уравнения находятся по формуле

[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1.]

Пример 1

Решить уравнение: $x^{3} =8$.

Решение:

Так как $A>0$, то $x_{k} =sqrt[{3}]{8} cdot left(cos frac{2kpi }{3} +icdot sin frac{2kpi }{3} right),, , , k=0,..,2$.

При $k=0$ получаем $x_{0} =sqrt[{3}]{8} cdot left(cos 0+icdot sin 0right)=sqrt[{3}]{8} =2$.

При $k=1$ получаем

[x_{1} =sqrt[{3}]{8} cdot left(cos frac{2pi }{3} +icdot sin frac{2pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=-1+sqrt{3} cdot i.]

При $k=2$ получаем

[x_{2} =sqrt[{3}]{8} cdot left(cos frac{4pi }{3} +icdot sin frac{4pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=-1-sqrt{3} cdot i.]

Пример 2

Решить уравнение: $x^{3} =1+i$.

«Квадратное уравнение с комплексными корнями» 👇

Решение:

Так как $A$ – комплексное число, то

[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1,, , , k=0,..,2.]

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

[r=sqrt{1^{2} +1^{2} } =sqrt{1+1} =sqrt{2} ]

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac{1}{1} =arctg1=frac{pi }{4} ]

Подставим полученные значения и получим:

[A=sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]

Уравнение перепишем в виде:

[x^{3} =sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]

При $k=0$ получаем $x_{0} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4}{3} +icdot sin frac{pi /4}{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)=sqrt[{6}]{2} cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)$.

При $k=1$ получаем

[begin{array}{l} {x_{1} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+2pi }{3} +icdot sin frac{pi /4+2pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)} end{array}]

При $k=2$ получаем

[begin{array}{l} {x_{2} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+4pi }{3} +icdot sin frac{pi /4+4pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)} end{array}]

Определение 2

Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^{2} -4ac$, при этом

[x_{1,2} =frac{-bpm sqrt{D} }{2a} .]

Примечание 1

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

Пример 3

Решить уравнение $x^{2} +2x+5=0$ и изобразить корни на плоскости.

Решение:

Вычислим дискриминант:

[D=2^{2} -4cdot 1cdot 5=4-20=-16.]

Так как $D

[x_{1,2} =frac{-2pm sqrt{-16} }{2} =frac{-2pm icdot sqrt{16} }{2} =frac{-2pm icdot 4}{2} =-1pm 2i.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

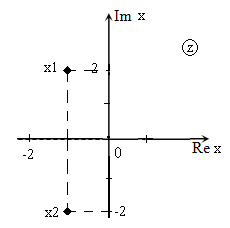
Рис. 1

Примечание 2

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Определение 3

Комплексное число вида $overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Примечание 3

Известно, что если $x_{1,2} $ являются корнями квадратного уравнения $ax^{2} +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_{1} )(x-x_{2} )=0$. В общем случае $x_{1,2} $ являются комплексными корнями.

Пример 4

Зная корни уравнения $x_{1,2} =1pm 2i$, записать исходное уравнение.

Решение:

Запишем уравнение следующим образом:

[(x-(1-2i))cdot (x-(1+2i))=0.]

Выполним умножение комплексных чисел

[x^{2} -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0][x^{2} -x+2icdot x-x-2icdot x+1-4i^{2} =0] [x^{2} -2x+1+4=0] [x^{2} -2x+5=0]

Следовательно, $x^{2} -2x+5=0$ – искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Пример 5

Решить уравнение: $z^{2} +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Решение:

Вычислим дискриминант:

[D=(1-2i)^{2} +4cdot 1cdot (1+i)=1-4i+4i^{2} +4+4i=1-4+4=1.]

Так как $D>0$, уравнение имеет два корня:

[x_{1} =frac{-(1-2i))-sqrt{1} }{2} =frac{-1+2i-1}{2} =frac{-2+2i}{2} =-1+i.] [x_{2} =frac{-(1-2i))+sqrt{1} }{2} =frac{-1+2i+1}{2} =frac{2i}{2} =i.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

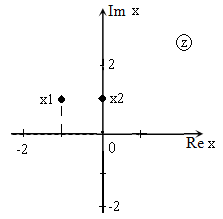
Рис. 2

Примечание 4

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Если
все корни отрицательные, то стечением
времени все члены уравнения (6,6),
содержащие множитель
,стремятся
к нулю, т.к.,а
отклонение регулируемой величины y(t)
стремится
к постоянному значению у_вын(t)
или
к нулю. Система в этом случае устойчива.

Если
хотя бы один из корней, например, p₁
положителен, то соответствующий член

с
течением времени неограниченно
возрастает и отклонение регулируемой
величины y(t)
= y_св(t)→∞.
Система в этом случае будет неустойчивой
(рис. 6.2),

Если
все вещественные корни отрицательны,
то каждая составляющая или множитель
стремятся к нулю приt→∞,
т.е.

Если
же вещественные части корней положительны
(p_i>0),
то

и
система неустойчивая.

2. Корни комплексные сопряжённые с отрицательной вещественной частью

где
α_i
–
показатель затухания колебаний;

Ω_i
– круговая частота затухающих колебаний.

В
этом
случае

(6.7)

Если
корни сопряженные комплексные, то в
этом случае при отрицательных
вещественных частях отклонение
регулируемой величины приходит к
установившемуся значению (к нулю) с
затухающими гармоническими колебаниями
(рис. 6.3).

Действительно,
если вещественные части α_i
всех
комплексных корней отрицательны, то
каждое слагаемое суммы (6.7) представляет
собой затухающее колебание и поэтому

т.е.
система устойчивая.

3. Корни комплексные, сопряжённые при положительной вещественной части

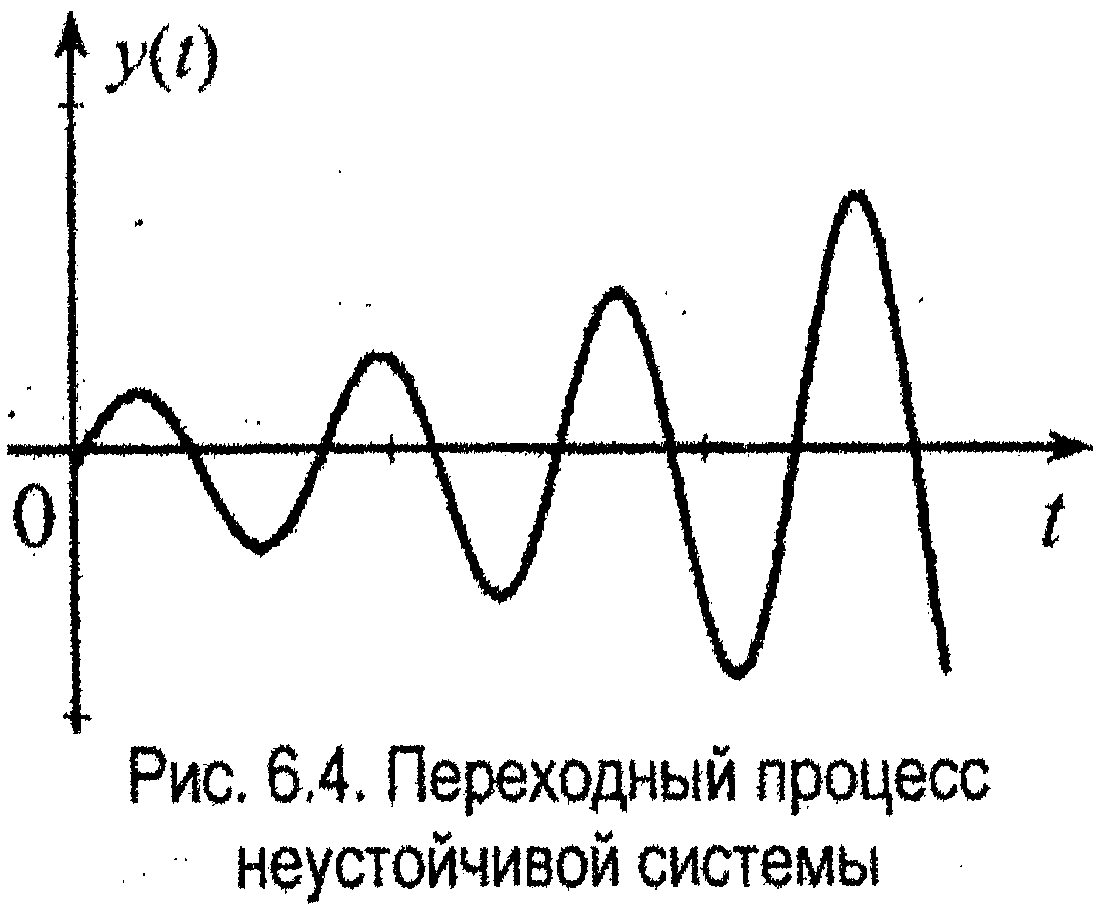
Если
хотя бы одна пара комплексных корней
имеет положительную вещественную
часть (α_i
> 0),
то в этом случае

(6.8)

т.е.
отклонение регулируемой величины
совершает колебания с неограниченно
возрастающей амплитудой. Система
неустойчива (рис. 8.4).

4.
Корни имеют нулевую вещественную часть
(α_i=
0),
т.е.

В
этом случае отклонение регулируемой
величины совершает незатухающие
колебания (автоколебания), т.е. система
находится на границе устойчивости (рис.
6.5).

Система
будет находиться на границе устойчивости
при наличии:

–
нулевого корня,

–
пары чисто мнимых корней,

–
бесконечного корня.

Таким
образом, условием устойчивости
системы автоматического управления
является отрицательность вещественных
частей всех корней характеристического
уравнения (т.е. расположение всех
корней характеристического уравнения
в левой полуплоскости комплексной
плоскости корней, рис. 6.6).

Корни
характеристического уравнения замкнутой
системы зависят только от параметров
системы (коэффициентов уравнения),
т.
е. от постоянных времени и коэффициентов
усиления звеньев.

Корни
характеристического уравнения можно
представить в виде векторов,
расположенных в комплексной плоскости.
Очевидно, что система будет устойчивой,
если все корни располагаются слева от
мнимой оси (рис, 6.7).

В
случае, если один вещественный корень
или пара комплексно сопряженных
корней располагается на мнимой оси,
система оказывается на границе
устойчивости. Системы, у которых
имеется одна пара мнимых корней, могут
совершать незатухающие колебания
(автоколебания). Если система имеет один
нулевой корень при всех остальных
корнях, расположенных левее мнимой
оси, систему называют нейтрально
устойчивой.

Для
того, чтобы все корни оказались в левой
полуплоскости,
можно воздействовать на коэффициенты
характеристического уравнения, которые
связаны с корнями непрерывными
зависимостями.

Задача
определения устойчивости может быть
решена различными методами. Можно
определять корни характеристического
уравнения и по ним устанавливать знаки
вещественных частей. Но такой метод
может быть использован, когда порядок
характеристического уравнения ниже
третьего. Уравнения более высоких
степеней вообще не имеют аналитического
решения и могут быть решены лишь
приближенно.

Но
для определения устойчивости совершенно
не обязательно знать значение корней.
Достаточно убедиться только в
отрицательности вещественных частей
корней. Для этого можно воспользоваться
методами, основанными на использовании
критериев
устойчивости.

Критерием
устойчивости
называется косвенный метод определения
знаков вещественной части корней
характеристического уравнения, не
требующий решения этого уравнения.

Все
известные критерии делятся на 2 группы:

1)
алгебраические,

2)
частотные,

К
алгебраическим относятся критерии:
Вышнеградского, Рауса-Гурвица. К частотным
относятся критерии Михайлова, Найквиста,
логарифмический критерий устойчивости.
Особое место занимает выделение областей
устойчивости. Применение того или
иного критерия зависит от конкретных
условий.

Соседние файлы в папке Лекции по ТАУ

Источник

Геометрическое представление и его сопряжённого на комплексной плоскости

Сопряжённые числа (комплексно-сопряжённые числа) — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине, но противоположными по знаку, мнимыми частями^[1]. Например, сопряжёнными являются числа и . Число, сопряжённое к числу , обозначается . В общем случае, сопряжённым к числу (где и — действительные числа) является .

Например:

На комплексной плоскости сопряжённые числа представлены точками, симметричными относительно действительной оси. В полярной системе координат сопряжённые числа имеют вид ${displaystyle re^{iphi }}$ и ${displaystyle re^{-iphi }}$ , что непосредственно следует из формулы Эйлера.