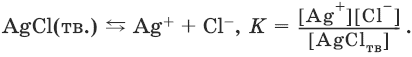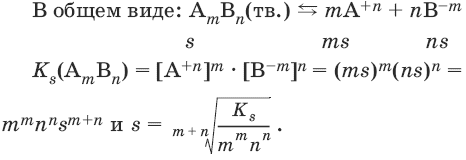Константа растворимости как найти

В
системе, состоящей из раствора и осадка,
идут два процесса – растворение осадка
и осаждение. Равенство скоростей этих
двух процессов является условием
равновесия.

Насыщенный
раствор – это раствор, который находится
в равновесии с осадком.

Применим
закон действия масс к равновесию между
осадком и раствором.

AgCl(тв.)


Ag⁺
+ Cl^–

Поскольку
[AgCl_тв]
= const, имеем:

К[AgCl_тв]
= K_SAgCl
=[Ag⁺][Cl^–]
В общем виде имеем:

A_mB_n(тв.)

mA⁺ⁿ
+ nB^-m
и K_S(A_mB_n)
= [A⁺ⁿ]^m[B^-m]ⁿ.

Константа
растворимости
K_S
(или
произведение растворимости ПР) –
произведение концентраций ионов в
насыщенном растворе малорастворимого
электролита – есть величина постоянная
и зависит лишь от температуры.

Примеры
величин K_S
для ряда солей:

K_S(AgCl)
= 1,610^-10

K_S(Ag₂CrO₄)
= 1,110^-12

K_S(Ag₂S)
= 610^-50.

Растворимость
малорастворимого
вещества s может быть выражена в молях
на литр. В зависимости от величины s
вещества могут быть разделены на
малорастворимые – s < 10^-4
моль/л, среднерастворимые – 10^-4
моль/л 
s 
10^-2
моль/л
и хорошо растворимые s >10^-2
моль/л.

Растворимость
соединений связана с их константой
растворимости. Для AgCl имеем:

AgCl(тв.)Ag⁺
+ Cl^–

s
s s

Растворимость
s – молярная концентрация AgCl в растворе:

s
= [AgCl_р–р]
= m/(MV)
[AgCl_р–р]
= s = [Ag⁺]
= [Cl^–].

Отсюда
K_S
AgCl
= [Ag⁺][Cl^–]
= s²
и
s=.

В
общем виде для A_mB_n
имеем: A_mB_n(тв.)mA⁺ⁿ
+ nB^-m

s
ms ns

K_S(A_mB_n)
= [A⁺ⁿ]^m[B^-m]ⁿ
=
(ms)^m(ns)ⁿ
= m^mnⁿs^m+n.

Пример.
Найти растворимость AgCl (K_S=1,610^-10)
и Ag₂CrO₄
(K_S=
1,210^-12).

Решение.
AgCl

Ag⁺
+ Cl^–
,

K_S
= s²,
s ==
1,3410^-5
моль/л.

Ag₂CrO₄


2Ag⁺
+ CrO₄^2-

s
2s s

K_S
= (2s)²s
= 4s³,
s =

= 6,510^-5
моль/л.

Хотя
обычно растворимость тем меньше, чем
меньше K_S,
в данном случае для соединений разных
типов s(AgCl) < s(Ag₂CrO₄),
хотя K_S(AgCl)
> K_S(Ag₂CrO₄).

Условие осаждения и растворения осадка

Для
равновесия между осадком и раствором
– насыщенного раствора – имеем в случае
AgCl:

AgClAg⁺
+ Cl^–
[Ag⁺][Cl^–]
= K_S.

Условие
осаждения записывается в виде: [Ag⁺][Cl^–]
> K_S

В
ходе осаждения концентрации ионов
уменьшаются до установления равновесия.

Условие
растворения осадка или существования
насыщенного раствора записывается в
виде: [Ag⁺][Cl^–]
< K_S.

В
ходе растворения осадка концентрация
ионов увеличивается до установления
равновесия.

Эффект общего иона

Добавление
общего иона уменьшает растворимость
малорастворимых соединений.

Пример.
Найдем растворимость AgCl в 0,1 М растворе
NaCl.

Решение.
AgCl

Ag⁺
+ Cl^–

s
s s+0,10,1

K_S
AgCl
= [Ag⁺][Cl^–]
= s 
0,1 = 1,610^-10,
s = 1,610^-9
моль/л.

Растворимость
AgCl в воде (см. выше) равна 1,3410^-5
моль/л, растворимость AgCl в 0,1М NaCl – 1,610^-9
моль/л, т.е. в 10⁴
раз меньше.

Солевой эффект

Увеличение
ионной силы раствора увеличивает
растворимость малорастворимых соединений.

Поскольку
концентрации ионов, образующихся при
диссоциации малорастворимых соединений,
а также ионная сила получаемых растворов
малы, то оказывается возможным использовать
в выражениях K_S
концентрации ионов, а не их активности.
В тех случаях, когда в растворе присутствуют
сильные электролиты, обусловливающие
большую ионную силу раствора, необходимо
в выражении для K_S
подставлять активность ионов.

Определим
растворимость AgCl в 0,1 М NaCl с учетом ионной
силы раствора

AgCl


Ag⁺
+ Cl^–

s
s s+0,10,1

Для
0,1М NaCl 
= 0,1 и f_Ag+
= f_Cl–
= 0,78.

K_S
= a_Ag+a_Cl–
= f_Ag+[Ag⁺]f_Cl-[Cl^–]
= 0,78s0,780,1
= 1,610^-10,

s
= 1,610^-9/(0,78)²
= 2,610^-9
M, т. е. в 1,64 раза больше, чем без учета
ионной силы раствора. Солевой эффект
значительно меньше эффекта одноименного
иона.

Пример.
Растворимость Mg(OH)₂
равна 0,012 г/л. Найти K_S.

Решение.
М(Mg(OH)₂)
= 58 г/моль, s = 0,12г/л / 58г/моль =

=
2,0710^-4М.

Mg(OH)₂


Mg²⁺
+ 2OH^–

K_S
= [Mg²⁺][OH^–]²
= s(2s)²
= 4s³
= 4(2,0710^-4)³
= 3,610^-11.

Пример.
Выпадает ли осадок PbCl₂
при смешивании равных объемов растворов
0,1M Pb(NO₃)₂
и 0,1M NaCl, если K_S(PbCl₂)
=

=
1,610^-5.

Решение.
После смешивания растворов концентрации
ионов уменьшатся в два раза, т.е. имеем:
[Pb²⁺]
= [Na⁺]
= [Cl^–]
= 0,05M, а [NO₃^–]
= 0,1 M. Находим ионную силу раствора:

 =
1/2(0,052²
+ 0,11²
+ 0,051²
+ 0,051²)
= 0,2.

Находим
коэффициенты активности: f_Pb2+
= 0,24 и f_Cl–
= 0,70.

Имея
для PbCl₂Pb⁺²
+ 2Cl^–

K_S
PbCl2
= a_Pb2+a_Cl–²,
вычисляем величину a_Pb2+a_Cl–²
для нашего раствора:

a_Pb2+a_Cl–²
= f_Pb2+[Pb²⁺](f_Cl-[Cl^–])²
= 0,240,050,70²0,05²
= 1,4710^-5
, что меньше, чем ПР_PbCl2
(1,610^-5),
поэтому осадка не образуется.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В системе, состоящей из раствора и осадка, идут два процесса – растворение осадка и осаждение. Равенство скоростей этих двух процессов является условием равновесия.

Насыщенный раствор – раствор, который находится в равновесии с осадком.

Закон действия масс в применении к равновесию между осадком и раствором дает:

Поскольку [AgCl_тв] = const,

К • [AgCl_тв] = K_s(AgCl) = [Ag⁺] • [Cl?].

В общем виде имеем:

А_mB_n(тв.) ? mA⁺ⁿ + nB^-m

K_s(A_mB_n) = [А⁺ⁿ]^m • [В^-m]ⁿ.

Константа растворимости K_s
(или произведение растворимости ПР) – произведение концентраций ионов в насыщенном растворе малорастворимого электролита – есть величина постоянная и зависит лишь от температуры.

Растворимость малорастворимого вещества s может быть выражена в молях на литр. В зависимости от величины s вещества могут быть разделены на малорастворимые – s < 10^-4 моль/л, среднерастворимые – 10^-4 моль/л ? s ? 10^-2 моль/л и хорошо растворимые s >10^-2 моль/л.

Растворимость соединений связана с их произведением растворимости.

Условие осаждения и растворения осадка

В случае AgCl: AgCl ? Ag⁺ + Cl?

K_s
= [Ag⁺] • [CI?]:

а) условие равновесия между осадком и раствором: [Ag⁺] • [Cl?] = K_s.

б) условие осаждения: [Ag⁺] • [Cl?] > K_s; в ходе осаждения концентрации ионов уменьшаются до установления равновесия;

в) условие растворения осадка или существования насыщенного раствора: [Ag⁺] • [Cl?] < K_s; в ходе растворения осадка концентрация ионов увеличивается до установления равновесия.

Перейти к содержанию

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Теоретическое введение

Примеры решения задач

Задачи для самостоятельного решения

Теоретическое введение

В насыщенных водных растворах малорастворимых соединений устанавливается равновесие:

PbCl_{2(кристалл.)}  ↔Pb²⁺_{(насыщ.р-р)} + 2 Cl^–_{(насыщ.р-р)}

которое описывается константой равновесия, называемой произведением растворимости (ПР). Величина ПР равна:

ПР = [Pb²⁺] [Cl^–]²

Понятие ПР используется только при описании гетерогенных равновесий в насыщенных растворах малорастворимых сильных электролитов и их твердых фаз. Растворимость вещества равна его концентрации в насыщенном растворе. Насыщенный раствор находится в равновесии с кристаллической фазой.

ПР связано с изменением энергии Гиббса процесса уравнением:

ΔG^о_T = – RT lnПР                   (1)

которое используется для расчетов ПР по термодинамическим данным.

Чем меньше величина ПР, тем в меньшей степени осуществляется переход вещества в раствор. Так, PbCl₂ более растворим, чем PbI₂ (при 25^оС ПР(PbCl₂) = 1,6·10^–5, ПР(PbI₂) = 8,2× 10^–9), поэтому количественно осаждать ионы Pb²⁺ лучше в виде йодида, а не хлорида свинца.

Из определенной опытным путем растворимости соединения можно рассчитать ПР и, наоборот, зная ПР соединения, можно рассчитать его растворимость в воде.

Рассмотрим растворение малорастворимого электролита К_nА_m. В насыщенном растворе этого электролита имеет место равновесие:

К_nА_m (к) + aq ↔ n К^m+_{(насыщ.р-р)} + m A^n-_{(насыщ.р-р)} 

Произведение растворимости К_nА_m запишется в виде:

ПР = [К^m+]ⁿ [A^n-]^m             (2)

Если обозначить растворимость электролита буквой Р, то концентрации катионов и анионов в насыщенном растворе составят:

[К^m+] = nP; [A^n-] = mP

В результате для величины ПР получаем

ПР = [nP]ⁿ [mP]^m = nⁿ m^m P^n+m             (3)

Растворимость симметричных электролитов (содержащих равнозарядные ионы, например, AgCl, BaSO₄, AlPO₄) рассчитывается как корень квадратный из ПР.

Добавление в раствор малорастворимого электролита, например, AgCl, веществ, содержащих одноименные ионы, в частности, BaCl₂ или AgNO₃, приводит к уменьшению растворимости этого электролита.

Примеры решения задач

Задача 1. Рассчитайте произведение растворимости карбоната бария, если известно, что при 298 К в 100 мл его насыщенного раствора содержится 1,38× 10^-3 г BaCO₃.

Решение. М(BaCO₃) = 197 г/моль. Растворимость Р карбоната бария равна:

Р(BaCO₃) = 7·10^–5 моль/л.

В насыщенном растворе карбоната бария:

ВаСО₃(к) + aq ↔ Ba²⁺_{(насыщ.р-р)} + СO₃^2–_{(насыщ.р-р)}

концентрации ионов бария и карбонат-ионов равны. Следовательно,

[Ba²⁺] = [СO₃^2-] = 7× 10^–5 моль/л

Таким образом, растворимость Р карбоната бария равна 7·10^–5 моль/л. Величина ПР составит:

ПР = [Ba²⁺][СO₃^2–] = Р× Р = (7× 10^–5)² = 4,9× 10^–9.

Задача 2. Вычислите растворимость PbCl₂ в воде (моль/л и г/л), если произведение растворимости при 298 К для этой соли равно 1,6·10^–5.

Решение.

PbCl₂(к) + aq ↔ Pb²⁺_{(насыщ.р-р)} + 2 Cl^—_{(насыщ.р-р)}

Пусть Р (моль/л) — растворимость PbCl₂. Тогда концентрации ионов соли в растворе составят:

[Pb²⁺] = Р; [Cl^–] = 2[Pb²⁺] = 2P.

ПР(PbCl₂) = [Pb²⁺][ Cl^—]² = Р(2Р)² = 1,6× 10^-5.

Р(PbCl₂) = 278× 1,6× 10^–2 = 4,413 г/л, где 278 — М(PbCl₂) (г/моль)

В этой задаче следует обратить внимание на то, что в квадрат возводится удвоенное значение растворимости: (2Р)², т.е. растворимость умножается на стехиометрический коэффициент, и полученная величина возводится в степень, равную стехиометрическому коэффициенту.

Задача 3. Вычислите растворимость (моль/л) PbCl₂ в 0,1 М растворе KCl, если ПР (PbCl₂) = 1,6× 10^–5 при 298 К.

Решение. Суммарная концентрация хлорид-ионов составляет

[Cl^–] = (2Р + 0,1) моль/л

Хлорид-ионы образуются при диссоциации PbCl₂. В его насыщенном растворе:

PbCl₂(к) + aq ↔ Pb²⁺_{(насыщ.р-р)} + 2 Cl^—_{(насыщ.р-р)}

а также за счет диссоциации неассоциированного электролита KCl в его 0,1М растворе:

KCl → K⁺ + Cl^—

Запишем выражение для ПР(PbCl₂): ПР = Р (2Р + 0,1)². Слагаемым 2Р по сравнению со вторым слагаемым 0,1 можно пренебречь. Следовательно, ПР = Р(0,1)². Растворимость PbCl₂, равная концентрации ионов Pb²⁺, составляет Р = 1,6·10^–3 моль/л.

В воде растворимость PbCl₂ равна 1,6× 10^–2 моль/л (см. предыдущую задачу), в растворе KCl растворимость PbCl₂ уменьшилась и составила 1,6× 10^–3 моль/л.

Задача 4. Смешали 100 мл 0,01 н раствора CuCl₂ и 300 мл 0,1 н раствора Na₂S. Выпадет ли осадок cульфида меди, если ПР(CuS) = 6,3× 10^–36? Примите, что соли в растворе диссоциированы полностью и объем полученного раствора равен 400 мл.

Решение. Осадок выпадет, если [Сu²⁺][S^2–] > ПР(СuS), т.е. если произведение концентраций ионов Сu²⁺ и S^2– в растворе будет больше ПР, то раствор окажется пересыщенным и из него будет выпадать осадок.

Молярные концентрации растворов равны:

С_м (СuCl₂) = 1/2× 0,01 = 0,005M

С_м (Na₂S) = 1/2× 0,1 = 0,05M

До смешения растворов: [Сu²⁺] = 0,005 M, [S^2–] = 0,05М.

После смешения растворов концентрации ионов изменятся и станут равными:

[Сu²⁺] = 0,005× 0,1:0,4 = 0,00125M

[S^2–] = 0,05× 0,3:0,4 = 0,0375М

Следовательно, произведение концентраций ионов равно:

[Сu²⁺][S^2–] = 0,00125× 0,0375 = 4,7× 10^–5(моль/л)²

Поскольку [Сu²⁺][S^2–] = 4,7·10^–5 >> 6,3·10^–36, то осадок выпадет.

Задача 5. При 298 К произведение растворимости BaSO₄ равно 1× 10^–10. Определите, в каком объеме воды растворяется 1 г сульфата бария.

Решение.

BaSO₄(к) + aq ↔ Ba²⁺_{(насыщ.р-р)} + SO₄^2– _{(насыщ.р-р)}

Примем растворимость BaSO₄ за Р моль/л.

Растворимость BaSO₄ равна концентрации ионов Ba²⁺ и SO₄^2– в растворе: [Ba²⁺] = [SO₄^2–].

ПР(BaSO₄) = [Ba²⁺]·[SO₄^2–] = Р·Р = 1× 10^-10

Р = √ПР = 1× 10^-5 моль/л или 233× 10^–5 = 2,33× 10^–3 г/л,

где 233 — М(BaSO₄) (г/моль).

Следовательно, 1 г BaSO₄ растворяются в 1/2,33× 10^–3 = 429,2 л воды.

Задачи для самостоятельного решения

1. При некоторой температуре растворимость карбоната серебра равна 10^-4 моль/л. Рассчитайте ПР этой соли.

2. При некоторой температуре в 20 л воды растворяется 4×10^-3 моль фторида кальция. Рассчитайте ПР этой соли.

3. При некоторой температуре в 10 л воды растворяется 1,112 г хлорида свинца. Рассчитайте ПР этой соли.

4. При некоторой температуре рН насыщенного раствора гидроксида кальция составляет 13. Рассчитайте величину ПР этого основания.

5. ПР сульфата серебра при комнатной температуре составляет 5,02× 10^-5. Рассчитайте растворимость этой сли в воде. Какой объем воды понадобится для растворения 1 г этой соли?

6. Вычислить растворимость Ag₂SO₄ в воде (моль/л и г/л), если произведение растворимости при 298 К для этой соли равно 1,2× 10^–5.

7. Вычислить растворимость (моль/л) Ni(OH)₂ в 0,15 М растворе Ni(NO₃)₂, если ПР(Ni(OH)₂) = 1,2× 10^–16 при 298 К.

8. Смешали 150 мл 0,1 н раствора FeCl₂ и 350 мл 0,01 М раствора NaOH. Выпадет ли осадок Fe(OH)₂, если ПР(Fe(OH)₂) = 1,6× 10^–15. Принять, что объем полученного раствора равен 500 мл (осаждение гидроксида проводят в инертной атмосфере).

Произведение концентраций ионов равно: [Fe2+][OH–]2 = 0,015× 0,0072 = 7,35× 10–7(моль/л)2. Поскольку 7,35× 10–7 >> 1,6× 10–15, то осадок выпадет.

9. При 298 К произведение растворимости Ag₂CrO₄ равно 4,7× 10^–12. Определить, сколько г Ag₂CrO₄ можно растворить в 100 л воды при этой температуре.

10. При 298 К растворимость PbS в 0,015 М водном растворе K₂S равна 4,1× 10^–26 моль/л. Определить G^o₂₉₈ процесса растворения PbS.

Содержание

• Что такое $ K_s_p $?
• Как рассчитать $ K_s_p $?
• Написание выражений $ K_s_p $
• Пример 1
• Пример 2
• Пример 3
• Пример 4
• Решение для $ K_s_p $ с растворимостью
• Какие факторы влияют на $ K_s_p $?
• Температура
• Давление
• Размер молекулы
• Почему важен $ K_s_p $?
• Чтобы найти растворимость растворенных веществ
• Предсказать, образуется ли осадок в результате реакции
• Чтобы понять общий ионный эффект
• Таблица констант произведения растворимости
• Заключение: $ K_s_p $ Руководство по химии

Вы изучаете химию, но не совсем понимаете константу произведения растворимости или хотите узнать о ней больше? Не знаете, как рассчитать молярную растворимость по $ K_s_p $? Константа растворимости, или $ K_s_p $, является важной частью химии, особенно когда вы работаете с уравнениями растворимости или анализируете растворимость различных растворенных веществ. Когда у вас есть четкое представление о $ K_s_p $, на эти вопросы станет намного легче ответить!

В этом руководстве по $ K_s_p $ химии мы объясним определение химии $ K_s_p $, как решить его (с примерами), какие факторы на него влияют и почему это важно. Внизу этого руководства у нас также есть таблица со значениями $ K_s_p $ для длинного списка веществ, чтобы облегчить вам поиск значений констант растворимости.

Что такое $ K_s_p $?

$ K_s_p $ известен как константа растворимости или произведение растворимости. Это константа равновесия, используемая для уравнений, когда твердое вещество растворяется в жидком / водном растворе. Напоминаем, что растворенное вещество (то, что растворяется) считается растворимым, если более 1 грамма его можно полностью растворить в 100 мл воды.

$ K_s_p $ используется для растворенных веществ, которые слабо растворяется и не растворяется полностью в растворе. (Растворенное вещество нерастворимый если в растворе ничего или почти ничего не растворяется.) $ K_s_p $ представляет, сколько растворенного вещества растворяется в растворе.

Значение $ K_s_p $ варьируется в зависимости от растворенного вещества. Чем более растворимо вещество, тем выше его химическое значение $ K_s_p $. А что такое единицы $ K_s_p $? Собственно, единицы нет! Значение $ K_s_p $ не имеет единиц измерения, потому что молярные концентрации реагентов и продуктов различны для каждого уравнения. Это означало бы, что единица $ K_s_p $ будет отличаться для каждой проблемы и ее будет трудно решить, поэтому, чтобы упростить задачу, химики обычно вообще отбрасывают единицы $ K_s_p $. Как мило с их стороны!

Как рассчитать $ K_s_p $?

В этом разделе мы объясняем, как записывать химические выражения $ K_s_p $ и как найти значение $ K_s_p $. Для большинства уроков химии вам редко нужно будет решать значение $ K_s_p $; большую часть времени вы будете записывать выражения или использовать значения $ K_s_p $ для определения растворимости (что мы объясняем, как это сделать, в разделе «Почему важен $ K_s_p $»).

Написание выражений $ K_s_p $

Ниже приведено уравнение произведения растворимости, за которым следуют четыре химические задачи $ K_s_p $. так что вы можете увидеть, как записывать выражения $ K_s_p $.

Для реакции $ A_aB_b $ (s) ⇌ $ aA ^ b ^ {+} $ (aq) + $ bB ^ a ^} $ (aq)

Выражение растворимости: $ K_s_p $ = $ [A ^ b ^ {+}] ^ a $ $ [B ^ a ^ {] ^ b $

Первое уравнение известно как уравнение диссоциации, а второе – сбалансированное выражение $ K_s_p $.

Для этих уравнений:

• А и B представляют собой разные ионы и твердые вещества. В этих уравнениях они также называются «продуктами».
• а и б представляют коэффициенты, используемые для балансировки уравнения
• (водный) и (s) указывают, в каком состоянии находится продукт (водный или твердый, соответственно)
• Скобки обозначают молярную концентрацию. Итак, [AgCl] представляет собой молярную концентрацию AgCl.

Чтобы правильно писать выражения $ K_s_p $, вам необходимо хорошо знать химические названия, многоатомные ионы и заряды, связанные с каждым ионом. Кроме того, в этих уравнениях важно знать, что каждая концентрация (представленная квадратными скобками) возводится в степень своего коэффициента в сбалансированном выражении $ K_s_p $.

Давайте посмотрим на несколько примеров.

Пример 1

$ PbBr_2 $ (s) ⇌ $ Pb ^ 2 ^ {+} $ (aq) + $ 2Br ^ {¯} $ (aq)

$ K_s_p $ = $ [Pb ^ 2 ^ {+}] $ $ [Br¯] ^ 2 $

В этой проблеме не забудьте возвести Br в квадрат в уравнении $ K_s_p $. Вы делаете это из-за коэффициента «2» в уравнении диссоциации.

Пример 2

CuS (s) ⇌ $ Cu ^ {+} $ (водн.) + S¯ (водн.)

$ K_s_p $ = [$ Cu ^ {+} $] [S¯]

Пример 3

$ Ag_2CrO_4 $ (s) ⇌ 2 $ Ag ^ {+} $ (водн.) + $ CrO_4 ^ 2 ^} $ (водн.)

$ K_s_p $ = $ [Ag ^ {+}] ^ 2 $ [$ CrO_4 ^ 2 $]

Пример 4

$ Cu_3 $ $ (PO_4) ^ 2 $ (s) ⇌ $ 3Cu ^ 2 ^ {+} $ (водн.) + $ 2PO_4 ^ 3 ^ {¯} $ (водн.)

$ K_s_p $ = $ [Cu ^ 2 ^ {+}] ^ 3 $ [$ PO_4 ^ 3 ^ ¯ $] $ ^ 2 $

Решение для $ K_s_p $ с растворимостью

Чтобы вычислить значение для $ K_s_p $, вам необходимо иметь значения молярной растворимости или уметь их найти.

Вопрос: Определите $ K_s_p $ AgBr (бромид серебра), учитывая, что его молярная растворимость составляет 5,71 x $ 10 ^ {¯} ^ 7 $ моль на литр.

Во-первых, нам нужно записать два уравнения.

AgBr (s) ⇌ $ Ag ^ {+} $ (aq) + $ Br ^ {¯} $ (aq)

$ K_s_p $ = [$ Ag ^ {+} $] [$ Br ^ {¯} $]

Теперь, поскольку в этой задаче мы решаем фактическое значение $ K_s_p $, мы подставляем полученные значения растворимости:

$ K_s_p $ = (5,71 x $ 10 ^ {¯} ^ 7 $) (5,71 x $ 10 ^ {¯} ^ 7 $) = 3,26 x $ 10 ^ {¯} ^ 13 $

Значение $ K_s_p $ равно 3,26 x $ 10 ^ {¯} ^ 13 $.

Какие факторы влияют на $ K_s_p $?

В этом разделе мы обсудим основные факторы, влияющие на значение константы растворимости.

Температура

Большинство растворенных веществ становятся более растворимыми в жидкости при повышении температуры. Если вам нужны доказательства, посмотрите, насколько хорошо растворимый кофе смешивается в чашке с холодной водой по сравнению с чашкой горячей воды. Температура влияет на растворимость как твердых веществ, так и газов. но не было обнаружено определенного влияния на растворимость жидкостей.

Давление

Давление также может влиять на растворимость, но только для газов, находящихся в жидкостях. Закон Генри гласит, что растворимость газа прямо пропорциональна парциальному давлению газа.

Закон Генри записан как п=kc, куда

• п парциальное давление газа над жидкостью
• k константа закона Генри
• c это концентрация газа в жидкости

Закон Генри показывает, что по мере уменьшения парциального давления концентрация газа в жидкости также уменьшается, что, в свою очередь, снижает растворимость. Таким образом, меньшее давление приводит к меньшей растворимости, а большее давление приводит к большей растворимости.

Вы можете увидеть закон Генри в действии, если откроете банку газировки. Когда баллон закрыт, газ находится под большим давлением, и появляется много пузырьков, потому что большая часть газа растворяется. Когда вы открываете банку, давление снижается, и, если вы оставите газировку стоять достаточно долго, пузырьки в конечном итоге исчезнут, потому что растворимость уменьшилась, и они больше не растворяются в жидкости (они пузырились из напитка) .

Размер молекулы

Как правило, растворенные вещества с более мелкими молекулами более растворимы, чем вещества с частицами молекул. Растворителю легче окружать более мелкие молекулы, поэтому эти молекулы могут растворяться быстрее, чем более крупные.

Почему важен $ K_s_p $?

Почему имеет значение константа растворимости? Ниже приведены три основных случая, когда вам нужно будет использовать химию $ K_s_p $.

Чтобы найти растворимость растворенных веществ

Хотите знать, как рассчитать молярную растворимость по $ K_s_p $? Зная значение $ K_s_p $, вы можете определить растворимость различных растворенных веществ. Вот пример: Значение $ K_s_p $ сульфата серебра $ Ag_2SO_4 $ составляет 1,4 × 10 $ ^ } ^ 5 $. Определите молярную растворимость.

Сначала нам нужно написать уравнение диссоциации: $ K_s_p $ = $ [Ag ^ {+}] ^ 2 $ $ [SO_4 ^ 2] $

Затем мы вставляем значение $ K_s_p $, чтобы создать алгебраическое выражение.

1,4 × $ 10 ^ { ^ 5 $ = $ (2x) ^ 2 $ $ (x) $

1,4 × $ 10 ^ } ^ 5 $ = $ 4x ^ 3 $

$ x $ = [$ SO_4 ^ 2 $] = 1,5x $ 10 ^ {^ 2 $ M

$ 2x $ = [$ Ag ^ {+} $] = 3,0x $ 10 ^} ^ 2 $ M

Предсказать, образуется ли осадок в результате реакции

Когда мы знаем значение $ K_s_p $ растворенного вещества, мы можем выяснить, произойдет ли осадок, если раствор его ионов будет смешан. Ниже приведены два правила, определяющих образование осадка.

• Ионный продукт> $ K_s_p $, тогда выпадет осадок
• Ионный продукт <$ K_s_p $, тогда осаждения не будет

Чтобы понять общий ионный эффект

$ K_s_p $ также является важной частью общего ионного эффекта. Эффект общего иона заключается в том, что при смешивании двух растворов с общим ионом первым выпадает растворенное вещество с меньшим значением $ K_s_p $.

Например, предположим, что в раствор добавлены BiOCl и CuCl. Оба содержат ионы $ Cl ^ {$. Значение $ K_s_p $ для BiOCl составляет 1,8 × $ 10 ^ { ^ 31 $, а значение $ K_s_p $ для CuCl составляет 1,2 × $ 10 ^ {-} ^ 6 $. BiOCl имеет меньшее значение $ K_s_p $, поэтому он будет выпадать в осадок раньше, чем CuCl.

Таблица констант произведения растворимости

Ниже приведена диаграмма, показывающая значения $ K_s_p $ для многих распространенных веществ. Значения $ K_s_p $ приведены для веществ с температурой около 25 градусов Цельсия, что является стандартным. Поскольку значения $ K_s_p $ настолько малы, в их значениях могут быть незначительные различия в зависимости от того, какой источник вы используете. Данные в этой диаграмме получены на химическом факультете Университета Род-Айленда.

Вещество	Формула	$ K_s_p $ Значение
Гидроксид алюминия	$ Al (OH) _3 $	1.3×$10^{–}^33$
Фосфат алюминия	$ AlPO_4 $	6.3×$10^{–}^19$
Карбонат бария	$ BaCO_3 $	5.1×$10^{–}^9$
Хромат бария	$ BaCrO_4 $	1.2×$10^{–}^10$
Фторид бария	$ BaF_2 $	1.0×$10^{–}^6$
Гидроксид бария	$ Ba (OH) _2 $	5×$10^{–}^3$
Сульфат бария	$ BaSO_4 $	1.1×$10^{–}^10$
Сульфит бария	$ BaSO_3 $	8×$10^{–}^7$
Тиосульфат бария	$ BaS_2O_3 $	1.6×$10^{–}^6$
Висмутилхлорид	$ BiOCl $	1.8×$10^{–}^31$
Гидроксид висмутила	$ BiOOH $	4×$10^{–}^10$
Карбонат кадмия	$ CdCO_3 $	5.2×$10^{–}^12$
Гидроксид кадмия	$ Cd (OH) _2 $	2.5×$10^{–}^14$
Оксалат кадмия	$ CdC_2O_4 $	1.5×$10^{–}^8$
Сульфид кадмия	$ CdS $	8×$10^{–}^28$
Карбонат кальция	$ CaCO_3 $	2.8×$10^{–}^9$
Хромат кальция	$ CaCrO_4 $	7.1×$10^{–}^4$
Фторид кальция	$ CaF_2 $	5.3×$10^{–}^9$
Гидрофосфат кальция	$ CaHPO_4 $	1×$10^{–}^7$
Гидроксид кальция	$ Ca (OH) _2 $	5.5×$10^{–}^6$
Оксалат кальция	$ CaC_2O_4 $	2.7×$10^{–}^9$
Фосфат кальция	$ Ca_3 (PO_4) _2 $	2.0×$10^{–}^29$
Сульфат кальция	$ CaSO_4 $	9.1×$10^{–}^6$
Сульфит кальция	$ CaSO_3 $	6.8×$10^{–}^8$
Гидроксид хрома (II)	$ Cr (OH) _2 $	2×$10^{–}^16$
Гидроксид хрома (III)	$ Cr (OH) _3 $	6.3×$10^{–}^31$
Карбонат кобальта (II)	$ CoCO_3 $	1.4×$10^{–}^13$
Гидроксид кобальта (II)	$ Co (OH) _2 $	1.6×$10^{–}^15$
Гидроксид кобальта (III)	$ Co (OH) _3 $	1.6×$10^{–}^44$
Сульфид кобальта (II)	$ CoS $	4×$10^{–}^21$
Хлорид меди (I)	$ CuCl $	1.2×$10^{–}^6$
Цианид меди (I)	$ CuCN $	3.2×$10^{–}^20$
Иодид меди (I)	$ CuI $	1.1×$10^{–}^12$
Арсенат меди (II)	$ Cu_3 (AsO_4) _2 $	7.6×$10^{–}^36$
Карбонат меди (II)	$ CuCO_3 $	1.4×$10^{–}^10$
Хромат меди (II)	$ CuCrO_4 $	3.6×$10^{–}^6$
Ферроцианид меди (II)	$ Cu [Fe (CN) _6] $	1.3×$10^{–}^16$
Гидроксид меди (II)	$ Cu (OH) _2 $	2.2×$10^{–}^20$
Сульфид меди (II)	$ CuS $	6×$10^{–}^37$
Карбонат железа (II)	$ FeCO_3 $	3.2×$10^{–}^11$
Гидроксид железа (II)	$ Fe (OH) _2 $	8.0$10^{–}^16$
Сульфид железа (II)	$ FeS $	6×$10^{–}^19$
Арсенат железа (III)	$ FeAsO_4 $	5.7×$10^{–}^21$
Ферроцианид железа (III)	$ Fe_4 [Fe (CN) _6] _3 $	3.3×$10^{–}^41$
Гидроксид железа (III)	$ Fe (OH) _3 $	4×$10^{–}^38$
Фосфат железа (III)	$ FePO_4 $	1.3×$10^{–}^22$
Свинец (II) арсенат	$ Pb_3 (AsO_4) _2 $	4×$10^{–}^6$
Азид свинца (II)	$ Pb (N_3) _2 $	2.5×$10^{–}^9$
Бромид свинца (II)	$ PbBr_2 $	4.0×$10^{–}^5$
Карбонат свинца (II)	$ PbCO_3 $	7.4×$10^{–}^14$
Хлорид свинца (II)	$ PbCl_2 $	1.6×$10^{–}^5$
Хромат свинца (II)	$ PbCrO_4 $	2.8×$10^{–}^13$
Свинец (II) фторид	$ PbF_2 $	2.7×$10^{–}^8$
Гидроксид свинца (II)	$ Pb (OH) _2 $	1.2×$10^{–}^15$
Иодид свинца (II)	$ PbI_2 $	7.1×$10^{–}^9$
Сульфат свинца (II)	$ PbSO_4 $	1.6×$10^{–}^8$
Сульфид свинца (II)	$ PbS $	3×$10^{–}^28$
Карбонат лития	$ Li_2CO_3 $	2.5×$10^{–}^2$
Литий фторид	$ LiF $	3.8×$10^{–}^3$
Фосфат лития	$ Li_3PO_4 $	3.2×$10^{–}^9$
Фосфат магния-аммония	$ MgNH_4PO_4 $	2.5×$10^{–}^13$
Арсенат магния	$ Mg_3 (AsO_4) _2 $	2×$10^{–}^20$
Карбонат магния	$ MgCO_3 $	3.5×$10^{–}^8$
Фторид магния	$ MgF_2 $	3.7×$10^{–}^8$
Гидроксид магния	$ Mg (OH) _2 $	1.8×$10^{–}^11$
Оксалат магния	$ MgC_2O_4 $	8.5×$10^{–}^5$
Фосфат магния	$ Mg_3 (PO_4) _2 $	1×$10^{–}^25$
Карбонат марганца (II)	$ MnCO_3 $	1.8×$10^{–}^11$
Гидроксид марганца (II)	$ Mn (OH) _2 $	1.9×$10^{–}^13$
Сульфид марганца (II)	$ MnS $	3×$10^{–}^14$
Бромид ртути (I)	$ Hg_2Br_2 $	5.6×$10^{–}^23$
Хлорид ртути (I)	$ Hg_2Cl_2 $	1.3×$10^{–}^18$
Иодид ртути (I)	$ Hg_2I_2 $	4.5×$10^{–}^29$
Сульфид ртути (II)	$ HgS $	2×$10^{–}^53$
Карбонат никеля (II)	$ NiCO_3 $	6.6×$10^{–}^9$
Гидроксид никеля (II)	$ Ni (OH) _2 $	2.0×$10^{–}^15$
Сульфид никеля (II)	$ NiS $	3×$10^{–}^19$
Фторид скандия	$ ScF_3 $	4.2×$10^{–}^18$
Гидроксид скандия	$ Sc (OH) _3 $	8.0×$10^{–}^31$
Ацетат серебра	$ Ag_2CH_3O_2 $	2.0×$10^{–}^3$
Арсенат серебра	$ Ag_3AsO_4 $	1.0×$10^{–}^22$
Азид серебра	$ AgN_3 $	2.8×$10^{–}^9$
Бромид серебра	$ AgBr $	5.0×$10^{–}^13$
Хлорид серебра	$ AgCl $	1.8×$10^{–}^10$
Хромат серебра	$ Ag_2CrO_4 $	1.1×$10^{–}^12$
Цианид серебра	$ AgCN $	1.2×$10^{–}^16$
Йодат серебра	$ AgIO_3 $	3.0×$10^{–}^8$
Йодид серебра	$ AgI $	8.5×$10^{–}^17$
Нитрит серебра	$ AgNO_2 $	6.0×$10^{–}^4$
Сульфат серебра	$ Ag_2SO_4 $	1.4×$10^{–}^5$
Сульфид серебра	$ Ag_2S $	6×$10^{–}^51$
Сульфит серебра	$ Ag_2SO_3 $	1.5×$10^{–}^14$
Тиоцианат серебра	$ AgSCN $	1.0×$10^{–}^12$
Карбонат стронция	$ SrCO_3 $	1.1×$10^{–}^10$
Хромат стронция	$ SrCrO_4 $	2.2×$10^{–}^5$
Фторид стронция	$ SrF_2 $	2.5×$10^{–}^9$
Сульфат стронция	$ SrSO_4 $	3.2×$10^{–}^7$
Бромид таллия (I)	$ TlBr $	3.4×$10^{–}^6$
Хлорид таллия (I)	$ TlCl $	1.7×$10^{–}^4$
Иодид таллия (I)	$ TlI $	6.5×$10^{–}^8$
Гидроксид таллия (III)	$ Tl (OH) _3 $	6.3×$10^{–}^46$
Гидроксид олова (II)	$ Sn (OH) _2 $	1.4×$10^{–}^28$
Сульфид олова (II)	$ SnS $	1×$10^{–}^26$
Карбонат цинка	$ ZnCO_3 $	1.4×$10^{–}^11$
Гидроксид цинка	$ Zn (OH) _2 $	1.2×$10^{–}^17$
Оксалат цинка	$ ZnC_2O_4 $	2.7×$10^{–}^8$
Фосфат цинка	$ Zn_3 (PO_4) _2 $	9.0×$10^{–}^33$
Сульфид цинка	$ ZnS $	2×$10^{–}^25$

Заключение: $ K_s_p $ Руководство по химии

Что такое $ K_s_p $ в химии? Константа произведения растворимости, или $ K_s_p $, является важным аспектом химии при изучении растворимости различных растворенных веществ. $ K_s_p $ представляет, сколько растворенного вещества растворяется в растворе, и чем более растворимо вещество, тем выше химическое значение $ K_s_p $.

Чтобы вычислить константу произведения растворимости, вам сначала нужно написать уравнение диссоциации и сбалансированное выражение $ K_s_p $, а затем подставить молярные концентрации, если они вам известны.

На константу растворимости могут влиять температура, давление и размер молекул, и это важно для определения растворимости, прогнозирования образования осадка и понимания общего ионного эффекта.

Есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделитесь этой статьей!