Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.
Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти площадь квадрата можно найти по сторонам, площадь ромба легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:
Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.
Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий. Подставим данные:
На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:
Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см. Для начала найдем полупериметр:
используем найденное значение для расчета площади:
Площадь четырехугольника, заданного координатами
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
Дан квадрат ABCD, расположенный в системе координат XY. Найти площадь фигуры, если координаты вершин A(2;10); B(10;8); C(8;0); D(0;2).
Мы знаем, что все стороны фигуры равны, и формула площади квадрата находится по формуле:
Найдем одну из сторон, к примеру, AB:
Подставим значения в формулу:
Знаем, что все стороны одинаковые. Подставляем значение в формулу расчета площади:
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так: p={(a+b+c+d)}/2
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:
S=sqrt{(p-a)(p-b)(p-c)(p-d)}
Иконка карандаша 24×24Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см. Для начала найдем полупериметр:
p={(5+4+3+6)}/2=18/2=9 cm
используем найденное значение для расчета площади:
S=sqrt{(9-5)(9-4)(9-3)(9-6)}=sqrt{4*5*6*3}=sqrt{360}=19{cm}^2
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  |
S = ab | |
 |
|||
 |
|||
| Параллелограмм |  |
||
 |
|||
 |
|||
| Квадрат |  |
S = a 2 | |
 |
S = 4r 2 | ||
 |
|||
 |
|||
| Ромб |  |
||
 |
|||
 |
|||
 |
|||
 |
|||
| Трапеция |  |
||
 |
S = m h | ||
 |
|||
 |
|||
| Дельтоид |  |
S = ab sin φ | |
 |
 |
||
 |
|||
 |
|||
| Произвольный выпуклый четырёхугольник |  |
||
| Вписанный четырёхугольник |  |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
 |
|
 |
|
 |
|
| Параллелограмм | |
 |
|
 |
|
 |
|
| Квадрат | |
 |
S = a 2
где |
 |
S = 4r 2 |
 |
|
 |
|
| Ромб | |
 |
|
 |
|
 |
|
 |
|
 |
|
| Трапеция | |
 |
|
 |
|
 |
|
 |
|
| Дельтоид | |
 |
|
 |

где |
 |
|
 |
|
| Произвольный выпуклый четырёхугольник | |
 |
|
| Вписанный четырёхугольник | |
 |
| Прямоугольник |
 |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Квадрат
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
Ромб
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
Дельтоид
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
Произвольный выпуклый четырёхугольник
φ – любой из четырёх углов между ними
Вписанный четырёхугольник
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Формулы вычисления площади произвольного четырёхугольника
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов – квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео
Разобраться в этой теме вам поможет видео.
[spoiler title=”источники:”]
http://www.resolventa.ru/spr/planimetry/sqf.htm
http://liveposts.ru/articles/education-articles/matematika/formuly-vychisleniya-ploshhadi-proizvolnogo-chetyryohugolnika
[/spoiler]
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
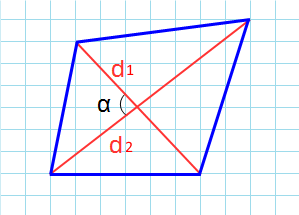
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
d1, d2 – диагонали; α – угол между диагоналями.
Через стороны и противолежащие углы
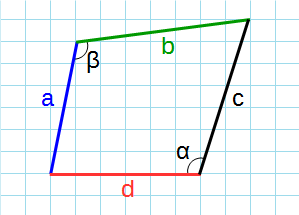
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
Площадь вписанного четырехугольника в окружность
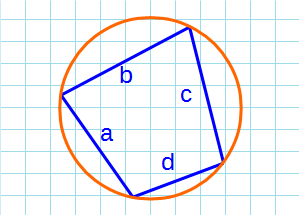
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через радиус
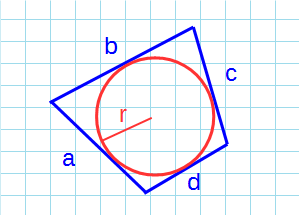
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
p – полупериметр четырехугольника; r – радиус вписанной окружности; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через стороны и противолежащие углы
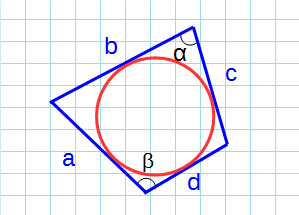
Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Содержание:
- Определения и соглашения
- Нахождение площади четырёхугольника различными способами и методами
- Заключение
- Видео
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
S = ((a + b+ c + d)/2)*r
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов – квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео
Разобраться в этой теме вам поможет видео.










































 Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.