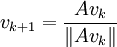Свойства собственных векторов линейных операторов (преобразований)
1. Собственные векторы линейного преобразования, принадлежащие различным собственным значениям, линейно независимы.
Аналогичное утверждение было доказано для собственных векторов матрицы (см. свойство 1).
2. Все собственные векторы линейного преобразования , принадлежащие одному собственному значению, совместно с нулевым вектором образуют линейное подпространство, инвариантное относительно преобразования
. Такое линейное подпространство называется собственным для преобразования
.
В самом деле, условие (9.5) можно записать в виде , где
— тождественное преобразование. Множество векторов
, удовлетворяющих последнему равенству, составляет ядро линейного преобразования
, т.е. является линейным подпространством
(собственное подпространство, отвечающее собственному значению
). Покажем, что это подпространство инвариантно относительно преобразования
. Действительно, любой вектор
в силу равенств
отображается в коллинеарный ему вектор
, также принадлежащий
.
3. Для собственного значения линейного преобразования
существует цепочка инвариантных подпространств
(9.8)
где ;
— некоторое натуральное число
.
Все перечисленные в цепочке (9.8) множества , являются линейными подпространствами по свойству ядра линейного преобразования. Каждое из подпространств
инвариантно относительно преобразования
, поскольку для любого вектора
его образ
, так как в силу перестановочности многочленов от одного и того же линейного преобразования (см. пункт 2 замечаний 9.3)
так как согласно определения ядра оператора.
Докажем включение . Если
, то
, при этом очевидно, что
то есть
Остальные включения доказываются аналогично.
Из цепочки (9.8) “расширяющихся” подпространств следует, что их размерности не убывают
поэтому в силу конечномерности пространства существует такое
, что
, т.е.
. Покажем, что дальнейшего “увеличения” подпространств нет, т.е.
для любого натурального
. Предположим противное. Пусть
и для некоторого
пространства не совпадают:
, то есть существует вектор
, который не принадлежит пространству
. Обозначим
. Тогда, с одной стороны,
, так как
, поскольку
. С другой стороны,
, так как
, поскольку
. Следовательно, и
и
одновременно, что противоречит предположению
.
Таким образом, в цепочке (9.8) размерности пространств , возрастают. Поэтому
.
Корневым подпространством линейного преобразования для собственного значения
называется линейное подпространство
с наименьшим натуральным показателем
, для которого
.
4. Если — собственное значение линейного преобразования
, то пространство
можно представить в виде прямой суммы
, где
— корневое подпространство, а
— инвариантное относительно
подпространство, в котором нет собственных векторов, принадлежащих собственному значению
.
В самом деле, покажем, что пересечение этих подпространств есть нулевой вектор: . Выберем вектор
. Так как вектор
, то существует такой вектор
, что
. Поскольку
, то
. Тогда
. Следовательно, вектор
, но
, так как
— корневое подпространство. Значит,
то есть
По теореме 9.1 о размерности ядра и образа получаем, что . Следовательно, пространство
можно представить в виде прямой суммы подпространств
(см. признаки прямых сумм подпространств).
Докажем, что в нет собственных векторов, принадлежащих собственному значению
. Действительно, пусть
— собственный вектор, соответствующий собственному значению
. Тогда
и в силу (9.8)
. Подпространство
имеет с
только один общий вектор (нулевой). Поэтому
, так как
. Инвариантность подпространства
следует из перестановочности операторов
и
(см. пункт 2 замечаний 9.3). В самом деле, для любого вектора
существует прообраз
. Поэтому в силу перестановочности операторов
поскольку и
. Таким образом, инвариантность подпространства
доказана, так как
.
Теорема (9.5) о разложении пространства в сумму корневых подпространств
Если все различные корни характеристического уравнения линейного преобразования
являются его собственными значениями, то пространство
можно разложить в прямую сумму инвариантных (корневых) подпространств:
(9.9)
где — корневое подпространство, соответствующее собственному значению
.
В самом деле, по свойству 4 можно “отщепить” корневое подпространство , т.е. представить пространство
в виде прямой суммы инвариантных подпространств
, причем в
нет собственных векторов, принадлежащих собственному значению
. В пространстве
определено сужение
преобразования
. Применяя свойство 4 к сужению
, аналогичным образом можно “отщепить” корневое подпространство
, т.е. представить пространство
в виде прямой суммы инвариантных подпространств:
. Этот процесс следует продолжить до тех пор, пока не исчерпаются все корни характеристического уравнения.
Следствие. Если все различные корни характеристического уравнения линейного преобразования
являются его собственными значениями, то существует базис пространства
, в котором матрица
линейного преобразования имеет блочно-диагональный вид
где — матрицы сужений
, преобразования
на корневые подпространства.
Согласно следствию из теоремы 9.2, такой базис можно получить, записывая последовательно базисы корневых подпространств (9.9).
Алгебраическая и геометрическая кратности собственных значений
Алгебраической кратностью собственного значения линейного оператора (преобразования)
называется кратность корня
характеристического многочлена
(или, что то же самое, кратность корня характеристического уравнения
).
Геометрической кратностью собственного значения линейного оператора (преобразования)
называется размерность собственного подпространства
, соответствующего этому собственному значению.
Теорема 9.6 о кратностях собственных значений оператора. Геометрическая кратность собственного значения не превосходит его алгебраической кратности.
Представим пространство в виде прямой суммы
(см. свойство 4) и обозначим
. Выбрав базис пространства
, дополним его до базиса всего пространства. В этом базисе, согласно следствию теоремы 9.5, матрица
преобразования
будет иметь блочно-диагональный вид
, где квадратная матрица
порядка
является матрицей сужения
преобразования
на подпространство
, а матрица
является матрицей сужения
. Характеристический многочлен матрицы
имеет вид (см. определитель блочно-диагональной матрицы)
где — многочлены степеней
и
соответственно. Так как сужение
не имеет собственных значений, отличных от
, то
, в силу того, что
и основной теоремы алгебры. Поскольку сужение
не имеет собственных векторов, принадлежащих собственному значению
, то
. Следовательно,
-алгебраическая кратность собственного значения
. Тогда утверждение теоремы следует из включения (9.8):
, так как
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
|
|
Найти собственные значения и корневые подпространства A
|
|
14/09/16 |
Оператор задан матрицей: C собственными значениями проблем нет: И соответственно: Как теперь найти корневые подпространства?
|
|
|
|
|
Xaositect |
Re: Найти собственные значения и корневые подпространства A
|
||
06/10/08 |
А что такое корневое подпространство?
|
||
|
|
|||
|
tremor |
Re: Найти собственные значения и корневые подпространства A
|
|
14/09/16 |
А что такое корневое подпространство? Ну в каких-то книжках его еще собственным называют, если я правильно помню.
|
|
|
|
|
Xaositect |
Re: Найти собственные значения и корневые подпространства A
|
||
06/10/08 |
Ну в каких-то книжках его еще собственным называют, если я правильно помню. Нет, корневые и собственные подпространства – это разные вещи, а я Вас просил привести определение.
|
||
|
|
|||
|
tremor |
Re: Найти собственные значения и корневые подпространства A
|
|
14/09/16 |
Ну в каких-то книжках его еще собственным называют, если я правильно помню. Нет, корневые и собственные подпространства – это разные вещи, а я Вас просил привести определение. Ядро линейного оператора вида Где
|
|
|
|
|
Xaositect |
Re: Найти собственные значения и корневые подпространства A
|
||
06/10/08 |
Это собственные подпространства, и найти их легко – надо решить уравнения Корневые подпространства – это немного посложнее. Вы по какому учебнику учитесь?
|
||
|
|
|||
|
tremor |
Re: Найти собственные значения и корневые подпространства A
|
|
14/09/16 |
Это собственные подпространства, и найти их легко – надо решить уравнения Корневые подпространства – это немного посложнее. Вы по какому учебнику учитесь? По Ильину-Позняку (потому что физфак)
|
|
|
|
|
Xaositect |
Re: Найти собственные значения и корневые подпространства A
|
||
06/10/08 |
|||
|
|
|||
|
tremor |
Re: Найти собственные значения и корневые подпространства A
|
|
14/09/16 |
Вместо
|
|
|
|
|
Xaositect |
Re: Найти собственные значения и корневые подпространства A
|
||
06/10/08 |
|||
|
|
|||
|
tremor |
Re: Найти собственные значения и корневые подпространства A
|
|
14/09/16 |
Да. Да, все сходится, ну а кратность характеристического многочлена как я понял из экспериментов должна совпадать с кратностью собственного значения которое подставляем.
|
|
|
|
|
Brukvalub |
Re: Найти собственные значения и корневые подпространства A
|
||
01/03/06 |
кратность характеристического многочлена Что это за термин?
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Определение.
Подпространство линейного пространства
называетсяинвариантным относительно
линейного оператора ,
если линейный операторэлементы подпространства отображает
в элементы этого же подпространства.
Теорема. Множество
всех корневых векторов линейного
пространстваV/K,
принадлежащих одному собственному
значению линейного оператора,
образует подпространство линейного
пространстваV, инвариантное
относительно линейного оператора.
Доказательство. Для
доказательства первой части теоремы
достаточно проверить все аксиомы
линейного пространства.
Если (-)hc=, то
(-)h
(с)
=((-)hc)
=()
=,
т.е. еслис– корневой вектор, то
ис
– тоже корневой вектор, принадлежащий
тому же собственному значению. ■
Обозначим через
множество всех корневых векторов
линейного пространстваV/K,
принадлежащих собственному значениюлинейного оператора.
– корневое подпространство,
принадлежащее собственному значениюлинейного оператора.
Теорема. Пусть1,
… ,m
– все попарно различные собственные
значения линейного оператора,
действующего в линейном пространствеV/KТогда
линейное пространствоVесть прямая сумма корневых подпространств:
V=
…
(2)
Доказательство. Так
как1,
… ,m
– все различные собственные значения
линейного оператора,
то его характеристический многочлен
имеет вид:
(х) = (х-1)… (x-m)
и
многочлены
1(х) = (x-2)(x-3)
… (x-m)
,
2(х) = (x -1)(x-3)
… (x-m)
,
m(х) = (x
-1)(x-m
–2)(x-m)
взаимно простые. По
теореме о линейном представлении НОД
существуют многочлены v1(x),
…,vm(x)
изKx,
для которых
1(x)v1(x)
+ … +m(x)vm(x)
= 1 или1()v1()
+ … +m()vm()
=.
Для любого элемента
a из линейного
пространстваV
получим
1()v1()a
+
+ m()vm()a
= a.
Введем
обозначения:
1()v1()a
= a1,
, m()vm()a
= am.
Тогда a
= a1+
… +am.
Так как (-i)i
()
=(),
а по теореме Гамильтона-Кэли линейный
оператор()
– нулевой, то
(
– i
)ai
= ,
т.е. ,
1
i
m
V
+
… +
V=
+ … +
.
Предположим, что y1
+ … +ym
=,
yi
,
1
i
m. Тогдау1
=,
…, ym
=.
В противном случае получаем противоречие
с тем, что ненулевые векторыy1,, ym
линейно независимы. Из единственности
представления нулевого вектора в виде
суммы элементов из подпространств
следует, что сумма прямая. ■
Замечание. Из
доказательства следует, что если
(х) = (х-1)… (x-m)
,
то
V = Ker(
–1)
Ker(
–2)
Ker(
–m).
Упражнения
-
Докажите, что сумма
и пересечение подпространств, инвариантных
относительно линейного оператора ,
также инвариантны относительно. -
Докажите, что ядро
и образ линейного оператора, действующего
в линейном пространстве, инвариантны
относительно . -
Докажите, что
линейные операторы
и –
имеют одни и те же инвариантные
подпространства,
–любое число. -
Докажите, что если
линейный оператор
невырожден, то
и -1
имеют одни и те же инвариантные
подпространства. -
Пусть с–
корневой вектор линейного оператора, принадлежащий
собственному значению
и имеющий высотуh
> 0. Докажите, что линейная оболочка
для векторов
(
- )h
–1c,
( -
)h
–2
c, …, (
- )c
является
инвариантным подпространством линейного
оператора .
-
Докажите, что
корневое подпространство линейного
оператора является
инвариантным подпространством любого
линейного оператора, перестановочного
с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение: Вектор X¹θ пространства V называется корневым вектором линейного оператора , если
и
(*).
Таким образом, в частности всякий собственный вектор является корневым (M-1). Наименьшее (min) M, при котором выполняется равенство (*) называется высотой корневого вектора Х.
Утверждения:
1) Cобственный вектор – корневой вектор высоты 1 (M=1).
2) Если справедливо , то λ – собственное значение оператора φ.
Доказательство:
Пусть Х– корневой вектор высоты M, тогда , при этом
, тогда
отсюда У – собственный вектор, отвечающий собственному значению λ. #
Говорят, что корневой вектор Х принадлежит собственному значению λ.
Определение: Подпространство – корневой вектор оператора φ, отвечающий собственному значению λ или X = θ} называется корневым подпространством.
Теорема 1: (о корневом подпространстве).
Корневое подпространство является подпространством пространства V.
Подпространство инвариантно относительно любого оператора
, где
.
Доказательство:
1) Нулевой элемент по определению
2) Если , то
3) Если и
, то
если
, отсюда
, т. е.
– подпространство пространства V.
Докажем, что инвариантно относительно любого оператора
, где
.
Пусть , тогда
, обозначим
. Запишем

– инвариантно относительно любого оператора
, кроме того
#
Определение: Пусть V1 подпространство пространства V, инвариантное относительно линейного оператора φ, т. е. . В этом случае определен оператор
, действующий по формуле
. Линейный оператор
называется ограничением оператора φ на инвариантном подпространстве V1 (по другому оператор φ индуцирует преобразование
На инвариантном подпространстве V1).
Замечание:
1) Если V1 и V2 – подпространства пространства V, инвариантные относительно линейного оператора φ и , то в базисе
пространства V матрица
оператора φ имеет вид:

,
.
,
– матрицы оператора φ, инвариантные на V1 и V2 соответственно.
2) Если же V1 – подпространство пространства V, то инвариантное относительно линейного оператора φ и других подпространств нет, то дополняя базис подпространства V1 векторами
до базиса пространства V, получим матрицу
оператора φ в пространстве V:

Лемма 1: Если , то
. Иначе если
и
, то
если
(здесь λ – собственное значение оператора φ).
Доказательство:
Пусть , т. е.
и
Тогда и т. к.
, то
#
Пусть – различные собственные значения оператора φ и
,
,…,
– соответствующие им корневые подпространства.
Утверждение: Сумма корневых подпространств является прямой, т. е.
, если равенство
справедливо тогда и только тогда когда
, где
.
Доказательство: Без доква
Следствие: Пусть – корневые векторы, принадлежащие попарно различным собственным значениям
. Тогда векторы
– л. н.з.
Доказательство:
Запишем равенство , тогда по утверждению получаем что
и значит
. #
Лемма 2: Пусть – корневые векторы, принадлежащие одному собственному значению λ, с попарно различными высотами
(
). Тогда векторы
– л. н.з.
Доказательство:
Проведем доказательство методом математической индукции по K.
Рассмотрим в порядке возрастания высоты корневых векторов, т. е. пусть
1) При K=1: – верно
2) При K=2: . Пусть
и
. Тогда
а из
что и
.
3) Пусть утверждение справедливо для (K-1) векторов.
4) Для K векторов.
. Пусть
и
.
Тогда 
#
Теорема 2:
Пусть – собственные значения линейного оператора φ с кратностями
, соответственно, а
,
,…,
– корневые подпространства. Тогда
,
,…,
и
.
Доказательство:
Без доказательства.
Следствие: Максимальная высота корневого вектора, отвечающего собственному значению λ, не превосходит кратности Nλ
Доказательство: Пусть с высотой M>Nλ (доказываем методом от противного). Тогда векторы
– корневые векторы, принадлежащие одному собственному значению λ с попарно различными высотами M, M-1,…, 2, 1. В самом деле, если
, то корневой вектор высоты M, тогда
корневой вектор высоты M-1.
– корневой вектор высоты M-2.
– корневой вектор высоты 1.
Тогда по Лемме 2 Эти векторы л. н.з. и их всего M>Nλ штук. Это противоречит тому, что #
Схемы нахождения корневых векторов.
1) Ищем собственные значения
2) Для каждого собственного значения λi решаем систему уравнений , где Ki<Ni, Ni – кратность λi как корня характеристического уравнения. Тогда находим корневые векторы максимальной высоты Ki из условия
.
| < Предыдущая | Следующая > |
|---|
Красным цветом обозначен собственный вектор. Он, в отличие от синего, при деформации не изменил направление и длину, поэтому является собственным вектором, соответствующим собственному значению λ = 1. Любой вектор, параллельный красному вектору, также будет собственным, соответствующим тому же собственному значению. Множество всех таких векторов (вместе с нулевым) образует собственное подпространство.
Содержание
- 1 Определения собственного числа, собственного и корневого вектора линейного оператора
- 2 Свойства собственных значений, собственных и корневых векторов и пространств
- 2.1 Общий случай
- 2.2 Конечномерные линейные пространства
- 2.3 Гильбертовы пространства над полем комплексных чисел и нормальные операторы
- 2.4 Положительные матрицы
- 3 Литература
Определения собственного числа, собственного и корневого вектора линейного оператора
Пусть L — линейное пространство над полем K, 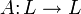
Собственным вектором линейного преобразования A называется такой ненулевой вектор 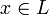
- Ax = λx
Собственным значением линейного преобразования A называется такое число 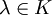
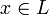
Собственным подпространством линейного преобразования A для данного собственного числа 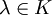
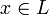
где E — единичный оператор.
Корневым вектором линейного преобразования A для данного собственного значения 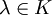
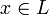
Если m является наименьшим из таких натуральных чисел (то есть 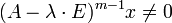
Корневым подпространством линейного преобразования A для данного собственного числа 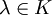
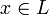
где
Свойства собственных значений, собственных и корневых векторов и пространств
Общий случай
Подпространство 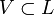
.
- Собственные подпространства Eλ, корневые подпространства Vλ и подпространства Vm,λ линейного оператора A являются A-инвариантными.
- Собственные векторы являются корневыми (высоты 1):
;
- Корневые векторы могут не быть собственными: например, для преобразования двумерного пространства, заданного матрицей
- (A − 1)2 = 0, и все векторы являются корневыми, соответствующими собственному числу 1, но A имеет единственный собственный вектор (с точностью до умножения на число).
- Для разных собственных значений корневые (и, следовательно, собственные) подпространства имеют тривиальное (нулевое) пересечение:
если
.
Конечномерные линейные пространства
Выбрав базис в n-мерном линейном пространстве L, можно сопоставить линейному преобразованию 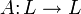
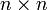
.
Пусть числовое поле алгебраически замкнуто (например, является полем комплексных чисел). Тогда характеристический многочлен разлагается в произведение n линейных множителей
- где
— собственные значения; некоторые из λi могут быть равны. Кратность собственного значения λi — это число множителей равных λ − λi в разложении характеристического многочлена на линейные множители (называется также алгебраическая кратность собственного значения).
- Размерность корневого пространства
равна кратности собственного значения.
- Векторное пространство L разлагается в прямую сумму корневых подпространств (по теореме о жордановой форме):
- где суммирование производится по всем λi — собственным числам A.
Гильбертовы пространства над полем комплексных чисел и нормальные операторы
Наличие скалярного произведения позволяет выделить важные классы операторов, собственные значения и собственные векторы которых обладают рядом дополнительных полезных свойств.
Нормальным оператором называется оператор A, коммутирующий со своим сопряжённым A * :
- AA * = A * A.
Частными классами нормальных операторов являются самосопряжённые (эрмитовы) операторы (A = A * ), антиэрмитовы операторы (A = − A * ) и унитарные операторы (A − 1 = A * ), а также их вещественные варианты: симметричные операторы, антисимметричные операторы и ортогональные преобразования.
- Все корневые векторы нормального оператора являются собственными.
- Собственные векторы нормального оператора A, соответствующие различным собственным значениям, ортогональны. То есть если Ax = λx, Ay = μy и
, то (x,y) = 0. (Для произвольного оператора это неверно.)
- Все собственные значения самосопряжённого оператора являются вещественными.
- Все собственные значения антиэрмитового оператора являются мнимыми.
- Все собственные значения унитарного оператора лежат на единичной окружности | λ | = 1.
- В конечномерном случае, сумма размерностей собственных подпространств нормального оператора
, соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств:
- где суммирование производится по всем λi — собственным числам A, а
взаимно ортогональны для различных λi.
- Последнее свойство для нормального оператора над
является характеристическим: оператор нормален тогда и только тогда, когда его матрица имеет диагональный вид в каком-нибудь ортонормированном базисе (в конечномерном случае).
Положительные матрицы
Квадратная вещественная 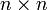
Теорема Перрона (частный случай теоремы Перрона-Фробениуса): Положительная квадратная матрица A имеет положительное собственное значение r, которое имеет алгебраическую кратность 1 и строго превосходит абсолютную величину любого другого собственного значения этой матрицы. Собственному значению r соответствует собственный вектор er, все координаты которого строго положительны. Вектор er — единственный собственный вектор A (с точностью до умножения на число), имеющий неотрицательные координаты.
Собственный вектор er может быть вычислен посредством прямых итераций: выберем произвольный начальный вектор v0 с положительными координатами. Положим:
Последовательность vk сходится к нормированному собственному вектору 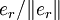
Другая область применения метода прямых итераций — поиск собственных векторов положительно определённых симметричных операторов.
Литература
- Гантмахер Ф. Р. Теория матриц. — М.: Наука, 1966. — 576 с.
- Уилкинсон Д. Х. Алгебраическая проблема собственных значений. — М.: Наука, 1970. — 564 с.
Wikimedia Foundation.
2010.




 Соответствующее собственное значение?
Соответствующее собственное значение? .
. Подставляются найденные собственные значения, я правильно понял?
Подставляются найденные собственные значения, я правильно понял?
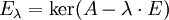
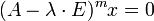
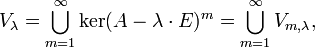

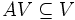 .
.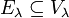 ;
;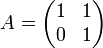
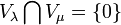 если
если 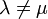 .
.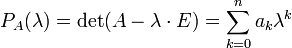 .
.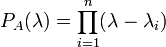
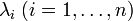 — собственные значения; некоторые из
— собственные значения; некоторые из 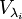 равна кратности собственного значения.
равна кратности собственного значения.
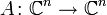 , соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств:
, соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств: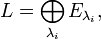
 взаимно ортогональны для различных
взаимно ортогональны для различных 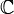 является характеристическим: оператор нормален тогда и только тогда, когда его матрица имеет диагональный вид в каком-нибудь ортонормированном базисе (в конечномерном случае).
является характеристическим: оператор нормален тогда и только тогда, когда его матрица имеет диагональный вид в каком-нибудь ортонормированном базисе (в конечномерном случае).