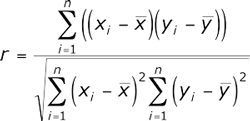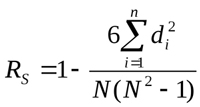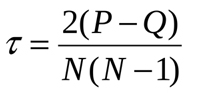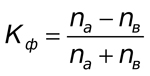Применяем корреляцию в ритейле
Время на прочтение
5 мин
Количество просмотров 13K
На данный момент система высшего образования свела математику до одноразового применения — сломать мозг студентов младших курсов непрофильных специальностей и благополучно выветрится к следующей сессии. Некоторые, правда, потом еще помнят что такие науки как математика и статистика это реальная сила, но мало кто это понимает и тем более применяет в своей деятельности.
В Datawiz.io, собрав несколько мат-гиков, мы решили попытаться изменить сложившуюся ситуацию. Интересно же использовать свои знания на чем-то реальном, измеримом, и даже, возможно, приносящем пользу обществу. Остановились мы на ритейл индустрии. Ритейл предлагает множество данных для обработки, просто водопад цифр: продажи, чеки, ценообразование, покупатели, программы лояльности,… Есть с чем порезвится.
Простая визуализация ритейл данных это тоже достаточно скучно. Традиционная аналитика может показать данные вчерашнего дня и выглядит круто в отчетах, но она никогда не покажет завтрашний день.
Модели машинного обучения действуют иначе. Они дают Вам возможности контроля и взаимодействия. Вы можете играть с моделями, изменять параметры и смотреть как это влияет на результат, изучать возможные последствия различных комбинаций факторов. Чем не общение с оракулом?
Начнем с простого.
Возможно ли определить продажи каких товаров могут влиять на общую выручку магазина?
Имеем исходные данные по двум магазинам, назовем их Гастроном и Универсам:
1. объем продаж товаров определенной категории;
2. количество упоминаний в чеках товаров определенной категории.
Составляем таблицы:
ряды — недели;
колонки — категории;
ячейки -количество проданных товаров или упоминаний в чеках.
Итого — 4 таблицы, по 2 на каждый магазин.
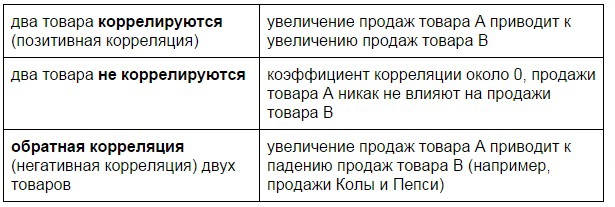
Сначала разберемся с корреляцией продаж. как влияют продажи товаров на общий оборот магазина и на продажи других категорий. Тут возможны 3 варианта развития событий.
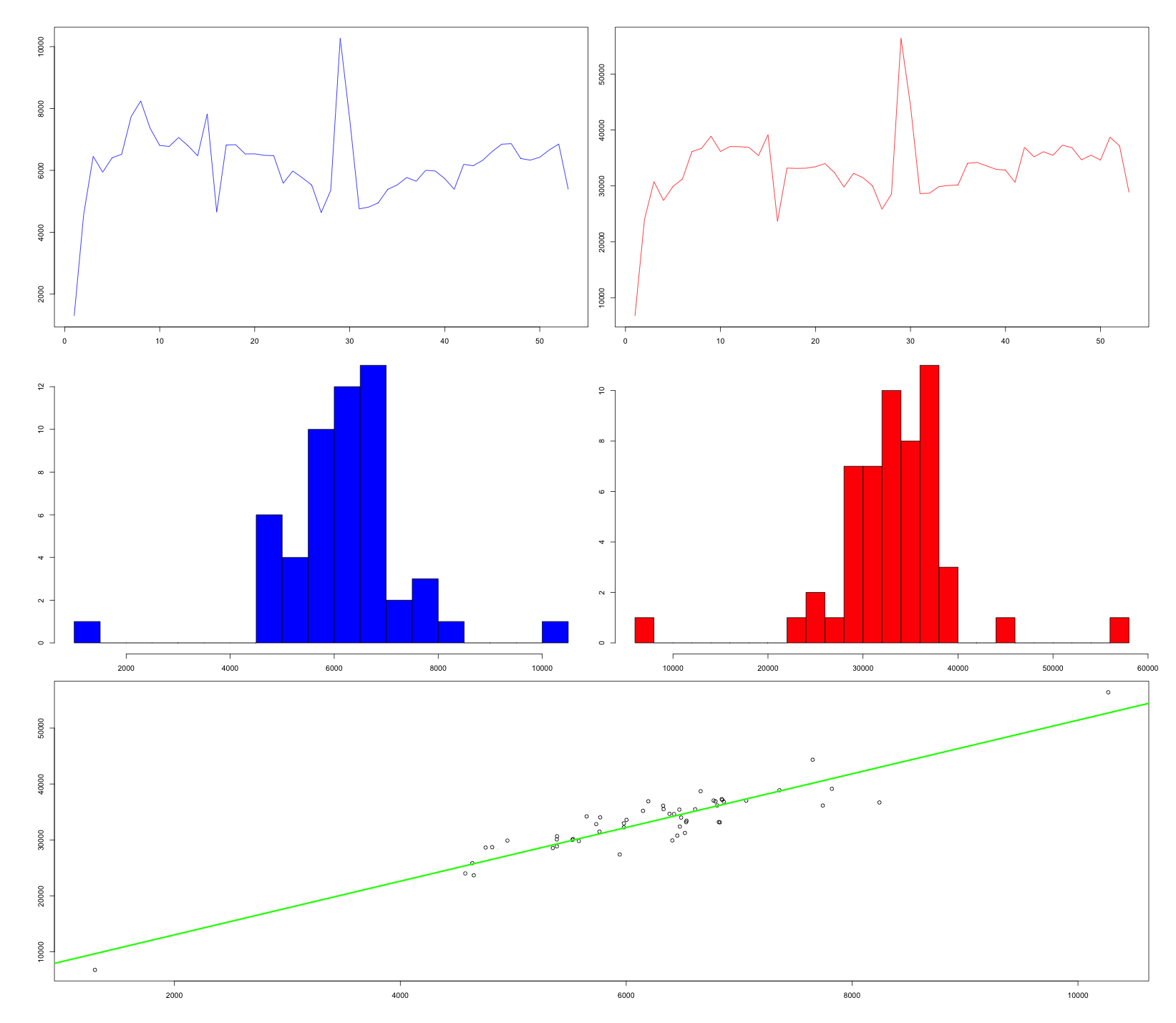
Мы знаем что практически любой магазин продает большое количество молока. Примем гипотезу, что продажи молока и оборот магазина прямо коррелируются. Мы обозначим данные о продажах молока синим, а данные об обороте красным.
plotPair <- function(x,y,namesX,namesY){
par(mfrow=c(2,1))
plot(x,type='l',col='red',main=namesX,xlab='')
plot(y,type='l',col='blue',main=namesY,xlab='')
par(mfrow = c(3,2),
oma = c(5,4,0,0) + 1,
mar = c(0,0,1,1) + 1
)
layout(matrix(c(1,2,3,4,5,5), 3,2, byrow = TRUE))
plot(x,type='l',col='blue',ylab='log sales qty',main=namesX,xlab='')
plot(y,type='l',col='red',main=namesY,xlab='')
hist(x,col='blue',main=names(x),breaks=20)
hist(y,col='red',main=names(y),breaks=20)
m<-lm(y~x)
plot(x,y,xlab=namesX,ylab=namesY)
abline(m,col='green',lwd=3)
}
plotPair(x=moloko_df$Молоко.и.молочная.продукция',
y=moloko_df$sum,
namesX='Молоко.и.молочная.продукция',
namesY='Оборот') Сравним левый и правый графики, они практически одинаковы, что видно на рисунке.
На нижней диаграмме мы отобразили по горизонтали “Молоко и молочную продукцию”, а по вертикали “Оборот”, и тут так же мы можем наблюдать линейную зависимость. А значит наша гипотеза была верна.
Покупатели приходят в магазин за молоком, но так же покупают и другие товары, а значит для магазина выгодно привлекать покупателей даже за счет снижения цены на молочные продукты.
Но теперь нас интересует вопрос, как найти все товары подверженные корреляции, и как продажи товаров коррелируются с оборотом магазина? Используем корреляционную матрицу.
corr<-function(df){
cr <-cor(df, use="complete.obs")
par(cex = 0.9)
corrplot.mixed(corr=cr,upper="ellipse", tl.pos="lt", col = colorpanel(50, "red", "gray60", "blue4"),
cl.cex=0.5,tl.cex=1.1)
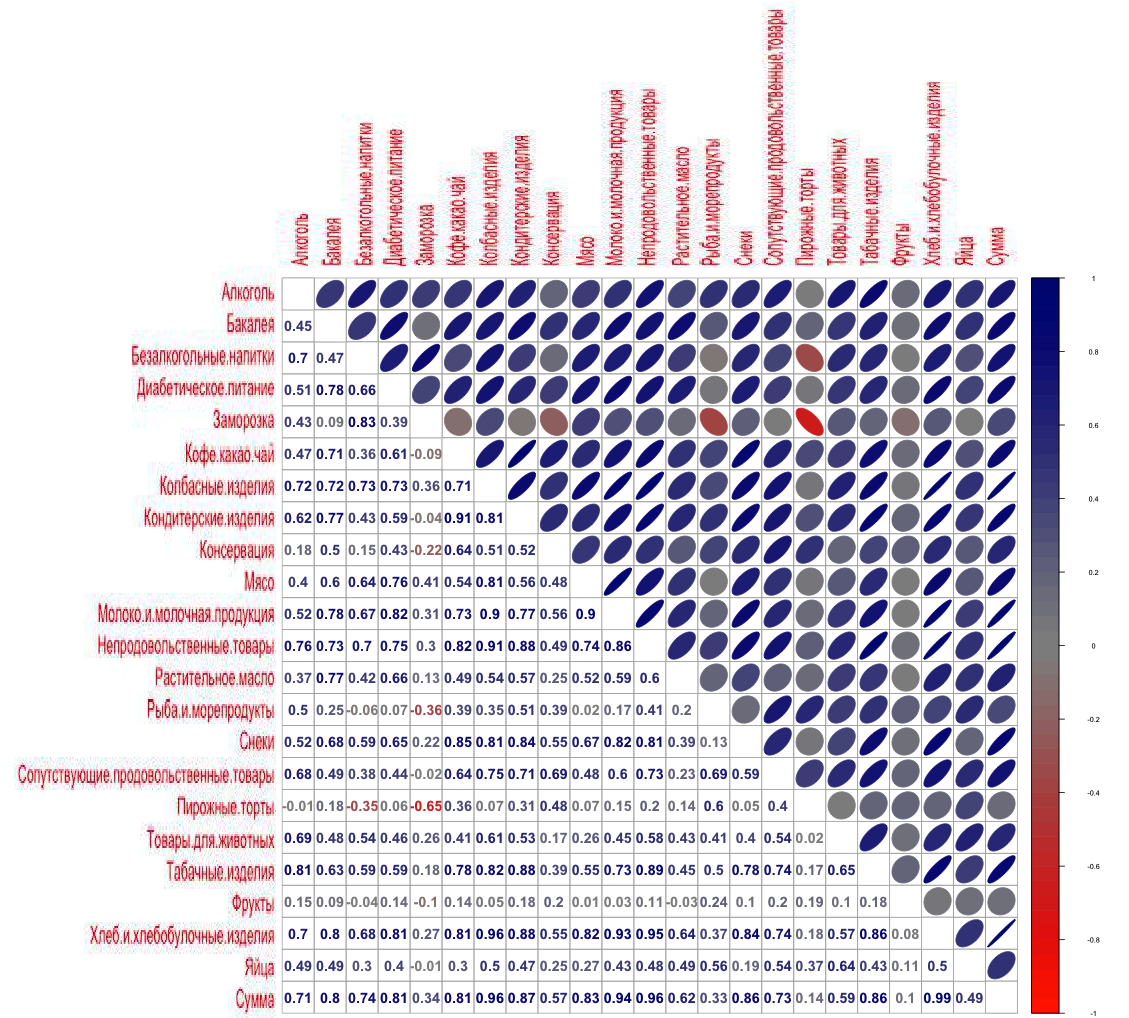
}Корреляция продаж товаров по Гастроному
*При построении матрицы корреляция близкая к нулю обозначается кругом и серым цветом (используя выбранную нами цветовую гамму), а магнитуда колебаний от нуля определяется эллипсом и его цветом: синий в случае позитивной корреляции, красный в случае негативной.
На основе матрицы можем выделить топ товаров, продажи которых коррелированы с оборотом магазина
Хлеб и хлебобулочные изделия 0.977
Непродовольственные товары 0.950
Молоко и молочная продукция 0.934
Колбасные изделия 0.930
Снеки 0.870
Табачные изделия 0.835
Кондитерские изделия 0.802
Диабетическое питание 0.794
Бакалея 0.782
По нашему опыту хлеб, пакеты (непродовольственные товары), молоко и колбасные изделия имеют высокий коэффициент корреляции практически в любом магазине мира. Каждый, кто приходит в магазин, как правило, покупает один или несколько из этих товаров. А вот снеки, табачные и кондитерские изделия отличаются в этом конкретном случае, значит у Гастронома есть покупатели которые приходят в магазин именно за этими группами товаров.
Теперь применим анализ по частоте упоминаний товаров в чеках — ориентированный на покупателя, а не товар, подход.
Корреляция частоты упоминаний товаров в чеках по Гастроному
Выделяем из этой матрицы топ частоты упоминаний товаров в чеках:
Хлеб и хлебобулочные изделия 0.986
Колбасные изделия 0.961
Непродовольственные товары 0.956
Молоко. и молочная продукция 0.944
Кондитерские изделия 0.867
Снеки 0.864
Табачные изделия 0.858
Мясо 0.829
Диабетическое питание 0.812
Как видим топ категорий и даже цифры по категориям остались практически те же.
Применим тот же подход ко второму магазину.
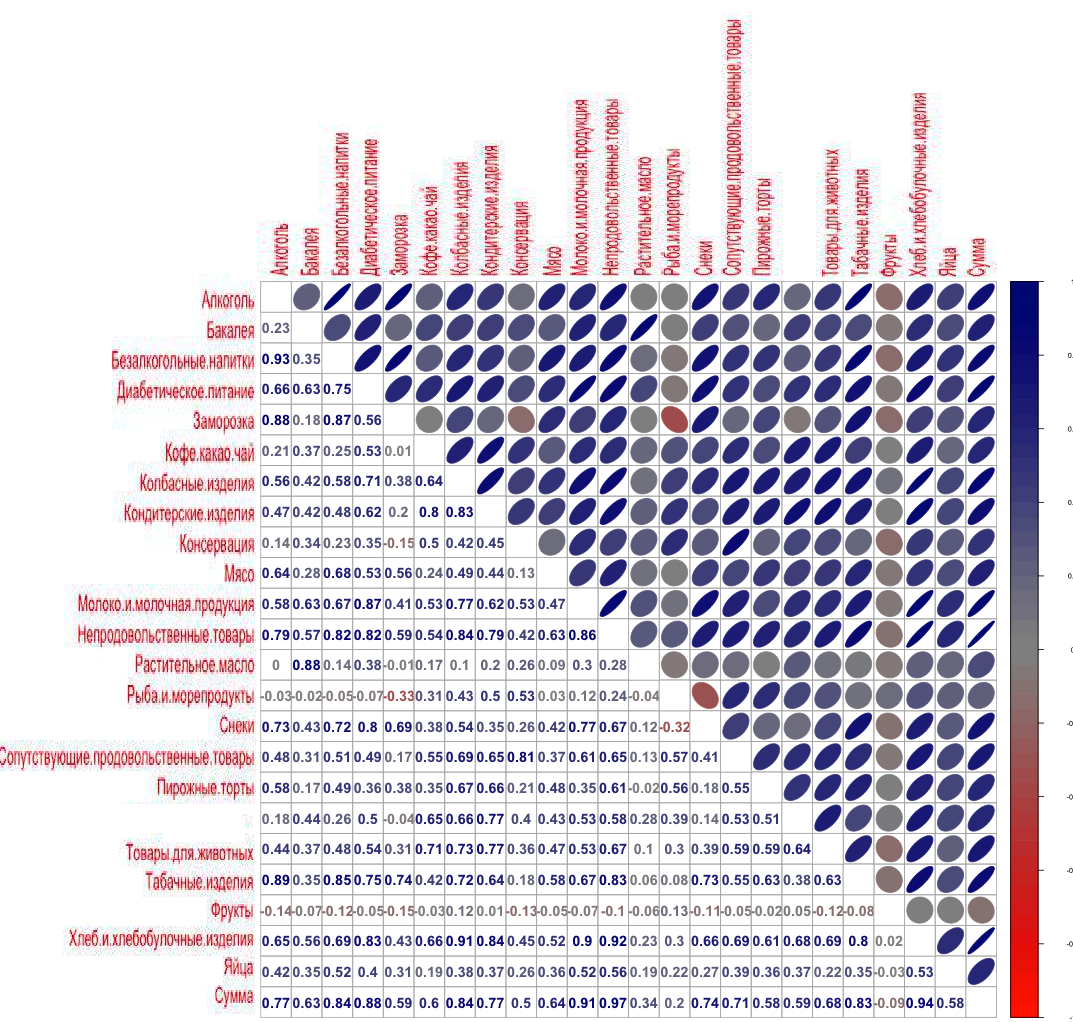
Корреляция продаж товаров по Универсаму
А вот тут мы уже видим существенную разницу с Гастрономом.
Матрица по Универсаму показывает другой топ продаж товаров:
Непродовольственные товары 0.966
Хлеб и хлебобулочные изделия 0.943
Молоко и молочная продукция 0.908
Диабетическое питание 0.882
Колбасные изделия 0.840
Безалкогольные напитки 0.837
Табачные изделия 0.835
Кондитерские изделия 0.775
Алкоголь 0.773
Корреляция частоты упоминаний товаров в чеках по Универсаму
Топ частоты упоминаний товаров в чеках по Универсаму:
Непродовольственные товары 0.975
Хлеб и хлебобулочные изделия 0.968
Молоко и молочная продукция 0.948
Колбасные изделия 0.927
Диабетическое питание 0.905
Кондитерские изделия 0.899
Табачные изделия 0.858
Безалкогольные напитки 0.819
Алкоголь 0.785
Как видим, в Универсаме в топ вошли 2 новые категории — Безалкогольные напитки и Алкоголь вместо Бакалеи и Снеков у Гастронома.
Возможно это зависит от местоположения магазинов и конкурентной среды.
Корреляционные матрицы дают нам широкие возможности для анализа.
На чем хотели бы заострить внимание, при анализе данных матриц стоит учитывать не только корреляцию (позитивную или негативную), не коррелируемые товары, так же стоит анализировать. Например, растительное масло не коррелируется как ни с одной другой категорией товаров, так и с общим оборотом магазина. Анализ чеков аналогично показывает, что есть покупатели который приходят в магазин исключительно за растительным маслом. А значит маркетолог может разместить его в торговом зале где угодно и покупатель все равно отыщет нужный ему товар.
Еще один аспект, некоторые товары имеют обратную корреляцию, как, например, рыба и снеки. Это легко объяснить тем, что люди, как правило, в зависимости от своих предпочтений берут либо пиво+снеки, либо пиво+рыбу. Очень редко кто-то покупает и рыбу и снеки одновременно. Схожая ситуацию с мороженой и свежей рыбой, мороженым и тортами.
Детальный анализ связей между товарами дает большое количество таких фактов, которые могут быть полезны.
Корреляционный анализ показывает текущую ситуацию, товары значительно влияющие на оборот магазина. Но какие из них являются наиболее значимыми? Это проще рассмотреть с помощью построения линейных моделей, что будет темой нашей следующей статьи.
Содержание
- Введение
- Понятие корреляции
- Виды корреляций
- Реализация индикаторов
- Торговая система на основе корреляций
- Тестирование торговой системы
- Выводы
- Заключение
Введение
Суть любой торговли, так или иначе сводится к тому, что приходится прогнозировать дальнейшее развитие событий на рынке и потенциальная прибыль сильно зависит от успешности прогноза. В начале своей статьи Торговые идеи на основе направления и скорости движения цен я описывал такую идею — каждое движение имеет такие характеристики как направление, ускорение и скорость. Это и касается движений цен на валютных и других рынках.
Любое движение имеет свои признаки начала движения, определенную скорость, инерционность и окончание. Успешными являются те торговые стратегии, которые максимально рано определяют начавшее движение и входят в рынок, а также четко идентифицируют его окончание. Тем не менее ни одна стратегия не может со стопроцентной вероятностью определить точки входа и выхода. Здесь мы может только говорить о благоприятном шансе, возможности. Поэтому в данной статье мы рассмотрим один из инструментов теории вероятности — корреляцию, которую будем применять в рамках финансовых рынков.
Понятие корреляции
Корреляция — это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин является коэффициент корреляции. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Коэффициент корреляции может принимать значения от -1 до +1. Чем ближе значение корреляции к 1, тем выше взаимосвязь исследуемых величин. Причем если значение стремится к 1, то связь считается положительной, а к -1 отрицательной. То есть при положительной, как правило, увеличение одной из исследованных величин влечет увеличение второй, а в случае отрицательной наоборот — увеличение одной снижает значение второй.
Иными словами, корреляция помогает идентифицировать зависимость одной величины от другой на основе имеющихся данных. Чем же может помочь корреляция на финансовых рынках?
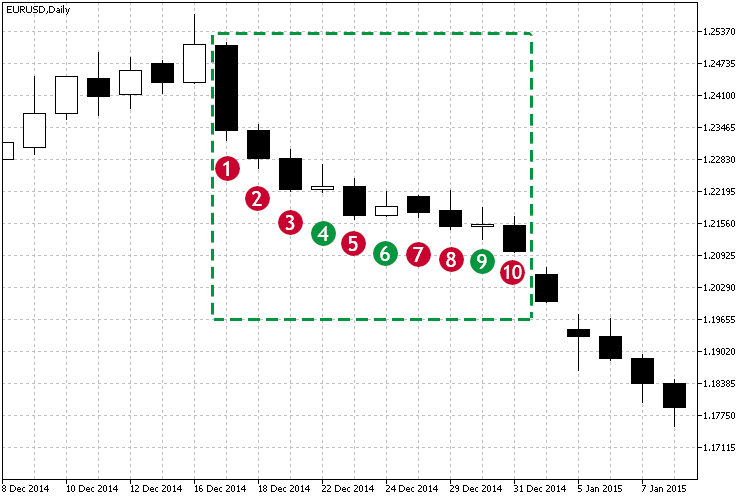
Давайте рассмотрим рис.1 и отмеченную зону нисходящего тренда.
Рис.1 Пример нисходящего тренда.
Как видно на отмеченной области, начиная со свечи №1, цена закрытия в подавляющем случае ниже, нежели цена открытия, или говоря по-другому — каждая следующая цена закрытия ниже предыдущей. Соответственно, с течением времени цена падает. В данном случае визуально видно, что происходит нисходящий тренд, но как же понять, насколько сильна зависимость? Тем более что тренд неидеален, и по свечам №№4,6,9 видно что небольшие попытки движения вверх были. Как же нам поможет корреляция? В данном случае ее коэффициент будет служить показателем силы текущего движения. Исходя из наблюдения за коэффициентом корреляции во времени можно делать сразу несколько выводов:
- Сила текущего тренда. Непосредственно по текущему значению корреляции.
- Длительность тренда. По наблюдениям во времени выбранного порогового значения. Например, порог более 0,75 и не спадает в течение 3-4 свечей.
Виды корреляций
Для определения связи между исследуемыми переменными виды корреляций могут быть следующими:
- Линейные и нелинейные. Линейной называется корреляция, при которой одна величина увеличивается или убывает, при этом вторая также соответственно изменяется. При нелинейной зависимости изменение одной не приводит к прямому изменению другой и может описываться другими функциями.
- Положительной и отрицательной корреляцией называется как раз характер зависимости. Так, при положительной рост одной из взаимосвязанных величин приводит к росту другой.
Примером может служить рис.1 где изображения линейная, отрицательная корреляция. Далее мы рассмотрим несколько видов расчета и выяснения взаимосвязи между двумя величинами.
Линейный коэффициент корреляции (коэффициент корреляции Пирсона)
Данный метод расчета позволяет установить прямую связь между переменными величинами по их абсолютным значениям. Расчет построен таким образом, что если взаимосвязь между величинами имеет линейный характер, то коэффициент Пирсона это покажет. В контексте финансовых рынков эта связь означала бы наличие движения в ту или иную сторону во времени. Для расчета коэффициента корреляции Пирсона применяется следующая формула:
А теперь в качестве примера рассчитаем коэффициент корреляции Пирсона для данных, представленных на рис.1, чтобы уже количественно измерить зависимость цен закрытия с течением времени. Для этого занесем данные в таблицу:
| Цена закрытия | Номер свечи |
|---|---|
| 1,23406 | 1 |
| 1,22856 | 2 |
| 1,22224 | 3 |
| 1,22285 | 4 |
| 1,21721 | 5 |
| 1,21891 | 6 |
| 1,21773 | 7 |
| 1,21500 | 8 |
| 1,21546 | 9 |
| 1,20995 | 10 |
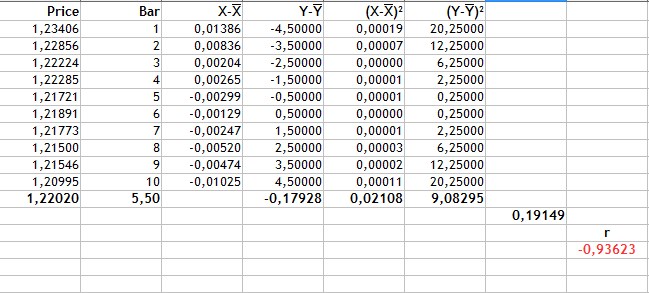
Весь расчет приведен на следующем рисунке.
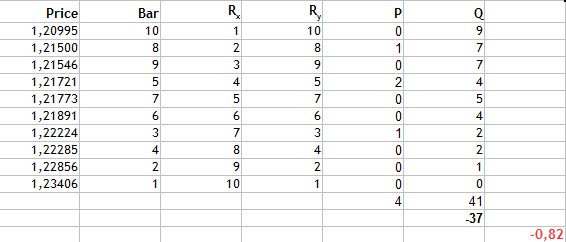
Рис.2 Расчет коэффициента корреляции Пирсона.
Очередность расчета выглядит следующим образом:
- Находим среднее значение цены(Price) и номера свечи. Это 1,22020 и 5,5 соответственно.
- Находим для каждого вида переменных отклонение от среднего(столбцы 3-4).
- Значение -0,17928 сумма произведений отклонений цены и номера свечи. Это числитель формулы.
- Столбцы 5 и 6 квадраты отклонений. Значения 0,02108 и 9,08295 это корни из суммы квадратов отклонений.
- Знаменатель формулы или произведение корней сумм квадратов отклонений равен 0,19149.
- Коэффициент корреляции Пирсона получается -0,93623.
Исходя из полученных результатов можно сделать вывод, что в данном случае присутствует сильная линейная, отрицательная взаимосвязь.
Коэффициент ранговой корреляции Спирмена
Этот метод расчета позволяет устанавливать линейную связь между случайными величинами. Для оценки взаимосвязи используются не числовые значения исследуемых признаков, а соответствующие им ранги. Также как и коэффициент Спирмена, его величина лежит в пределах от -1 до 1. Абсолютное значение характеризует тесноту связи, а знак — направленность связи между двумя признаками. Рассчитывается он по формуле:
Где Di — разница рангов между исследуемыми признаками. Рассмотрим пример расчета ранговой корреляции на всё том же рис.1 и занесем показания в новую таблицу:
| Цена закрытия | Номер свечи | Ранг цены закрытия | Ранг номера свечи |
|---|---|---|---|
| 1,23406 | 1 | 10 | 1 |
| 1,22856 | 2 | 9 | 2 |
| 1,22224 | 3 | 7 | 3 |
| 1,22285 | 4 | 8 | 4 |
| 1,21721 | 5 | 4 | 5 |
| 1,21891 | 6 | 6 | 6 |
| 1,21773 | 7 | 5 | 7 |
| 1,21500 | 8 | 2 | 8 |
| 1,21546 | 9 | 3 | 9 |
| 1,20995 | 10 | 1 | 10 |
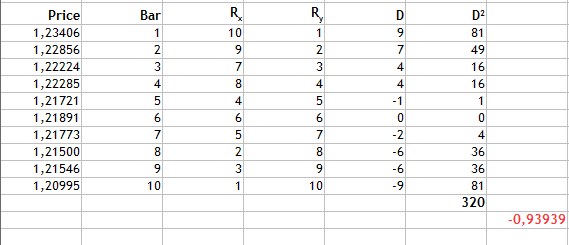
Как видно из таблицы, мы проранжировали значения цены закрытия, присвоив ранг 1 наименьшему значению и так далее. Согласно формуле рассчитаем разность рангов D исследуемых признаков и подставим полученные значения в формулу.
Рис.3 Расчет коэффициента ранговой корреляции Спирмена.
Как видно из рис.3, мы находим разности рангов, затем квадраты полученных разностей и суммируем, получаем 320. Подставляем полученные значения в формулу и получаем результат -0,93939.
Исходя из полученного значения коэффициента корреляции, вывод всё тот же — сильная линейная, отрицательная взаимосвязь. В данном случае теснота связи получилась сопоставима коэффициенту корреляции Пирсона, но следует учитывать тот факт, что существует один недостаток расчета данного метода. Это то, что одинаковым разностям рангов могут соответствовать несопоставимые значения разностей значений. К примеру ранжирование баров сопоставимо, а вот значения рангов цены не равномерно, но разброс признака цена у нас небольшой и отличается на тысячные доли. Потому в данном случае метод расчета уместен.
Коэффициент ранговой корреляции Кенделла
Также как и у Спирмена, коэффициент ранговой корреляции Кенделла есть мера линейной связи между случайными величинами. Аналогично происходит ранжирования значений проверяемых на взаимосвязь признаков, однако метод расчет несколько иной. Формула для расчета коэффициента такова:
Где P — сумма совпадений, а Q — сумма инверсий. Чтобы понять что это означает, вновь обратимся к исследуемому нами примеру из рис.1 и для начала сделаем следующую сортировку в таблице данных:
| Цена закрытия | Номер свечи | Ранг цены закрытия | Ранг номера свечи |
|---|---|---|---|
| 1,20995 | 10 | 1 | 10 |
| 1,21500 | 8 | 2 | 8 |
| 1,21546 | 9 | 3 | 9 |
| 1,21721 | 5 | 4 | 5 |
| 1,21773 | 7 | 5 | 7 |
| 1,21891 | 6 | 6 | 6 |
| 1,22224 | 3 | 7 | 3 |
| 1,22285 | 4 | 8 | 4 |
| 1,22856 | 2 | 9 | 2 |
| 1,23406 | 1 | 10 | 1 |
Как видно, таблица была отсортирована по столбцу Ранга цены закрытия. Далее определяем количество рангов выше текущего, начиная с первой строки в столбце Ранг номера свечи. То есть берем 10 и смотрим, есть ли ранги выше — их нет. Далее берем 8 и находим всего один ранг, это 9. И так далее. Это будут совпадения P.
Таким же образом считаем количество рангов ниже. Так для 10 рангов ниже будет 9, так как это самый большой ранг, для 8 будут семь — 5,7,6,3,4,2,1. Это будут инверсии Q. Заносим получившиеся данные в таблицу и рассчитываем коэффициент:
Рис.4 Расчет коэффициента ранговой корреляции Кенделла.
Суммируем получившиеся значения совпадений и значения инверсий. Находим их разницу -37 и подставив в формулу получаем следующее значение коэффициента корреляции Кенделла -0,82. Снова прослеживается сильная линейная отрицательная связь, тем не менее результат говорит о том, что данный метод расчета более избирателен, нежели два предыдущих, так как само абсолютное значение оказалось меньше.
Коэффициент корреляции знаков Фехнера
Данный метод основывается на оценке степени согласованности направления отклонений значений признаков от среднего значения и подсчете знаков отклонений, соответствующим значениям признаков. Формула для расчета очень проста:
Где Na — количество совпадений по знаку, а Nb — количество несовпадений по знаку. Для более ясного понимания, также рассчитаем коэффициент корреляции для нашего примера из рис.1.
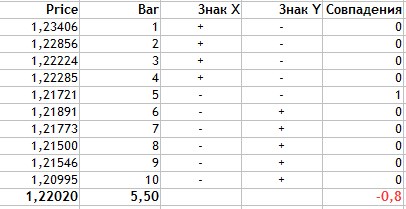
Рис.5 Расчет коэффициента корреляции знаков Фехнера.
Давайте рассмотрим более подробно расчет:
- Находим средние значения данных по двум признакам. Для Цены это 1,2202, для свечи 5,5.
- В столбце Знак Х ставим + если текущее значение признака Цена больше среднего значения и минус, если меньше.
- Аналогично поступаем со значениями номеров свечей.
- Подсчитываем количество совпадений знаков для сопоставленных значений двух признаков.
- Как видно, что совпадение знаков произошло лишь однажды, значит Na = 1, а Nb = 9.
- Подставляем полученные значения в формулу.
Как видно, метод расчета коэффициента корреляции Фехнера достаточно прост и его значение равно -0,8. Что, как и в предыдущих методах, говорит о сильной линейной, отрицательной зависимости Цены закрытия от номера свеча или во времени.
Реализация индикаторов
Итак давайте реализуем средствами MQL5 все методы расчета корреляций.
Коэффициент корреляции Пирсона
Так как расчет данного метода имеет большую формулу, то для лучшей визуализации и понимания этапов расчета она была разбита на два этапа расчета — расчет числителя и знаменателя.
double Numerator(double &Ranks[],int N) { double Y[],dx[],dy[],mx=0.0,my=0.0,sum=0.0,sm=0.0; ArrayResize(Y,N); ArrayResize(dx,N); ArrayResize(dy,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0;j<N;j++) { dx[j]=Y[j]-mx; dy[j]=Ranks[j]-my; sm+=dx[j]*dy[j]; } return sm; } double Denominator(double &Ranks[],int N) { double Y[],dx2[],dy2[],mx=0.0,my=0.0,sum=0.0,smx2=0.0,smy2=0.0; ArrayResize(Y,N); ArrayResize(dx2,N); ArrayResize(dy2,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0;j<N;j++) { dx2[j]=MathPow(Y[j]-mx,2); dy2[j]=MathPow(Ranks[j]-my,2); smx2+=dx2[j]; smy2+=dy2[j]; } return(MathSqrt(smx2*smy2)); }
Финальный метод расчета и логика расчета визуализации индикатора выглядит следующим образом на листинге ниже:
int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=PearsonCalc(PriceInt,rangeN); } return(rates_total); } double PearsonCalc(double &Ranks[],int N) { double ch,zn; ch=Numerator(Ranks,N); zn=Denominator(Ranks,N); return (ch/zn); }
Коэффициент ранговой корреляции Спирмена
Для создания индикатора на основе данного метода было решено не изобретать заново велосипед, поэтому некоторые методы расчета были взяты отсюда.
int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=limit; i>=0; i--) { for(int k=0; k<rangeN; k++) PriceInt[k]=int(price[i+k]*multiply); RankPrices(TrueRanks,PriceInt); ExtLineBuffer[i]=SpearmanCalc(R2,rangeN); } return(rates_total); } double SpearmanCalc(double &Ranks[],int N) { double sumd2=0.0; for(int i=0; i<N; i++) sumd2+=MathPow(Ranks[i]-i-1,2); return(1-6*sumd2/(N*(MathPow(N,2)-1))); }
Коэффициент ранговой корреляции Кенделла
При расчете данного метода поступим вариативно и используем внутренние резервы самого mql5. А именно используем встроенную библиотеку матстатистики и применим ее к нашим расчетам.
int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=KendallCalc(PriceInt,rangeN); } return(rates_total); } double KendallCalc(double &Ranks[],int N) { double Y[],t; ArrayResize(Y,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } MathCorrelationKendall(Ranks,Y,t); return (t); }
Коэффициент корреляции знаков Фехнера
Данный метода расчета, как мы помним, основан на подсчете совпадающих знаков отклонений от среднего значения. И последующее сравнение на совпадение.
int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=FechnerCalc(PriceInt,rangeN); } return(rates_total); } double FechnerCalc(double &Ranks[],int N) { double Y[],res,mx,my,sum=0.0,markx[],marky[]; double Na=0.0,Nb=0.0; ArrayResize(Y,N); ArrayResize(markx,N); ArrayResize(marky,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0; j<N; j++) { markx[j]=(Y[j]>mx)?1:-1; marky[j]=(Ranks[j]>my)?1:-1; if(markx[j]==marky[j]) Na++; else Nb++; } res=(Na-Nb)/(Na+Nb); return (res); }
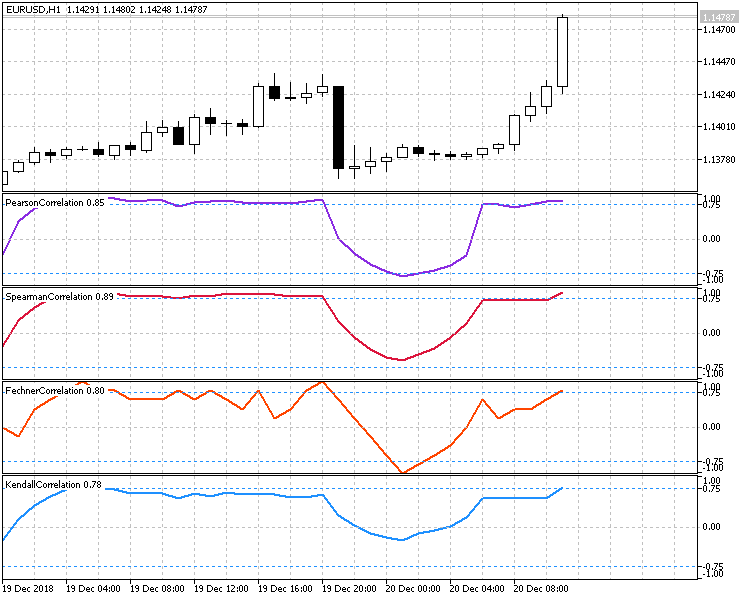
На рис.6 продемонстрирована работа всех четырех методов расчета корреляции Цены закрытия свечи и времени. На всех индикаторах установлен период 10, поэтому можно наглядно увидеть их работу в одинаковых условиях.
Рис.6 Сравнительная демонстрация работы всех методов работы.
Торговая система на основе корреляций
При создании торговой стратегии на основе корреляций нужно тщательно изучить специфику работы индикаторов и методов расчета, и выявить возможные неблагоприятные или рискованные условия входа в рынок.
Практически для всех индикаторов в реальном времени брать большой период расчета нецелесообразно, потому что индикатор будет сильно запаздывать, либо при резком развороте мы увидим лишь слабую корреляцию. Из-за того, что индикаторы все еще учитывают значения завершившегося противоположного движения.
Так как очень часто анализируют цену не в текущий момент, а в совокупности нескольких значений за период времени, то и нет большого смысла рассматривать текущее значение корреляции, как абсолютную оценку. Нужно рассматривать в динамике, в чем нам, собственно и помогают осцилляторы, построенные на значениях текущего и всех предыдущих коэффициентов корреляции.
Поэтому было решено строить стратегию исходя из характера поведения осциллятора коэффициентов корреляции. А именно в момент пробития неких предустановленных уровней. И тут можно пойти двумя путями:
- На падении коэффициента. Продавать при падении положительного коэффициента и пробитии ключевого предустановленного уровня, и покупать при росте отрицательного с пробитием уровня симметричного установленного в положительной области.
- На росте коэффициента. Продавать при падении коэффициента в отрицательной области и пробитии уровня, и покупать при росте коэффициента с пробитием положительного симметричного уровня.
Для ясности понимания потенциальные входы представлены на скриншотах ниже.
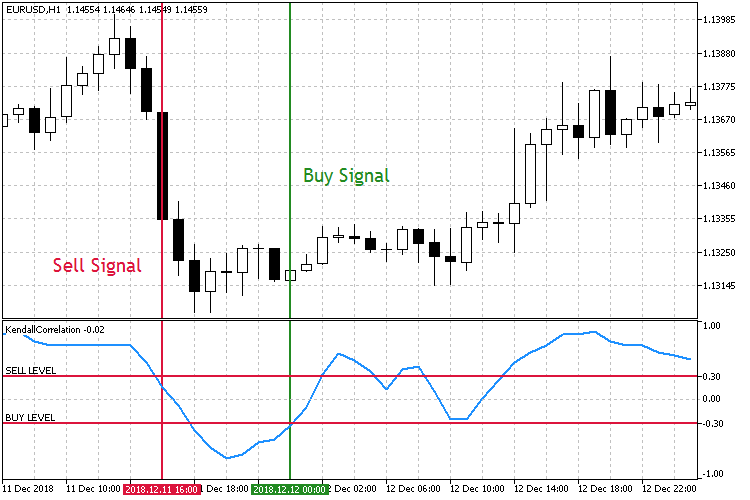
Рис.7 Торговля на падении коэффициента корреляции.
Как видно на скриншотах, есть два установленных симметричных уровня коэффициента корреляции Sell Level 0,3 и Buy Level -0,3. При пробитии Sell Level сверху вниз открываем ордер на продажу, а при пробитии Buy Level снизу вверх на покупку.
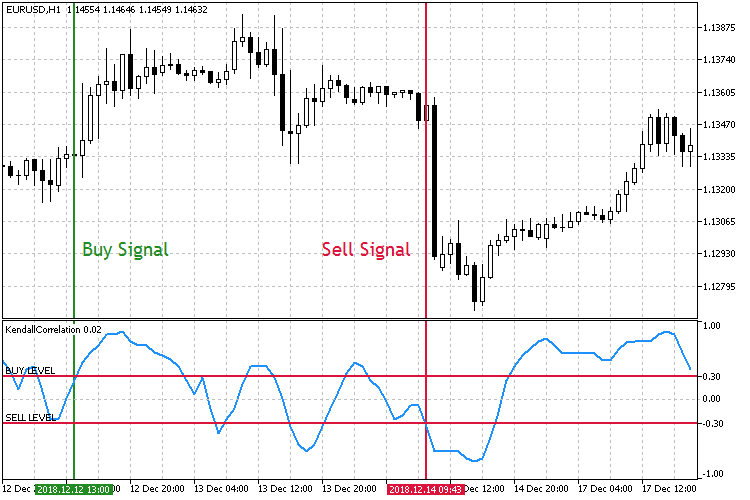
Рис.8 Торговля на росте коэффициента корреляции.
При другом режиме торговли, как показано на рис. 8, ключевые уровни для входа в рынок меняются местами. Теперь при пробитии Buy Level снизу вверх открывается ордер на покупку, а при пробитии Sell Level сверху вниз на продажу.
Итак, при реализации торгового эксперта следует учесть выбор использования одной из предложенных стратегий, а также выбор метода расчета корреляции.
enum Strategy_type { DECREASE = 1, INCREASE }; enum Corr_method { PEARSON = 1, SPEARMAN, KENDALL, FECHNER };
Во входных параметрах помимо параметров советника добавим выбор метода расчет, тип стратегии, ключевой уровень и настраиваемый выбор рабочего таймфрейма.
input string Inp_EaComment="Correlation Strategy"; input double Inp_Lot=0.01; input MarginMode Inp_MMode=LOT; input Corr_method Inp_Corr_method=1; input Strategy_type Inp_Strategy_type=1; input string Inp_Str_label="===EA parameters==="; input int Inp_MagicNum=1111; input int Inp_StopLoss=40; input int Inp_TakeProfit=60; input int Inp_RangeN=10; input double Inp_KeyLevel=0.2; input ENUM_TIMEFRAMES Inp_Timeframe=PERIOD_CURRENT;
При инициализации торгового эксперта добавим проверку ключевого уровня на корректность, а именно нахождение его в диапазоне от 0 до 1. Так как для ключевого уровня мы будем использовать абсолютное значение.
if(Inp_KeyLevel>1 || Inp_KeyLevel<0) { Print(Inp_EaComment,": Incorrect key level!"); return(INIT_FAILED); }
Далее выбираем выбранный в настройках метод расчета корреляции:
switch(Inp_Corr_method) { case 1: ind_type="Correlation\PearsonCorrelation"; break; case 2: ind_type="Correlation\SpearmanCorrelation"; break; case 3: ind_type="Correlation\KendallCorrelation"; break; case 4: ind_type="Correlation\FechnerCorrelation"; break; default: break; } InpInd_Handle=iCustom(Symbol(),Inp_Timeframe,ind_type,Inp_RangeN); if(InpInd_Handle==INVALID_HANDLE) { Print(Inp_EaComment,": Failed to get indicator handle"); Print("Handle = ",InpInd_Handle," error = ",GetLastError()); return(INIT_FAILED); }
После этого уже настраиваем условия входа и логику работы торгового эксперта.
void OnTick() { if(!GetIndValue()) return; if(!Trade.IsOpenedByMagic(Inp_MagicNum)) { if(BuySignal()) Trade.BuyPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment); if(SellSignal()) Trade.SellPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment); } } bool BuySignal() { bool res=false; if(Inp_Strategy_type==1) res=(corr[1]>Inp_KeyLevel && corr[0]<Inp_KeyLevel)?true:false; else if(Inp_Strategy_type==2) res=(corr[0]>Inp_KeyLevel && corr[1]<Inp_KeyLevel)?true:false; return res; } bool SellSignal() { bool res=false; if(Inp_Strategy_type==1) res=(corr[1]<-Inp_KeyLevel && corr[0]>-Inp_KeyLevel)?true:false; else if(Inp_Strategy_type==2) res=(corr[0]<-Inp_KeyLevel && corr[1]>-Inp_KeyLevel)?true:false; return res; }
Тестирование
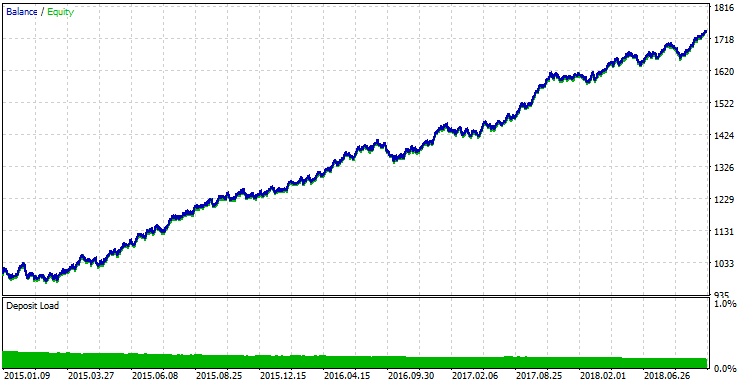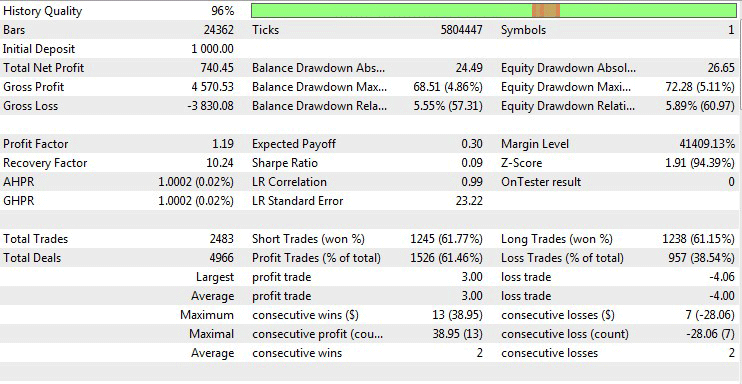
Для тестировании получившегося торгового эксперта выберем начальные предустановки:
- Интервал: Для режима Uptrend 01.01.2015 — 01.12.2018.
- Валютная пара: EURUSD.
- Режим торговли: Без задержки. Представленные стратегии не относятся к высокочастотным, поэтому влияние задержек было бы очень мало.
- Тестирование: OHLC на М1. Предварительное тестирование на реальных тиках оказалось почти неотличимо от этого режима.
- Начальный депозит: 1000 USD.
- Плечо: 1:500.
- Сервер: MetaQuotes-Demo.
- Котировки: 5-значные.
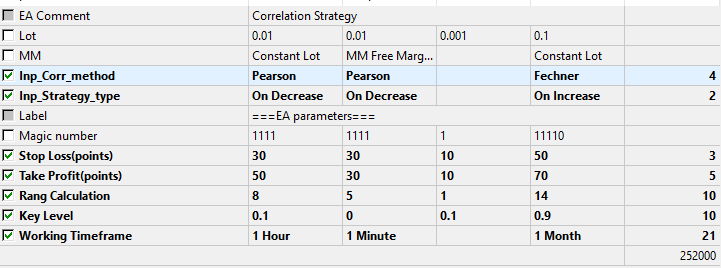
Также определимся с параметрами, которые будут тестироваться и оптимизироваться.
Рис.9 Набор оптимизируемых параметров.
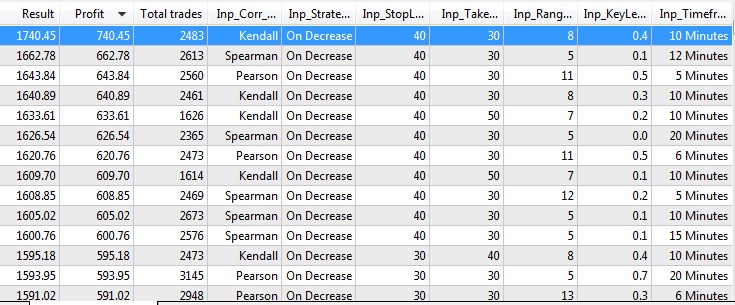
По результатам оптимизации можно выяснить какой из методов расчета и типов стратегии оказался более предпочтителен. Итак, по результатам тестирования и оптимизации получились следующие результаты.
Рис.10 Результаты тестирования и оптимизации.
Также проведем тестирование лучших параметров оптимизации.
Рис.11 Результаты тестирования лучших параметров.
Выводы
На основе полученных результатов можно сделать следующие наблюдения:
- Лучшие результаты тестов показывает стратегия на падении коэффициента корреляции, режим On Decrease. Такой результат можно объяснить лишь тем, что на падении коэффициентов происходит более раннее реагирование на движения рынка. Как уже говорилось выше, осцилляторы на основе коэффициентов корреляции, особенно с большими периодами, заметно запаздывают.
- Бросается в глаза, что самый простой расчет коэффициента корреляции по Фехнеру в первой двадцатке не присутствует. Лучший по данному методу находится на 99-м месте.
- Наилучшие результаты получились на мелких таймфреймах с небольшими тейк-профита и стоп-лоссами.
- Какой-либо зависимости величины прибыли от выбранного периода и предустановленного ключевого уровня не найдены, тем не менее превалируют небольшие периоды, в частности — нижняя граница диапазона оптимизации с периодом 5 в лучших результатах встречается постоянно. Это еще раз говорит о том, что при больших периодах индикаторы на основе корреляции сильно запаздывают со входом и дают слабые результаты.
Заключение
В конце статьи приложен архив со всеми перечисленными файлами, отсортированными по папкам. Поэтому для корректной работы достаточно положить папку MQL5 в корень терминала.
Программы, используемые в статье:
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Correlation.mq5 | Эксперт | Торговый эксперт, включающий в себя 4 метода расчета корреляции и 2 стратегии на их основе. |
| 2 | Trade.mqh | Библиотека | Класс торговых функций. |
| 3 | FechnerCorrelation.mq5 | Индикатор | Индикатор расчета коэффициента корреляции Фехнера |
| 4 | KendallCorrelation.mq5 | Индикатор | Индикатор расчета коэффициента корреляции Кенделла |
| 5 | PearsonCorrelation.mq5 | Индикатор | Индикатор расчета коэффициента корреляции Пирсона |
| 6 | SpearmanCorrelation.mq5 | Индикатор | Индикатор расчета коэффициента корреляции Спирмена |
Что такое корреляция на финансовом рынке, чем обусловлено её появление, как она определяется и используется в трейдинге. Примеры использования и особенности.
На финансовых рынках существует множество внутренних взаимосвязей. Например, изменение цены нефти влияет на курс рубля и прочих сырьевых валют, а динамика индекса S&P 500 определяет поведение акций американских компаний. Эта связь называется корреляцией и широко используется не только в трейдинге, но и в инвестиционной деятельности. Этот прием помогает снизить риски и повысить доходность инвестиционного портфеля.
Краткий гид:
- Что такое Корреляция простыми словами
- Положительная и отрицательная корреляция
- Причины возникновения
- Взаимозависимость валютных пар
- Межгрупповая корреляция на глобальном финансовом рынке
- Взаимозависимость инструментов фондового рынка
- Как определить корреляцию
- Как использовать корреляцию в трейдинге
- Что означает значение коэффициента корреляции
- Как использовать корреляцию в краткосрочной торговле (Биржа и Форекс)
- Как применять корреляцию при портфельном инвестировании
- Основные стратегии
Что такое Корреляция простыми словами
Корреляция – это статистическая связь между 2 и более величинами.
Понятие корреляции часто встречается и используется в статистике, изучающей те или иные явления, процессы, закономерности.
Если говорить простыми словами, то корреляция показывает, в какой мере изменение одной величины приводит к изменению других величин. Знание этой закономерности позволяет прогнозировать поведение соответствующих переменных в тех или иных ситуациях.
Например, падение стоимости нефти всегда совпадает с падением канадского доллара. Национальная валюта Канады зависит в том числе и от цены на черное золото так как страна входит в число крупнейших экспортеров нефти. В этом примере есть прямая зависимость курса USDCAD от цены нефти.
Другой пример – в зимнее время при гололеде возрастает травматизм людей и аварийность на дорогах, между ними наблюдается прямая корреляция. Эти явления не зависят друг от друга, но есть общая причина, влияющая на обе величины.
Корреляция – это то, что позволяет прогнозировать изменение одной величины, опираясь в том числе и на поведение связанной с ней величины.
Она может наблюдаться между 3, 4 и большим числом явлений. Например, поведение американского индекса S&P 500 коррелирует с динамикой изменения курса акций большинства акций американских компаний.
Положительная и отрицательная корреляция
Взаимодействие между рыночными ценами финансовых активов может проявляться по-разному:
- Положительная (или прямая) корреляция. В случае с финансовыми рынками это означает, что графики цен 2-х инструментов движутся синхронно или очень близко по динамике. Речь не идет о 100%-ном копировании друг друга, но большая часть движений совпадает. Характерным примером положительной корреляции считается взаимодействие валютных пар EURUSD и GBPUSD – данные инструменты часто демонстрируют синхронное повышение курса или одновременно дешевеют.
- Отрицательная (или обратная) корреляция обозначает зеркальную связь между величинами. Хороший пример устойчивой обратной связи – USDJPY и GBPUSD. Также валютные пары EURUSD и USDCHF. Когда растет EURUSD, пара USDCHF снижается и наоборот.
Также выделяют линейный и нелинейный тип связи. Линейная корреляция – такой тип связи, который может быть описан линейным уравнением регрессии (уравнение вида Y = a + b∙X, где a и b – коэффициенты, Y и X – связанные величины).
Нелинейная связь означает невозможность описать корреляцию между 2 и более величинами линейным уравнением регрессии. Зависимость может описываться, например, уравнение параболы или иной, более сложной кривой.
В трейдинге и инвестиционной деятельности тип связи не особо важен. Первостепенное значение имеет коэффициент корреляции (% совпадения динамики).
Корреляция ценовых движений: причины возникновения на разных рынках
Взаимосвязь активов финансового рынка предопределяется фундаментальными экономическими факторами. При этом важная роль принадлежит развитию торговых отношений между разными странами, интегрированными в систему мирового хозяйства. Таким образом, динамика рыночных котировок валюты, товаров, ценных бумаг находится под сильным влиянием процессов, происходящих как в международной экономике, так и в экономических системах отдельных стран.
Взаимозависимость валютных пар рынка Форекс
Движения курсов на Форекс часто взаимодействуют, отражая тесное экономическое сотрудничество стран – эмитентов соответствующих денежных единиц. Примером такой корреляции может считаться вышеупомянутая взаимосвязь валютных инструментов EURUSD (евро/доллар) и GBPUSD (фунт/доллар). Несмотря на некоторые противоречия, Великобритания является близким торговым партнером стран Европейского Союза (ЕС). Это значит, что знаковые события и ключевые процессы, происходящие в ЕС, неизбежно отражаются на курсовых позициях GBPUSD.
Межгрупповая корреляция на глобальном финансовом рынке
Взаимосвязь между активами, принадлежащими к разным сегментам финансового рынка, также предопределяется экономическими предпосылками. Актуальный пример – валютные котировки денежных единиц нефтедобывающих стран падают, если нефть на мировом рынке дешевеет. Сила такой корреляции напрямую определяется тем, в какой степени экономика конкретной страны зависит от экспорта углеводородного сырья.
Типичная ситуация – зависимость курсовых позиций российского рубля от динамики мировых нефтяных котировок. Как известно, экономика РФ характеризуется большим удельным весом поступлений от экспорта углеводородов. Это значит, что удешевление нефти приводит к адекватному падению курса отечественного рубля (RUB) относительно американского доллара (USD). Важный нюанс – углеводородное сырье на мировом рынке котируется именно в USD. Таким образом, падение нефтяных цен способствует росту котировок USD.
Взаимозависимость инструментов фондового рынка
Если деловая активность повышается или снижается для всей экономики, а также в её отдельных секторах, можно наблюдать корреляцию целых индексов фондового рынка. Однако решающее значение в этом случае имеет порядок вычисления индекса. При этом ценные бумаги и фондовые индексы могут пребывать в корреляции с Форекс.
Например, в США нередко реализуется программа «количественного смягчения». Она предусматривает выкуп ФРС ценных бумаг с одновременным наполнением американской экономики денежной ликвидностью. Такая программа часто сопровождается корреляцией пары EURUSD с большинством индексов американского рынка ценных бумаг. В данном случае можно констатировать обратную корреляцию инструмента EURUSD c индексом американского доллара и котировками казначейских облигаций США, поскольку такие облигации номинируются в USD.
Как определить корреляцию
Количественная оценка взаимосвязи определенных величин (например, изменений рыночных курсов конкретных акций) выражается значением коэффициента корреляции.
Чтобы определить данный показатель вручную, нужно выполнить пошаговый алгоритм математических вычислений, используя сложную формулу.
в этой формуле:
- К – коэффициент корреляции;
- X и Xср – значение первой величины в определенный промежуток времени и ее среднее значение;
- Y и Yср – значение первой величины в определенный промежуток времени и ее среднее значение.
Трейдеры финансового рынка могут избежать подобных трудностей, воспользовавшись для расчета корреляции такими доступными опциями:
- Индикаторы технического анализа в терминалах для трейдинга или компьютерные программы особого назначения, позволяющие точно рассчитать показатель корреляции для двух и более выбранных активов. Для вычислений используются исторические котировки.
- В Excel есть функция CORREL, автоматизирующая расчет. Нужно лишь заполнить таблицу, указав массив значений для 2 диапазонов ячеек. Например, в столбец №1 поместить цены Close каждой 4-часовой свечи валютной пары EURUSD за последние 3 месяца, а в столбец №2 – цены Close любого другого финансового инструмента. Функция КОРРЕЛ мгновенно рассчитает значение корреляции для этих данных.
- Простейший способ узнать коэффициент корреляции – онлайн-сервисы megatrader.org или mataf.net. Можно рассчитать показатели для самых разных инструментов валютного, товарно-сырьевого и фондового рынков.
Еще один метод – построить график спреда (разницы), вычтя один график из другого. При наличии корреляции график спреда должен находиться примерно у одной величины, ненадолго отклоняясь от нее. Можно использовать и другие арифметические действия, например, разделить график одного актива на другой. Численные значения не важны, нужно лишь понять колеблется результат вокруг одного значения или наблюдаются значимые расхождения и зависимости между величинами нет.
Производить математические действия с котировками и строить синтетические графики можно прямо на живом графике цен, который обладает соответствующим функционалом.
Результаты вычисления корреляции можно применять как своеобразный фильтр, который позволяет выявить пары взаимосвязанных инструментов (активов) с наилучшим потенциалом извлечения прибыли. Однако случайные корреляции также нельзя исключать.
Влияние ГЭПов на корреляцию
В случае, если на обоих графиках наблюдается большой ГЭП или просто солидный импульсный рывок, коэффициент корреляции будет искусственно завышен. После импульса движение график может быть вообще не связано друг с другом, но расчетное значение корреляции будет оставаться высоким. Лишь с течением времени он понизится.
Можно обойти эту проблему, если в расчетной формуле использовать не непосредственно цены, а их приращения. Значение корреляции в этом случае будет меньше зависеть от случайных сильных импульсных движений.
Как использовать корреляцию в трейдинге
Как метод технического анализа, корреляция нередко используется в трейдинге. Однако инвесторы, предпочитающие диверсифицировать свои вложения, также руководствуются данными расчета корреляции при выборе подходящих активов. Учет взаимосвязи между различными финансовыми инструментами благоприятствует принятию верных торговых решений.
В торговле явление корреляции используется:
- Как подсказка при поиске торговых сигналов. Если 2 инструмента обладают высокой прямой либо обратной корреляцией, то наметившееся движение на одном из них можно использовать как ориентир и искать точки входа в соответствующем направлении на втором инструменте;
- Как основа торговой системы. При высоком и стабильном значении коэффициента корреляции в моменты максимального спреда между инструментами можно торговать в расчете на его снижение. Например, стратегия парного трейдинга полностью основана на этом явлении;
- Для общей оценки состояния рынка.
Важно то, что корреляцию можно интегрировать в любую торговую стратегию. Эффективность этого приема не зависит от использования индикаторов или инструментов графического анализа.
Что означает значение коэффициента корреляции
Расчет дает число в долях единицы, которое и является численным выражением связи между 2 величинами. В зависимости от значений принята следующая классификация:
- 1,0 – полная корреляция, на финансовых рынках встречается крайне редко. Даже в ETF, практически на 100% копирующих биржевые индексы, нет 100%-ного совпадения изменения цен акций самого фонда и бенчмарка;
- Если значения коэффициента находятся в диапазоне от (+0.8) до (+1.0), это позволяет говорить о сильной прямой взаимосвязи между конкретными активами, цены которых синхронно меняются на рынке в едином векторе. В этом случае один актив можно приобрести (BUY), а второй – продать (SELL). Обе сделки открываются одновременно.
- 0,7 – сильная корреляция. Большая часть изменений одной величины вызывает схожие изменения в другой величине;
- 0,3-0,7– средний уровень связи;
- Если показатель составляет от 0 до (+0.5), положительная корреляция считается слабой.
- Если значение коэффициента пребывает в интервале от (-1.0) до (-0.8), это говорит о сильной отрицательной корреляции между соответствующими инструментами, цены которых меняются на рынке в разных направлениях. При такой взаимосвязи для обоих инструментов можно открывать однонаправленные сделки – одновременно купить оба актива или одновременно продать их.
Например, значение корреляции 0,90 для пар EURUSD и GBPUSD означает, что в 90% случаев восходящее движение на EURUSD совпадает с восходящим движением на GBPUSD.
Также корреляция может выражаться в процентах. Например, в характеристиках ETF фондов используется такой показатель как R-squared, он показывает уровень корреляции между бенчмарком и акциями фонда. R-squared выражается в процентах.
При этом корреляция может быть как случайной, так и экономически обоснованной. Случайные корреляции могут возникать на произвольных участках истории между несвязанными с собой активами. Например, на отдельных участках истории может возникать корреляция между акциями Apple и валютной парой AUDNZD. Но такая связь неустойчива и не носит систематический характер.
Устойчивая корреляция формируется между связанными экономически инструментами. Например, индекс RTS является барометром для российского фондового рынка. Между ним и акциями «голубых фишек» России есть устойчивая связь. Растет индекс – растет и стоимость бумаг крупных российских компаний.
Как использовать корреляцию в краткосрочной торговле (Биржа и Форекс)
В краткосрочном трейдинге (и на Форекс, и на фондовой бирже) связь между 2 инструментами используется и как основа торговой системы, и как фильтр. Один из самых популярных приемов – выявление ведомого и ведущего активов.
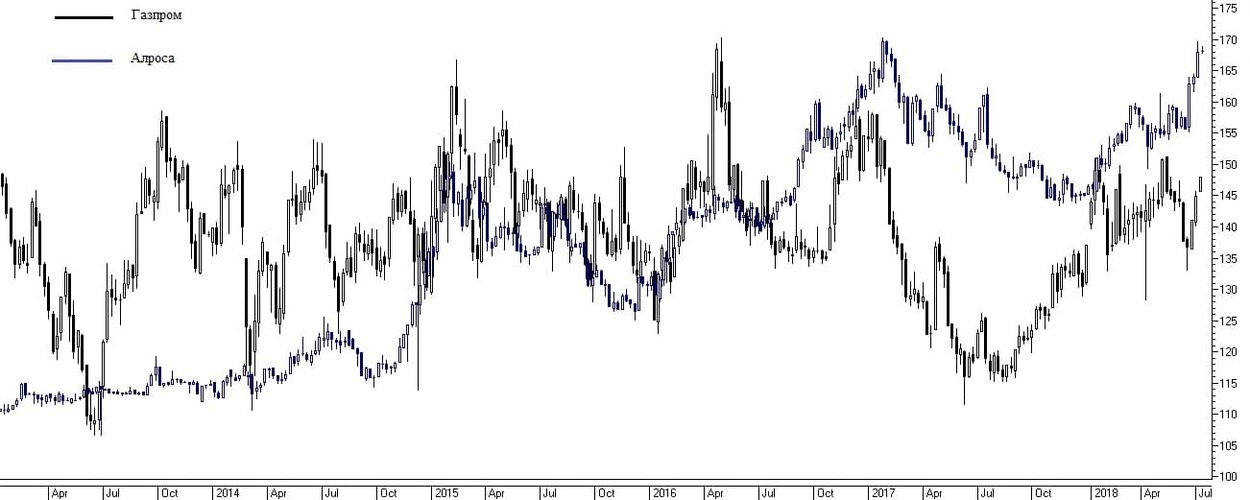
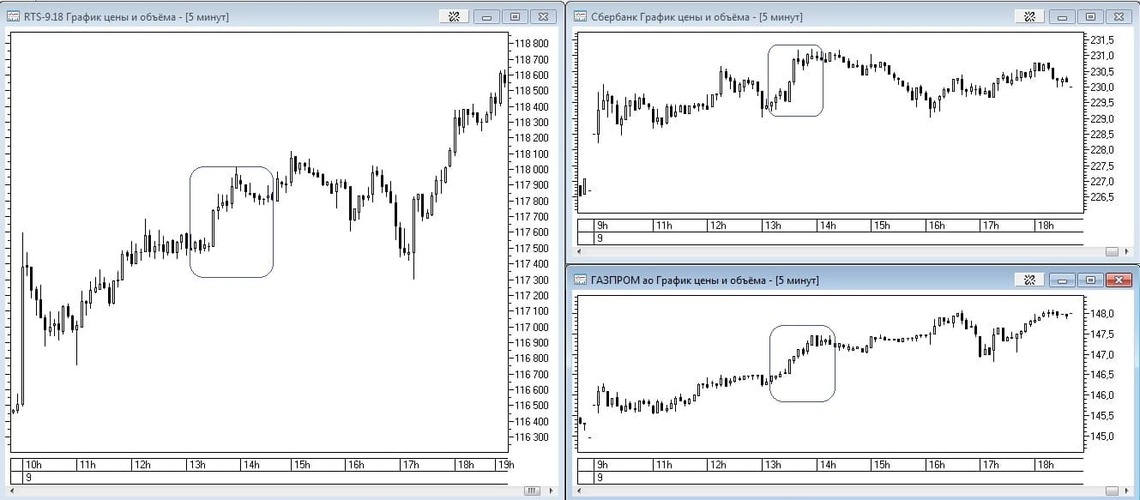
Выявляется устойчивая зависимость между 2 и более инструментами. Если есть небольшое запаздывание между движениями, это можно использовать, заключая сделки на более «медленном» инструменте. Например, фьючерсы на RTS резко упали в цене, а фьючерсы на акции Газпрома еще стоят на месте – можно открыть короткую позицию по Газпрому.
Диверсификация рисков. Здесь есть 2 варианта:
- Выбирать для торговли активы с практически отсутствующей корреляцией. Например, у AUDUSD и USDJPY низкая корреляция, доллар может одновременно расти в паре с австралийцем и падать в паре с японской иеной, можно одновременно открывать короткие позиции по AUDUSD и по USDJPY;
- Либо открывать разнонаправленные позиции по инструментам с высокой корреляцией. Между парами EURJPY и GBPJPY высокая прямая корреляция, нет смысла одновременно открывать сделки на покупку по обеим парам. Если трейдер не уверен в отработке сигнала, то лучше открыть позицию в противоположном направлении по другой паре (возможно, меньшим объемом).
Парный трейдинг – эта методика предусматривает работу во время расширения спреда между 2 активами с высокой корреляцией.
Как применять корреляцию при портфельном инвестировании
Портфельное инвестирование, как известно, также не обходится без учета ценовой корреляции финансовых активов. Взаимосвязь между ценами доходных инструментов часто принимается во внимание портфельными инвесторами, проявляющими интерес к ценным бумагам.
На всех уровнях проводится диверсификация (отраслевая, страновая, по классам активов, по уровню риска). Коэффициент корреляции между разными классами инструментов или инструментами одно группы используется при ребалансировке портфеля.
Это не непосредственно торговля по корреляции, а скорее методика подбора «весов» компонентов инвестпортфеля. За счет этого снижается отклонение от средней доходности, иногда удается получить дополнительную прибыль.
Включим в тестовый портфель 2 инструмента – ETF фонды, копирующие американский S&P 500. Примерно половина инвестируемой суммы направлена в SPY, а остаток – в фонд с тикером SH (Proshares Trust Short S&P 500), он растет при падении индекса и наоборот, то есть движется зеркально. Между SPY и SH почти все время наблюдается высокая обратная корреляция.
Для наглядности взят сложный кризисный период 2007-2010 гг., результат следующий:
- Старт – покупка 100 акций SPY по цене $130, на это уходит $13000, также приобретается 100 бумаг SH по цене $134 ($13400). Стоимость портфеля в этот момент составляет $26400;
- Первая ребалансировка выполняется при снижении обратной корреляции и максимальном расхождении стоимостей акций двух ETF фондов. В этот момент стоимость акции SPY составила $70, а SH – $182,00, портфель в этот момент оценивается в $25477, падение составило 3,50%. Проводится ребалансировка, прибыль, полученная за счет роста бумаг SH, перенаправляется в акции SPY, докупается 78 акций SPY по цене $70,00 (перед этим продается 30 акций SH, что дает $5460). После ребалансировки в портфеле будет 178 акций SPY, и 70 бумаг фонда SH;
- Со временем спред между бумагами снижается, коэффициент корреляция возвращается в район значений -01,00. Мир начинает выходить из кризиса, к дате очередной ребалансировки стоимость портфеля окажется равной $120,00×178 + $95,00×70 = $21360 + $6650 = $28010. За счет грамотной ребалансировки доход составил 6,09%.
Если бы деньги на этом временном промежутке вкладывались только в один ETF фонд, то было бы зафиксировано снижение стоимости инвестпортфеля. Пример выбран упрощенный, в реальности все сложнее – корреляция меняется со временем, к тому же в портфеле находится сразу несколько инструментов. В итоге задача ребалансировки сводится к тому, что нужно решить систему из N уравнений с N неизвестными.
Статистика доказывает, что лучший результат показывают комбинации инструментов с отрицательной корреляцией в районе -0,50. В этом случае стандартное отклонение доходности наименьшее. Простыми словами – комбинация этих активов позволяет получить тот же процент доходности с наименьшим риском.
Основные стратегии торговли с использованием корреляции
Есть несколько полноценных торговых тактик, полностью построенных на связи между 2 или группой активов. К ним относятся:
- Статистический арбитраж – подбираются активы с высокой прямой либо обратной связью и торгуются значимые расхождения между графиками. При максимальном расхождении растет вероятность, что оно снизится, на этом и построена работа;
- Парный трейдинг – его можно рассматривать как подвид статистического арбитража;
- Частичное либо полное хеджирование – с использованием фактора корреляции выполняется страховка от рисков части инвестиционного портфеля, либо всей инвестированной суммы.
По сути, все сводится к 2 подходам – созданию рыночно-нейтральной стратегии либо страховке части стоимости портфеля (или всей его стоимости). Парные корреляции используются во всех перечисленных случаях.
Статистический арбитраж
Статистический арбитраж – это методика онлайн-трейдинга, подразумевающая открытие позиции BUY (покупка) по одному активу с одновременным открытием позиции SELL (продажа) по второму активу. Чтобы реализовать данную стратегию, трейдер выбирает исключительно те финансовые инструменты, которые статистически связаны друг с другом. Иными словами, между торгуемыми активами должна быть определенная корреляция.
В пользу статистического арбитража говорят 2 фактора:
- Поведение отдельного инструмента спрогнозировать сложно. Вероятность правильности прогноза колеблется около 50%. Речь идет о математическом прогнозировании, без учета фундаментальных факторов;
- Если выявить пару инструментов с высокой связью, то вероятность прогнозирования их поведения выше 50%. За счет этого и удается создать рыночно-нейтральную стратегию – систему, в которой прибыль трейдера формируется независимо от направления движения ценовых графиков.
Стратегии статистического арбитража отличаются только методикой подбора инструментов для портфеля. Крупные хедж-фонды могут разрабатывать собственные алгоритмы отбора акций и прочих инструментов для инвестпортфеля, эти методики могут патентоваться.
Интересное по теме:
- Корреляция валютных пар на Форекс – Таблицы и как торговать на корреляции
- Что показывает Коэффициент Швагера и Примеры использования (+нормы значений)
- Что такое Коэффициент Кальмара (Calmar Ratio) – Примеры использования и нюансы
- Что такое Коэффициент Шарпа – Примеры использования, Нормы значений
- Что такое Коэффициент Сортино (Sortino ratio) и Что он показывает
Что касается торговой тактики, то торгуется спред. То есть между инструментами с высокой корреляцией измеряется разница и затем при ее увеличении более дорогой актив продается, а дешевый покупается в расчете на то, что спред должен уменьшиться. При сужении спреда до минимальных значений заключаются зеркальные сделки.
Это касается и валютных пар, и акций, и сырьевого рынка, и драгоценных металлов. Описанная тактика не имеет ограничений по классу актива. Заработок растет независимо от направления движения цены, важно только, чтобы было хоть какое-то движение.
Парный трейдинг
Эта стратегия – частный случай статистического арбитража. Используется пара инструментов с прямой либо обратной связью, это могут быть и валюты, и биржевой индекс + валютная пара. Используется та же логика, что и в статистическом арбитраже, но за счет того, что не нужно анализировать десятки инструментов работать можно и вручную.
Простейший пример – валютные пары EURUSD и USDCHF, между ними существует устойчивая обратная корреляция. Когда EURUSD растет пара USDCHF падает и наоборот.
Для определения моментов максимального расхождения EURUSD и USDCHF понадобится график спреда. Можно построить график EURUSD/USDCHF или EURUSD/USDCHF.
Далее с графиком спреда работа ведется по обычной схеме. Можно строить уровни поддержки и сопротивления, и открывать сделки по обеим валютным парам при развороте графика спреда от уровня. Можно использовать индикаторы, например, полосы Боллинджера, торговать при приближении синтетического графика к его границе и формировании разворота.
График EURUSD-USDCHF подошел к нижней границе ВВ. Это значит, что франк ослаб в паре с американским долларом, а евро укрепилось. Сделки заключаются в расчете на то, что спред между парами начнет снижаться:
- По USDCHF открывается короткая позиция – расчет на укрепление франка;
- По EURUSD открывается сделка на покупку – расчет на ослабление евро.
После подхода графика спреда к противоположной границе полос Боллинджера обе сделки закрываются. В примере прогноз оправдался, сделки принесли профит в 195 и 118 пунктов.
Этот же принцип можно перенести на фондовый рынок, коррелирующими валютами дело не ограничивается. Например, следить за индексом, отражающим состояние рынка какой-либо страны и следить за акциями отстающих от него компаний.
Методика работает. Показателен пример трейдера с никнеймом CIS. Не имея профильного образования стартовые 1 млн. японских иен он смог превратить в 20+ млрд иен. При этом анализу рынка он практически не уделял время, точки входа определялись исключительно по методике парного трейдинга.
Частичное хеджирование
Методика немного напоминает парный трейдинг, но цели ставятся иные. Если трейдер пытается заработать за счет статистического арбитража, то инвестор хочет минимизировать риски. Значимость корреляции велика, на ее основе подбираются инструменты, с помощью которых будет выполняться хеджирование. Частичным оно называется из-за того, что страхуется не вся стоимость инвестпортфеля.
Пример – собран простейший портфель из акций IT гигантов (Apple + Google + Amazon + Microsoft). Стоимость портфеля составляет $1 млн. Инвестор хочет подстраховаться на случай кризиса и падения стоимости ценных бумаг.
Нужно подобрать актив, хорошо коррелирующий со всеми 4 инструментами или подбирать отдельный хеджирующий актив под каждый пункт инвестпортфеля. В примере бумаги всех перечисленных компаний в целом коррелируют с поведением индекса S&P 500, он подходит для хеджирования.
Так как инвестпортфель ориентирован на рост, открыты длинные позиции, то при хеджировании нужно продавать S&P 500. Можно делать это с помощью фьючерсов. При полном хеджировании размер короткой позиции должен быть равен стоимости инвестпортфеля, при частичном – нет.
В заключении
Если разобраться в вопросе, что такое корреляция глубже, то окажется, что это не просто любопытная закономерность, а основа для прибыльной торговой стратегии. Основная проблема в том, что нужно понять является закономерность случайной или устойчивой, обусловленной фундаментальными зависимостями между двумя величинами. Решение этой задачи облегчается различными онлайн-сервисами, рассчитывающими корреляцию в режиме реального времени.
Еще одно преимущество корреляции в том, что пользу из нее можно извлечь независимо от используемой торговой стратегии. Используя фактор устойчивой связи между двумя инструментами можно и снизить торговые риски, и повысить прибыль.
Что касается методики использования корреляции, то по сути все сводится к разным подвидам статистического арбитража. Существуют десятки стратегий, но базовая логика одна и та же.
Загрузка…
Автор: Максим Галански
Трейдер, инвестор, частный предприниматель. “Финансовые рынки объединяют разные интересы, бизнес, континенты. Это то место, где всегда можно найти, чем заняться, что и как сделать или создать.”
1. Коэффициент корреляции это лишь одна характеристика из множества параметров и не нужно переоценивать его значения
Приходящие с биржевых терминалов потоки ценовой информации указывают на наличие как хаотичного случайного компонента в поведении цен, так и неко- торой их согласованности с ценами других активов. Математическая статистика позволяет выявить эле- менты связности поведения временных рядов. Для этого можно проводить анализ Фурье или оценивать другие параметры. Наиболее удобным и простым является коэффициент регрессии (корреляции) К. Он часто используется для анализа степени связанности двух временных рядов. Этот коэффициент может быть определен для любых двух совокупностей (в том числе случайных) величин Xi и Yi, где i пробега- ет значения от 1 до n. По выборке длиной n можно определить эмпирической коэффициент корреляции, который определяется по следующей формуле:
K= , где Mx и Му – оценки математического ожидания случайных ве- личин {X} и {Y}, а – величины их среднеквадратичных отклонений. К изменяется в пределах (-1, 1).
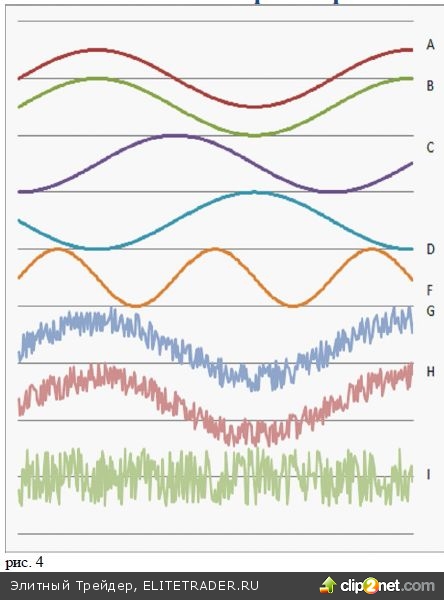
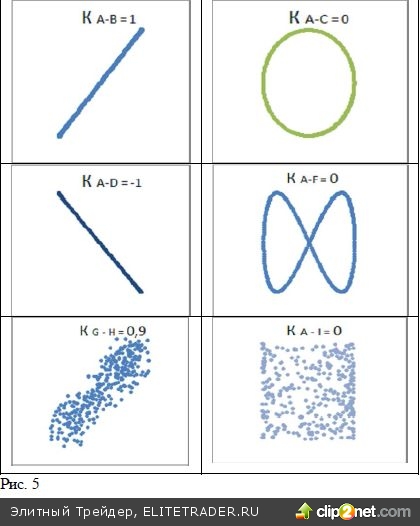
Коэффициент корреляции оказывается равным едини- це для наборов двух величин X(ti) и Y(ti), значения которых синфазно изменяются со временем, таких как обозначенные буквами А и В синусоиды на рисунке 4. На серии рисунков 5 эти наборы зависимостей X(ti) и Y(ti) представлены в координатах (Х и У). Для проти- вофазных колебаний (кривые А и D) коэффициент корреляции равен -1. При смещении фазы одного из процессов коэффициент корреляции уменьшается, чтобы стать близким к нулю для ортогональных коле- баний sin(t) и cos(t) (кривые А и C). Аналогично, нулевую корреляцию обнаружим у колебаний с отли- чающимися в два раза периодами колебаний sin(t) sin(2t) (Кривые А и F). Коэффициент корреляции уменьшается и за счет «зашумления» колебаний двух разных процессов. Так, для синхронно колеблющихся кривых G и H, в которых имеется случайный шум, рассчитанный коэффициент корреляции оказывается уже меньшим единицы. Чаще именно подобное зашумленное поведение наблюдается для цен различных активов. Корреляция набора чисто случайных чисел Yi с любой зависимостью X(ti) будет стремиться к нулю по мере роста выборки, а «график» пар чисел X(ti) и Yi не будет давать даже намеков на зависимость, как это изображено на последнем графике для «зависимости» пар чисел Xi и Yi, где Xi бралось с верхней синусоидальной кривой А, а Yi считывалось с кривой I, представляющей собой набор равномерно распределенных случайных чисел.
2. Следует помнить о возможной точности определения корреляции
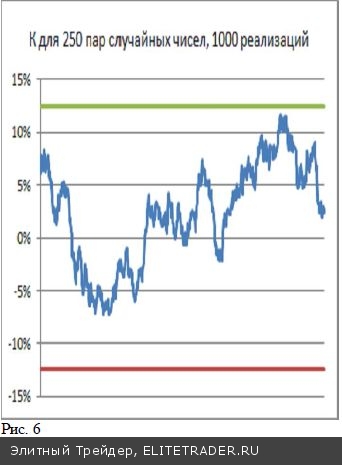
В рыночных зависимостях кроме детерминированных компо- нент, которые приводят к часто наблюдаемой связанности их поведения, присутствуют также другие слагаемые, которые можно трактовать как «число случайные». Случайные слагае- мые тоже дают вклад в определяемый коэффициент корреляции К. Так, при расчете К для конечной выборки раз- мером N между двумя наборами Xi и Yi случайных величин, равномерно распределенных на интервале (0-1), тоже будут получаться отличные от нуля значения. Значение Кj(250) (для выборки размером 250 пар) будет зависеть от номера j самой выборки. Коэффициент корреляции К будет случайной вели- чиной, реализации которого Kj согласно закону больших чисел оказываются распределенными по нормальному закону. На представленном рисунке видим, как изменялись коэффициен- ты корреляций Кj(250) между выборками по 250 пар случайных величин для тысячи реализаций (j=1,2,3…1000). Среднеквадратичное отклонение ?? случайной величины К (250) близко к 0,062, а значит, что в 77% случаев эмпирическое значение коэффициента корреляции Кj(250) для 250 пар случайных величин будет находиться в пределах ±2??. (Ли- нии ±0,124 приведены на рисунке). А за пределы 3*?? (±0,186) случайная величина Кj(250) будет выходить только в 1,35% случаев. Таким образом, значе- ние К(250) для набора 250 пар чисел, большее по модулю 0,2, скорее всего, не может быть связанным со случайными обстоятельствами, и для временных рядов с К>0,2 приходится отбрасывать идею об их случайном изменении и можно ис- кать возможные причины их коррелированного поведения. Для нормально распределения Kj(N) величина ?? обратно пропорциональна квадратному корню из размера выборки N. Поэтому для выборки размером в 1000 пар случайных чисел ?? уменьшится в два раза по сравнению с выборкой из 250 пар случайных чисел, а выборки меньшей в четыре раза, размером в 62 пары точек ??, напротив, вырастет в два раза. Если считать, что в цене акций имеется заданный детерминированный компонент и случайное слагаемое, то увеличивая объем выборки можно уменьшить добавку в коэффициент корреляции, которая возникает за счет случайного слагаемого. В случае временного ряда, для сниже- ния вклада случайных компонентов нужно увеличивать период, с которого берутся используемые точки. Однако слишком увеличивать период исследования тоже нельзя, поскольку на большом интервале вполне может изменяться характер согласованности кривых. Понятно, что с помощью коэффициента корреляции оценивается только среднее значение корреляции за период. Поэтому в качестве окна изучения чаще всего используют годовой интервал, дающий с учетом выходных и праздничных нера- бочих дней около 250 дневных цен закрытия. Выбирая годовой интервал, следует помнить, что в полученном коэффициенте корреляции К(250) могут давать вклад случайные компоненты цены, величина которого на выборке в 250 точек легко может составлять ±0,1, а в отдельных (пусть и редких) случаях дос- тигать даже ±0,2. Поэтому реально при вычислении коэффициента корреляции на годовом интервале есть смысл удерживать только одну значащую цифру по- сле запятой, а все остальное может быть связано со статистическими погрешностями. Если же коэффициент корреляции К(250) оказывается меньшим 10%, то о взаимосвязи исходных величин лучше не думать. (Нет смысла искать неслучайных вещей там, где доминирует случайность).
3. Корреляции индексов
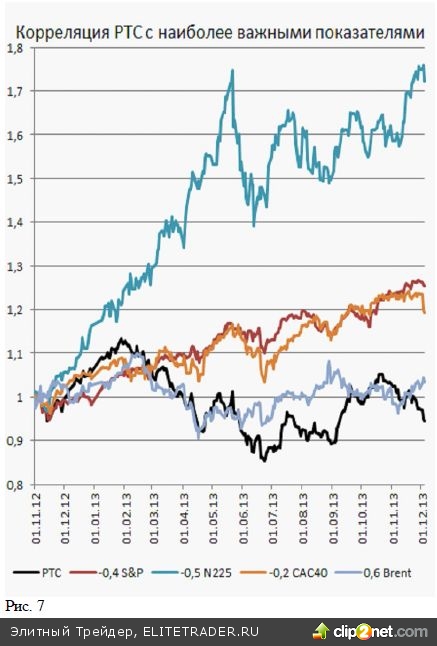
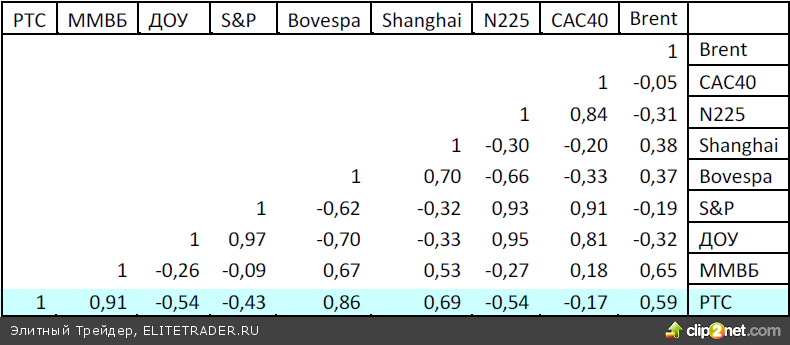
С учетом приведенной выше оценки точности можно рассчитать коэффициенты корреляции потенциально наиболее значимых для индекса РТС величин. На приведенном рисунке изображены относительные изменения индекса РТС, американского индекса S&P 500, японского Nikkei225 и французского CAC40. Оказывается, что в последний год коэффициент кор- реляции индекса РТС с указанными индексами составлял отрицательную величину. (Значения К для РТС с указанными выше индексами приведены в подписях к кривым на рисунке). Отрицательной величина корреляции становится за счет длительных периодов разнонаправленных движений индексов. Так, индекс РТС в первой половине года снижался, в то время как индексы указанных стран показывали рост. Особенно сильно подрос индекс N225, что и дало высокий отрицательный коэффициент К. По- ложительным коэффициент корреляции (из приведенных кривых) оказался только для цен нефти марки Brent. Хотя коэффициент К с нефтью +0,6 оказывается не столь высоким, как это можно было бы предположить, с учетом зависимости нашей эко- номики от цен на это сырье.
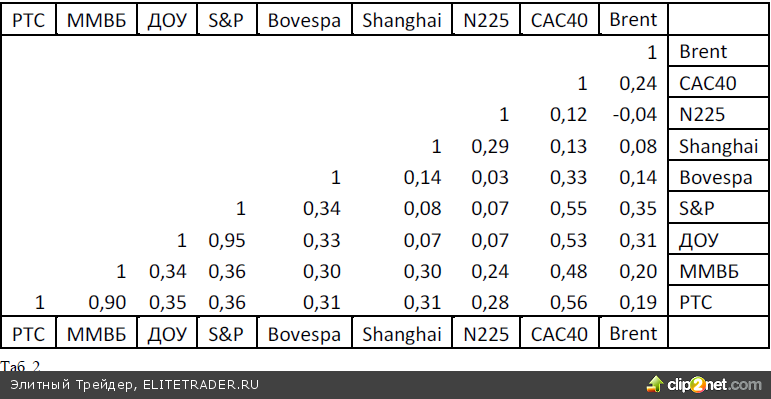
Из приведенной Таблицы 1 попарных корреляций видим, что указанные активы распределяются на две группы. В одной располагаются индексы развитых стран, которые имеют между собой достаточно высокие положительные значения по- парной корреляции. Так, коэффициент корреляции индекса S&P 500 и индекса САС 40 очень высок и составляет +0,9. В то время как коэффициенты корреля- ции с индексами стран BRICS для них оказываются отрицательными.
В другую группу выделяются индексы стран BRICS. На совместном графике относительных изменений индексов хорошо видно их согласованное поведение. Коэффициент корреляции РТС с индексами Китая и Бразилии оказывается даже чуть большим, чем зави- симость индекса РТС от цен нефти. Это указывает на достаточно высокую связанность поведения индексов стран BRICS. Из приведенных на двух рисунках кривых и коэффи- циентов корреляции этих кривых с индексом РТС можно сделать предположение, что на годовом гори- зонте решение об инвестировании в фондовый рынок России, Бразилии и Китая набором основных инве- сторов, определявших динамику индексов, принимались по схожим соображениям. Аналогично, как и решения об инвестировании в рынки США, Японии и Франции.
4. Корреляции приращений цен
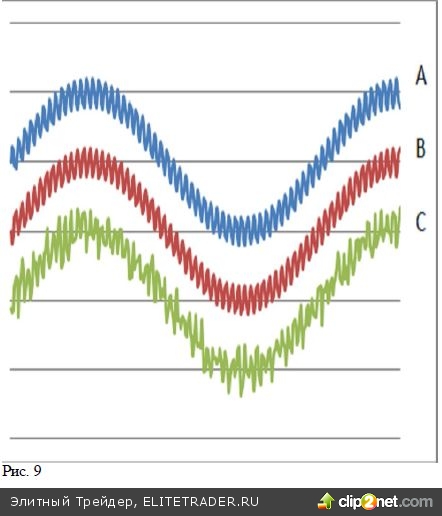
Важно обратить внимание еще на одну важную осо- бенность. Для спекулянта гораздо большее значение имеет не корреляция цен акций, но корреляция днев- ных изменений цен. А это совсем не одно и то же. На рисунке 9. представлены три модельных графика. Каждый из них представляет сумму длиннопериод- ной синусоиды (годовые изменения) с соответствующей добавкой. А вот добавка для трех графиков разная. Для графика А – это «недельная» синусоида с периодом в 5 дней. Для графика В и С – недельная синусоида имеет отрицательный знак, так что на графиках А она находится в противофазе с добавкой на графиках В и С. На графике С, кроме того, имеется случайная добавка. Амплитуды всех добавок выбраны равной пятой части амплитуды основного колебания. Попарные коэффициенты кор- реляции кривых, несмотря на добавки, близки к единице и равны КА-В=+0,92; КА-С=+0,9; КB-С= + 0,9.
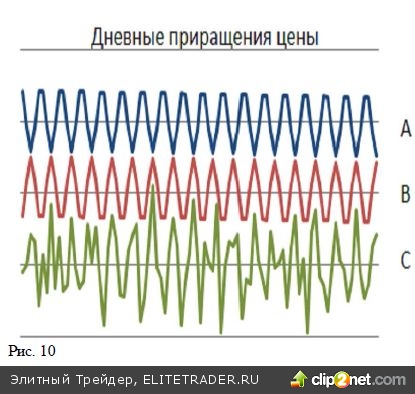
А вот для «дневных приращений цены», приведенных на втором графике картина, совсем иная. Точки на кривых А, В, С на рис. 10 получены в результате вычисления разностей последовательных по времени значений на кривых рис.9: Арис.10=Арис.9(t)-A рис.9(t-?t). Как видим, дневные приращения цен гораздо меньше зависят от годовых трендов, но в большей мере опре- деляются короткими колебаниями, имеющими период в несколько дней. Для указанных разностных кривых (рис.10) коэффициенты корреляции имеют совсем другие значения КА-В= -1,0; КА-С= -0,7; КB-С= + 0,7. Коэффициенты корреляции вычислены по вы- боркам в 250 пар. (С учетом предыдущего пункта ограничиваемся одним знаком после запятой для кривых содержащих случайную компоненту).
Аналогично можно поступить с использовавшимися выше индексами и обра- зовать из них наборы дневных приращений. Для полученных рядов относительных приращений были рассчитаны значения коэффициентов кор- реляции. Как видим из приведенной ниже таблицы 2, значения коэффициентов корреляции принципиально отличаются от соответствующих величин, приведенных в таблице 1.
Главное отличие состоит в большей устойчивости таких коэффициентов. Кроме того, корреляции приращений в основном оказываются положитель- ными. Исключением оказалось отрицательная величина корреляции приращений цены нефти и приращений японского индекса Nikkei 225. Однако абсолютные значения коэффициентов корреляции для приращений оказыва- ются, как правило, заметно меньшими, чем для самих величин и, в большинстве случаев, лишь немногим превышают возможные значения для наборов чисто случайных величин.
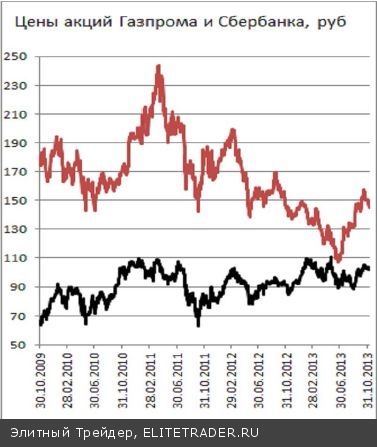
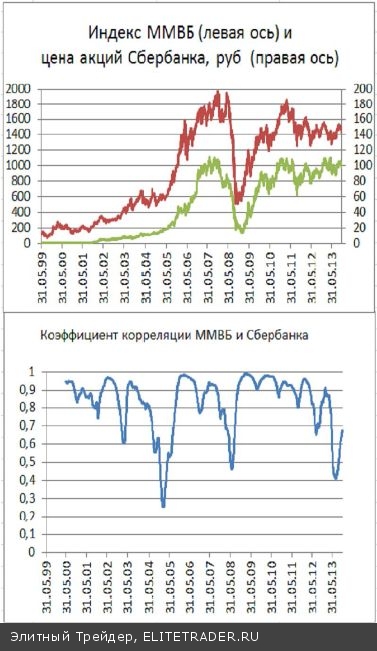
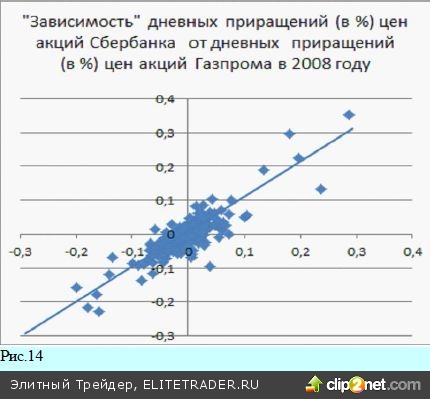
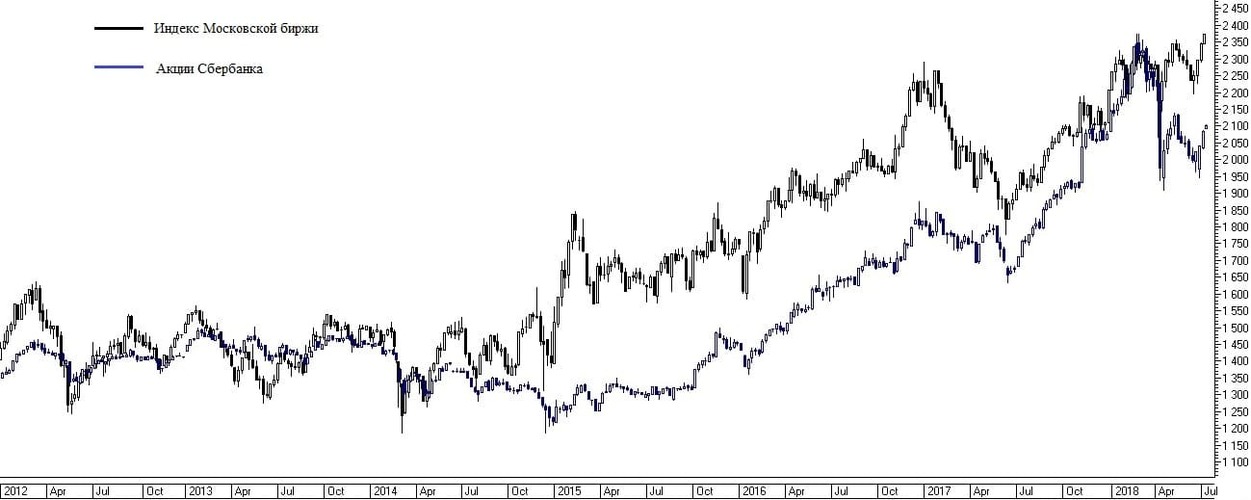
Степень устойчивости коэффициента корреляции можно продемонстрировать на их временных зави- симостях. Как уже упоминалось, коэффициент корреляции зависит от времени. Так, для двух наибо- лее ликвидных бумаг российского рынка, цен акций Сбербанка и Газпрома коэффициент корреляции (вычисленный по предыдущим 250 дням – пример- ный годовой интервал) сильно изменяется со временем. Например, в конце 2008 года коэффициент корреляции приближался к +1. Значит, в 2008 году в динамике цен акций преобладала согласованная ком- понента. Однако были периоды, когда коэффициент корреля- ции опускался в отрицательную область. Значит, в течение года, предшествовавшего таким провалам, значений корреляции, цены акций Газпрома и Сбер- банка изменялись в большей мере разнонаправленно. Такого рода разнонаправленность является довольно частым явлением на нашем рынке. Так часто проти- вофазное рынку движение показывали акции Сургутнефтегаза, Норильского Никеля или некото- рые другие акции. Это происходило либо по специфическим корпоративным причинам, либо, когда инвесторы на рынке выбирали какие-либо ак- ции в качестве защитного актива. А вот краткосрочные изменения цен акций, пусть даже в среднем, не являются столь высоко согласо- ванными, но зато демонстрируют большую устойчивость коэффициента корреляции в разные периоды времени. Такое отличие можно увидеть, сопоставляя поведение корреляции как самих цен акций Сбербанка и Газпрома (рис. 12), так и их изме- нений (рис.13). Рис.14 Стоит отметить, что даже для периодов высокой корреляции «зависимость» приращений цен одних акций от приращения цен других акций выглядит совсем не как динамическая кривая. Тем не менее, при больших К с достаточно большой вероятностью будет работать линейная регрессионная зависимость. В результате, можно, например, по приращению цен акций Газпрома оценить приращение акций Сбербан- ка (и наоборот). Однако беда такой зависимости состоит в том, что приращения цен указанных акций происходят за один временной интервал. И оценка вероятности приращения цены акций Сбербанка в определенный день возможна только при завершении этого же дня для акций Газпрома.
Определение коэффициентов корреляции между различными рядами данных позволяет быстро выявить наиболее простые зависимости и найти активы, ко- торые коррелируют с изучаемым. Так, по изменениям индексов зарубежных рынков или цен на товарные группы можно делать оценки вероятности теку- щих изменений индексов на нашем рынке. Но вот с самым главным – возможностью делать вероятностные прогнозы по уже произошедшим событиям все немного хуже. А ведь именно такого рода прогнозы имеют наибольшую ценность. Для этого нужно изучать корреляции сегодняшних приращений индекса с прошлыми приращениями индексов дру- гих рынков или приращениями цен товарных групп. Но по факту оказывается, что информация о прошлом довольно быстро девальвирует со временем. Из- вестная «максима» технического анализа «история цен содержат всю информацию о рынке», работает с большой натяжкой и при условии учета про- исходящих on-line событий. Реально прошлые цены определяют будущую динамику лишь в ограниченной мере. Для определения того, какое прошлое наиболее существенным образом влияет на настоящее, для начального анализа можно пытаться выстраивать корреля- цию текущих приращений с изменениями значений индексов, цен акций в предыдущие моменты времени. По факту оказывается, что уровни корреляции приращений из разных временных интервалов, как правило, имеют довольно низкие значения.
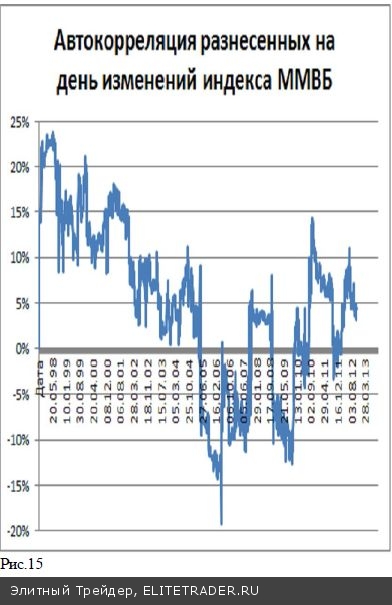
Это можно проиллюстрировать на примере автокорреля- ционной функции приращений индекса ММВБ. Корреляция берется для двух последовательных рядов дневных изменений индекса ММВБ. И если в качестве значений Xi берется дневное приращение индекса ММВБ за текущий день, то в качестве Yi выступают приращения индекса за предыдущий день. Из приведенного на рисунке 15 графика видим, что, во- первых, величина автокорреляции не сильно превышает значения коэффициента корреляции для пар чисто слу- чайных чисел. Во-вторых, К может изменять знак. И все же в длительные периоды знаковой определенно- сти коэффициента корреляции, с его использованием можно заработать на рынке деньги. Для этого, при поло- жительных К, достаточно покупать индекс под занавес торгов в дни, когда он закрывается с положительным приращением, и продавать в дни, когда индекс имеет отрицательное приращение. В результате, на периоде положительной определенности К можно получить ста- тистически значимое положительное приращение счета. В периоды отрицательного К, работоспособной будет контр трендовая к изменениям прошедшего дня методика.
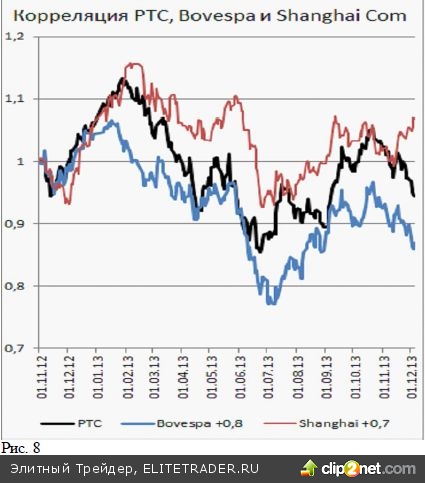
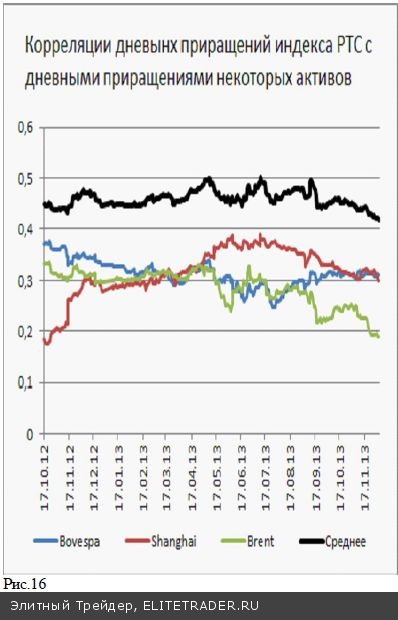
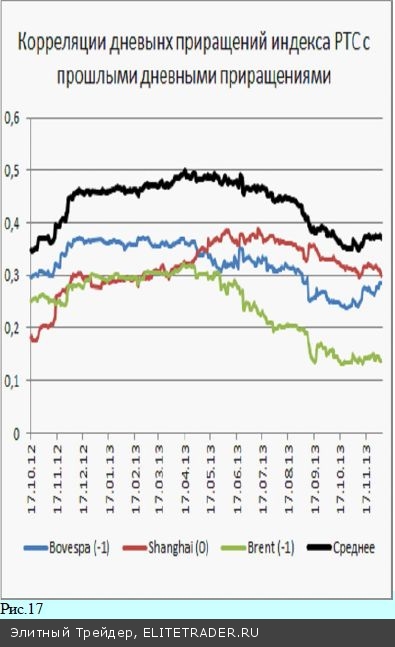
В заключение отметим, что из рядов данных, имеющих наибольшую корреляцию с изучаемым активом, можно отобрать наборы, имеющие наибольшие по модулю ко- эффициенты корреляции. Тогда, (взвешивая, например, пропорционально величине К) можно строить синтетиче- ские активы, которые будут потенциально иметь более глубокую связь с интересующим нас активом, и иметь большее значение коэффициента корреляции. На рис. 16 приведены рассчитанные за предыдущий прошедший год коэффициенты корреляции приращений индекса РТС к приращениям индекса Bovespa, Shanghai Com., цен нефти марки Brent. Видим, что все три указанных коэффициен- та в течение последнего года изменялись в окрестности значений 0,3. Образовав гипотетический актив, изменения которого равны среднему значению изменений трех указанных величин, так же можно рассчитать коэффициент корре- ляции для дневных приращений полученного актива. Рассчитанные по тем же правилам значения коэффици- ента корреляции приращений индекса РТС и указанного синтетического актива приведены на рис. 16 жирной линией. Видим, что уровни корреляции вновь образован- ного актива оказались систематически большими, чем для входящих в него слагаемых. На таком пути можно образовывать другие активы добиваясь получения более высоких значений коэффициентов корреляции. Наиболее очевидное практическое значение имеет ком- бинирование таких синтетических активов из уже ушедших в историю рядов данных. Так, в пару к Xi – изменениям индекса РТС можно, например, составить актив Yi из трех величин: изменений цен нефти и индек- са Bovespa в предыдущий день и значения индекса Shanghai Сomp., но уже в текущий торговый день, кото- рый в Китае заканчивается намного раньше, чем закрываются торги в Москве. Как и в предыдущем слу- чае, коэффициент корреляции приращений индекса РТС с такой синтетической переменной оказывается выше попарных корреляций с каждой из этих величин по от- дельности. Тем самым коэффициент корреляции помогает найти более тесно связанную с изменениями индекса РТС переменную, значения которой появляются раньше по времени, чем время закрытия индекса РТС. Поступая аналогичным образом можно отбирать наборы таких переменных, выбирая из них наиболее связанную пару с интересующим активом.
(Нужно быть готовым к кропотливой работе по предварительной очистке данных, учету праздничных дней, торговле в выходные дни, как это проис- ходит по нефти марки Brent и т.д.). И еще: правильнее брать не среднее значение входящих величин, а их взвешенные значения по средней величине коэффициента корреляции. Лучше ввести изменяемые параметры, подбирая которые можно добиться лучших результатов. Однако оптимизацию лучше проводить уже не по величине коэффициента корреляции, а по потенциаль- ной прибыли, которую можно получить, используя ту или иную торговую методику. Можно уже на этапе подбора исходных данных использовать нейросети, когда оптимизирующая система на этапе обучения сама подбира- ет наиболее подходящие коэффициенты. Но все это уже скорей относится к созданию торговой системы. В данном же тексте продемонстрировано то, как можно использовать коэффициенты корреляции.
РЕЗЮМЕ
Определение коэффициентов корреляции позволяет установить степень связанности изу- чаемых временных рядов. Большие значения коэффициентов корреляции свидетельствуют о высокой коррелированности поведения двух активов. Коэффициент корреляции К изме- няется со временем, но, к сожалению, определение К на малых интервалах может давать большие случайные отклонения. Поэтому реально приходится рассчитывать средние значе- ния К по временному интервалу. Для наборов дневных данных наиболее оптимальным для определений К является годовой интервал. Коэффициент корреляции позволяет проводить регрессионные прямые, которые в некото- рых случаях позволяют прогнозировать вероятность изменения интересующего актива по изменениям других активов. Особенно интересным это становится в случаях, когда можно получить значимые коэффициенты корреляции с рядами данных, которые для текущего момента уже стали историей. Для этого бывает полезным образование «синтетических акти- вов». Таким образом, коэффициент корреляции может быть полезным элементом предваритель- ного анализа исходных рядов цен, которые будут служить исходными данными для будущей торговой системы.
(C)
Источник
При копировании ссылка обязательна | Не является индивидуальной инвестиционной рекомендацией
Поддержите нас – ссылаясь на материалы и приводя новых читателей
Нашли ошибку: выделите и Ctrl+Enter
Добавьте Элиттрейдер в избранное Дзен новостей
Трейдинг19 февраля 2020 в 16:0016 051
Корреляция, индексы, акции
Корреляция в краткосрочной торговле и при построении портфеля ценных бумаг
Определение и логика корреляции
Рис. 1. Пример прямой корреляции.
Рис. 2. Пример обратной корреляции.
Рис. 3. Пример околонулевой корреляции.
Корреляция в краткосрочной торговле
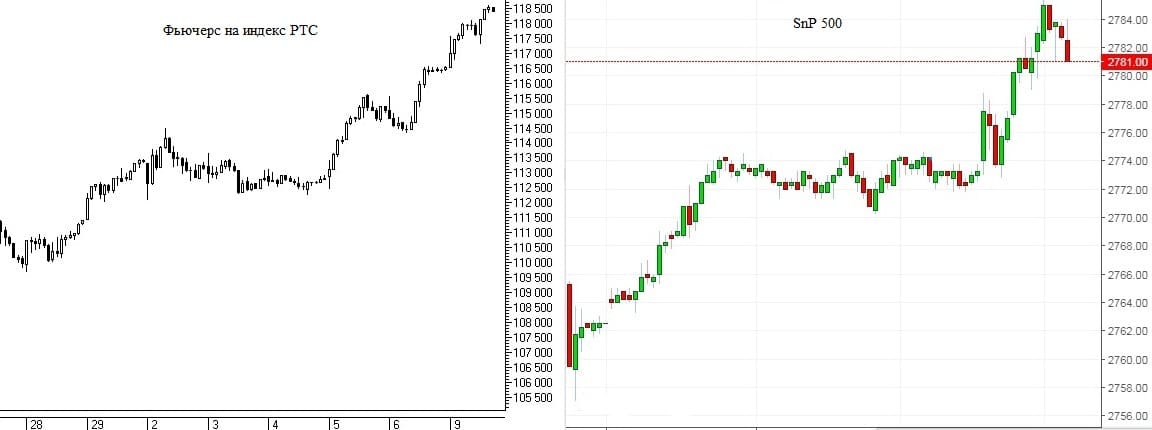
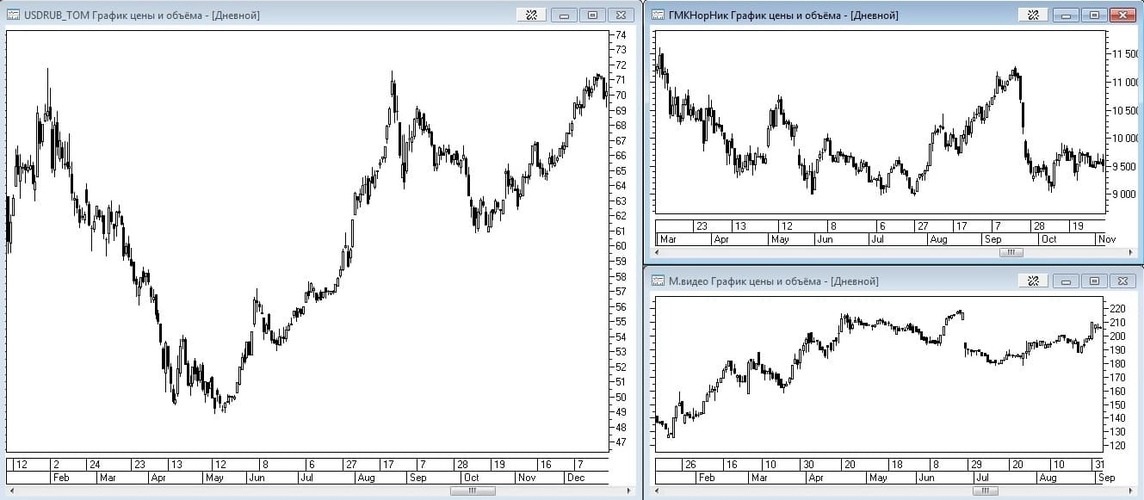
Рис. 4. Пример корреляции фьючерса на индекс РТС и индекса SnP.
Рис. 5. Пример корреляции фьючерса на индекс РТС и акций «Газпрома» и «Сбербанка».
Корреляция при построении портфеля ценных бумаг
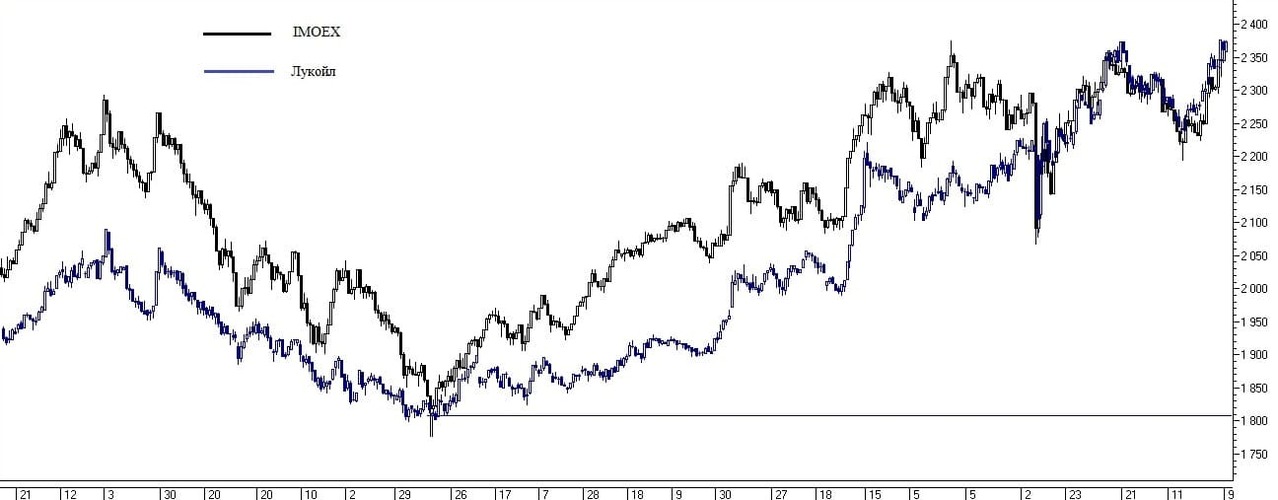
Рис. 6. Пример динамики акции от поддержки по индексу.
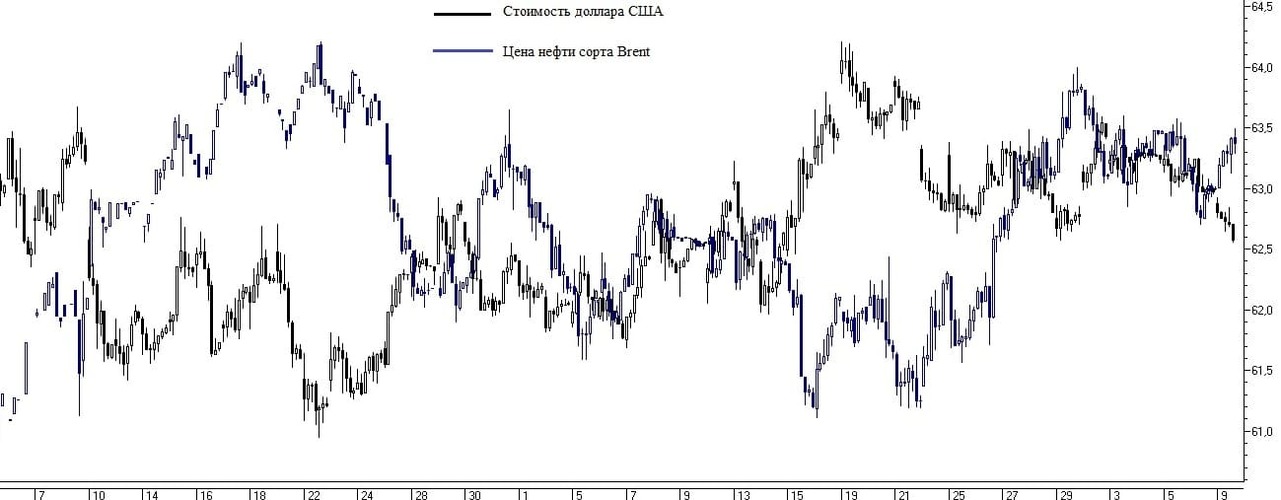
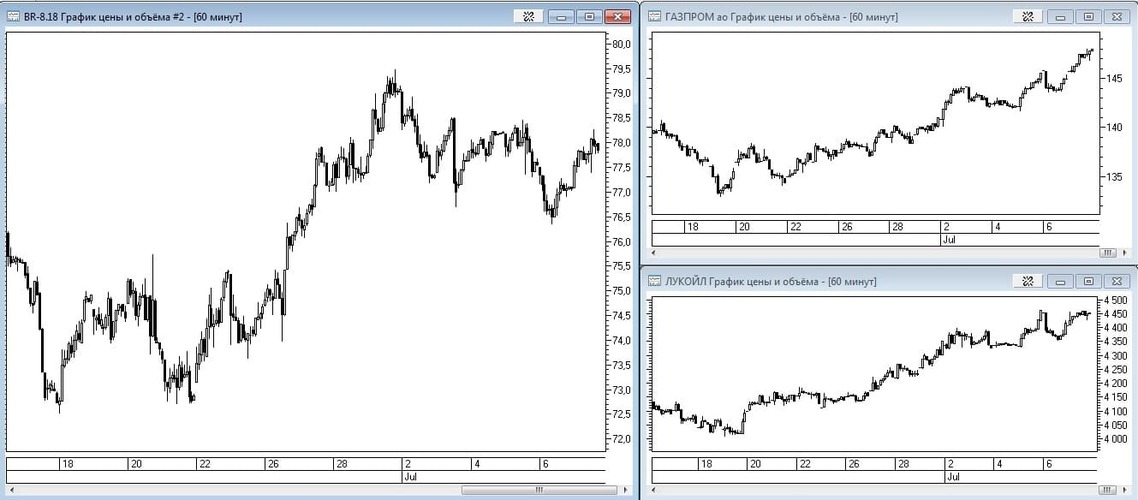
Рис. 7. Пример корреляции нефти и бумаг нефтегазового сектора.
Рис.8 Пример корреляции доллара США, бумаг экспортера и компании внутреннего спроса.