Вы отправили работу на проверку эксперту. Укажите номер телефона на него придет СМС
Отправить
Незнайка → ЕГЭ → Математика → Базовая → Вариант 6 → Задание 5
Задание № 4461
Найдите cos 720°.
Показать ответ
Комментарий:
Косинус – функция периодическая [math]T=360^o=2pi[/math]
[math]cos(720^circ)=cos(360^circ+360^circ)=cos;0=1[/math]
Ответ: 1
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
2 301 257
Уже готовятся к ЕГЭ, ОГЭ и ВПР.
Присоединяйся!
Мы ничего не публикуем от вашего имени
Единичная окружность

О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Математика для блондинок
Математика – это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
Страницы
воскресенье, 24 октября 2010 г.
У меня 720 градусов, как дальше найти синус и косинус альфа?
“А что если при нахождении значения альфа равному 4пи, у меня 720 градусов, как дальше найти синус и косинус альфа??” – такой вопрос был задан в комментариях. Действительно, как найти тригонометрическую функцию, если угол альфа больше 360 градусов?
Представьте, что все углы больше 360 градусов или 2 пи – это клубок пряжи. Для того, чтобы узнать значения тригонометрических функций для таких углов, этот клубок пряжи нужно сначала размотать. Один виток пряжи равняется углу в 360 градусов или 2 пи. Разматывать клубок нужно до тех пор, пока значение угла не станет меньше 360 градусов или 2 пи. После этого по таблице значений тригонометрических функций или по тригонометрическому кругу находим значение нужной тригонометрической функции.
Этот же фокус с углами в радианах будет выглядеть так:
Для угла 720 градусов или 4 пи получается, что синус и косинус такие же, как и для угла 0 градусов. Решение можно записать так:
Синус 720 градусов или 4 пи равен синусу нуля градусов и равен нулю. Косинус 720 градусов или 4 пи равен косинусу нуля градусов и равен единице.
Зачем нужны все эти заморочки с такими большими углами? Я не зря упомянул о клубочке пряжи. Давайте вместе попробуем его не только распутать, но и посмотрим, как же он наматывается и зачем вообще нужен.
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
[/spoiler]
The value of cos 720 degrees is 1. Cos 720 degrees in radians is written as cos (720° × π/180°), i.e., cos (4π) or cos (12.566370. . .). In this article, we will discuss the methods to find the value of cos 720 degrees with examples.
- Cos 720°: 1
- Cos (-720 degrees): 1
- Cos 720° in radians: cos (4π) or cos (12.5663706 . . .)
What is the Value of Cos 720 Degrees?
The value of cos 720 degrees is 1. Cos 720 degrees can also be expressed using the equivalent of the given angle (720 degrees) in radians (12.56637 . . .)
We know, using degree to radian conversion, θ in radians = θ in degrees × (pi/180°)
⇒ 720 degrees = 720° × (π/180°) rad = 4π or 12.5663 . . .
∴ cos 720° = cos(12.5663) = 1

Explanation:
For cos 720°, the angle 720° > 360°. Given the periodic property of the cosine function, we can represent it as cos(720° mod 360°) = cos(0°). The angle 720°, coterminal to angle 0°, lies on the positive x-axis.
Thus cos 720 degrees value = 1
Similarly, cos 720° can also be written as, cos 720 degrees = (720° + n × 360°), n ∈ Z.
⇒ cos 720° = cos 1080° = cos 1440°, and so on.
Note: Since, cosine is an even function, the value of cos(-720°) = cos(720°).
Methods to Find Value of Cos 720 Degrees
The value of cos 720° is given as 1. We can find the value of cos 720 degrees by:
- Using Trigonometric Functions
- Using Unit Circle
Cos 720° in Terms of Trigonometric Functions
Using trigonometry formulas, we can represent the cos 720 degrees as:
- ± √(1-sin²(720°))
- ± 1/√(1 + tan²(720°))
- ± cot 720°/√(1 + cot²(720°))
- ±√(cosec²(720°) – 1)/cosec 720°
- 1/sec 720°
Note: Since 720° lies on the positive x-axis, the final value of cos 720° will be positive.
We can use trigonometric identities to represent cos 720° as,
- -cos(180° – 720°) = -cos(-540°)
- -cos(180° + 720°) = -cos 900°
- sin(90° + 720°) = sin 810°
- sin(90° – 720°) = sin(-630°)
Cos 720 Degrees Using Unit Circle
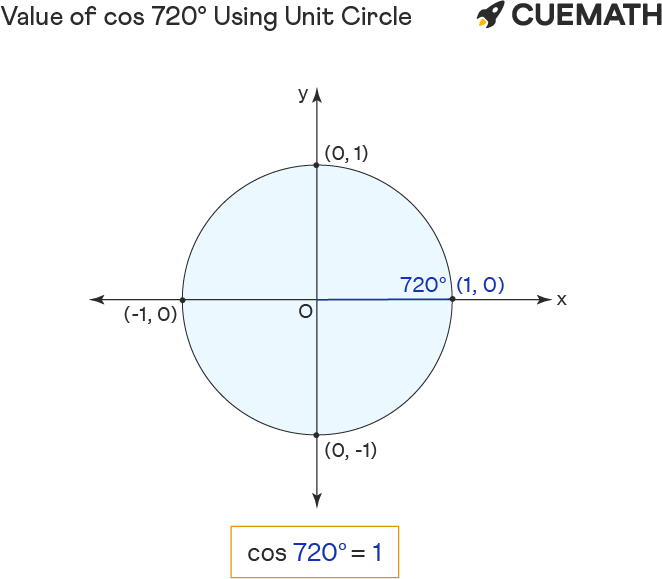
To find the value of cos 720 degrees using the unit circle, represent 720° in the form (2 × 360°) + 0° [∵ 720°>360°] ∵ cosine is a periodic function, cos 720° = cos 0°.
- Rotate ‘r’ anticlockwise to form 0° or 720° angle with the positive x-axis.
- The cos of 720 degrees equals the x-coordinate(1) of the point of intersection (1, 0) of unit circle and r.
Hence the value of cos 720° = x = 1
☛ Also Check:
- cos 37 degrees
- cos 30 degrees
- cos 150 degrees
- cos 320 degrees
- cos 6 degrees
- cos 720 degrees
FAQs on Cos 720 Degrees
What is Cos 720 Degrees?
Cos 720 degrees is the value of cosine trigonometric function for an angle equal to 720 degrees. The value of cos 720° is 1.
What is the Value of Cos 720 Degrees in Terms of Tan 720°?
We know, using trig identities, we can write cos 720° as 1/√(1 + tan²(720°)). Here, the value of tan 720° is equal to 0.
What is the Value of Cos 720° in Terms of Sec 720°?
Since the secant function is the reciprocal of the cosine function, we can write cos 720° as 1/sec(720°). The value of sec 720° is equal to 1.
How to Find Cos 720° in Terms of Other Trigonometric Functions?
Using trigonometry formula, the value of cos 720° can be given in terms of other trigonometric functions as:
- ± √(1-sin²(720°))
- ± 1/√(1 + tan²(720°))
- ± cot 720°/√(1 + cot²(720°))
- ± √(cosec²(720°) – 1)/cosec 720°
- 1/sec 720°
☛ Also check: trigonometric table
How to Find the Value of Cos 720 Degrees?
The value of cos 720 degrees can be calculated by constructing an angle of 720° with the x-axis, and then finding the coordinates of the corresponding point (1, 0) on the unit circle. The value of cos 720° is equal to the x-coordinate (1). ∴ cos 720° = 1.

