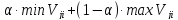Критерий
Сэвиджа использует матрицу рисков ||
rij
||. Элементы данной матрицы можно
определить по формулам (23), (24), которые
перепишем в следующем виде:
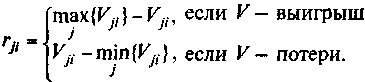 (31)
(31)
Это
означает, что rij
есть разность между наилучшим значением
в столбце i
и значениями Vji
при том же i.
Независимо от того, является ли Vji
доходом (выигрышем) или потерями
(затратами), rji
в обоих случаях определяет величину
потерь лица, принимающего решение.
Следовательно, можно применять к rji
только минимаксный критерий. Критерий
Сэвиджа рекомендует в условиях
неопределенности выбирать ту стратегию
Rj, при которой величина риска принимает
наименьшее значение в самой неблагоприятной
ситуации (когда риск максимален).
Пример
6. Рассмотрим пример 4. Заданная матрица
определяет потери (затраты). По формуле
(31) вычислим элементы матрицы рисков
|| rij
||:
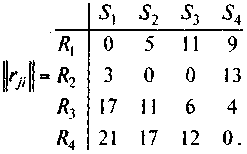
Полученные
результаты вычислений с использованием
критерия минимального риска Сэвиджа
оформим в следующей таблице:
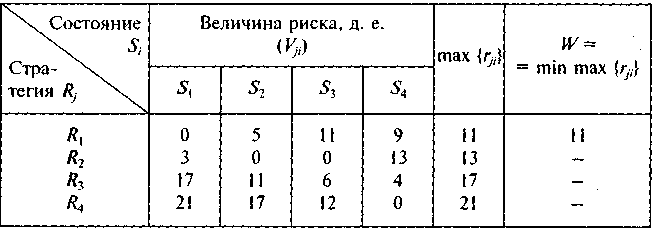
Введение
величины риска rji,
привело к выбору первой стратегии
R1,
обеспечивающей наименьшие потери
(затраты) в самой неблагоприятной
ситуации (когда риск максимален).
Применение
критерия Сэвиджа позволяет любыми
путями избежать большого риска при
выборе стратегии, а значит, избежать
большего проигрыша (потерь).
4.Критерий Гурвица.
Критерий
Гурвица
основан
на следующих двух предположениях:
«природа» может находиться в самом
невыгодном состоянии с вероятностью
(1 — α) и в самом выгодном состоянии с
вероятностью α, где α — коэффициент
доверия. Если результат Vji
— прибыль, полезность, доход и т. п., то
критерий Гурвица записывается так:
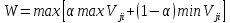
j
i
i
 Когда
Когда
Vji
представляет затраты (потери), то выбирают
действие, дающее
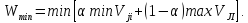
j
i
i
Если
α = 0, получим пессимистический критерий
Вальда.
Если
α = 1, то приходим к решающему правилу
вида max max Vji,
или к так называемой стратегии «здорового
оптимиста», т. е. критерий слишком
оптимистичный.
Критерий
Гурвица устанавливает баланс между
случаями крайнего пессимизма и
крайнего оптимизма путем взвешивания
обоих способов поведения соответствующими
весами (1 — α) и α, где 0≤α≤1.
Значение α от 0 до 1 может определяться
в зависимости от склонности лица,
принимающего решение, к пессимизму или
к оптимизму. При отсутствии ярко
выраженной склонности α = 0,5 представляется
наиболее разумной.
Пример
7. Критерий Гурвица используем в примере
4. Положим α = 0,5. Результаты необходимых
вычислений приведены ниже:
|
Wj |
min i |
max i |
i |
min j |
|
W1 |
6 |
24 |
15 |
15 |
|
W2 |
7 |
28 |
17,5 |
– |
|
W3 |
15 |
23 |
19 |
– |
|
W4 |
15 |
27 |
21 |
– |
Оптимальное
решение заключается в выборе W.
Таким
образом, в примере предстоит сделать
выбор, какое из возможных решений
предпочтительнее:
по
критерию Лапласа — выбор стратегии R2,
по
критерию Вальда — выбор стратегии R3;
по
критерию Сэвиджа — выбор стратегии R1;
по
критерию Гурвица при α = 0,5 — выбор
стратегии R1,
а если лицо, принимающее решение, —
пессимист (α = 0), то выбор стратегии R3.
Это
определяется выбором соответствующего
критерия (Лапласа, Вальда, Сэвиджа
или Гурвица).
Выбор
критерия принятия решений в условиях
неопределенности является наиболее
сложным и ответственным этапом в
исследовании операций. При этом не
существует каких-либо общих советов
или рекомендаций. Выбор критерия должно
производить лицо, принимающее решение
(ЛПР), с учетом конкретной специфики
решаемой задачи и в соответствии со
своими целями, а также опираясь на
прошлый опыт и собственную интуицию.
В
частности, если даже минимальный риск
недопустим, то следует применять
критерий Вальда. Если, наоборот,
определенный риск вполне приемлем и
ЛПР намерено вложить в некоторое
предприятие столько средств, чтобы
потом оно не сожалело, что вложено
слишком мало, то выбирают критерий
Сэвиджа.
Задание
для самостоятельного решения
: написать программу на языке С++ для
выбора наиболее эффективного проекта
легкового автомобиля для производства,
используя критерии Лапласа, Вальда,
Сэвиджа и Гурвица.
Намечается
крупномасштабное производство легковых
автомобилей. Имеются четыре варианта
проекта автомобиля
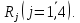
Определена
экономическая эффективность Vji
каждого проекта в зависимости от
рентабельности производства. По истечению
трех сроков
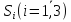 рассматриваются как некоторые состояния
рассматриваются как некоторые состояния
среды (природы). Значения экономической
эффективности для различных проектов
и состояний природы приведены в следующей
таблице (д.е.):
|
Проекты |
Состояния |
||
|
S1 |
S2 |
S3 |
|
|
R1 |
20 |
25 |
15 |
|
R2 |
25 |
24 |
10 |
|
R3 |
15 |
28 |
12 |
|
R |
9 |
30 |
20 |
Требуется
выбрать лучший проект для производства,
используя критерии Лапласа, Вальда,
Сэвиджа и Гурвица при ɑ=0,1. Сравните
решения и сделайте выводы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Любую хозяйственную деятельность
человека можно рассматривать как игру с природой. В широком смысле под природой
будем понимать совокупность неопределенных факторов, влияющих на эффективность
принимаемых решений.
Управление любым объектом
осуществляется путем принятия последовательности управленческих решений. Для принятия решения
необходима информация (совокупность сведений о состоянии объекта управления и
условиях его работы). В тех случаях когда отсутствует
достаточно полная информация, возникает неопределенность в принятии решения. Причины этого могут быть
различны: требующаяся для полного обоснования решения информация принципиально
не может быть получена (неустранимая неопределенность); информация не может быть
получена своевременно, к моменту принятия решения; затраты, связанные с
получением информации, слишком высоки. По мере совершенствования средств сбора, передачи и обработки информации неопределенность
управленческих решении будет уменьшаться. К этому нужно стремиться.
Существование неустранимой неопределенности связано со случайным характером
многих явлений. Например, в торговле, случайный характер изменения спроса
делает невозможным его точное прогнозирование, a, следовательно, и формирование
идеально точного заказа на поставку товара. Принятие решения в этом случае
связано с риском. Приемка партии товара на основании выборочного контроля также
связана с риском принятия решения в условиях неопределенности. Неопределенность
может быть снята путем полного контроля всей партии, однако это может оказаться
слишком дорогостоящим мероприятием. В сельском хозяйстве, например, с целью
получения урожая человек предпринимает ряд действии (пашет землю, вносит
удобрения, борется с сорняками и т. п.). Окончательный результат (урожай)
зависит от действий не только человека, но и природы (дождь, засуха, вечер и т.
п.). Из приведенных примеров видно, что
полностью исключить неопределенность в управлении экономической системой
нельзя, хотя, повторим, к этому нужно стремиться. В каждом конкретном случае
следует принимать во внимание степень риска при принятии управленческих
решений, по возможности максимально учитывать имеющуюся информацию с целью
уменьшения неблагоприятных последствий, которые могут возникнуть из-за
ошибочных решений.
Две стороны, участвующие в игре,
будем называть игрок I и игрок II. Каждый из игроков располагает конечным
набором действий (чистых стратегий), которые он может применять в процессе
игры. Игра имеет повторяющийся,
циклический характер. о
каждом цикле игроки выбирают одну из своих стратегии, что однозначно определяет
платеж
. Интересы игроков
противоположны. Игрок I старается вести игру так, чтобы платежи были как можно
большими. Для игрока II желательны как можно меньшие значения платежей (с
учетом знака). Причем в каждом цикле выигрыш одного из игроков в точности
совпадает с проигрышем другого. Игры такого типа называются играми с нулевой
суммой.
Решить игру – значит определить
оптимальное поведение игроков. Решение игр является предметом теории игр.
Оптимальное поведение игрока инвариантно относительно изменения всех элементов
платежной матрицы на некоторую величину.
В общем случае определение оптимального
поведения игроков связано с решением двойственной пары задач линейного
программирования. В отдельных случаях могут быть использованы более простые
методы. Часто платежную матрицу удается упростить путем удаления из нее строк и
столбцов, соответствующих доминируемым стратегиям
игроков, доминируемой называется стратегия, все
платежи которой не лучше соответствующих платежей некоторой другой стратегии и
хотя бы один из платежей хуже соответствующего платежа этой другой стратегии,
называемой доминирующей.
В обычной стратегической игре
принимают участие «разумные и антагонистические» противники (противоборствующие
стороны). В таких играх каждая из сторон предпринимает именно те действия,
которые наиболее выгодны ей и менее выгодны противнику. Однако очень часто неопределенность, сопровождающая
некоторую операцию, не связана с сознательным противодействием противника, а
зависит от некой, не известной игроку I объективной действительности (природы).
Такого рода ситуации принято называть играми с природой. Игрок II – природа – в
теории статистических игр не является разумным игроком, так как рассматривается
как некая незаинтересованная инстанция, которая не выбирает для себя
оптимальных стратегий. Возможные состояния природы (ее стратегии) реализуются
случайным образом. В исследовании операций оперирующую сторону (игрока I) часто
называют статистиком, а сами операции – играми статистика с природой или
статистическими играми.
Рассмотрим игровую постановку
задачи принятия решения в условиях неопределенности. Пусть оперирующей стороне
необходимо выполнить операцию в недостаточно известной обстановке относительно
состояний которой можно сделать
предположений. Эти предположения
будем рассматривать как стратегии природы.
Оперирующая сторона в своем распоряжении имеет
возможных стратегий –
. Выигрыши игрока I
при каждой паре стратегий
и
– предполагаются известными и заданы платежной
матрицей
.
Задача заключается в определении
такой стратегии (чистой или смешанной), которая лри
ее применении обеспечила бы оперирующей стороне наибольший выигрыш.
Выше уже говорилось, что
хозяйственная деятельность человека может рассматриваться как игра с природой.
Основной особенностью природы как игрока является ее не заинтересованность в
выигрыше.
Анализ матрицы выигрышей игры с
природой начинается с выявления и отбрасывания
дублирующих и заведомо невыгодных стратегий лица, играющего с природой. Что
касается стратегий природы, то ни одну из них отбросить нельзя, так как каждое
из состояний природы может наступить случайным образом, независимо от действий
игрока I. Ввиду того что природа не противодействует
игроку I, может показаться, что игра с природой проще стратегической игры. На
самом деле это не так. Противоположность интересов игроков в стратегической
игре в некотором смысле как бы снимает неопределенность, чего нельзя сказать о
статистической игре. Оперирующей стороне в игре с природой легче в том
отношении, что она скорее .всего выиграет больше, чем
в игре против сознательного противника. Однако ей труднее принять обоснованное
решение, так как в игре с природой неопределенность ситуации сказывается в
гораздо более сильной степени.
После упрощения платежной матрицы
игры с природой целесообразно не только оценить выигрыш при той или иной
игровой ситуации, но и определить разность между максимально возможным
выигрышем при данном состоянии природы и выигрышем, который будет получен при
применении стратегии
в тех же условиях. Эта разность в теории игр
называется риском.
Природа меняет состояние
стихийно, совершенно не заботясь о результате игры. В антагонистической игре мы
предполагали, что игроки пользуются оптимальными (в определенном выше смысле)
смешанными стратегиями. Можно предположить, что природа применяет наверняка не
оптимальную стратегию. Тогда какую? Если бы существовал ответ на этот вопрос,
то принятие решения лицом, принимающим решения (ЛПР) сводилось бы к
детерминированной задаче.
Если вероятности
состояний
природы известны, то пользуются критерием
Байеса, в соответствии с которым оптимальной считается чистая стратегия
, при которой максимизируется
средний выигрыш:
Критерий Байеса предполагает, что
нам хотя и неизвестны условиях выполнения операций (состояния природы)
, но известны их вероятности
.
С помощью такого приема задача о
выборе решения в условиях неопределенности превращается в задачу о выборе
решения в условиях определенности, только принятое решение является оптимальным
не в каждом отдельном случае, а в среднем.
Если игроку
представляются в равной мере правдоподобными
все состояния
природы, то иногда полагают
и, учитывая, «принцип недостаточного
основания» Лапласа, оптимальной считают чистую стратегию
, обеспечивающую:
Если же смешанная стратегия
природы неизвестна, то в зависимости от гипотезы о поведении природы можно
предложить ряд подходов для обоснования выбора решения ЛПР. Свою оценку
характера поведения природы будем характеризовать числом
, которое можно связывать со
степенью активного «противодействия» природы как игрока Значение
соответствует наиболее пессимистичному
отношению ЛПР в смысле «содействия» природы в достижении им наилучших
хозяйственных результатов. Значение
соответствует наибольшему оптимизму ЛПР. Как
известно, в хозяйственной деятельности указанные крайности опасны. Скорее
всего, целесообразно исходить из некоторого промежуточного значения
. В этом случае используется
критерий Гурвица, согласно которому наилучшим решением ЛПР является чистая
стратегия
, соответствующая условию:
Критерий Гурвица (критерий
«оптимизма-пессимизма») позволяет руководствоваться при выборе рискового
решения в условиях неопределенности некоторым средним результатом
эффективности, находящимся в поле между значениями по критериям «максимакса» и «максимина» (поле между этими значениями
связано посредством выпуклой линейной функции).
В случае крайнего пессимизма ЛПР
указанный критерий называется критерием
Вальда. Согласно этому критерию, наилучшей считается максиминная
стратегия. Это критерий крайнего
пессимизма. По этому критерию ЛПР выбирает ту стратегию, которая гарантирует в
наихудших условиях максимальный выигрыш:
Такой выбор соответствует
наиболее робкому поведению ЛПР, когда он предполагает наиболее, неблагоприятное
поведение природы, боится больших потерь. Можно предположить, что он не получит
больших выигрышей. Согласно критерию Сэвиджа, следует
выбирать чистую стратегию
соответствующую условию:
где риск
.
Критерий Сэвиджа
(критерий потерь от «минимакса») предполагает, что из всех возможных вариантов
«матрицы решений» выбирается та альтернатива, которая минимизирует размеры
максимальных потерь по каждому из возможных решений. При использовании этого
критерия «матрица решения» преобразуется в «матрицу риска», в которой вместо
значений эффективности проставляются размеры потерь при различных вариантах
развития событий.
Недостатком критериев Вальда, Сэвиджа и Гурвица
является субъективная оценка поведения природы. Хотя указанные критерии и дают
некоторую логическую схему принятия решений, резонно все же задать вопрос: «А
почему сразу не выбрать субъективное решение, вместо того чтобы иметь дело с
разными критериями?» Несомненно, определение решения по различным критериям помогает
ЛПР оценить принимаемое решение с различных позиций и избежать грубых ошибок в
хозяйственной деятельности.
Задача
После
нескольких лет эксплуатации оборудование может оказаться в одном из трех
состояний:
-
требуется профилактический ремонт;
требуется замена отдельных деталей и узлов;
требуется капитальный ремонт.
В
зависимости от ситуации руководство предприятия может принять следующие
решения:
-
отремонтировать оборудование своими силами, что потребует затрат
;
вызвать специальную бригаду ремонтников, расходы в этом случае составят
;
заменить оборудование новым, реализовав устаревшее по остаточной стоимости.
Совокупные затраты на этот мероприятие составят
.
Требуется
найти оптимальное решение данной проблемы по критерию минимизации затрат с
учетом следующих предположений:
|
|
|
|
|
| a | 4 | 6 | 9 |
| b | 5 | 3 | 7 |
| c | 20 | 15 | 6 |
| q | 0.4 | 0.45 | 0.15 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Игра парная, статистическая. В игре участвуют
2 игрока: руководство предприятия и природа.
Под природой в данном случае понимаем
совокупность внешних факторов, которые определяют состояние оборудования.
Стратегия руководства:
–
отремонтировать оборудование своими силами
–
вызвать бригаду специалистов
–
заменить оборудование новым
Стратегия природы – 3 возможных состояния
оборудования.
– требуется профилактический ремонт;
– следует заменить отдельные детали и узлы;
– требуется капитальный ремонт.
Расчет платежной матрицы и матрицы рисков
Поскольку элементы матрицы – затраты,
то будем считать их выигрышными но со знаком минус. Платежная матрица:
|
|
|
|
|
|
|
|
-4 | -6 | -9 | -9 |
|
|
-5 | -3 | -7 | -7 |
|
|
-20 | -15 | -6 | -20 |
|
|
0.4 | 0.45 | 0.15 |
Составляем матрицу рисков:
|
|
|
|
|
|
|
|
(-4)-(-4)=0 | (-3)-(-6)=3 | (-6)-(-9)=3 | 3 |
|
|
(-4)-(-5)=1 | (-3)-(-3)=0 | (-6)-(-7)=1 | 1 |
|
|
(-4)-(-20)=16 | (-3)-(-15)=12 | (-6)-(-6)=0 | 16 |
Критерий Байеса
Определяем средние выигрыши:
По критерию Байеса оптимальной является стратегия
–
вызвать бригаду специалистов
Критерий Лапласа
Примем
Определим средние выигрыши:
По критерию Лапласа оптимальной является стратегия
– вызвать бригаду специалистов
Критерий Вальда
По критерию Вальда оптимальной является стратегия
– вызвать бригаду специалистов
Критерий Сэвиджа
По критерию Сэвиджа оптимальной
является стратегия
-вызвать
бригаду специалистов.
Критерий Гурвица
:
По критерию Гурвица оптимальной является стратегия
–
вызвать бригаду специалистов
Ответ: По всем критериям
оптимальной является стратегия «Вызвать бригаду специалистов».
Основные критерии применяемые в процессе принятия решений в условиях неопределённости и риска, а также в игре с природой
Критерий среднего выигрыша
Формула критерия среднего выигрыша
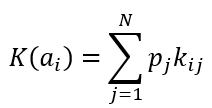
Формула оптимального решения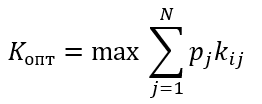
Пример

Пусть даны вероятности, p1=0.2 p2=0.1 p3=0.3 p4=0.2, тогда получаем
K(a1)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.4=0.3
K(a2)=0.2*0.3+0.1*0.2+0.3*0.3+0.2*0.5=0.27
K(a3)=0.2*0.6+0.1*0.3+0.3*0.3+0.2*0.2=0.28
K(a4)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.3=0.25
Kопт=max{0.27; 0.48; 0.43; 0.51}=0.51
В итоги оптимальным вариантом выбора программы по критерию среднего выигрыша является вариант первой программы.
Критерий Вальда или пессимизма
Формула критерия Вальда или максимина
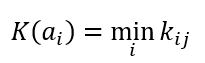
Формула оптимального решения по критерию Лапласа
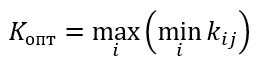
Пример

K(a1)=min(0.4;0.5;0.3;0.4)=0.3
K(a2)=min(0.3;0.2;0.3;0.5)=0.2
K(a3)=min(0.6;0.3;0.3;0.2)=0.2
K(a4)=min(0.4;0.5;0.2;0.3)=0.2
Kопт=max{0.3; 0.2; 0.2; 0.2}=0.3
По критерию Вальда оптимальным решением является выбор первой программы.
Критерий максимакса или оптимизма
Формула критерия максимакса
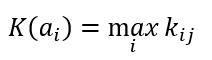
Формула оптимального решения по критерию максимакса
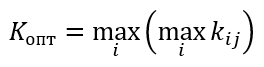
Пример

K(a1)=max(0.4;0.5;0.3;0.4)=0.5
K(a2)= max (0.3;0.2;0.3;0.5)=0.5
K(a3)= max (0.6;0.3;0.3;0.2)=0.6
K(a4)= max (0.4;0.5;0.2;0.3)=0.5
Kопт=max{0.5; 0.5; 0.6; 0.5}=0.6
По критерию максимакса оптимальным решением является выбор третьей программы.
Критерий Лапласа
Формула критерия Лапласа
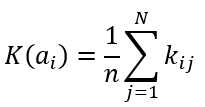
Формула оптимального решения по критерию Лапласа

Пример

Решение
K(a1)=0.25*(0.4+0.5+0.3+0.4)=0.4
K(a2)=0.25*(0.3+0.2+0.3+0.5)=0.325
K(a3)=0.25*(0.6+0.3+0.3+0.2)=0.35
K(a4)=0.25*(0.4+0.5+0.2+0.3)=0.35
Kопт=max{0.4; 0.325; 0.35; 0.35}=0.4
По критерию Лапласа оптимальным решением является выбор первой программы.
Критерий Гурвица
Пример

Формула критерия Гурвица
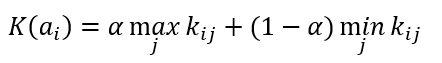
Формула оптимального решения по Гурвица критерию

Коэффициент α принимает значения от 0 до 1. Если α стремится к 1, то критерий Гурвица приближается к критерию Вальда, а при α стремящемуся к 0, то критерий Гурвица приближается к критерию максимакса.
Пусть α=0.7
K(a1)= 0.7* 0.5+(1-0.7)*0.3=0.44
K(a2)= 0.7* 0.5+(1-0.7)*0.2=0.41
K(a3)= 0.7* 0.6+(1-0.7)*0.2=0.48
K(a4)= 0.7* 0.5+(1-0.7)*0.2=0.41
Kопт=max{0.44; 0.41; 0.48; 0.41}=0.48
По критерию Гурвица оптимальным решением является выбор третьей программы.
Критерий Сэвиджа или минимакса (критерий потерь)
Формула критерия Сэвиджа для построения матрицы потерь

Формула для выбора максимального значения из матрицы потерь

Формула оптимального решения по критерию Сэвиджа
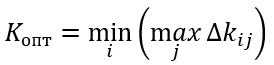
Для примера

Строим матрицу потерь по столбцам выбираем максимальное значение и поочередно вычитаем значения каждой ячейки соответствующего столбца согласно формуле, в итоге получим матрицу вида

K(a1)= max{0.2; 0; 0; 0.1}=0.2
K(a2)= max{0.3; 0.3; 0; 0}=0.3
K(a3)= max{0; 0.2; 0; 0.3}=0.3
K(a4)= max{0.2; 0; 0.1; 0.2}=0.2
Kопт=min{0.2; 0.3; 0.3; 0.2}=0.2
По критерию Сэвиджа оптимальным решением является выбор первой или четвёртой программы.
Таким образом, в соответствии со всеми приведёнными критериями большинство решений указывает на выбор первой программы.
Аннотация: Рассмотрена методика выбора наименее рискованного инвестиционного проекта на основе вероятностных критериев.
Цель лекции: освоить методику расчета вероятностных критериев риска и выбора наименее рискованного варианта инвестирования.
Практика хозяйственной деятельности нередко вынуждает принимать решения, связанные с выбором оптимального варианта инвестирования в условиях риска и неопределенности. Инвестор, имеющий некоторую сумму, выбирает между несколькими инвестиционными проектами. Предприятие может стоять перед выбором направления инвестирования в основной, человеческий или природный капитал. Если направление инвестирования выбрано, возникают другие вопросы: так, если речь идет об инвестициях в основной капитал, то возникает проблема выбора конкретной техники и технологии. Инвестиции в человеческий капитал могут быть выражены либо в улучшении системы социального обеспечения работников предприятия, либо в их дополнительном образовании. Инвестиции в природный капитал могут быть направлены на строительство очистных сооружений или на приобретение нового оборудования, которое позволит снизить ресурсоемкость производства, и т.п. При этом неопределенность существует практически всегда. Параметры нового оборудования, уровень готовности персонала к работе на нем, затраты на монтаж можно прогнозировать, но зачастую реальные значения существенно отличаются от прогнозных. Оценка эффективности инвестиций в природный и человеческий капитал вообще является достаточно сложной экономической проблемой из-за трудности денежной оценки результата таких инвестиций. Кроме того, инвестор, как правило, не может прогнозировать макроэкономические изменения: структурные сдвиги, смену экономических циклов, процессы на международном валютно-финансовом рынке
[
13
]
. Таким образом, выбор оптимального варианта инвестирования — это нахождение проекта, удовлетворяющего инвестора с точки зрения доходности и риска.
Существенную помощь в решении подобных задач оказывают экономико-математические методы, а именно – использование теории игр и статистических решений. Методы теории игр позволяют глубже разобраться в ситуации, оценить каждое решение с разных точек зрения. В конечном итоге решающее значение имеет позиция инвестора относительно цели реализации проекта: либо он рассчитывает на оптимистический сценарий и хочет извлечь максимум выгоды (но в случае реализации негативных прогнозов он понесет существенные убытки), либо он хочет получить относительно небольшую, но гарантированную прибыль
[
14
]
.
В ситуации выбора оптимального варианта инвестирования целесообразно рассчитать несколько критериев: критерий Вальда, критерий Сэвиджа, критерий Гурвица, критерий Байеса, критерий Лапласа.
Предположим, имеется 4 варианта инвестирования — проекты А, Б, В, Г. По каждому проекту возможны 4 сценария развития ситуации — оптимистический, консервативный, пессимистический и смешанный. Для расчета вероятностных критериев риска нужно составить матрицу доходности и матрицу рисков. Элементами матрицы доходности являются индексы доходности (ИД). Строки матрицы доходности обозначают варианты инвестирования, а столбцы – сценарии развития ситуации (
таблица
13.1).
Матрица рисков имеет такую же структуру, как и матрица доходности (в строках – инвестиционные проекты, в столбцах – сценарии). Элементом матрицы рисков является разность между максимально возможным индексом доходности по данному сценарию и индексом доходности данного проекта по этому же сценарию (
таблица
13.2).
Критерий Вальда олицетворяет позицию “крайнего пессимизма”, позволяя определить, какой проект даст наибольший доход при реализации пессимистического сценария:
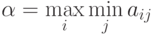
где  – элементы матрицы доходности.
– элементы матрицы доходности.
Критерий Сэвиджа также является критерием “крайнего пессимизма”, но этот критерий советует при выборе оптимального решения ориентироваться не на доходность, а на риск. Использование критерия Сэвиджа оправдано в том случае, если инвестор хочет в любом случае избежать большого риска и готов ради этого упустить некоторую выгоду. Оптимальным считается тот инвестиционный проект, для которого величина риска при реализации пессимистического сценария минимальна:
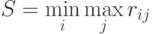
где 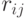 – элементы матрицы рисков.
– элементы матрицы рисков.
Критерий Гурвица рекомендует не рассматривать ситуацию ни с позиции “крайнего пессимизма”, ни “крайнего оптимизма”, то есть советует не рассчитывать ни на наилучшее, ни на наихудшее развитие событий. При расчете критерия Гурвица используется так называемый “коэффициент пессимизма” 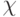 , значения которого находятся в интервале между нулем и единицей:
, значения которого находятся в интервале между нулем и единицей:
![H=max_{i}[lambdamin_{j}a_{ij}+(1-lambda)max_{j}a_{ij}]](https://intuit.ru/sites/default/files/tex_cache/145b72ef263911fc46a05b180622ad7a.png)
При 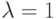 критерий Гурвица превращается в критерий Вальда, то есть в критерий “крайнего пессимизма”. При
критерий Гурвица превращается в критерий Вальда, то есть в критерий “крайнего пессимизма”. При 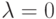 – в критерий “крайнего оптимизма”, рекомендующий выбирать инвестиционный проект, дающий наибольший доход при реализации оптимистического сценария. Коэффициент пессимизма ? выбирается исходя из склонности инвестора к риску – чем меньше эта склонность, тем ближе к единице значение
– в критерий “крайнего оптимизма”, рекомендующий выбирать инвестиционный проект, дающий наибольший доход при реализации оптимистического сценария. Коэффициент пессимизма ? выбирается исходя из склонности инвестора к риску – чем меньше эта склонность, тем ближе к единице значение 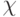 .
.
Критерий Байеса рекомендует выбирать тот инвестиционный проект, для которого математическое ожидание индекса доходности максимально:
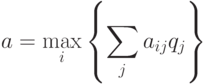
где  – элементы матрицы доходности;
– элементы матрицы доходности;
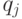
– вероятности наступления сценариев.
Критерий Лапласа отличается от критерия Байеса тем, что вероятности наступления сценариев принимаются равными.
Пример. Дана матрица доходности (
таблица
13.3). Составить матрицу рисков и рассчитать критерии Вальда, Сэвиджа, Гурвица, Байеса, Лапласа. Коэффициент пессимизма равен 0,6. Вероятность наступления оптимистического сценария – 0,2, пессимистического – 0,2, смешанного – 0,1, консервативного – 0,5.
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
|---|---|---|---|---|
| Проект А | 2,03 | 1,03 | -0,3 | 1,01 |
| Проект Б | 2,04 | 1,04 | -0,4 | 1,02 |
| Проект В | 2,05 | 1,05 | -0,5 | 1,15 |
| Проект Г | 2,06 | 1,06 | -0,6 | 1,32 |
Решение.
1. Определим максимальное значение по каждому столбцу матрицы доходности. Получим 2,06 для оптимистического сценария, 1,06 – для консервативного, -0,3 – для пессимистического и 1,32 для смешанного. Далее вычитаем из максимального по столбцу значения каждый элемент этого столбца. Например, определим риск по проекту А для оптимистического сценария:
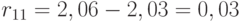
Аналогично определяем каждый элемент матрицы рисков и сводим полученные значения в таблицу 13.4 .
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
|---|---|---|---|---|
| Проект А | 0,03 | 0,03 | 0,00 | 0,31 |
| Проект Б | 0,02 | 0,02 | 0,10 | 0,30 |
| Проект В | 0,01 | 0,01 | 0,20 | 0,17 |
| Проект Г | 0,00 | 0,00 | 0,30 | 0,00 |