-
Проверка гипотез
-
Гипотеза.
Прежде
всего, выдвигается гипотеза
о том, что
распределение
удовлетворяет некоторому свойству. При
этом, если есть возможность, желательно
сразу конкретизировать альтернативное
утверждение
относительно
.
Например,
-
– распределение
в точности совпадает с некоторым
известным распределением F0.
Так, вполне уместно рассмотреть гипотезу
о том, что случайные числа, выдаваемые
функцией Random
языка программирования Pascal,
действительно имеют равномерное на
отрезке [0;1] распределение; -
–
распределение
принадлежит некоторому известному
семейству распределений
.
Весьма популярна на практике гипотеза
о том, что наблюдаемая в эксперименте
выборка имеет нормальное распределение
с некоторыми неизвестными значениями
среднего и дисперсии. Варианты альтернатив
как в этом, так и в предыдущем примере
очень разнообразны и зависят от
предпочтений исследователя. Наиболее
естественная альтернатива здесь –
семейство всех возможных распределений
на числовой прямой (в предыдущем примере
– на отрезке [0;1]); -
– значение
неизвестного параметра
принадлежит некоторому подмножеству
.
В качестве примера здесь можно привести
задачу проверки гипотезы о том, что
вероятность рождения мальчика больше
½, при альтернативе – меньше или равна
½. Другой пример, связанный с медициной,
– исследование эффективности нового
препарата при лечении пациентов с
повышенным артериальным давлением в
сравнении со стандартной методикой
лечения. Здесь в качестве гипотезы
лучше выдвинуть утверждение, что новый
препарат идентичен старому, при
альтернативе, что новый лучше старого.
-
Критерий.
После
выдвижения гипотезы строится критерий
проверки этой гипотезы. Критерий
– функция выборочных
данных
,
принимающая значение 1, если гипотезу
следует отвергнуть, и значение 0, если
гипотезу следует принять. Вместо критерия
часто строят критическую
область
A
– область, при попадании в которую
выборочных данных гипотеза отвергается.
Обычно
критерий строится с помощью некоторой
тестовой
статистики
,
и в этом случае гипотеза отвергается,
если значение статистики больше (или
меньше) критической
константы
Cкрит.
Величина константы выбирается в
соответствии с требованиями
на качество критерия.
-
Ошибки.
Качество
критерия (критической области)
характеризуется двумя величинами –
вероятностями ошибок первого и второго
рода.
-
Вероятность
ошибки 1-ого рода
– вероятность отвергнуть гипотезу,
если на самом деле она верна.
Вероятность
ошибки 2-ого рода
– вероятность принять гипотезу, если
на самом деле верна альтернатива.
Понятно, что если альтернатива не
конкретизирована, то вычислить эту
вероятность невозможно. Поэтому чаще
всего контролируется только ошибка
первого рода.
-
Максимальная
вероятность ошибки 1-го рода среди всех
“гипотетических” распределений
(распределений, удовлетворяющих
требованиям проверяемой гипотезы)
называется размером
критерия. -
Критерий,
размер которого не превосходит некоторого
наперед заданного малого значения
,
называется критерием
уровня,
а заданная заранее константа
называется уровнем
значимости.
Таким
образом, для критерия уровня
маловероятно (не больше
)
отвержение справедливой гипотезы:
для
всех
.
Поскольку
на практике чаще всего контролируется
только вероятность ошибки 1-го рода, то
в качестве нулевой гипотезы следует
выбирать утверждение, противоположное
ожидаемому. Например, при исследовании
нового лечебного препарата следует
проверять гипотезу о его полной
неэффективности. В этом случае критерий
уровня
будет обеспечивать низкую вероятность
принятия неэффективного препарата.
Чем
меньше уровень значимости, тем выше
надежность статистического вывода.
Однако слишком малые значения
могут привести к слишком частому принятию
неверной гипотезы, то есть к увеличению
вероятности ошибки 2-ого рода. Чтобы
контролировать обе эти ошибки, часто
требуется проведение большого числа
наблюдений, что не всегда допустимо.
Наиболее
популярное на практике значение
(- 5%-ый уровень значимости). Иногда
рассматривают значения
и
.
-
Тестовая
статистика.
Если
критерий построен на основе статистики
и критическая
область имеет вид
,
то критическая константа выбирается
из условия на вероятность ошибки 1-го
рода
|
|
(*) |
которое
должно выполняться для всех распределений
F
, удовлетворяющих предположениям
гипотезы
.
Если распределение статистики
известно, то значение критической
константы легко найти из таблиц этого
распределения. Таким образом, для
построения критерия проверки гипотезы
необходимо
-
выбрать
тестовую статистику
и вид критической области (например,);
-
найти
критическую
константу
по таблице распределения
из условия
(*) на вероятность ошибки 1-го рода; -
после
проведения статистического эксперимента
и вычисления значения
принять (если
)
или отвергнуть (если
)
проверяемую гипотезу.
Замечание.
Не зная
,
нельзя проверить гипотезу, как бы не
было соблазнительно значение
,
полученное в эксперименте. Например,
если из двух баскетболистов один попал
в 25% бросков с игры, а второй – в 50%, то
ещё нельзя сказать, что первый баскетболист
хуже второго, так как для подобного
вывода надо знать (чтобы вычислить
)
количество бросков каждого из игроков.
-
Критический
уровень значимости.
Другой
способ проверки гипотезы состоит в
вычислении критического
уровня значимости,
который тесно связан с видом критерия
и применительно к рассмотренному выше
критерию равен
(часто
обозначается через
и называется
–значением).
Гипотеза
отвергается, если
.
Другими
словами, критический уровень значимости
равен размеру критерия, при вычислении
которого критическая константа
заменена полученным в эксперименте
выборочным значением статистики
.
Если вспомнить определение константы
,
то критический уровень значимости можно
определить как
наименьший
уровень значимости, при котором гипотеза
отвергается.
В
общем случае
можно понимать как вероятность того,
что тестовая статистика T
примет значение “хуже”, чем полученное
в эксперименте. Слово “хуже” означает,
что такие значения статистики
свидетельствуют больше в пользу
альтернативы, чем гипотезы. Такое
понимание поможет правильно сориентироваться
в определении вида критической области
(
,
или
)
при вычислении
-значения.
Основное
преимущество этого способа (кроме
очевидного преимущества, связанного с
вычислением прямой, а не обратной функции
распределения) состоит в том, что мы
можем не делать жестких выводов типа
“да, гипотеза верна” или “нет, гипотеза
не верна”, а принять более гибкое
решение. Здесь можно предложить следующую
градацию высказываний о справедливости
гипотезы:
–
хорошее согласие с гипотезой;
– нет
оснований отвергать гипотезу;
– слабо
значимое расхождение с гипотезой;
–
значимое расхождение с гипотезой;
– высоко
значимое расхождение с гипотезой.
Следует
предостеречь, что учет только ошибки
1-го рода может привести к весьма
парадоксальным результатам. Можно
предложить простой критерий, который
будет иметь заданный уровень значимости
сразу для всех гипотез. Для этого,
например, достаточно 5 раз подбросить
правильную монету и отвергать гипотезу,
если все 5 раз монета упадет “гербом”
вверх. Легко понять, что вероятность
этого события равна 1/25.
Следовательно, размер такого (ну, очень
смешного) критерия приблизительно равен
0.03, что, конечно, можно считать очень
хорошим значением. Подчеркнем, что этот
критерий может быть применен к проверке
любой гипотезы, например, гипотезы о
том, что на Луне есть жизнь. Чтобы избежать
подобных нелепых ситуаций, необходимо
либо применять критерии, у которых мала
ошибка 2-го рода, вычисленная хотя бы
для некоторых более или менее правдоподобных
альтернатив, либо, в крайнем случае,
использовать тестовые статистики,
свидетельствующие в той или иной степени
о близости данных к гипотезе. Например,
если в эксперименте подсчитывается
частота рождения мальчиков, то достаточно
большое отклонение этой частоты от ½
несомненно будет свидетельствовать
против гипотезы о равенстве вероятностей
рождения мальчиков и девочек.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
10.02.20152.79 Mб19k_5New.pdf
- #
- #
- #
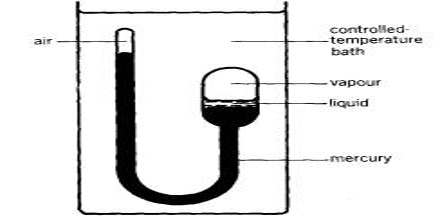
Determination of Critical Constants
Long before Andrews performed his experiments with carbon dioxide, Caignard de La Tour (1822) observed that when ether was heated in a sealed tube, the surface of separation between liquid and its vapor disappeared at a particular temperature; but on cooling the surface reappeared at about the same temperature. The significance of these observations was not realized until Andrews correlated this with his work on carbon dioxide. He observed that the temperature at which the surface of separation between liquid and its vapor disappears is the same at which he observed the Critical phenomenon.
These observations have been utilized for the determination of the critical constants. Critical pressure and temperature may be determined fairly easily by using an apparatus as shown in the figure; similar to Caignard de La Tour’s apparatus.
It consists of a thick-walled glass U-tube one limb of which is longer than the other. The liquid is contained in the bulb and the rest of the apparatus is filled with mercury and the upper and of the bulb is preserved leaving a little air in it. The shorter end containing the liquid in contact with its saturated vapor is sealed and is surrounded by a heating jacket. The other limb of the U-tube, which serves as a manometer, has aired at its upper-end A, the rest of the tube being filled with mercury.
The temperature of the bulb is raised gradually. The end B is gradually heated by passing hot air or vapor through the jacket and the temperature at which the meniscus separating liquid and vapor just disappears and at which it reappears on cooling is noted. On cooling this mixture, a mist first forms and the liquid appear quickly. The average of the two is the critical temperature. The volume of the air in the limb A is also noted at this temperature and the critical pressure is calculated from this. The critical temperature, (Tc), is characteristic of every gas and might be defined as: “The temperature beneath which the constant enlarge of pressure on gas ultimately brings about liquefaction and above which no liquefaction can take place no issue what so ever pressure be applied”.
When the liquid and its vapor are gradually heated the density of the liquid decreases, but the density of the vapor increases, because of compression until at the critical temperature and pressure the densities of both liquid and vapor, become equal, and the liquid and vapor become indistinguishable from each other. The mean of the temperature of the evaporation and return of the liquid in the bulb is critical temperature. The pressure read on the manometer is “critical pressure”. The pressure required to liquefy the gas at critical temperature is called critical pressure and the volume occupied by 1 mole of gas under these conditions is called the critical volume. This is the reason why at the critical point the surface of separation vanishes. The critical constants of liquid explosives cannot be calculated in a straight line because of the obdurate nature of the substances concerned.
Книга содержит подробную классификацию растворителей эмпирические и теоретические уравнения, выражающие температурную зависимость плотности, показателя преломления поверхностного натяжения, вязкости и теплоты испарения, й также данные по критическим температурам и критическим давлениям, температурам замерзания, электрическим и оптическим свойствам таблицы физических констант и отдельные таблицы температур кипения и замерзания, диэлектрических постоянных и дипольных моментов для 254 растворителей. Кроме того, в книге приведены критерии чистоты, методы сушки и способы определения влажности растворителей и собраны наиболее надежные из описанных в литературе методов очистки растворителей книга снабжена обширной библиографией, состоящей из ссылок более чем на 2000 книг и журнальных статей. [c.4]
Вириальное уравнение —удобный способ представления зависимости р—V при заданной температуре. В литературе имеются таблицы экспериментально определенных вторых вириальных коэффициентов . Предложены полуэмпирические формулы, связывающие эти величины с критическими константами вещества. [c.162]
| Таблица 2.5 Критические константы НгО [255] и ВгО [258] | ![Таблица 2.5 Критические константы НгО [255] и ВгО [258]](https://www.chem21.info/pic2/184159055049031204024064127139041015170170154137.png) |
Том I (1962 г.) содержит общие сведения атомные веса и распространенность элементов единицы измерения физических величин соотношения между единицами измерения физических величин измерение температуры и давления математические таблицы и формулы важнейшие химические справочники и периодические издания основные данные о строении вещества и структуре кристаллов физические свойства (плотность и сжимаемость жидкостей и газов, термическое расширение твердых тел, жидкостей и газов равновесные температуры и давления критические величины и константы Ван-дер-Ваальса энергетические свойства теплопроводность электропроводность и числа переноса диэлектрическая проницаемость дипольные моменты вязкость поверхностное натяжение показатели преломления) краткие сведения по лабораторной технике. Имеется предметный указатель. [c.23]
ТАБЛИЦА 41 Критические константы некоторых газов [c.204]
Критические константы некоторых веществ приведены в таблице 3. [c.24]
ТАБЛИЦА 31. ЗНАЧЕНИЕ КРИТИЧЕСКИХ НАПРЯЖЕНИЙ а ,р МПа И КОНСТАНТЫ К, МПа.Ч В]УРАВНЕНИИ КОРРОЗИОННОГО РАСТРЕСКИВАНИЯ [c.72]
Обобщен обширный материал по термодинамическим свойствам веществ, относящихся к различным классам кислородсодержащих органических соединений. Даны критические обзоры литературных данных и таблицы рекомендуемых значений. Приводятся величины теплоемкости, энтальпии, энтропии, энергии Гиббса, теплот фазовых превращений, теплот образования и термодинамических констант для твердого, жидкого и газообразного состояния вещества. [c.304]
Поскольку электронные структуры ксенона и иодид-иона аналогичны, а электронные структуры ковалентно связанных атомов фтора, хлора и брома похожи на электронные структуры неона, аргона и криптона соответственно, то можно воспользоваться силовыми постоянными для инертных газов, приняв я = 9 [42]. Тогда получаются константы отталкивания, приведенные в третьем столбце табл. 8.19. С помощью данных по кажущимся энергиям активации реакций между иодид-ионами и тремя замещенными метилбромидами, в ацетоновом растворе получим энергии, соответствующие пространственным эффектам, которые приведены во втором столбце той же таблицы. Рассчитанные значения критического расстояния а (четвертый столбец) превосходят кристаллографический радиус иодид-иона (2,32 А) на значения, которые очень близки ковалентным радиусам атомов фтора, хлора и брома. [c.232]
Из сделанных выше замечаний мы видим, что общепринятые трактовки подобия твердых тел не приходится считать безупречными. Даже использование характеристической температуры 0 сопряжено с осложнениями так как, в отличие от критической температуры (или даже Тпл), величина 0 не является строго фиксированной константой, характеризующей свойства вещества, но зависит от его теплового состояния и в особенности от его плотности. Ниже помещена табл. 16 наиболее применяемых сейчас значений 0 для металлов и некоторых ионных кристаллов (для некоторых веществ взяты средние значения из указываемых разными авторами). Почти все значения в таблице получены сопоставлением расчетов с измеренными теплоемкостями тел. [c.289]
В табл. 2.24 приведены значения поверхностного натяжения сжиженных газов. Данные таблицы получены по приведенному выше уравнению, при этом константа с была определена через молекулярную массу того или иного углеводорода. С повышением молекулярной массы поверхностное натяжение вещества увеличивается, а с увеличением температура уменьшается и становится равным нулю при критической температуре, т. е. в точке, где исчезает разница между жидкостью и паром. [c.76]
Критическое рассмотрение литературных данных по взаимодействию редкоземельных элементов с комплексонами позволило составить таблицу констант нестойкости их комплексонатов и сделать вывод о перспективности применения комплексонатов для разделения редкоземельных элементов. [c.334]
В третьем томе книги Цейзе содержится обширная критическая сводка опубликованных до 1953 г. данных о термодинамических свойствах различных неорганических и органических веществ преимущественно в состоянии идеального газа при низких, обычных и высоких температурах теплоемкость (Ср), энтальпия (Я°г – Яо), энтропия (5г), функция (Сг —Яо)/ . Кроме того, приведены данные о равновесии некоторых гомогенных газовых реакций при разных температурах (константа равновесия, степень диссоциации). Все они представлены в виде таблиц, большей частью взятых непосредственно из оригинала. Для сопоставления влияния температуры на теплоемкости некоторых веществ и на константы равновесия некоторых реакций в книге помещены графики. [c.77]
Графики рис. 14 и 15 в сочетании с таблицами критических параметров можно использовать для приближенного определения объема любого газа. Критические параметры даны в Приложении вместе с константами уравнения Ван-дер-Ваальса. [c.220]
Среди других интересных работ, посвященных вириальному уравнению, следует отметить работу Эпштейна [58], который. в уравнении (П. 22) ограничился членами с тремя вириальными коэффициентами и добавил остаточный член, выраженный в функции Т и критических констант. Дерог (Gyorog) и Оберт [59] обобщили вириальные коэффициенты для сферически симметричных молекул, а Дэвид, Хаманн [60] и Блэк [61 составили таблицы второго вириального коэффициента в зависимости от температуры для различных веществ. Питцер и Керл [62] представили второй вириальный коэффициент в виде ряда, употребив в нем фактор ацентричности, который весьма часто используется в качестве характеристики неполярных или слабо полярных веществ [c.94]
Тогда метод Майзика и Тодоса сводится к нахождению оптимальной функциональной зависимости между ky и Тг, Ср и Z . Найдено несколько уравнений для различных тщюв соединений и для разных областей приведенной температуры. Сводка этих уравнений приведена в табл. IX. 2 и, поскольку величина ky не является безразмерной, то необходимо использовать соответствующую систему единиц, приведенных в этой таблице. Критические константы можно найти в приложении I или определить с помощью методов, изложенных в гл. I. Теплоемкость при низком давлении Ср может быть рассчитана как это показано в гл. IV. Точность и области применения указанных уравнений рассматриваются на стр. 505. [c.502]
Третий компонент — метилциклопентан неполярен, поэтому на первой карте содержатся только критические свойства и наименование компонента. На второй карте (вторая строка в таблице) указаны молярные объемы жидкости при двух температурах 0°С и 40 °С другие данные об этом компоненте недостаточно достоверны. В этом случае параметр VL1Q (3,3) полагается равным нулю, вследствие чего температурная зависимость для метилциклопе тана будет линейной. Третья строка содержит константы уравнения Рейделя для аппроксимации давления паров. Данные о компоненте с самой высокой критической температурой — бензоле представлены аналогичным образом. [c.122]
Затем измеряют А/г акс для толуола при температуре термостата 30, 40, 50 и 60° С. Из уравнения (6) получают ряд значений о, по которым рассчитывают температурный коэффициент, принимая Д0 вместо da и АТ вместо dT. Полученные значения Ао АТ сводят в таблицу, вычисляют среднюю величину и рас-считывак т отклонение отдельных измерений от нее. Величина отклонений свидетельствует о точности измерений. Зная критическую температуру толуола и пользуясь опытными данными а при различной температуре, можно рассчитать коэффициенты К и а в уравнении (9) или же построить график зависимости о от Т опыта в координатах (Гкр—7)—g и определить константы уравнения графически. [c.21]
Так как уравнение ван-дер-Ваальса только приближенное, то значенпп константы зависят от физических данных, использованных для ее вычисления. Приведенные в таблице данные основаны на критических свойствах. Значения, полученные из теплоты испарения и плотности ншдкости в точке кипения при атмосферном давлении, в два или три раза больше, хотя соотношение это уменьшается с повышением точки кипения. [c.85]
Константы конечных продуктов крекинга приведены в таблице. 91. Определиы критические условия для исходного сырья. [c.434]
В отличие от большинства других справочников и сводок, имеющих компилятивный характер, все таблицы термодинамических свойств, приведенные в настоящем Справочнике, вычислены его авторами. Расчеты были выполнены на основании значений исходных постоянных, принятых в результате критического анализа данных, опубликованных в литературе до конца 1960 г. (частично были использованы также данные, опубликованные в 1961 г.). Выбор метода расчета в каждом случае определялся полнотой данных, необходимых для расчета. В Справочнике дано обоснование выбора всех постоянных, принятых в расчетах, описаны методы расчета, применявшиеся для каждого конкретного случая, а результаты расчетов сопоставлены с известными ранее в литературе. Для всех таблиц термодинамических функций и констант равновесия указана точность с учетом погрешности принятых в расчетах постоянных и примененных методов расчета. Для всех веществ, рассмотренных в Справочнике (за исключением А1аОз), вычислены таблицы термодинамических свойств соответствующих идеальных газов. [c.20]
В практике лабораторной и производственной работы не всегда представляется возможным и необходимым пользоваться обширными и громоздкими справочниками, как например, многотомным Справочником физико-технических величин , таблицами Ландоль-та — Бернштейна или Международными критическими таблицами . В этих справочниках для каждой константы обычно дается ряд цифр, и выбор из них предоставляется самому читателю. [c.5]
Члены правой стороны уравнения распадаются на две группы те, которые содержат множитель у представляют собой эффект Пойнтинга. Они все, кроме первого, исчезают, если добавляемый газ является идеальным. Члены с В12, Сцг и Ощг и 1т. д. представляют собой взаимодействие в газовой фазе одной молекулы твердого вещества с одной, двумя и т. д. молекулами газа. Это уравнение может быть написано в более простом виде, аналогичном уравнению (15). Коэффициент Dui2 не мог быть подсчитан, а остальные вириальные коэффициенты подсчитывались на основании свойств чистых компонентов при использовании таблиц [25], вычисленных для потенциала Леннард-Джонса, при этом были использованы также следующие соотношения между критическими постоянными и константами потенциала Леннард-Джонса [c.462]
Мне кажется, что из сделанного выше обзора развития теории соответственных состояний напрашивается еш е одно заключение. А именно, в по-следуюш ем нужно отказаться от попыток Iсвязывать эту теорию с каким-либо конкретным уравнением состояния. Понятно, что не приходится возражать против того или иного использования уравнений состояния типа уравнений Леннард-Джонса и Девоншайра, как и любого другого с более или менее строго вычисленными вириальными коэффициентами. Но рассматривать законы соответственных состояний как следствие одного из этих уравнений и на этом основании для определения приведенных параметров -пользоваться вместо критических величин константами молекулярного потенциала — в этом нет необходимости такой подход ведет только к бесполезным пересчетам он не дает ничего нового, ничего интересного и только затрудняет сопоставление. таблиц и диаграмм, полученных разными авторами. [c.278]
В следующей таблице приведены некоторые значения атомных рефракций, данные Ауерсом и Эйзенлором [4], которые произвели критический перерасчет этих констант. [c.484]
Критическая константа
Cтраница 3
При отсутствии в литературе значений критических констант, необходимых для определения величины р, они могут быть рассчитаны по формулам, приводимым в курсах химической термодинамики и физической химии.
[31]
Большое внимание уделяется методу измерения критических констант, так как для одного вещества могут быть получены совершенно разные результаты из-за разницы в аппаратуре и методах наблюдений.
[32]
При отсутствии в литературе значений критических констант, необходимых для определения величины 3, они могут быть рассчитаны по формулам, приводимым в курсах химической термодинамики и физической химии.
[33]
Сопоставление рассчитанных и экспериментальных значений критических констант Ткр, Ркр, VKf индивидуальных углеводородов ( табл. 4.6) показывает достаточно высокую адекватность предложенной математической модели, применимой и для узких нефтяных фракций.
[34]
Имеющиеся в литературе данные по критическим константам были получены различными методами и процедурами.
[35]
С другой стороны, если известны критические константы, то летучести можно найти по обобщенным диаграммам, после чего можно вычислить K.
[37]
Давление насыщенного пара, плотности и критические константы 2 2 4-триметилпентана.
[38]
Биетти и соавторы [21] определили также критические константы изобутана, применив для этой цели метод построения изотерм вблизи критической точки. Приводим найденные ими значения: / Кр 134 98 0 05 С; Ркр 36 00 0 05 ата; с / кр 0 221 г / мл. Найденные Биетти и соавторами значения критических констант изобутана следует считать наиболее надежными.
[39]
Установлено, что концентрационный хаос искажает критические константы фазовых переходов, определяемые из классов универсальности. Показана статистическая корреляция между параметрами порядка фазовых переходов первого рода и кинетических фазовых переходов второго рода. Обнаружен эффект пространственно-временного совмещения фазовых переходов в многокомпонентных высокомолекулярных системах с концентрационным хаосом.
[40]
Постоянные а и b вычисляются из критических констант. В табл. 23 приведены объемы V 1 моля двуокиси углерода при различных давлениях и температуре 40, найденные экспериментально, а также значения, вычисленные по уравнению состояния идеальных газов и по уравнению состояния Ван-дер – Ваальса.
[41]
Псевдокритические параметры рассчитываются обычно исходя из истинных критических констант индивидуальных компонентов и молярных долей последних методом У.
[42]
В литературе встречаются разные данные в значении критических констант этилового спирта.
[43]
Если экспериментальные данные полностью отсутствуют, но известны критические константы ( или могут быть определены), то объем жидкости при любой температуре может быть определен с помощью одного из следующих способов: 1) значение Vb рассчитывается по методам, изложенным в разделе II. Бенсона [ уравнение (11.82) ], Гольдхаммера [ уравнение (11.85) ] или Лидерсена, Гринкорна и Хоугена [ уравнение ( II. Второй способ более предпочтителен при давлениях, превышающих давление насыщения.
[44]
Уравнение Дюкло дает также возможность вычислить тройную точку и критические константы, если известна кривая давления насыщенного пара.
[45]
Страницы:
1
2
3
4
До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.
Так был изобретен критерий χ2 (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.
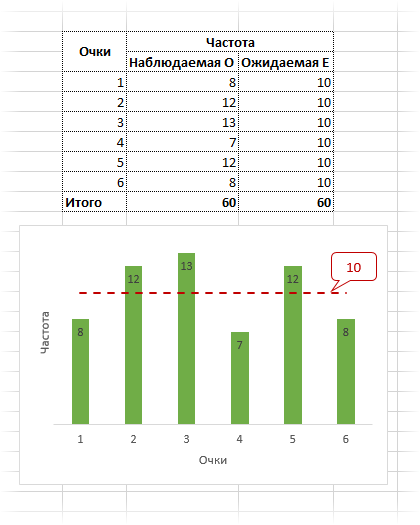
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.
- Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
- Распределение этой меры при справедливости гипотезы о том, что различий нет.
Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной Ei будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение
имеет стандартное нормальное распределение.
Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
Это и есть статистика для критерия Хи-квадрат Пирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.
«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.
Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ2 – это целое семейство распределений.
И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).
Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.
Таким образом, распределение хи квадрат (χ2) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
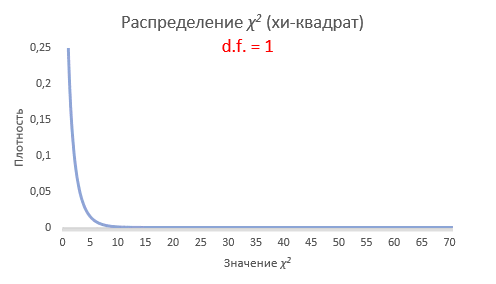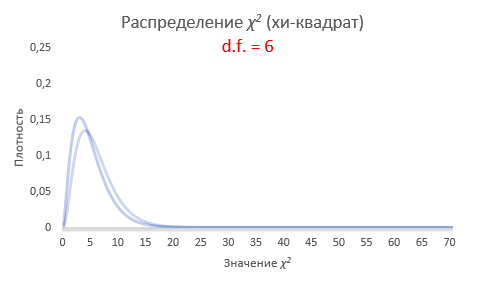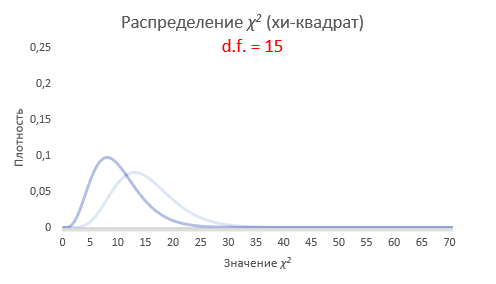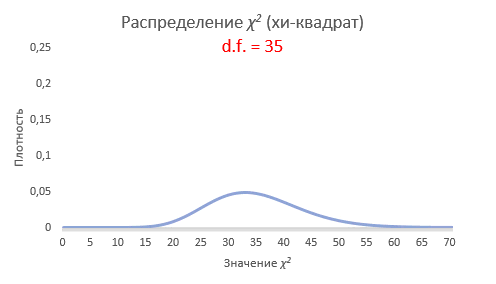
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).
Проверка гипотезы по критерию Хи квадрат Пирсона
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.
Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.
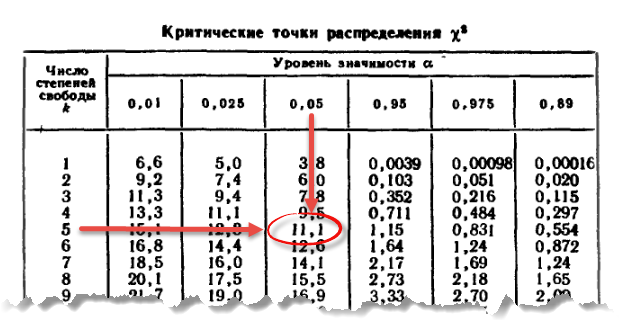
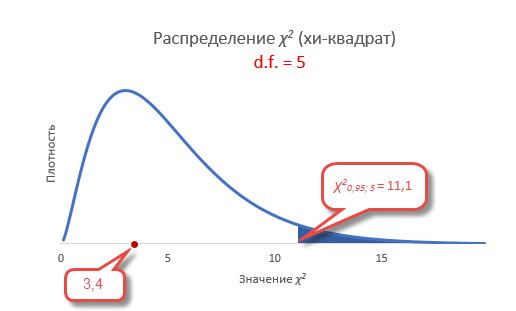
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ20,05; 5 = 11,1.
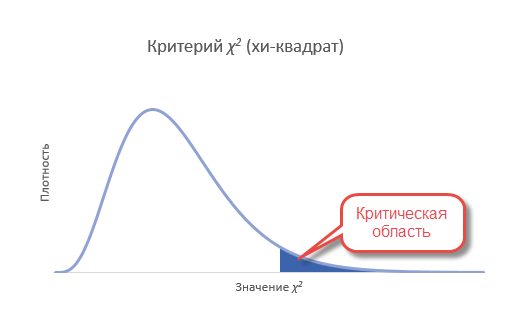
Сравним фактическое и табличное значение. 3,4 (χ2) < 11,1 (χ20,05; 5). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.
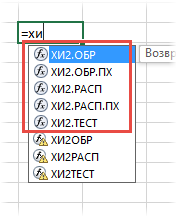
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.
Ниже их краткое описание.
ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)
ХИ2.ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ХИ2.РАСП – p-value слева (можно рассчитать плотность).
ХИ2.РАСП.ПХ – p-value справа.
ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.
Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:
=ХИ2.ОБР(0,95;5)
Или так
=ХИ2.ОБР.ПХ(0,05;5)
Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).
Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ2 = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
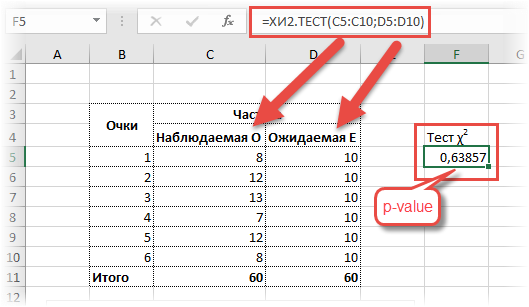
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857
Значит, при 5-ти степенях свободы вероятность получить значение критерия χ2 = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.
А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.
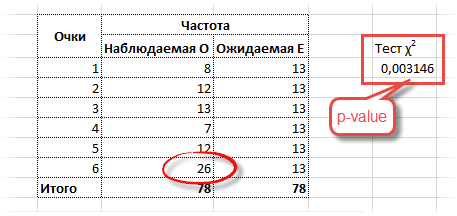
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).
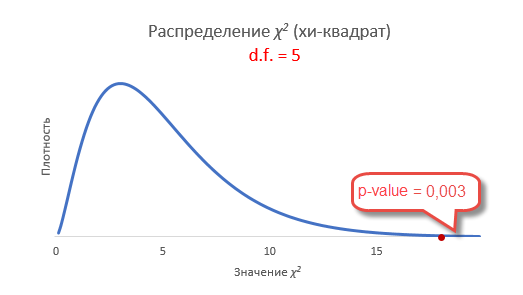
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.
Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).
Надеюсь, мне удалось объяснить, что такое критерий согласия χ2 (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.
Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.
Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.
Скачать файл с примером.
Поделиться в социальных сетях: