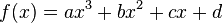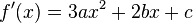Кубическая парабола как найти вершину параболы - Сайт, где вы сможете решить свои вопросы

Формула нахождения вершины параболы

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение 1

Парабола – это геометрическое множество точек, равноудалённых от точки F, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.

Что значит вершина параболы

Определение 2

Вершина параболы – это точка, ближайшая к директрисе параболы. Она является центром отрезка, ограниченного точкой фокуса параболы $F$ и директрисой $d$.

Производная в вершине квадратичной параболы равна нулю.

Каноническое уравнение параболы $y^2 = 2px$ справедливо для параболы, вершина которой находится в центре осей.

Для того, чтобы определить, принадлежит ли точка графику заданной параболы, необходимо подставить её координаты в формулу $y = ax^2 + bx + c$.

Если равенство выполняется — точка принадлежит графику.

Как найти вершины параболы, задающейся квадратичной функцией

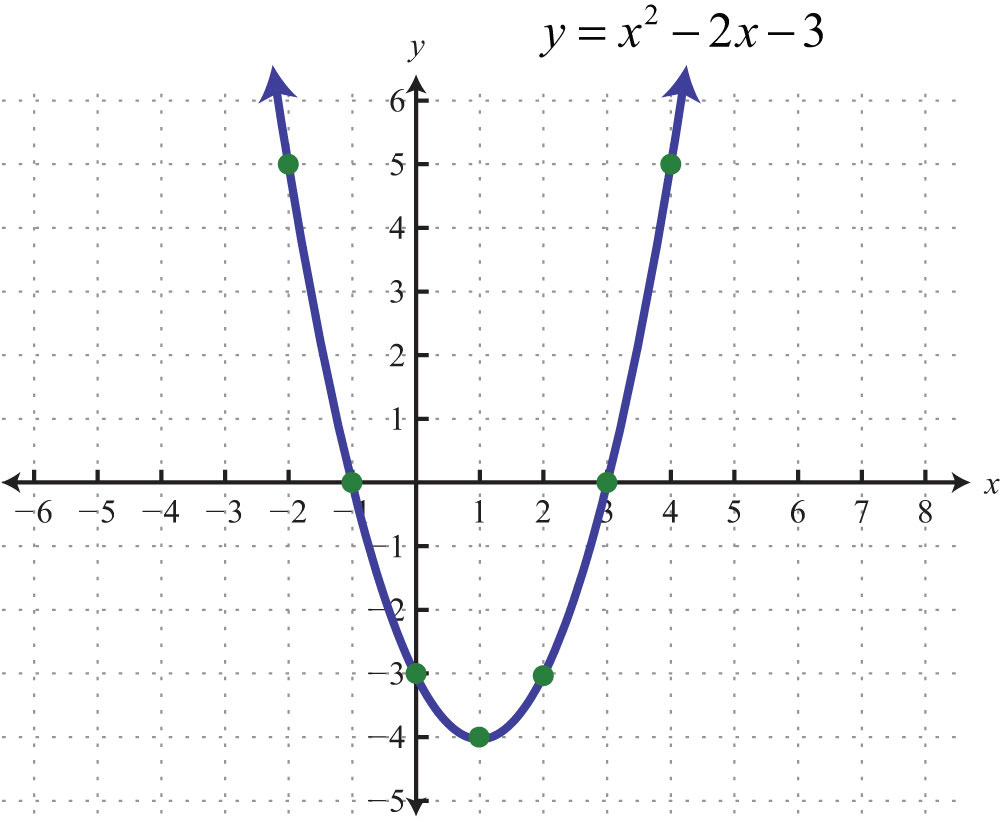
Рисунок 1. Пример уравнения и графика квадратичной параболы

Довольно часто парабола задаётся квадратичной функцией вида $y = ax^2 + bx + c$, вершина такой параболы находится в произвольной точке.

Какой-то единой формулы для нахождения сразу обеих координат вершины параболы нет, но при этом определить координаты вершины параболы по уравнению довольно просто.

Алгоритм для нахождения вершины параболы такой:

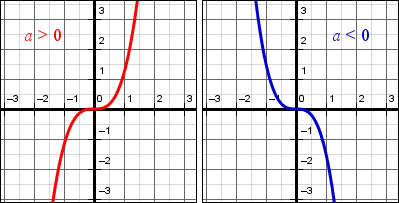
Запишите коэффициенты $a, b, c$ из уравнения. Если коэффициент $a$ при $y$ положительный, то ветви параболы будут смотреть вверх, а если отрицательный, то вниз.
Найдите абсциссу вершины параболы ($x$ вершины) по формуле $x = – frac{b}{2a}$, для этого воспользуйтесь коэффициентами $a, b, c$ из уравнения.
Подставьте найденный $x$ в уравнение параболы и вычислите ординату вершины параболы $y$.
Запишите полученные координаты x и y вершины параболы в форме точки $(x; y)$.

Пример 1

Рассмотрим уравнение параболы $y = x^2 – 5x + 7$

Коэффициенты этой параболы $a = 1$, $b = -5$, $c = 7$.
Для вычисления x вершины параболы подставьте $a = 1$ и $b = -5$ в формулу $x = – frac{b}{2a}= frac{5}{2}=2.5$
Подставьте найденный $x$ в исходное уравнение:
$y = 2,5^2 – 5 cdot 2.5 + 7$
$y = 0,75$
Координаты вершины этой параболы $(2.5;0.75)$.

Вершина кубической параболы

Чтобы найти вершины (точки локальных минимумов и максимумов) кубической параболы, необходимо найти её производную, приравнять её к нулю и затем вычислить $x$ и $y$.

Если же необходимо найти точку перегиба кубической параболы, необходимо найти вторую производную и также приравнять её к нулю.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 04.12.2022

Источник

Понятие вершины параболы

Парабола – это геометрическое множество точек, которые равноудалены от точки F, и которая не является частью параболы и прямой, а также не проходит через центр отрезка.

Вершина параболы — это некая точка, которая расположена ближе всего в директрисе параболы. Данная точка является центром любого отрезка, который ограничен точками фокуса параболы и директрисой.

Формула

Каноническое уравнение параболы выглядит следующим образом:

[y^{2}=2 p x]

Где: [p] — параметр параболы; [x] — ось данной параболы.

Данное уравнение будет справедливо только для параболы, вершина которой проходит через центр осей.

Чтобы определить принадлежность точки к графику заданной параболы, нужно точку подставить в уравнение:

[y=a x^{2}+b x+c]

где:

a, b, c — заданные коэффициенты;
х — ось координатной прямой.

Определение вершины кубической параболы

Определение

Кубическая парабола – плоская алгебраическая кривая третьего порядка.

Ее каноническое уравнение в прямоугольной декартовой системе координат имеет вид у = ах³, где а ≠ 0.

Для кубической параболы характерен центр симметрии в самом начале координат. Данная точка является точкой перегиба кривой. Касательная к кубической параболе, в этой же точке именуется как ось абсцисс.

Рисунок 1. Графики кубической параболы

Для того, чтобы определить точки вершин кубической параболы, нужно вычислить ее производную. Точки вершин, иначе еще называют точками минимума и максимума.

После того, как определится производная, нужно ее значение приравнять к нулевому. Затем можно приступать к вычислению значений x и y.

Определение вершин параболы, которая задана квадратичной функцией

Рисунок 2. Уравнение и график параболы квадратичной функции

Квадратичная функция вида: [y=a x^{2}+b x+c] очень часто используется для того, чтобы задать значения параболы.

Вершина такой функции, всегда находится в произвольной точке.

В технических науках не существует единой формулы, чтобы вычислить сразу две вершины параболы. Однако, довольно легко определяются координаты вершины, по уже упомянутому уравнению.

Нет времени решать самому?

Наши эксперты помогут!

Алгоритм решения задач по определению точек вершин параболы

Необходимо выписать коэффициенты a, b, c по условию заданного уравнения. При условии, что коэффициент а будет иметь положительное значение, можно сделать вывод: ветви параболы направлены вверх. Следовательно, если значение отрицательное, то ветви будут направлены вниз.
Вторым действием определяется абсцисса вершины параболы.
(x) по следующей формуле [x=-frac{b}{2 a}], для этого необходимо применить коэффициенты a, b, c из заданного по заданию уравнения.
Найденное значение x нужно подставить в уравнение, решить его, и тем самым будет выполнен окончательный расчет.
В ответ записать найденные координаты вершин параболы x и y.

Пример решения уравнения параболы

Рассмотрим подробно на примере, решение задач данной категории.

Запишем данное уравнение следующего вида: [y=x^{2}-5 x+7].

Воспользуемся алгоритмом решения, и выполним следующие действия:

Зададим коэффициенты параболы. Они равны следующим значениям: a=1, b=-5, с=7.
Чтобы вычислить вершину x параболы, нужно известные коэффициенты a=1, b=-5 подставить в формулу: [x=-frac{b}{2 a}=frac{-5}{2}=2,5].
Вычисленное значение х, нужно подставить в исходное уравнение: [y=2,5^{2}-5 cdot 2,5+7=0,75]
Координаты вершины параболы будут равняться следующим значения: (0,75 и 2,5).

Источник

Как найти вершину в куб. параболе? Очень нужно, срочно. Заранее спасибо

Дмитрий Минаев

Знаток

(279),
на голосовании

8 лет назад

Голосование за лучший ответ

Алексашка

Гуру

(2934)

8 лет назад

http://znanija.com/task/4779942

Дмитрий МинаевЗнаток (279)

8 лет назад

Мне не квадратная нужна, а кубическая.. (

Алексашка
Гуру
(2934)
извини! Ошибся!

Булатова Римма

Искусственный Интеллект

(126427)

8 лет назад

Абсцисса вершины параболы х (о) =-b/2a.
А ординату вершины находим, подставляя в функцию значение абсциссы вершины параболы: у (о) =f(x(o)).

Дмитрий МинаевЗнаток (279)

8 лет назад

Это кубической?

Булатова Римма
Искусственный Интеллект
(126427)
Нет. Квадратичной функции. Я невнимательно прочитала задачу.

лиза стаинова

Профи

(525)

3 года назад

пипяууууууууу

Похожие вопросы

Источник

График кубической функции (кубическая парабола)

Куби́ческая фу́нкция в математике — это числовая функция вида

$f(x)=ax^{3}+bx^{2}+cx+d,quad xin {mathbb {R}},$

где aneq 0.
Другими словами, кубическая функция задаётся многочленом третьей степени.

Аналитические свойства[править | править код]

Производная кубической функции $f(x)=ax^{3}+bx^{2}+cx+d$ имеет вид $f'(x)=3ax^{2}+2bx+c$ . В случае, когда дискриминант ${frac {D}{4}}=b^{2}-3ac$ полученного квадратного уравнения f'(x)=0 больше нуля, оно имеет два различных решения, которые соответствуют критическим точкам функции . При этом, одна из этих точек является точкой локального минимума, а другая точкой локального максимума. Равенство нулю второй производной f'' определяет точку перегиба x=-b/3a .

График[править | править код]

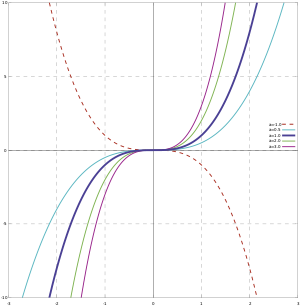
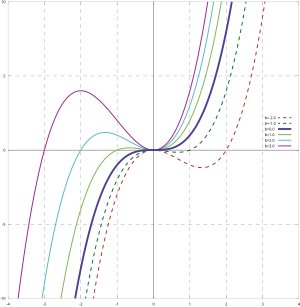
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции $y=ax^{3}$ или $y=x^{3}$ . Легко видеть, что, применяя параллельный перенос, можно привести кубическую параболу к виду, когда она будет задаваться уравнением $y=ax^{3}-px$ . Путём применения аффинных преобразований плоскости можно добиться, чтобы a=1 и p=0 . В этом смысле все определения будут эквивалентны.

Кроме того, кубическая парабола

центрально-симметрична относительно точки перегиба,
всегда пересекает линию абсцисс хотя бы в одной точке,
не имеет общих точек со своей касательной в точке перегиба, кроме как в самой точке касания.

Поведение графика при изменении коэффициентов


Коэффициент при кубе	Коэффициент при квадрате	Коэффициент при первой степени

Коллинеарность[править | править код]

Касающиеся прямые в трёх коллинеарных точках графика кубической функции пересекают график снова в коллинеарных точках.^[1]

Применение[править | править код]

Кубическую параболу иногда применяют для расчёта переходной кривой на транспорте, так как её вычисление намного проще, чем построение клотоиды.

См. также[править | править код]

Парабола
Кубика
Кубическое уравнение
Сплайн

Примечания[править | править код]

↑ Whitworth, William Allen. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866). http://www.forgottenbooks.com/search?q=Trilinear+coordinates&t=books Архивная копия от 24 марта 2016 на Wayback Machine

Литература[править | править код]

Л. С. Понтрягин, Кубическая парабола // «Квант», 1984, № 3.
И. Н. Бронштейн, К. А. Семендяев, «Справочник по математике», издательство «Наука», М. 1967, с. 84

Источник

Кубическая парабола задается функцией y=x³
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции y=a x^3 или y=x^3
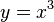
Перечислим основные свойства функции
1.Область определения – любое действительное число:.

2.Область значений – любое действительное число:.

3.Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием .
Производная кубической функции имеет вид . В случае, когда дискриминант $frac{D}{4}=b^2-3ac$ полученного квадратного уравнения f'(x)=0 больше нуля, оно имеет два различных решения, которые соответствуют критическим точкам функции . При этом, одна из этих точек является точкой локального минимума, а другая точкой локального максимума. Равенство нулю второй производной f'' определяет точку перегиба x=-b/3a .