Содержание
- Геометрические фигуры. Квадрат.
- Свойства квадрата.
- Диагональ квадрата.
- Квадрат, свойства и формулы, площадь и периметр
- Квадрат, свойства и формулы, площадь и периметр.
- Квадрат (понятие, определение), диагональ квадрата:
- Свойства квадрата:
- Формулы квадрата. Площадь квадрата. Периметр квадрата:
- Квадрат — определение и свойства
- Квадрат. Онлайн калькулятор
- Свойства квадрата
- Диагональ квадрата
- Окружность, вписанная в квадрат
- Формула вычисления радиуса вписанной окружности через сторону квадрата
- Формула вычисления сторон квадрата через радиус вписанной окружности
- Окружность, описанная около квадрата
- Формула радиуса окружности описанной вокруг квадрата
- Формула стороны квадрата через радиус описанной около квадрата окружности
- Периметр квадрата
- Признаки квадрата
- Квадрат
- Свойства квадрата
- Признаки квадрата
- Описанная окружность
- Вписанная окружность
- Площадь квадрата
Геометрические фигуры. Квадрат.
Квадрат — правильный четырёхугольник. У квадрата все углы и стороны одинаковы.
Квадраты различаются лишь длиной стороны, а все 4 угла прямые и равны 90°.
Квадратом может стать параллелограмм, ромб либо прямоугольник, когда у них одинаковые длины диагоналей, сторон и равные углы.
Свойства квадрата.
— у всех 4-х сторон квадрата одинаковая длина, т.е. стороны квадрата равны:
— противолежащие стороны квадрата параллельны:
— каждый уг ол квадрата прямой:
— сумма углов квадрата равна 360°:
— каждая диагональ квадрата имеет такую же длину, как и другая:
— каждая из диагоналей квадрата делит квадрат на 2 одинаковые симметричные фигуры.
— угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
AC┴BD;AO = BO = CO = DO = d/2
— точку пересечения диагоналей называют центр квадрата и она оказывается центром вписанной и описанной окружностей.
— все диагонали делят угол квадрата на две равные части, таким образом, они оказываются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
— диагонали делят квадрат на 4 одинаковых треугольника, кроме того, полученные треугольники в одно время и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата.
Диагональю квадрата является всякий отрезок, который соединяет 2-е вершины противолежащих углов квадрата.
Диагональ всякого квадрата больше стороны этого квадрата в √2 раз.
Формулы для определения длины диагонали квадрата:
1. Формула диагонали квадрата через сторону квадрата:
2. Формула диагонали квадрата через площадь квадрата:
3. Формула диагонали квадрата через периметр квадрата:
4. Сумма углов квадрата = 360°:
5. Диагонали квадрата одной длины:
6. Все диагонали квадрата делят квадрат на 2-е одинаковые фигуры, которые симметричны:
7. Угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
8. Формула диагонали квадрата через длину отрезка l:
9. Формула диагонали квадрата через радиус вписанной окружности:
10. Формула диагонали квадрата через радиус описанной окружности:
R – радиус описанной окружности;
D – диаметр описанной окружности;
11. Формула диагонали квадрата через линию, которая выходит из угла на середину стороны квадрата:
C – линия, которая выходит из угла на середину стороны квадрата;
Вписанный круг в квадрат – это круг, примыкающий к серединам сторон квадрата и имеющий центр на пересечении диагоналей квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Радиус окружности описанной вокруг квадрата больше радиуса вписанной окружности в √2 раз.
Радиус окружности описанной вокруг квадрата равен 1/2 диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Источник
Квадрат, свойства и формулы, площадь и периметр
Квадрат, свойства и формулы, площадь и периметр.
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат (понятие, определение), диагональ квадрата:
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат – это четырехугольник, имеющий равные стороны и углы.
Все углы квадрата прямые. Каждый из них прямой и равен 90°.
Таким образом, все квадраты отличаются друг от друга только длиной стороны.
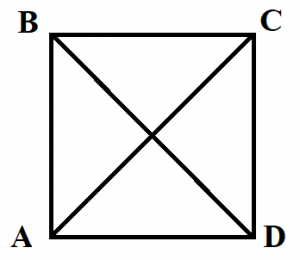
Рис. 2. Квадрат и диагонали квадрата
Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.
Квадрат – это равносторонний прямоугольник.
Квадрат – это ромб с прямыми углами.
Свойства квадрата:
1. Длины всех сторон равны.
2. Противоположные стороны квадрата параллельны.
3. Все углы квадрата прямые. Каждый из них равен 90°.
4. Сумма углов квадрата равна 360 градусам.
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
5. Диагонали квадрата равны между собой.
6. Диагонали квадрата взаимно перпендикулярны.
7. Диагонали квадрата точкой пересечения делятся пополам.
8. Угол между диагональю и стороной квадрата равен 45 градусам.
9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.
10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.
11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.
Формулы квадрата. Площадь квадрата. Периметр квадрата:
Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.
Формула диагонали квадрата:





Формула радиуса вписанной окружности квадрата:
Радиус вписанной окружности квадрата равен половине его стороны.

Формула радиуса описанной окружности квадрата:

Формула периметра квадрата:



Формула площади квадрата:





Источник
Квадрат — определение и свойства
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Перечислим свойства квадрата:
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
Очевидно, радиус окружности равен половине диагонали квадрата.
Диаметр окружности равен стороне квадрата.
Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.
Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Источник
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
Изложеннные свойства изображены на рисунках ниже:
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
Из равенства (1) найдем d:
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
Из формулы (5) найдем R:
или, умножая числитель и знаменатель на 
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
Эти реугольники также равнобедренные. Тогда
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Источник
Квадрат

Квадрат – прямоугольник с равными сторонами.
Квадрат – параллелограмм, у которого все стороны равны и все углы равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.
Признаки квадрата
Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:
1. Все стороны равны и среди внутренних углов есть прямой угол.
2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.
Описанная окружность
Около квадрата можно описать окружность. Сторона и радиус
окружности связаны соотношением:
Вписанная окружность
В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:
Площадь квадрата
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Источник
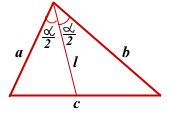
Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.
I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.
Утверждение 1
Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
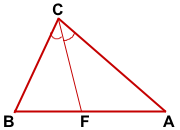
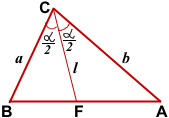
ΔABC,
СF — биссектриса ∠ABC
Доказать:
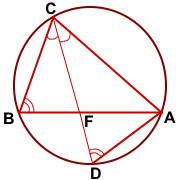
Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.
Рассмотрим треугольники BCF и DCA.
∠BCF=∠DCA (по условию);
∠CBF=∠CDA (как вписанные углы, опирающиеся на одну дугу AC).
Значит, треугольники BFC и DCA подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
По свойству пересекающихся хорд
Отсюда
Что и требовалось доказать.
II. Через три стороны треугольника
Утверждение 2
Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле
Доказательство:
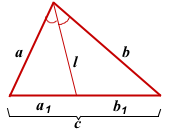
a1+b1=c, b1=c-a1, поэтому
Согласно утверждению 1,
откуда
Что и требовалось доказать.
Аналогично,
III Через две стороны треугольника и угол между ними.
Утверждение 3
Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле
Доказательство:
Найдем площади треугольников BCF, ACF и ABC.
Так как
то
Что и требовалось доказать.
Квадрат — определение и свойства
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Перечислим свойства квадрата:
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
Очевидно, радиус окружности равен половине диагонали квадрата.
Диаметр окружности равен стороне квадрата.
Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.
Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Источник
Чему равна биссектриса квадрата
Квадрат — прямоугольник, у которого все стороны равны (ромб, у которого углы прямые).
Из всех прямоугольников одного и того же периметра квaдрат имеет наибольшую площадь.
Из всех прямоугольников определенной площади квадрaт имеет наименьший периметр.
Слово «квaдрaт» происходит от латинского «gudratus» — четырехугольник.
Квадрaт был первым четырехугольником, который рассматривался в геометрии.
Любой квадрат можно разрезать на два равных квадрата.
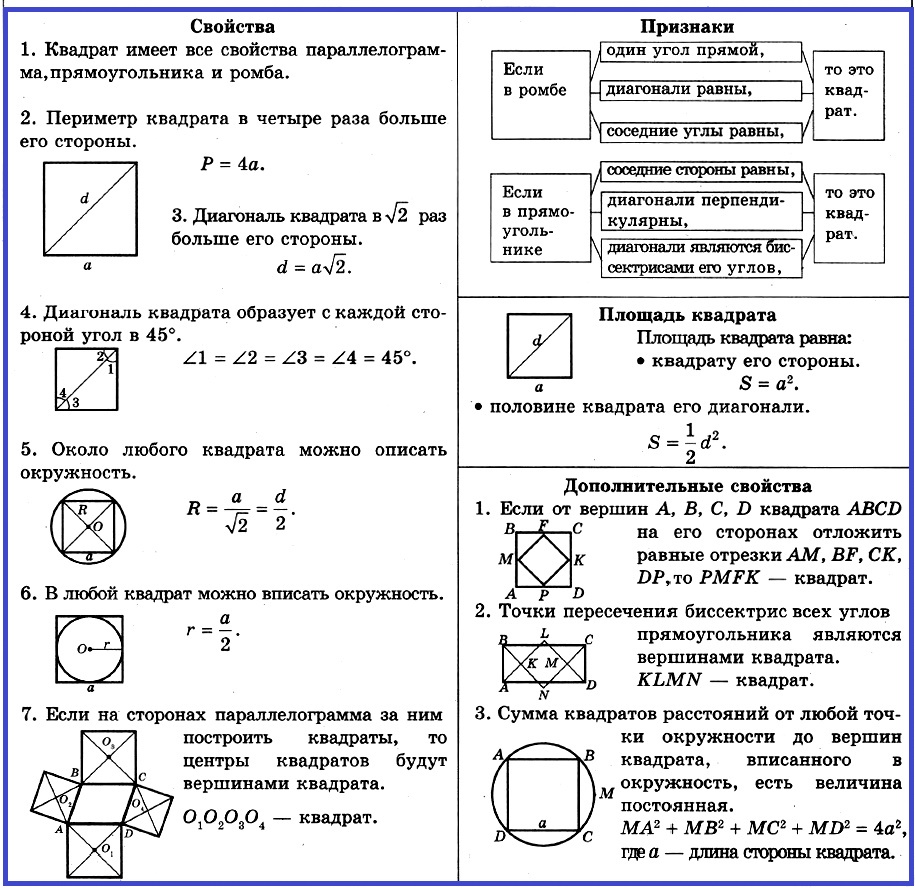
Свойства и признаки квадрата
Свойства квадрата:
1. Квадрaт имеет все свойства параллелограмма, прямоугольника и ромба.
2. Периметр квадрата в четыре раза больше его стороны.
3. Диагональ квадрата в √2 раз больше его стороны.
4. Диагональ квадрата образует с каждой стороной угол в 45°.
5. Около любого квадрата можно описать окружность.
6. В любой квадрат можно вписать окружность.
7. Если на сторонах параллелограмма за ним построить квадраты, то центры квадратов будут вершинами квадрата.
Признаки квадрата:
Если в ромбе один угол прямой,
Если в ромбе диагонали равны,
Если в ромбе соседние углы равны,
Если в прямоугольнике соседние стороны равны,
Если в прямоугольнике диагонали перпендикулярны,
Если в прямоугольнике диагонали являются биссектрисами его углов.
Дополнительные свойства
1. Если от вершин А, В, С, D квадрата ABCD на его сторонах отложить равные отрезки AM, BF, СК, DP, то PMFK — квадрат.
2. Точки пересечения биссектрис всех углов прямоугольника являются вершинами квадрата.
3. Сумма квадратов расстояний от любой точки окружности до вершин квадрата, вписанного в окружность, есть величина постоянная.
Это конспект по теме «Квадрат и его свойства». Выберите дальнейшие действия:
Источник
Что такое квадрат: определение и свойства
В данной публикации мы рассмотрим определение и свойства (с рисунками) одной из основных геометрических фигур – квадрата.
Определение квадрата
Свойства квадрата
Свойство 1
Диагонали квадрата равны, расположены под прямым углом друг к другу, в точке пересечения делятся пополам.
Свойство 2
Диагонали квадрата являются биссектрисами его углов. Для рисунке выше:
Свойство 3
Центром описанной вокруг и вписанной в квадрат окружностей является точка пересечения его диагоналей (в нашем случае – E).
При этом радиусы окружностей можно вычислить через длину стороны или диагонали квадрата:
Также, один радиус можно выразить через другой:
Свойство 4
Зная длину стороны или диагонали квадрата, можно найти его площадь или периметр.
Периметр (P) квадрата через сторону:
P = a + a + a + a = 4 ⋅ a
Периметр (P) квадрата через диагональ:
Площадь (S) квадрата через сторону:
Площадь (S) квадрата через диагональ:
Источник
Геометрические фигуры. Квадрат.
Квадрат — правильный четырёхугольник. У квадрата все углы и стороны одинаковы.
Квадраты различаются лишь длиной стороны, а все 4 угла прямые и равны 90°.
Квадратом может стать параллелограмм, ромб либо прямоугольник, когда у них одинаковые длины диагоналей, сторон и равные углы.
Свойства квадрата.
— у всех 4-х сторон квадрата одинаковая длина, т.е. стороны квадрата равны:
— противолежащие стороны квадрата параллельны:
— каждый уг ол квадрата прямой:
— сумма углов квадрата равна 360°:
— каждая диагональ квадрата имеет такую же длину, как и другая:
— каждая из диагоналей квадрата делит квадрат на 2 одинаковые симметричные фигуры.
— угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
AC┴BD;AO = BO = CO = DO = d/2
— точку пересечения диагоналей называют центр квадрата и она оказывается центром вписанной и описанной окружностей.
— все диагонали делят угол квадрата на две равные части, таким образом, они оказываются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
— диагонали делят квадрат на 4 одинаковых треугольника, кроме того, полученные треугольники в одно время и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата.
Диагональю квадрата является всякий отрезок, который соединяет 2-е вершины противолежащих углов квадрата.
Диагональ всякого квадрата больше стороны этого квадрата в √2 раз.
Формулы для определения длины диагонали квадрата:
1. Формула диагонали квадрата через сторону квадрата:
2. Формула диагонали квадрата через площадь квадрата:
3. Формула диагонали квадрата через периметр квадрата:
4. Сумма углов квадрата = 360°:
5. Диагонали квадрата одной длины:
6. Все диагонали квадрата делят квадрат на 2-е одинаковые фигуры, которые симметричны:
7. Угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
8. Формула диагонали квадрата через длину отрезка l:
9. Формула диагонали квадрата через радиус вписанной окружности:
10. Формула диагонали квадрата через радиус описанной окружности:
R – радиус описанной окружности;
D – диаметр описанной окружности;
11. Формула диагонали квадрата через линию, которая выходит из угла на середину стороны квадрата:
C – линия, которая выходит из угла на середину стороны квадрата;
Вписанный круг в квадрат – это круг, примыкающий к серединам сторон квадрата и имеющий центр на пересечении диагоналей квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Радиус окружности описанной вокруг квадрата больше радиуса вписанной окружности в √2 раз.
Радиус окружности описанной вокруг квадрата равен 1/2 диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Источник
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
Изложеннные свойства изображены на рисунках ниже:
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
Из равенства (1) найдем d:
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
Из формулы (5) найдем R:
или, умножая числитель и знаменатель на 
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
Эти реугольники также равнобедренные. Тогда
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Источник
Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
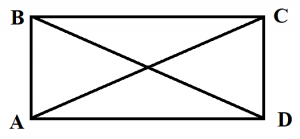
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.

- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
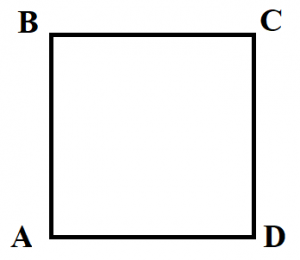
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 . . |
(1) |
Из равенства (1) найдем d:
 . . |
(2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 |
(3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 |
(4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
(5) |
Из формулы (5) найдем R:
 |
(6) |
или, умножая числитель и знаменатель на 
 . . |
(7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 . . |
(8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 |
(9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 |
(10) |
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 |
(12) |
Эти реугольники также равнобедренные. Тогда
Из (13) следует, что
 |
(14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Все, что нужно знать о свойствах четырехугольников
В этой статье мы рассмотрим все основные свойства и признаки четырехугольников.
Для начала я расположу все виды четырехугольников в виде такой сводной схемы:
Схема замечательна тем, что четырехугольники, стоящие в каждой строке обладают ВСЕМИ СВОЙСТВАМИ ЧЕТЫРЕХУГОЛЬНИКОВ, РАСПОЛОЖЕННЫХ НАД НИМИ. Поэтому запоминать надо совсем немного.
Трапеция – это четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны называются основаниями трапеции, а не параллельные – боковыми сторонами.
1. В трапеции сумма углов, прилежащих к боковой стороне равна 180°: А+В=180°, C+D=180°
2. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне:
3. Биссектрисы смежных углов трапеции пересекаются под прямым углом.
4.Трапеция называется равнобедренной, если ее боковые стороны равны:
В равнобедренной трапеции
- углы при основании равны,
- проекции боковых сторон на основание равны: .
5. Площадь трапеции равна произведению полусуммы оснований на высоту:
Параллелограм – это четырехугольник, у которого противоположные стороны попарно параллельны: В параллелограмме:
- противоположные стороны и противоположные углы равны
- диагонали параллелограмма делятся точкой пересечения пополам:
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.
Площадь параллелограмма равна произведению основания на высоту:
или произведению сторон на синус угла между ними:
:
Ромб – это параллелограмм, у которого все стороны равны:
- противоположные углы равны
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали ромба являются биссектрисами углов
Площадь ромба равна половине произведения диагоналей:
или произведению квадрата стороны на синус угла между сторонами:
Прямоугольник – это параллелограмм, у которого все углы прямые:
- Диагонали прямоугольника равны.
- Диагонали точкой пересечения делятся пополам.
Площадь прямоугольника равна произведению его сторон:
.
Квадрат – это прямоугольник, у которого все стороны равны
Квадрат – это ромб, у которого все углы прямые.
Соответственно: квадрат обладает свойствами ромба и прямоугольника:
- все углы равны 90 градусов
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали являются биссектрисами углов
- диагонали равны
Площадь квадрата равна квадрату его стороны.
Площадь квадрата равна половине произведения диагоналей.
И.В. Фельдман, репетитор по математике.
[spoiler title=”источники:”]
http://matworld.ru/geometry/kvadrat.php
http://ege-ok.ru/2012/05/14/vse-chto-nuzhno-znat-o-svoystvah-chetyirehugolnikov
[/spoiler]
Квадрат. Формулы и свойства квадрата
Определение.
Квадрат – это четырехугольник у которого все четыре стороны и углы одинаковы.
Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.
Основные свойства квадрата
Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.
1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:
AB = BC = CD = AD
2. Противоположные стороны квадрата параллельны:
AB||CD, BC||AD
3. Все четыре угла квадрата прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4. Сумма углов квадрата равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Диагонали квадрата имеют одинаковой длины:
AC = BD
6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:
| AC┴BD | AO = BO = CO = DO = | d | |
| 2 |
8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности
9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
10. Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата
Определение.
Диагональю квадрата называется любой отрезок, соединяющий две вершины противоположных углов квадрата.
Диагональ любого квадрата всегда больше его стороны в√2 раз.
Формулы определения длины диагонали квадрата
1. Формула диагонали квадрата через сторону квадрата:
d = a·√2
2. Формула диагонали квадрата через площадь квадрата:
d = √2S
3. Формула диагонали квадрата через периметр квадрата:
4. Формула диагонали квадрата через радиус описанной окружности:
d = 2R
5. Формула диагонали квадрата через диаметр описанной окружности:
d = Dо
6. Формула диагонали квадрата через радиус вписанной окружности:
d = 2r√2
7. Формула диагонали квадрата через диаметр вписанной окружности:
d = Dв√2
8. Формула диагонали квадрата через длину отрезка l:
Периметр квадрата
Определение.
Периметром квадрата называется сумма длин всех сторон квадрата.
Формулы определения длины периметра квадрата
1. Формула периметра квадрата через сторону квадрата:
P = 4a
2. Формула периметра квадрата через площадь квадрата:
P = 4√S
3. Формула периметра квадрата через диагональ квадрата:
P = 2d√2
4. Формула периметра квадрата через радиус описанной окружности:
P = 4R√2
5. Формула периметра квадрата через диаметр описанной окружности:
P = 2Dо√2
6. Формула периметра квадрата через радиус вписанной окружности:
P = 8r
7. Формула периметра квадрата через диаметр вписанной окружности:
P = 4Dв
8. Формула периметра квадрата через длину отрезка l:
Площадь квадрата
Определение.
Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.
Площадь квадрата больше площади любого четырехугольника с таким же периметром.
Формулы определения площади квадрата
1. Формула площади квадрата через сторону квадрата:
S = a2
2. Формула площади квадрата через периметр квадрата:
3. Формула площади квадрата через диагональ квадрата:
4. Формула площади квадрата через радиус описанной окружности:
S = 2R2
5. Формула площади квадрата через диаметр описанной окружности:
6. Формула площади квадрата через радиус вписанной окружности:
S = 4r2
7. Формула площади квадрата через диаметр вписанной окружности:
S = Dв2
8. Формула площади квадрата через длину отрезка l:
Окружность описанная вокруг квадрата
Определение.
Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.
Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√2 раз.
Радиус окружности описанной вокруг квадрата равен половине диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Формулы определения радиуса окружности описанной вокруг квадрата
1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата:
2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата:
3. Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:
4. Формула радиуса круга описанного вокруг квадрата через диагональ квадрата:
5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности:
6. Формула радиуса круга описанного вокруг квадрата через радиус вписанной окружности:
R = r √2
7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности:
8. формула радиуса круга описанного вокруг квадрата через длину отрезка l:
Окружность вписанная в квадрата
Определение.
Кругом вписанным в квадрат называется круг, который примыкает к серединам сторон квадрата и имеет центр на пересечении диагоналей квадрата.
Радиус вписанной окружности равен половине стороны квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в 4/π раза.
Формулы определения радиуса круга вписанного в квадрат
1. Формула радиуса круга вписанного в квадрат через сторону квадрата:
2. Формула радиуса круга вписанного в квадрат через диагональ квадрата:
3. Формула радиуса круга вписанного в квадрат через периметр квадрата:
4. Формула радиуса круга вписанного в квадрат через площадь квадрата:
5. Формула радиуса круга вписанного в квадрат через радиус описанной окружности:
6. Формула радиуса круга вписанного в квадрат через диаметр, описанной окружности:
7 Формула радиуса круга вписанного в квадрат через диаметр вписанной окружности:
8. Формула радиуса круга вписанного в квадрат через длину отрезка l:






































































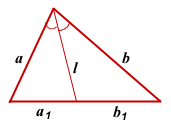
![Rendered by QuickLaTeX.com [ l = sqrt {frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c)} , ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-18591dd13191b4e7e6e02d8ea7855cc4_l3.png)