Мы начнем с матрицы
размером
:
Попробуем найти ее определитель. Его обозначают так:
-
— самый частый вариант
-
— такое обозначение тоже встречается, но реже
Далее мы по шагам разберем, как найти определитель.
Шаг 1: Выбираем опорную строку
Для начала выберем одну строку или столбец — это будет наша опорная строка. Это выбор не влияет на результат: мы получим один и тот же ответ независимо от того, какую строку или какой столбец выберем в качестве опоры.
В качестве опорной строки выберем первую строку нашего примера:
Шаг 2: Составляем новую матрицу
Теперь с помощью опорной строки нужно составить новую матрицу. Она будет размером
, потому что мы вычеркиваем:
-
Саму опорную строку
-
Столбец, который содержит первый элемент опорной строки (он обозначается как
)
Новая матрица будет выглядеть так:
Шаг 3: Находим минор
Выше мы не только выбрали опорную строку, но и выбрали элемент, с которым будет работать далее. Это
— первый элемент первой строки.
Теперь нам нужно найти минор этого элемента. Минором называют определитель не всей матрицы, а ее части. В нашем случае
— это одновременно:
-
И определитель матрицы
-
И минор матрицы
Как только мы найдем минор, нам будет намного проще найти полный определитель.
Чтобы найти минор, воспользуемся такой формулой:
Эта формула работает для такой матрицы:
Применим формулу к нашему примеру:
Это число
и есть минор.
Далее умножим полученный минор на выбранный элемент
. Получаем:
Шаг 4: Определяем знак
На предыдущем шаге мы нашли минор. Теперь надо найти знак ответа. Для этого надо умножить:
-
Либо на
-
Либо на
На что умножать? Все зависит от того, где элемент был в матрице. Вот простая таблица знаков, чтобы отслеживать, какой элемент на что умножать:
Мы выбрали элемент
, отмеченный знаком
, поэтому мы умножаем число на
. Ответ по-прежнему равен
.
Шаг 5: Повторяем шаги для второго элемента опорной строки
Повторим этот процесс для второго элемента в опорной строке. Вернемся к исходной матрице
:
Вспомним, что в качестве опорной строки мы выбрали первую строку нашего примера:
С первым элементом опорной строки мы уже поработали — это был элемент
. Возьмем следующий элемент —
со значением
.
Вычеркнем опорную строку и второй столбец, потому что он содержит
. Получится такая матрица
:
Найдем минор этой матрицы по формуле
:
Умножим минор на выбранный элемент матрицы —
:
Определим знак по таблице знаков. Мы выбрали элемент
, который на таблице знаков имеет знак
. Мы должны изменить знак нашего ответа:
Шаг 6: Повторяем шаги для третьего элемента опорной строки
Попробуйте самостоятельно повторить все те же шаги с третьим элементом (
со значением
):
-
Вычеркните из начальной матрицы опорную строку и третий столбец
-
Составьте новую матрицу
-
Найдите минор по формуле
-
Умножьте минор на
-
Определите знак по таблице
В итоге у вас должно получится
.
Шаг 7: Складываем все значения
Последним шагом нужно сложить все значения:
Таким образом, мы нашли определитель для нашей матрицы — это
.
Определи́тель (детермина́нт) в линейной алгебре — скалярная величина, которая характеризует ориентированное «растяжение» или «сжатие» многомерного евклидова пространства после преобразования матрицей; имеет смысл только для квадратных матриц. Стандартные обозначения определителя матрицы 



Определитель квадратной матрицы 










История[править | править код]
Теория определителей возникла в связи с задачей решения систем линейных уравнений.
К понятию определителя близко подошли авторы древнекитайского учебника «Математика в девяти книгах»[2].
В Европе определители матриц 2 × 2 встречаются у Кардано в XVI веке.
Для старших размерностей определение детерминанта дано Лейбницем в 1693 году.
Первая публикация принадлежит Крамеру. Теория определителей создана Вандермондом, Лапласом, Коши и Якоби. Термин «определитель» в современном его значении ввёл О. Коши (1815), хотя ранее (1801) «детерминантом» К. Гаусс назвал дискриминант квадратичной формы.
Японский математик Сэки Такакадзу ввёл определители независимо в 1683 году[3].
Определения[править | править код]
Через перестановки[править | править код]
Для квадратной матрицы 


,
где суммирование проводится по всем перестановкам 



Таким образом, в определитель входит 
Эквивалентная формула:
,
где коэффициент 
- 0, если не все индексы
различны,
- 1, если все индексы
различны и подстановка
чётна,
- −1, если все индексы
различны и подстановка
нечётна.
Аксиоматическое построение (определение на основе свойств)[править | править код]
Понятие определителя может быть введено на основе его свойств. А именно, определителем вещественной матрицы называется функция 
— кососимметрическая функция строк (столбцов) матрицы
.
— полилинейная функция строк (столбцов) матрицы
.
, где
— единичная
-матрица.
Значение определителя матрицы[править | править код]
Для матрицы первого порядка значение детерминанта равно единственному элементу этой матрицы:
Матрицы 2 x 2[править | править код]

Схема расчета определителя матрицы 2×2.

Площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма.
Для матрицы 
Эта матрица A может быть рассмотрена как матрица линейного отображения, преобразующего единичный квадрат в параллелограмм с вершинами (0, 0), (a, b), (a + c, b + d), и (c, d).
Абсолютное значение определителя 
Значение определителя со знаком (ориентированная площадь параллелограмма) помимо коэффициента масштабирования также показывает, выполняет ли преобразование A отражение.
Матрицы 3 x 3[править | править код]
Определитель матрицы 
Для более удобного вычисления определителя третьего порядка можно воспользоваться правилом Саррюса или правилом треугольника.
Определитель матрицы, составленной из векторов 

Матрицы N × N[править | править код]
В общем случае, для матриц более высоких порядков (выше 2-го порядка) 
-
, где
— дополнительный минор к элементу
. Эта формула называется разложением по строке.
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
Также справедливо и аналогичное разложение по любой строке (столбцу):
Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым 
Альтернативные методы вычисления[править | править код]
- Метод конденсации Доджсона, основанный на рекурсивной формуле:
.
Основные свойства определителей[править | править код]
Следующие свойства отражают основные результаты теории определителей, применение которых выходит далеко за пределы этой теории:
(Определитель единичной матрицы равен 1);
(Определитель является однородной функцией степени
на пространстве матриц размера
);
(Определитель матрицы не меняется при её транспонировании);
(Определитель произведения матриц равен произведению их определителей,
и
— квадратные матрицы одного и того же порядка);
, причём матрица
обратима тогда и только тогда, когда обратим её определитель
;
- Существует ненулевое решение уравнения
тогда и только тогда, когда
(или же
должен быть нетривиальным делителем нуля в случае, если
— не целостное кольцо).
Определитель как функция строк (столбцов) матрицы[править | править код]
При изучении теории определителей полезно иметь в виду, что в основе этой теории лежит техника манипулирования со строками и столбцами матриц, разработанная К.Ф. Гауссом (преобразования Гаусса). Суть этих преобразований сводится к линейным операциям над строками (столбцами) и их перестановке. Эти преобразования достаточно простым образом отражаются на определителе, и при их изучении удобно “расчленить” исходную матрицу на строки (или столбцы) и считать определитель функцией, определённой над наборами строк (столбцов). Далее буквами 

- 1. Определитель — полилинейная функция строк (столбцов) матрицы. Полилинейность означает линейность функции по каждому аргументу при фиксированных значениях остальных аргументов:
- 2. Определитель — кососимметрическая функция строк (столбцов) матрицы, то есть при перестановке двух строк (столбцов) матрицы её определитель умножается на −1:
- 3. Если две строки (столбца) матрицы совпадают, то её определитель равен нулю:
Замечание. Свойства 1-3 являются основными свойствами определителя как функции строк (столбцов), они легко доказываются непосредственно из определения. Свойство 2 (кососимметричность) является логическим следствием свойств 1 и 3. Свойство 3 является логическим следствием свойства 2, если в кольце 
- 4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя (следствие свойства 1).
- 5. Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю (следствие свойства 4).
- 6. Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю (следствие свойств 1 и 3).
- 7. При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится (следствие свойств 1 и 6).
Фактом, имеющим фундаментальное значение, является универсальность определителя как полилинейной кососимметрической функции полного ранга, аргументами которой являются элементы конечномерного векторного пространства 


- Теорема. Пусть
— свободный
-модуль ранга
(
-мерное векторное пространство над
, если
— поле). Пусть
—
-значная функция на
, обладающая свойствами 1-3. Тогда при выборе базиса
пространства
существует константа
такая, что при всех значениях
справедливо равенство:
,
где 


Одним из важнейших следствий универсальности определителя является следующая теорема о мультипликативности определителя.
- Теорема. Пусть
— матрица размера
. Тогда
для любой матрицы
размера
.
Доказательство
Рассмотрим на пространстве столбцов 



■
Определитель и ориентированный объём[править | править код]
Пусть 



Функция ориентированного объёма 

Функция 














Применяя теорему об универсальности определителя как кососимметрической полилинейной функции, получаем, что при выборе ортонормированного базиса 

,
где 

Таким образом, определитель матрицы коэффициентов векторов относительно ортонормированного базиса имеет смысл ориентированного объёма параллелепипеда, построенного на этих векторах.
Всё вышесказанное без существенных изменений переносится на пространство 
Разложение определителя по строке/столбцу и обращение матриц[править | править код]
Формулы разложения определителя по строке/столбцу позволяют сводить вычисление определителей к рекурсивной процедуре, использующей вычисление определителей меньших порядков. Для вывода этих формул сгруппируем и просуммируем в формуле для определителя матрицы 


,
где 



Так как произвольный элемент 



.
Величина 

Учитывая, что каждый член разложения определителя с ненулевым коэффициентом содержит ровно один элемент из i-ой строки, можно разложить определитель по членам этой строки:
— Формула разложения определителя по i-ой строке
Аналогично, учитывая, что каждый член разложения определителя с ненулевым коэффициентом содержит ровно один элемент из j-го столбца, можно разложить определитель по членам этого столбца:
— Формула разложения определителя по j-ому столбцу
Если элементы k-й строки матрицы 
— Формула “фальшивого” разложения определителя по i-ой строке (
).
Аналогично для столбцов:
— Формула “фальшивого” разложения определителя по j-ому столбцу (
)
Полученные формулы полезно записать в матричном виде. Введём матрицу алгебраических дополнений к элементам матрицы 

Тогда, согласно с полученными формулами,
.
Следствие 1 (Критерий обратимости матриц). Квадратная матрица 



Следствие 2. Если произведение матриц равно нулю 


Решение систем линейных алгебраических уравнений с помощью определителей[править | править код]
Формула Крамера позволяет выразить решение системы линейных алгебраических уравнений в виде отношения определителей, в знаменателе которого стоит определитель системы, а в числителе — определитель матрицы системы, в которой столбец коэффициентов при соответствующей переменной заменён на столбец из правых частей уравнений.
Формула Крамера. Пусть задана система линейных алгебраических уравнений в матричном виде: 





Из этой формулы следует, в частности, что если 
Одной из важнейших теорем в теории определителей является следующая теорема о решениях однородной системы линейных уравнений.
Теорема. Пусть 


Доказательство
Необходимость условия содержится в следствии 2 предыдущего раздела. Докажем необходимость.
Если матрица 

Пусть 


Введём вектора 

Поскольку матрица 



Введём две матрицы:
и
.
У матрицы 








Из соотношения 



Тогда 

Данная теорема используется, в частности, для нахождения собственных значений и собственных векторов матриц.
Критерий полноты и линейной независимости системы векторов[править | править код]
Тесно связанными с понятием определителя является понятие линейной зависимости и полноты систем векторов в векторном пространстве.
Пусть 








Теорема (Критерий полноты и линейной независимости системы векторов).
- (1) Система векторов
линейно зависима тогда и только тогда, когда
.
- (2) Система векторов
полна, тогда и только тогда, когда матрица
не вырождена (
).
Доказательство
(1) Доказательство основано на том, что вектор 


Если 




Обратно, если 



(2) Если матрица 





Обратно, пусть матрица 







■
Следствие. В векторном пространстве 

- (1) всякая система, состоящая менее, чем из
векторов, не полна;
- (2) всякая система, состоящая более, чем из
векторов, линейно зависима;
- (3) всякий базис пространства
содержит ровно
векторов.
Таким образом, размерность векторного пространства 
Некоторые специальные свойства определителей[править | править код]
- Определитель матрицы равен произведению её собственных значений.
- Если квадратная матрица выражает линейное преобразование, то её определитель не меняется при замене базиса линейного пространства.
Алгоритмическая реализация[править | править код]
- Прямые методы вычисления определителя могут быть основаны непосредственно на его определении, как суммы по перестановкам, или на разложении Лапласа по определителям меньшего порядка. Однако такие методы очень неэффективны, так как требуют О(n!) операций для вычисления определителя
-го порядка. В то же время они универсальны, применимы в тех случаях, когда элементы матрицы не являются числами (функции, многочлены, дифференциальные формы чётной степени и т. д.), и не требуют выполнения операций деления.
- Можно вычислить определитель и выполнив меньшее количество операций умножения; точнее, можно для матрицы
обойтись лишь количеством слагаемых, равным количеству разбиений числа
вместо
, например 5 вместо 6 для
[6]:
.
- Один из наиболее быстрых численных методов вычисления определителя заключается в простой модификации метода Гаусса. Следуя методу Гаусса, произвольную матрицу
можно привести к ступенчатому виду (Верхнетреугольная матрица), используя лишь две следующие операции над матрицей — перестановку двух строк и добавление к одной из строк матрицы другой строки, умноженной на произвольное число. Из свойств определителя следует, что вторая операция не изменяет определителя матрицы, а первая лишь меняет его знак на противоположный. Определитель матрицы, приведённой к ступенчатому виду, равен произведению элементов на её диагонали, так как она является треугольной, поэтому определитель исходной матрицы равен:
- где
— число перестановок строк, выполненных алгоритмом, а
— ступенчатая форма матрицы
, полученная в результате работы алгоритма. Сложность этого метода, как и метода Гаусса, составляет
, для его реализации необходимо использование операции деления.
- Определитель можно вычислить, зная LU-разложение матрицы. Если
, где
и
— треугольные матрицы, то
. Определитель треугольной матрицы равен просто произведению её диагональных элементов.
- Если доступен алгоритм, выполняющий умножение двух матриц порядка
за время
, где
, для некоторого
, то определитель матрицы порядка
может быть вычислен за время
.[7] В частности это означает, что, используя для умножения матриц алгоритм Копперсмита — Винограда, определитель можно вычислить за время
.
Специальные виды определителей[править | править код]
- Определитель Вронского (Вронскиан)
- Определитель Вандермонда
- Определитель Грама
- Определитель Якоби (Якобиан)
См. также[править | править код]
- Циркулянт
- Перманент
- Пфаффиан
- Результант
Примечания[править | править код]
- ↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — 13-е изд., исправленное. — М.: Наука, 1986.
- ↑ Э. И. Березкина. Математика древнего Китая. — М.: Наука, 1980.
- ↑ H. W. Eves. An Introduction to the History of Mathematics. — Saunders College Publishing, 1990.
- ↑ Скорняков Л. А. Элементы алгебры. — М.: Наука, 1986. — С. 16-23. — Тираж 21 000 экз.
- ↑ Определитель матрицы и геометрический смысл определителя матрицы (рус.). Математика для всех.
- ↑ Houston, Robin; Goucher, Adam P. & Johnston, Nathaniel (2023), A New Formula for the Determinant and Bounds on Its Tensor and Waring Ranks, arΧiv:2301.06586 [math.CO].
- ↑ J. R. Bunch and J.E. Hopcroft. Triangular factorization and inversion by fast matrix multiplication, Mathematics of Computation, 28 (1974) 231—236.
Литература[править | править код]
- В. А. Ильин, Э. Г. Позняк Линейная алгебра, М.: Наука — Физматлит, 1999.
- Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2000.
- Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры: Учебник для вузов. М.: Физматлит, 2004.
- Боревич З. И. Определители и матрицы. – М.: Наука, 1988.
Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
Перед тем как находить и считать определитель, дадим определение определителю матрицы.
Что такое определитель матрицы или детерминант матрицы? Определитель матрицы — это некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.
|А|, ∆, det A – символы, которыми обозначают определитель матрицы.
Как найти определитель матрицы? Вычислить определитель или найти определитель можно с помощью разных способов (в том числе онлайн и при помощи калькулятора). Конкретный способ поиска и того, как решать, выбирают в зависимости от порядка матрицы.
Определитель матрицы второго порядка можно вычислять по формуле:
А=1-231.
Решение матрицы:
det A=1-231=1×1-3×(-2)=1+6=7
Определитель матрицы 3-го порядка: правило треугольника
Нахождение определителя матрицы 3-го порядка осуществляется по одному из правил:
- он может считаться по правилу треугольника;
- расчет также проводится по правилу Саррюса.
Как найти определитель матрицы третьего порядка по методу треугольника (определитель матрицы 3×3)?
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
А=13402115-1
Решение:
det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицы четвертого порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
det A=ai1×Ai1+ai2×Ai2+…+аin×Аin
Разложение матрицы по элементам столбца:
det A=а1i×А1i+а2i×А2i+…+аni×Аni
Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
А=01-132100-24513210
Решение:
- раскладываем по 2-ой строке:
А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310
- раскладываем по 4-му столбцу:
А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321
Свойства определителя
Свойства определителя:
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
В рамках темы советуем обратиться к модулю определителя.
А=134021005
Решение:
det А=134021005=1×5×2=10
Матричныый определитель, который содержит нулевой столбец, равный нулю (представляет собой минор).
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы  второго порядка, надо от произведения
второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
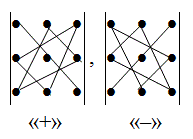
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком “минус”:
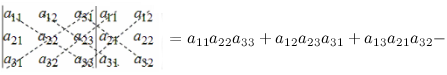
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение. 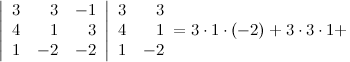
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
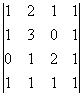
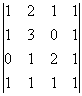
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
1.1. Определители и матрицы
1.1.1. Понятие числовой матрицы
1.1.2. Определители второго порядка
1.1.3. Подматрица, минор, алгебраическое дополнение
1.1.4. Определители третьего порядка
1.1.5. Свойства определителей
1.1.6. Определители порядка n
1.2. Решение систем линейных уравнений методом Крамера
1.2.1. Понятие системы линейных уравнений
1.2.2. Формулы Крамера
1.3. Матрицы. Операции над матрицами
1.3.1. Умножение матрицы на число
1.3.2. Сложение матриц
1.3.3. Произведение матриц
1.3.4. Транспонирование матриц
1.3.5. Понятие обратной матрицы
1.3.6. Нахождение обратной матрицы методом Крамера
1.3.7. Алгоритм нахождения обратной матрицы методом Крамера
1.3.8. Элементарные преобразования матриц
1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований
1.4. Решение системы линейных уравнений
1.4.1. Системы линейных уравнений. Основные понятия
1.4.2. Метод Гаусса
1.5. Исследование систем линейных уравнений
1.5.1. Теоремы о ранге матриц
1.5.2. Исследование систем линейных уравнений
1.5.3. Теорема Кронекера-Капелли
1.5.4. Однородные системы линейных уравнений
1.5.5. Свойства решений линейной однородной системы уравнений
1.1. Определители и матрицы
1.1.1. Понятие числовой матрицы
Числовая матрица – прямоугольная таблица чисел, состоящая из строк и столбцов. Размеры матрицы обозначаются M * N, где M-число строк, N-число столбцов.
Пример:
A= 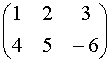 или A=
или A=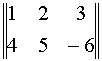
Общее обозначение:
A=![]() или A=
или A=![]() , где
, где ![]() – элемент матрицы, находящийся на пересечении i-ой строки и j-ого столбца:
– элемент матрицы, находящийся на пересечении i-ой строки и j-ого столбца: ![]()
![]()
Если M=N, то матрица называется квадратной. В этом случае N – ее порядок. В квадратной матрице выделяются две диагонали – главная и побочная:
![]() . . .
. . .
. ![]()
. . ![]() главная
главная
. . ![]() .
.
побочная
. . ![]()
![]() . .
. .
Пример:
A = 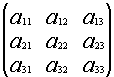 главную диагональ образуют эл-ты:
главную диагональ образуют эл-ты:
![]() , а побочную
, а побочную ![]()
1.1.2. Определители второго порядка
Пусть дана матрица второго порядка
A= 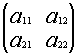 .
.
Определителем второго порядка называется число, вычисляемое по правилу:
![]()
Определитель второго порядка равен произведению элементов Главной диагонали минус произведение элементов Побочной диагонали.
![]() =
=
1*(-4)-6 = -10
1.1.3. Подматрица, минор, алгебраическое дополнение
Пусть дана какая-либо матрица (например, порядка 3):
А= 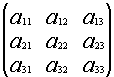
Подматрицей матрицы А называется часть этой матрицы, полученная вычеркиванием какого-либо количества строк, и(или) какого-либо количества столбцов.
Например, если вычеркнуть первую строку и второй столбец, то получим подматрицу данной матрицы:
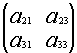
Минором ![]() элемента
элемента ![]() определителя
определителя ![]() называется определитель, полученный вычеркиванием i-ой строки и j-ого столбца.
называется определитель, полученный вычеркиванием i-ой строки и j-ого столбца.
Алгебраическим дополнением элемента ![]() называется минор, взятый со знаком “+” или “- ” в зависимости от места этого элемента в определителе.
называется минор, взятый со знаком “+” или “- ” в зависимости от места этого элемента в определителе.
Обозначение: ![]() =
=![]()
![]()
Если i+j – четное число , то знак алгебраического дополнения и минора одинаковы, если нечетное , то их знаки противоположны.
Символически покажем положительные и отрицательные места в определителе:
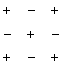 или
или 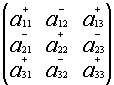
1.1.4. Определители третьего порядка
Определителем третьего порядка называется число, вычисляемое по правилу:
![]() =
= 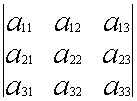 =
= ![]()
Определитель третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения.
Заменим алгебраические дополнения на миноры:
![]() =
= ![]()
![]() =
= ![]()
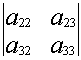 –
– ![]()
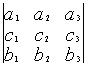 +
+ ![]()
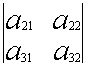
Вычисляя миноры, получим:
![]() =
= ![]()
![]()
1.1.5. Свойства определителей
Свойство 1. При замене строк на столбцы определитель не меняется.
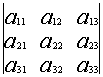 =
= 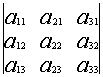
(такая операция называется транспонированием).
Следствие: строки и столбцы равноправны, т.е любые свойства или утверждения относительно строк справедливы и для столбцов и наоборот.
Свойство 2. При перестановке двух строк определитель меняет знак на противоположный.
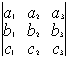 = –
= – 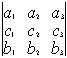
Следствие: любую строку (столбец) можно поставить первой (первым)
Свойство 3. Определитель с двумя равными строками равен нулю.
 = 0
= 0
Свойство 4. Общий множитель элементов строки можно выносить за знак определителя.
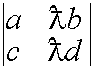
![]()
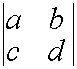
Следствие: Постоянный множитель можно внести в какую-нибудь строку
![]()
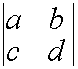
![]()
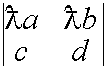
Свойство 5. Если элементы какой–либо строки состоят из двух слагаемых, то определитель можно представить в виде суммы двух определителей.
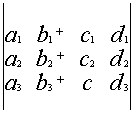
![]()
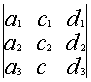
![]()
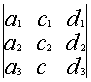
Свойство 6. Определитель не меняется, если любую строку умножить на любое число и прибавить к любой другой строке.
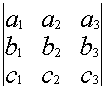
![]()
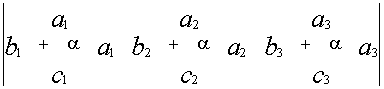
Случаи, когда определитель равен нулю:
- Все элементы какой-либо строки равны нулю
- Две строки одинаковы
- Элементы двух строк пропорциональны
1.1.6. Определители порядка n
![]() Вычисление определителей порядка n.
Вычисление определителей порядка n.
Для вычисления порядка n используется метод разложения по cтроке.
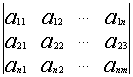
![]()
![]()
Алгебраическое дополнение получается вычеркиванием i-строки и j-столбца. Этот процесс мы будем продолжать до тех пор пока не получим определители порядка 2 или 3

![]()
![]()
Формулу (1) используют как правило при i=1
Пример:

![]()
![]()
1.2. Решение систем линейных уравнений методом Крамера
1.2.1. Понятие системы линейных уравнений
Система линейных уравнений порядка n имеет вид:
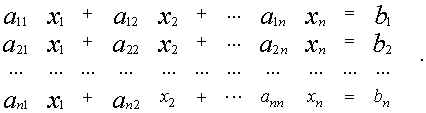
![]()
![]() При этом числа – называются коэффициентами
При этом числа – называются коэффициентами
при неизвестных
![]()
![]() – свободные члены
– свободные члены
![]()
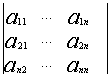 Матрица называется матрицей системы
Матрица называется матрицей системы
Числа 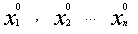 – решение системы, если при подстановке этих чисел в систему каждое из уравнений системы превращается в верное числовое тождество.
– решение системы, если при подстановке этих чисел в систему каждое из уравнений системы превращается в верное числовое тождество.
Система линейных уравнений называется совместной, если она имеет по крайней мере одно решение.
Если система линейных уравнений не имеет решений, то система называется несовместной.
1.2.2. Формулы Крамера
Рассмотрим систему уравнений (*). И пусть А – матрица системы
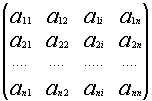
Если i – столбец заменим свободными членами, то соответствующую матрицу обозначим
![]()
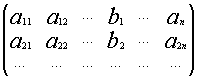
Если система линейных уравнений (*) такова, что определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, которое находится по формуле:
![]()
![]()
![]()
1.3. Матрицы. Операции над матрицами
Две матрицы A и B называются равными, если они имеют один и тот же порядок и если элементы стоящие на соответствующих местах равны.
![]()
![]()
![]()
К линейным операциям относятся:
1.3.1. Умножение матрицы на число
Для того чтобы умножить матрицу на число нужно каждый элемент матрицы умножить на это число:
![]()
![]()
![]()
1.3.2. Сложение матриц
Складывать можно только матрицы одинаковых размеров:
![]()
Свойства линейных операций
![]()
![]()
![]()
![]()
![]()
Если матрица в качестве элементов имеет нули, то такая матрица называется нулевой.
1.3.3. Произведение матриц
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
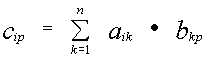
Пример:
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() =
=![]() =
=![]()
![]()
![]() .
.![]() =
=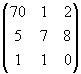
![]() .
.
Если для матриц А и В выполняется равенство А*В=В*А, то матрицы называются перестановочными.
Если для матриц А, В, С имеет смысл операция произведения, то выполняются равенства
A(B*C)=(A*B)*C
A(B+C)=AB+AC
(B+C)A=BA+CA
1.3.4. Транспонирование матриц
Рассмотрим матрицы
![]()

![]()

AT называется транспонированной по отношению к A
Если AT получена из матрицы А заменой строк на столбцы то
![]()
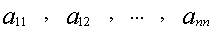 называют главной диагональю
называют главной диагональю
Очевидно:
Если для квадратной матрицы выполняется условие
![]()
то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.
1.3.5. Понятие обратной матрицы
Обратные матрицы существуют только для квадратных матриц. Квадратная матрица, у которой на главной диагонали стоят единицы, а
вне главной диагонали – нули, называется единичной матрицей.
Например, единичная матрица второго порядка:
![]()
![]()
Теорема.
Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:
![]()
Определение обратной матрицы:
Матрица В называется обратной для матрицы А, если А и В перестановочны и А*В=В*А=Е
Обозначение обратной матрицы:
![]()
![]()
Теорема.
Если матрица А имеет обратную, то ее определитель отличен от нуля.
Доказательство.
Так как А имеет обратную матрицу, то
![]()
![]()
Воспользуемся теоремой о том, что определитель произведения равен произведению определителей.
![]()
![]()
что и требовалось доказать.
1.3.6. Нахождение обратной матрицы методом Крамера
Теорема.
Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.
Доказательство.
![]() Пусть матрица А такова, что её определитель отличен от нуля.
Пусть матрица А такова, что её определитель отличен от нуля.
Докажем, что существует матрица В, такая что:
![]()
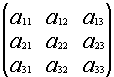 *
*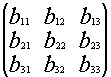 =
=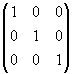
![]()
Отсюда, в частности, следует:
![]()
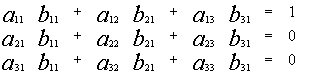
![]()
Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля, то эту систему можно решить методом Крамера ![]() причем решение (3) – единственно.
причем решение (3) – единственно.
Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.
1.3.7. Алгоритм нахождения обратной матрицы методом Крамера
Первоначально находим определитель матрицы А и если он равен нулю, то обратной матрицы не существует.
Если определитель отличен от нуля, то находим союзную
![]() матрицу
матрицу
состоящую из алгебраических дополнений элементов матрицы А.
![]()
![]()
![]()
1.3.8. Элементарные преобразования матриц
Эквивалентные матрицы.
К элементарным преобразованиям относятся:
-
- умножение любой строки матрицы на число, отличное от нуля;
пример
![]() =
= ![]()
- к любой строке можно добавить любую другую строку, умноженную на любое число;
- перестановка двух строк.
Матрицы, полученные с помощью элементарных преобразований называются эквивалентными
А~
В, В~
С, А~
С
1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований
Рассмотрим квадратную матрицу А и предположим, что
![]()
тогда используя элементарные преобразования эту матрицу можно привести к единичной матрице. Таким образом единичная матрица эквивалентна любой невырожденной матрице того же порядка.
Теорема
Если элементарные преобразования:
![]()
переводят невырожденную матрицу А в единичную, то те же самые преобразования, взятые в том же порядке, переводят единичную матрицу в обратную для A.
Доказательство:
![]()
![]()
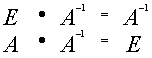
отсюда
![]()
![]()
1.4. Решение системы линейных уравнений
1.4.1. Системы линейных уравнений. Основные понятия
Система уравнений вида:
![]()
![]()
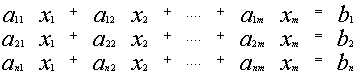
называется линейной системой из n уравнений с m неизвестными.
(aij) коэффициенты при неизвестных x1, x2,…,xm
b1,b2,…,bn – свободные члены
Матрица А системы (*) состоит из коэффициентов aij, размера n*m .
Если неизвестные и свободные члены представим в виде:
![]()
![]()
![]()
![]() ,
,
то систему уравнений (*) мы можем переписать в виде: ![]() (3)
(3)
Запись системы в виде (3) называют матричной формой записи системы линейных уравнений (*). Следует особо обратить внимание на то, что m может быть неравно n. Если m=n и матрица А является невырожденной , то из соотношения (3) вытекает: ![]() (4)
(4)
Равенство (4) получается умножением (3) слева на А-1. Система (*) называется совместной, если она имеет по крайней мере одно решение. В противном случае система называется несовместной.
Решить систему – означает найти все её решения.
1.4.2. Метод Гаусса
Рассмотрим систему (*):![]()

Припишем к матрице А
матрицу-столбец В ![]()
![]()
Припишем к матрице А матрицу-столбец
В: ![]()
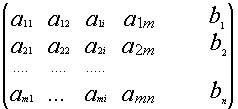
Матрица H называется расширенной матрицей системы. Матрица, у которой ниже главной диагонали стоят нули называется треугольной. Метод Гаусса (метод исключения неизвестных) состоит в том, что расширенную матрицу системы с помощью элементарных преобразований мы приводим к треугольному виду. Если у нас при этом получается матрица вида: 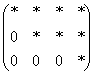 то, система решений не имеет.
то, система решений не имеет.
Если треугольная матрица получается вида: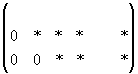 , то система имеет бесконечно много решений. При этом какие-то неизвестные
, то система имеет бесконечно много решений. При этом какие-то неизвестные
объявляются свободными, а остальные неизвестные могут быть выражены через них. Свободные неизвестные могут принимать любые значения. Если матрица примет вид: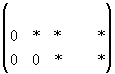 , то в этом случае система имеет единственное решение.
, то в этом случае система имеет единственное решение.
Пример: ![]()
Элементарные преобразования расширенной матрицы системы, приводящие её к треугольному виду, могут быть такими:
 ~
~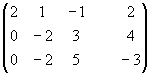 ~
~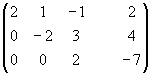
В итоге получим систему: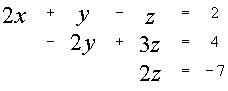
Откуда получим значения неизвестных: y = -7,25 x = 2,875 ![]()
Пример: 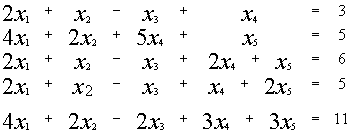
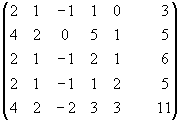 ~
~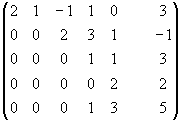 ~
~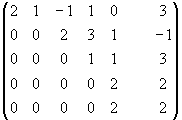 ~
~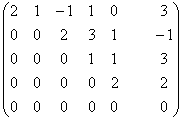
![]()
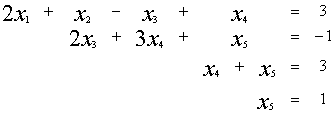
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1.5. Исследование систем линейных уравнений
Рассмотрим систему линейных уравнений.
Задача: определить:
- Совместна или нет данная система
- Если совместна, то сколько имеет решений а) единственное б) бесконечное множество
Понятие ранга матрицы
А=(![]() ) i=
) i=![]() j=
j=![]()
Возьмем в матрице К строк и К столбцов, тогда элементы матрицы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка К. Определитель этой квадратной матрицы называется минором порядка К для матрицы А.
Опр.1. Наибольший порядок минора матрицы, отличный от нуля называется рангом матрицы.
Опр.2. Число r(A)=k называется рангом матрицы А, если среди миноров порядка k есть по крайней мере один, отличный от нуля, а все миноры большего порядка равны нулю.
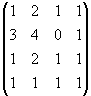 М=
М=![]() =0 М=
=0 М=![]() =-2
=-2![]() 0 М=
0 М=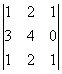 =0 М=
=0 М=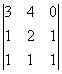 =3 Ранг равен 3.
=3 Ранг равен 3.
Совершенно очевидно, что нулевой ранг имеет только нулевая матрица. Если матрица не нулевая то её ранг![]() 1.
1.
С другой стороны если матрица имеет порядок MxN, то r(A)![]() min(M,N).
min(M,N).
1.5.1. Теоремы о ранге матриц
Теорема 1
Если матрица А эквивалентна матрице B, то ранг матрицы А равен рангу матрицы B (элементарные преобразования не изменяют ранга матрицы).
Доказательство
Для доказательства достаточно доказать, что каждое из преобразований не может изменить ранга матрицы.
1) А~B B получена умножением строки(столбца) на отличное от нуля число.
А=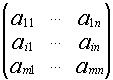 B=
B=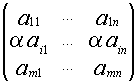
Если i-я строка не входит в выделенный минор то миноры матриц А и B совпадают. Если i-я строка входит в выделенный минор ![]() В=
В=![]() А (по св-ву определителей). Если минор
А (по св-ву определителей). Если минор ![]() А был отличен от нуля, то
А был отличен от нуля, то ![]() В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.
В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.
2) A~B B получена прибавлением строк
А=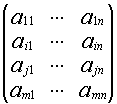 В=
В=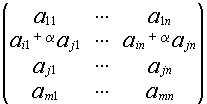
Если выбранные строки не содержат i-й строки, то соответствующие миноры матриц А и В полностью совпадают. Если минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А![]() 0, то и минор матрицы В
0, то и минор матрицы В![]() 0.
0.
Если выбранные миноры содержат i-ю и j-ю строки, тогда
М(А)=![]() А=
А=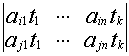
![]() В=
В=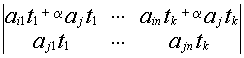
минор ![]() В получен из
В получен из ![]() А путем прибавления строки.
А путем прибавления строки.
Элементарные преобразования получаются с помощью конечного числа преобразований 1 и 2 типа и по уже доказанному на каждом из шагов ранг матрицы не меняется. Следовательно, он не изменится и за конечное число шагов. Ранг матрицы не меняется, если произведено конечное число элементарных преобразований.
Теорема 2
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Вычисление ранга матрицы
Используя утверждение доказанной теоремы, легко вычислить ранг матрицы
- с помощью элементарных преобразований матрица приводится к ступенчатому виду.
- считается число ненулевых строк ступенчатой матрицы
Ясно, что если матрица является квадратной и невырожденной, то её ранг равен порядку этой матрицы.
ПРИМЕР
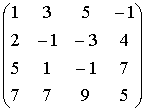 ~
~ 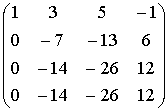 ~
~ 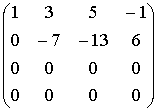
Ответ: r(A)=2
1.5.2. Исследование систем линейных уравнений
Рассмотрим систему линейных уравнений
(*)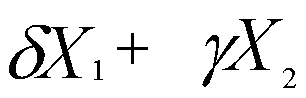
А=(![]() )
)
H=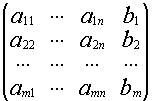
1.5.3. Теорема Кронекера-Капелли
Система ур-ний (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H)
Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса.
Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных объявляются свободными неизвестными (принимают любые значения), оставшиеся k неизвестных выражаются через эти свободные неизвестные.
1.5.4. Однородные системы линейных уравнений
Если в системе (*) все свободные члены ![]() равны нулю, то такая система является однородной.
равны нулю, то такая система является однородной.
Однородные системы всегда совместны т.к. ![]() =
=![]() =
=![]() =
=![]() =0 всегда является решением. Такое решение называется тривиальным.
=0 всегда является решением. Такое решение называется тривиальным.
1) ![]()
![]() то
то 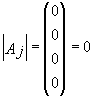
2) Если ранг матрицы А меньше числа неизвестных,то система имеет бесконечно много решений
1.5.5. Свойства решений линейной однородной системы уравнений
1) Если 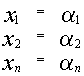 является решением системы, то
является решением системы, то 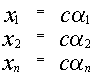 также является решением.
также является решением.
Доказательство.
![]()
![]()
![]()
2) Если 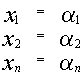 является решением системы
является решением системы
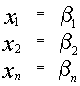 также является решением той же самой системы, то и
также является решением той же самой системы, то и
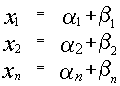 также является решением системы
также является решением системы
Доказательство.
![]()
+
![]()
откуда получим ![]()
3) Если 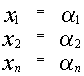 и
и 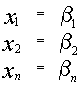
два различных решения системы, то их линейная комбинация, равная 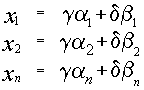
также является решением системы.
Доказательство.
![]()
+
![]()
откуда получим ![]()
Каждое из решений системы можно записать в виде строки матрицы![]() , тогда на основании свойств можно утверждать, что матрицы
, тогда на основании свойств можно утверждать, что матрицы ![]() есть решения, то
есть решения, то ![]() также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.
также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.
Пример.
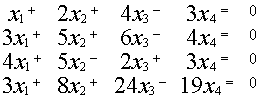
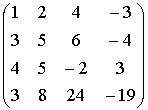 ~
~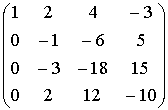 ~
~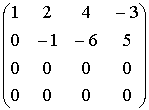
{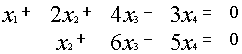 {
{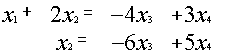
![]()
![]() {
{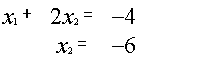 {
{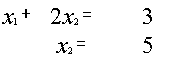
![]()
![]()












