Эту задачу можно решать в уме, она не требует сложных математических выкладок. Просто порассуждайте, каким должно быть это число. Итак, формулировка задачи следующая:
Формулировка задачи
Какое наименьшее четырехзначное натуральное число делится и на 5, и на 9 и состоит только из четных цифр?
Решение 1
Целое число делится и на 5, и на 9 ровно тогда, когда оно делится на 45.
Поскольку мы ищем число, имеющее только четные цифры, его последняя цифра — одна из 0, 2, 4, 6 или 8, поэтому само число четное. Таким образом, мы ищем четное число, кратное 45.
Четное число кратно 45 ровно тогда, когда оно кратно 90. Это означает, что мы ищем наименьшее четырехзначное число, кратное 90, которое имеет только четные цифры.
Наименьшее четырехзначное число, кратное 90, равно 1080, но первая цифра этого числа равна 1, что нечетно. Каждое из следующих 10 кратных 90 имеет первую цифру, равную 1, поэтому искомое число должно быть больше 2000.
Четырёхзначные числа, кратные 90, которые имеют тысячную цифру 2 это 2070, 2160, 2250, 2340, 2430, 2520, 2610, 2700, 2790, 2880, 2970, а единственное число в этом списке, у которого все четные цифры, — это 2880.
Следовательно, 2880 — это наименьшее четырехзначное число, кратное 5, кратное 9 и имеющее только четные цифры.
Решение 2
Предположим, что это число abcd, где a, b, c и d — цифры. Поскольку число делится на 5, мы должны иметь, что d = 0 или d не равно 5.
Наименьшее значение а равно 2, поскольку оно должно быть четным и больше 0 (четырехзначное число не может иметь а = 0). Итак, мы попытаемся найти такое число где a = 2.
Чтобы число делилось на 9, мы должны иметь сумму a + b + c + d, делящуюся на 9. Подставив a = 2 и d = 0, получим, что
2 + b + c + 0 = 2 + b + c делится на 9.
Так как b и c четны, то 2 + b + c четно, а значит, не может равняться 9. Таким образом, мы попытаемся найти b и c так, чтобы 2 + b + c = 18, что является наименьшим кратным 9, которое больше 9. Это уравнение преобразуется в b + c = 16.
Поскольку b и c четны и удовлетворяют условию 0 ≤ b ≤ 9 и 0 ≤ c ≤ 9, то единственная возможность это b = c = 8.
Получаем ответ: 2880
Получилось ли у вас решить задачку самостоятельно? 😁
20 апреля 2020
Отдых
Разгадайте логику построения цепочек и добавьте на место пропусков недостающие числа.
![]()
Анастасия Сукманова

Избранное
– 1 –
Показать ответ
Скрыть ответ
– 2 –
Показать ответ
Скрыть ответ
– 3 –
Показать ответ
Скрыть ответ
– 4 –
Показать ответ
Скрыть ответ
– 5 –
Показать ответ
Скрыть ответ
– 6 –
Показать ответ
Скрыть ответ
– 7 –
Показать ответ
Скрыть ответ
– 8 –
Показать ответ
Скрыть ответ
– 9 –
Показать ответ
Скрыть ответ
– 10 –
Показать ответ
Скрыть ответ
Читайте также 🔥
- 10 хитрых головоломок со спичками для тренировки воображения
- Ответьте на вопрос Илона Маска и узнайте, взяли бы вас в SpaceX
- Решите головоломку и узнайте, сможете ли попасть на закрытую вечеринку
Как решать логические и математические задачи
Решение задач на логику — отличная гимнастика для ума детей и взрослых на каждый день.
На ЛогикЛайк более 3500 заданий с ответами и пояснениями, полноценный учебный комплекс для развития логики и способностей к математике.
Решаем логические задачи
Чтобы научиться решать типовые логические задачи, простые и нестандартные математические задачи, важно знать основные приемы и методы их решения. Ведь решить одну и ту же задачу и прийти к правильному ответу во многих случаях можно разными способами.
Знание и понимание различных методов решения поможет определить, какой способ подойдет лучше в каждом конкретном случае, чтобы выбрать наиболее быстрый и простой путь получения ответа.
К «классическим» логическим задачам относятся текстовые задачи, цель решения которых состоит в распознавании объектов или расположении их в определенном порядке в соответствии с заданными условиями.
Более сложными и увлекательными типами заданий являются задачи, в которых отдельные утверждения являются истинными, а другие ложными. Задачи на перемещение, перекладывание, взвешивание, переливание — самые яркие примеры широкого ряда нестандартных задач на логику.
Основные методы решения логических задач
- метод рассуждений;
- с помощью таблиц истинности;
- метод блок-схем;
- средствами алгебры логики (алгебры высказываний);
- графический (в том числе, «дерево логических условий», метод кругов Эйлера);
- метод математического бильярда.
Давайте рассмотрим подробнее с примерами три популярных способа решения логических задач, которые мы рекомендуем использовать в начальной школе (детям 6-12 лет):
- метод последовательных рассуждений;
- разновидность метода рассуждений — «с конца»;
- табличный способ.
Метод последовательных рассуждений
Самый простой способ решения несложных задач заключается в последовательных рассуждениях с использованием всех известных условий. Выводы из утверждений, являющихся условиями задачи, постепенно приводят к ответу на поставленный вопрос.
Пример:
На столе лежат Голубой, Зеленый, Коричневый и Оранжевый карандаши.
Третьим лежит карандаш, в имени которого больше всего букв. Голубой карандаш лежит между Коричневым и Оранжевым.
Разложи карандаши в описанном порядке.

Решение:
Рассуждаем. Последовательно используем условия задачи для формулирования выводов о позиции, на которой должен лежать каждый следующий карандаш.
- Больше всего букв в слове «коричневый», значит, он лежит третьим.
- Известно, что голубой карандаш лежит между коричневым и оранжевым. Справа от коричневого есть только одна позиция, значит, расположить голубой между коричневым и другим карандашом возможно только слева от коричневого.
- Следующий вывод на основе предыдущего: голубой карандаш лежит на второй позиции, а оранжевый — на первой.
- Для зеленого карандаша осталась последняя позиция — он лежит четвертым.
Метод «с конца»
Такой способ решения является разновидностью метода рассуждений и отлично подходит для задач, в которых нам известен результат совершения определенных действий, а вопрос состоит в восстановлении первоначальной картины.
Пример:
Бабушка испекла для троих внуков рогалики и оставила их на столе. Коля забежал перекусить первым. Сосчитал все рогалики, взял свою долю и убежал.
Аня зашла в дом позже. Она не знала, что Коля уже взял рогалики, сосчитала их и, разделив на троих, взяла свою долю.
Третьим пришел Гена, который тоже разделил остаток выпечки на троих и взял свою долю.
На столе осталось 8 рогаликов.
Сколько рогаликов из восьми оставшихся должен съесть каждый, чтобы в результате все съели поровну?

Решение:
Начинаем рассуждение «с конца».
Гена оставил для Ани и Коли 8 рогаликов (каждому по 4). Получается, и сам он съел 4 рогалика: 8 + 4 = 12.
Аня оставила для братьев 12 рогаликов (каждому по 6). Значит, и сама она съела 6 штук: 12 + 6 = 18.
Коля оставил ребятам 18 рогаликов. Значит, сам съел 9: 18 + 9 = 27.
Бабушка положила на стол 27 рогаликов, рассчитывая, что каждому достанется по 9 штук. Поскольку Коля уже съел свою долю, Аня должна съесть 3, а Гена — 5 рогаликов.
Решение логических задач с помощью таблиц истинности
Суть метода состоит в фиксации условий задачи и полученных результатов рассуждений в специально составленных под задачу таблицах. В зависимости от того, является высказывание истинным или ложным, соответствующие ячейки таблицы заполняются знаками «+» и «-» либо «1» и «0».
Пример:
Три спортсмена (красный, синий и зеленый) играли в баскетбол.
Когда мяч оказался в корзине, красный воскликнул: «Мяч забросил синий».
Синий возразил: «Мяч забросил зеленый».
Зеленый сказал: «Я не забрасывал».
Кто забросил мяч, если только один из троих сказал неправду?
Решение:
Сначала таблицу составляют: слева записывают все утверждения, которые содержатся в условии, а сверху — возможные варианты ответа.

Затем таблицу последовательно заполняют: верные утверждения отмечают знаком «+», а ложные утверждения — знаком «-«.

Рассмотрим первый вариант ответа («мяч забросил красный«), проанализируем утверждения, записанные слева, и заполним первый столбик.
Исходя из нашего предположения («мяч забросил красный«), утверждение «мяч забросил синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый» также ложь. Заполняем ячейку знаком «-«.
Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».
Рассмотрим второй вариант ответа (предположим, что мяч забросил зеленый) и заполним второй столбик.
Утверждение «мяч забросил Синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый« — истина. Заполняем ячейку знаком «+».
Утверждение зеленого «Я не забрасывал» – ложь. Ставим в ячейке «-«.
И, наконец, третий вариант: предположим, что «мяч забросил синий«.
Тогда утверждение «мяч забросил синий« — истина. Ставим в ячейке «+».
Утверждение «мяч забросил зеленый» — ложь. Заполняем ячейку знаком «-«. Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».
Так как по условию лишь один из троих ребят сказал неправду, в заполненной таблице выбираем такой вариант ответа, где будет только одно ложное утверждение (в столбце один знак «-«). Подходит третий столбец.
Значит, правильный ответ – мяч забросил синий.
Метод блок-схем
Метод блок-схем считается оптимальным вариантом для решения задач на взвешивание и на переливание жидкостей. Альтернативный способ решения этого типа задач — метод перебора вариантов — не всегда является оптимальным, да и назвать его системным довольно сложно.
Порядок решения задач по методу блок-схем выглядит следующим образом:
- графически (блок-схемой) описываем последовательность выполнения операций;
- определяем порядок их выполнения;
- в таблице фиксируем текущие состояния.
Подробнее об этом и других способах решения логических задач с примерами и описанием хода решения мы рассказываем в полном Курсе ЛогикЛайк по развитию логического мышления.
Отгадывайте самые интересные загадки на логику, собранные специально для постоянных читателей нашего блога и учеников LogicLike, решайте логические задачи онлайн вместе с тысячами детей и взрослых!
Задание № 20. Задачи на логику и смекалку
Тип № 17 (про страницы)
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 372, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Решение.
Из числа 372 можно составить числа 327, 273, 237, 723, 732. Числа 327, 273 и 237 не подходят, поскольку они меньше числа 372. Номер первой страницы после выпавших листов должен быть нечётным, поскольку номер последней страницы перед выпавшими листами чётный. Следовательно, нам подходит только число 723. Вычтем из числа 723 одну страницу, поскольку страница 723 не выпала, а является первой страницей после выпавших листов. Теперь можно найти количество выпавших листов:
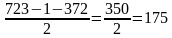
Ответ: 175.
Задания для самостоятельного решения
1. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 276, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
2. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 274, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
3. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 294, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Тип № 18 (про натуральные числа)
Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 165. Какое число было загадано?
Решение.
Числа А, В и С могут быть равны 5, 6 или 7.
Пусть загадали натуральное число Х, тогда Х · А + В – С = 165 или Х · А = 165 + (C – B). Рассмотрим различные случаи.
1) С – В = 0 (7 – 7 = 0, 6 – 6 = 0 или 5 – 5 = 0), тогда Х · А = 165. Число 165 делится нацело на A = 5, значит, Х = 33.
2) С – В = 1 (7 – 6 = 1 или 6 – 5 = 1), тогда Х · А = 166. Число 166 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.
3) С – В = –1 (6 – 7 = –1 или 5 – 6 = –1), тогда Х · А = 164. Число 164 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.
4) С – В = 2 (7 – 5 = 2), тогда Х · А = 167. Число 167 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.
5) С – В = –2 (5 – 7 = –2), тогда Х·А = 163. Число 163 не делится нацело на A = 5, на 6 и на 7, значит, этот случай не подходит.
Ответ: 33.
Задания для самостоятельного решения
1. Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 417. Какое число было загадано?
2. Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 213. Какое число было загадано?
3. Про натуральные числа A, B и С известно, что каждое из них больше 6, но меньше 10. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 186. Какое число было загадано?
Математические задачи – Вычисления
Найти наибольшее число
На доске выписаны числа от 1 до 2150. Каждую минуту каждое число подвергается следующей операции: если число делится на 100, то его делят на 100, если же не делится, то из него вычитают 1. Найдите наибольшее среди чисел на доске через 87 минут.
- Ответ на задачу
Число e
Присмотритесь к этой картинке:

Выражение в скобках, состоящее из всех десяти цифр, даёт 1,8⋅1025 верных знаков для числа е≈2,71828, т.е. точность приближения просто фантастическая. Можете ли вы это объяснить?
- Ответ на задачу
Поезд в тоннеле
Имеется ж/д тоннель длиной 1 км, в котором на глубине 600 м находятся 2 человека (т.е. на расстояние 600 м от одного края тоннеля и 400 м от другого). Внезапно они услышали шум приближающегося поезда и начали бежать в разные стороны. Каждый из них едва успел выскочить из тоннеля и остался жив. Какова была скорость поезда, если люди бежали со скоростью 10 км/ч?
- Ответ на задачу
Кратные числа
Три мальчика, на груди которых написаны цифры 3, 1 и 6 соответственно, стоят в одну шеренгу.
Известно, что:
1. Один из мальчиков поменял свое положение, в результате чего получилось число, кратное 7.
2. Один из мальчиков поменял свое положение, в результате чего получилось число, кратное 27.
Возможно ли такое? Ответ обосновать.
- Ответ на задачу
Встреча
Коля и Петя, встретившись на улице, увидели написанное мелом на асфальте двузначное число. Петя прибавил к нему 4 и затем поделил на 7, а Коля поделил его на 9 и затем отнял 1. Результаты совпали. Какое число было написано?
- Ответ на задачу
Поезд в туннеле
Человек хочет пройти через туннель для поездов. Он начинает свой путь в начале туннеля, и когда он пройдет четверть пути, то услышит, что сзади приближается поезд. Неизвестно – как быстро поезд едет, и насколько он далеко.
Известно только вот что:
Если человек развернется и побежит назад, то он достигнет начала туннеля одновременно с поездом.
Если человек побежит вперед, то конца туннеля он также достигнет одновременно с поездом.
Считайте, что человек ускоряется мгновенно и бегает с постоянной и одинаковой скоростью в обе стороны туннеля, поезд также едет с постоянной скоростью. Вопрос – насколько быстрее движется поезд по сравнению с человеком?
- Ответ на задачу
Разбитая витрина
Два хулигана, Славик и Димон бьют витрину, состоящую из цельного стекла. За один удар Славик разбивает стекло (или осколок) на 7 осколков, а Димон за один удар на 10 осколков. Существует ли такая последовательность ударов, чтобы в результате получилось 2000 осколков?
- Ответ на задачу
Расстояние между деревьями
Учительница математики, проводящая отпуск за рулём, ехала по проселочной дороге, направляясь к старинному замку, когда она заметила, что деревья на обочине были посажены на равном расстоянии друг от друга. Она взглянула на часы, когда машина была на полпути между деревьями и сосчитала, сколько деревьев она проехала за минуту. “Как интересно! – сказала она себе. – Если умножить число деревьев на 10, получается скорость моей машины в милях в час”. Предполагая, что скорость автомобиля была постоянной и что минута закончилась на полпути между деревьями, каково расстояние между ними?
- Ответ на задачу
Числа и буквы-2
Одно трехзначное число состоит из различных цифр, а в его названии все слова начинаются с одной и той же буквы. Другое трехзначное число, наоборот, состоит из одинаковых цифр, но в его названии все слова начинаются с разных букв. Какие это числа?
- Ответ на задачу
Чему равна сумма?
Пусть a и b – заданные натуральные числа, ни одно из которых не делится без остатка на 10, и для которых выполняется равенство a*b = 10000.
Чему равна сумма a + b?
- Ответ на задачу
Яблоки, бананы и кокосы
Не так давно крупные зарубежные издания представили математическую задачку, которая вызвала бурные обсуждения среди их читателей. Задачку про яблоки, бананы и кокосы обычно задают детям, но взрослым они выносят мозг гораздо эффективнее.
Итак, чему же равно последнее выражение?
P.S. Прежде чем начать решать – внимательно посмотрите, что нарисовано на картинке.

- Ответ на задачу
Число Пи
Знает или не знает современная наука точное значение числа Пи = 3,14…?
Одни ученые правильно говорят “ЗНАЕТ”, другие ученые так же правильно говорят “НЕ ЗНАЕТ И НИКОГДА НЕ УЗНАЕТ”. Почему ученые отвечают неодинаково? Как устранить логическое противоречие?
Автор задачи – Александр Шестаков
- Ответ на задачу
Монеты и кошельки
У вас есть 1000 монет и десять пустых кошельков. Вам нужно распределить все монеты между кошельками таким образом, чтобы по запросу вы могли выдать любое число монет от 1 до 1000. Причем выдавать монеты можно только вместе с кошельками, перекладывать монеты между кошельками нельзя. Как это сделать?
- Ответ на задачу
Заполнить пустые клетки
Заполните пустые клетки числами от 1 до 9 таким образом, чтобы выполнялись следующие условия:
а) Сумма четырех чисел вокруг каждого черного ромба равнялась 20
б) Все наборы слагаемых, образующих число 20, различны. Т.е. если вокруг какого-то ромба расположены числа 1, 3, 7 и 9, то этот набор нельзя использовать для другого ромба
в) Числа в соседних клетках (включая диагональные) должны быть различными

- Ответ на задачу
