Машина атвуда как что найти - Сайт, где вы сможете решить свои вопросы

Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.

Что такое машина Атвуда?

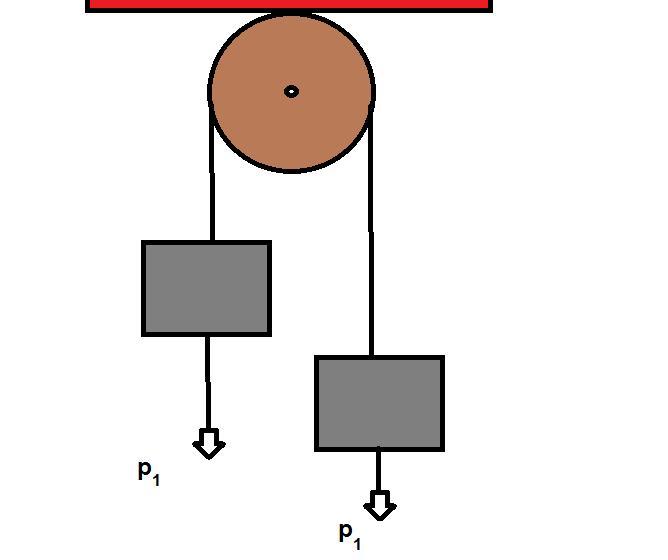
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Вам будет интересно:Пространственная экономика: описание специальностей и структура

Вам будет интересно:Что такое подполье? Подпольная организация “Молодая гвардия”. Антифашистское движение

Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.

Уравнения динамики

Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:

F = m*a.

Где m – инерционная масса тела, a – ускорение.

Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.

Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:

F1 – T = m1*a.

Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:

T – F2 = m2*a.

Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.

Расчет уравнений динамики для равноускоренного движения

Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.

Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:

F1 – T = m1*a;

T – F2 = m2*a.

Чтобы выразить значение ускорения a, сложим оба равенства, получаем:

F1 – F2 = a*(m1 + m2) =>

a = (F1 – F2)/(m1 + m2).

Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:

a = g*(m1 – m2)/(m1 + m2).

Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:

a = na*g.

Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.

Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:

h = a*t2/2.

Откуда ускорение определяется однозначно:

a = 2*h/t2.

Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:

acp = ∑i=1mai/m.

Где m – количество измерений.

Приравнивая это равенство и полученное ранее, приходим к следующему выражению:

acp = na*g.

Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.

Расчет силы тяжести

Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:

g = a/na.

Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:

g = 2*h/(t2*na).

Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:

F1 = 2*h*m1/(t2*na).

Определение силы натяжения нити

Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:

F1 – T = m1*a;

T – F2 = m2*a.

Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:

(F1 – T)/m1 = (T – F2)/m2 =>

T = (m2*F1 + m1*F2)/(m1 + m2).

Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:

T = 2*m1*m2*g/(m1 + m2).

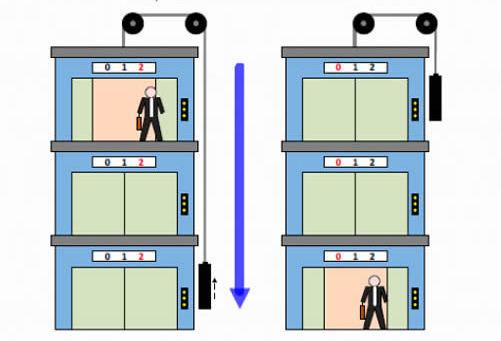
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 августа 2021 года; проверки требуют 2 правки.

Машина Атвуда — лабораторное устройство для изучения поступательного движения с постоянным ускорением. Была изобретена в 1784 году английским физиком и математиком Джорджем Атвудом.

Описание[править | править код]

Для проведения опытов по свободному падению тел требуется большая высота экспериментальной установки, вследствие большого ускорения свободного падения. Машина Атвуда позволяет избежать этой трудности и замедлить движение до удобных скоростей. Идеальная Машина Атвуда имеет следующую конструкцию: через невесомый блок, в оси которого отсутствует трение, укрепленный на некоторой высоте над столом, переброшена нерастяжимая и невесомая нить, к концам которой привязаны два тела с массами m_1 и m_2 .

Когда массы тел равны ( $m_{1}=m_{2}$ ) система находится в состоянии безразличного равновесия вне зависимости от положения грузов.

Если $m_{1}neq m_{2}$ , грузы приходят в поступательное движение.

Формула для нахождения ускорения[править | править код]

Это движение описывается с помощью второго закона Ньютона, представленного в общем виде:

$sum limits _{{i=1}}^{n}{{vec F}_{i}}=m{vec a}.$

Применительно к нашей задаче для левого и правого тел уравнение движения запишется в виде двух уравнений в проекциях на ось :

$left{{begin{array}{r}-m_{1}a_{1}=-m_{1}g+T_{1},\m_{2}a_{2}=-m_{2}g+T_{2}.end{array}}right.$

Мы считаем, что нить идеальна (то есть невесома и нерастяжима) и блок невесом, значит $T_{1}=T_{2}=T$ и $a_{1}=a_{2}=a$ , получим:

$a=g{m_{1}-m_{2} over m_{1}+m_{2}}.$

Формула для нахождения ускорения свободного падения[править | править код]

Измерив время прохождения грузами определённого расстояния, можно вычислить их ускорение. Отсюда:

$g=a{m_{1}+m_{2} over m_{1}-m_{2}}.$

Формула для нахождения силы натяжения нити[править | править код]

Для нахождения натяжения нити в любое из уравнений подставляем выражение для ускорения, полученное выше. Например, подставляя в первое уравнение системы выражение для ускорения, получаем:

$T={2m_{1}m_{2}g over m_{1}+m_{2}}$

См. также[править | править код]

Машина Обербека

Литература[править | править код]

Г. Голдстейн. Классическая механика. — 1975. — 413 с.
Атвудова машина // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт. — М. : Советская энциклопедия, 1926—1947.

Ссылки[править | править код]

Атвудова машина // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Источник

ФЕДЕРАЛЬНОЕ
АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ

ДОНСКОЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра
физики

Определение ускорения свободного падения на машине Атвуда.

Методические
указания к лабораторной работе №20

(Раздел
“Механика”)

Ростов-на-Дону
2010

Составители:
В.С. Ковалёва, В.С. Кунаков, О.А. Лещёва,

О.М.
Холодова.

УДК
530.1

ОПРЕДЕЛЕНИЕ
УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ НА МАШИНЕ
АТВУДА: Метод. указания. -Ростов н/Д:

Издательский
центр ДГТУ, 2010. – 11 с.

Указания
содержат краткое описание рабочей
установки и методику определения
ускорения свободного падения с помощью
машины Атвуда.

Методические
указания предназначены для студентов
инженерных специальностей всех форм
обучения при выполнении лабораторных
работ по физике (раздел «Механика и
молекулярная физика»).

Печатается
по решению методической комиссии
факультета «Нанотехнологии и композиционные
материалы»

Научный
редактор канд. хим. наук, доц.
А.Я. Шполянский

Лабораторная
работа №20

Определение ускорения свободного падения на машине Атвуда.

Цель
работы:
экспериментально определить ускорение
свободного падения.

Приборы
и принадлежности:
машина Атвуда ФПН02-ПС, набор основных
и дополнительных грузиков, электронный
секундомер.

Теоретическая часть.

Свободным
падением
называется движение, которое совершало
бы тело только под действием силы
тяжести. Такое движение может быть,
например, в трубке, из которой выкачали
воздух. При свободном падении тела с
небольшой высоты

от поверхности Земли (,
где
– радиус Земли) оно движется с постоянным
ускорением
,
направленным по вертикали вниз.

Ускорение

называется
ускорением
свободного падения.
Оно одинаково для всех тел и зависит
лишь от высоты над уровнем моря и от
географической широты на поверхности
Земли. Ускорение
максимально на полюсах и минимально
на экваторе Земли.

Впервые
ускорение свободного падения было
экспериментально определено итальянским
физиком Г.Галилеем.

Описание метода и экспериментальной установки для определения ускорения свободного падения.

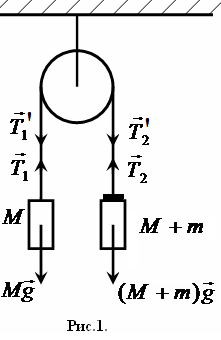Метод
основан на исследовании движения двух
грузов, связанных нитью, перекинутой
через неподвижный блок (рис.1).

Грузы
имеют одинаковые массы
,
величина которых значительно превышает
массу нити. Если на один из грузов
положить дополнительный груз (перегрузок)
массы
,то
они начинают двигаться прямолинейно и
равно-ускоренно с некоторым ускорением
,
а блок начинает вращаться с угловым
ускорением.

Применяя
второй закон Ньютона, запишем уравнения
движения грузов в проекциях на оси:

а)
для груза без перегрузка:

,
(1)

б)
для груза с перегрузком:

, (2)

где

– ускорение движения грузов,

и

– силы натяжения нити (см. рис.1),

–
ускорение свободного падения.

Уравнение
вращения блока (т.к. по 3-му закону Ньютона

и
):

,
(3)

где

– момент инерции блока,

– угловое ускорение блока,

– радиус блока.

Решая
систему уравнений (1), (2) и (3), получим
формулу для определения ускорения
свободного падения в виде:

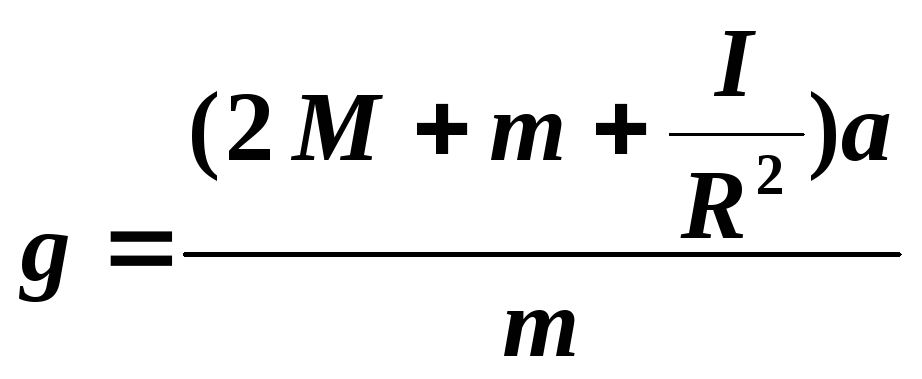
(4)

Из
выражения (4) следует, что для определения
ускорения свободного падения необходимо
знать массы грузов
и перегрузка,
момент инерции блокаи
ускорение движения грузов.

Ускорение
движения грузов определяется из формулы
пути при равноускоренном движении:

,
откуда (5)

где

– время, в течение которого грузы
перемещаются на величину.

Подставив
в формулу (4) выражение ускорения (5),
получим:

(6).

Силы
натяжения нити
иимеют различные значения и могут быть
определены из уравнений (1) и (2)

(7)

(8)

Если
момент инерции блока настолько мал, что
величиной
можно пренебречь по сравнению с массой
грузов,
то выражение (6) получает вид:

(9)

Силы
натяжения нити при условии
имеют одинаковые значения.
Определить силу натяжения можно из
формул (7) либо (8).

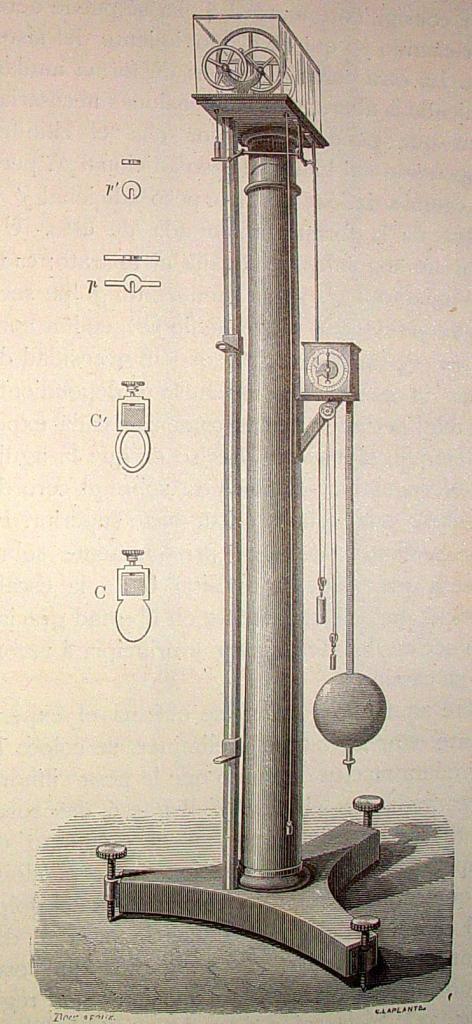
Общий
вид машины Атвуда приведен на рис.2.

Её
конструкция была предложена Д.Атвудом
и названа в его честь. Машина представляет
собой настольный прибор с вертикальной
стойкой 1, на которой крепятся все
основные элементы машины Атвуда, и
основание 2. На вертикальной стойке 1
расположены два кронштейна: нижний 3 и
верхний 4. На верхнем кронштейне 4 крепится
блок с узлом подшипников

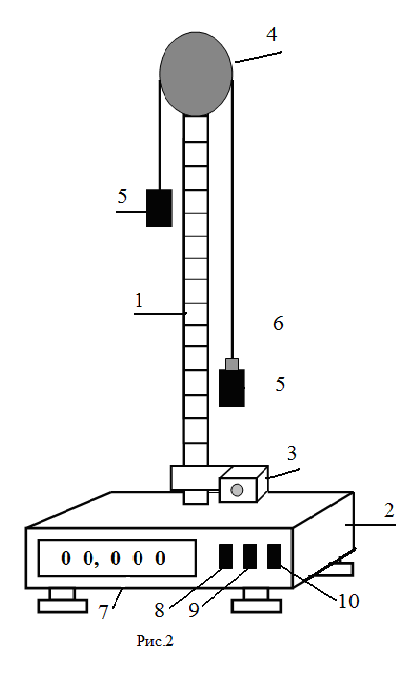
качения,
через блок перекинута нить с грузами 5
одинаковой массы. Перегрузок 6 кладут
на правый груз 5. На верхнем кронштейне
находится электромагнит, который с
помощью фрикциона при подаче на него
напряжения, удерживает систему с грузами
в неподвижном состоянии. На нижнем
кронштейне 3 крепится фотодатчик,
который выдает электрический сигнал
окончания счета времени равноускоренного
движения грузов. Нижний кронштейн 3
представляет собой площадку с резиновым
амортизатором, о который ударяется груз
при его остановке. Нижний кронштейн
имеет возможность свободного перемещения
и фиксации на вертикальной стойке по
всей ее свободной длине. На вертикальной
стойке 1 укреплена миллиметровая линейка,
по которой определяют начальное и
конечное положения грузов, а следовательно,
и пройденный путь. Начальное положение
определяют визуально по нижнему срезу
грузов, конечное положение – по индексу
нижнего кронштейна. Секундомер 7 выполнен
самостоятельным прибором и соединен
кабелем с датчиком (фотоэлектрическим).
На установке кнопка 8 – “сброс времени”,
кнопка 9 – “пуск”, кнопка 10 – “сеть”

Соседние файлы в папке Лаб.мех

Источник

Описание лабораторной работы

Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Основные законы динамики материальных точек – это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:

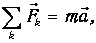
называют основным уравнением динамики.

Эскиз машины Атвуда показан на рис. 1.

Рис. 1. Эскиз машины Атвуда

Два одинаковых груза с массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m (в виде шайбы), то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на соответствующий груз с силой натяжения Т ₁ или Т ₂ , а на блок – с силами Т ’₁ и Т ’₂ . Тогда на каждый груз действует сила тяжести и сила натяжения нити.

Основное уравнение динамики для груза с перегрузком имеет вид:

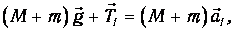
а для другого груза (без перегрузка):

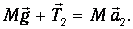
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:

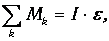
где S M_k – алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I – момент инерции блока относительно оси вращения; e – его угловое ускорение.

Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим

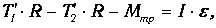
где: R – радиус блока; М_тр – момент силы трения.

Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:

Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:

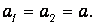
Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:

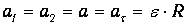
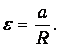
Проецируя уравнения (2) и (3) на ось у , направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4а):

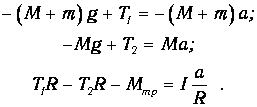
Умножая первое из уравнений (8) на (-1) , и складывая все уравнения (8), получим

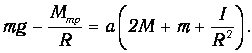
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство

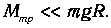
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:

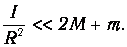
Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m :

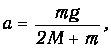
а модули сил натяжения нити Т₁ и Т₂ по обе стороны блока равны:

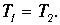
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).

Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:

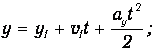
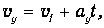
Исключая из этих уравнений время t , при условии v₁=0 , получим

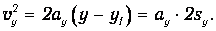
Система грузов перемещается на величину s_y=L₁ , двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).

В точке с координатой у₂ и скоростью v₂ перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину L₂ за время t , измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу

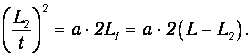
При изменении L₂ меняется время t , измеряемое секундомером, но ускорение а должно оставаться неизменным.

С помощью формулы (15) найдём расчётную формулу для величины ускорения а грузов с перегрузком:

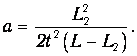
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

К основанию 1 экспериментальной установки (см. рис. 2), которая стоит на ножках 2 , прикреплена вертикальная стойка 3 . К стойке крепится кронштейн 4 , который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.

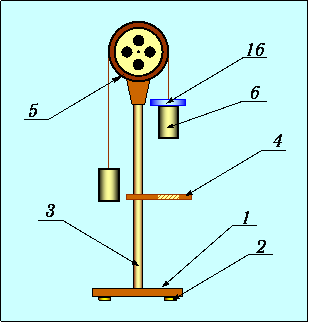
Рис. 2. Схема экспериментальной установки

На верхнем конце стойки находится неподвижный блок 5 . Для наблюдения ускоренного движения грузов на правый груз 6 помещают перегрузок 7 и поднимают их в верхнее положение путем нажатия кнопок «+» или «-». Значение массы перегрузка показывается в окне «масса После нажатия кнопки «ПУСК» начинается ускоренное движение грузов и перегрузка до того момента, когда столик 4 подхватит перегрузок. Одновременно включается миллисекундомер, измеряющий время равномерного движения грузов до остановки. Итак, во время равноускоренного движения грузы проходят расстояние L₁ (см. рис. 1) и приобретают скорость v₂ , с которой, двигаясь равномерно, проходят расстояние L₂ за время t , измеренное миллисекундомером в секундах и показанное в окне «время».

Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ

1. Измерьте расстояние L с помощью линейки и занесите результат в таблицу измерений 1. Цена деления линейки 1 см .

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.

2. Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г . Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г .

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.

3. Установите, взяв мышкой, кронштейн со столиком на некотором расстоянии L₂ от нижнего фиксатора расстояний. Возможные пределы варьирования расстояния от 12 до 25 см . Измерьте установленное расстояние L₂ по линейке, взяв отсчёт по красной черте. Результаты измерения запишите в таблицу 1 результатов измерений 1 . Цена деления линейки 1 см .

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.

5. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «время». Время необходимо записывать в системе СИ, то есть в секундах. Погрешность миллисекундомера составляет 0.001 с .

6. Нажмите кнопку «СБРОС».

7. Повторите пункты 3 – 5 ещё четыре раза, не меняя расстояние L₂ .

8. Вычислите среднее значение времени t >. Результат занесите в таблицу расчетов 2.

Изучение законов поступательного движения на машине Атвуда: формулы и пояснения

Что такое машина Атвуда?

Вам будет интересно: Пространственная экономика: описание специальностей и структура

Вам будет интересно: Что такое подполье? Подпольная организация “Молодая гвардия”. Антифашистское движение

Уравнения динамики

Где m – инерционная масса тела, a – ускорение.

Расчет уравнений динамики для равноускоренного движения

Чтобы выразить значение ускорения a, сложим оба равенства, получаем:

F1 – F2 = a*(m1 + m2) =>

a = (F1 – F2)/(m1 + m2).

a = g*(m1 – m2)/(m1 + m2).

Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:

Проверка решения уравнений динамики

Откуда ускорение определяется однозначно:

Где m – количество измерений.

Приравнивая это равенство и полученное ранее, приходим к следующему выражению:

Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.

Расчет силы тяжести

Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:

Определение силы натяжения нити

Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:

(F1 – T)/m1 = (T – F2)/m2 =>

T = (m2*F1 + m1*F2)/(m1 + m2).

Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:

T = 2*m1*m2*g/(m1 + m2).

Изучение прямолинейного движения тел на машине Атвуда

Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Лабораторная работа по курсу “Общая физика”

ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ

НА МАШИНЕ АТВУДА

Преподаватель Студент группы

___________ /____________. / / ____________ /

___________2010 г. __________ 2010 г.

Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1.

На вертикальной стойке 1 крепится легкий блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. На корпусе среднего кронштейна имеется риска, совпадающая с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На вертикальной стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положения грузов. Начальное положение определяют по нижнему срезу груза, а конечное – по риске на корпусе среднего кронштейна.

Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе.

Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Среднее значение времени прохождения системой некоторого расстояния S определяется согласно соотношения:

(3.1)

где – порядковый номер измерения времени, =1.. n , n – номер последнего измерения, количество измерений.

Аналогично для квадрата времени:

(3.2)

Случайная погрешность измерений:

(3.3)

г де – случайная погрешность измерения времени, – случайная погрешность измерения квадрата времени, – коэффициент Стьюдента, – количество значений, – доверительная вероятность, – средняя квадратичная погрешность среднего значения времени, – средняя квадратичная погрешность среднего значения квадрата времени.

Средние квадратические погрешности средней величины:

(3.4)

Согласно теории вероятности, если абсолютная погрешность некоторого измерения больше утроенной среднеквадратической погрешности, тогда такое измерение считается промахом и в дальнейшем исключается из обработки. Таким образом, необходимо чтобы для всех выбранных измерений соблюдалось условие:

(3.5)

Приборная погрешность измерения времени:

(3.6)

где – цена деления секундомера (в данной работе =0,001 с).

Общая погрешность измерений:

(3.7)

Относительная погрешность измерений:

(3.8)

Ускорение движения системы, согласно руководства по лабораторной работе, определим по формуле:

(3.9)

где и значения, определенные с помощью полученного графика линеаризованной зависимости .

Поскольку график зависимости теоретически должен проходить через начало системы координат, тогда для того, чтобы оценить погрешность вычисления ускорения движения системы необходимо для полученных данных найти такие две графические зависимости, для которых их угловой коэффициент (а это и есть, собственно, ускорение) был бы максимальным и минимальным. Большее из отклонений углового коэффициента от рассчитанного значения а и принимается как абсолютная погрешность Δа.

Относительная погрешность определения ускорения движения системы:

(3.10)

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ

Измеренные значения и результаты их обработки приведены в таблице.

Таблица 4.1 – Результаты прямых и косвенных измерений

= 6 , 32 см1/2

= 5 , 48 см1/2

=4, 47 см1/2

= 3 , 8 7, см1/2

= 3 ,1 6 , см1/2

Таблица 4.2 – Результаты первичного расчета погрешностей измерений

= 6 , 32 см1/2

= 5 , 48 см1/2

=4, 47 см1/2

= 3 , 8 7, см1/2

= 3 ,1 6 , см1/2

, c

, c2

, c

, c2

, c

, c2

, c

, c2

, c

, c2

, c

, c2

Поскольку для всех полученных значений выполняется условие (3.5), тогда можно приступать к дальнейшей обработке результатов.

Исходя из того, что для каждого выбранного значения пути перемещения S было выполнено по n =5 измерений, тогда при доверительной вероятности α=0,95 коэффициент Стьюдента будет равен .

Таблица 4.5 – Результаты расчета погрешностей

= 6 , 32 см1/2

= 5 , 48 см1/2

=4, 47 см1/2

= 3 , 8 7, см1/2

= 3 ,1 6 , см1/2

, c

, %

, c2

, %

Как видно из приведенных расчетов в данной лабораторной работе можно пренебречь приборной погрешностью вследствие её малости по сравнению со случайной погрешностью.

Согласно полученным данным построим графики зависимостей , , :

Согласно полученному графику линеаризованной зависимости , пользуясь формулой (3.9), получим:

(см/с2);

Для оценки абсолютной погрешности определения ускорения движения системы, мысленно проведем прямые, проходящие через начало координат системы и каждую экспериментально найденную точку зависимости и вычислим для каждой из них свой угловой коэффициент (3.9):

1) для прямой проходящей через точки (0;0) и (2,307; 3,16) угловой коэффициент равен 3,75 см/с2;

2) для прямой проходящей через точки (0;0) и (2,828; 3,87) угловой коэффициент равен 3,75 см/с2;

3) для прямой проходящей через точки (0;0) и (3,276; 4,47) угловой коэффициент равен 3,72 см/с2;

4) для прямой проходящей через точки (0;0) и (4,006; 5,48) угловой коэффициент равен 3,74 см/с2;

5) для прямой проходящей через точки (0;0) и (4,589; 6,32) угловой коэффициент равен 3,79 см/с2;

1) максимальный угловой коэффициент:

(см/с2);

2) минимальный угловой коэффициент:

(см/с2);

Соответственно получим отклонения:

(см/с2);

В конечном итоге абсолютная погрешность определения углового ускорения движения системы:

см/с2;

(см/с2);

Относительная погрешность определения ускорения, согласно выражению (3.10):

;

В ходе данной лабораторной работы с помощью машины Атвуда был изучен закон прямолинейного равноускоренного движения тел под действием сил земного тяготения. В результате проведенных испытаний удалось получить графики зависимости перемещения от времени , перемещения от квадрата времени , корня квадратного от времени . Также в ходе выполнения работы было рассчитано ускорение движения системы (см/с2) с относительной погрешностью , что является отличным результатом. В заключение необходимо сказать, что поставленная цель работы была достигнута полностью, на что указывают относительные погрешности определения времени движения системы для различных перемещений (все менее 5%), а также допустимая точность определения искомого ускорения движения 2,4%.

6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие силы действуют на груз с перегрузком во время движения?

На груз с перегрузком во время движения действуют сила земного тяготения и сила натяжения нити. Действием всех остальных сил в данной работе пренебрегаем (силы трения, сопротивления воздуха и т. д.)

2. Запишите уравнение движения для каждого из грузов.

Уравнение движения груза с перегрузком:

;

Уравнение движения груза без перегрузка:

;

где – масса каждого груза без перегрузка, – масса перегрузка, – ускорение свободного падения, и – силы натяжения нитей на грузе с перегрузком и грузе без перегрузка соответственно, и – ускорения движения грузов с перегрузком и без соответственно.

В силу не растяжимости нити ; при невесомом блоке .

3. Укажите возможные причины, обуславливающие несовпадение теоретических выводов с результатами измерений.

Среди причин, обуславливающих несовпадение теоретических выводов с результатами измерений можно назвать такие как: пренебрежение весом блока, пренебрежение силами трения и сопротивления в системе, пренебрежение весом, физическими и геометрическими свойствами нити, а также, что естественно, определенную погрешность вносят погрешности измерения всех величин.

4. Каким образом из линеаризованного графика можно оценить систематическую погрешность измерения времени?

Систематическая погрешность измерения времени может быть определена из линеаризованного графика зависимости по точке пересечения графика с координатной осью времени t .

5. Укажите физические допущения, используемые при теоретическом анализе движения грузов в машине Атвуда.

При теоретическом анализе движения грузов в машине Атвуда считается, что блок и нить невесомы, нить нерастяжима, силы трения малы; в силу чего допускается, что ускорение движения грузов и силы натяжения нити по разные стороны блока одинаковы.

К работе прилагается регистрационный файл (*. REG ).

[spoiler title=”источники:”]

http://1ku.ru/obrazovanie/52155-izuchenie-zakonov-postupatelnogo-dvizhenija-na-mashine-atvuda-formuly-i-pojasnenija/

http://pandia.ru/text/79/388/43500.php

[/spoiler]

Источник

Что такое машина Атвуда?

Уравнения динамики

Расчет уравнений динамики для равноускоренного движения

Проверка решения уравнений динамики

Расчет силы тяжести

Определение силы натяжения нити

Описание[править | править код]

Формула для нахождения ускорения[править | править код]

Формула для нахождения ускорения свободного падения[править | править код]

Формула для нахождения силы натяжения нити[править | править код]

См. также[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Определение ускорения свободного падения на машине Атвуда.

Определение ускорения свободного падения на машине Атвуда.

Теоретическая часть.

Описание метода и экспериментальной установки для определения ускорения свободного падения.

Описание лабораторной работы

Изучение законов поступательного движения на машине Атвуда: формулы и пояснения

Что такое машина Атвуда?

Уравнения динамики

Расчет уравнений динамики для равноускоренного движения

Проверка решения уравнений динамики

Расчет силы тяжести

Определение силы натяжения нити

Изучение прямолинейного движения тел на машине Атвуда

Вам также может понравиться

Как исправить тугоухость

Как мне найти кирпич в майнкрафт

Как найти плюсы в школе

Добавить комментарий Отменить ответ