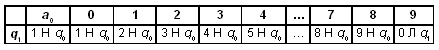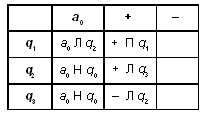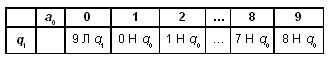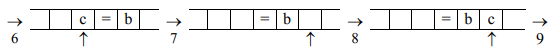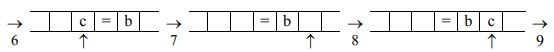#статьи
- 25 янв 2023
-
0
Машина Тьюринга — что это: роскошь или средство вычисления?
Рассказываем о концепции, которая легла в основу всех современных компьютеров.
Иллюстрация: Wikimedia Commons / Colowgee для Skillbox Media
Востоковед, интересующийся IT. В прошлом редактор раздела «Системный блок» журнала «Fакел», автор журналов Computer Gaming World RE, Upgrade Special, руководитель веб-ресурсов компании 1С-Softclub.
Любой, кто интересуется информатикой, компьютерами и IT, рано или поздно встретит термин «машина Тьюринга». Понять, что это, с помощью соответствующей страницы в «Википедии» категорически невозможно, даже не пытайтесь. Поэтому мы решили справиться сами — и вам рассказать.
Всё, что нужно знать о машине Тьюринга
- Зачем она нужна
- Как устроена
- Принцип работы
- Роль в истории
- Полнота по Тьюрингу
- Примеры реализации
- При чём тут грибы?
В XVII веке знаменитый математик Готфрид Лейбниц мечтал о создании машины, которая могла бы определять истинность математических утверждений.
Три века спустя другой выдающийся математик, Давид Гильберт, мечтая о том же, сформулировал задачу. Он хотел найти алгоритм, который принимал бы в качестве входных данных описание любой проблемы разрешимости. А после конечного числа шагов останавливался бы и выдавал один из двух ответов: «истина» или «ложь».
Фото: Wikimedia Commons
Чуть позже, в 1930-е годы, к этому же вопросу обратился третий, не менее знаменитый, математик Макс Ньюман. Он преподавал в Кембридже, был криптоаналитиком и одним из создателей Colossus — самого большого компьютера тех времён.
«Есть ли конкретный метод или механический процесс, который можно применить к математическому утверждению и он ответит, доказуемо ли это утверждение?»
Из лекций Макса Ньюмана,
цитата по книге Чарльза Петцольда «Читаем Тьюринга»
Фото: Wikimedia Commons
Среди студентов Ньюмана был пока ещё никому не известный математик Алан Тьюринг. Валяясь на лугах Гранчестера, где любили отдыхать тогдашние хипстеры, он размышлял над словами Ньюмана. Итогом этих раздумий стала статья On Computable Numbers, with an Application to the Entscheidungsproblem
«Я предполагаю, что Тьюринг с самого начала своей работы ставил перед собой цель доказать неразрешимость Entscheidungsproblem. Он сказал мне, что „главная идея“ статьи пришла к нему, когда он лежал на лугах Гранчестера летом 1935 года. Главной идеей мог быть либо его анализ вычислений, либо осознание существования универсальной машины, а значит, и диагональный аргумент для доказательства неразрешимости».
Из воспоминаний ученика и друга Тьюринга Робина Ганди,
цитата по книге The Universal Turing Machine. A Half-Century Survey (1995), Rolf Herken
Фото: Christie’s
Именно в этой статье, опубликованной в 1936 году, была впервые описана машина Тьюринга. Правда, сам автор использовал понятие «вычислительная машина» (computing machine); в честь него модель назовут чуть позже.
Фото: Wikimedia Commons
Тьюринг пошёл не по привычному пути формул и доказательств, а начал с описания машины, которая совершает несколько простых операций. Хотя компьютеров тогда не было, если не считать прообразов вычислительных машин, созданных Чарльзом Бэббиджем и Вэниваром Бушем.
Машина Тьюринга — это абстрактная вычислительная машина, мысленный эксперимент для решения проблемы математической логики. Она состоит из трёх элементов:
- бесконечной ленты с ячейками;
- автомата или головки для чтения и записи;
- программы.
Изображение: Computational Error and Complexity in Science and Engineering / V. Lakshmikantham, S. K. Sen / Mathematics in Science and Engineering, 2005
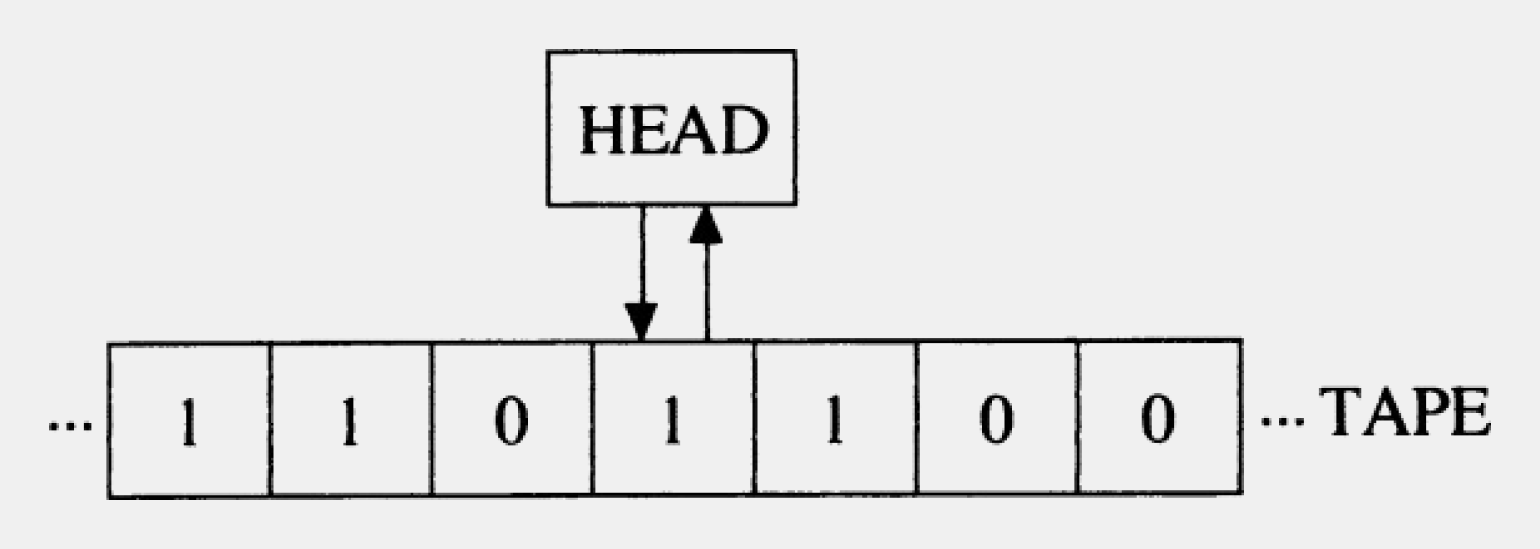
Машина работает следующим образом: головка может прочитать содержимое конкретной ячейки, стереть, перезаписать и/или передвинуться на ячейку влево или вправо и повторить считывание/запись.
«В некоторых конфигурациях, в которых ячейка пуста (то есть не содержит символа), машина записывает новый символ в эту ячейку: в других конфигурациях она стирает символ. Машина может также поменять ячейку, но только путём смещения его на одно место вправо или влево».
А. Тьюринг,
«О вычислительных числах, с приложением к проблеме принятия решений»
Действия головки определяются программой. Она записывается в виде таблицы, где есть внешний и внутренний алфавиты и таблица переходов между ними. Внешний алфавит — это конечное множество, элементы которого называются буквами или символами. Внутренний алфавит — это конечное множество состояний головки. Таблица переходов описывает поведение головки. Команда, которую должна выполнить головка, определяется пересечением внешнего и внутреннего алфавитов в таблице.
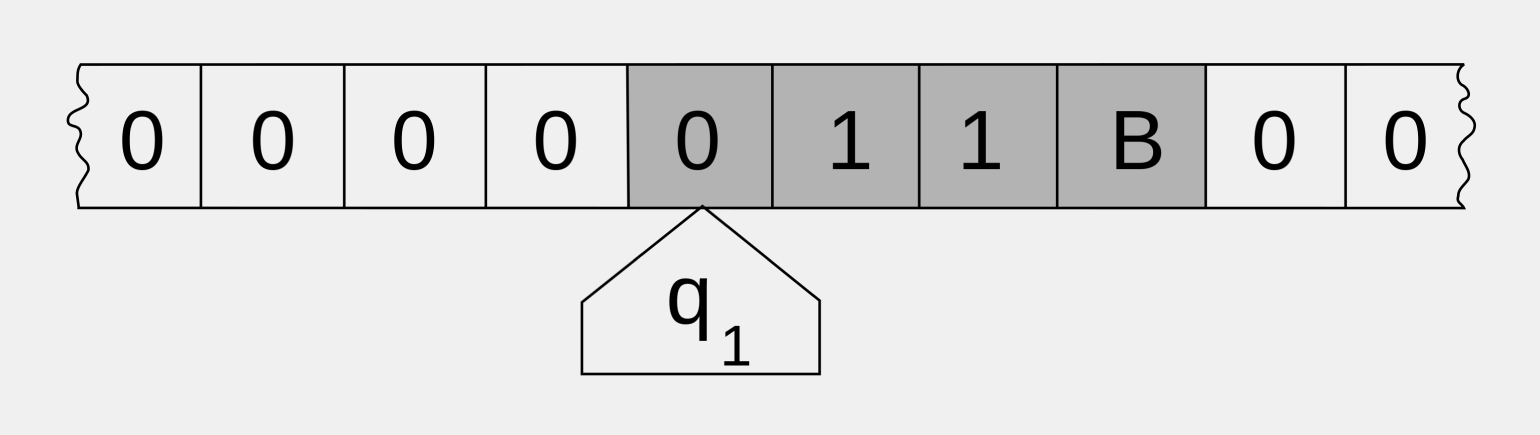
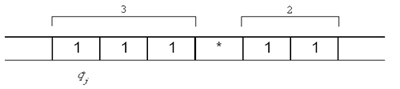
На рисунке выше изображена лента, входная информация (11В) расположена так, что в каждой клетке по одному символу. До и после неё — нулевые ячейки. Исходное состояние головки — q1. Это состояние запускает работу машины. Головка может сдвинуться влево и вместо 0 записать цифру или букву. Также она может сдвинуться вправо и перезаписать 1 другой цифрой или буквой. Или передвинуться ещё на ячейку влево/вправо без перезаписи.
Головка может также остаться на месте и ничего не делать. Выполнение операций прекращается после того, как головка считывает пассивное состояние — q0.
В чём же важность этой, на первый взгляд, нехитрой конструкции?
Историческое значение машины Тьюринга в том, что это первая математическая модель универсальных вычислений. Другими словами, всё, что можно вычислить, описывается как машина Тьюринга. Это не единственная модель вычислений, но, пожалуй, самая известная и популярная. И ещё это описание работы компьютера, которое Тьюринг дал до появления компьютеров.
«Его машины предлагали мост, связь между абстрактными символами и физическим миром».
Эндрю Ходжес,
«Алан Тьюринг: Энигма»
Также новаторство Тьюринга было в том, что его машина использовала двоичную систему во времена, когда преобладала десятичная. Привычные для нас двоичные числа для большинства читателей в 1936 году были не столь знакомы. Так, компьютер ENIAC (1943–1945) использовал десятичную систему. А слово «бит» (сокращение от binary digit, «двоичная цифра») появилось в публикациях только в 1948 году.
Важность работы Тьюринга была ещё и в том, что он описал универсальный компьютер «общего назначения». Это революционная концепция. В то время компьютеры разрабатывались специально для определённых видов работ. Например, Вэнивар Буш со студентами в 1920-е годы придумал аналоговый компьютер, известный как дифференциальный анализатор. Он решал обыкновенные дифференциальные уравнения — и это было всё, что он делал.
«Не нужно разрабатывать разные машины для выполнения различных вычислительных процессов. Все они могут быть выполнены с помощью одного цифрового компьютера, соответствующим образом запрограммированного для каждого случая».
А.Тьюринг,
«Вычислительная техника и интеллект»
Никто не доказал, что существует более эффективная модель вычислений, чем машина Тьюринга. Она отвечает на вопрос, какие минимальные условия нам нужны для выполнения любого вычисления. Ответ на этот вопрос показывает нам ограничения компьютеров. Если мы можем произвести определённое вычисление на машине Тьюринга, значит, его можно сделать на любом другом компьютере. Это называется «полнота по Тьюрингу».
Полнота по Тьюрингу — одно из базовых понятий в информатике. Полный по Тьюрингу язык программирования или компьютер способен имитировать машину Тьюринга. Он теоретически может выразить все задачи, решаемые компьютерами; почти все языки программирования Тьюринг-полные, если не обращать внимания на ограничения памяти.
Другими словами, можно написать на Java или C++ программу, которая будет действовать как машина Тьюринга. «Полными» также являются и HTML5, и CSS3. А вот SQL не полный — на нём пишутся в основном запросы к базе данных, а не полноценные программы.
Несмотря на то что данная разработка — это мысленный эксперимент, нашлись энтузиасты, которые попытались сконструировать её физический прототип.
Пожалуй, наиболее впечатляющую модель воспроизвел Ричард Ридел. У него ушло на её создание шесть месяцев.
Фото: Wikimedia Commons
Другие умельцы реализовали машину Тьюринга в Excel:
Несмотря на то что машина Тьюринга была придумана почти 100 лет назад, эта концепция не только не устарела, но и используется сейчас. Робототехник Джошуа Бонгард и биолог Майкл Левин в своих работах предлагают уйти от узкого понимания компьютеров и рассматривать живые организмы тоже как вычислительные машины.
И для того, чтобы определить, можно ли причислить этих крабов к компьютерам, они рассматривают их как машину Тьюринга. Правда, здесь у учёных возникают сложности, потому что в случае с грибами или жидкостями сложно определить, где лента, где считывающая головка, а где программа.
Кроме того, биологические системы эволюционируют и меняются со временем, что также усложняет применение к ним жёстких математических определений.
Но ничего лучше машины Тьюринга, похоже, не придумали, поэтому Бонгарду и Левину придётся найти, где у крабов лента, а где считывающая головка.
Высшее образование со Skillbox
Программа бакалавриата по аналитике данных и машинному обучению от РАНХиГС. Стань востребованным IT-специалистом, получи диплом государственного вуза и измени мир с помощью высоких технологий.
Узнать подробнее


189
Рис. 6.3. Повторение алгоритмов
Также без доказательства примем следующую теорему.
Теорема 6.4. Повторение нормального алгоритма, управляемое нормальным алгоритмом, есть нормальный алгоритм.
Основным и важнейшим результатом этого параграфа является то, что различные операции (комбинации) над нормальными алгоритмами снова приводят к нормальному алгоритму.
Стремясь найти точное определение понятия алгоритма, Тьюринг выделил некоторый класс абстрактных машин, о которых высказал предположение, что они пригодны для осуществления любой “механической” вычислительной процедуры. Эти машины называются теперь в честь их изобретателя машинами Тьюринга.
|
S0 |
Пусть имеется лента, потенциально |
||||||||||
|
q0 |
бесконечная в обе стороны* и разделенная |
||||||||||
|
на ячейки (квадраты), см. Рис. 6.4. |
|||||||||||
|
Рис. 6.4. |
Потенциальная |
бесконечность |
ленты |
||||||||
|
понимается в том смысле, что в каждый |
|||||||||||
данный момент времени она имеет конечную длину, и вместе с тем к ней всегда как слева, так и справа могут быть добавлены новые квадраты.
Имеется некоторое конечное множество символов S0,S1,..,Sn, которое называется алфавитом машины. В каждой ячейке может быть записан только один из символов – букв алфавита машины.
Машина обладает некоторым конечным множеством внутренних состояний {q0,q1,…,qm}. В каждый данный момент времени машина находится только в одном из этих состояний. Считаем, что внутренним
*) Тьюринг определил машину с лентой потенциально бесконечной вправо и ограниченной слева. Потенциальная бесконечность ленты в обе стороны упрощает дальнейшее описание работы машины. Можно показать, что вводимая машина эквивалентна машине, определенной Тьюрингом.
190
состоянием q0 обладает каждая машина и q0 называется начальным состоянием.
Машина имеет читающую головку, которая в каждый данный момент времени находится на одном из квадратов ленты и воспринимает символ, записанный на этом квадрате. Будем предполагать, что среди символов S0,S1,..,Sn имеется символ, означающий пустой квадрат, например, S0. Положим, что символ S0 принадлежит алфавиту каждой машины Тьюринга и S0 не может быть записан ни в каком квадрате ленты. Когда мы пишем, что читающая головка обозревает квадрат с символом S0 или записывает в квадрат символ S0, то имеем в виду, что читающая головка соответственно обозревает пустой квадрат (воспринимая его как S0) или оставляет квадрат без символов (воспринимая его как S0). Машина действует не непрерывно, а лишь в дискретные моменты времени.
Если в какой-то момент времени t читающая головка воспринимает квадрат (т.е. стоит на квадрате), содержащий символ Si, и машина находится во внутреннем состоянии qj, то действие машины определено, и она совершает один из следующих четырех действий:
1)головка стирает символ Si и записывает на том же квадрате символ Sk;
2)головка перемещается в соседний слева квадрат;
3)головка перемещается в соседний справа квадрат;
4)машина останавливается.
В случаях 1)-3) машина переходит во внутреннее состояние qr и готова к действию в следующий момент времени t+1.
Первые три из возможных актов действия машины могут быть описаны соответственно следующими упорядоченными четверками символов, которые в дальнейшем будем называть командами:
1)qj Si Sk qr;
2)qj Si L qr;
3)qj Si R qr.
Любая машина имеет конечное (непустое) множество команд.
Машина останавливается, если она находится в некотором внутреннем состоянии qj, читающая головка обозревает какой-то символ Sk, а среди команд машины нет команды, начинающейся с qjSk.
Если на ленте имеется какое-нибудь слово Р (в частности, пустое слово), читающая головка помещена на квадрат с первой левой буквой слова Р и машина приведена во внутреннее состояние q0, то машина начинает оперировать на ленте: ее головка стирает и пишет символы и перемещается из одного квадрата в другой (соседний). Если при этом машина когда-нибудь останавливается, то находящееся в момент остановки слово на ленте считается результатом применения машины Т к данному слову Р и обозначается через Т(Р). Если процесс переработки машиной Т слова Р бесконечен, то говорят, что машина Т не применима к слову Р.

191
§ 8. Задание машины Тьюринга
Машина Тьюринга Т считается заданной, если задано непустое конечное множество упорядоченных четверок символов (команд), удовлетворяющих условиям:
а) каждая четверка символов принадлежит к одному из трех типов команд, приведенных выше (в § 7),
б) никакие две четверки одной машины не имеют совпадающие первые два символа,
в) среди команд любой машины всегда есть хотя бы одна команда, начинающаяся с q0.
Множество всех символов типа Sm, входящих в команды машины, называется алфавитом заданной машины, а входящие в эти команды символы qi называются внутренними состояниями заданной машины Т.
Считаем, что в исходном (начальном) состоянии машина обладает внутренним состоянием q0.
Для преобразования слова Р машиной Т обязательно указывается положение слова на ленте относительно читающей головки. Если это не сделано, то предполагается, что читающая головка находится на первой (самой левой) букве слова Р.
Рассмотрим несколько примеров.
1. Пусть задана машина Т командами:
q01Rq1 q1S01q0,
а на ленте записано слово Р=1, см. Рис.6.5. Легко убедиться, что машина Т, начав работу с первой буквы слова Р, приписывает к нему слева по одной букве 1 на каждом шаге, никогда при этом не останавливаясь. Следовательно, эта машина неприменима к слову Р.
|
2. Машина, заданная командами: |
q0S0Rq0 |
|||||||||||
|
q0S1Rq0 |
||||||||||||
|
q0S2Rq0 |
||||||||||||
|
q0SkRq0 |
||||||||||||
|
……… |
||||||||||||
|
q011q1, |
где ни одно из Si (1≤ i≤ k) не совпадает с символом 1, двигается по ленте вправо, пока не встретит вхождение (если такое вообще имеется) символа 1, после чего останавливается.
3. Машина Т, заданная командами
q0aRq0 q0bRq0 q0S0aq1,
как легко убедиться, приписывает к любому слову Р алфавита {a,b} справа букву а и останавливается.

192
§9. Алгоритм Тьюринга. Вычислимость по Тьюрингу
Скаждой машиной Тьюринга можно связать некоторый алгоритм AT,A в алфавите А машины Т. Возьмем произвольное слово Р алфавита А и запишем его слева направо в квадратах чистой ленты, причем так, чтобы первая (самая левая) буква Р находилась под читающей головкой. Приведем машину Т во
внутреннее состояние q0. Машина начинает работать. Если она когда-нибудь остановится, то появившееся в результате на ленте слово алфавита А является
значением алгоритма AT,A. Такой алгоритм AT,A называется алгоритмом Тьюринга.
Будем говорить, что машина Тьюринга Т с алфавитом А, включающим 1
и*, частично вычисляет частичную арифметическую функцию f(x1,x2,…,xn), если для любых натуральных k1,k2,…,kn и некоторых r и m имеем:
|
A |
( |
) = S r |
S m , |
(Si |
= S S …S |
), |
||||||||||||||
|
k |
1 |
,k |
2 |
,…,k |
n |
f ( k |
1 |
,k |
2 |
,…,k |
n |
) |
0 |
|||||||
|
T ,A |
0 |
0 |
0 |
0 0 |
||||||||||||||||
|
14243 |
i раз
тогда и только тогда, когда определена хотя бы одна из частей этого равенства. Это означает, что применение алгоритма Тьюринга AT,A к слову
( k1 ,k2 ,…,kn ) даст слово, означающее с точностью до слов S0r и S0m значение
функции f(k1,k2,…,kn) (S0 – интерпретируется как изображение пустого квадрата ленты).
Арифметическая функция f(x1,x2,…,xn) называется вычислимой по Тьюрингу, если для любых натуральных k1,k2,…,kn и некоторых r и m имеем:
|
A |
( |
) = S r |
Sm , |
(Si |
= S S …S |
). |
||||||||||||||
|
k |
1 |
,k |
2 |
,…,k |
n |
f ( k |
1 |
,k |
2 |
,…,k |
n |
) |
0 |
|||||||
|
T ,A |
0 |
0 |
0 |
0 0 |
||||||||||||||||
|
14243 |
i раз
Это означает, что применение алгоритма Тьюринга AT,A к слову ( k1 ,k2 ,…,kn ) даст слово, означающее с точностью до слов S0r и S0m значение функции
f(k1,k2,…,kn), т.е. существует машина Тьюринга, вычисляющая эту функцию для любых значений её аргументов.
Пример. Рассмотрим всюду определенную функцию сложения f(x,y)=x+y. Покажем, что эта функция вычислима по Тьюрингу. Для этого построим машину Тьюринга:
q0 1 S0 q0 q0 S0 R q1 q1 1 R q1 q1 * 1 q2 q2 1 R q2 q2 S0 L q3 q3 1 S0 q3.
Художественное представление машины Тьюринга
Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать всех исполнителей (с помощью задания правил перехода), каким-либо образом реализующих процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
То есть всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга[1].
Устройство[править | править код]
В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки[2][3], и управляющее устройство (также называется головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, оставаться в неподвижном положении, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм,
реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку
новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и
ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.
Описание машины Тьюринга[править | править код]
Конкретная машина Тьюринга задаётся перечислением букв алфавита A, множеством состояний Q и набором правил перехода, по которым работает машина. Они имеют вид: qiaj→qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации <qi, aj> имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое, машина останавливается. Кроме того, необходимо указать начальное и конечное состояния, начальную конфигурацию на ленте и расположение головки машины.
Пример[править | править код]
Пример машины Тьюринга для умножения чисел в унарной системе счисления.
Запись правила перехода «qiaj→qi1aj1R/L/N» следует понимать так: qi — состояние, при котором выполняется это правило, aj — данные в ячейке, в которой находится головка, qi1 — состояние, в которое нужно перейти, aj1 — что нужно записать в ячейку, R/L/N — команда на перемещение.
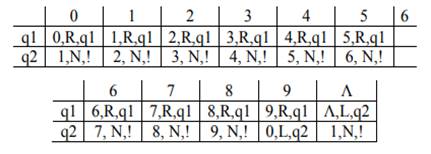
Машина работает по следующему набору правил:
| q0 | q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | q01→q01R | q11→q2aR | q21→q21L | q31 → q4aR | q41→q41R | q71→q2aR | |||
| × | q0×→q1×R | q2×→q3×L | q4×→q4×R | q6×→q7×R | q8×→q9×N | ||||
| = | q2=→q2=L | q4=→q4=R | q7=→q8=L | ||||||
| a | q2a→q2aL | q3a→q3aL | q4a→q4aR | q6a→q61R | q7a→q7aR | q8a→q81L | |||
| * | q0*→q0*R | q3*→q6*R | q4*→q51R | ||||||
| q5 →q2*L |
Описание состояний:
| Начало | |
| q0 | начальное состояние. Ищем «x» справа. При нахождении переходим в состояние q1 |
|---|---|
| q1 | заменяем «1» на «а» и переходим в состояние q2 |
| Переносим все «1» из первого числа в результат | |
| q2 | ищем «х» слева. При нахождении переходим в состояние q3 |
| q3 | ищем «1» слева, заменяем её на «а» и переходим в состояние q4.
В случае, если «1» закончились, находим «*» и переходим в состояние q6 |
| q4 | переходим в конец (ищем «*» справа), заменяем «*» на «1» и переходим в состояние q5 |
| q5 | добавляем «*» в конец и переходим в состояние q2 |
| Обрабатываем каждый разряд второго числа | |
| q6 | ищем «х» справа и переходим в состояние q7. Пока ищем, заменяем «а» на «1» |
| q7 | ищем «1» или «=» справа,
при нахождении «1» заменяем его на «а» и переходим в состояние q2 при нахождении «=» переходим в состояние q8 |
| Конец | |
| q8 | ищем «х» слева. При нахождении переходим в состояние q9. Пока ищем, заменяем «а» на «1» |
| q9 | терминальное состояние (остановка алгоритма) |
Умножим с помощью МТ 3 на 2 в единичной системе.
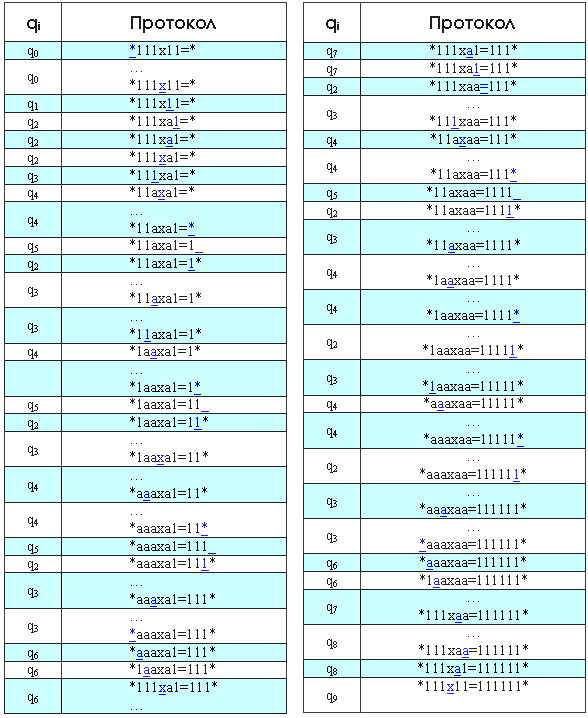
В протоколе указаны начальное и конечное состояния МТ, начальная конфигурация на ленте и расположение головки машины (подчёркнутый символ).
Начало. Находимся в состоянии q0, ввели в машину данные: *111×11=*, головка машины располагается на первом символе *.
1-й шаг. Смотрим по таблице правил, что будет делать машина, находясь в состоянии q0 и над символом «*». Это правило из 1-го столбца 5-й строки — q0*→q0*R. Это значит, что мы переходим в состояние q0 (то есть не меняем его), символ станет «*» (то есть не изменится) и смещаемся по введённому нами тексту «*111×11=*» вправо на одну позицию (R), то есть на 1-й символ 1. В свою очередь, состояние q01 (1-й столбец 1-я строка) обрабатывается правилом q01→q01R. То есть снова происходит просто переход вправо на 1 позицию. Так происходит, пока мы не станем на символ «х». И так далее: берём состояние (индекс при q), берём символ, на котором стоим (подчёркнутый символ), соединяем их и смотрим обработку полученной комбинации по таблице правил.
Простыми словами, алгоритм умножения следующий: помечаем 1-ю единицу 2-го множителя, заменяя её на букву «а», и переносим весь 1-й множитель за знак равенства. Перенос производится путём поочерёдной замены единиц 1-го множителя на «а» и дописывания такого же количества единиц в конце строки (слева от крайнего правого «*»). Затем меняем все «а» до знака умножения «х» обратно на единицы. И цикл повторяется. Действительно, ведь A умножить на В можно представить как А+А+А В раз. Помечаем теперь 2-ю единицу 2-го множителя буквой «а» и снова переносим единицы. Когда до знака «=» не окажется единиц — значит, умножение завершено.
Полнота по Тьюрингу[править | править код]
Можно сказать, что машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам перехода преобразует входные данные с помощью последовательности элементарных действий.
Элементарность действий заключается в том, что действие меняет лишь небольшой фрагмент данных в памяти (в случае машины Тьюринга — лишь одну ячейку), и число возможных действий конечно. Несмотря на простоту машины Тьюринга, на ней можно вычислить всё, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой.
Один из естественных способов доказательства того, что алгоритмы вычисления, которые можно реализовать на одной машине, можно реализовать и на другой, — это имитация первой машины на второй.
Имитация заключается в следующем. На вход второй машине подаётся описание программы (правил работы) первой машины 


Как было сказано, на машине Тьюринга можно имитировать (с помощью задания правил перехода) все другие исполнители, каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
На машине Тьюринга можно имитировать машину Поста, нормальные алгоритмы Маркова и любую программу для обычных компьютеров, преобразующую входные данные в выходные по какому-либо алгоритму. В свою очередь, на различных абстрактных исполнителях можно имитировать Машину Тьюринга. Исполнители, для которых это возможно, называются полными по Тьюрингу (Turing complete).
Есть программы для обычных компьютеров, имитирующие работу машины Тьюринга. Но данная имитация неполная, так как в машине Тьюринга присутствует абстрактная бесконечная лента. Бесконечную ленту с данными невозможно в полной мере имитировать на компьютере с конечной памятью: суммарная память компьютера — оперативная память, жёсткие диски, различные внешние носители данных, регистры и кэш процессора и др. — может быть очень большой, но тем не менее всегда конечна. Теоретический предел количества информации, которая может находиться внутри заданной поверхности, с точностью до множителя 
Варианты машины Тьюринга[править | править код]
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
Машина Тьюринга, работающая на полубесконечной ленте[править | править код]
В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте (то есть на ленте, бесконечной в одну сторону).
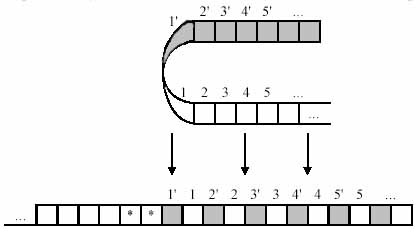
Рассмотрим доказательство, приведённое Ю. Г. Карповым в книге «Теория автоматов». Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых, произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:
Затем перенумеруем ячейки, причём будем считать, что символ «*» не содержится в словаре МТ:
Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ ‘*’, значит головка считывания-записи достигла границы зоны:
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров «*» лента в эквивалентной машине Тьюринга не используется.
Двумерные машины Тьюринга[править | править код]
- Муравей Лэнгтона
См. также[править | править код]
- JFLAP кроссплатформенная программа — симулятор автоматов, машины Тьюринга, грамматик, рисует граф автомата
- Универсальная машина Тьюринга
- Недетерминированная машина Тьюринга
- Вероятностная машина Тьюринга
- Квантовая машина Тьюринга
- Теория алгоритмов
- Тьюринговская трясина
- Диаграмма Тьюринга
- Машина Минского
Другие абстрактные исполнители и формальные системы вычислений[править | править код]
- Нормальный алгоритм Маркова (продукционное программирование)
- Машина Поста (автоматное программирование)
- Рекурсивная функция (теория вычислимости)
- Лямбда-исчисление (функциональное программирование)
- Brainfuck (императивное программирование)
Примечания[править | править код]
- ↑ Нефёдов, 1992, с. 97.
- ↑ Нефёдов, 1992, с. 94.
- ↑ Эббинхауз, 1972, с. 24.
Литература[править | править код]
- Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман. Глава 8. Введение в теорию машин Тьюринга // Введение в теорию автоматов, языков и вычислений = Introduction to Automata Theory, Languages, and Computation. — М.: Вильямс, 2002. — 528 с. — ISBN 0-201-44124-1.
- Карпов Ю. Г. Теория автоматов. — Питер, 2003. — ISBN 5-318-00537-3.
- Эббинхауз Г. Д., Якобс К., Ман Ф. К., Хермес Г. Машины Тьюринга и рекурсивные функции. — М.: Мир, 1972. — 262 с.
- Нефёдов В. Н., Осипова В. А. Курс дискретной математики. — М.: МАИ, 1992. — 260 с.
Ссылки[править | править код]
- Машина Тьюринга // Лекция Александра Шеня в проекте ПостНаука (06.04.2013)
ПРЕДЛАГАЮ КОЛЛЕГАМ
Тема “Машина Тьюринга” в школьном
курсе информатики
И.Н. Фалина,
Москва
Во многих учебниках по информатике при
изучении понятия и свойств алгоритма
присутствуют фразы такого содержания:
“…существует много разных способов для записи
одного и того же алгоритма, например, запись в
виде текста, запись в виде блок-схемы, запись на
каком-либо алгоритмическом языке, представление
алгоритма в виде машины Тьюринга или машины
Поста…”. К сожалению, такого типа фразы являются
единственными, где упоминается машина Тьюринга.
Без сомнения, объем часов, отводимых на изучение
алгоритмов, не позволяет включать в эту тему еще
и изучение способов записи алгоритма в виде
машины Тьюринга. Но эта тема крайне интересна,
важна и полезна для школьников, особенно
увлекающихся информатикой.
Тема “Машина Тьюринга” может
изучаться в 8–11-х классах в рамках темы
“Информационные процессы. Обработка
информации”, на факультативных занятиях, в
системе дополнительного образования, например, в
школах юных программистов. Изучение этой темы
может сопровождаться компьютерной поддержкой,
если у учителя есть программный
тренажер-имитатор “Машина Тьюринга”. В классах
с углубленным изучением программирования
школьники могут самостоятельно написать
программу “Машина Тьюринга”. В рамках этой
статьи вашему вниманию предлагается практикум
по решению задач на тему “Машина Тьюринга”.
Теоретический материал по данной теме не раз
печатался на страницах газеты “Информатика”,
например, в № 3/2004 статья И.Н. Фалиной “Элементы
теории алгоритмов”.
Краткий теоретический материал
Машина Тьюринга — это строгое
математическое построение, математический
аппарат (аналогичный, например, аппарату
дифференциальных уравнений), созданный для
решения определенных задач. Этот математический
аппарат был назван “машиной” по той причине, что
по описанию его составляющих частей и
функционированию он похож на вычислительную
машину. Принципиальное отличие машины Тьюринга
от вычислительных машин состоит в том, что ее
запоминающее устройство представляет собой
бесконечную ленту: у реальных вычислительных
машин запоминающее устройство может быть как
угодно большим, но обязательно конечным. Машину
Тьюринга нельзя реализовать именно из-за
бесконечности ее ленты. В этом смысле она мощнее
любой вычислительной машины.
В каждой машине Тьюринга есть две
части:
1) неограниченная в обе стороны лента,
разделенная на ячейки;
2) автомат (головка для
считывания/записи, управляемая программой).
С каждой машиной Тьюринга связаны два
конечных алфавита: алфавит входных символов A =
{a0, a1, …, am}и алфавит состояний Q =
{q0, q1, …, qp}. (С разными машинами
Тьюринга могут быть связаны разные алфавиты A
и Q.) Состояние q0 называется пассивным.
Считается, что если машина попала в это
состояние, то она закончила свою работу.
Состояние q1 называется начальным.
Находясь в этом состоянии, машина начинает свою
работу.
Входное слово размещается на ленте по
одной букве в расположенных подряд ячейках.
Слева и справа от входного слова находятся
только пустые ячейки (в алфавит А всегда
входит пустая буква а0 — признак того, что
ячейка пуста).
Автомат может двигаться вдоль ленты
влево или вправо, читать содержимое ячеек и
записывать в ячейки буквы. Ниже схематично
нарисована машина Тьюринга, автомат которой
обозревает первую ячейку с данными.
Автомат каждый раз “видит” только
одну ячейку. В зависимости от того, какую букву ai
он видит, а также в зависимости от своего
состояния qj автомат может выполнять
следующие действия:
- · записать новую букву в обозреваемую
ячейку; - · выполнить сдвиг по ленте на одну
ячейку вправо/влево или остаться неподвижным; - · перейти в новое состояние.
То есть у машины Тьюринга есть три вида
операций. Каждый раз для очередной пары (qj,
ai) машина Тьюринга выполняет команду,
состоящую из трех операций с определенными
параметрами.
Программа для машины Тьюринга
представляет собой таблицу, в каждой клетке
которой записана команда.
Клетка (qj, ai)
определяется двумя параметрами — символом
алфавита и состоянием машины. Команда
представляет собой указание: куда передвинуть
головку чтения/записи, какой символ записать в
текущую ячейку, в какое состояние перейти машине.
Для обозначения направления движения автомата
используем одну из трех букв: “Л” (влево), “П”
(вправо) или “Н” (неподвижен).
После выполнения автоматом очередной
команды он переходит в состояние qm
(которое может в частном случае совпадать с
прежним состоянием qj). Следующую
команду нужно искать в m-й строке таблицы на
пересечении со столбцом al (букву al
автомат видит после сдвига).
Договоримся, что когда лента содержит
входное слово, то автомат находится против
какой-то ячейки в состоянии q1. В процессе
работы автомат будет перескакивать из одной
клетки программы (таблицы) в другую, пока не
дойдет до клетки, в которой записано, что автомат
должен перейти в состояние q0. Эти
клетки называются клетками останова. Дойдя
до любой такой клетки, машина Тьюринга останавливается.
Несмотря на свое простое устройство,
машина Тьюринга может выполнять все возможные
преобразования слов, реализуя тем самым все
возможные алгоритмы.
Пример. Требуется построить машину
Тьюринга, которая прибавляет единицу к числу на
ленте. Входное слово состоит из цифр целого
десятичного числа, записанных в
последовательные ячейки на ленте. В начальный
момент машина находится против самой правой
цифры числа.
Решение. Машина должна прибавить
единицу к последней цифре числа. Если последняя
цифра равна 9, то ее заменить на 0 и прибавить
единицу к предыдущей цифре. Программа для данной
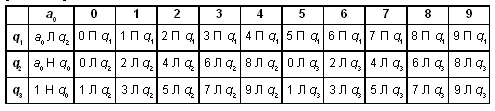
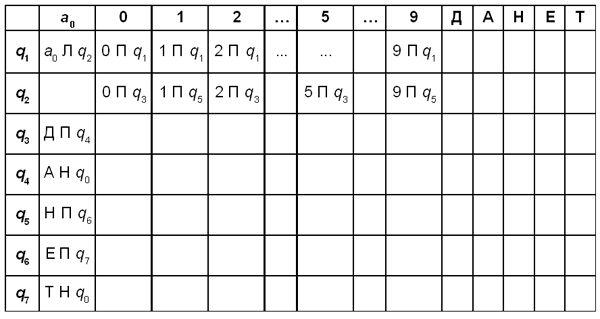
машины Тьюринга может выглядеть так:
В этой машине Тьюринга q1 —
состояние изменения цифры, q0 —
состояние останова. Если в состоянии ql
автомат видит цифру 0..8, то он заменяет ее на 1..9
соответственно и переходит в состояние q0,
т.е. машина останавливается. Если же он видит
цифру 9, то заменяет ее на 0, сдвигается влево,
оставаясь в состоянии ql. Так
продолжается до тех пор, пока автомат не встретит
цифру меньше 9. Если же все цифры были равны 9, то
он заменит их нулями, запишет 0 на месте старшей
цифры, сдвинется влево и в пустой клетке запишет
1. Затем перейдет в состояние q0, т.е.
остановится.
Практические задания
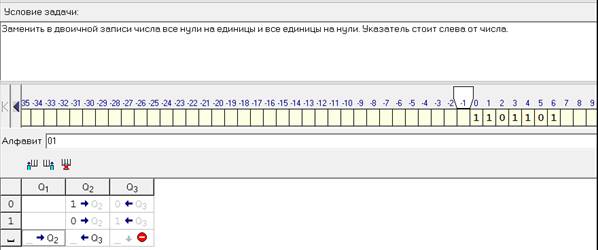
1. На ленте машины Тьюринга содержится
последовательность символов “+”. Напишите
программу для машины Тьюринга, которая каждый
второй символ “+” заменит на “–”. Замена
начинается с правого конца последовательности.
Автомат в состоянии q1 обозревает один
из символов указанной последовательности. Кроме
самой программы-таблицы, описать словами, что
выполняется машиной в каждом состоянии.
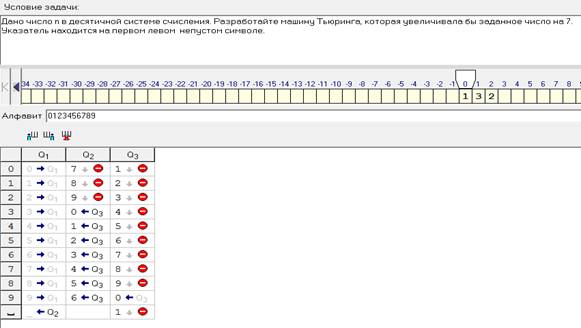
2. Дано число n в восьмеричной
системе счисления. Разработать машину Тьюринга,
которая увеличивала бы заданное число n на 1.
Автомат в состоянии q1 обозревает некую
цифру входного слова. Кроме самой
программы-таблицы, описать словами, что
выполняется машиной в каждом состоянии.
3. Дана десятичная запись натурального
числа n > 1. Разработать машину Тьюринга,
которая уменьшала бы заданное число n на 1.
Автомат в состоянии q1 обозревает
правую цифру числа. Кроме самой
программы-таблицы, описать словами, что
выполняется машиной в каждом состоянии.
4. Дано натуральное число n > 1.
Разработать машину Тьюринга, которая уменьшала
бы заданное число n на 1, при этом в выходном
слове старшая цифра не должна быть 0. Например,
если входным словом было “100”, то выходным
словом должно быть “99”, а не “099”. Автомат в
состоянии q1 обозревает правую цифру
числа. Кроме самой программы-таблицы, описать
словами, что выполняется машиной в каждом
состоянии.
5. Дан массив из открывающих и
закрывающих скобок. Построить машину Тьюринга,
которая удаляла бы пары взаимных скобок, т.е.
расположенных подряд “( )”.
Например, дано “) ( ( ) ( ( )”, надо
получить “) . . . ( ( ”.
Автомат в состоянии q1
обозревает крайний левый символ строки. Кроме
самой программы-таблицы, описать словами, что
выполняется машиной в каждом состоянии.
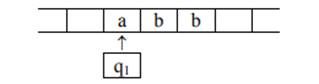
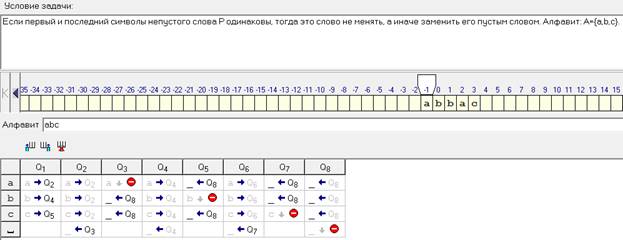
6. Дана строка из букв “a” и “b”.
Разработать машину Тьюринга, которая переместит
все буквы “a” в левую, а буквы “b” — в
правую части строки. Автомат в состоянии q1
обозревает крайний левый символ строки. Кроме
самой программы-таблицы, описать словами, что
выполняется машиной в каждом состоянии.
7. На ленте машины Тьюринга находится
число, записанное в десятичной системе
счисления. Умножить это число на 2. Автомат в
состоянии q1 обозревает крайнюю левую
цифру числа. Кроме самой программы-таблицы,
описать словами, что выполняется машиной в
каждом состоянии.
8. Даны два натуральных числа m и n,
представленные в унарной системе счисления.
Соответствующие наборы символов “|” разделены
пустой клеткой. Автомат в состоянии q1обозревает
самый правый символ входной последовательности.
Разработать машину Тьюринга, которая на ленте
оставит сумму чисел m и n. Кроме самой
программы-таблицы, описать словами, что
выполняется машиной в каждом состоянии.
9. Даны два натуральных числа m и n,
представленных в унарной системе счисления.
Соответствующие наборы символов “|” разделены
пустой клеткой. Автомат в состоянии q1
обозревает самый правый символ входной
последовательности. Разработать машину
Тьюринга, которая на ленте оставит разность
чисел m и n. Известно, что m > n.
Кроме самой программы-таблицы, описать словами,
что выполняется машиной в каждом состоянии.
10. На ленте машины Тьюринга находится
десятичное число. Определить, делится ли это
число на 5 без остатка. Если делится, то записать
справа от числа слово “да”, иначе — “нет”.
Автомат обозревает некую цифру входного числа.
Кроме самой программы-таблицы, описать словами,
что выполняется машиной в каждом состоянии.
Решения заданий
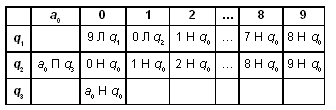
Задача 1
В состоянии q1 машина ищет
правый конец числа, в состоянии q2 —
пропускает знак “+”, при достижении конца
последовательности — останавливается. В
состоянии q3 машина знак “+” заменяет
на знак “–”, при достижении конца
последовательности она останавливается.
Задача 2
Решение этой задачи аналогично
рассмотренному выше примеру.
Задача 3
Состояние q1 — уменьшаем
младшую (очередную) цифру на 1. Если она не равна
нулю, то после уменьшения сразу — останов, если
же младшая цифра равна 0, то вместо нее пишем 9,
смещаемся влево и вновь выполняем вычитание. В
клетку [a0, q1] машина Тьюринга
никогда не попадет, поэтому ее можно не
заполнять.
Задача 4 (усложнение задачи 3)
Состояние q1 — уменьшаем
младшую (очередную) цифру на 1. Если она больше 1,
то после уменьшения — сразу останов, если же
младшая цифра равна 0, то вместо нее пишем 9,
смещаемся влево и вновь выполняем вычитание.
Если уменьшаемая цифра равна 1, то вместо нее
пишем 0 и переходим в состояние q2.
Состояние q2 — после записи
“0” в каком-либо разряде надо проанализировать,
не является ли этот ноль старшей незначащей
цифрой (т.е. не стоит ли слева от него в записи
выходного слова a0).
Состояние q3 — если
записанный “0” является старшей незначащей
цифрой, то его надо удалить из записи выходного
слова.
Те клетки, в которые машина Тьюринга
никогда не попадает, оставляем пустыми.
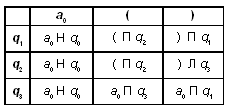
Задача 5
Состояние q1: если встретили
“(”, то сдвиг вправо и переход в состояние q2;
если встретили “a0”, то останов.
Состояние q2: анализ символа
“(” на парность, в случае парности должны
увидеть “)”. Если парная, то возврат влево и
переход в состояние q3.
Состояние q3: стираем сначала
“(”, затем “)” и переходим в q1.
Задача 6
Решение этой задачи обычно вызывает у
школьников затруднение. При разборе решения этой
задачи можно пойти, например, следующим путем.
Рассмотрите со школьниками следующие
варианты входных слов и попросите их
сформулировать, что должна делать машина
Тьюринга, каков внешний вид выходного слова, чем
с точки зрения машины Тьюринга эти варианты
различаются:
aaa —> выходное слово совпадает с
входным, просматриваем входное слово до тех пор,
пока оно не заканчивается.
a —> выходное слово совпадает с
входным, просматриваем входное слово до тех пор,
пока оно не заканчивается.
bbb —> выходное слово совпадает с
входным, просматриваем входное слово до тех пор,
пока оно не заканчивается.
b —> выходное слово совпадает с
входным, просматриваем входное слово до тех пор,
пока оно не заканчивается.
ab —> выходное слово совпадает с
входным, просматриваем входное слово до тех пор,
пока оно не заканчивается.
Результат обсуждения. Машина
Тьюринга должна “понимать”, по цепочке каких
букв она идет, т.е. у нее должно быть как минимум
два состояния. Пусть состояние q1 —
движение по цепочке из букв “a”, а q2
— состояние движения по цепочке из букв “b”.
Заметим, что цепочка может состоять и из одной
буквы. Если мы дошли до конца строки в состоянии q1
или q2, т.е. встретили a0, машина
должна остановиться, мы обработали всю строку.
Рассмотрим следующие варианты входных
слов:
bba —> abb
bbbaab —> aabbbb
aabbbaab —> aaaabbbb
Результат обсуждения. Первый
вариант входного слова можно последовательно
обработать следующим образом: bba —> bbb
—> вернуться к левому концу цепочки из букв “b”
—> abb (заменить первую букву в этой цепочке
на “a”). Для выполнения этих действий нам
потребуется ввести два новых состояния и, кроме
того, уточнить состояние q2. Таким
образом, для решения этой задачи нам нужно
построить машину Тьюринга со следующими
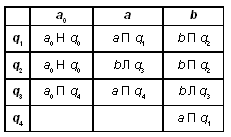
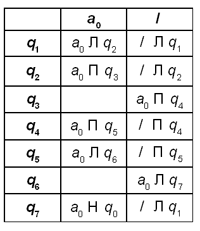
состояниями:
q1 — идем вправо по цепочке
букв “a”. Если цепочка заканчивается a0,
то переходим в q0; если заканчивается
буквой “b”, то переходим в q2;
q2 — идем вправо по цепочке
букв “b”, если цепочка заканчивается a0,
то переходим в q0; если заканчивается “a”,
то заменяем букву “a” на “b”, переходим в
состояние q3 (цепочку вида заменили на цепочку вида
);
q3 — идем влево по цепочке
букв “b” до ее левого конца. Если встретили a0
или “a”, то переходим в q4;
q4 — заменяем “b” на “a”
и переходим в q1 (цепочку вида заменяем на цепочку вида
.
Задача 7
состояние q1 — поиск правой
(младшей) цифры числа;
состояние q2 — умножение
очередной цифры числа на 2 без прибавления 1
переноса;
состояние q3 — умножение
очередной цифры числа на 2 с прибавлением 1
переноса.
Задача 8
Машина Тьюринга для этой программы
выглядит тривиально просто — в ней всего одно
состояние. Такая машина Тьюринга выполняет
следующие действия: стирает самый правый штрих,
ищет разделитель (пустую ячейку) и в эту пустую
ячейку помещает штрих, тем самым сформирована
непрерывная последовательность штрихов длины n
+ m.
Однако, как ни странно, решение этой
задачи вызывает большие трудности. Очень часто
ученики строят машину Тьюринга, которая
выполняет циклические действия: последовательно
пододвигают правые n штрихов к левым.
В этом случае их программа выглядит
следующим образом:
состояние q1 — поиск
разделителя;
состояние q2 — передвинули
штрих;
состояние q3 — проверка
на конец (все ли штрихи передвинули).
На примере этой задачи четко видно, как
часто дети пытаются решить задачу уже знакомыми
способами. Мне кажется, что, предлагая ученикам
задачи на составление машин Тьюринга, мы
развиваем способность к нахождению необычных
решений, развиваем способность творчески думать!
Задача 9
Эта задача кажется школьникам
достаточно легкой, но трудности возникают с
остановом машины Тьюринга. Ниже приведен один из
возможных вариантов машины Тьюринга для этой
задачи.
Идея решения (условие останова). На
ленте есть два исходных массива штрихов.
Штрихи начинаем стирать с левого конца
массива m. И поочередно стираем самый левый
штрих в массиве m и самый правый штрих в
массиве n. Но прежде чем стереть правый штрих
в массиве n, проверяем, единственный он (т.е.
последний, который надо стереть) или нет.
Опишем сначала состояния машины
Тьюринга, которые необходимы для решения нашей
задачи, а затем составим программу-таблицу.
Состояние q1 — поиск
разделителя между массивами штрихов при
движении справа налево;
состояние q2 — поиск левого
штриха в массиве m;
состояние q3 — удаление
левого штриха в массиве m;
состояние q4 — поиск
разделителя при движении слева направо;
состояние q5 — поиск правого
штриха в массиве n;
состояние q6 — проверка
единственности этого штриха в массиве n, т.е.
определяем, был ли он последним;
состояние q7 — если он был
последним, то останов, иначе переход на новый
цикл выполнения алгоритма.
Задача 10
При решении этой задачи следует
обратить внимание на правильное выписывание
алфавита:
A = {a0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, Д, А,
Н, Е, Т}.
Состояние q1 — поиск
правого конца числа;
состояние q2 — анализ
младшей цифры числа; если она равна “0” или “5”,
т.е. число делится на 5, то переход в состояние q3,
иначе переход в состояние q5;
состояние q3 — запись
буквы “Д” справа от слова на ленте;
состояние q4 — запись
буквы “А” справа от слова и останов машины;
состояние q5 — запись
буквы “Н” справа от слова;
состояние q6 — запись
буквы “Е” справа от слова;
состояние q7 — запись
буквы “Т” справа от слова и останов машины.
Свойства машины Тьюринга как
алгоритма
На примере машины Тьюринга хорошо
прослеживаются свойства алгоритмов. Попросите
учащихся показать, что машина Тьюринга обладает
всеми свойствами алгоритма.
Дискретность. Машина Тьюринга
может перейти к (к + 1)-му шагу только после
выполнения к-го шага, т.к. именно к-й шаг
определяет, каким будет (к + 1)-й шаг.
Понятность. На каждом шаге в ячейку
пишется символ из алфавита, автомат делает одно
движение (Л, П, Н), и машина Тьюринга переходит в
одно из описанных состояний.
Детерминированность. В каждой
клетке таблицы машины Тьюринга записан лишь один
вариант действия. На каждом шаге результат
определен однозначно, следовательно,
последовательность шагов решения задачи
определена однозначно, т.е. если машине Тьюринга
на вход подают одно и то же входное слово, то
выходное слово каждый раз будет одним и тем же.
Результативность. Содержательно
результаты каждого шага и всей
последовательности шагов определены однозначно,
следовательно, правильно написанная машина
Тьюринга за конечное число шагов перейдет в
состояние q0, т.е. за конечное число шагов
будет получен ответ на вопрос задачи.
Массовость. Каждая машина Тьюринга
определена над всеми допустимыми словами из
алфавита, в этом и состоит свойство массовости.
Каждая машина Тьюринга предназначена для
решения одного класса задач, т.е. для каждой
задачи пишется своя (новая) машина Тьюринга.
ОТ РЕДАКЦИИ
Все приведенные в статье задачи можно
решить просто в тетради, начертив информационную
ленту и программу-таблицу. Но можно сделать этот
процесс более увлекательным и наглядным:
воспользоваться машинной реализацией —
интерпретатором машины Поста и машины Тьюринга
“Algo2000”, созданным Радиком Зартдиновым.
Программа обладает интуитивно понятным
интерфейсом, и требования у нее самые умеренные:
компьютер IBM PC AT 486 и выше, наличие операционной
системы Windows’95/98/NT.
Посмотрим в общих чертах, как работает
“Algo2000”.
В меню программы выберем пункт Интерпретатор
и укажем, с какой машиной мы хотим работать (в
нашем случае это “машина Тьюринга”).
Перед нами появится поле машины
Тьюринга.
Теперь необходимо задать внешний
алфавит, т.е. в строке Внешний алфавит
указать, какие символы в него входят (если строка Внешний
алфавит не видна, нужно выбрать пункт меню Вид
| Внешний алфавит). Каждый символ можно указать
только один раз. После окончания ввода внешнего
алфавита формируется первый столбец таблицы: он
заполняется символами внешнего алфавита в том же
порядке. При редактировании внешнего алфавита
автоматически изменяется таблица: вставляются,
удаляются или меняются местами строки.
Не забудем, что нужно как-то расставить
символы внешнего алфавита по секциям ленты
(можно все секции оставить пустыми) и поставить
каретку против одной из секций, т.е. надо задать
программу и некоторое состояние машины.
Теперь можно приступить
непосредственно к записи алгоритма решения
задачи. Он задается в виде таблицы: в каждый
столбец верхней строчки заносятся символы
внутреннего алфавита, в каждую строчку первого
столбца — символы внешнего алфавита. В ячейках
на пересечении других столбцов и строчек
помещаются команды. Если на пересечении
какой-либо строки и какого-либо столбца мы
получим пустую клетку, то это означает, что в
данном внутреннем состоянии данный символ
встретиться не может.
Например, мы составляем алгоритм
нахождения разности двух целых положительных
чисел (в десятичной системе счисления), если
известно, что первое число больше второго, а
между ними стоит знак минус.
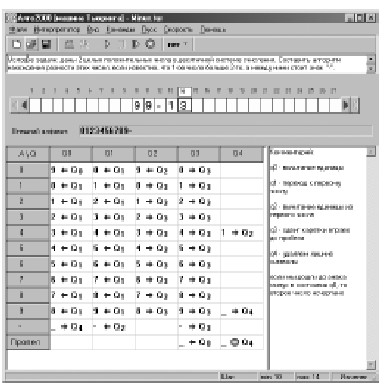
Поле программы будет выглядеть так:
Формат команды в каждой ячейке — aKq.
Здесь:
a — новое содержание текущей ячейки (новый символ
внешнего алфавита, который заносится в текущую
ячейку), K — команда лентопротяжного механизма
машины Тьюринга (влево, вправо, стоп), q — новое
внутреннее состояние машины Тьюринга.
Кнопка запустит
программу. Если выполнение не было
приостановлено, то оно всегда начинается с
нулевого внутреннего состояния Q0.
Программу можно выполнить по шагам.
Для этого нажмите на кнопку на панели инструментов (если
кнопки не видны, нужно выбрать пункт меню Вид |
Панель инструментов) или выберите в главном
меню Пуск | Пошагово. Если необходимо
полностью прервать выполнение программы, то это
можно сделать с помощью кнопки на панели
инструментов или с помощью главного меню (Пуск |
Прервать). Пункт меню Скорость позволяет
регулировать скорость выполнения программы.
Выполнение программы будет идти до тех
пор, пока не встретится команда “Стоп” или не
возникнет какая-нибудь ошибка.
При возникновении вопросов в ходе работы с
программой-интерпретатором обращайтесь к
справочному файлу Algo2000.hlp. Его, так же, как и
саму программу “Algo2000”, можно найти на сайте
газеты “Информатика” https://inf.1sept.ru
в разделе “Download”.
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МАШИНЫ ТРЬЮРИНГА
§1. История создания машины Тьюринга
Алан Мэтисон Тьюринг ˗ английский математик, криптограф,
логик, оказавший огромное влияние на развитие информатики. Данный ученый родился
в 1912 году недалеко от Лондона и прожил достаточно короткую, внешне не очень
яркую, но чрезвычайно насыщенную практическими и интеллектуальными достижениями
жизнь.
Заслуги Алана Тьюринга по расшифровке немецких военных кодов,
которые спасли жизни сотен тысяч людей, во время Второй мировой войны были
проигнорированы. Однако официальные публичные извинения были принесены только спустя
55 лет после его смерти. Математика с его смертью лишилась одного из самых
ярких и оригинальных мыслителей. Алан М. Тьюринг не только решил одну из
труднейших математических проблем, а фактически он предложил намного большее –
новый метод решения математических задач (машину Тьюринга), который в конечном
счете привел к возникновению computer science и современных компьютеров.
Алан Тьюринг стоял у самых истоков искусственного интеллекта
и программирования. У данного ученого него не было учеников в общепринятом
смысле, но определенно можно утверждать, что любой программист или же человек,
непосредственно связанный с информатикой, даже не осознавая того, является
если и не учеником, но уж точно его последователем. Именем Алана Тьюринга
названа своего рода Нобелевская премия в области computer science , которая
называется премией Тьюринга. Данной награды удостаиваются те, кто внес
выдающийся вклад в эту область исследований.
Для решения любой
проблемы не надо думать, и уж тем более ˗
угадывать, именно к этому сводятся большинство исследований этого ученого, а достаточно
разработать определенный метод. Правильное решение можно будет получить гораздо
быстрее, если механически следовать этому порядку действий. Алан Тьюринг ввел
понятие «определительного метода», который позже получил название «алгоритм», а
так же разработал свои собственные логические ходы.
В 1936 году
этим ученым была построена логическая модель знаменитой машины, которая и
называется машиной Тьюринга. Необходимо заметить и то, что в те годы под словом
«Computer» подразумевался человек, проводящий однообразные вычисления по
определенным инструкциям. Например, так называли бухгалтеров, счетоводов. Идея
Алана Мэтисона Тьюринга состояла в том, что для проведения данных действий
присутствие человека не требуется.
Предыстория
создания этой работы связана с формулировкой Давидом Гильбертом на
Международном математическом конгрессе в Париже в 1900 году неразрешенных
математических проблем. Одной из них была задача доказательства
непротиворечивости системы аксиом обычной арифметики, которую Гильберт в
дальнейшем уточнил как «проблему разрешимости» – нахождение общего метода, для
определения выполнимости данного высказывания на языке формальной логики.
Статья
Тьюринга как раз и давала ответ на эту проблему – вторая проблема Гильберта
оказалась неразрешимой. Но значение статьи Тьюринга выходило далеко за рамки
той задачи, по поводу которой она была написана.
Приведем
характеристику этой работы, принадлежащую Джону Хопкрофту: «Работая над
проблемой Гильберта, Тьюрингу пришлось дать четкое определение самого понятия
метода. Отталкиваясь от интуитивного представления о методе как о некоем
алгоритме, т.е. процедуре, которая может быть выполнена механически, без
творческого вмешательства, он показал, как эту идею можно воплотить в виде
подробной модели вычислительного процесса. Полученная модель вычислений, в
которой каждый алгоритм разбивался на последовательность простых, элементарных
шагов, и была логической конструкцией, названной впоследствии машиной
Тьюринга».
Машина Тьюринга является достаточно простым вычислительным устройством.
Она состоит из ленты бесконечной длины, разделенной на ячейки,
и головки, которая перемещается вдоль ленты и способна читать и записывать
символы. Также у машины Тьюринга существует и такая характеристика, как состояние,
которое может выражаться целым числом от нуля до некоторой максимальной
величины. В зависимости от состояния, машина может выполнить одно из трех
действий: записать символ в ячейку, передвинуться на одну ячейку влево или
вправо, а также установить внутреннее состояние.
Устройство машины
Тьюринга довольно просто, однако на ней можно выполнить практически любую
программу. Для выполнения всех этих действий предусмотрена
специальная таблица правил, в которой прописано, что нужно делать при
различных комбинациях текущих состояний и символов, прочитанных с ленты.
В 1947 году Алан Тьюринг
расширил определение, описав «универсальную машину Тьюринга». Позже для решения
определенных классов задач была введена ее разновидность, которая позволяла
выполнять не одну задачу, а несколько.
Машина Тьюринга может
решить любую проблему, которая может быть разбита на элементарные логические
шаги, но при наличии достаточного количества времени и памяти. Также важно
отметить, что конструкция этой машины не претендует на создание чего-то
координально нового.
Алан Мэтисон
Тьюринг высказал предположение, которое заключается в следующем: любой алгоритм
в интуитивном смысле данного слова может быть представлен эквивалентной машиной
Тьюринга. Это предположение более известно как тезис Черча–Тьюринга. Каждый
компьютер может моделировать машину Тьюринга (операции перехода и сравнения к
дркгой соседней ячейке, перезаписи ячеек с учетом изменения состояния машины).
Следовательно, автомат может моделировать алгоритмы в любом формализме, и из
этого тезиса следует, что все компьютеры (независимо от мощности, архитектуры и
т.д.) эквивалентны с точки зрения принципиальной возможности решения алгоритмических задач.
§2. Структура и такт работы машины Тьюринга
Машина Тьюринга (МТ)
состоит из двух частей – ленты и автомата (см. рис.1):
Рисунок 1.
Лента в машине Тьюринга
используется для хранения информации. Она является бесконечной в обе стороны и
разбита на клетки, которые никак не именуются и не номеруются. В свою очередь,
в каждой клетке может быть записан один символ или же не записано ничего. Содержимое
клетки может меняться, то есть в неё можно записать другой символ или стереть
находящийся там символ.
Пустое содержимое клетки
назовем символом «пусто» и обозначим знаком («лямбда»).
В связи с этим изображение ленты, показанное на рисунке 1 справа, такое же, как
и на рисунке слева. Данное соглашение удобно тем, что операцию стирания символа
в некоторой клетке можно рассматривать как запись в эту клетку символа , поэтому вместо длинной фразы
«записать символ в клетку или стереть находящийся там символ» можно говорить
просто «записать символ в клетку».
Автомат является активной
частью Машины Тьюринга. В каждый момент он размещается под одной из клеток
ленты и видит её содержимое. Такая клетка называется видимой, а находящийся в
ней символ – видимым символом. Содержимое же соседних и других клеток автомат
не видит. Кроме того, в каждый момент автомат находится в одном из состояний, которые
будем обозначать буквой номерами
.
Находясь в каком-либо из
состояний, автомат выполняет некоторую определённую операцию, например,
перемещается направо по ленте, заменяя все символы на
, а, в свою очередь, находясь в
другом состоянии – другую операцию.
Пару из видимого символа и текущего состояния автомата
будем называть конфигурацией и
обозначать .
Автомат может
выполнять три элементарных действия:
1. записывать в видимую клетку новый
символ, (то есть менять содержимое других клеток автомат не может);
2. сдвигаться на одну клетку вправо или
влево (то есть «перепрыгивать» сразу через несколько клеток автомат не может);
3. переходить в новое состояние.
Никакие другие действия
автомат выполнять не умеет, поэтому другие, наиболее сложные операции так или
иначе должны сводиться к этим трём элементарным действиям.
Такт работы машины
Тьюринга (МТ) работает по шагам (тактами), которые выполняются один за другим.
На каждом такте автомат машины Тьюринга выполняет три четко определенных действия,
причем обязательно в указанном порядке:
1. записывает некоторый символ в видимую клетку (в частности,
может быть записан тот же символ, что и был в ней, тогда содержимое этой клетки
не меняется);
2. сдвигается на одну клетку влево
(обозначение –, от left), либо на одну
клетку вправо (обозначение – , от right),
либо остается неподвижным (обозначение – ).
3. переходит в некоторое состояние (в частности, может остаться в
прежнем состоянии).
Формально действия одного
такта будем записывать в виде тройки: ,
,
,
где конструкция с квадратными скобками означает возможность записи в этом месте
любой из букв или
.
Например, такт *, означает запись символа * в
видимую клетку, сдвиг на одну клетку влево и переход в состояние . Запись такта для конфигурации
называют командой машины Тьюринга.
На примере машины
Тьюринга хорошо прослеживаются свойства алгоритмов.
Можно выделить
следующие свойства машины Тьюринга как алгоритма:
1. Дискретность.
Машина Тьюринга (МТ)
может перейти к (k+1) шагу только
после выполнения каждого шага, так как именно каждый шаг определяет, каким
будет, в свою очередь, (k+1)-й
шаг;
2. Понятность.
На каждом шаге в ячейку
записывается один символ, автомат делает одно движение (L, R, N), и машина
Тьюринга таким образом переходит в одно из описанных состояний;
3. Детерминированность.
В каждой ячейке таблицы
машины Тьюринга записан лишь один вариант действия. На каждом шаге результат
определен однозначно, следовательно, последовательность шагов решения задачи
определена однозначно, то есть, если машине Тьюринга на вход подают одно и то
же входное слово, то выходное слово каждый раз будет одним и тем же;
4. Результативность.
Содержательно результаты
всей последовательности шагов и каждого шага определены однозначно,
следовательно, правильно написанная машина Тьюринга за конечное число шагов
перейдет в состояние , то есть за конечное число шагов
будет получен ответ на вопрос задачи;
5. Массовость.
Каждая машина Тьюринга
определена над всеми доступными словами из алфавита, именно в этом и состоит
свойство массовости. Каждая машина Тьюринга предназначена для решения одного
класса задач, то есть для каждой задачи пишется своя, новая машина Тьюринга.
§3. Программа для машины Тьюринга и правила ее выполнения
Машина Тьюринга сама по
себе не совершает никаких операций. Для того чтобы увидеть ее работу,
необходимо написать программу для данной машины. Эта программа записывается в
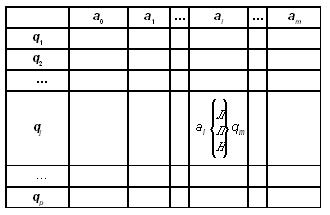
виде следующей таблицы:
Таблица 1. Программа для МТ.
|
|
|
… |
|
… |
|
|
|
|
|
|||||||
|
… |
|||||||
|
|
|
||||||
|
… |
|||||||
|
|
В данной таблице слева
перечисляются все состояния, в которых может находиться автомат, а сверху, в
свою очередь, все символы (в том числе и ),
которые автомат может видеть в ленте. Какие именно состояние и символы
указывать в таблице определяет сам автор программы. На пересечениях же, то есть
в ячейках таблицы, указываются те акты, которые непосредственно должен
выполнить автомат, когда он видит на ленте соответствующий символ и находится в
соответствующем состоянии.
В целом таблица полностью
определяет действия машины Тьюринга при всех возможных конфигурациях и, таким
образом, можно сказать, что полностью задает поведение машины Тьюринга.
Описать алгоритм в виде машины Тьюринга тем самым значит предъявить такую таблицу.
Необходимо сделать
следующее замечание: очень часто машину Тьюринга определяют как машину, которая
состоит из ленты, автомата и программы, именно поэтому при разных программах
получаются разные машины Тьюринга. Однако, будем считать, что машина Тьюринга
одна (в духе современных компьютеров), но она может выполнять различные
программы.
Правила выполнения
программы:
К моменту начала
выполнения программы машина Тьюринга находится в начальной конфигурации. Данная
начальная конфигурация определена определенным образом.
Во-первых, на ленте записано входное слово, к которому
будет применена программа. Входное слово, в свою очередь, является конечной
последовательностью символов, записанных в соседних клетках ленты. Внутри
входного слова пустых клеток быть не должно, а справа и слева от него должны
быть только пустые клетки. Пустое входное слово означает, что все клетки ленты
пусты.
Во-вторых, автомат
установлен в состояние , которое указано в
таблице первым, и размещен под его первым (самым левым) символом входного
слова:
Рисунок 2.
Если входное слово пустое, то автомат
может смотреть в любую клетку, так как они все пусты.
После данных
предварительных действий начинается выполнение программы. Так как автомат
находится в состоянии , то в таблице
отыскивается ячейка на пересечении первой строки и того столбца, который
соответствует первому символу входного слова (это необязательно должен быть левый
столбец таблицы), и выполняется такт, указанный в этой ячейке. В результате
автомат окажется в новой конфигурации. Далее такие же действия повторяются,
только уже для новой конфигурации: в таблице отыскивается ячейка, которая
соответствует состоянию и символу этой конфигурации, и выполняется такт из этой
ячейки. И так далее.
Для того, чтобы
выполнялось завершение программы, введем понятие такта остановки.
Такт остановки ничего не
меняет: автомат записывает в видимую клетку тот же символ, что и был в ней
раньше, не сдвигается и остается в прежнем состоянии, то есть это такт для конфигурации
. Таким образом, попав на такт
остановки, машина Тьюринга останавливается, завершая свою работу.
Вообще говоря, возможны
два исхода работы машины Тьюринга над входным словом:
1. Первый исход (считается «хорошим»):
При данном исходе в
какой-то момент машина Тьюринга останавливается, то есть попадает на такт
остановки. В данном случае говорят, что машина Тьюринга применима к заданному
входному слову. А то слово, которое к этому моменту получено в ленте, считается
входным словом, то есть результатом работы машины Тьюринга, ответом.
Будем считать, что в
момент остановки должны выполняться следующие условия:
a) внутри выходного слова не должно быть
пустых клеток . Так же необходимо отметить, что во время выполнения программы
внутри обрабатываемого слова пустые клетки могут быть, но в конце их уже не
должно остаться;
b) автомат обязан остановиться под одним
из символов выходного слова (под каким именно – не играет роли), а если слово
пустое – под любой клеткой ленты.
2. Второй исход (считается «плохим»):
При данном исходе машина
Тьюринга зацикливается,
никогда не попадая на такт остановки. В качестве примера можно привести тот
случай, когда автомат на каждом шаге сдвигается вправо и потому не может остановиться,
т.к. лента 7 бесконечна. В данном случае говорят, что машина Тьюринга
неприменима к заданному входному слову. Никакого результата при таком исходе
быть не может. Необходимо
отметить, что один и тот же алгоритм, то есть программа машины Тьюринга, может
быть применим к одним входным словам, то есть останавливаться, и неприменимым к
другим, то есть зацикливаться. Таким образом, применимость или же
неприменимость зависит не только от самого алгоритма, но и от входного слова.
Алгоритм должен останавливаться
на тех словах, которые относятся к допустимым исходным данным решаемой задачи,
для которых задача является осмысленной. Однако, на ленте могут быть записаны
любые входные слова, в том числе и те, для которых задача не имеет смысла. На
таких словах поведение алгоритма не фиксируется, он может остановиться (при
любом результате), а может и зациклиться.
§4. Примеры на составление программ для машины Тьюринга
Для сокращения
формулировки задач введем следующие обозначения:
1. Буквой будем
обозначать входное слово;
2. Буквой будем
обозначать алфавит входного слова, то есть набор тех символов, из которых может
состоять . Однако, необходимо отметить, что
в выходных и промежуточных словах могут появляться и другие символы.
Пример 1:
Перемещение автомата.
Замена символов.
Пусть , а
˗ это непустое слово. Значит
˗ это последовательность из десятичных цифр, то есть
запись целого неотрицательного числа в десятичной системе. Необходимо получить
на ленте запись числа, которое на 1 больше числа .
Решение:
Для решения данной задачи
необходимо выполнить ряд действий:
1. Перегнать автомат под последнюю цифру
числа;
2. Если это цифра от 0 до 8, то заменить
ее цифрой на 1 больше и остановиться;
Рисунок 3.
3. Если же это цифра 9, то заменить ее
на 0 и сдвинуть автомат к предыдущей цифре, после чего таким же способом
увеличить на 1 эту предпоследнюю цифру;
Рисунок 4.
4. Особый случай составляет тот, когда в
имеются только девятки (например,
99). В данном случае автомат будет сдвигаться влево, заменяя девятки на нули, и
в конце концов окажется под пустой клеткой. Тогда именно в эту пустую клетку
необходимо записать 1 и остановиться (ответом будет 100):
Рисунок 5.
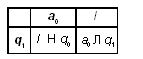
В виде программы для МТ эти действия
описываются следующим образом:
Рисунок 6.
Пояснения: ˗
это состояние, в котором автомат переходит под последнюю цифру числа. Для этого он постоянно движется
вправо, не меняя видимые цифры и оставаясь в том же состоянии. Однако,
определить последнюю цифру автомат может, только попав на соседнюю пустую
клетку. Поэтому, дойдя до пустой клетки, он возвращается под последнюю цифру и
переходит в состояние .
˗ это состояние, в котором автомат прибавляет 1 к той
цифре, которую в данный момент видит. Сначала это последняя цифра, если она
находится в диапазоне от 0 до 8, то он прибавляет к ней 1 и останавливается,
если нет, то возвращается и проверяет предпоследнюю цифру и т.д.
Пример 2:
Пусть . Необходимо перенести первый
символ непустого слова в его конец.
Например,
Рисунок 7.
Решение:
Для решения данной задачи
необходимо выполнить ряд следующих действий:
1. На
первом шаге необходимо запомнить первый символ слова ,
а затем стереть данный символ.
2. На
втором шаге необходимо перегнать автомат вправо под первую пустую клетку за и записать в неё символ, который
был запомнен на первом шаге.
Для того, чтобы запомнить
первый символ необходимо использовать различные состояния автомата. Если первым
символом оказался символ , то необходимо
перейти в состояние , в котором автомат бежит вправо и записывает в конце
. Если же первым символом оказался
символ , тогда необходимо перейти в состояние
, где происходят все те же действия, только
в конце записывается символ . Если же, в свою очередь, первый символ был
, тогда необходимо перейти в состояние
, в котором автомат дописывает в
конце слова символ . Следовательно, фиксируется
переводом автомата в разные состояния именно то, каким был первый символ. Это один
из типичных приёмов при программировании на машине Тьюринга.
С учетом всего
вышеприведенного программа будет выглядеть следующим образом:
Таблица 2. Программа для задачи 2.
|
|
|
|
|
комментарий |
|
|
|
|
|
|
|
Анализ 1-го символа, удаление его, разветвление |
|
|
|
|
|
|
Запись |
|
|
|
|
|
|
Запись |
|
|
|
|
|
|
Запись |
Так же можно рассмотреть
поведение данной программы на входных словах, которые содержат не более одного
символа.
Если входное слово пусто
(такое слово называется «плохим» для задачи), то в данном случае программа
зациклится, то есть автомат, находясь в состоянии и
все время попадая на пустые клетки, будет двигаться бесконечно вправо.
Если же входное слово
оказывается равным только одному символу, то в таком случае автомат сотрет
данный символ, сдвинется на одну клетку вправо и запишет в нее этот символ:
Рисунок 8.
Таким образом, можно
сказать, что в том случае, если слово состоит из одного символа, то оно просто
сдвинется на одну клетку вправо. Это допустимо, так как клетки не нумерованы.
Именно поэтому местоположение слова в ленте никак не фиксируется и перемещение
слова вправо или влево относительно исходного положения заметить невозможно. В
связи с данной особенностью совсем необязательно, чтобы выходное слово
находилось там же, где и находилось входное. Результат может оказаться правее
или левее этого места.
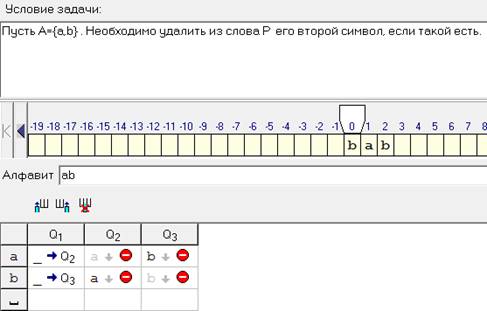
Пример 3:
Пусть . Необходимо удалить из слова
его второй символ, если такой
есть.
Решение:
С первого взгляда на
данную задачу, кажется, что решить ее довольно просто: для этого нужно сдвинуть
автомат под клетку со вторым символом и затем, после проделанного, очистить
данную клетку:
Рисунок 9.
Однако, необходимо
сказать, что внутри входного слова не должны находиться пустые клетки. Именно поэтому,
после удаления второго символа необходимо «сжать» слово, тем самым перенеся
первый символ на одну клетку вправо. Для этого автомат должен вернуться к
первому символу, запомнить его и стереть, а затем, опять сдвинувшись вправо
записать его в ячейку, где находился второй символ. Однако заметим то, что
начальный шаг вправо ко второму символу, чтобы его стереть, и последующий
возврат к первому символу являются лишними действиями, так как нет разницы
между переносом первого символа в пустую клетку и клетку с каким-то символом.
Именно поэтому необходимо зразу запомнить первый символ, стереть его и записать
вместо второго символа:
Рисунок 10.
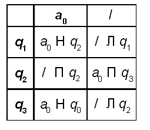
В виде программы для
машины Тьюринга это можно записать следующим образом:
Таблица 3. Программа для задачи 3.
|
|
|
|
комментарий |
|
|
|
|
|
|
Анализ и удаление первого символа |
|
|
|
|
|
Замена второго символа на |
|
|
|
|
|
Замена |
Пример 4.
Пусть .
Если является непустым словом, то
необходимо за его первым символом вставить символ .
Решение:
Понятно, что между вторым
и первым символами слова необходимо
освободить ячейку для нового символа . Для этого на
одну позицию влево нужно перенести первый символ (но на старом месте его можно
пока не удалять), а далее, вернувшись на прежнее место, записать символ :
Рисунок 11.
Перенос символа на одну позицию влево схож с переносом
символа вправо. Так же необходимо отметить, что в состояниях автомат может видеть только пустую
клетку, а в состоянии он видит первый символ входного
слова, но никак не пустую клетку.
В виде программы для машины Тьюринга данную задачу можно
записать следующим образом:
Таблица 4. Программа для примера 4.
|
|
|
|
|
комментарий |
|
|
|
|
|
|
|
Анализ первого символа для переноса |
|
|
|
|
|
|
Приписать |
|
|
|
|
|
|
Приписать |
|
|
|
|
|
|
Приписать |
|
|
|
|
|
|
Заменить бывший первый символ на |
Пример 5:
Пусть алфавит состоит из
следующего набора символов: . Необходимо
удалить из слова все вхождения символа
, если такие имеются.
Решение:
В машине Тьюринга довольно сложно
реализуются удаления символов из слов и вставки символов в слова. Поэтому иногда проще не сжимать или
раздвигать входное слово, а формировать выходное слово в другом, свободном
месте ленты.
Конкретно необходимо
выполнить следующий ряд действий:
1. Выходное слово строится справа от
входного. Чтобы разграничить эти слова, необходимо отделить их некоторым
вспомогательным символом, например знаком =, который отличен от всех символов
алфавита . На ленте могут быть записаны не только символы из
алфавита входного слова.
2. После этого необходимо вернуться к
началу входного слова:
Рисунок 12.
3. На данном этапе нужно перенести в
цикле все символы входного слова, кроме символа ,
вправо за знак равенства в формируемое выходное слово.
Для этого необходимо проанализировать
первый символ входного слова. Если это символ ,
то стираем его и переходим к следующему символу. Если же первый символ ˗ это символ или
, тогда нужно стереть его и
«пройти» вправо до первой пустой клетки , куда и записать данный символ.
Рисунок 13.
Далее необходимо
вернуться налево к тому символу, который стал первым во входном слове, и
повторить те же самые действия, но уже по отношению к этому символу.
Рисунок 14.
4. Данный цикл завершается, когда при
возврате налево в качестве первого символа появляется знак равенства. Это
признак того, что полностью просмотрено входное слово и перенесены все его
символы, которые отличны от , в формируемое
справа выходное слово. Этот знак необходимо стереть, сдвинуться вправо под
выходное слово и остановиться.
Рисунок 15.
С учётом всего сказанного
и строится программу для машины Тьюринга. При этом необходимо отметить, что
помимо символов в процессе решения
задачи на ленте появляется знак равенства, поэтому в таблице должен быть
предусмотрен столбец и для этого знака.
Таблица 5. Программа для примера 5.
|
|
|
|
= |
|
комментарий |
|
|
|
|
|
|
|
|
Записать справа знак = |
|
|
|
|
|
|
|
Влево к первому символу слова |
|
|
|
|
|
|
|
Анализ и удаление его, разветвление |
|
|
|
|
|
|
|
Запись |
|
|
|
|
|
|
|
Запись |
§5. Примеры решения задач
Пример 1:
Заменить в двоичной
записи числа все нули на единицы и все единицы на нули. Указатель стоит слева
от числа.
Решение:
Рисунок 16.
Пример 2:
Дано три числа,
разделенные пробелами. Необходимо пробелы, разделяющие данные числа заменить на
запятые. Указатель стоит на первом левом непустом символе.
Решение:
Рисунок 17.
Пример 3:
Дано число n в десятичной системе счисления.
Разработайте машину Тьюринга, которая увеличивала бы заданное число на 7. Указатель
находится на первом левом непустом символе.
Решение:
Рисунок 18.
Пример 4:
Пусть . Если первый и последний символы
слова совпадают, то данное слово не
менять, а иначе заменить то слово пустым символом.
Решение:
Рисунок 19.
Пример 5:
Пусть . Необходимо удалить
из слова его второй символ, если такой
есть.
Решение:
Рисунок 20.
Пример 6:
Пусть . Если
˗ непустое слово, то
необходимо за его первым символом вставить символ .
Решение:
Рисунок 21.
Пример 7:
Пусть .
Необходимо вставить в слово символ
за первым символом
, если такой есть.
Решение:
Рисунок 22.
Пример 8:
Пусть .
Необходимо перенести первый символ непустого слова в
его конец.
Решение:
Рисунок 23.
Заключение
Машина Тьюринга ˗ это строгое математическое
построение, математический аппарат, созданный для решения определенных задач.
Данная тема занимает весомое место в школьном курсе информатики. Для
учителя является важным то, что данный вопрос может изучаться в 8-11 классах в
рамках темы «Информационные процессы. Обработка информации», на факультативных
занятиях, в системе дополнительного образования.
Подводя итоги
проделанного, необходимо отметить, что в данной работе удалось:
охарактеризовать специфику работы машины Тьюринга, определить основные понятия,
относящиеся к данной теме, рассмотреть особенности работы машины Тьюринга с
помощью практических заданий.
Во введении
курсовой работы были обозначены цели и задачи, актуальность данной темы, а так
же причины создания такого математического аппарата, как машина Тьюринга. В
первом параграфе данной работы был приведен краткий исторический очерк о
создании машины Тьюринга. Во втором параграфе были изложены структура работы
машины Тьюринга а так же ее такт. В третьем параграфе рассмотрена
непосредственно программа для данной машины и, соответственно, правила ее
выполнения. В четвертом и пятом параграфах, в свою очередь, приводятся
практические задания, касающиеся данной темы.
Таким образом, в ходе
работы были выполнены все поставленные задачи:
– найти
материал по данной теме в учебных и научных источниках;
–
проанализировать изученную литературу;
– изучить
историю создания машины Тьюринга;
– рассмотреть
структуру и такт работы машины Тьюринга;
–
проанализировать программу для МТ и правила ее выполнения;
– рассмотреть
различные примеры решения задач с помощью МТ;
– изложить
материал в форме курсовой работы.
А так же была
достигнута цель курсовой работы.
Список литературы
1. Бильгаева Н.Ц. Теория алгоритмов,
формальных языков, грамматик и автоматов. Улан-Удэ.: ВСГТУ, 2000. 51 с.
2. Брауэр В. Введение в теорию конечных
автоматов. М.: Радио и связь, 1987. 357 с.
3. Варпаховский
Ф.Л.
4. Гэри М.
Вычислительные машины и труднорешаемые задачи. М.: ЦНИИ Электроника, 2016. 519
с.
5. Игошин В.И. Математическая логика и
теория алгоритмов. М.: Академия, 2008. 448 с.
6. Ильиных А.П. Теория алгоритмов:
учебное пособие. Екатеринбург.: Уральский государственный университет, 2006.
149 с.
7. Карпов Ю.Г. Теория автоматов. СПб.:
Питер, 2003. 208 с.
8. Крупский В.Н. Теория алгоритмов. М.:
Академия, 2009. 320 с.
9. Крючкова Е.Н. Теория алгоритмов. М.:
Статистика, 2000. 270 с.
10. Петцольд
Чарльз. Классика программирования. Путешествие по исторической статье Тьюринга
о вычислимости и машинах Тьюринга. М.: Академия, 2014. 440 с.
11. Рассел
Джесси. Машина Тьюринга. М.: VSD, 2012.
137 с.
12.
Рощин А.Г., Половов Р.М.
Теория автоматов. Тексты лекций. М.: МГТУ ГА, 2001. 76 с.
13. Савельев А.Я. Основы информатики:
Учебник для вузов. М.: Издательство МГТУ им. Баумана, 2001. 328 с
14. Фалина
И.Н. Машина Тьюринга. М.: Академия, 2005. 53 с.
15. Фалевич Б.Я. Теория алгоритмов. М.: ИНФРА-М, 2006. 324 с.
16. Шеннон,
К.Э. Машина Тьюринга (часть 2). М.: Научное книгоиздательство, 2015. 520 с.
Скачано с www.znanio.ru