Машинная бесконечность как найти

Определяем машинный ноль, машинную бесконечность и машинный эпсилон

Доверять расчёту, сделанному на компьютере, без тени понимания того, как именно выполнен этот расчёт – одна из худший вещей, которые может допустить в своей работе инженер. К сожалению, уже нередки “специалисты”, которых не смущает ненулевой результат, полученный при умножении на ноль, или, напротив, ноль там, где теоретически нуля быть не должно.

Поэтому повторим в этой заметке несколько азбучных истин о представлении вещественных чисел в компьютере и правилах выполнения операций с ними.

В IBM-совместимой ЭВМ для вещественных чисел используется двоичная система счисления и принята форма представления чисел с плавающей точкой вида

x = m*2p, где мантисса m = ± (g1*2-1 +
g2*2-2 + ... +
gt*2-t),

g1, ..., gt – двоичные цифры, причём, g1=1, а целое значение p называется двоичным порядком. Количество цифр t, которое отводится для записи мантиссы, называется разрядностью мантиссы. Диапазон представления чисел в ЭВМ ограничен конечной разрядностью мантиссы и значением числа p.

Все представимые на ЭВМ вещественные числа x удовлетворяют неравенствам
0 < X0 ≤ |x| < X∞, где
X0 = 2-pmax+1,
X∞ = 2pmax, а значение pmax соответствует разрядности вычислительной системы.

Все числа, по модулю большие X∞, не представимы на ЭВМ и рассматриваются как машинная бесконечность. Все числа, по модулю меньшие X0, для компьютера не отличаются от нуля и рассматриваются как машинный ноль. Машинным эпсилон εM называется относительная точность ЭВМ, то есть граница относительной погрешности представления вещественных чисел. Можно показать, что εM ≈ 2-t. Пусть
x* = m*2p. Тогда граница абсолютной погрешности представления этого числа равна Δ(x*) ≈ 2-t-1*2p. Поскольку 1/2≤m<1, то величина относительной погрешности представления оценивается как
δ(x*) ≈ Δ(x*) / |x*| ≈ (2-t-1*2p) / (m*2p) = 2-t-1 / m ≤ 2-t-1 / 2-1 = 2-t.

Машинное эпсилон определяется разрядностью мантиссы и способом округления чисел, реализованным на конкретной ЭВМ.

Примем следующие способы определения приближённых значений искомых величин:

• положим X∞ = 2n, где n – первое натуральное число, при котором произошло переполнение;
• положим X0 = 2-m, где m – первое натуральное число , при котором 2-m совпадает с нулем;
• положим εM = 2-k, где k – наибольшее натуральное число, при котором сумма вычисленного значения 1+2-k ещё больше 1. Фактически, εM есть граница относительной погрешности представления числа x* ≈ 1.

Дальше задаём это в нужной среде (пакете) и подбираем значения параметров, вот пример для моего MathCAD 15:

машинный ноль, машинная бесконечность и машинный эпсилон в MathCAD 15

А вот что вышло в Visual Studio 2010 при использовании проекта Windows Forms, C++/CLI, библиотеки System::Math и типа данных long double:

Inf: 1024
Zero: 1075
Eps: 53

Код:

//Функции для подсчёта
long double inf (int n) { return Math::Pow(2.,n); }
long double zero (int m) { return Math::Pow(2.,-m); }
long double eps (int k) { return 1.+Math::Pow(2.,-k); }

//...
//Расчёт, сделанный по нажатию кнопки с выводом результатов в метку label1
 label1->Text = "";

 int n=1,m=1,k=1;
 long double res;
 while (1) {
  res=inf(n);
  if (res==Double::PositiveInfinity) break;
  else n++;
 };
 label1->Text +=  "Inf: " + n + Environment::NewLine;

 while (1) {
  res=zero(m);
  if (res==0.) break;
  else m++;
 };
 label1->Text +=  "Zero: " + m + Environment::NewLine;

 while (1) {
  res=eps(k);
  if (res==1.) break;
  else k++;
 };
 label1->Text +=  "Eps: " + k + Environment::NewLine;

Ну и пара стандартных напоминаний напоследок:

К вещественным значениям в общем случае неприменима операция == (“сравнение”) из-за неточного представления этих значений в памяти компьютера. Поэтому для вещественных переменных отношение вида a==b обычно заменяется на fabs(a-b)≤eps, где fabs() – функция вычисления модуля вещественного числа, а eps – малая величина, определяющая допустимую погрешность.

Допустимую погрешность можно ввести в расчёт также через стандартный метод округления round, например, левый расчёт произведения чисел в MathCAD не даст нуля, а правый – да:

учёт погрешностей через метод round (Mathcad)

27.10.2015, 17:32 [26281 просмотр]

---

Относительная
погрешность частного не превышает суммы
относительных погрешностей делимого
и делителя.

Если 
,
то 
.

Таким
образом, предельная относительная
погрешность частного равна сумме

предельных
относительных погрешностей делимого
и делителя

2.7.В
каком
случае может произойти полная потеря
точности вычислений.

Алгоритм
следует составлять таким образом, чтобы
избежать вычитание близких чисел и
деление на слишком большие или маленькие
числа.

2.8.Что такое «машинный ноль» и «машинная бесконечность»

Машинный
ноль – числовое значение, меньше
которого невозможно задавать точность
для любого алгоритма, возвращающего
вещественные числа,Х₀
называется наименьшее представимое на
компьютере положительное число, т.е.
для любого другого представимого числа
х на компьютере будет выполняться
неравенство

Х₀



|Х
|

Ситуация,
при которой результат какого-либо
действия, выполняемого на компьютере,
оказывается меньше Х_0,
называется
исчезновением порядка.

Машинная
бесконечность

– наименьшее из чисел удовлетворяющих
неравенству |X|
,
где – Х любое число, которое можно
представить на компьютере.

Ситуация,
при которой результат какого-либо
действия, выполняемого на компьютере,
оказывается больше или равен

_,
называется
переполнением.

2.9.Какую задачу называют хорошо обусловленной.

Под обусловленностью
вычислительной задачи понимают
чувствительность ее решения к малым
изменениям входных данных. Задачу
называют хорошо
обусловленной, если
при малых изменениях входных данных
отвечают малые погрешности решения и
результат также изменяется незначительно.

2.10.
Какую
задачу называют плохо обусловленной.

Задача
называется плохо
обусловленной, если
малые изменения входных данных могут
привести к большим изменениям решения.

2.11.Плохо
обусловленная задача на примере системы
линейных алгебраических уравнений.

вычислить
у(100) – ?

СЛАУ

,

2.12.
Пояснить графически хорошо и плохо
обусловленных задач.

2.13.
Дать определение количественной меры
обусловленности.

Дать
определение количественной меры
обусловленности задачи является числом
обусловленности, которое можно
интерполировать как коэффициент
возможного возрастания погрешности
решения, по отношению и вызвавшим его
погрешностям начальных данных.

(y*) = Ji

(x*)

(y*)

Jg
(x*)

2.14.
Мера
обусловленности системы линейных
алгебраических уравнений.

Для
количественной характеристики зависимости
погрешности 
 решения
системы от погрешности 
 свободного
вектора вводятся понятия обусловленности
системы и обусловленности матрицы
системы. 

Под
мерой обусловленности системы понимают
следующую величину

,
где 
. 

3.1.
Назначение задачи приближения функции.

Задача
приближения функции
-восстановление аналитической
зависимости, неизвестного вида функции,
по известным значениям ее, в некоторых
точках.

3.2.Что
такое интерполирование.

Интерполирование
– способ
решения задач о приближении функции,
основанный на критерии совпадения
значений функций в узлах таблицы.

3.3.
Какая функция называется интерполируемой,
а какая –интерполирующей.

Интерполирующая
функция –
это функция g
(x),
для которой выполняется условие,
совпадение с учетом узлов таблицы g(

)=
f(

)
i=

Интерполируемая
функция– это
функция f
(x)
задана таблицей своих значений f
(
)=

i
=

3.4.
Записать условие интерполирования.

, 
. 

3.5.Дать
определение обобщенного многочлена.

g
(x)=

(x)+

3.6.
Какие функции называются базовыми.

3.7.
Сформулировать постановку задачи
алгебраического интерполирования для
каждого узла таблицы.

Пусть
неизвестная функция f(x)заданная
значениями ,требуется найти полином ,
чтобы выполнялось условие интерполирования

…….+

3.8.
Записать условие алгебраического
интерполирования для каждого узла
таблицы.

)
=

3.9.
При каком условии в задаче алгебраического
интерполирования система линейных
алгебраических уравнений (СЛАУ) будет
иметь единственное решение.

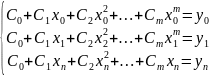
3.10.Из
чего следует единственность
интерполяционного многочлена.

Для
выполнения должно выполняться два
условия :

1. n=m,
   2)∆≠0

3.11.Какие
формы записи алгебраического
интерполяционного многочлена вам
известны

Интерполяционный
член в форме Ньютона

Интерполяционный
член в форме Лагранжа

3.12.Приведите
общий вид интерполяционного многочлена
степени n
в форме Лагранжа.

3.13.Каким
образом выбираются узлы интерполирования
для построения многочленов Лагранжа(на
примере)

Выберем 2
близлежащие точки (Первые опорные точки
от х*) Нужно выбрать n+1
точку (из нах-я из таблицы m)

3.14.Запишите
многочлены Лагранжа первой, второй, и
третьей степени в канонической форме.

3.15.Записать
неравенство, использующее на практике
при оценке погрешности интерполирования
функции многочленом степени n
в точке х*.

f
(
)-

4.1.
Сформулируйте задачу о наилучшем
приближении функции по известной таблице
значений.

Задача
приближения (аппроксимации) функций
заключается в том, чтобы для данной
функции построить другую, отличную от
нее функцию, значения которой достаточно
близки к значениям данной функции

f(x)=f(

4.2
Какие нормы вектора используются чаще
всего в численных методах

Норма
вектора должна быть минимальна

– вектор отклонения

– отклонение нашей
функции от истинной в каждой точке

– норма вектора
должна быть минимальна

Определение
нормы может быть разным. Мы определяем,
как корень квадратный из суммы квадратов
разностей координат

4.3
В чем заключается простейший подход к
решению линейной задачи метода наименьших
квадратов

Простейший
подход к решению этой задачи (линейной
задачи метода наименьших квадратов)
состоит в использовании условия минимума
функции нескольких переменных

4.4
Записать функцию невязки для метода
наименьших квадратов

-невязка
(среднеквадратичное отклонение)

4.5
Сформулируйте условие минимума для
функции невязки

=0;

;
все частные производные должны быть
равны нулю

4.6
К какой системе алгебраических уравнений
сводится условие минимума невязки

4.7
Сформулировать алгоритм построения
многочлена наилучшего среднеквадратичного
приближения первой степени

– вспомогательная
функция,

=0;

При
m=1

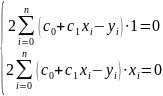
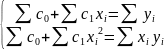
4.8
Сформулировать алгоритм построения
многочлена наилучшего среднеквадратичного
приближения второй степени

– вспомогательная
функция,

=0;

При
m=2

4.9
Как формулируется задача Коши для
обыкновенного ДУ I
порядка

ДУ
I
– общ.вид:

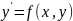
Общее
решение:

– совокупность интегральных кривых

+см.след
вопрос

4.10
Отличие формулировок задачи Коши для
обыкновенного ДУ I
порядка, решаемой аналитическими и
численными методами

Аналитическими:

Численными:

4.11
Дать определение сетки на отрезке

Сеткой

на отрезке

называется
упорядоченное множество точек, такое,
что

– граничные точки (входят в сетку);

– шаг сетки.

4.12
Какая сетка называется равномерной?

Если
шаг сетки

равен постоянной величине и вычисляется
как

,
сетка называется равномерной и все узлы
вычисляются по формуле

4.13
Какие функции называются сеточными

Функции,
вычисленные в узлах сетки, называются
сеточными функциями

4.14
Какие выражения называются разностными
производными?

Ра́зностное
уравне́ние — уравнение, связывающее
значение некоторой неизвестной функции
в любой точке с ее значением в одной или
нескольких точках, отстоящих от данной
на определенный интервал

Разностными
производными называют выражения
следующего вида:

– правая
разностная производная О(h)

– левая
разностная производная О(h)

– центральная
разностная производная О(
)

Погрешность
центральной разностной производной
меньше, чем у левой и правой О(
)<
О(h)

– обозначение
для различения формул

О(h)
– порядок (оц.погрешности)

– узел сетки

– узел сетки

– сеточные функции

– равномерная
сетка

4.15
Привести расчетную формулу левой
разностной производной

– левая
разностная производная О(h)

4.16
Привести расчетную формулу правой
разностной производной

– правая
разностная производная О(h)

4.17
Привести расчетную формулу центральной
разностной производной

– центральная
разностная производная О(
)

4.18.
Записать дискретный аналог произвольного
дифференциального уравнения I
порядка.

4.19.
Определение разностной схемы.

Семейство
уравнений, зависящее от параметра h,
называется разностной схемой.

задано

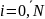
4.20.
Определение разностной задачи.

Разностная
схема при конкретном значении h
называется разностной заачей

задано

5.1.
Какие разностные методы называются k
– шаговыми?

Разностные
методы называются k
– шаговыми, если для вычисления последнего
значения решения требуется k
предыдущих значений.

5.2.
Какие разностные методы называются
одношаговыми?

Разностные
методы называются одношаговыми, если
для вычисления очередного значения
решения требуется только одно предыдущее
значение решения.

5.3.
Какие разностные методы решения задачи
Коши называются явными?

Разностные
методы решения задачи Коши называются
явными, если сеточная функция в разностном
уравнении не содержит вычисляемого
значения решения.

5.4.
Какие разностные методы решения задачи
Коши называются неявными?

Разностные
методы решения задачи Коши называются
неявными, если сеточная функция в
разностном уравнении содержит вычисляемого
значения решения.

5.5.
Для каких функций задача сводится к
решению дифференциального уравнения
в частных производных.

Для
функций многих переменных f(x,
y)

5.6.
Общий вид линейного дифференциального
уравнения II
порядка для функций с двумя независимыми
переменными.

5.7.
Общий вид однородного линейного
дифференциального уравнения II
порядка для функций с двумя независимыми
переменными.

*

5.8.
Что означают начальные условия в задачах
математической физики.

Начальные
условия представляют собой картину
изучаемого процесса в фиксированный
момент времени.

5.9.
Что означают граничные условия в задачах
математической физики.

Граничные
условия представляют собой описание
режима протекания процесса на границе
области

5.10.
Что является краевой задачей математической
физики.

часто
встречающаяся в математической физике
задача, в которой из класса функций,
определенных в данной области, требуется
найти функцию, удовлетворяющую на
границе (крае) этой области заданным
условиям.

5.11.
Что называется краевой задачей
математической физики.

Уравнения
математической физики расчета вместе
с начальными и граничными условиями
называется краевой задачей.

5.12.
Запишите канонический вид уравнения
гиперболического типа.

5.13.
Запишите канонический вид уравнения
параболического типа.

5.14
Запишите канонический вид уравнения
эллиптического типа

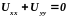
5.15Описать
дискретзацию области решения краевой
задачи

Соседние файлы в папке Мат.мод 313

• #

  22.08.20221.15 Кб0func10.m

• #
• #
• #
• #

  22.08.2022128 б0matlab.mat

• #
• #

  22.08.202257 б0model.m

• #
• #
• #
• #

  22.08.202218.38 Кб0Лаб3.docx

Category:

• Компьютеры
• Cancel

Определяем машинный ноль, машинную бесконечность и машинный эпсилон

17:32 27.10.2015

Доверять расчёту, сделанному на компьютере, без тени понимания того, как именно выполнен этот расчёт – одна из худший вещей, которые может допустить в своей работе инженер. К сожалению, уже нередки “специалисты”, которых не смущает ненулевой результат, полученный при умножении на ноль или напротив, ноль, там где теоретически нуля быть не должно.

Поэтому повторим в этой заметке несколько азбучных истин о представлении вещественных чисел в компьютере и правилах выполнения операций с ними.

В IBM-совместимой ЭВМ для вещественных чисел используется двоичная система счисления и принята форма представления чисел с плавающей точкой вида

x = m*2p, где мантисса m = ± (g1*2-1 +
g2*2-2 + ... +
gt*2-t),

g1, ..., gt – двоичные цифры, причём, g1=1, а целое значение p называется двоичным порядком. Количество цифр t, которое отводится для записи мантиссы, называется разрядностью мантиссы. Диапазон представления чисел в ЭВМ ограничен конечной разрядностью мантиссы и значением числа p.

Все представимые на ЭВМ вещественные числа удовлетворяют неравенствам
0 < X0 ≤ |x| < X∞, где
X0 = 2-pmax+1,
X∞ = 2pmax.

Все числа, по модулю большие X∞, не представимы на ЭВМ и рассматриваются как машинная бесконечность. Все числа, по модулю меньшие X0, для компьютера не отличаются от нуля и рассматриваются как машинный ноль. Машинным эпсилон εM называется относительная точность ЭВМ, то есть граница относительной погрешности представления вещественных чисел. Можно показать, что εM ≈ 2-t. Пусть
x* = m*2p. Тогда граница абсолютной погрешности представления этого числа равна Δ(x*) ≈ 2-t-1*2p. Поскольку 1/2≤m<1, то величина относительной погрешности представления оценивается как
δ(x*) ≈ Δ(x*) / |x*| ≈ (2-t-1*2p) / (m*2p) = 2-t-1 / m ≤ 2-t-1 / 2-1 = 2-t.

Машинное эпсилон определяется разрядностью мантиссы и способом округления чисел, реализованным на конкретной ЭВМ.

Примем следующие способы определения приближенных значений искомых величин:

читать далее в блоге ПерСа