Масштаб векторной диаграммы как найти

1. Построение
   векторных диаграмм начинаем с выбора
   масштаба для тока и напряжения.:
   m_I
   = 1 А/ см, m_U
   = 5 B/ см.
   Здесь и масштабные коэффициенты. Они
   означают, сколько ампер или вольт
   содержится в 1 см. Масштаб можно задавать
   и графически, смотри рисунок.

От
точки 0 горизонтально вправо проводим
вектор тока I
общий для всей цепи. В выбранном масштабе
его длина будет l_I
=
I
/ m_I
= 2 А / (1 А / см)= 2 см

1. Вектор
   активного напряжения U_R1
   совпадает
   по фазе с током, угол сдвига фаз между
   ними равен 0, поэтому откладываем его
   вдоль вектора тока от точки 0 вправо.
   Его длина l_UR1
   = U_R1
   /
   m_U
   =18 В / (5 В / см)=3,6 см

2. От
   конца вектра U_R1
   
   откладываем вправо вдоль вектора тока
   вектор активного напряжения U_R2.
   Его длина l_UR2
   = U_R2
   /
   m_U=
   22 В / (5 В / см) = 4,4 см

3. От
   конца вектора U_R2
   откладывае вертикально вверх вектор
   напряжения U_L
   на
   индуктивном сопротивлении, так как он
   опережает ток на угол 90.

Его
длина
l_U
L
= U_L
/ m_U
= 24 см / (5 В/см) = 4, 8 см.

1. От
   конца вектора U_L
   откладываем вертикально вниз вектор
   падения напряжения U_C
   на емкостном сопротивлении, так как
   он отстает от тока на угол 90º.

Его
длина l_UC
= /
m_U
=54 В / (5 В/см) = 10, 8 см.

Геометрическая
сумма векторов
U_R1,

U_R2,

U_L,
U_C
должна
быть равна полному напряжению U,
приложенному к зажимам цепи, т. е. U
= U_R1+
U_R2+
U_L
+U_C

Измерив
длину этого вектора, убеждаемся, что
она l_U
=
10 см. Это значит, что с учетом масштаба
его величина будет U
=
10 см. ∙ 5 В/ см = 50 В.

По условию задачи
именно такое напряжения приложено к
зажимом цепи.

Примечание.
Если в выбранном масштабе вектор
суммарного напряжения не будет равен
приложенному к зажимам цепи напряжения,
то это будет означать об ошибке,
допущенной при решении задачи или в
построении векторной диаграммы. Ее
нужно найти и устранить. Чаще всего
наблюдаются ошибки, связанные с
искажением масштабов при построении
векторной диаграммы. Учтите это, и при
построении вектоной диаграммы пользуйтесь
чертежным инструментом. Выполняйте
постоение точно и аккуратно.

10. Расчет параллельных цепей переменного тока

Методика (с
примером) решения задач на тему:
Электрические цепи с параллельным
соединением активного, емкостного и
индуктивного сопротивлений

Цель. Рассчитать
напряжения, токи на элементах цепи.
Построить диаграмму напряжений и токов.

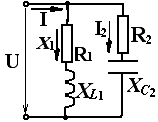
Теория к работе.

Для такой цепи
характерно, что электроприемники,
соединенные параллельно, находятся
под одинаковым (общим) напряжением.
(При отсутствии на параллельных цепях
какого-либо элемента вместо них в
формулах будет стоять, естественно,
нуль!).

Ток каждой ветви
определяется по закону Ома:

I₁
=
U
/Z₁,
где
Z₁
=
,

I₂
=
U
/Z₂,
где
Z₂
=

Углы
сдвига фаз
φ₁
и
φ₂

между током и напряжением каждой ветви
определяются с помощью тригонометрических
функций:

cos
φ₁=
R₁
/ Z₁
и
sin
φ₁=
X_L1
/
Z₁,

cos
φ₂=
R₂
/ Z₂
и
sin
φ₂=
– X_C2
/
Z₂

Угол
сдвига фаз обязательно следует проверять
по синусу во избежание потери знака
угла
(cos
является четной функцией), но находить
его тоже нужно. Он потребуется в
дальнейшем расчете цепи.

Общий
ток цепи следует из I закона Кирхгофа,
он равен векторной
сумме токов ветвей: I
= I₁
+
I₂

Векторная диаграмма
этих токов:

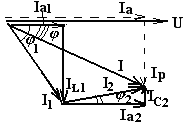
Общий
суммарный или результирующий ток можно
найти не только графически (диаграмма
строится в масштабе), но и математически,
на основании теоремы Пифагора: I
=
,
где Iа
– проекция вектора общего тока на
вектор напряжений, она называется
активной составляющей общего тока.

Iр
– проекция вектора общего тока на
линию, перепндикулярную линии напряжения,
она называется реактивной составляющей
общего тока.

Из
диаграммы видно, что Iа
= Iа₁
+ Iа₂
, Iр = I_L1
 Iс₂.
В
этих формулах: Iа₁
и Iа₂
–
активные составляющие токов первой и
второй ветви.

I_L1
–
реактивные составляющие тока первой
ветви. Она носит индуктивный характер
и поэтому взята знаком “плюс”.

Iс₂
–
реактивные составляющие тока второй
ветви. Она носит емкостной характер и
поэтому взята знаком “минус”.

Введем
в формулу общего
тока
его составляющие, тогда I
=

Значения составляющих
токов ветвей можно определять по
формулам:

Iа₁
= I₁
cos
φ₁;
Iа₂
=
I₂
cos φ₂;
I_L1
= I₁
sin
φ₁;
I_C2
= I₂
sin
φ₂
;

Активная мощность
цепи равна арифметической сумме активных
мощностей ветвей:

Р
= Р₁
+ Р₂,
где
Р₁
= U
I₁
cos
φ₁
или
Р₁

= I₁²R₁,
Р₂
= U
I₂
cos
φ₂
или
Р₂

= I₂²R₂

Реактивная
мщность цепи равна алгебраической
сумме реактивных мощностей ветвей:
Q =Q_L1
–
Q_C2
,
где

Q_L1=

U
I₁
sin φ₁
или

Q_L1=I₁²
Х
L₁,

Q
_C2=

U
I₂
sin φ₂
или

Q_С2=I₂²
Х
_С2

Активную
и
реактивную мощность можно найти и так:
Р
= U
I
cos
φ
или
Q=

U
I
sin φ

Где
cos
φ
=
,
sin φ=
;
cos
φ
и sin
φ
используют
также для определения угла сдвига фаз
между общим током и напряжением.

Полная
мощность цепи: S
=U I или S =

Угол
сдвига фаз между общим токомм и
напряжением можно определять и из
выражений:
cos
φ
= Р / S,
sin
φ
=
Q/ S

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Векторная диаграмма токов и напряжений

Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.

Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.

Определение

Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.

Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.

Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.

Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.

Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.

Разновидности

Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:

1. Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
2. Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.

Векторную диаграмму токов можно построить 2 разными способами:

1. Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.
2. Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.

Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.

Построение

Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.

1. Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
2. Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
3. Напряжение резистора UR 10 вольт, его направление совпадает с током I.
4. Сила тока в цепи I равняется 3 ампера.

Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.

1. Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.
2. Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.
3. Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.
4. Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.
5. Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.

Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.

Способ 2

Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:

• Резистора UR;
• Конденсатора UC;
• Катушки UL.

1. На плоскости Im откладывается вектор UR (резистор). Его направление точно совпадает с током, поэтому это будет горизонтальная линия.
2. От точки отсчета откладывается вниз вектор UC (конденсатор). Вектор откладывается под углом 90 градусов вниз, так как он имеет указанное ранее опережение 90°.
3. От этой же точки отсчета откладывается вектор UL (катушка индуктивности). Ее значение откладывается ровно на 90 градусов вертикально, так как есть сдвиг фазы на 90 градусов.

Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.

1. Показать результат сложения вектора UL и UC.
2. При увеличении величины сопротивления определить разницу между напряжением и сопротивлением можно, используя новый вектор Um.
3. Кроме того можно определить угол сдвига фазы φ в цепи.

Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.

Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:

1. На оси ОХ откладываются настоящие значения величин, а на оси OY мнимые значения.
2. Угловая величина обозначается как W.
3. Также присутствует сам вектор Im и угол сдвига фаз φ.

Далее нужно сделать:

1. На плоскости выбрать точку отсчета.
2. От нее отложить вектор Im, учитывая угол сдвига фаз равный 90°.
3. Длина вектора Im равна значению его напряжения и откладывается в выбранном масштабе.

Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.

Заключение

Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.

Видео по теме

Построение векторной диаграммы

Вы будете перенаправлены на Автор24

Разновидности векторных диаграмм и правила их построения

Векторная диаграмма – это совокупность векторов на комплексной прямой, которая соответствует комплексным параметрами и/или величинам электрической цепи.

Векторные диаграммы могут быть:

Построение точечных диаграмм осуществляется с соблюдением масштаба всех величин согласно результатам численного анализа. Основное назначение точечных диаграмм – проверка результатов расчета. Качественные векторные диаграммы строятся с учетом взаимосвязей между комплексными величинами. Построение данного вида диаграмм, как правило, заменяет расчет, или предшествует ему. В качественных векторных диаграммах значения параметров (или величин) и масштаб изображения несущественны. Основное требование к ним заключается в том, чтобы все связи между величинами были отображены корректно. Этот вид диаграмм является одним из основных инструментов анализа цепей переменного тока.

Векторные диаграммы делятся на круговые и линейные. В круговой векторной диаграмме геометрическим местом точек перемещения конца вектора является окружность или полуокружность. В линейных векторных диаграммах геометрическим местом точек конца вектора является прямая линия.

Перед построением векторной диаграммы сначала вычерчивается и анализируется схема замещения, которая эквивалентна принципиальной схеме электрической цепи. На данной схеме обязательно отмечаются каждый элемент электрической цепи, наносятся направления всех напряжений и токов. Векторные диаграммы токов и напряжений должны чертиться в крупных масштабах, выбор которого осуществляется по самой большой вычисленной или измеренной величине электрического тока или напряжения.

Построение векторной диаграммы

В основе метода векторных диаграмм лежит тот факт, что любую меняющуюся величину, которая изменяется по синусоидальному закону определяется, как проекция на выбранное направление вектора, вращающийся вокруг своей начальной скорости, равной угловой частоте колебаний изображаемой переменной величины.

Готовые работы на аналогичную тему

Угловая скорость – это векторная величина, которая характеризует направление и быстроту вращения материальной точки вокруг центра вращения.

Рассмотрим электрическую цепь, которая состоит из последовательно соединенных резистора, источника тока, конденсатора и индуктивности. Схема данной цепи изображена на рисунке ниже.

Рисунок 1. Схема электрической цепи. Автор24 — интернет-биржа студенческих работ

Здесь U – мгновенное значение переменного напряжения; i – электрический ток в настоящий момент времени.

Изменение мгновенного значения переменного напряжения можно рассчитать по следующей формуле:

По закону сохранения заряда ток имеет одно и тоже значение в любой момент времени. Таким образом, на каждом элементе электрической цепи будет падать напряжение:

1. UL на индуктивности.
2. UR на активном сопротивлении.
3. UC на конденсаторе.

По второму правилу Кирхгофа напряжение источника тока равно:

По второму закону Ома:

Для активного сопротивления значение R зависит от свойств проводника (не зависит от момента времени, электрического тока), поэтому оно совпадает с напряжением по фазе, таким образом:

$UR = Im • R • Coswt.$

Конденсатор в электрической цепи переменного тока обладает емкостным реактивным сопротивлением, а напряжение на конденсаторе отстает по фазе от тока на П/2, поэтому:

Рисунок 2. Уравнение. Автор24 — интернет-биржа студенческих работ

Напряжение на катушке индуктивности опережает ток по фазе на величину П/2, поэтому

Рисунок 3. Уравнение. Автор24 — интернет-биржа студенческих работ

Получается, что сумму падения напряжений можно вычислить по следующей формуле:

По закону сохранения заряда ток всегда одинаков во всех частях, таким образом векторная диаграмма токов будет иметь следующий вид:

Рисунок 4. Векторная диаграмма токов. Автор24 — интернет-биржа студенческих работ

Im – амплитудное значение электрического тока.

Напряжение (на активном сопротивлении) совпадает с током по фазе, поэтому их векторы будут сонаправлены и откладываются из одной точки

Рисунок 5. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Так как напряжение на конденсаторе отстает от электрического тока на величину П/2, то его вектор должен быть отложен под прямым углом вниз, перпендикулярно по отношению к вектору напряжения на активном сопротивлении.

Рисунок 6. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Напряжение на катушке индуктивности опережает ток на П/2, поэтому его вектор откладывается под прямым углом вверх, перпендикулярно вектору напряжения на активном сопротивлении.

Рисунок 7. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Складываем векторы напряжений на активных элементах цепи и получаем разницу (принимаем, что UL>UC), которая будет направлена вверх.

Рисунок 8. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Затем прибавляем вектор напряжения на активном сопротивлении, и получаем вектор суммарного напряжения (по правилу векторного сложения).

Рисунок 9. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ

Затем по закону Ома и Теореме Пифагора, получаем формулу для расчета амплитудного значения тока:

Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ

где, Z – сопротивление общее сопротивление.

Затем, преобразуя данное уравнение получаем формулу для расчета полного сопротивления

Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 27 02 2022

Эксперт по предмету «Электроника, электротехника, радиотехника» , преподавательский стаж — 5 лет

Как построить векторы в масштабе

Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит надежным контролем корректности хода решения и позволяет легко определить квадрант, в котором находятся определяемые векторы.

При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока (см. лекцию № 8), а к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый (отправной) вектор следует принять вектор напряжения (см. лекцию № 8), ориентируя относительно него векторы токов в параллельных ветвях.

Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.

В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы, расчет которой был приведен в лекции № 5 (см. рис. 1).

Параметры схемы:

При данных параметрах и заданном напряжении на входе схемы найденные значения токов (см. лекцию № 5) равны: ; ; .

При построении векторной диаграммы зададимся масштабами токов и напряжений (см. рис. 2). Векторную диаграмму можно строить, имея запись комплекса в показательной форме, т.е. по значениям модуля и фазы . Однако на практике удобнее проводить построения, используя алгебраическую форму записи, поскольку при этом вещественная и мнимая составляющие комплексной величины непосредственно откладываются на соответствующих осях комплексной плоскости, определяя положение точки на ней.

Построение векторной диаграммы токов осуществляется непосредственно на основании известных значений их комплексов. Для построения топографической диаграммы предварительно осуществим расчет комплексных потенциалов (другой вариант построения топографической диаграммы предполагает расчет комплексов напряжений на элементах цепи с последующим суммированием векторов напряжений вдоль контура непосредственно на комплексной плоскости).

При построении топографической диаграммы обход контуров можно производить по направлению тока или против. Чаще используют второй вариант.

В этом случае с учетом того, что в электротехнике принято, что ток течет от большего потенциала к меньшему, потенциал искомой точки равен потенциалу предыдущей плюс падение напряжения на элементе между этими точками. Если на пути обхода встречается источник ЭДС, то потенциал искомой точки будет равен потенциалу предыдущей плюс величина этой ЭДС, если направление обхода совпадает с направлением ЭДС, и минус величина ЭДС, если не совпадает. Это вытекает из того, что напряжение на источнике ЭДС имеет направление, противоположное ЭДС.

Обозначив на схеме по рис. 1 точки между элементами цепи e и a и приняв потенциал точки а за нуль( ), определим потенциалы этих точек:

или

Таким образом, в результате проведенных вычислений получено, что . Но разность потенциалов точек е и а равно напряжению U, приложенному к цепи, а оно равно 120 В. Таким образом, второй закон Кирхгофа выполняется, а следовательно, вычисления выполнены верно. В соответствии с полученными результатами строится топографическая диаграмма на рис. 2. Следует обратить внимание на ориентацию векторов, составляющих топографическую диаграмму, относительно векторов тока: для резистивных элементов соответствующие векторы параллельны, для индуктивного и емкостных – ортогональны.

В заключение заметим, что векторы напряжений ориентированы относительно точек топографической диаграммы противоположно положительным направлениям напряжений относительно соответствующих точек электрической цепи. В этой связи допускается не указывать на топографической диаграмме направления векторов напряжений.

Потенциальная диаграмма применяется при анализе цепей постоянного тока. Она представляет собой график распределения потенциала вдоль участка цепи или контура, при этом по оси абсцисс откладываются сопротивления резистивных элементов, встречающихся на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих точек. Таким образом, каждой точке рассматриваемого участка или контура соответствует точка на потенциальной диаграмме.

Рассмотрим построение потенциальной диаграммы на примере схемы на рис. 3.

При параметрах схемы ; ; ; ; и токи в ветвях схемы равны: ; ; .

Построим потенциальную диаграмму для контура abcda.

Для выбора масштаба по оси абсцисс просуммируем сопротивления резисторов вдоль рассматриваемого контура: после чего определим потенциалы точек контура относительно потенциала произвольно выбранной точки a, потенциал которой принят за нуль:

Таким образом, координаты точек потенциальной диаграммы: а(0;0);b(4;-20); c(4;17); d(7;2). С учетом выбранных масштабов на рис. 4 построена потенциальная диаграмма для выбранного контура.

Преобразование линейных электрических схем

Для упрощения расчета и повышения наглядности анализа сложных электрических цепей во многих случаях рационально подвергнуть их предварительному преобразованию. Очевидно, что преобразование должно приводить к упрощению исходной схемы за счет уменьшения числа ее ветвей и (или) узлов. Такое преобразование называется целесообразным. При этом при любых способах преобразований должно выполняться условие неизменности токов в ветвях участков схемы, не затронутых этими преобразованиями. Из последнего вытекает, что, если преобразованию подвергаются участки цепи, не содержащие источников энергии, то мощности в исходной и эквивалентной схемах одинаковы. Если в преобразуемые участки входят источники энергии, то в общем случае мощности в исходной и преобразованной цепях будут различны.

Рассмотрим наиболее важные случаи преобразования электрических цепей.

1. Преобразование последовательно соединенных элементов

Рассмотрим участок цепи на рис. 5,а. При расчете внешней по отношению к этому участку цепи данную ветвь можно свести к виду на рис. 5,б, где

При этом при вычислении эквивалентной ЭДС k-я ЭДС берется со знаком “+”, если ее направление совпадает с направлением эквивалентной ЭДС, и “-”, если не совпадает.

2. Преобразование параллельно соединенных ветвей

Пусть имеем схему на рис. 6,а.

Согласно закону Ома для участка цепи с источником ЭДС

,

где .

причем со знаком “+” в (4) записываются ЭДС и ток , если они направлены к тому же узлу, что и ЭДС ; в противном случае они записываются со знаком “-”.

3. Взаимные преобразования “треугольник-звезда”

В ряде случаев могут встретиться схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному типу (см. рис. 7). В таких случаях преобразования носят более сложный характер: преобразование треугольника в звезду и наоборот.

Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными в звезду между теми же точками. При этом на участках схемы, не затронутых этими преобразованиями, токи должны остаться неизменными.

Без вывода запишем формулы эквивалентных преобразований

Треугольник звезда

Звезда треугольник

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш.шк., 1978. –528с.

Контрольные вопросы и задачи

1. Что представляют собой векторные диаграммы?
2. Что такое топографические диаграммы, для чего они служат?
3. В чем сходство и различие топографической и потенциальной диаграмм?
4. Какой практический смысл преобразований электрических цепей?
5. В чем заключается принцип эквивалентности преобразований?
6. Построить потенциальные диаграммы для левого и внешнего контуров цепи рис.3.

Полагая в цепи на рис. 8 известными ток и параметры всех ее элементов, качественно построить векторную диаграмму токов и топографическую диаграмму потенциалов для нее.

Определить входное сопротивление цепи на рис. 8, если .

Ответ: .

Определить сопротивления ветвей треугольника, эквивалентного звезде между узлами a,c и d в цепи на рис. 8.

Ответ: ; ; .

Определить сопротивления ветвей звезды, эквивалентной треугольнику в цепи на рис. 8, состоящему из элементов , и .

Ответ: ; ; .

[spoiler title=”источники:”]

http://spravochnick.ru/elektronika_elektrotehnika_radiotehnika/postroenie_vektornoy_diagrammy/

http://toehelp.ru/theory/toe/lecture09/lecture09.html

[/spoiler]

Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС,
напряжения, токи и т. д., называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов
можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит
надежным контролем корректности хода решения и позволяет легко определить квадрант, в котором находятся определяемые векторы.

При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока (см. лекцию
№ 8), а к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый
(отправной) вектор следует принять вектор напряжения (см. лекцию № 8), ориентируя относительно него векторы токов в параллельных ветвях.

Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они
представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме,
представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор
падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.

В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы, расчет которой был приведен в лекции № 5 (см. рис. 1).

Параметры схемы:

При данных параметрах и заданном напряжении на входе схемы найденные значения токов (см.
лекцию № 5) равны: ; ; .

При построении векторной диаграммы зададимся масштабами токов и напряжений
(см. рис. 2). Векторную диаграмму можно строить, имея запись комплекса в показательной
форме, т.е. по значениям модуля и фазы . Однако на практике удобнее проводить
построения, используя алгебраическую форму записи, поскольку при этом вещественная
и мнимая составляющие комплексной величины непосредственно откладываются на
соответствующих осях комплексной плоскости, определяя положение точки на ней.

Построение векторной диаграммы токов осуществляется непосредственно на основании
известных значений их комплексов. Для построения топографической диаграммы предварительно
осуществим расчет комплексных потенциалов (другой вариант построения топографической
диаграммы предполагает расчет комплексов напряжений на элементах цепи с последующим
суммированием векторов напряжений вдоль контура непосредственно на комплексной
плоскости).

При построении топографической диаграммы обход контуров можно
производить по направлению тока или против. Чаще используют второй вариант.

В этом случае с учетом того, что в электротехнике
принято, что ток течет от большего потенциала к меньшему, потенциал искомой
точки равен потенциалу предыдущей плюс падение напряжения на элементе между
этими точками. Если на пути обхода встречается источник ЭДС, то потенциал искомой
точки будет равен потенциалу предыдущей плюс величина этой ЭДС, если направление
обхода совпадает с направлением ЭДС, и минус величина ЭДС, если не совпадает.
Это вытекает из того, что напряжение на источнике ЭДС имеет направление, противоположное
ЭДС.

Обозначив на схеме по рис. 1 точки между элементами цепи e и a и приняв потенциал
точки а за нуль( ), определим потенциалы этих точек:

или

Таким образом, в результате проведенных вычислений получено, что . Но разность потенциалов точек
е и а равно напряжению U, приложенному к цепи, а оно равно 120
В. Таким образом, второй закон Кирхгофа выполняется, а следовательно, вычисления
выполнены верно. В соответствии с полученными результатами строится топографическая
диаграмма на рис. 2. Следует обратить внимание на ориентацию векторов, составляющих
топографическую диаграмму, относительно векторов тока: для резистивных элементов
соответствующие векторы параллельны, для индуктивного и емкостных – ортогональны.

В заключение заметим, что векторы напряжений ориентированы относительно точек
топографической диаграммы противоположно положительным направлениям напряжений
относительно соответствующих точек электрической цепи. В этой связи допускается
не указывать на топографической диаграмме направления векторов напряжений.

Потенциальная диаграмма

Потенциальная диаграмма применяется при анализе цепей постоянного тока. Она
представляет собой график распределения потенциала вдоль участка цепи или контура,
при этом по оси абсцисс откладываются сопротивления резистивных элементов, встречающихся
на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих
точек. Таким образом, каждой точке рассматриваемого участка или контура соответствует
точка на потенциальной диаграмме.

Рассмотрим построение потенциальной диаграммы на примере схемы на рис. 3.

При параметрах схемы ; ; ; ; и токи в ветвях схемы равны: ; ; .

Построим потенциальную диаграмму для контура abcda.

Для выбора масштаба по оси абсцисс просуммируем сопротивления резисторов вдоль
рассматриваемого контура: после чего определим потенциалы
точек контура относительно потенциала произвольно выбранной точки a,
потенциал которой принят за нуль:

Таким образом, координаты точек потенциальной диаграммы: а(0;0);b(4;-20);
c(4;17); d(7;2). С учетом выбранных масштабов на рис. 4 построена потенциальная
диаграмма для выбранного контура.

Преобразование линейных электрических схем

Для упрощения расчета и повышения наглядности анализа сложных электрических
цепей во многих случаях рационально подвергнуть их предварительному преобразованию.
Очевидно, что преобразование должно приводить к упрощению исходной схемы за
счет уменьшения числа ее ветвей и (или) узлов. Такое преобразование называется
целесообразным. При этом при любых способах преобразований должно выполняться
условие неизменности токов в ветвях участков схемы, не затронутых этими преобразованиями.
Из последнего вытекает, что, если преобразованию подвергаются участки цепи,
не содержащие источников энергии, то мощности в исходной и эквивалентной схемах
одинаковы. Если в преобразуемые участки входят источники энергии, то в общем
случае мощности в исходной и преобразованной цепях будут различны.

Рассмотрим наиболее важные случаи преобразования электрических цепей.

1. Преобразование последовательно соединенных элементов

Рассмотрим участок цепи на рис. 5,а. При расчете внешней по отношению к этому
участку цепи данную ветвь можно свести к виду на рис. 5,б, где

(1)

или

.

(2)

При этом при вычислении эквивалентной ЭДС k-я ЭДС берется со знаком “+”,
если ее направление совпадает с направлением эквивалентной ЭДС, и “-”, если
не совпадает.

2. Преобразование параллельно соединенных ветвей

Пусть имеем схему на рис. 6,а.

Согласно закону Ома для участка цепи с источником ЭДС

,

где .

Тогда

 ,

где

причем со знаком “+” в (4) записываются ЭДС и ток , если они направлены к тому же
узлу, что и ЭДС ; в противном случае они записываются
со знаком “-”.

3. Взаимные преобразования “треугольник-звезда”

В ряде случаев могут встретиться
схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному
типу (см. рис. 7). В таких случаях преобразования носят более сложный характер:
преобразование треугольника в звезду и наоборот.

Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных
в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными
в звезду между теми же точками. При этом на участках схемы, не затронутых этими
преобразованиями, токи должны остаться неизменными.

Без вывода запишем формулы эквивалентных преобразований

Треугольник звезда

Звезда треугольник

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
   С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические
   цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
   специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш.шк., 1978. –528с.

Контрольные вопросы и задачи

1. Что представляют собой векторные диаграммы?
2. Что такое топографические диаграммы, для чего они служат?
3. В чем сходство и различие топографической и потенциальной диаграмм?
4. Какой практический смысл преобразований электрических цепей?
5. В чем заключается принцип эквивалентности преобразований?
6. Построить потенциальные диаграммы для левого и внешнего контуров цепи рис.3.



7. Полагая в цепи на рис. 8 известными
   ток и параметры всех ее элементов,
   качественно построить векторную диаграмму токов и топографическую диаграмму
   потенциалов для нее.
8. Определить входное сопротивление цепи на рис. 8, если .

Ответ: .

9. Определить сопротивления ветвей треугольника, эквивалентного звезде между
   узлами a,c и d в цепи на рис. 8.

Ответ: ; ; .

10. Определить сопротивления ветвей звезды, эквивалентной треугольнику в цепи
    на рис. 8, состоящему из элементов , и .

Ответ: ; ; .

Векторные диаграммы и комплексное представление

Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел. При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy — оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица).

Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ0 запишется как комплексное число, а его действительная часть — есть гармоническое колебание с циклической частотой ω и начальной фазой φ0.

Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.

• Метод векторных диаграмм может излагаться отдельно в курсах электротехники или элементарной физики, если по тем или иным причинам (обычно связанным с умеренным уровнем математической подготовки учащихся и недостатком времени) надо избежать использования комплексных чисел (в явном виде) вообще.

• Метод комплексного представления (который при необходимости или желании может включать и графическое представление, что, правда, совершенно не обязательно и иногда излишне) вообще говоря более мощен, т.к. естественно включает в себя, например, составление и решение систем уравнений любой сложности, в то время как метод векторных диаграмм в чистом виде всё же ограничен задачами, подразумевающим суммирование, которое можно изобразить на одном чертеже.

• Однако метод векторных диаграмм (в чистом виде или в качестве графической составляющей метода комплексного представления) — более нагляден, а значит в некоторых случаях потенциально более надежен (позволяет до некоторой степени избежать грубых случайных ошибок, которые могут встречаться при абстрактных алгебраических вычислениях) и позволяет в некоторых случаях достичь в каком-то смысле более глубокого понимания задачи.

Разновидности векторных диаграмм

Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.

С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.

Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.

Круговая диаграмма

Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.

Линейная диаграмма

Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.

Примеры применения

Механика; гармонический осциллятор

• Гармонический осциллятор в механике и гармонический осциллятор любой природы формально представляют точную аналогию, поэтому рассмотрим их в одном параграфе на примере механического гармонического осциллятора.
• Применение векторных диаграмм в механике сводится в основном к случаю гармонического осциллятора (в том числе имеется в виду и случай осциллятора с линейной по скорости силой трения); впрочем, векторные диаграммы могут быть до некоторой степени полезны и для исследования нескольких осцилляторов в том числе и в пределе бесконечного их количества (для колебаний или волн в распределенных системах).
• С современной точки зрения применение векторных диаграмм к гармоническому осциллятору представляет скорее только исторический и педагогический интерес, однако тем не менее в принципе они здесь вполне применимы.
• В механике применение векторных диаграмм (обычно подразумевается их применение к одномерному осциллятору) имеет ту особенность, что добавляющаяся вторая координата для превращения колебаний во вращение может иметь не только чисто формальный абстрактный смысл, но для одномерной механической системы такого сорта может быть указана механическая же двумерная система, для которой векторная диаграмма первой реализуется как вполне реальное двумерное механическое движение, и все векторы реально двумерны (а после проецирования всех их и движения точки двумерной системы на одну ось, мы получаем мгновенные значения соответствующих величин – в том числе положения – для соответствующей одномерной системы); таким образом, для механической одномерной системы возможна не только формальная математическая, но и реальная механическая модель, переводящая колебательное одномерное движение во вращательное движение в двумерном пространстве, реализующая в себе векторную диаграмму для одномерной системы.

Разберем два основных случая простого применения векторных диаграмм в механике (как замечено выше, также применимых к гармоническому осциллятору не только механической, но любой природы): осциллятор без затухания и без внешней силы и осциллятор с (линейным) затуханием (вязкостью), и внешней вынуждающей силой.

Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.

Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции

i(t) = 10 sin(ωt + 30°).

Данный синусоидальный сигнал можно представить в виде комплексной величины

I = 10∠30°.

Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.

Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.

Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.

Последовательное соединение элементов цепи

Составим уравнение для данной цепи по второму закону Кирхгофа:

UR + UL + UC = E.

По закону Ома падение напряжений на элементах определяется по следующим выражениям:

UR = I ∙ R,

UL = I ∙ jXL,

UC = −I ∙ jXC.

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.

Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.

При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.

Падение напряжения на резисторе UR совпадает по направлению с током I (т.к. UR = I ∙ R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. UL = I ∙ jXL, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. UC = −I ∙ jXC, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелке).

Векторная диаграмма напряжений при последовательном соединении элементов цепи

Следует обратить внимание, что на одной векторной диаграмме изображают только векторы тех величин, у которых частота совпадает!

Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.

Параллельное соединение элементов цепи

Составим уравнение для данной цепи по первому закону Кирхгофа:

I­­ – IR – IL – IC = 0,

откуда

I­­ = IR + IL + IC.

Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:

IR = E / R,

IL = E / (jXL) = −j ∙ E / XL,

IC = E / (−jXC) = j ∙ E / XC,

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.

При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.

Ток в резисторе IR совпадает по направлению с ЭДС E (т.к. IR = E / R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. IL = −j ∙ E / XL, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелки). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. IC = j ∙ E / XC, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.

Векторная диаграмма токов при параллельном соединении элементов цепи

Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.

Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.

Свободные гармонические колебания без затухания

Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.

Гармонический осциллятор с затуханием и внешней вынуждающей силой

В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.

Расчет электрических цепей

Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.

Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).

Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.

Дифракция

Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.

Как построить векторную диаграмму токов и напряжений

Расчеты в цепях с синусоидальными напряжениями и токами упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами (рис. 1).

Проекция конца вектора на ось координат совершает синусоидальные колебания : каждое мгновенное значение тока, соответствующее моменту времени  и фазовому углу , можно рассматривать как проекцию на ось ординат вектора, повернувшегося на фазовый угол относительно оси абсцисс.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Таким образом, синусоидальная функция условно представляется вектором, длина которого определяется максимальным или действующим ее значением, а направление — ее начальной фазой; положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов (против часовой стрелки). Векторы токов и напряжений, вращаясь с одной и той же

угловой скоростью , неподвижны относительно друг друга. Условное изображение синусоидально изменяющихся во времени токов и напряжении при помощи векторов позволило записать в векторной форме первый и второй законы Кирхгофа.

Алгебраическому суммированию синусоид, т.е. суммированию их мгновенных значений, соответствуют геометрические действия над изображающими их векторами. Применение в этой форме законов Кирхгофа даст возможность путем построения векторных диаграмм достаточно просто и наглядно рассчитывать электрические цепи. Приступая к графическому расчету пеней переменного тока, следует помнить, что физические процессы на участках цепи с сопротивлением, индуктивностью, емкостью весьма различны.

Соответственно вектор тока и вектор напряжения имеют одно направление.

В индуктивном элементе ток отстает от напряжения на и соответственно располагаются векторы (рис.3). Закон Ома для участка цепи только с индуктивными сопротивлением записывается .

В емкостном элементе в активном сопротивлении ток и напряжение совпадают по фазе (рис.2), ток опережает напряжение на ( расположение вектора напряжения и тока показано на рис.4); закон Ома для участка цепи только с емкостным сопротивлением записывается
или .

Построение ВД напряжений и токов

В качестве примера построения ВД рассмотрим последовательную цепочку из сопротивления R, индуктивности L и конденсатора C. Схема приведена на рисунке ниже.

Напряжения на элементах схемы — UR, UL, UC. Ток в цепи — i.

Напряжение на выходе U = UR + UL + UC.

Пускай в цепи протекает синусоидальный ток с частотой ω и с нулевым сдвигом фазы. Для ненулевого сдвига фазы ВД просто повернётся на этот начальный угол, а общий её вид не изменится. Амплитуды напряжений на каждом элементе в форме закона Ома:

|U|R = R* |i|

|U|L = 1/ωC*|i|

|U|С = ωL* |i|

Соответствующие этим амплитудам длины векторов наносятся на ВД. При этом каждый вектор наносится с учетом своего фазового сдвига. Суммарный вектор оказался равен U = UR + UL + UC, но это теперь доказано геометрически на диаграмме.

Модуль суммарного вектора равен длине гипотенузы в прямоугольном треугольнике со сторонами |U|R, (|U|L – |U|С). Воспользовавшись теоремой Пифагора, можно вычислить |U|:

|U|2 = UR2 + (UL – UC)2

Применив формулы, указанные выше, получим:

|U|2 = (i0 * R)2 + (i0 * ωL – i0/ ωC)2

Можно вынести за скобки i0 (амплитуда тока — длина вектора i), тогда:

|U|2 = i02 * (R2 + (ωL – 1/ ωC)2

Пользуясь последней формулой, можно вычислять амплитуду синусоидального напряжения. Полученные формулы справедливы для случая обратной задачи, когда требуется найти ток в цепи с известным источником напряжения.

Алгоритм создания лучевой векторной диаграммы в Excel

Чтобы упростить наш урок, давайте предположим, что мы говорим об отношениях не между четырнадцатью как на графике, а пока только с 4-ма людьми по имени Антон, Алиса, Борис и Белла.

Наша матрица уровня отношений и связей между ними выглядит следующим образом:

• 0 значит отсутствие отношений;
• 1 означает слабые отношения (например: Антон и Алиса просто знают друг друга);
• 2 означает крепкие отношения (например, Борис и Алиса друзья).

Как можно геометрически смоделировать визуализацию этих исходных данных? Если бы мы нарисовали отношения между этими четырьмя людьми (Антон, Алиса, Борис и Белла), это схематически выглядело бы так:

2 критерия, которые нам нужно определить:

1. Расположение точек (где печатаются имена людей).
2. Линии (начальная и конечная точка соединения линий).

Определение и построение точек

Сначала нам нужно построить наши точки таким образом, чтобы промежуток между каждой точкой был одинаковым. Это создаст сбалансированный график.

Какая геометрическая фигура максимально удовлетворяет нашу потребность в таких равных промежутках? Конечно же круг!

Вы можете возразить, что на готовой модели диаграммы нет фигуры круга. Да действительно нет –вот так. Нам не нужно рисовать круг. Нам просто нужно построить точки вокруг него.

Таким образом, у нас есть 4 заинтересованные стороны, нам нужно 4 точки:

1. Если у нас 12 заинтересованных сторон, нам нужно 12 точек.
2. Если у нас есть 20, нам нужно 20 точек.

Предполагая, что источником нашего круга является (x, y), радиус – это r, а тета – 360, деленная на количество нужных нам точек. Первая точка (x1, y1) на окружности будет в этой позиции:

• x1 = x + r * COS (тета);
• y1 = y + r * SIN (тета).

Как только все точки рассчитаны и подключены к XY-диаграмме (точечная диаграмма), давайте двигаться дальше.

Построение линий на лучевой диаграмме

Допустим, у нас в сети есть n человек. Это означает, что каждый человек может иметь максимум n-1 отношений.

Таким образом, общее количество возможных линий на нашем графике равно n * (n-1) / 2.

Нам нужно разделить его на 2, как будто A знает B, тогда B тоже знает A. Но нам нужно нарисовать только 1 линию.

Шаблон лучевой диаграммы для анализа сетевого графика настроен для работы с 20 людьми. Его можно скачать в конце статьи и использовать как готовый аналитический инструмент визуализации данных связей. Это означает, что максимальное количество строк, которое мы можем иметь, будет равно 190.

Каждая строка требует добавления отдельной серии на график. Это означает, что нам нужно добавить 190 серий данных только для 20 человек. И это удовлетворяет только одному типу линии (пунктирная или толстая). Если нам нужны разные линии в зависимости от типа отношений, нам нужно добавить еще 190 серий.

Это больно и смешно одновременно. К счастью, выход есть!

Мы можем использовать гораздо меньшее количество серий и по-прежнему строить один и тот же график.

Допустим, у нас есть 4 человека – A,B,C и D. Ради простоты, давайте предположим, что координаты этих 4-х участников следующие:

• А – (0,0);
• B – (0,1);
• С – (1,1);
• Д – (1,0).

И скажем, A имеет отношения с B, C и D.

Это означает, что нам нужно нарисовать 3 линии, от A до B, от A до C и A до D.

Теперь, вместо того, чтобы поставить 3 серии для диаграммы, что если мы поставим одну длинную серию, которая выглядит следующим образом:

(0,0), (0,1), (0,0), (1,1), (0,0), (1,0)

Это означает, что мы просто рисуем одну длинную линию от A до B, от A до C, от A до D. Договорились, что это не прямая линия, но точечные диаграммы Excel могут нарисовать любую линию, если вы предоставите ей набор координат.

Таким образом, вместо 190 рядов данных для диаграммы нам просто нужно 20 рядов.

На последнем графике мы имеем 40 + 2 + 1 ряд данных. Это потому что:

• 20 линий для слабых отношений (пунктирные линии);
• 20 линий для прочных отношений (толстые линии);
• 1 строка для выделения синим цветом слабых отношений выделенного участника;
• 1 строка для выделения зеленым цветом сильных отношений выделенного участника;
• 1 комплект без линий, а просто точек для подписей данных на графике.

Как сгенерировать все 20 серий данных:

Это требует следующей логики:

• Предполагая, что нам нужны линии для отношений человека n.
• Точка этого человека будет (Xn, Yn) и уже рассчитана ранее (в точках на графике вокруг круга).
• Нам нужно всего 40 строк данных.
• Каждая нечетная строка будет иметь (Xn, Yn).
• Для каждого четного ряда:

• разделите номер строки на 2, чтобы получить номер человека (скажем, m
• (Xn, Yn), если нет отношений между n и m
• (Xm, Ym), если есть отношения.

Нам нужны формулы MOD и INDEX для выражения этой логики в Excel.

Как только все координаты линии будут рассчитаны, добавьте их к нашему точечному графику как новые ряды используя инструмент из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«КОНСТРУКТОР»-«Выбрать данные» в окне «Выбор источника данных» используйте кнопку «Добавить» для добавления всех 43-х рядов.

Реализовывать создание такой лучевой диаграммы связей будем в 3 этапа:

1. Подготовка исходных данных.
2. Обработка данных.
3. Визуализация.

Подготовка данных для лучевой диаграммы

Как уже упоминалось выше данный шаблон будет обладать возможностью визуального построения связей до 20-ти участников (компаний, филиалов, контрагентов и т.п.). На листе книги шаблона «Данные» предоставленная таблица для заполнения входящих значений. Например, заполним ее для 14-ти участников рынка:

На этом же листе создадим дополнительную таблицу, которая представляет собой матрицу связей всех возможных участников, сгенерированную формулой:

С подготовкой данных мы закончили переходим к обработке.

Как вычислить сумму векторов?

Вектора и матрицы в электронной таблице хранятся в виде массивов.

Известно, что сумма векторов – это вектор, координаты которого равны суммам соответствующих координат исходных векторов:

Для вычисления суммы векторов нужно выполнить следующую последовательность действий:

– В диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора.

– Выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы.

– Ввести в выделенный диапазон формулу перемножения диапазонов

– = Адрес_Вектора_1 + Адрес_Адрес_Вектора_2

– Нажать комбинацию клавиш [Ctrl] + [Shift] +[Enter].

Пример.

Даны два вектора:

Требуется вычислить сумму этих векторов.

Решение:

– В ячейки диапазона А2:A4 введем значения координат вектора a1, а в ячейки диапазона С2:С4 – координаты вектора a2.

– Выделим ячейки диапазона, в которых будет вычисляться результирующий вектор С (E2:E4) и введем в выделенный диапазон формулу:

=A2:A4+C2:C4

– Нажмем комбинацию клавиш [Ctrl] + [Shift] +[Enter]. В ячейках диапазона E2:E4 будут вычислены соответствующие координаты результирующего вектора.

Сложение и вычитание векторов

Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями

Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:

Im = Im1 + Im2

Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.

Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).

Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):

При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.

Заключение

Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.