Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Уравнение движения математического маятника
Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Скажите плиз Формулу максимальной скорости математического маятника!!!?
Ученик
(204),
закрыт
9 лет назад
Андрей Ясашных
Мудрец
(17167)
11 лет назад
Тут майл не даст по-человечески формулу написать!… Ноль потенциальной энергии в самой нижней точке маятника. Там же макс. кинетическая (m*v^2)/2. Вот и приравниваем потенциальную энергию (можете выразить как из высоты маятника над нулём пот. энергии, так и из угла отклонения) и выразите скорость.
Трудное детство
Оракул
(70151)
11 лет назад
уравнение колебаний математического маятника длинной L следующее s=Ssin(wt) (1), где s и S мгновенные и максимальное (амплитуда) смещения маятника, w=(g/L)^1/2 – циклическая частота колебаний маятника. скорость это первая производная смещения по времени v=ds/dt=Swcos(wt), величина Sw=S*(g/L)^1/2 равна максимальной скорости.
PS. S=La, где а – угол отклонения маятника выраженный в радианах. а должно быть не больше 15 град, чтобы (1) было верно.
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 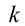
Если груз, который находится в равновесии, потянем вправо на расстояние 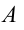
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
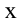
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 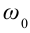
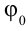
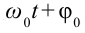
Из математики известно, что 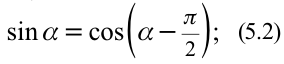
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 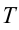

б) частота колебания 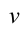
Единица
c) циклическая частота 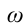
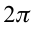
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
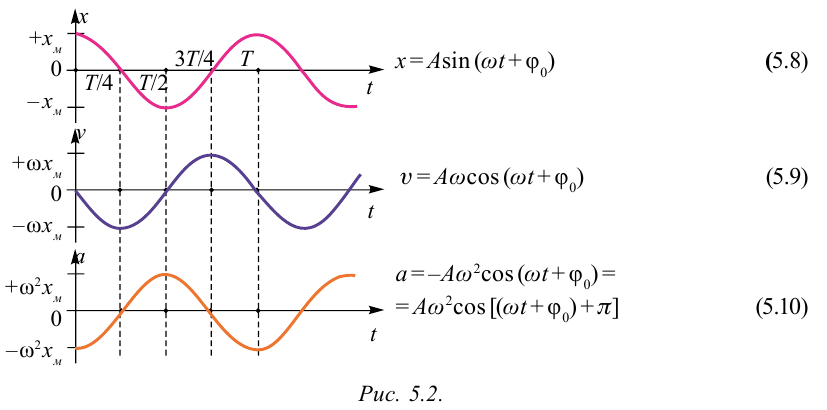
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
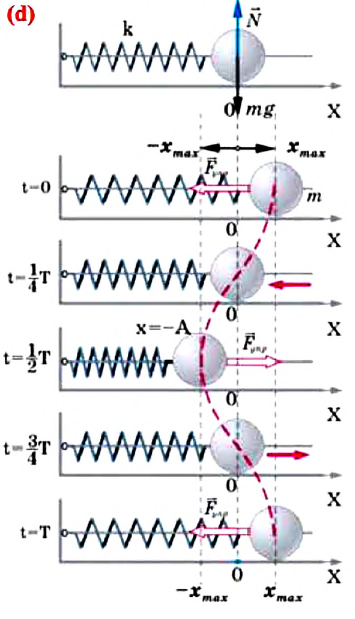
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 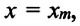
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 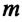
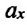
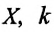
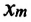
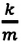
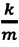
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 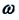
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 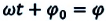
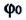

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник – это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
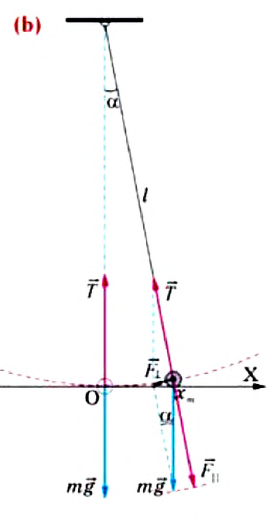
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 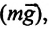
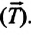
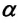
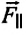
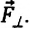
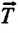
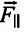
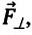
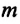
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 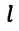
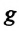
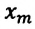
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
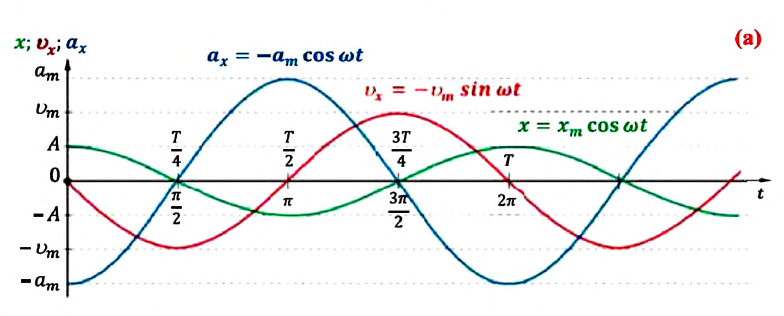
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 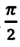
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 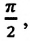
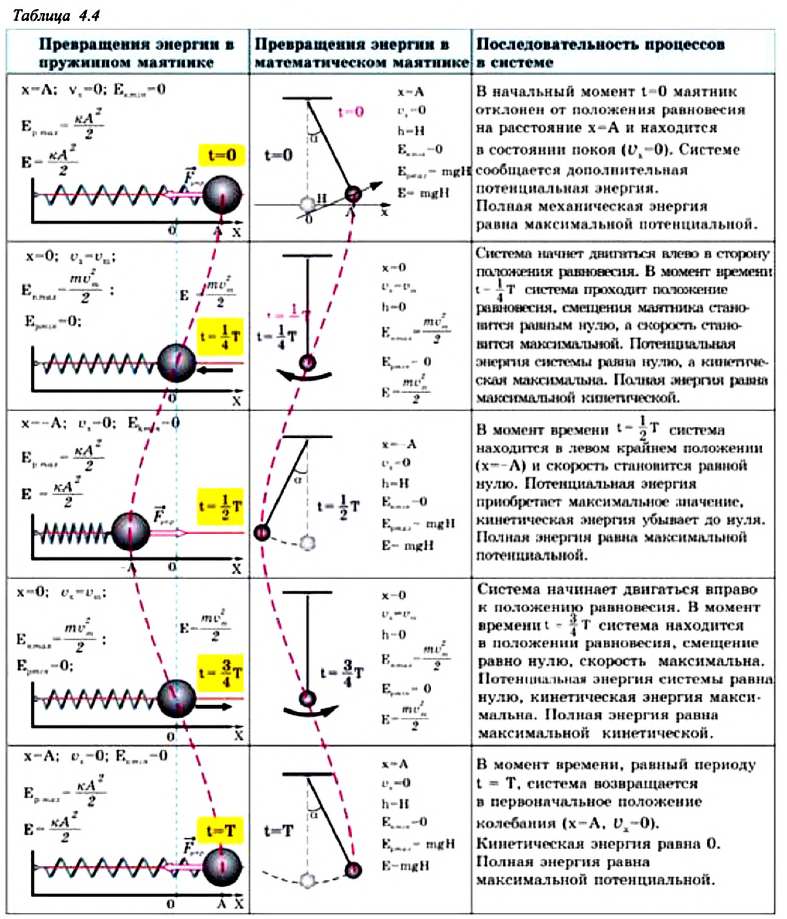
Превращения энергии при гармонических колебаниях
Теоретический материал
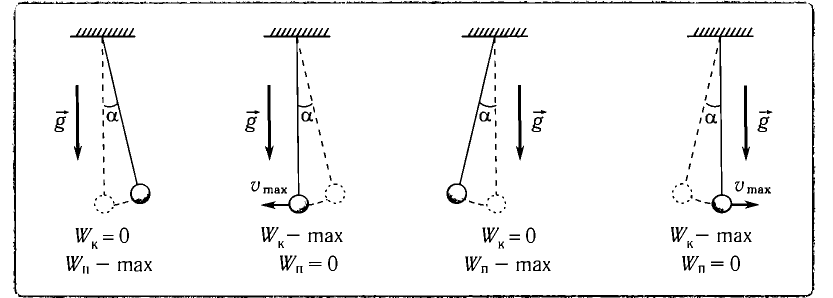
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 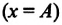
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 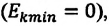
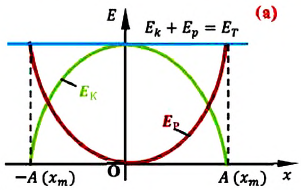
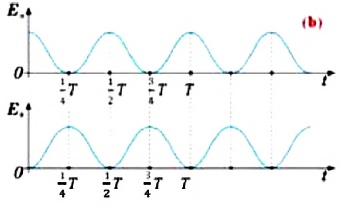
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 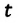
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
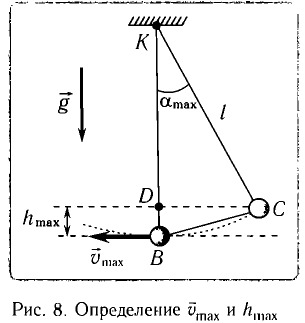
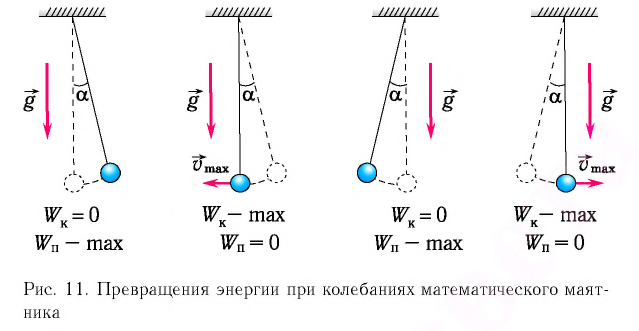
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
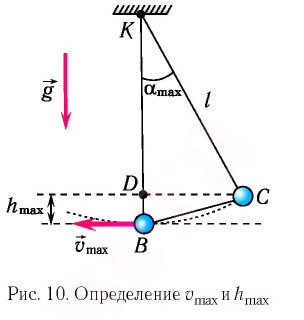
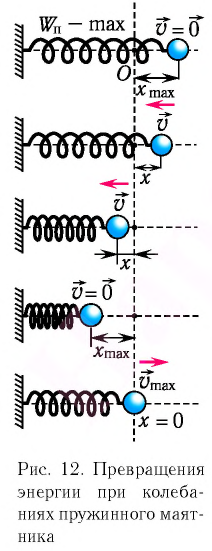
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
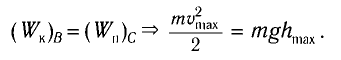
Отсюда найдем модуль максимальной скорости маятника:
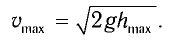
Высоту 
Если колебания малые, то 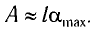
Отсюда
Подставив выражение для 
Подставляя выражения для 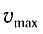

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
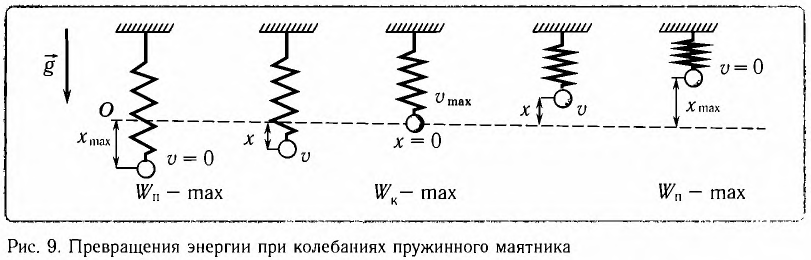
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 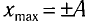
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 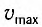
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 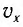
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 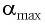
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 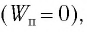
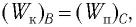
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 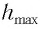
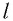
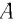
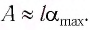
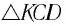
или
Подставив выражение (3) для 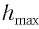
Подставляя выражения (3) для 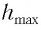
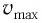
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 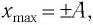
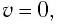
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 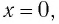
где 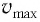
В положениях между крайними точками полная энергия
С учетом выражений для координаты 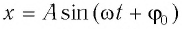
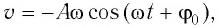
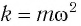
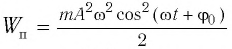
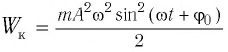
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 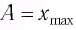
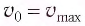
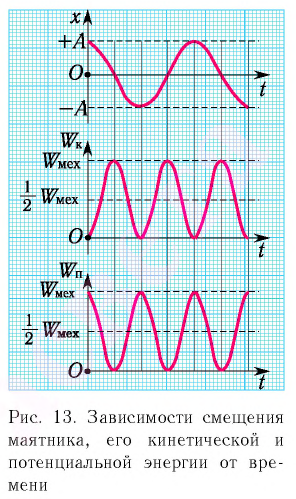
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 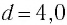
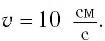
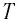
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 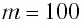
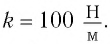
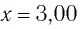
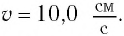
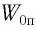
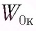
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
В начальный момент времени 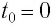
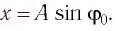
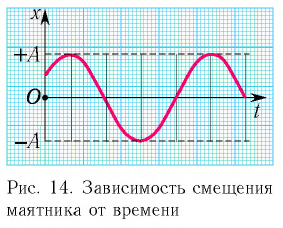
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
Скорость математического маятника
Сергей Феликсович Савельев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Математическим маятником (осциллятором) называется раскачиваемая механическая система из нерастяжимой нити с пренебрежительно малой массой и подвешенного на ней тела с точечной массой. При описании свойств такого идеального маятника пренебрегают также силами трения и прочими потерями, возникающими при проведении аналогичных опытов в реальных условиях.
Колебания идеального маятника (зависимость угла отклонения от времени) описываются уравнением:
$phi(t) = phi_0 cdot cos(omega_0 cdot t + alpha)$,
где:
- $phi(t)$ – угол отклонения от нижнего положения равновесия в момент $t$,
- $omega_0$ – циклическая частота,
- $alpha$ – исходный угол отклонения,
- $phi_0$ – амплитуда.
Свойства математического маятника
Эксперименты, проведенные над маятниками со свойствами, близкими к идеальным, показали их следующие свойства:
- период колебаний зависит не от массы подвешенного груза, а только от длины нити;
- при небольших углах отклонения частота колебаний не зависит и от амплитуды (это явление называется изохронизмом).
Период колебаний идеального маятника можно определить по формуле:
$T = 2pi cdot sqrt{frac{l}{g}}$,
где $l$ – длина нити математического маятника, $g$ – ускорение свободного падения.
Применение маятников на практике
Маятники применяют для создания хронометров. В таких часах период колебаний, отсчитывающих время, регулируют изменением расстояния между точкой крепления подвеса к неподвижной оси и центром тяжести подвешенного груза.
Замечание 1
Колебания маятника математически впервые описал в XVII в. Христиан Гюйгенс, который применил свои теоретические разработки для создания точных механических часов.
«Скорость математического маятника» 👇
В геодезии зависимость частоты колебаний маятников от изменения силы гравитации используется при определении географической широты.
Пример 1
Уточнить ускорение свободного падения для данной географической широты, если математический маятник длиной 1 м, совершает колебания с частотой 0,5 Гц (амплитуда колебаний достаточно мала).
Выразим ускорение из уравнения периода колебаний математического маятника:
$g = frac{4 cdot pi^2 cdot l}{T^2}$
Частота $omega$ – величина обратная периоду колебаний, значит
$T = frac{1}{omega}$
Подставив значения, получим
$T = frac{1}{0,5} = 2 с$
Таким образом,
$g = frac{4 cdot pi^2 cdot 1}{2^2} = frac{4 cdot pi^2 cdot 1}{2^2} = 3.14159265359^2 approx 9,8696$
Ответ: ускорение приблизительно равно $9,8696 м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 03.04.2023
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 февраля 2023 года; проверки требует 1 правка.
Математический маятник. Чёрный пунктир — положение равновесия, 
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения[1]. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен
и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.
Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.
Характер движения маятника[править | править код]
Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, следовательно, является системой с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, получится система с двумя степенями свободы (так как становятся возможными колебания по двум горизонтальным координатам).
При колебаниях в одной плоскости маятник движется по дуге окружности радиуса 
Уравнение колебаний маятника[править | править код]
Маятник (схема с обозначениями)
Если в записи второго закона Ньютона 

,
так как 

,
где неизвестная функция 




.
Для решения ДУ второго порядка, то есть для определения закона движения маятника, необходимо задать два начальных условия — угол 


Решения уравнения движения[править | править код]
Возможные типы решений[править | править код]
В общем случае решение ДУ с начальными условиями для маятника может быть получено численно. Варианты движения (в случае, если маятник — это материальная точка на лёгком стержне), качественно, представлены на анимации. В каждом окне вверху показана зависимость угловой скорости 

-
Маятник висит
-
Малые колебания (размах 45°)
-
Колебания с размахом 90°
-
Колебания с размахом 135°
-
Колебания с размахом 170°
-
Фиксация в верхнем положении
-
Движение близкое к сепаратрисе
-
Вращение маятника
Гармонические колебания[править | править код]
Уравнение малых колебаний маятника около нижнего положения равновесия, когда уместна замена 
,
где 


.
Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону[2]:
,
где 

Если пользоваться переменной 







Случай нелинейных колебаний[править | править код]
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 


Параметр 
.
Период колебаний нелинейного маятника составляет
,
где K — эллиптический интеграл первого рода.
Для вычислений практически удобно разлагать эллиптический интеграл в ряд:
где 

При углах до 1 радиана (≈ 60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:
.
Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года[3]:
,
где 

Движение по сепаратрисе[править | править код]
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.
Факты[править | править код]
Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.
- Если амплитуда колебания маятника близка к
, то есть движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения[4].
- Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
- В условиях вращения Земли при достаточно длинной нити подвеса плоскость, в которой маятник совершает колебания, будет медленно поворачиваться относительно земной поверхности в сторону, противоположную направлению вращения Земли (маятник Фуко).
См. также[править | править код]
- Физический маятник
- Маятник Фуко
- Маятник Дубошинского
Примечания[править | править код]
- ↑ 1 2 Главный редактор А. М. Прохоров. Маятник // Физический энциклопедический словарь. — М.: Советская энциклопедия. — 1983. — Статья в Физическом энциклопедическом словаре
- ↑ Скорость и ускорение маятника при гармонических колебаниях также изменяются во времени по синусоидальному закону.
- ↑ Adlaj S. An Eloquent Formula for the Perimeter of an Ellipse (англ.) // Notices of the AMS. — 2012. — Vol. 59, no. 8. — P. 1096—1097. — ISSN 1088-9477.
- ↑ В. В. Вечеславов. Хаотический слой маятника при низких и средних частотах возмущений // Журнал технической физики. — 2004. — Т. 74, № 5. — С. 1—5. Архивировано 14 февраля 2017 года.
Ссылки[править | править код]
- Коллекция Java-апплетов, моделирующая поведение математических маятников, в частности маятника Капицы.
- Java-апплет, моделирующий колебание математического маятника при наличии вязкого трения с черчением фазовой траектории.
- Учебный фильм «Математический и физический маятник», производство СССР


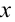


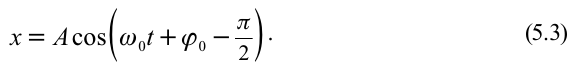

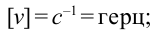

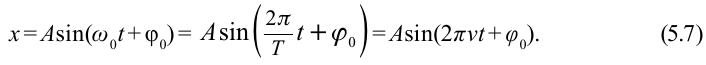
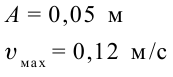
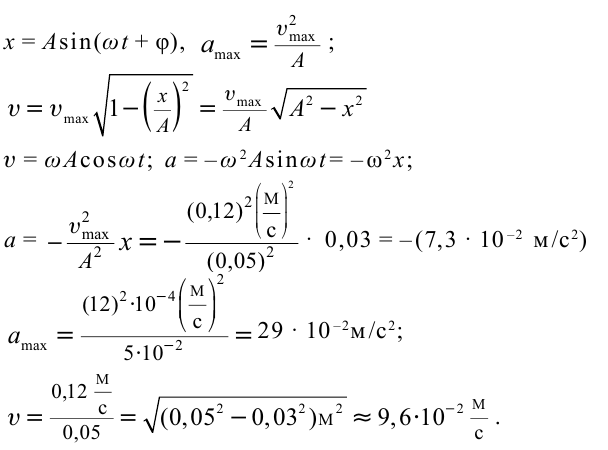
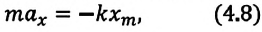
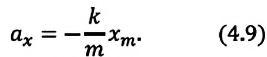
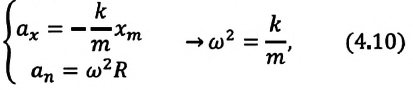
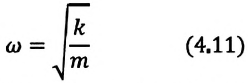
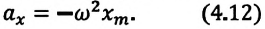
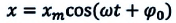
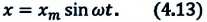
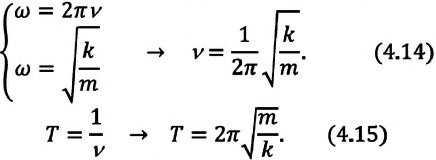
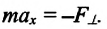
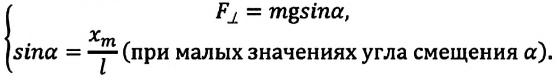
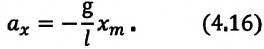
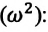


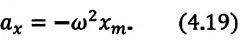
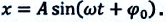
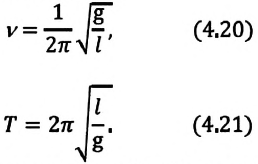
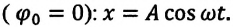
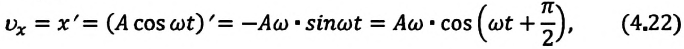
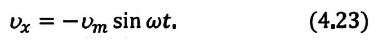

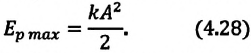
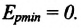
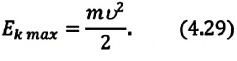
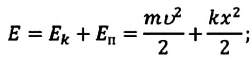
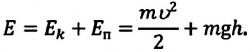
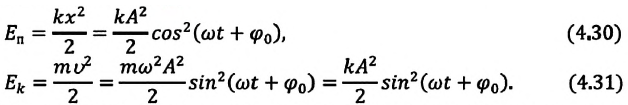
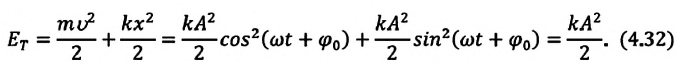
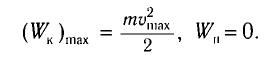
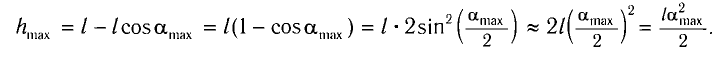
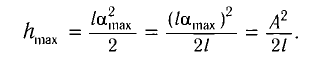
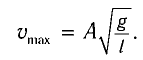
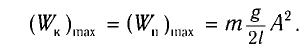
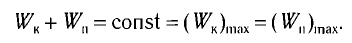
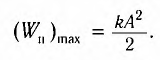
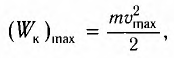
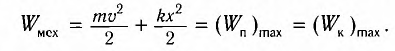
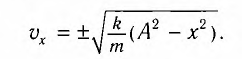
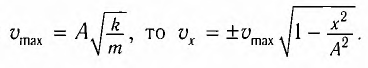
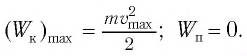
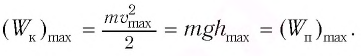
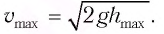
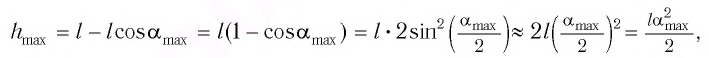
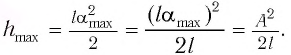
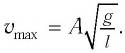
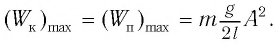
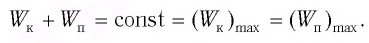
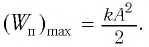
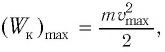
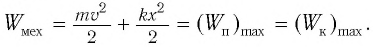
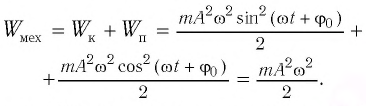
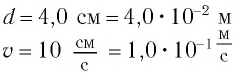
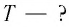
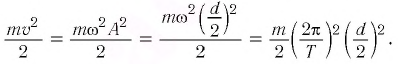
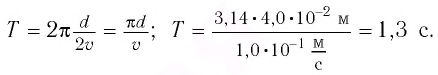

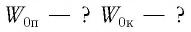
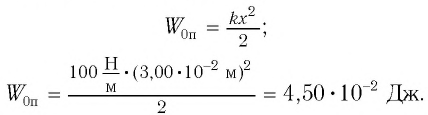
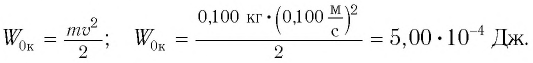
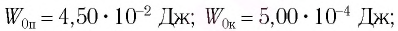
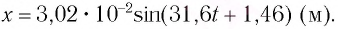




















![{displaystyle T=T_{0}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {theta _{0}}{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {theta _{0}}{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {theta _{0}}{2}}right)+dots right}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5346cf06ad62d5c061cf5527d53a86e61cf89478)



