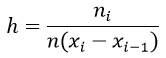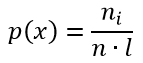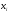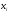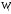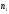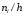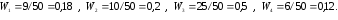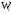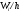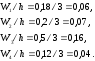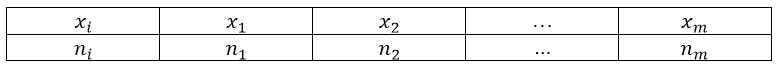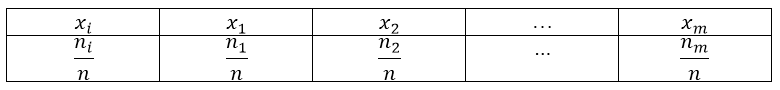Математический полигон как найти - Сайт, где вы сможете решить свои вопросы

Построение полигона, гистограммы, кумуляты, огивы

Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.

Полигон
Гистограмма
Кумулята и огива

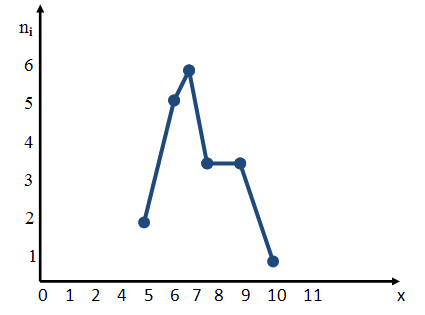
Полигон

Полигоном частот называют
ломаную, отрезки которой соединяют точки

. Для построения полигона частот на оси
абсцисс откладывают варианты

, а на оси ординат – соответствующие им
частоты

. Такие точки

соединяют
отрезками прямых и получают полигон частот.

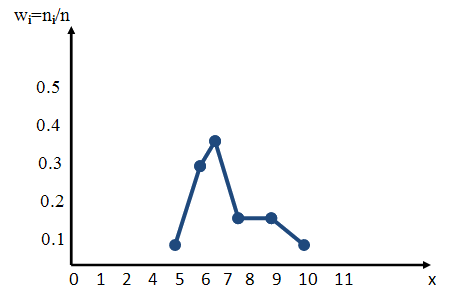
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки

. Для построения полигона относительных
частот на оси абсцисс откладывают варианты

, а на оси ординат – соответствующие им
относительные частоты (частости)

. Такие точки

соединяют
отрезками прямых и получают полигон частот.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Пример 1

Построить полигон частот и
полигон относительных частот (частостей):

Решение

Вычислим относительные
частоты (частости):

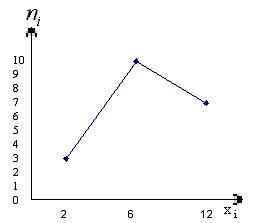
Полигон частот

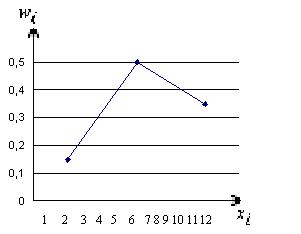
Полигон относительных частот

В случае интервального ряда для
построения полигона в качестве

берутся середины интервалов.

Гистограмма

В случае интервального
статистического распределения целесообразно построить гистограмму.

Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною

, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты

. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.

В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте

, а в случае неравных интервалов высота
равна плотности относительной частоты

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Пример 2

Построить гистограмму
частот и относительных частот (частостей)

Гистограмма частот

Гистограмма относительных частот

Пример 3

Построить гистограмму
частот (случай неравных интервалов).

Решение

Вычислим плотности
частоты:

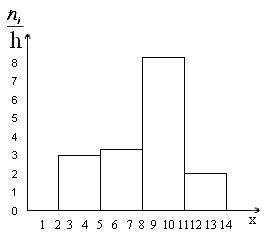
Гистограмма частот

Кроме этой задачи на другой странице сайта есть

пример построения полигона и гистограммы на одном графике для интервального вариационного ряда

Кумулята и огива

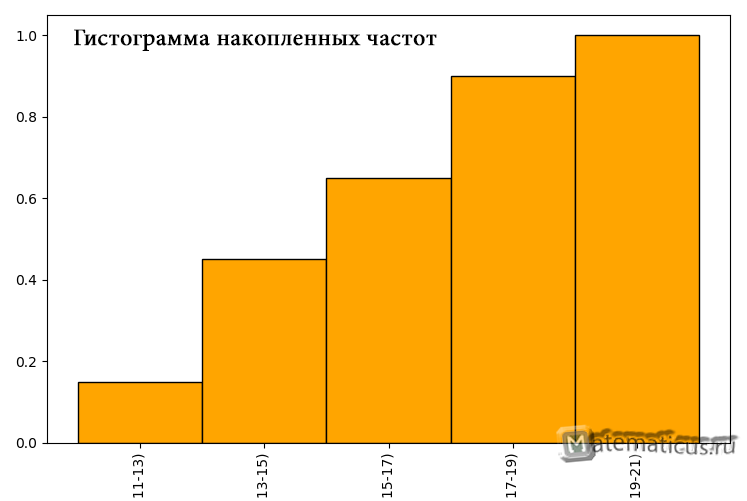
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.

Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.

Пример 4

Построить кумулятивную
кривую:

Решение

Вычислим накопленные
частоты:

Кумулятивная кривая

Источник

Гистограмма представляет собой ступенчатую фигуру в виде прямоугольников. Длина каждого прямоугольника представляет собой равный одинаковый частотный интервал и вычисляется по формуле:

x_i-x_i-1

Высоты гистограммы определяется по формуле:

Формула размаха выборки R:

R=x_max−x_min

Количество интервалов в выборке определяется по формуле:

k≈1+log₂n≈1+3,221·lgn

Длина l интервала гистограммы, формула:

l=R/n

Формула эмпирической плотности распределения выборки имеет вид:

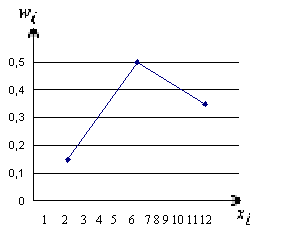
х_i — значения частот;

n_i — частоты;

w_i — относительные частоты;

n — объём выборки;

В водоёме проведены измерения температуры воды в течение 20 дней.

Статистика отчета измерений:

11, 15, 18, 14, 12, 13, 11, 14, 18, 19, 18, 14, 15, 16, 14, 18, 21, 17, 13, 16

Построить гистограмму относительных, абсолютных и накопленных частот выборки, вычислить эмпирическую плотность распределения частот.

Решение.

По условию задачи объем выборки равен 20.

Отсортируем и упорядочим вариационный ряд, начиная от самого минимального значения, получим:

11, 11, 12, 13, 13, 14, 14, 14, 14, 15, 15, 16, 16, 17, 18, 18, 18, 18, 19, 21

Найдем размах выборки

R=21-11=10

Количество интервалов в выборке равно:

k≈log₂20+1≈5,32

Округляя до целого числа, имеем

k=5

Определим длину каждого интервала

l=10/5=2

Получаем таблицу интервалов

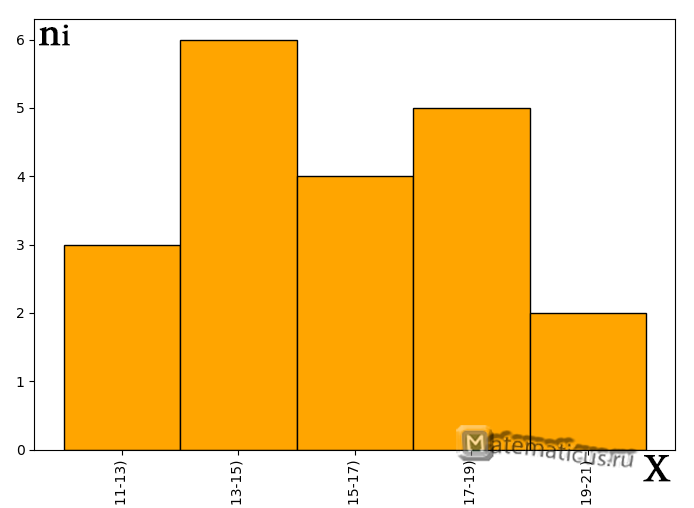
Номер интервала	Абсолютная частота, n_i	Частотный интервал
1.	3	[11;13)
2.	6	[13;15)
3.	4	[15;17)
4.	5	[17;19)
5.	2	[19;21)

Таблица относительных частот и эмпирическая плотность распределения частоты

Частотный интервал	Относительная частота, w_i=n_i/n	Эмпирическая плотность распределения частоты n_i/Δ
[11;13)	0.15	1.5
[13;15)	0.3	3
[15;17)	0.2	2
[17;19)	0.25	0.25
[19;21)	0.1	0.1

График гистограммы абсолютных частот

График гистограммы относительных частот

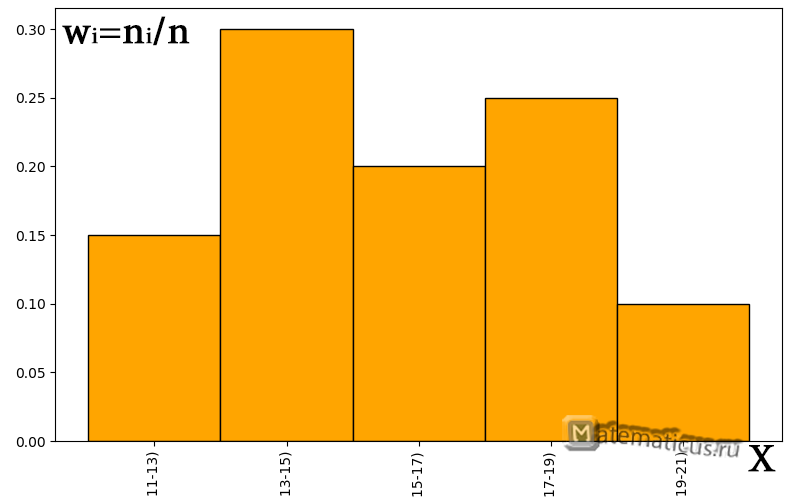
График гистограммы накопленных частот

Полигон в статистике — это график (или ломанная линия), отрезки которой соединяют точки с координатами х_i, w_i в прямоугольной системе координат между собой (см. рисунок ниже) и наглядно показывает распределение частот как для количественных, так и порядковых значений переменных, то плотность распределения случайной величины.

Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат — соответствующие им частоты n_i и соединяют точки.

Пример графика полигона частот х_i, n_i

Пример графика полигона относительных частот х_i, w_i

22684

Источник

Для
наглядности строят различные графики
статистического распределения, в
частности, полигон и гистограмму.

Определение.
Полигоном
частот называют ломаную, отрезки которой
соединяют точки (x₁,
n₁),
(x₂,
n₂),
…, (x_k,
n_k).

Для
построения полигона частот на оси
абсцисс откладывают варианты x_i,
а на оси ординат – соответствующие им
частоты n_i.
Точки (x_i,
n_i)
соединяют отрезками прямых и получают
полигон частот.

Определение.
Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки (x₁,
w₁),
(x₂,
w₂),
…, (x_k,
w_k).

Для
построения полигона частот на оси
абсцисс откладывают варианты x_i,
а на оси ординат w_i.
Точки (x_i,
w_i)
соединяют отрезками прямых и получают
полигон относительных частот.

На
рисунке изображен полигон относительных
частот следующего распределения:

x	1,5	3,5	5,5	7,5
w	0,1	0,2	0,4	0,3

Рис.
6. Полигон относительных частот.

В
случае непрерывного признака целесообразно
строить гистограмму, для чего интервал,
в котором заключены все наблюдаемые
значения признака, разбивают на несколько
частичных интервалов длинной h
и находят для каждого частичного
интервала n_i–
сумму частот вариант, попавших в i-ый
интервал.

Определение.
Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
(плотность частоты).

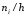
Рис.
7. Гистограмма частот.

Для
построения гистограммы частот на оси
абсцисс откладывают частичные интервалы,
а над ними проводят отрезки, параллельные
оси абсцисс, на расстоянии
.

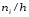
Площадь
i-го
частичного прямоугольника равна
=─ сумме частот вариантi-го
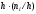
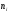
интервала; следовательно, площадь
гистограммы частот равна сумме всех
частот, то есть объему выборки n.

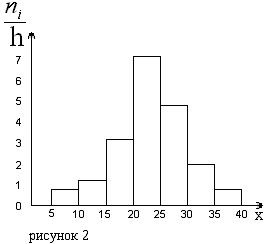
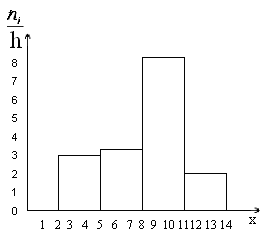
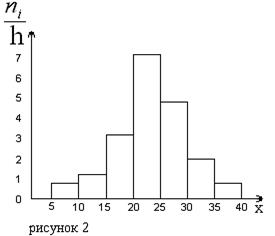
На
рисунке 2 изображена гистограмма частот
распределения объема n=100,
приведенного в таблице 1.

Частичный интервал, длиною h=5	Сумма частот вариант частичного интервала	Плотность частоты
5 – 10	4	0,8
10 – 15	6	1,2
15 – 20	16	3,2
20 – 25	36	7,2
25 – 30	24	4,8
30 – 35	10	2,0
34 – 40	4	0,8

Определение.
Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длинною h,
а высоты равны отношению
(плотность относительной частоты).

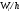
Для
построения гистограммы относительных
частот на оси абсцисс откладывают
частичные интервалы, а над ними проводят
отрезки, параллельные оси абсцисс на
расстоянии
.
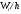
Площадьi-го
частичного прямоугольника равна
=─ относительной частоте вариант,
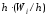
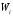
попавших вi-й
интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, то
есть единице.

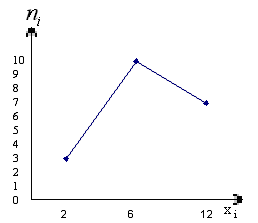
Примеры.

В
результате выборки получена следующая
таблица распределения частот.

	2	6	12
	3	10	7

Построить
полигоны частот и относительных частот
распределения.

Для
начала построим полигон частот.

Рис.
8. Полигон частот.

Чтобы
построить полигон относительных частот
найдем относительные частоты, для чего
разделим частоты на объем выборки n.

n
=
3
+
10
+
7
=
20.

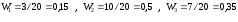
Получаем

	2	6	12
	0,15	0,50	0,35

Построим
полигон относительных частот.

Рис.
9. Полигон относительных частот.

2.
Построить гистограммы частот и
относительных частот распределения.

Найдем
плотность частоты
:

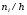
Частичный интервал, длиною h = 3	Сумма частот вариант частичного интервала	Плотность частоты
2 – 5	9	3
5 – 8	10	3,3
8 – 11	25	8,3
11 – 14	6	2

Построим
гистограмму частот.

Рис.
10. Гистограмма частот.

Чтобы
построить гистограмму относительных
частот, нужно найти относительные
частоты. Для этого найдем объем выборки
n.

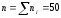
Теперь
найдем относительные частоты
:

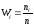
Получим:

Частичный интервал	Сумма относительных частот	Плотность частоты
2 – 5	0,18	0,06
5 – 8	0,2	0,07
8 – 11	0,5	0,16
11 – 14	0,12	0,04

Плотности
частот
нужно вычислить. При этомh
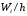
= 3.

Построим
гистограмму относительных частот.

Рис.11.
Гистограмма относительных частот.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Полигон частот и гистограмма частот

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Полигон частот

Пусть нам дан ряд распределения, записанный с помощью таблицы:

Рисунок 1.

Определение 1

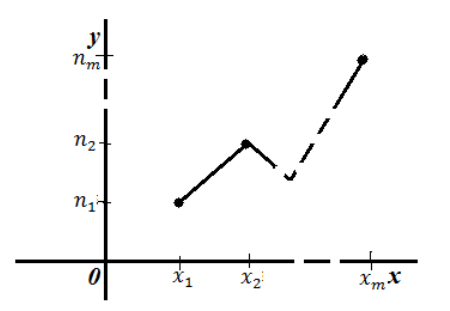
Полигон частот — ломанная, которая соединяет точки $(x_m,n_m)$ ($m=1,2,dots ,m)$.

То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие частоты. Полученные точки соединяют ломанной:

Рисунок 2. Полигон частот.

Помимо обычной частоты существует еще понятие относительной частоты.

Получаем следующую таблицу распределения относительных частот:

Рисунок 3.

Определение 2

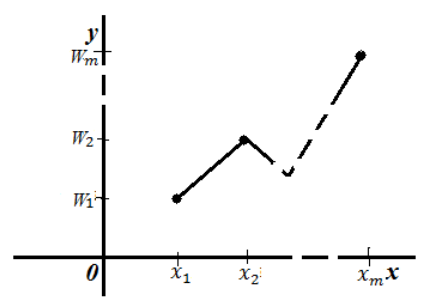
Полигон относительных частот — ломанная, которая соединяет точки $(x_m,W_m)$ ($m=1,2,dots ,m)$.

То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие относительные частоты. Полученные точки соединяют ломанной:

Рисунок 4. Полигон относительных частот.

Гистограмма частот

Помимо понятия полинома для непрерывных значений существует понятие гистограммы.

Определение 3

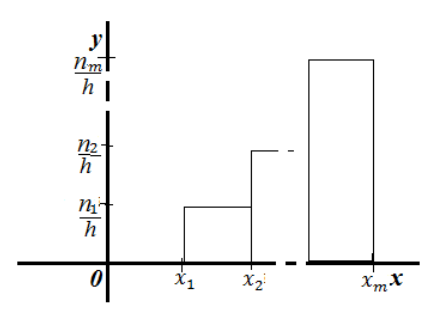
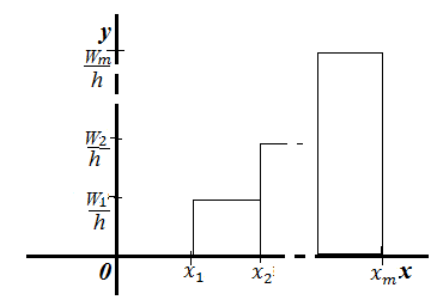
Гистограмма частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{n_i}{h}$:

Рисунок 5. Гистограмма частот.

«Полигон частот и гистограмма частот» 👇

Заметим, что площадь одного такого прямоугольника $frac{n_ih}{h}=n_i$. Следовательно, площадь всей фигуры равна $sum{n_i}=n$, то есть равна объему выборки.

Определение 4

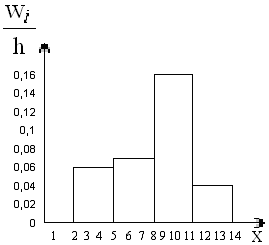
Гистограмма относительных частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{W_i}{h}$:

Рисунок 6. Гистограмма относительных частот.

Заметим, что площадь одного такого прямоугольника $frac{W_ih}{h}=W_i$. Следовательно, площадь всей фигуры равна $sum{W_i}=W=1$.

Примеры задачи на построение полигона и гистограммы

Пример 1

Пусть распределение частот имеет вид:

Рисунок 7.

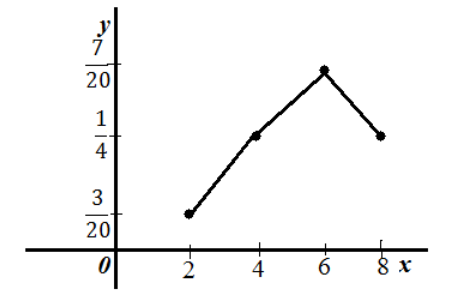
Построить полигон относительных частот.

Решение.

Построим сначала ряд распределения относительных частот по формуле $W_i=frac{n_i}{n}$

Рисунок 8.

Получим следующий полигон относительных частот.

Рисунок 9.

Пример 2

Дан ряд непрерывного распределения частот:

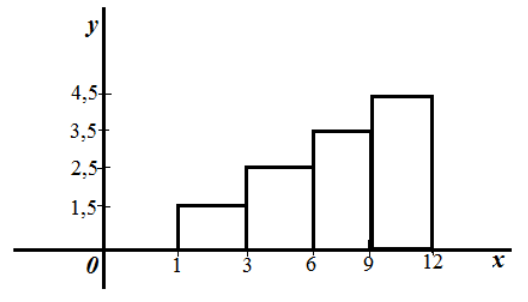
Рисунок 10.

Решение.

Очевидно, что данном случае длина частичного интервала $h=2.$ Найдем высоты прямоугольников каждой точки разбиения.

При $x=1$: $frac{3}{2}=1,5$.

При $x=3$: $frac{5}{2}=2,5.$

При $x=6$: $frac{7}{2}=3,5.$

При $x=9$: $frac{9}{2}=4,5.$

Получаем следующую гистограмму частот:

Рисунок 11.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 25.02.2023

Источник

Полигон и гистограмма

Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

Определение . Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁, n₁), (x₂, n₂), (x_k, n_k).

Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат – соответствующие им частоты n_i. Точки (x_i, n_i) соединяют отрезками прямых и получают полигон частот.

Определение . Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁, w₁), (x₂, w₂), (x_k, w_k).

Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат w_i. Точки (x_i, w_i) соединяют отрезками прямых и получают полигон относительных частот.

На рисунке изображен полигон относительных частот следующего распределения:

x	1,5	3,5	5,5	7,5
w	0,1	0,2	0,4	0,3

Рис. 6. Полигон относительных частот.

В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинной h и находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i-ый интервал.

Определение . Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность частоты).

Рис. 7. Гистограмма частот.

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на расстоянии .

Площадь i-го частичного прямоугольника равна = — сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки n.

На рисунке 2 изображена гистограмма частот распределения объема n =100, приведенного в таблице 1.

Частичный интервал, длиною h=5	Сумма частот вариант частичного интервала	Плотность частоты
5 – 10	0,8
10 – 15	1,2
15 – 20	3,2
20 – 25	7,2
25 – 30	4,8
30 – 35	2,0
34 – 40	0,8

Определение . Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длинною h, а высоты равны отношению (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i-го частичного прямоугольника равна = — относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.

1. В результате выборки получена следующая таблица распределения частот.

Построить полигоны частот и относительных частот распределения.

Для начала построим полигон частот.

Рис. 8. Полигон частот.

Чтобы построить полигон относительных частот найдем относительные частоты, для чего разделим частоты на объем выборки n.

n = 3 + 10 + 7 = 20.

Построим полигон относительных частот.

Рис. 9. Полигон относительных частот.

2. Построить гистограммы частот и относительных частот распределения.

Найдем плотность частоты :

Частичный интервал, длиною h = 3	Сумма частот вариант частичного интервала	Плотность частоты
2 – 5
5 – 8	3,3
8 – 11	8,3
11 – 14

Построим гистограмму частот.

Рис. 10. Гистограмма частот.

Чтобы построить гистограмму относительных частот, нужно найти относительные частоты. Для этого найдем объем выборки n.

Полигон частот

Полиго́н часто́т (в математической статистике) — один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.

Ссылки

См. также

Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).
Проставить интервики в рамках проекта Интервики.

Математическая статистика

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Полигон частот» в других словарях:

Полигон (значения) — Полигон: Полигон участок суши или моря, который предназначен для испытаний различных видов техники. Военный полигон объект для проведения войсковых учений или испытаний вооружений и военной техники. Полигон оборудованная территория,… … Википедия

полигон — 3.30 полигон: Испытательное средство и средство обучения персонала заказчика. Обеспечивает создание готовой к внедрению и предварительно проверенной (в условиях полигона) АСУТП или ее компонентов. Полигон АСУТП, оснащенный специальными средствами … Словарь-справочник терминов нормативно-технической документации

полигон кумулятивных частот — 2.19. полигон кумулятивных частот Ломаная линия, получаемая при соединении точек, абсциссы которых равны верхним границам классов, а ординаты либо кумулятивным абсолютным частотам, либо кумулятивным относительным частотам Источник: ГОСТ Р… … Словарь-справочник терминов нормативно-технической документации

ПОЛИГОН — – ломаная линия, соединяющая точки, соответствующие величинам частот, откладываемых по осям ординат [2, c. 67; 16, c.46; 89, c. 175] … Современный образовательный процесс: основные понятия и термины

ЧАСТОТ ПОЛИГОН — Способ рисуночного представления плотности распределения. Частота каждого интервала класса (см. групповая плотность распределения) откладывается на графике, и проводится линия, соединяющая эти точки. Эта линия называется гистограммой … Толковый словарь по психологии

РАСПРЕДЕЛЕНИЯ ПОЛИГОН — график распределения частот для порядковых и количественных переменных ( также Шкала измерительная). Представляет собой ломаную линию, наглядно демонстрирующую распределение частот. Линия Р.П. соединяет точки, координаты которых для дискретных и… … Социология: Энциклопедия

РАСПРЕДЕЛЕНИЕ ЧАСТОТЫ — Любое распределение, основанное на перечислении частоты встречаемости значений, согласно классам или категориям. Таким образом, каждому набору классов присваивается номер, который представляет наблюдаемую частоту. Независимо от метода… … Толковый словарь по психологии

НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ СТАТИСТИКИ — методы математич. статистики, не предполагающие знания функционального вида генеральных распределений. Название непараметрические методы подчеркивает их отличие от классических параметрических методов, в к рых предполагается, что генеральное… … Математическая энциклопедия

Гистограмма — Пример гистограммы У этого термина существуют и другие значения, см. Гистограмма (значения). Гистограмма (от др. греч … Википедия

КРИВАЯ РАСПРЕДЕЛЕНИЯ — – это предел, к которому стремится полигон частот при неограниченном увеличении объема статистической совокупности и уменьшения интервалов (увеличение точности измерения, переход от дискретной величины к непрерывной) [73, c. 16; 89, c. 178] … Современный образовательный процесс: основные понятия и термины

Полигон и гистограмма

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4 / 5. Количество оценок: 14

Оценок пока нет. Поставьте оценку первым.

9048

Полигон частот и гистограмма частот

ГОСТ

Полигон частот

Пусть нам дан ряд распределения, записанный с помощью таблицы:

Полигон частот — ломанная, которая соединяет точки $(x_m,n_m)$ ($m=1,2,dots ,m)$.

Рисунок 2. Полигон частот.

Помимо обычной частоты существует еще понятие относительной частоты.

Получаем следующую таблицу распределения относительных частот:

Полигон относительных частот — ломанная, которая соединяет точки $(x_m,W_m)$ ($m=1,2,dots ,m)$.

Рисунок 4. Полигон относительных частот.

Гистограмма частот

Помимо понятия полинома для непрерывных значений существует понятие гистограммы.

Гистограмма частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac$:

Рисунок 5. Гистограмма частот.

Готовые работы на аналогичную тему

Заметим, что площадь одного такого прямоугольника $frac=n_i$. Следовательно, площадь всей фигуры равна $sum=n$, то есть равна объему выборки.

Гистограмма относительных частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac$:

Рисунок 6. Гистограмма относительных частот.

Заметим, что площадь одного такого прямоугольника $frac=W_i$. Следовательно, площадь всей фигуры равна $sum=W=1$.

Примеры задачи на построение полигона и гистограммы

Пусть распределение частот имеет вид:

Построить полигон относительных частот.

Построим сначала ряд распределения относительных частот по формуле $W_i=frac$

Получим следующий полигон относительных частот.

Дан ряд непрерывного распределения частот:

Источник

Построение полигона, гистограммы, кумуляты, огивы

Полигон

Гистограмма

Кумулята и огива

Полигон частот и гистограмма частот

Полигон частот

Гистограмма частот

Примеры задачи на построение полигона и гистограммы

Полигон и гистограмма

Полигон частот

Ссылки

См. также

Полезное

Смотреть что такое «Полигон частот» в других словарях:

Полигон и гистограмма

Полигон частот и гистограмма частот

Полигон частот

Гистограмма частот

Готовые работы на аналогичную тему

Примеры задачи на построение полигона и гистограммы

Вам также может понравиться

Как найти справочник строительных компаний

Minecraft как найди деревню

Как найти прикольные стикеры в вотсапе

Добавить комментарий Отменить ответ