Содержание
- – Как найти длину дуги окружности 6 класс?
- – Как вычислить длину дуги окружности?
- – Как найти длину окружности?
- – Как найти градусную меру дуги?
- – Как найти длину дуги окружности зная хорду?
- – Как рассчитать длину дуги для навеса?
- – Какая формула описывает длину окружности?
- – Как вычислить длину окружности и площадь круга?
- – Как найти длину окружности и площадь?
- – Как найти радиус окружности зная длину дуги и центральный угол?
Мы имеем формулу для вычисления длины окружности, если известен диаметр: C = π ⋅ d . Если вспомним, что d = 2 r , то формула длины окружности будет выглядеть так: C = 2 π ⋅ r .
Как вычислить длину дуги окружности?
Если измерение дуги (или центрального угла) задано в радианах, то формула для длины дуги окружности является произведением радиуса и измерения дуги. где r-радиус окружности, а m-мера дуги (или центрального угла) в градусах.
Как найти длину окружности?
Формула Чтобы найти длину окружности, нужно либо диаметр окружности умножить на $pi approx 3,1415926535 dots$, либо найти удвоенное произведение радиуса и числа $pi$.
Как найти градусную меру дуги?
Дугу окружности можно измерять в градусах. Градусная мера дуги — это градусная мера соответствующего ей центрального угла. NMB = 360° – ∠NOB = 360° – 135° = 225°. AMB + ALB = 360°.
Как найти длину дуги окружности зная хорду?
Существует также формула Гюйгенса для расчета длины дуги окружности через хорду. Для того чтобы ей воспользоваться нужно провести перпендикуляр из середины хорды, соединяющий ее с самой дугой, а из точки соединения перпендикуляра с дугой провести еще два отрезка к концам хорды.
Как рассчитать длину дуги для навеса?
Формула будет иметь вид P=pi*r*n/180, где:
- Р — длина дуги (применительно к нашему случаю — длина листа поликарбоната или профильной трубы, которая станет элементом каркаса).
- pi — число «пи» (в расчетах, в которых не требуется крайне высокая точность, обычно принимаемое равным 3,14).
- r — радиус дуги.
Какая формула описывает длину окружности?
= π. Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам.
Как вычислить длину окружности и площадь круга?
Вычислить длину окружности и площадь круга одного и того же заданного радиуса R. Далее пишем простейшую программу: program z_1; var P, R, S: real; begin write(‘Введите радиус круга: ‘); read(R); writeln(‘Длина окружности: ‘, 2*pi*R); writeln(‘Длина окружности: ‘, pi*R*R); end.
Как найти длину окружности и площадь?
Так как длина всей окружности равна C = 2 π ⋅ R , то длина дуги в 1° равна 2 π R 360 ° = π R 180 ° . Если градусная мера дуги равна α градусам, то длина такой дуги ∪ AB = l выражается формулой l = π R 180 ° ⋅ α . Площадь круга определяется по формуле S = π ⋅ R 2 .
Как найти радиус окружности зная длину дуги и центральный угол?
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Интересные материалы:
Как увеличить урожай клубники в 10 раз?
Как увеличить звук на Honor?
Как увидеть информацию на флешке?
Как узаконить уже сделанную перепланировку в Екатеринбурге?
Как узнать 4к монитор или нет?
Как узнать дату создания файла JPG?
Как узнать есть ли в земле кабель?
Как узнать есть ли вода под натяжным потолком?
Как узнать имя беспроводной сети SSID?
Как узнать Кбе банка?
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром,
радиусом и диаметром окружности.
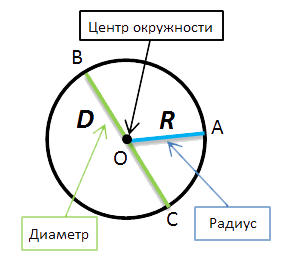
- (·)O — называется центром окружности.
- Отрезок, который соединяет
центр и любую точку окружности, называется радиусом окружности.
Радиус окружности обозначается буквой «R». На рисунке выше —
это отрезок «OA». - Отрезок, который соединяет
две точки окружности и проходит через её центр, называется
диаметром окружности.Диаметр окружности обозначается буквой «D».
На рисунке выше — это отрезок «BC».На рисунке также видно, что диаметр равен двум радиусам. Поэтому
справедливо выражение «D = 2R».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что
такое число π (читается как «Пи»), которое
так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность
и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π ≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,
округленное до разряда сотых
π ≈ 3,14…
Теперь, зная, что такое число π, мы
можем записать формулу длины окружности.
Запомните!
Длина окружности
— это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С» (читается как «Це»).
C = πD
C = 2πR
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Разбор примера
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число
π
округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.
Разбор примера
Условие задачи:
Определите диаметр окружности, если
её длина равна 56,52 дм.
(π ≈ 3,14).
Выразим из формулы длины окружности диаметр.
C = πD
D = С / π
D = 56,52 / 3,14 = 18 дм
Хорда и дуга окружности
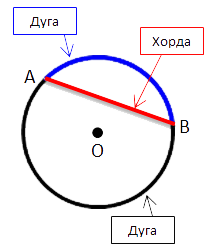
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность
на две части, каждую из которых называют дугой.
Это синяя дуга «AB» и черная дуга «AB».
Точки «A» и «B» называют концами дуг.
Соединим точки «A» и «B» отрезком. Полученный отрезок называют
хордой.
Важно!
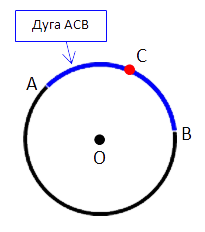
Точки «A» и «B» делят окружность на две дуги. Поэтому важно
понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на
нужной дуге и обращаются к ней по трем точкам.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 мая 2020 в 10:27
Владислав Заступневич
Профиль
Благодарили: 0
Сообщений: 1
Владислав Заступневич
Профиль
Благодарили: 0
Сообщений: 1
, Радиус одной окружности равен 12 см, а второй-36см.Чему равно отношения длины первой окружности к длине второй окружности?
0
Спасибо
Ответить
6 мая 2020 в 15:48
Ответ для Владислав Заступневич
Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
С=2πR
если длину одной окружности разделить на дилну другой, то 2π сократится, следовательно длины будут относится так же как радиусы, то есть 12:36=
0
Спасибо
Ответить
22 сентября 2016 в 19:03
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Помогите 2) чему равен деаметр если радиус равен а)12см б)10 децеметров
1) начертить окружность радиусом а)2 см пот буквой б)4см 5мм (начертиь!)
3)Чему равен радиус если деаметр равен а)6см б)9см в)12мСРОЧНО СЕГОДНЯ! ПРОШУ!!!
0
Спасибо
Ответить
23 сентября 2016 в 14:51
Ответ для Вика Камалова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Радиус равен половине диаметра. Обратно диаметр равен двум радиусам. Подробнее здесь.
1) а) 12см · 2=24см б)10дм · 2 = 20дм
2) ответил в теме.
3) а) 6см: 2 = 3см б) 9см: 2 = 4см 5 мм в)12м: 2 = 6м
0
Спасибо
Ответить
22 сентября 2016 в 18:54
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
1)Начертить окружность радиусом а)2 см пот буквой б)4 см 5 мм
0
Спасибо
Ответить
23 сентября 2016 в 14:46
Ответ для Вика Камалова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Радиус окружности это расстояние от центра до любой точки окружности. Подробнее можно посмотреть вот здесь. На линейке циркулем отмеряем необходимый радиус и чертим окружность.
0
Спасибо
Ответить
24 января 2016 в 13:45
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Длина окружности и площадь круга.
Я не понимаю как найти площадь круга.
0
Спасибо
Ответить
19 сентября 2016 в 10:56
Ответ для Инна Шабрашина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
7 сентября 2015 в 21:08
Игорь Желтоновский
Профиль
Благодарили: 0
Сообщений: 1
Игорь Желтоновский
Профиль
Благодарили: 0
Сообщений: 1
радиус — 2,1 м.Найти длинну круга и его площадь(помогите плз)
0
Спасибо
Ответить
2 сентября 2016 в 15:18
Ответ для Игорь Желтоновский
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Длина окружности(l) вычисляется по формуле: l=2?r
Площадь круга(S) вычисляется по формуле: S=?r2
Подставляем значения и считаем, приняв ?=3,14
l=2 · 3,14 · 2,1 = 13,188
S = 3,14 · 2,12=13,8474
Более подробно можно прочитать здесь: math-prosto.ru/index.php?page=pages/circle/square_of_circle.php
0
Спасибо
Ответить

{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
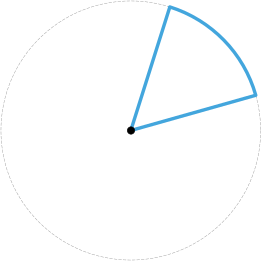
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.
-
Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
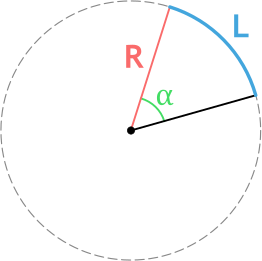
Формула длины дуги окружности через радиус и угол
{L = dfrac{pi R alpha}{180degree}}
R – радиус окружности
α – центральный угол (угол между радиусами) в градусах
{L = R alpha}
R – радиус окружности
α – центральный угол (угол между радиусами) в радианах
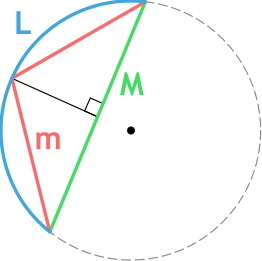
Формула длины дуги окружности по формуле Гюйгенса
{L approxeq 2m + dfrac{2m-M}{3}}
m – длина хорды m
M – длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Дуга окружности – это фрагмент окружности. Если на окружности отметить две точки A И B, то она разобьётся на 2 части, называемые дугами окружности.
Для того, чтобы найти длину дуги окружности, необходимо использовать значение центрального угла, измеряемого в радианах или градусах.
Существует 2 формулы длины дуги окружности:
1) Если дан центральный угол в радианах: l = R*α, где R – радиус, α – величина угла AOB в радианах.
2) Если дан центральный угол в градусах: l = R*π*C/180, где R – радиус, C – величина угла AOB в градусах.
Пример
Дано:
1) радиус окружности R = 6 дм.
2) центральный угол AOB = 45°.
Найти:
Длину дуги AB.
Решение:
l = 6*3,14*1/4 дм. = 4,71 дм.
Длина дуги
Онлайн калькулятор

радиус r =
угол α =
Теория
Чему равна длина дуги окружности L если её радиус r, а угол между двумя прямыми, проведёнными от центра окружности к конечным точкам дуги – центральный угол α?
Формула
Если угол в градусах:
Если угол в радианах:
Пример
Для примера посчитаем чему равна длина дуги окружности с радиусом r = 2 см и центральным углом α = 45° :
L = 3.14 ⋅ 2 ⋅ 45/180 = 6.28 ⋅ 0.25 = 1.57 см
Площадь круга и его частей. Длина окружности и ее дуг
Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
Как найти длину дуги окружности ?
r – радиус окружности
α – угол AOB, в градусах
Формула длины дуги ( L ):
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
[spoiler title=”источники:”]
http://www.resolventa.ru/demo/diaggia6.htm
http://www-formula.ru/2011-09-21-06-50-23
[/spoiler]