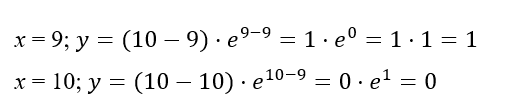Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
По мнению выпускников, задание № 11 — самое сложное в первой части ЕГЭ по математике. Ведь там… производная! На деле не стоит бояться — все задания можно решить, зная только 2 алгоритма. В этой статье я о них расскажу! А еще поделюсь полезным лайфхаком, как решать некоторые задания на производную в ЕГЭ, вообще не используя алгоритм и экономя драгоценное время.
В этой статье:
Почему задания на производную решает только 40% выпускников?Два прототипа задания № 11 ЕГЭ по математикеПоиск точек экстремумаПоиск наибольшего / наименьшего значения функцииЛайфак, чтобы решать задания на производную в ЕГЭ
До ЕГЭ все меньше времени, и 11-классники уже на финишной прямой. Усилить подготовку и написать на максимальный балл поможет «ЕГЭ-гонка» 🏁 На экспресс-марафоне вы повторите ключевые разделы предмета, прорешаете множество заданий и попробуете симуляцию экзамена, а также узнаете все секреты ЕГЭ-2023 от преподавателей, написавших работу в досрочный период. Записывайтесь на марафон и придите первыми в гонке ЕГЭ!
Почему задания на производную решает только 40% выпускников?
Ни для кого не секрет, что профильный ЕГЭ по математике состоит из частей с кратким и развёрнутым ответом. В первой части всего 11 заданий. В том числе и интересующее нас задание № 11.
Задание № 11 проверяет, умеют ли выпускники работать с производной. По статистике его решают около 40% всех сдающих экзамен, что для первой части ЕГЭ по математике очень мало.
Проблема этого задания в том, что производную проходят только в середине 11 класса, когда уже активно идет подготовка к ЕГЭ по другим темам. Из-за этого школьники не успевают ее отработать.
Два прототипа задания № 11 ЕГЭ по математике
В этом номере есть всего два типа заданий, которые можно решить с помощью простых алгоритмов. Ученикам нужно лишь запомнить их и выучить таблицу производных.
Сначала необходимо понять, что именно от нас хотят в задании — расскажу небольшой лайфхак. Многие ученики путают понятия «точка максимума / минимума» и «наибольшее / наименьшее значение». Дело в том, что точка экстремума – это x, а наибольшее или наименьшее значение – это у. Как не запутаться? Обрати внимание на слово-маркер «точка». Если ты видишь его, то речь идет об х, если этого слова нет, то речь об у.
Поиск точек экстремума
Теперь, когда мы разобрались, как не запутаться и понять, что необходимо найти в задаче, приступим к разбору самих заданий и алгоритмов к ним. Начнём с поиска точек экстремума. Чтобы провести анализ функции, необходимо определить основные этапы. У функции есть точки экстремума, в них производная равна нулю. Единственный способ, определить, является ли данная точка точкой максимума или минимума – это определить знаки производной до и после неё, если знак производной меняется с «–» на «+», то это будет точка минимума, а если с «+» на «–», то точка максимума. Таким образом общий порядок действий будет следующим:
Данному алгоритму подчиняются абсолютно все задания, в которых нужно найти точки экстремума.
Поиск наибольшего / наименьшего значения функции
Перейдём ко второму прототипу, в котором нужно найти наибольшее/наименьшее значение функции. Интересно, что второй прототип можно отличить даже визуально, потому что кроме самой функции вам будет дан ещё промежуток, ограничивающий функцию в двух точках [a; b]. Так как мы про эти точки ничего не знаем, их придётся дополнительно учитывать. В остальном начало этого алгоритма будет совпадать с предыдущим. Начинать всегда будем именно с точек экстремума, потом проверим, как ведёт себя функция в каждой точке экстремума, а также в начале и конце заданного промежутка, и в итоге запишем в ответ нужное значение функции.
Лайфак, чтобы решать задания на производную в ЕГЭ
Давайте посмотрим на некоторые задания, которые можно решить гораздо быстрее, не прибегая к использованию алгоритмов. Лайфхаки не работают на абсолютно всех заданиях, поэтому будьте аккуратны, применяя их!
Лайфхак, которые мы рассмотрим сегодня, будет опираться на знание формата экзамена. № 11 – задание из части с кратким ответом, ответ на который мы пишем в клеточки на бланке, а чего в этих клеточках не может быть? Очевидно, что бесконечную дробь, буквы 𝑒, ln(…), log(…), 𝜋, sin𝑥, бесконечность и прочие знаки мы не сможем записать, и это очень сильно упрощает нам задачу.
Разбираем лайфхак на примере
Чтобы выполнить данное задание, необходимо знать таблицу производных и немного порассуждать логически. Если мы пойдём по алгоритму, нам придётся брать производную от e в степени (x-9), а производная от данной функции будет равна тому же самому. И получается, что мы никак не можем избавиться от символа, которого просто не может быть в ответе.
Или можем? Есть замечательная степень, которая абсолютно любое основание может превратить в единицу — это 0. Таким образом, мы можем избавиться от е, если представим её степень (х – 9) равной нулю. Получается х – 9 = 0, тогда х = 9.
Но единственный ли это способ избавиться от «е»? На самом деле нет, так как есть ещё один множитель – скобка. Ее можно занулить, тогда занулится и всё произведение. Получим 10 – х = 0, тогда х = 10. Но не стоит забывать, что найти нас просят наименьшее значение ФУНЦИИ, поэтому теперь подставим найденные х в исходную функцию.
При х = 9 получаем 1, а при х = 10 получаем 0. Видим, что значение 0 меньше, чем 1, а значит именно его мы запишем в ответ. Обратите внимание, что оно достигается при х = 10, поэтому критично важно учитывать как степень экспоненты, так и множитель-скобку.
В этой статье мы рассмотрели два алгоритма, с помощью которых можно решить абсолютно любое задание № 11 ЕГЭ по математике. А еще вы узнали лайфхак, как можно выполнить задание на производную в ЕГЭ, не прибегая к использованию алгоритма, и сэкономить время!
- Учите производную
- Пользуйтесь алгоритмами
- Не забывайте про крутые лайфхаки, но будьте внимательны, применяя их!
Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:
$f'(x_0)={lim}↙{△x→0}{△f(x_0)}/{△x}$
Дифференцированием называют операцию нахождения производной.
Таблица производных некоторых элементарных функций
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^{n-1}$ |
| ${1}/{x}$ | $-{1}/{x^2}$ |
| $√x$ | ${1}/{2√x}$ |
| $e^x$ | $e^x$ |
| $lnx$ | ${1}/{x}$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | ${1}/{cos^2x}$ |
| $ctgx$ | $-{1}/{sin^2x}$ |
Основные правила дифференцирования
1. Производная суммы (разности) равна сумме (разности) производных
$(f(x) ± g(x))’= f'(x)±g'(x)$
Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$
Производная суммы (разности) равна сумме (разности) производных.
$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx – {1}/{x^2}$
2. Производная произведения
$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$
Найти производную $f(x)=4x·cosx$
$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$
3. Производная частного
$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$
Найти производную $f(x)={5x^5}/{e^x}$
$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))’=f'(g(x))·g'(x)$
$f(x)= cos(5x)$
$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$
Физический смысл производной
Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.
$v(t) = x'(t)$
Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?
Решение:
1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции
$v(t) = x'(t) = 1,5·2t -3 = 3t -3$
2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:
$3t-3 = 12$
$3t = 15$
$t = 5$
Ответ: $5$
Геометрический смысл производной
Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.
$k = tgα$
Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:
$f'(x_0) = k$
Следовательно, можем составить общее равенство:
$f'(x_0) = k = tgα$
На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.
На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.
На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение:
Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$
Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.
Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)
$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$
$f'(x_0) = tg ВАС = 0,25$
Ответ: $0,25$
Производная так же применяется для нахождения промежутков возрастания и убывания функции:
Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.
Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.
В ответ запишите количество данных точек.
Решение:
Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.
В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.
Ответ: $2$
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
2
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.
3
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
4
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
5
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Пройти тестирование по этим заданиям
Выпускники, прошедшие через ЕГЭ по математике, отмечают, что задание под номером 11 – самое сложное в первой части профильного варианта. Весь сыр-бор из-за производной.
Переживать из-за производной не стоит, пользуясь всего лишь двумя алгоритмами, можно решить абсолютно любое задание с ней, эта статья посвящена им. Также в материале будут представлены интересные хитрости, позволяющие быстро решать задачи из ЕГЭ на производную, без каких-либо алгоритмов.
В этом материале:
- Почему только 40 процентов сдающих успешно справляются с производной в ЕГЭ
- Как выглядят два прототипа 11 задания из первой части профильной математики ЕГЭ
- Как найти две точки экстремума функции
- Как найти наибольшее или наименьшее значение функции
- Хитрость, помогающая быстро разобраться с производной в ЕГЭ
Все, кто хоть немного знаком с темой выпускного госэкзамена (например, те, кто ходят на онлайн занятия по математике к репетитору), в курсе, что профильный вариант математики содержит две части: с кратким ответом и подробным ответом. Краткая часть содержит 11 заданий, последнее связано с производной, вот на нем следует остановиться подробнее.
Задача задания: выяснить, знают ли сдающие школьники понятие производной и умеют ли они вычислять ее. Статистика показывает, что 60% из них не в состоянии успешно выполнить это задание, это большая цифра.
В оправдание сдающих можно сказать то, что тема производной впервые рассматривается на уроках математики в выпускном классе, в середине года, у школьников просто не хватает времени хорошо проработать тему.
Как выглядят два прототипа 11 задания из первой части профильной математики ЕГЭ?
Для упрощения задачи выпускникам составители придумали сделать два вида задания, каждое из них решается по одному и тому же алгоритму, отличаются только числа и буквы. Чтобы успешно справиться с одним из прототипов, требуется только запомнить таблицу производных, также стоит походить на онлайн занятия математикой.
Прежде чем приступить к решению, стоит разобраться в сути задания. Существует небольшая хитрость для этого. Выпускники плохо ориентируются в понятиях, они не могут отличить «точку максимума» от «точки минимума», «наибольшее» или «наименьшее значение» функции.
Точку экстремума (максимума или минимума) функции принято обозначать буквой x, а наибольшее или наименьшее значение принято обозначать буквой y. Здесь легко растеряться и ошибиться. Чтобы этого избежать, нужно обратить внимание на слово «точка экстремума». Слово «точка» – маркер, если оно есть в задании, значит требуется найти x, в противном случае – y.
Для работы в Учи.Дома мы тщательно отбираем онлайн репетиторов по математике, которые зажигают в детях интерес к предмету. Их профессионализм и энергичность дают потрясающий результат: ученики с нетерпением ждут новых занятий и без напоминаний выполняют домашние задания.
Как найти две точки экстремума функции?
Если ученик понял разницу между x и y, нужно перейти к следующей части – поиску точек экстремума. Математическая функция содержит две точки, в которых производная равняется нулю. Чтобы понять, где точка минимума, а где максимума – нужно обратить внимание на то, какой знак у производной до и после точки. Если до знак был «+», а стал «-», то это точка максимума, и наоборот, если знак до точки был «-» – это точка минимума. Алгоритм работает следующим образом:
Он универсален для каждого прототипа 11 задания, где требуется найти точки максимума или минимума. Такой метод часто репетиторы разбирают на онлайн занятиях математикой.
Как найти наибольшее или наименьшее значение функции?
Второй тип задания отличается от первого даже своим видом, а не только формулировкой. Сдающему представляется не только сама функция, но и ее отдельный промежуток вида [a, b]. Изначально про точки этого промежутка нет никакой информации, но на них следует обратить внимание.
Начало алгоритма похоже на предыдущий: нужно найти точки максимума и минимума, определить изменение функций в этих точках. После этого нужно приступить к данному в задании промежутку – определить поведение функции в его точках.
Хитрость, помогающая быстро разобраться с производной в ЕГЭ
Для части заданий можно проигнорировать указанные выше алгоритмы, сделать все проще и быстрее с помощью маленькой хитрости. Стоит быть внимательным при ее использовании чтобы не ошибиться, она не работает для всех заданий.
Хитрость относится к формату ЕГЭ, задание номер 11 требует краткого ответа. Это значит, что в бланк ответов нельзя вписать бесконечную дробь, некоторые математические знаки, обозначающие числа (например, число Пи или число Е), знаки для синуса, логарифма и т.д. Для подкованного выпускника – это упрощение решения.
Хотите, чтобы ваш ребенок полюбил математику с младших классов? Запишите его на бесплатный вводный урок, где мы покажем, каким увлекательным может быть этот «сложный» предмет.
Пример использования хитрости
Для успешного выполнения ученик должен наизусть помнить таблицу производных, далее – простая логика.
В задании есть число Е, значит, придется брать производную от него, причем ответ будет тем же самым числом. Поскольку в бланке ответов число Е вписать нельзя, становится понятно, что основная задача – это избавиться от него. Но возможно ли это сделать? Да, если вспомнить свойства степеней и одну хитрость.
В указанном примере нужно превратить число в единицу, поскольку Е – это основание степени, нужно, чтобы его показатель был равен нулю. Получается – (x – 9) = 0. При таком раскладе даже второклассник сможет найти икс, он равен 9.
Можно по-другому избавиться от числа. Скобки в примере – тоже своего рода множитель. Если представить, что результат действий в скобках равен нулю, то получается, что 10 – x = 0. Икс находится так же просто, он равен уменьшаемому – десяти.
На этом решение не заканчивается. В задании потребовалось найти наименьшее значение функции – нужно подставить икс в данную функцию.
В первом примере, когда икс равен 9 – значение функции игрек равно 1, в другом примере, где икс равен 10, игрек равен 0. Второе значение меньше первого, значит нужно именно его вписать в ответ.
Чтобы вписать правильный ответ, нужно применить оба метода для того, чтобы найти именно наименьшее или наибольшее значение.
Применяя оба метода, довольно легко можно решить любое 11 задание в ЕГЭ. Не стоит забывать и про хитрости формата, для упрощения задачи. Но лучше все же ходить и на онлайн занятия математикой к репетиторам, чтобы быть уверенным в успешной сдаче экзамена.
Что следует запомнить:
- Нужно учить таблицы производных;
- Алгоритмы – удобный и верный способ решения;
- При использовании хитростей нужно обращать внимание на производную.