Математика как найти в задаче площадь – Сайт, где вы сможете решить свои вопросы

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Запомните!
$!$

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S = a · a

Пример:

$площадь квадрата$
S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Запомните!
$!$

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S = a · b

Пример:

$площадь прямоугольника$
S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Запомните!
$!$

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Запомните!
$!$

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

$площадь фигуры$

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

$площадь сложной фигуры$
S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Запомните!
$!$

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Рассмотрим прямоугольник:

$диагональ прямоугольника делит на равные треугольники$

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
$знак треугольника$
ABC и
$знак треугольника$ ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см²

S_ABC =
S_ACD = 10 см²

Ваши комментарии

Важно!
$Галка$

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

$Пришелец пожимает плечами$

Оставить комментарий:

3 декабря 2015 в 22:54

Ирина Петренко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Ирина Петренко
Профиль
Благодарили: 0

Сообщений: 1

как написать правильно площадь треугольника? $undecided$

0
Спасибо $thanks$
Ответить

9 декабря 2015 в 19:41
Ответ для Ирина Петренко

Тима Клюев
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Тима Клюев
Профиль
Благодарили: 0

Сообщений: 8

S(рисуешь мини треугольник) = ,,,,,

0
Спасибо $thanks$
Ответить

Источник

Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8-9 класс. Задачи на нахождение площади треугольника. Они встречаются в 15 задании ОГЭ по математике.

В статье будут рассмотрены несколько формул вычисления площади треугольника.

Первая теорема

Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена.

Задача №1

Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника

Решение

Задача №2

У треугольника со сторонами 2 и 10 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 5. Чему равна высота, проведённая ко второй стороне?

Решение

Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена. Поэтому площадь треугольника в каждом случае будет одинаковой.

Задача №3

На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.

Решение

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла, делит треугольник на два треугольника, площади которых относятся как m:n:

Отрезок AD относиться к отрезку DC как 6:10. Значить площадь треугольника ABD составляет 6 частей от площади треугольника АВС, а площадь треугольника DBC – 10 частей. Вся площадь треугольника ABC равна 16 частей. По условию площадь треугольника АВС равна 48. Значит площадь треугольника ВСD=(48/16)*10=30.

Ответ 30

Задача №4

Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.

Решение

Вторая теорема

Площадь прямоугольного треугольника равна половине произведения его катетов.

Ответ 20

Задача №5

В прямоугольном треугольнике один из катетов равен 4, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника

Решение:

Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.

Значит в треугольнике катеты равны 4 ( a=b=4). Найдем площадь равнобедренного прямоугольного треугольника:

Ответ 8

Задача №6

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 8 и 17.

Решение

Вспомним что такое катет и гипотенуза.

Стороны прямоугольного треугольника, которые образуют прямой угол, называются катеты, а третья сторона – гипотенуза.

Чтобы вычислить площадь прямоугольного треугольника, необходимо вычислить второй катет. Для этого воспользуемся теоремой Пифагора.

Теорема Пифагора

Квадрат гипотенузы равен сумме квадратов катетов.

Зная оба катета прямоугольного треугольника, вычислим его площадь:

Ответ 60

Задача №7

Катеты прямоугольного треугольника равны 21 и 72. Найдите высоту, проведенную к гипотенузе.

Решение

В этой задаче, чтобы найти высоту, проведенную к гипотенузе, необходимо воспользоваться двумя формулами нахождения площади треугольника. Первая формула (для прямоугольного треугольника): половина произведения его катетов. Вторая формула: половина произведения высоты на сторону, к которой эта высота проведена. Площадь, вычисленная разными формулами одной фигуры, одинаковая. Для решения, нам понадобятся размеры гипотенузы. Вычислим ее:

Теперь найдем, чему будет равна высота:

Ответ 20,16

Задача №8

Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.

Решение.

В этой задаче, площадь треугольника найдем по формуле Герона. Для этого нужно знать полупериметр (периметр, деленный на 2) треугольника и длину каждой стороны.

В равнобедренном треугольнике, боковые стороны равны. Найдем периметр треугольника. Периметр треугольника – это сумма всех длин сторон треугольника

Ответ 168

Задача №9

В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.

Решение

В нашем случает получается треугольник прямоугольный и равнобедренный т.е. катеты треугольника равны. Найдем катеты прямоугольного треугольника через теорему Пифагора.

Пусть катеты прямоугольного треугольника это Х

Ответ 1681

Задача №10

Решение

Третья теорема. Теорема о площади треугольника (9 класс)

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Ответ 50

Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог

Источник

Решение задач на вычисление площадей многоугольников чаще всего сводится к поиску величин отдельных элементов рассматриваемых фигур и дальнейшему применению соответствующих формул площадей.

Во многих задачах наряду с сугубо геометрическими приемами решения (дополнительные построения, применение равенства фигур и т. п.) используются и методы алгебры (составление уравнений или систем уравнений на основе метрических соотношений между элементами фигуры).

В ходе решения особое внимание следует уделить тому, однозначно ли данные задачи определяют взаимное расположение элементов фигуры.

Пример:

Найдите площадь трапеции, в которой одно из оснований равно 24 см, высота 12 см, а боковые стороны — 13 см и 20 см.

Решение:

Пусть 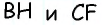Решение задач на вычисление площадей с примерами вычисления и определения

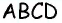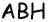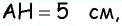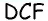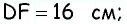1) Для трапеции Решение задач на вычисление площадей с примерами вычисления и определения (рис. 152, а): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем Решение задач на вычисление площадей с примерами вычисления и определения тогда

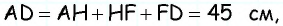
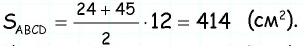
Решение задач на вычисление площадей с примерами вычисления и определения

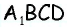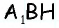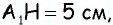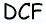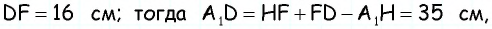
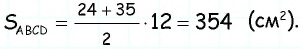
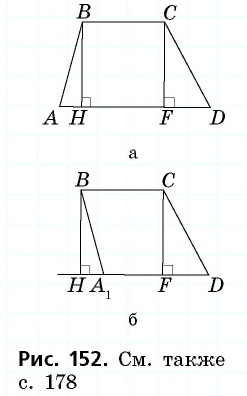
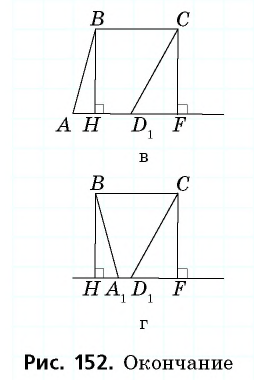
2) Для трапеции Решение задач на вычисление площадей с примерами вычисления и определения (рис. 152, б): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем Решение задач на вычисление площадей с примерами вычисления и определения

Решение задач на вычисление площадей с примерами вычисления и определения

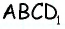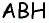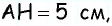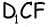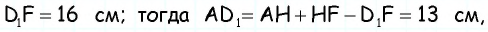
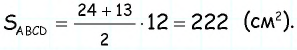
3) Для трапеции Решение задач на вычисление площадей с примерами вычисления и определения (рис. 152, в): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем Решение задач на вычисление площадей с примерами вычисления и определения

Решение задач на вычисление площадей с примерами вычисления и определения

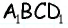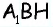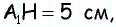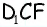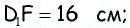4) Для трапеции Решение задач на вычисление площадей с примерами вычисления и определения (рис. 152, г): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем Решение задач на вычисление площадей с примерами вычисления и определения тогда 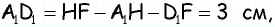т.е. точки 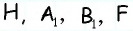расположены на прямой в указанном порядке.

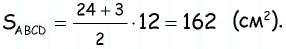
Решение задач на вычисление площадей с примерами вычисления и определения
Ответ: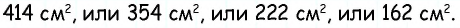

Решение задач на вычисление площадей с примерами вычисления и определения

Рассмотренная задача наглядно демонстрирует одну из причин, по которым в процессе решения геометрической задачи может возникать многовариантность. Но даже если такая ситуация не возникает, взаимное расположение элементов фигур нуждается в обосновании.

Пример:

Основания трапеции равны 10 см и 35 см, а боковые стороны — 15 см и 20 см. Найдите площадь трапеции.

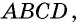
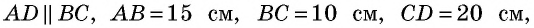
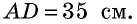
Прежде всего заметим, что решение данной задачи фактически сводится к нахождению высоты трапеции. Итак, пусть дана трапеция Решение задач на вычисление площадей с примерами вычисления и определения

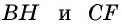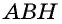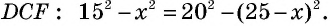
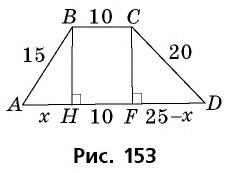
Естественно было бы провести, как в предыдущей задаче, высоты Решение задач на вычисление площадей с примерами вычисления и определения (рис. 153) и составить уравнение на основании теоремы Пифагора, примененной к треугольникам Решение задач на вычисление площадей с примерами вычисления и определения и

Решение задач на вычисление площадей с примерами вычисления и определения

Такое решение позволит получить правильный ответ, но не будет полным, ведь принадлежность точек 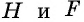Решение задач на вычисление площадей с примерами вычисления и определения отрезку 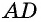нужно обосновать. Попробуем избежать необходимости такого обоснования, применив для решения другое дополнительное построение.

Решение:

Проведем через вершину 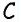Решение задач на вычисление площадей с примерами вычисления и определения прямую 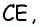параллельную (рис. 154).

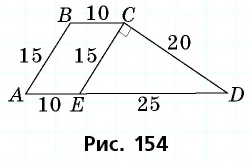
Решение задач на вычисление площадей с примерами вычисления и определения

Поскольку по построению 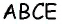Решение задач на вычисление площадей с примерами вычисления и определения — параллелограмм, то 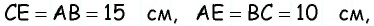следовательно, 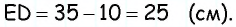Стороны треугольника 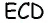пропорциональны числам 3, 4, 5, следовательно, по теореме, обратной теореме Пифагора, он является прямоугольным с гипотенузой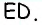 Решение задач на вычисление площадей с примерами вычисления и определения

По формуле 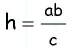Решение задач на вычисление площадей с примерами вычисления и определения находим высоту этого треугольника, которая одновременно является и высотой трапеции: 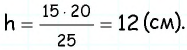Следовательно,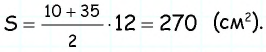 Решение задач на вычисление площадей с примерами вычисления и определения

Ответ: 270 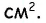Решение задач на вычисление площадей с примерами вычисления и определения

Как видим, этот способ намного более рационален, в частности, с точки зрения вычислений. Рассмотрим еще одну задачу, для решения которой используется дополнительное построение.

Пример:

Диагонали трапеции равны 30 см и 40 см и пересекаются под прямым углом. Найдите площадь трапеции.

Попробуем решить эту задачу чисто геометрическими методами. Основная сложность заключается в том, что данные отрезки не являются сторонами одного треугольника. Попробуем «исправить» эту ситуацию.

Решение:

Пусть дана трапеция 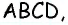Решение задач на вычисление площадей с примерами вычисления и определения в которой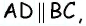 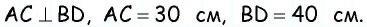Проведем через вершину 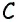прямую 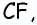параллельную диагонали 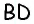(рис. 155).

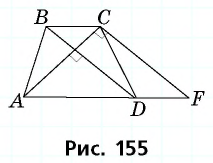
Решение задач на вычисление площадей с примерами вычисления и определения

Очевидно, что по построению угол 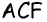Решение задач на вычисление площадей с примерами вычисления и определения будет прямым, т.е. треугольник 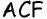прямоугольный с гипотенузой 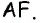С другой стороны, 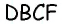— параллелограмм, тогда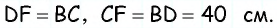 Решение задач на вычисление площадей с примерами вычисления и определения

Обратим внимание на то, что треугольники 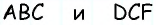Решение задач на вычисление площадей с примерами вычисления и определения равновеликие, поскольку 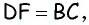а высоты, проведенные к этим сторонам, являются высотами трапеции. Таким образом, 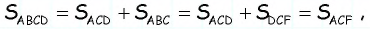Решение задач на вычисление площадей с примерами вычисления и определения т.е. искомая площадь трапеции равна площади треугольника которая, в свою очередь, равна полупроизведению его катетов:
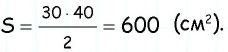
Решение задач на вычисление площадей с примерами вычисления и определения
Ответ: 600

Применение площадей

Теорема (об отношении площадей подобных треугольников)

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство:

Пусть 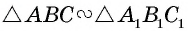Решение задач на вычисление площадей с примерами вычисления и определения с коэффициентом 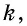т.е. 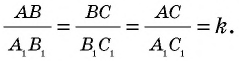Докажем, что

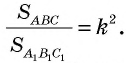
Решение задач на вычисление площадей с примерами вычисления и определения

Проведем в данных треугольниках высоты 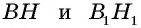Решение задач на вычисление площадей с примерами вычисления и определения (рис. 161).

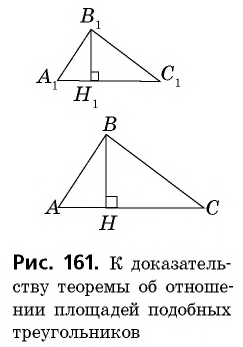
Решение задач на вычисление площадей с примерами вычисления и определения

Прямоугольные треугольники 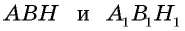Решение задач на вычисление площадей с примерами вычисления и определения подобны, поскольку 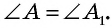Это означает, что 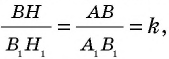т.е. 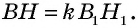Учитывая, что 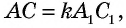имеем:

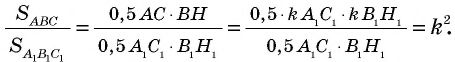
Решение задач на вычисление площадей с примерами вычисления и определения

Пример:

Средняя линия отсекает от данного треугольника треугольник с площадью 8 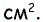Решение задач на вычисление площадей с примерами вычисления и определения Найдите площадь данного треугольника.

Решение:

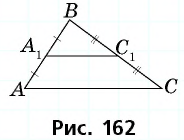
Пусть 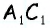Решение задач на вычисление площадей с примерами вычисления и определения — средняя линия треугольника 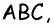параллельная стороне (рис. 162),

Решение задач на вычисление площадей с примерами вычисления и определения

Треугольники 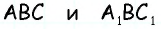Решение задач на вычисление площадей с примерами вычисления и определения подобны по двум сторонам и углу между ними, причем 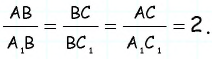Тогда по доказанной теореме 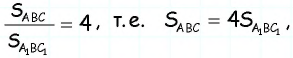откуда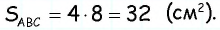 Решение задач на вычисление площадей с примерами вычисления и определения
Ответ:

Метод площадей

Понятия площади и формулы ее вычисления могут применяться даже в тех задачах, в условиях которых площадь не упоминается. Рассмотрим такой пример.

Пример:

Стороны параллелограмма равны 16 см и 12 см. Высота параллелограмма, проведенная к большей стороне, равна 3 см. Найдите высоту, проведенную к меньшей стороне.

Решение:

Пусть дан параллелограмм со сторонами 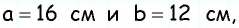Решение задач на вычисление площадей с примерами вычисления и определения к которым проведены высоты длину которой необходимо найти (рис. 163).

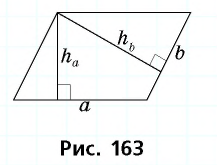
Решение задач на вычисление площадей с примерами вычисления и определения

По формуле площади параллелограмма 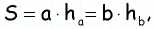Решение задач на вычисление площадей с примерами вычисления и определения откуда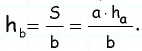

Таким образом, 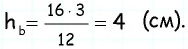Решение задач на вычисление площадей с примерами вычисления и определения

Ответ: 4 см.

При решении этой задачи площадь параллелограмма вычислялась двумя разными способами. Поскольку площадь многоугольника независимо от способа ее вычисления определяется однозначно, то полученные выражения приравнивались, благодаря чему удалось связать известные величины с искомой. Такой метод, основанный на использовании площади как вспомогательной величины, называется методом вспомогательной площади или просто методом площадей.

Заметим, что из формул площади параллелограмма 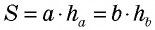Решение задач на вычисление площадей с примерами вычисления и определения и площади треугольника 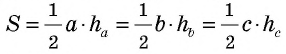следует важное утверждение: в параллелограмме (треугольнике) большей является высота, проведенная к меньшей стороне, меньшей — высота, проведенная к большей стороне.

Метод площадей используется как в задачах на вычисление, так и для доказательства утверждений.

Пример:

Сумма расстояний от точки, взятой внутри равностороннего треугольника, до его сторон не зависит от выбора точки и равна высоте треугольника. Докажите.

Решение:

Пусть точка 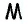Решение задач на вычисление площадей с примерами вычисления и определения лежит внутри равностороннего треугольника 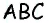со стороно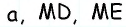й и 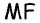— расстояния от данной точки до сторон треугольника (рис. 164).

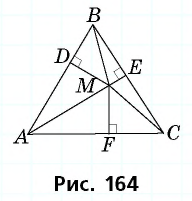
Решение задач на вычисление площадей с примерами вычисления и определения

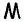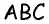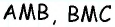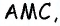Соединим точку Решение задач на вычисление площадей с примерами вычисления и определения с вершинами треугольника. Площадь треугольника равна сумме площадей треугольников и Решение задач на вычисление площадей с примерами вычисления и определения в которых отрезки 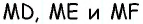являются высотами. Имеем:

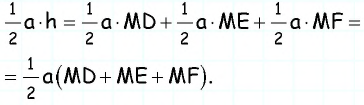
Решение задач на вычисление площадей с примерами вычисления и определения

Отсюда 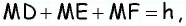Решение задач на вычисление площадей с примерами вычисления и определения т.е. сумма рассматриваемых расстояний равна высоте треугольника и не зависит от выбора точки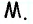 Решение задач на вычисление площадей с примерами вычисления и определения

Другие доказательства теоремы Пифагора

Исторически появление и доказательство теоремы Пифагора связаны с вычислением площадей. Поэтому в классической формулировке этой теоремы речь идет не о квадратах сторон прямоугольного треугольника, а о площадях соответствующих фигур:

площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

Рисунок 165, который наглядно воплощает эту формулировку, стал своеобразным символом геометрии и среди гимназистов позапрошлого столетия получил название «пифагоровы штаны».

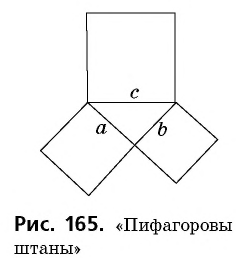
Решение задач на вычисление площадей с примерами вычисления и определения

Шутливый стишок про «пифагоровы штаны» школьники запоминали на всю жизнь.

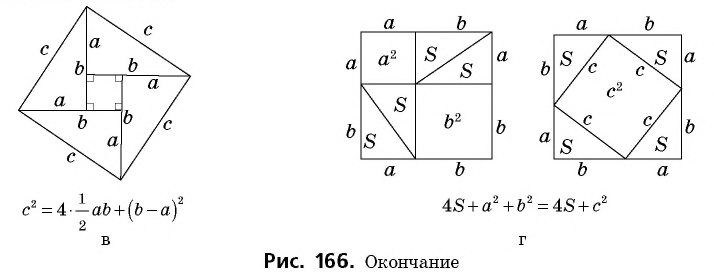
Докажем теорему Пифагора с помощью площадей.

Доказательство:

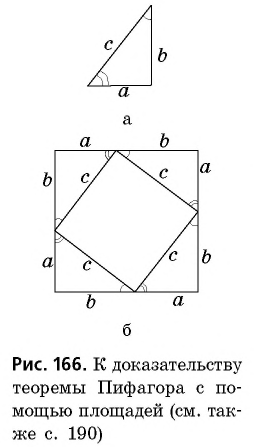
Решение задач на вычисление площадей с примерами вычисления и определения

Пусть дан прямоугольный треугольник с катетами 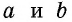Решение задач на вычисление площадей с примерами вычисления и определения и гипотенузой 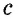(рис. 166, а). Достроим его до квадрата со стороной 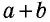так, как показано на рисунке 166, б. Площадь этого квадрата равна 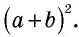Решение задач на вычисление площадей с примерами вычисления и определения Построенный квадрат состоит из четырех равных прямоугольных треугольников площадью 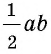и четырехугольника со сторонами длиной 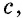Решение задач на вычисление площадей с примерами вычисления и определения который является квадратом (докажите это самостоятельно). Итак, имеем: ^

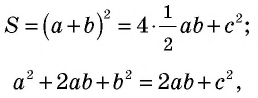
Решение задач на вычисление площадей с примерами вычисления и определения

т.е. Решение задач на вычисление площадей с примерами вычисления и определения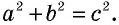

Теорема доказана.

На рисунках 166, в, г показаны другие способы доказательства теоремы Пифагора с помощью площадей. В трактатах индийского математика XII ст. Бхаскари один из них сопровождался только одним словом: «Смотри!». В целом сегодня известно более 150 разных способов доказательства этой знаменитой теоремы. Но каждый из вас может изобрести и свой собственный способ.

Решение задач на вычисление площадей с примерами вычисления и определения

Итоги главы 3.

Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону

Решение задач на вычисление площадей с примерами вычисления и определения
Сумма углов многоугольника
Сумма углов выпуклого 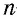-угольника равна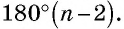

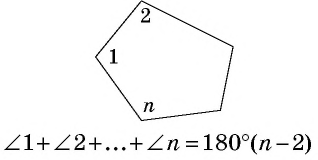
Решение задач на вычисление площадей с примерами вычисления и определения
Сумма внешних углов выпуклого 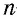-угольника, взятых по одному при каждой вершине, равна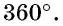

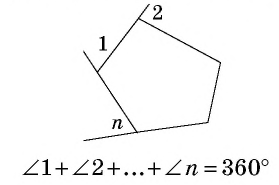
Решение задач на вычисление площадей с примерами вычисления и определения
Описанный многоугольник

Многоугольник называется вписанным в окружность, если все его вершины лежат в этой окружности.

Решение задач на вычисление площадей с примерами вычисления и определения

Описанный многоугольник.

Многоугольником называют описанным около окружностей, если все его стороны касаются этой окружности.

Решение задач на вычисление площадей с примерами вычисления и определения

Аксиомы площадей

Равные многоугольники имеют равные площади.
Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Площадь квадрата со стороной, равной единице длины, равна единице площади

Две фигуры называются равновеликими, если они имеют равные площади

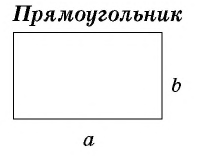
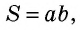Решение задач на вычисление площадей с примерами вычисления и определения где 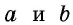– стороны прямоугольника.

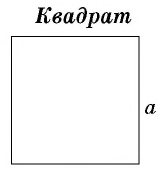
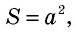Решение задач на вычисление площадей с примерами вычисления и определения где 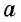— сторона квадрата

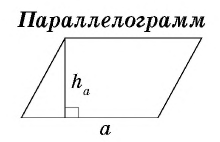
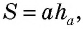Решение задач на вычисление площадей с примерами вычисления и определения где 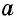— сторона параллелограмма,

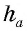Решение задач на вычисление площадей с примерами вычисления и определения — проведенная к ней высота

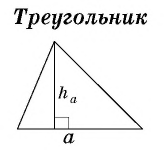
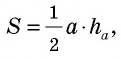Решение задач на вычисление площадей с примерами вычисления и определения где 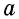– сторона треугольника, 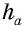– проведенная к ней высота.

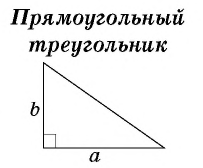
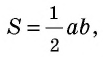
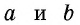Решение задач на вычисление площадей с примерами вычисления и определения – катеты прямоугольного треугольника.

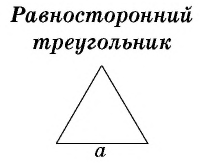
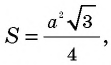Решение задач на вычисление площадей с примерами вычисления и определения где 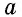– сторона треугольника.

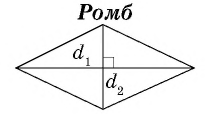
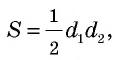Решение задач на вычисление площадей с примерами вычисления и определения где 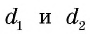– диагонали ромба.

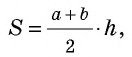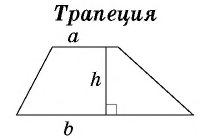
Решение задач на вычисление площадей с примерами вычисления и определения где 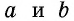основание трапеции, 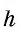– высота трапеции.

Теорема об отношении площадей подобных треугольников Отношение площадей подобных треугольников равно квадрату коэффициента подобия

Историческая справка:

Вычисление площадей многоугольников — первая среди тех практических задач, благодаря которым появилась геометрия как наука. Но не всегда представление об измерении площадей было таким, как сегодня.

Например, древние египтяне при вычислении площади любого треугольника брали половину произведения двух его сторон. Так же пять столетий назад измеряли площадь треугольника и в Древней Руси. Чтобы найти площадь четырехугольника, который не является квадратом, в Вавилоне использовали формулу произведения полусумм его противолежащих сторон.

В Средние века для вычисления площади треугольника со стороной и проведенной к ней высотой, которые выражаются целым числом 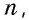Решение задач на вычисление площадей с примерами вычисления и определения брали сумму членов натурального ряда от 1 до 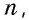т.е. число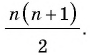

Кстати, в то время знали и правильную формулу площади этого треугольника 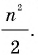Решение задач на вычисление площадей с примерами вычисления и определения Ее обосновал средневековый математик Герберт, который в X ст. даже занимал какое-то время престол Римского Папы под именем Сильвестра II.

Древние вавилоняне еще четыре тысячи лет назад умели правильно вычислять площадь квадрата, прямоугольника, трапеции. Немало формул площадей и объемов, с которыми вы познакомитесь в старших классах, открыл знаменитый греческий ученый Архимед (ок. 287-212 гг. до н. э.). И это все при том, что в те древние времена не было даже алгебраической символики!

Сегодня, благодаря значительно более широкому применению алгебры в геометрии, мы имеем возможность дать куда более простые и понятные решения многих задач, чем это было возможно в те далекие времена.

Тела вращения: цилиндр, конус, шар
Четырехугольник
Площади фигур в геометрии
Площади поверхностей геометрических тел
Эллипс
Гипербола
Парабола
Многогранник

Источник

Давайте вспомним, как найти площадь прямоугольника. Чтобы найти
площадь прямоугольника, надо длину умножить на ширину.

Вот формула для нахождения площади прямоугольника:

S = a · b

В этой формуле латинской буквой S обозначается площадь, буквами a и b – стороны прямоугольника.

Выполним задание, в котором надо найти площадь
прямоугольника со сторонами 5 см и 3 см.

Решение. Итак, чтобы найти площадь
прямоугольника, надо его длину умножить на ширину.

Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в
квадратных единицах. В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.

3 · 5 =
15 (см²)

Ответ: площадь прямоугольника равна 15 см².

Теперь давайте найдём площадь квадрата со стороной 4 см.

Решение. У этого квадрата каждая
сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата
равна 16 квадратным сантиметрам.

4 · 4 =
16 (см²)

Ответ: площадь квадрата равна 16 см².

Ну а сейчас перейдём к решению задач, в которых нам надо будет
найти площадь сложных фигур.

Найдите площадь фигуры, изображённой на рисунке.

Эта фигура не является ни прямоугольником, ни квадратом. Но мы
можем разделить эту фигуру на два прямоугольника, например, вот таким образом.

А площади прямоугольников мы легко можем найти с помощью
известной формулы.

Напомним, что противоположные стороны прямоугольника равны.

Итак, стороны первого прямоугольника равны 5 см и 4 см.

5 · 4 =
20 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

Ширина этого прямоугольника равна 2 см.

7 – 4 = 3 (см) – длина второго прямоугольника

3 · 2 = 6
(см²) – площадь второго прямоугольника

Мы нашли площади прямоугольников, из которых состоит сложная
фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.

20 + 6 = 26
(см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Площадь этой сложной фигуры найти другим способом. Можно разделить
её на два прямоугольника вот таким образом.

Найдём площадь первого прямоугольника.

Одна его сторона равна 4 см.

5 – 2 = 3 (см) – длина стороны первого прямоугольника

4 · 3 =
12 (см²) – площадь первого прямоугольника

Теперь найдём площадь второго прямоугольника.

7 · 2 =
14 (см²) – площадь второго прямоугольника

12 + 14 =
26 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Решим следующую задачу.

Найдём площадь ещё одной фигуры, изображённой на рисунке.

Чтобы найти площадь этой фигуры, тоже разделим её на простые
фигуры. Сделаем это вот таким образом.

Получилось 3 прямоугольника.

Найдём площадь первого прямоугольника.

7 · 2 =
14 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

7 – 4 = 3 (см) – длина одной стороны второго прямоугольника

8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника

Получается, что это квадрат, так как длина всех его сторон равна 3
см.

3 · 3 = 9
(см²) – площадь квадрата

И найдём площадь последнего прямоугольника.

Его ширина равна 3 см. Длина равна 7 см.

3 · 7 =
21 (см²) – площадь третьего прямоугольника

Таким образом, мы нашли площади всех трёх фигур, на которые
разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму
площадей трёх фигур.

14 + 9 + 21 =
44 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 44 см²

Отметим, что площадь этой фигуры можно было бы найти, разделив её
на простые фигуры и вот таким образом:

И решим ещё одну задачу.

Найдите площадь незаштрихованной фигуры.

На рисунке изображён прямоугольник со сторонами 9 см и 5 см.
Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см
и 3 см. Давайте найдём площадь каждого из них.

9 · 5 =
45 (см²) – площадь большего прямоугольника

5 · 3 =
15 (см²) – площадь меньшего прямоугольника

А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.

45 – 15 =
30 (см²) – площадь незаштрихованной фигуры

Ответ: площадь незаштрихованной фигуры равна 30 см².

Источник

ПЕРИМЕТР

Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.

Чаще всего периметр обозначается буквой P.

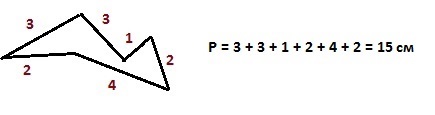
Периметр прямоугольника – удвоенная сумма длины и высоты – 2∙(a+b)

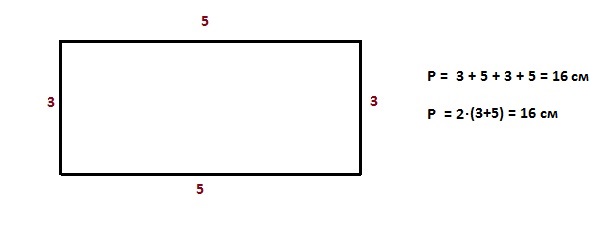
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.

ПЛОЩАДЬ

Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.

В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.

Чаще всего площадь обозначается буквой S.

Площадь прямоугольника – произведение длины на высоту.

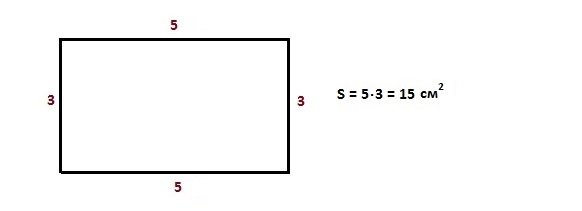
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Разделим этот прямоугольник на квадраты

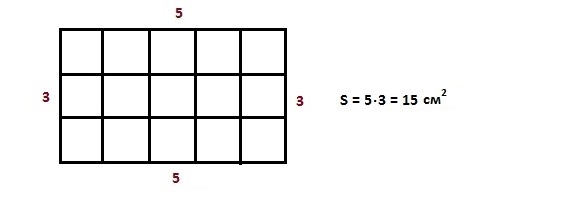
Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.

Площадь квадрата – произведение длины стороны на саму себя.

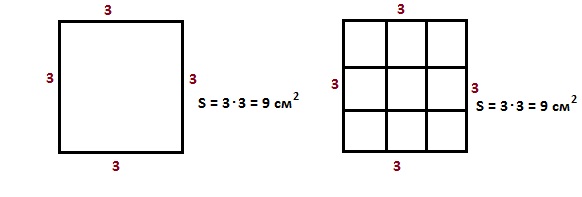
СОСТАВНЫЕ ФИГУРЫ

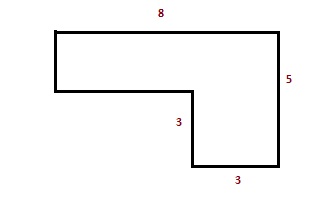
Разделим эту фигуру на прямоугольник и квадрат

Высота прямоугольника составит 5 – 3 = 2

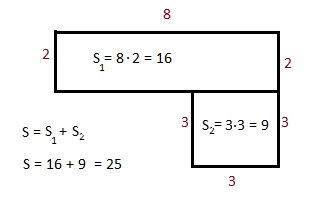
СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА

Фигуры с одной и той же площадью могут иметь разный периметр

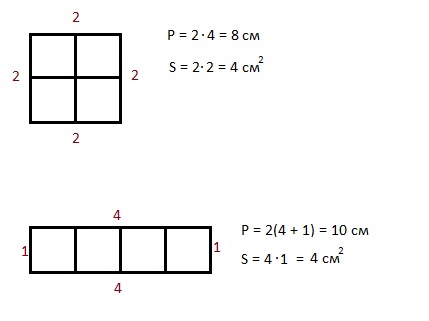
Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?

Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.

Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.

ОБЪЁМ

Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.

1 л = 1 дм³

Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.

Чаще всего объём обозначается буквой V.

Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.

Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты

Зная объём и две стороны, мы можем найти третью сторону:

c = (V:a):b = V:S

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

ЗАДАЧИ

Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.

x = 10 см – ширина

1. Найдём длину

y = 10 + 6 = 16 см

2. Найдём периметр

P = 2∙(10+16) = 52 см

3. Найдём площадь

S = 10∙16 = 160 см²

Ответ: P = 52 см, S = 160 см²

Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?

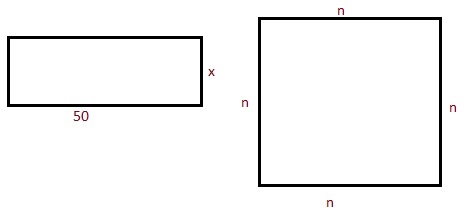
1. Вычислим сторону квадрата

4∙n = 80 – периметр

n = 20 см

2. Вычислим площадь квадрата

20∙20 = 400 см²

3. Вычислим ширину прямоугольника

50∙x = 400 см²

x = 8 см

Ответ: 8 см

Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?

1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм

1. Переведём длину прямоугольника в дм

x = 15∙10 = 150 дм

2. Найдём ширину прямоугольника

150∙y = 7500

y = 7500:150 = 50 дм

Ответ: 50 дм

Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.

1. Найдите площадь этого прямоугольника.

2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.

3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.

1. Найдём ширину прямоугольника

x = 60:3 = 20 см

2. Найдём площадь прямоугольника

S = 60∙20 = 1200 см

2. Найдём периметр прямоугольника

P = 2∙(60+20) = 160 см

3. Найдём сторону квадрата

y = 160:4 = 40 см

4. Найдём площадь квадрата

Sкв = 40∙40 = 1600 см²

5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:

Sкв₂ = 1200:12 = 100 см²

6. Найдём сторону такого квадрата

Площадь квадрата = 100 см²

Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см

7. Найдём периметр такого квадрата

P = 10∙4 = 40 см

Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.

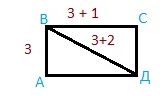
1. Найдём сторону ВС

ВС = 3+1 = 4

2. Найдём диагональ ВД

ВД = 3+2 = 5

3. Найдём периметр АВСД

P = 2∙(3+4) = 14 см

4. Найдём площадь АВСД

Sавсд = 3∙4 = 12 см²

5. Найдём периметр треугольника АВД

Pавд = 3 + 5 + 4 = 13 см

6. Найдём площадь треугольника АВД

Треугольник АВД занимает половину площади прямоугольника АВСД

Sавд = Sавсд:2

Sавд = 12:2 = 6 см²

Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?

Решение

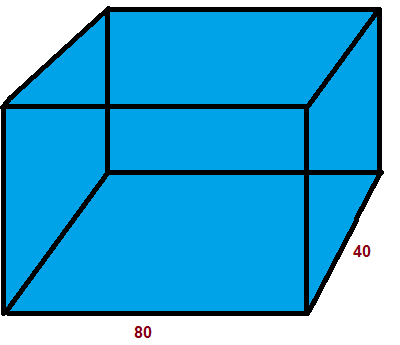
1. Переведём литры в кубические дециметры

1 л = 1 дм³, 160 л = 160 дм³

2. Переведём стороны аквариума в дециметры

1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм

3. Найдём высоту аквариума

V = a∙b∙c, a = 8, b = 4

c = (V:a):b

c = (160:8):4 = 5 дм

c = 5∙10 = 50 см

Ответ: 50 см

Источник

Площадь квадрата

Площадь прямоугольника

Площадь сложных фигур

Ваши комментарии

Применение площадей

Метод площадей

Другие доказательства теоремы Пифагора

ПЕРИМЕТР

ПЛОЩАДЬ

СОСТАВНЫЕ ФИГУРЫ

СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА

ОБЪЁМ

ЗАДАЧИ

Вам также может понравиться

Как составить комплекс ору с мячом

Как найти амплитуда колебаний напряжения на конденсаторе

Надоело одиночество как найти девушку

Добавить комментарий Отменить ответ