Математика
5 класс
Урок №30
Площадь прямоугольника. Единицы площади
Перечень рассматриваемых вопросов:
– понятие площади фигуры;
-единицы измерения площади;
– площадь прямоугольника, квадрата;
– приближенное измерение площади фигуры на клетчатой бумаге.
Тезаурус
Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам).
Квадрат – прямоугольник, у которого все стороны равны.
Площадь прямоугольника– число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.
Основная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Сегодня мы начнём занятие с задачи. Представим, что две девочки пришли в магазин, чтобы купить в подарок подруге на день рождения коробку конфет. На витрине были разложены самые разные наборы сладостей. Девочки решили купить ту коробку, которая больше. А какая из них больше? Как это измерить? Можно сравнить коробки по длине и ширине или просто положить их друг на друга. Но одна коробка оказалась длиннее, а другая – шире. Какая же из них больше? Как это узнать?
Чтобы ответить на эти вопросы, мы поговорим о вычислении площади прямоугольника.
Для начала введём понятие площади фигуры.
Если какую-нибудь площадь можно разбить на n квадратов со стороной, например, 1 см, то получится, что площадь фигуры равна n см2.
За единицу измерения площадей принимают не только квадратный сантиметр, но и квадратный миллиметр, квадратный дециметр, квадратный метр.
Это площади квадратов, длины сторон которых равны одному миллиметру, одному дециметру и одному метру соответственно.
Далее покажем, что подразумевается под площадью прямоугольника.
Площадью прямоугольника называют число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.
Называя величину площади, необходимо указывать единицу измерения.
Например, прямоугольник состоит из пятнадцати квадратов; площадь каждого квадрата составляет 1 см2. Следовательно, площадь всего прямоугольника равна 15 см2.
S = 15 см2
Решим задачу.
Найдём площадь прямоугольника ABCD, который имеет длину АВ = 6 см и ширину ВС = 7 см. Для этого разделим его на квадратные сантиметры. Сосчитаем, сколько квадратных сантиметров в нём содержится.
В прямоугольнике ABCD квадратный сантиметр содержится сорок два раза – значит, его площадь равна: S = 42 см2 = 6 см · 7 см = АВ · ВС.
Поэтому можно ввести формулу для нахождения площади прямоугольника.
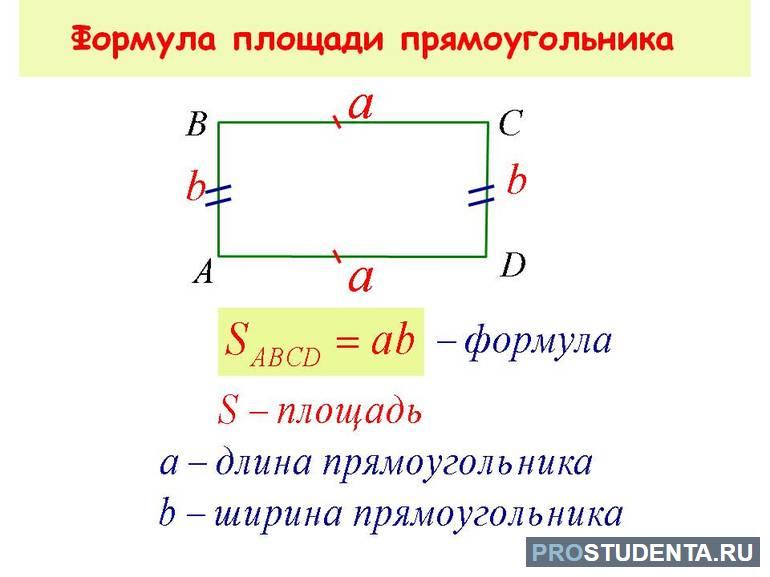
Чтобы найти площадь прямоугольника S, нужно умножить его длину a на ширину b.
S = а · b
Так как квадрат является прямоугольником, у которого все стороны равны, то его площадь можно вычислить как квадрат его стороны а.
S = а · а = а2
Далее найдём соотношение между единицами измерения площадей.
Так как 1 см = 10 мм, следовательно, 1 см2 = 102 мм2 = 100 мм2.
Соответственно, 1 дм2 = 102 см2 = 100 см2
1 м2 = 102 дм2 = 100 дм2
1 км2 = 10002 м2 = 1000000 м2.
Для измерения небольших площадей земельных участков используют специальную единицу измерения– ар, которая равна площади квадрата со стороной десять метров. В обиходе ар называют соткой, так как один ар– это сто квадратных метров.
1 ар = 102 м2 = 100 м2
Для обмера больших земельных территорий ввели единицу один гектар, которая соответствует площади квадрата со стороной сто метров.
1 га = 1002 м2 = 10000 м2 = 100 а
Решим задачу.
Найдём площадь прямоугольника.
При измерении окажется, что стороны с недостатком приближенно равны трём и пяти сантиметрам. Значит, площадь прямоугольника больше, чем произведение этих сторон, то есть пятнадцати квадратных сантиметров.
S (с недостатком) = 3 · 5 = 15 см2
Если взять стороны в приближении с избытком, то есть четыре и шесть сантиметров, то площадь будет меньше произведения сторон, а именно равна двадцати четырём квадратным сантиметрам.
S (с избытком) = 4 · 6 = 24 см2
Таким образом, площадь этого прямоугольника варьируется от пятнадцати до двадцати четырёх квадратных сантиметров.
15 см2 < S < 24 см2
Отметим, что равные прямоугольники имеют равную площадь.
Сравним площади закрашенных квадратов, изображённых на рисунке.
Решение: если посмотреть внимательно на рисунок, то можно заметить, что все фигуры расположены в одинаковых квадратах со стороной 9 клеток, следовательно, площади этих квадратов одинаковы. На верхнем рисунке шесть фигур – два квадрата и четыре треугольника. На нижнем рисунке пять фигур – квадрат и четыре треугольника.
Далее внимательно посмотрим на треугольники – все они одинаковы, следовательно, их площади одинаковы. И, если из больших квадратов, в которых расположены наши фигуры, мы отнимем сумму площадей равных треугольников, получится, что площади оставшихся фигур (квадратов) верхней и нижней части равны.
Примеры заданий из Тренировочного модуля
№ 1. В квадрате все стороны равны 5 см. Чему равна площадь квадрата?
Решение: Для нахождения площади квадрата воспользуемся следующей формулой:
S = а2 = 5см · 5 см = 25 см2
№ 2. Найдите площадь фигуры.
Решение: сначала следует разделить фигуру на три прямоугольника, далее найти площадь каждого по формулеS=а · b, а затем сложить площади трёх фигур. Или можно найти площадь прямоугольника со сторонами 10 см и 3 см, она равна 30 см2. Далее вычислить площадь вырезанной фигуры со сторонами 2см на 1 см, она составляет 2см2. И вычесть 2 см2 из 30см2.
Ответ: 28 см2.
Как найти площадь прямоугольника?
Анонимный вопрос
18 августа 2019 · 203,4 K
Редактор, автор и переводчик книг по математике · 18 авг 2019 ·
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину
Обрати внимание, что длина и ширина должны быть выражены в одних единицах. Если длина и ширина в сантиметрах, то площадь получится в сантиметрах квадратных; если длина и ширина в километрах, то площадь получится в квадратных километрах. Если длина и ширина выражены в разных единицах, сначала приведи к одинаковым, а потом уж умножай.
Очень полезно познакомиться с площадями прямоугольников на практике. Давай я попробую угадать: площадь твоего стола меньше одного квадратного метра. Площадь твоей кровати больше одного квадратного метра, но меньше двух. Площадь твоей комнаты больше 10 квадратных метров и меньше 20 квадратных метров. Мне не видно, и я могла ошибиться. Так что измерь, посчитай и проверь, правильно ли я угадала.
120,6 K
площадь- это длина умноженая на ширину
Комментировать ответ…Комментировать…
7,0 K
Комментировать ответ…Комментировать…
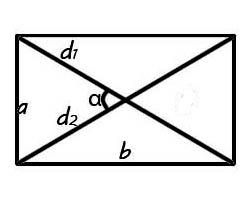
Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:
1) через две стороны
S=a*b
2) через диагонали и угол
S=1/2*d(в квадрате)*sin(α)… Читать далее
7,4 K
Комментировать ответ…Комментировать…
Надо длину умножить на ширину
Пример : 3*2 = 6 квадратных сантиметров ( квадратные сантиметры пишутся так : см и мелкая 2 на верху) так же есть и другие квадратные
5,5 K
Комментировать ответ…Комментировать…
Пример:
У прямоугольника есть 4 стороны. Первые 2 стороны равны друг другу, как и вторые 2 стороны.
Значит, прямоугольник делится на a и b. Представим, что сторона a – 3 сантиметра, а b – 2 сантиметра. Площадь будет буквой S. Чтобы вычислить площадь прямоугольника, нужно сторону a умножить на b. S=a*b. S=3*2. 3*2 это шесть. Площадь обозначается квадратными сантиметрами. S=6 см2
5,0 K
-Как найти площадь Ленина?
-Надо длину Ленина, умножить на ширину Ленина!
Комментировать ответ…Комментировать…
Геймер, програмер, учу английский, чуть-чуть ютубер · 4 мая 2021
У прямоугольника есть длина и ширина.
Длину и ширину надо перемножить.
Ответ надо записывать в квадратной величине (результат и маленькая двойка сверху)
Пример:
Ширина = 3 см
Длина = 7 см
7*3 = 21(см2)
Ответ: 21 см2. Читать далее
2,5 K
Возьмите 2 игральных кубика. Бросьте оба. Первый показывает вам ширину прямоугольника, второй – длину. А площадь -… Читать дальше
Комментировать ответ…Комментировать…
Чтобы найти площадь прямоугольника, нужно умножить две его неравные стороны друг на друга. Также это выражается формулой S = a * b, где S – площадь, a и b – две неравные стороны прямоугольника.
В общей сложности, площадь прямоугольника, можно найти с помощью пяти разных формул.
1. Через две смежные стороны
2. Через любую сторону и периметр
3. Через любую сторону и… Читать далее
9,4 K
Комментировать ответ…Комментировать…
Что бы найти площадь треугольника, нужно воспольщоваться формулой:
S= a•b
Например:
Длина прямоугольника равна 8 см
Ширина прямоугольника равна 4см
Площадь прямоугольника равна 8•4=32 Читать далее
1,5 K
Комментировать ответ…Комментировать…
Чтобы найти площадь прямоугольника надо умножить длину на ширину пример:
a-9 см
b-3 см
s-? см
s=a*b
9*3=27(см)
Ответ:27 сантиметров площадь прямоугольника. Читать далее
2,5 K
Комментировать ответ…Комментировать…
Я работаю сама на себя – плету из бисера украшения и продаю. · 25 окт 2022
Для того чтобы найти площадь прямоугольника надо одну сторону прямоугольника (ширину) умножить на вторую сторону (длина).
Ширина – а
Длина – б
площадь – S
S = а умножить на б
349
Комментировать ответ…Комментировать…
Площадь прямоугольника

4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. Особая роль отводится площади прямоугольника, так как эта фигура одна из наиболее простых в изучении.
Опыт работы учителем математики – более 33 лет.
Понятия площади
Любая фигура имеет свою площадь, а вычисление площади отталкиваются от единичного квадрата, то есть от квадрата с длиной стороны в 1 мм, либо 1 см, 1 дм и так далее. Площадь такой фигуры равна $1*1 = 1мм^2$, либо $1см^2$ и т. д. Площадь, как правило, обозначается буквой S.
Площадь показывает размер части плоскости, которую занимает фигура, очерченная отрезками.
Прямоугольником называется четырехугольник, у которого все углы одинаковой градусной меры и равны по 90 градусов, а противоположные стороны попарно параллельны и равны.
Особое внимание нужно обращать на единицы измерения длины и ширины. Они должны совпадать. Если единицы не совпадают, их переводят. Как правило переводят большую единицу в меньшую, например, если длина дается в дм, а ширина в см, то дм переводят в см, а результат получится в $см^2$.
Формула площади прямоугольника
Для того, чтобы найти площадь прямоугольника без формулы необходимо посчитать количество единичных квадратов, на которые разбита фигура.
Прямоугольник разбит на 15 квадратов, то есть его площадь равна 15 см2. Стоит обратить внимание, что в ширину фигура занимает 3 квадрата, а в длину 5, поэтому чтобы вычислить количество единичных квадратов, необходимо умножить длину на ширину. Меньшая сторона четырехугольника – ширина, большая длина. Таким образом, можно вывести формулу площади прямоугольника:
S = a · b, где a,b – ширина и длина фигуры.
К примеру, если длина прямоугольника 5 см, а ширина 4 см, то площадь будет равна 4*5=20 см2.
Расчет площади прямоугольника, с использованием его диагонали
Для того, чтобы рассчитать площадь прямоугольника через диагональ необходимо применить формулу:
$$S = {1over{2}} ⋅ d^2 ⋅ sin{α}$$
Если в задании дано значения угла между диагоналями, а также значение самой диагонали, то можно вычислить площадь прямоугольника по общей формуле произвольных выпуклых четырехугольников.
Диагональ – это отрезок, который соединяет противоположные точки фигуры. Диагонали прямоугольника равны, и точкой пересечения делятся пополам.
Примеры
Для закрепления темы рассмотрим примеры заданий:
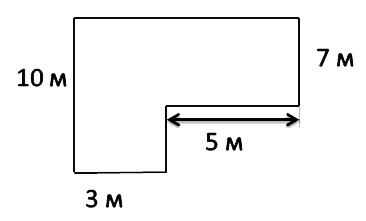
№1. Найти площадь огородного участка, такой формы как на рисунку.
Решение:
Для того чтобы вычесть площадь, необходимо фигуру разбить на два прямоугольника. Один из них будет иметь размеры 10 м и 3 м, другой 5 м. и 7 м. Отдельно находим их площади:
$S_1 =3*10=30 м^2$;
$S_2=5*7=35 м^2$.
Далее необходимо найти их сумму:
$30+35=65 м^2$
Это и будет площадь огородного участка $S = 65 м^2$.
№2. Вычислить площадь прямоугольника, если его диагональ d=6 см. а угол между диагоналями α =300.
Решение:
Значение $sin 30 ={1over{2}} $,
$ S ={1over{2}}⋅ d^2 ⋅ sinα$
$S ={1over{2}} * 6^2 * {1over{2}} =9 см^2$
Таким образом, $S=9 см^2$.
Диагонали разделяют прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести одну диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не являются биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.
Что мы узнали?
Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также не стоит забывать, что если в задании разные единицы измерения сторон, то необходимо перевести их одну.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Dima Erlichenkov
10/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
А какая ваша оценка?
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
При решении задач иногда возникает необходимость в определении площади прямоугольника. Формула для математики 5 класса довольно простая и позволяет находить не один параметр геометрической фигуры, а также широко применяется в строительстве, электротехнике и других отраслях человеческой жизни. Специалисты разработали специальный алгоритм, позволяющий не только выполнять правильно расчеты, но и контролировать размерность величин.
Общие сведения
Прямоугольник — геометрическая фигура, состоящая из четырех взаимно перпендикулярных и равных между собой сторон. Следует отметить, что у него углы между смежными сторонами равны 90 градусов. У любой фигуры есть понятие размерности, а прямоугольник не является исключением.
Найти площадь прямоугольника можно по очень простой формуле. Она имеет следующий вид: S=k*l, где S — площадь (искомая величина), k и l — длины наибольшей и наименьшей сторон соответственно. Формулировка формулы имеет следующий вид: размерность прямоугольника прямо пропорциональна произведению его сторон. Однако это не единственное соотношение для вычисления этого параметра.
Если неизвестны стороны, то можно найти площадь через диагонали. Для этого потребуется знать их длину, а также острый угол между ними (y). Следует отметить, что диагонали прямоугольника равны между собой, поэтому можно обозначить их одной литерой «q». В результате формула записывается следующим образом: S=q 2 * sin (y).
Звучит соотношение следующим образом: площадь прямоугольника эквивалентна произведению квадрата его диагонали на синус острого угла между диагоналями.
Применение формулы площади
Вычисление размерности прямоугольника применяется не только при решении задач, но и в строительстве. Например, чтобы выложить пол плиткой, нужно знать площадь комнаты, в которой будет выполняться эта операция. Следует отметить, что плитка в магазине продается в метрах квадратных.
Исходя из этого, требуется вычислить площадь комнаты, предварительно замерив стороны «прямоугольника». Однако на этом расчеты не заканчиваются, поскольку необходимо доказать, что пол комнаты является прямоугольником. Доказательство является очень простым, поскольку достаточно измерить диагонали. Если последние равны между собой, то плитку можно выкладывать от стены (ровно). В противном случае следует начинать работы с центра, и следить, чтобы углы изделия не совпадали с углами комнаты.
Следующий пример — расчет площади земельных участков. Вычисление происходит на основании базового соотношения определения площади через стороны.
Измеряется величина в сотках или гектарах, в которые нужно переводить метрические величины (длина и ширина участка — в метрах). Для правильности выполнения вычислений специалисты предлагают простой алгоритм измерения размерности.
Алгоритм нахождения размерности
Для вычисления площади прямоугольника нужно использовать специальный алгоритм, разработанный специалистами. Он имеет такой вид:
- Определить тип фигуры: у нее противолежащие стороны и диагонали не должны быть разными и углы внутри прямоугольника, образованные сторонами, — прямыми.
- Записать формулу площади: S=k*l=d 2 * sin (y).
- Определить размерность, то есть сантиметры, метры или километры.
- Подставить известные величины в одно из тождеств во втором пункте.
- Записать результат, вычислив величину размерности, которая может находиться по одной из формул.
Следует отметить, что каждый алгоритм должен быть реализован на практическом примере. Последний имеет следующий вид:
- Условие: диагонали четырехугольника и противоположные стороны равны (5 м и 7 м). Следовательно, фигура является прямоугольником.
- Формула размерности: S=l*k.
- Единица измерения — м2, поскольку стороны равны 5 м и 7 м.
- S=5*7=35 (м2).
- Результат: площадь прямоугольника со сторонами 5 и 7 метров эквивалентна 35 м2.
Следует отметить, что при отсутствии единицы измерения сторон необходимо указывать условные величины, то есть ед2. Далее необходимо рассчитать размерность фигуры на практическом примере при решении задачи.
Пример решения задачи
Для закрепления теоретического материала необходимо решить задачу. Она имеет следующее условие:
- Фигура состоит из прямоугольных треугольников, которые равны между собой.
- Периметр одного треугольника: 12.
- Разница между катетами составляет 1.
- Гипотенуза больше первого катета на 1, а второго — на 2.
Необходимо узнать площадь фигуры. Решение задачи выглядит следующим образом:
- Первый катет нужно приравнять к переменной m, тогда второй будет эквивалентен величине «m+1», а гипотенуза — «m+2».
- Составить уравнение для нахождения периметра: m+m+1+m+2=12. Его корень (значение переменной) равен 1, то есть m=3. Тогда второй катет эквивалентен числу 4, а гипотенуза — 5.
- Фигура является прямоугольником, так как состоит из равных треугольников.
- На основании третьего пункта алгоритма стороны прямоугольника эквивалентны 3 и 4.
- Площадь вычисляется по формуле: S=k*l=3*4=12 (ед2).
Cледует отметить, что фигура имеет одинаковые значения площади и периметра. Этот факт свидетельствует о том, что она была образована при помощи египетских треугольников (каждая сторона на единицу больше предыдущей).
Таким образом, определение площади прямоугольника необходимо осуществлять по алгоритму, предложенному специалистами. Кроме того, нужно внимательно следить за единицами измерения размерности.
При решении задач иногда возникает необходимость в определении площади прямоугольника. Формула для математики 5 класса довольно простая и позволяет находить не один параметр геометрической фигуры, а также широко применяется в строительстве, электротехнике и других отраслях человеческой жизни. Специалисты разработали специальный алгоритм, позволяющий не только выполнять правильно расчеты, но и контролировать размерность величин.
Общие сведения
Прямоугольник — геометрическая фигура, состоящая из четырех взаимно перпендикулярных и равных между собой сторон. Следует отметить, что у него углы между смежными сторонами равны 90 градусов. У любой фигуры есть понятие размерности, а прямоугольник не является исключением.
Найти площадь прямоугольника можно по очень простой формуле. Она имеет следующий вид: S=k*l, где S — площадь (искомая величина), k и l — длины наибольшей и наименьшей сторон соответственно. Формулировка формулы имеет следующий вид: размерность прямоугольника прямо пропорциональна произведению его сторон. Однако это не единственное соотношение для вычисления этого параметра.
Если неизвестны стороны, то можно найти площадь через диагонали. Для этого потребуется знать их длину, а также острый угол между ними (y). Следует отметить, что диагонали прямоугольника равны между собой, поэтому можно обозначить их одной литерой «q». В результате формула записывается следующим образом: S=q 2 * sin (y).
Звучит соотношение следующим образом: площадь прямоугольника эквивалентна произведению квадрата его диагонали на синус острого угла между диагоналями.
Применение формулы площади
Вычисление размерности прямоугольника применяется не только при решении задач, но и в строительстве. Например, чтобы выложить пол плиткой, нужно знать площадь комнаты, в которой будет выполняться эта операция. Следует отметить, что плитка в магазине продается в метрах квадратных.
Исходя из этого, требуется вычислить площадь комнаты, предварительно замерив стороны «прямоугольника». Однако на этом расчеты не заканчиваются, поскольку необходимо доказать, что пол комнаты является прямоугольником. Доказательство является очень простым, поскольку достаточно измерить диагонали. Если последние равны между собой, то плитку можно выкладывать от стены (ровно). В противном случае следует начинать работы с центра, и следить, чтобы углы изделия не совпадали с углами комнаты.
Следующий пример — расчет площади земельных участков. Вычисление происходит на основании базового соотношения определения площади через стороны.
Измеряется величина в сотках или гектарах, в которые нужно переводить метрические величины (длина и ширина участка — в метрах). Для правильности выполнения вычислений специалисты предлагают простой алгоритм измерения размерности.
Алгоритм нахождения размерности
Для вычисления площади прямоугольника нужно использовать специальный алгоритм, разработанный специалистами. Он имеет такой вид:
- Определить тип фигуры: у нее противолежащие стороны и диагонали не должны быть разными и углы внутри прямоугольника, образованные сторонами, — прямыми.
- Записать формулу площади: S=k*l=d 2 * sin (y).
- Определить размерность, то есть сантиметры, метры или километры.
- Подставить известные величины в одно из тождеств во втором пункте.
- Записать результат, вычислив величину размерности, которая может находиться по одной из формул.
Следует отметить, что каждый алгоритм должен быть реализован на практическом примере. Последний имеет следующий вид:
- Условие: диагонали четырехугольника и противоположные стороны равны (5 м и 7 м). Следовательно, фигура является прямоугольником.
- Формула размерности: S=l*k.
- Единица измерения — м2, поскольку стороны равны 5 м и 7 м.
- S=5*7=35 (м2).
- Результат: площадь прямоугольника со сторонами 5 и 7 метров эквивалентна 35 м2.
Следует отметить, что при отсутствии единицы измерения сторон необходимо указывать условные величины, то есть ед2. Далее необходимо рассчитать размерность фигуры на практическом примере при решении задачи.
Пример решения задачи
Для закрепления теоретического материала необходимо решить задачу. Она имеет следующее условие:
- Фигура состоит из прямоугольных треугольников, которые равны между собой.
- Периметр одного треугольника: 12.
- Разница между катетами составляет 1.
- Гипотенуза больше первого катета на 1, а второго — на 2.
Необходимо узнать площадь фигуры. Решение задачи выглядит следующим образом:
- Первый катет нужно приравнять к переменной m, тогда второй будет эквивалентен величине «m+1», а гипотенуза — «m+2».
- Составить уравнение для нахождения периметра: m+m+1+m+2=12. Его корень (значение переменной) равен 1, то есть m=3. Тогда второй катет эквивалентен числу 4, а гипотенуза — 5.
- Фигура является прямоугольником, так как состоит из равных треугольников.
- На основании третьего пункта алгоритма стороны прямоугольника эквивалентны 3 и 4.
- Площадь вычисляется по формуле: S=k*l=3*4=12 (ед2).
Cледует отметить, что фигура имеет одинаковые значения площади и периметра. Этот факт свидетельствует о том, что она была образована при помощи египетских треугольников (каждая сторона на единицу больше предыдущей).
Таким образом, определение площади прямоугольника необходимо осуществлять по алгоритму, предложенному специалистами. Кроме того, нужно внимательно следить за единицами измерения размерности.