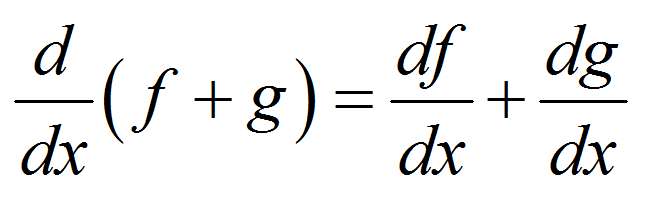Step-by-Step Examples
Calculus
Derivative Calculator
Step 1:
Enter the function you want to find the derivative of in the editor.
The Derivative Calculator supports solving first, second…., fourth derivatives, as well as implicit differentiation and finding the zeros/roots. You can also get a better visual and understanding of the function by using our graphing tool.
Chain Rule: ddx[f(g(x))]=f'(g(x))g'(x)
Step 2:
Click the blue arrow to submit. Choose “Find the Derivative” from the topic selector and click to see the result!
Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).
Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
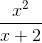
cos2(2x+π) ≡ (cos(2*x+pi))^2
Правила ввода функции, заданной в неявном виде
Примеры
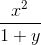
cos2(2x+y) ≡ (cos(2*x+y))^2
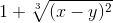
Если функция задана в виде y2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y).
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
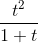
cos2(t) ≡ cos(t)^2
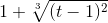
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
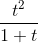
cos2(t) ≡ cos(t)^2
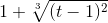
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функции y=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
.

В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции

Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию
Учитывая, что 
Но 

Пример 4. Найти производную функции y=xex
Решение.


Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Данный калькулятор вычисляет производную функции и затем упрощает ее.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, – вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже.
Упрощение полученной производной может занять некоторое время, для сложных функций — весьма продолжительное. Если ждать до конца нет сил — нажмите кнопку остановить. У меня получался достаточно простой вариант уже после 10-15 секунд работы алгоритма упрощения.
Калькулятор производных
Производная функции
Допустимые операции: + – / * ^
Константы: pi
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Показать детали вычисления
Показать шаги вычисления производной и упрощения формулы
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Синтаксис описания формул
В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, – — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.
Таблица синтаксиса математических выражений
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Вычисление производной
Вычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз…
Правила дифференцирования
1) производная суммы:
2) производная произведения:
3) производная частного:
4) производная сложной функции равна произведению производных:
Таблица производных
Производная степенной функции:
Производная показательной функции:
Производная экспонециальной функции:
Производная логарифмической функции:
Производные тригонометрических функций:
,
,
,
Производные обратных тригонометрических функций:
,
,
,
Производные гиперболических функций:
Данный онлайн калькулятор вычисляет производную функции. Программа не только вычисляет ответ, она производит пошаговое решение. Выбирается порядок дифференцирования.
Как пользоваться калькулятором для нахождения производных онлайн:
1. Введите математическое выражение с переменной x, в выражении используйте стандартные операции: + сложение, –
вычитание, / деление, * умножение, ^ – возведение в степень, а также математические функции.
2. Выберите порядок дифференцирования (решения производных от первого до пятого порядка включительно).
3. Нажмите кнопку – Вычислить производную.
4. Через несколько секунд внизу отобразится пошаговое решение производной с подробными комментариями.
При помощи нашего калькулятора вы можете найти производную онлайн как от элементарной функции, так и от сложной, не имеющей решения в аналитическом виде.
Калькулятор поможет найти производную функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
: x^a
модуль x: abs(x)
Для того, чтобы найти производную функции
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции 
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где 
Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.
- Примеры
- x*E^x, x;
- x^3*E^x, {x,17};
- x^3*y^2*Sin[x+y], x;
- x^3*y^2*Sin[x+y], y,
- x/(x+y^4), {x,6}.
Инструкции:
Используйте этот калькулятор производных для нахождения производной заданной вами функции, показывая все этапы процесса. Пожалуйста, введите функцию, для которой вы хотите вычислить производную, в поле ниже.
Производный калькулятор
Калькулятор производных проведет вас через все шаги и правила, используемые для нахождения производной заданной функции. Вы должны ввести функцию, например 3x + sin(x^2), или вы можете ввести определение всей функции, например f(x) = 3x^ 2 + 2tan(x^3).
Обратите внимание, что это можно назвать калькулятором первой производной, так же как и калькулятором производной. Первая производная и производная представляют собой одно и то же, и “первая” часть обычно опускается.
Функция может быть полностью упрощенной или нет, это не имеет значения, так как калькулятор сначала упростит функцию, если это необходимо, прежде чем вычислить ее производную.
Однажды
действующая функция
уже предоставлен, вам нужно просто нажать кнопку “Рассчитать”, подождать несколько секунд, и вам будут представлены все этапы расчета.
Дифференциация является основным инструментом, используемым в исчислении (наряду с интегрированием), и это важная операция, которая широко используется в более продвинутой математике. Некоторые очень распространенные приложения включают
расчет касательной
, максимумы и минимумы и многое другое.
Как вычислить производную функции?
Процесс вычисления производной функции называется
дифференциация
и заключается в определении мгновенной скорости изменения точки, в каждой точке области функции.
Что такое мгновенная скорость изменения функции? Что ж, давайте начнем с определения
скорость изменения
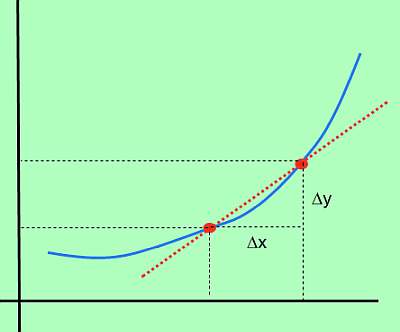
: Рассмотрим функцию (f) и предположим, что у нас есть две точки, (x_0) и (x_1). В точке (x_0) функция имеет вид (f(x_0)), а в точке (x_1) функция принимает значение (f(x_1))
Затем изменение f определяется как (Delta y = f(x_1) – f(x_0)) (которое также называют изменением y). Кроме того, изменение x определяется как (Delta x = x_1 – x_0)). Проще говоря, (Delta x) — это изменение x, тогда как (Delta y) — это изменение значения функции из-за изменения x.
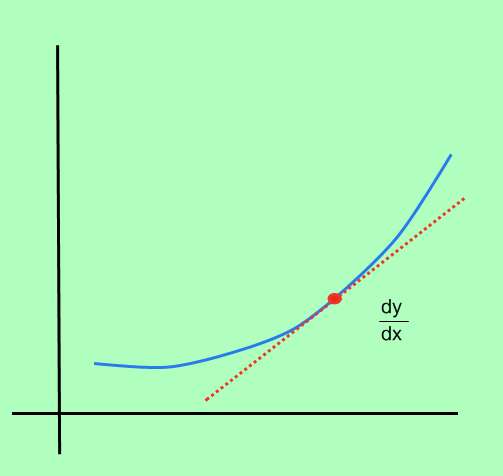
Графически:
Производная формула
Таким образом, если (Delta x) представляет собой изменение x, а (Delta y) представляет собой изменение значения функции из-за изменения x, соответствующее
скорость изменения
это:
[text{Rate of Change} = displaystyle frac{Delta y}{Delta x} ]
Итак, какова будет мгновенная скорость изменения? Это соответствует анализу того, что произойдет, если (Delta x) станет действительно маленьким. Можно было бы ожидать, что (Delta y) также станет маленьким, но что произойдет с курсом между (Delta y) и (Delta x)?
Итак, в данном контексте мгновенная скорость изменения определяется как
[text{Instant Rate of Change} = displaystyle lim_{x_1 to x_0}frac{Delta y}{Delta x} ]
Итак, с точки зрения непрофессионала, мы устанавливаем (x_0) фиксированным и вычисляем скорость изменения для значений (x_1), которые все ближе и ближе к (x_0). Используя эту идею мгновенной скорости изменения, мы можем дать следующую формулу для производной в точке (x_0).
[f'(x_0) = displaystyle lim_{x_1 to x_0}frac{Delta y}{Delta x} = displaystyle lim_{x_1 to x_0}frac{f(x_1) – f(x_0)}{x_1 – x_0} ]
Если вышеуказанный предел выходит за пределы, мы говорим, что функция f дифференцируема в (x_0). Также будем говорить, что функция дифференцируема на множестве А, если функция дифференцируема в каждой точке множества.
Шаги для использования формулы производной
-
Шаг 1:
Четко определите функцию f, которую вы хотите дифференцировать -
Шаг 2:
Убедитесь, что вы максимально упростили f, иначе нахождение требуемого предела может быть неоправданно усложнено -
Шаг 3:
Решите, будете ли вы работать с общей точкой x0, или вы задаете конкретную числовую точку для x0 -
Шаг 4:
На основе определения функции используйте формулу (f'(x_0) = displaystyle lim_{x_1 to x_0}frac{f(x_1) – f(x_0)}{x_1 – x_0} ). То есть подставьте значения x0 и x1 в f и посмотрите, как формула выглядит алгебраически. -
Шаг 5:
Упростите все, что можно, ДО того, как взять лимит -
Шаг 6:
Иногда проще задать x1 = x0 + h, а затем вычислить предел, когда h сходится к 0
Обратите внимание, что шаг 6 – это шаг, который некоторым людям нравится по умолчанию. Действительно, альтернативная формула производной, которая может показаться более простой для целей упрощения, такова:
[f'(x_0) = displaystyle lim_{h to 0} frac{f(x_0 + h) – f(x_0)}{h} ]
это формула, которую вы можете найти в своем учебнике, вместо другой.
Правила производных
Вычисление производной по формуле может показаться чертовски трудоемким занятием. И действительно, это может быть трудоемким процессом, если мы решим каждый процесс дифференцирования проводить по формуле производной.
К счастью, существует ряд функций (а именно
полиномы
,
Тригонометрические функции
), для которых мы точно знаем их производные.
Кроме того, у нас есть
правила дифференциации
которые позволяют нам найти производную функции, которая является
Составная функция
и/или комбинацию элементарных функций (для которых известна их производная), в терминах элементарных производных.
Каковы этапы вычисления производной?
-
Шаг 1:
Определите функцию f, которую вы хотите дифференцировать. Упростите как можно больше перед вычислением ее производной -
Шаг 2:
Определите, должны ли вы использовать формулу производной или нет -
Шаг 3:
Если вы должны использовать производную формулу, используйте (f'(x_0) = displaystyle lim_{x_1 to x_0}frac{f(x_1) – f(x_0)}{x_1 – x_0} ) или вы можете использовать (f'(x_0) = displaystyle lim_{h to 0}frac{f(x_0+h) – f(x_0)}{h} ), если это кажется более простым. -
Шаг 4:
Если вам не требуется использовать формулу производной, вы можете воспользоваться основными правилами дифференцирования: Линейность,Правило Продукта
,
Правило Квоты
и
Правило Цепи
, что поможет вам свести вычисление производной к использованию основных известных производных
Часто бывает так, что функция, которую вы пытаетесь
найти производную
for не является простой функцией, а представляет собой базовую комбинацию нескольких простых функций. Например, функция
[f(x) = x + cos(x) + sin(x)]
сама по себе не является элементарной функцией, но
Составная функция
из трех элементарных функций: (x), (sin x) и (cos x).
Применение деривативов
Можно подумать: “Ну, производные связаны с пределами, а это супертеоретически, поэтому они не должны иметь слишком много применений”, но вы будете совершенно неправы. Магия производных заключается в том, что они, по сути, представляют собой скорость изменения функций, которые могут представлять различные типы процессов.
Именно поэтому дифференциация позволяет изучить процесс изменения и сравнить изменяющиеся переменные, что имеет широкое применение.
Пример: вычисление производной
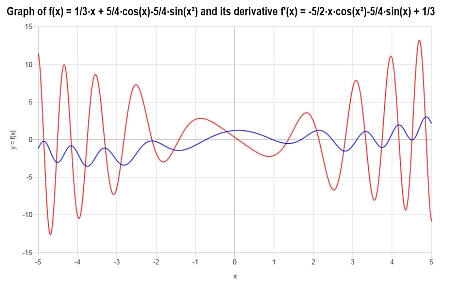
Вычислите производную по x для (f(x) = displaystyle frac{x}{3} + frac{5}{4} cos(x) – frac{5}{4} sin(x^2))
Отвечать:
Предусмотрена следующая функция: (displaystyle f(x)=frac{x}{3}+frac{5}{4}cosleft(xright)-frac{5}{4}sinleft(x^2right)), для которой нам нужно вычислить ее производную.
Начальный Этап:
В этом случае нам сначала нужно упростить заданную функцию (displaystyle f(x)=frac{x}{3}+frac{5}{4}cosleft(xright)-frac{5}{4}sinleft(x^2right) ), и для этого мы проведем следующие шаги упрощения:
( displaystyle f(x)=frac{x}{3}+frac{5}{4}cosleft(xright)-frac{5}{4}sinleft(x^2right))
Directly reorganizing/simplifying/expanding
( displaystyle = ,,)
(displaystyle frac{1}{3}x+frac{5}{4}cosleft(xright)-frac{5}{4}sinleft(x^2right))
После упрощения функции мы можем перейти к вычислению производной:
( displaystyle frac{d}{dx}left(frac{1}{3}x+frac{5}{4}cosleft(xright)-frac{5}{4}sinleft(x^2right)right))
By linearity, we know (frac{d}{dx}left( frac{1}{3}x+frac{5}{4}cos(x)-frac{5}{4}sin(x^2) right) = frac{d}{dx}left(frac{1}{3}xright)+frac{5}{4} cdot frac{d}{dx}left(cos(x)right)-frac{5}{4}cdot frac{d}{dx}left(sin(x^2)right)), so plugging that in:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(frac{1}{3}xright)+frac{5}{4} cdot frac{d}{dx}left(cosleft(xright)right)-frac{5}{4}cdot frac{d}{dx}left(sinleft(x^2right)right))
Using the Chain Rule: (frac{d}{dx}left( sinleft(x^2right) right) = frac{d}{dx}left(x^2right)cdot cosleft(x^2right)),directly differentiating: (frac{d}{dx}left( cosleft(xright) right) = -sinleft(xright)) and directly we get: (frac{d}{dx}left( frac{1}{3}x right) = frac{1}{3})
( displaystyle = ,,)
(displaystyle frac{1}{3}+frac{5}{4} left(-sinleft(xright)right)-frac{5}{4}cdot frac{d}{dx}left(x^2right)cdot cosleft(x^2right))
Using the Power Rule for polynomial terms: (frac{d}{dx}left( x^2 right) = 2x)
( displaystyle = ,,)
(displaystyle frac{1}{3}+frac{5}{4} left(-sinleft(xright)right)-frac{5}{4}cdot 2xcdot cosleft(x^2right))
( displaystyle = ,,)
(displaystyle frac{1}{3}+frac{5}{4}cdot left(-sinleft(xright)right)-frac{5}{4}cdot 2xcosleft(x^2right))
Grouping and operating all the integer terms and fractions: (displaystyle 2 times left(-frac{ 5}{ 4}right)=-frac{ 5}{ cancel{ 2} times 2} times cancel{ 2}=-frac{ 5}{ 2})
( displaystyle = ,,)
(displaystyle frac{1}{3}+frac{5}{4}cdot left(-sinleft(xright)right)-frac{5}{2}xcosleft(x^2right))
Directly reorganizing/simplifying/expanding
( displaystyle = ,,)
(displaystyle -frac{5}{2}xcosleft(x^2right)-frac{5}{4}sinleft(xright)+frac{1}{3})
Следующий график получается для (displaystyle f(x)=frac{1}{3}x+frac{5}{4}cosleft(xright)-frac{5}{4}sinleft(x^2right)) на интервале ([-5, 5]):
Пример: дифференцирование функции
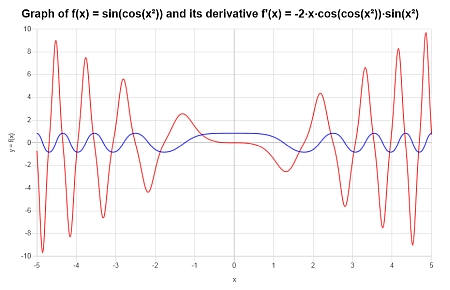
Вычислить производную от : (f(x) = sin(cos(x^2))) и представить график (f(x)) и (f'(x)).
Отвечать:
Теперь у нас есть (displaystyle f(x)=sinleft(cosleft(x^2right)right)).
Функция пришла уже упрощенной, поэтому мы можем перейти непосредственно к вычислению ее производной. Используя этот производный кал, мы получаем:
( displaystyle frac{d}{dx}left(sinleft(cosleft(x^2right)right)right))
Using the Chain Rule: (frac{d}{dx}left( sinleft(cosleft(x^2right)right) right) = frac{d}{dx}left(cosleft(x^2right)right)cdot cosleft(cosleft(x^2right)right))
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(cosleft(x^2right)right)cdot cosleft(cosleft(x^2right)right))
Using the Chain Rule: (frac{d}{dx}left( cosleft(x^2right) right) = frac{d}{dx}left(x^2right)cdot left(-sinleft(x^2right)right))
( displaystyle = ,,)
(displaystyle left(frac{d}{dx}left(x^2right)cdot left(-sinleft(x^2right)right)right) cosleft(cosleft(x^2right)right))
Using the Power Rule for polynomial terms: (frac{d}{dx}left( x^2 right) = 2x)
( displaystyle = ,,)
(displaystyle left(2xcdot left(-sinleft(x^2right)right)right) cosleft(cosleft(x^2right)right))
( displaystyle = ,,)
(displaystyle 2xcdot left(-sinleft(x^2right)right)cosleft(cosleft(x^2right)right))
Expanding and simplifying the expression
( displaystyle = ,,)
(displaystyle -2xcosleft(cosleft(x^2right)right)sinleft(x^2right))
Таким образом, мы получаем следующий график функции на интервале ([-5, 5]):
Пример: калькулятор производных
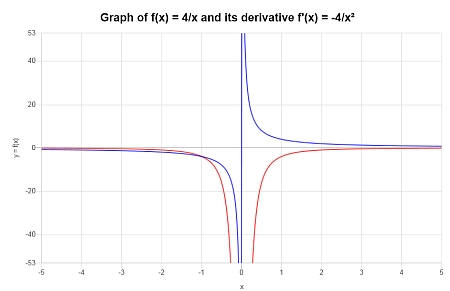
Найдите производную от ( f(x) = displaystyle frac{4}{x}). Везде ли он четко определен? График это.
Отвечать:
Предоставляемая функция, для которой требуется производная, — это (displaystyle f(x)=frac{4}{x}).
Дальнейшее упрощение не требуется, поэтому мы можем перейти непосредственно к вычислению его производной:
( displaystyle frac{d}{dx}left(frac{4}{x}right))
Using the Power Rule for a polynomial term with negative exponent: (frac{d}{dx}left( frac{4}{x} right) = -frac{4}{x^2})
( displaystyle = ,,)
(displaystyle -frac{4}{x^2})
Графически:
Подробнее о производных и функциях
Этот
производный калькулятор с шагами
окажется для вас очень полезным, так как проведет вычисление производной любой заданной функции, показывая все этапы процесса, применяя соответствующие
Правила производных
, и сообщать вам, когда они применяются и почему.
Этот калькулятор также можно назвать
dy dx калькулятор
или
калькулятор дифференциального коэффициента
поскольку это именно то, что он делает, он вычисляет предел отношения dy/dx, когда dx приближается к 0.
Функции — чрезвычайно важные конструкции в математике. Наряду с дифференцированием необходимо уметь
упростить функцию
обычно в качестве преамбулы других, более специализированных вычислений. Существуют специальные типы функций, которые позволяют выполнять конкретные операции, например, то, что вы делаете с
Полиномиальные операции
.
Интересно, что многие важные элементы, такие как нахождение координат
вершина параболы
которые можно вывести хитрым способом, используя геометрические аргументы, можно тривиально получить с помощью дифференцирования.
Также идея о
Касательная линия
и
Аппроксимация Первого Порядка
появляются естественным образом, вытекая из понятия производного и естественного расширения.

 : x^a
: x^a