|
0 / 0 / 0 Регистрация: 17.04.2020 Сообщений: 47 |
|
|
1 |
|
|
MathCAD 15 Найти сумму всех элементов матрицы А18.06.2020, 15:58. Показов 4712. Ответов 13
Найти сумму всех элементов матрицы А Изображения
0 |
|
8701 / 6308 / 3384 Регистрация: 14.01.2014 Сообщений: 14,473 |
|
|
18.06.2020, 17:01 |
2 |
|
РешениеВот так можно Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 17.04.2020 Сообщений: 47 |
|
|
18.06.2020, 17:15 [ТС] |
3 |
|
Не подскажите, как сделать знак суммы с 2 пустыми местозаполнителяями, а не 4. я делал комбинацию crtl+shift+4
0 |
|
8701 / 6308 / 3384 Регистрация: 14.01.2014 Сообщений: 14,473 |
|
|
18.06.2020, 17:17 |
4 |
|
С палитры “Матанализ” вводите знак суммы два раза!
1 |
|
0 / 0 / 0 Регистрация: 17.04.2020 Сообщений: 47 |
|
|
18.06.2020, 18:11 [ТС] |
5 |
|
Не подскажете как сделать тоже самое, но соединение организовать дописыванием вниз?
0 |
|
8701 / 6308 / 3384 Регистрация: 14.01.2014 Сообщений: 14,473 |
|
|
18.06.2020, 18:15 |
6 |
|
Вместо augment(A,B) используйте stack(A,B)
0 |
|
0 / 0 / 0 Регистрация: 17.04.2020 Сообщений: 47 |
|
|
19.06.2020, 09:04 [ТС] |
7 |
|
не ясно
0 |
|
8701 / 6308 / 3384 Регистрация: 14.01.2014 Сообщений: 14,473 |
|
|
19.06.2020, 09:31 |
8 |
|
Яснее ясного Миниатюры
0 |
|
0 / 0 / 0 Регистрация: 17.04.2020 Сообщений: 47 |
|
|
19.06.2020, 11:22 [ТС] |
9 |
|
Это точно к этому ответ? Ваш ответ на первый вопрос был другим решением.
0 |
|
8701 / 6308 / 3384 Регистрация: 14.01.2014 Сообщений: 14,473 |
|
|
19.06.2020, 11:32 |
10 |
|
Это был ответ на Ваш новый вопрос (похоже, что задали по ошибке не в той теме)
Не подскажете как сделать тоже самое, но соединение организовать дописыванием вниз?
0 |
|
0 / 0 / 0 Регистрация: 17.04.2020 Сообщений: 47 |
|
|
19.06.2020, 13:25 [ТС] |
11 |
|
нет. в той же. Там просто задание состоит из 2 частей. Первое(12 пункт) – Найти сумму всех элементов матрицы А
0 |
|
6630 / 4733 / 1975 Регистрация: 02.02.2014 Сообщений: 12,682 |
|
|
19.06.2020, 13:31 |
12 |
|
Повторить пункт 12, может, опечатка…
1 |
|
0 / 0 / 0 Регистрация: 17.04.2020 Сообщений: 47 |
|
|
19.06.2020, 14:14 [ТС] |
13 |
|
А если выдает ошибку размерности массива не совпадают?
0 |
|
6630 / 4733 / 1975 Регистрация: 02.02.2014 Сообщений: 12,682 |
|
|
19.06.2020, 14:21 |
14 |
|
показывайте, что у вас получилось…
0 |
Иногда бывает
нужно вычислить сумму всех элементов
вектора. Для этого существует
вспомогательный оператор, задаваемый
кнопкой VectorSum
(Сумма вектора)
на панели Matrix
(Матрица)
или сочетанием клавиш <Ctrl>+<4>.
Этот оператор чаще оказывается полезным
не в векторной алгебре, а при организации
циклов с индексированными переменными.
Сумму диагональных
элементов квадратной матрицы называют
следом
(trace)
матрицы. След можно найти с помощью
функции tr:
tr(A)
– след квадратной матрицы A.
Задание:
Найдите след квадратной матрицы A
=
![]() .
.
Решение:
![]()
![]()
9 Обращение квадратной матрицы
Поиск обратной
матрицы возможен, если матрица квадратная,
и ее определитель не равен нулю.
Произведение исходной матрицы на
обратную по определению является
единичной
матрицей. Для ввода оператора поиска
обратной матрицы нажмите кнопку Inverse
(Обратная матрица)
на панели инструментов Matrix
(Матрица).
10 Возведение матрицы в степень
К квадратным
матрицам можно формально применять
операцию возведения в степень n.
Для этого n
должно быть целым числом. Ввести оператор
возведения матрицы M
в степень n
можно точно так же, как и для скалярной
величины: нажав кнопку Raise
to Power
(Возвести в степень)
на панели Calculator
(Калькулятор)
или клавишу <^>.
После появления местозаполнителя в
него следует ввести значение степени
n.
11 Символьные преобразования
Все матричные и
векторные операторы, о которых шла речь
выше, допустимо использовать в символьных
вычислениях. Мощь символьных операций
заключается в возможности проводить
их не только над конкретными числами,
но и над переменными.
Пример:
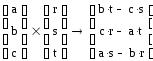
12 Генераторы матриц
Самым наглядным
способом создания
матрицы или вектора является применение
первой кнопки панели инструментов
Matrix (Матрицы).
Однако в большинстве случаев, в частности,
при программировании сложных проектов,
удобнее бывает создавать массивы с
помощью встроенных функций.
12.1
Создание матрицы на основе функции
Matrix(M,
N,
f)
– создание матрицы размера M×N,
каждый i,
j
элемент которой есть f(i,
j),
где:
-
M
– количество строк; -
N
– количество столбцов; -
f(i,
j)
– функция.
12.2
Генерация матриц специального вида
В Mathcad
легко создать матрицы определенного
вида с помощью одной из встроенных
функций:
-
identity(N)
– единичная матрица размера N×N; -
diag(V)
– диагональная
матрица, на диагонали которой находятся
элементы вектора
V; -
geninv(A)
– создание матрицы, обратной матрице
А; -
rref(A)
– преобразование матрицы или вектора
A
в ступенчатый вид, где:
N
– целое число;
V
– вектор;
A
– матрица из действительных чисел.
Примечание:
Размер N×M
матрицы A
для функции geninv
должен быть таким, чтобы N
M.
13 Выделение части матрицы
Часть матрицы
выделяется одним из следующих способов:
1) для выделения
одного
элемента
предназначен оператор нижнего индекса.
Оператор вводится нажатием кнопки
Subscript (Нижний
индекс) со значком
xn
на панели Matrix
(Матрица),
либо нажатием клавиши <[>;
2) для выделения
из матрицы столбца
примените оператор выделения столбца
нажатием кнопки Matrix
Column (Столбец
матрицы) с
изображением угловых скобок <>
на панели Matrix
(Матрица),
либо сочетанием клавиш <Ctrl>+<6>.
Этот оператор называют еще, по аналогии
с предыдущим, оператором верхнего
индекса;
3) чтобы выделить
из матрицы строку,
примените тот же оператор <>
к транспонированной матрице;
4) для выделения
подматрицы
используйте встроенную функцию
submatrix(A, ir,
jr, ic, js),
возвращающую часть матрицы A,
находящуюся между строками ir,
jr и столбцами
ic, jc
включительно.
Примечание:
выделить из
матрицы один столбец или одну строку
можно и с помощью функции submatrix.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Матрица в Mathcad
Для быстрого построения матрицы в Mathcad, нажмите Ctrl+M, появится окно Insert Matrix
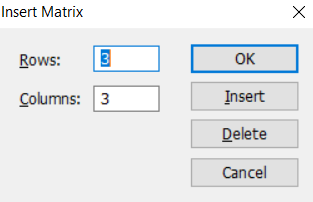
Указываем размерность матрицы, rows – количество строк, columns – количество столбцов. Жмем Ок.
Вводим значения
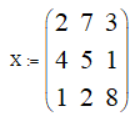
Последний элемент матрицы равен (нумерация первого элемента начинается с нуля)
![]()
Найдем максимальное значение матрицы max(X)
![]()
Найдем минимальное значение матрицы min(X)
![]()
Среднее значение матрицы равно
![]()
Первая матрица-столбец равна 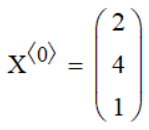
Транспонирование матрицы в Mathcad XT
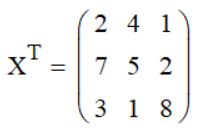
Вычисление обратной матрицы

Вычисление определителя матрицы
![]()
Умножение матрицы на матрицу
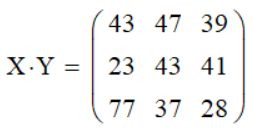
Сложение матриц — сумма элементов матрицы Mathcad
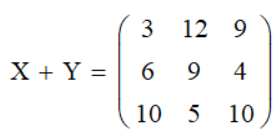
Возведение матрицы в степень
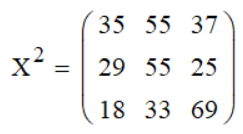
Далее, создадим две матрицы в виде векторов 3×1 и 1×3
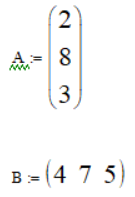
Здесь A – матрица-столбец; B – матрица-строка
Первый элемент вектора A (нумерация начинается с нуля) равен
![]()
Количество элементов в матрице-столбце через функцию length(A) равно
![]()
Найдем значения для функции ln x, подставив значения матрицы A
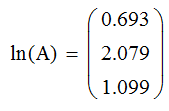
Сортировка вектора sort(А)
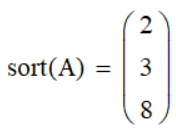
Количество элементов в векторе rows(A), cols(A)
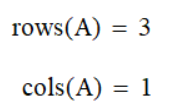
Сумма вектора
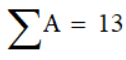
Векторное произведение в Mathcad
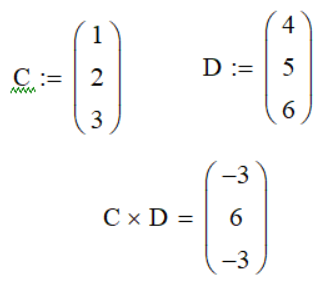
Скалярное произведение
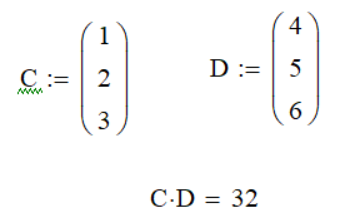
Векторизация
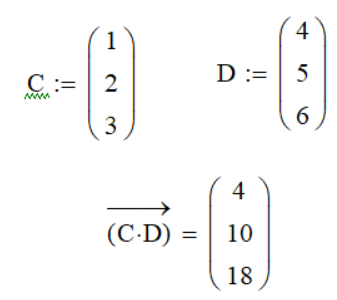
![]() 2836
2836
Векторы и матрицы в MathСad
Вы уже наверняка не раз сталкивались с такими понятиями как векторы и матрицы. Вектор – это обыкновенный столбец с числами. Матрица представляет собой сборный блок с объектами. Именно на работе с этими элементами построен принцип функционирования программы Excel. В этом уроке мы расскажем о том, как работать с такими вычислениями в программе Маткад и акцентируем внимание на том, почему процесс работы в данном ПО куда проще и удобнее.
Мы уже рассказывали в своих уроках о том, что все наши векторы начинались с элемента с нулевым значением. Сейчас же мы поставим номером первого элемента цифру один, ведь так нам гораздо проще будет сориентироваться в учебном материале.

Данное значение можно внести прямо в рабочее поле.

Посмотрите на матрицы на рисунке ниже.

Как вы можете заметить, в них входят и числа, и функции. Помимо этого, сюда можно внести и текст. Чтобы вывести элемент матрицы, воспользуйтесь подстрочным индексом.

Матрицы, описанные на скрине повыше, относятся к квадратному типу. Тем не менее, пользователь может самостоятельно устанавливать их размерные рамки.

Примите во внимание, что первое число обозначает общую нумерацию строчки, а второе – номер столбика.

Для векторного столбца второй индекс можно удалить. Для строки же он является обязательным.

Нужные команды, для всевозможного выделения строчек или столбиков вы всегда сможете отыскать во вкладке «Математика».


Большинство операций для векторных и матричных конструкций вполне соответствуют работе со стандартными числами и функциями. Для того, чтобы отыскать обратную матрицу, потребуется действовать по аналогии с операциями деления. Пользователь может записать операторы, задав им наименования матриц и векторов. Например, это может выглядеть так:

Более подробно мы рассмотрим данный опционал немного погодя. Стоит отметить, что такая функция нуждается в девяти операциях умножения и в таком же количестве деления. Согласитесь, что расписывать все эти процессы достаточно скучно. К тому же, с большими матрицами такой подход нерациональный.
Методика применения векторов отличается значительным разнообразием. Чтобы разработать вектор или матрицу, понадобится открыть вкладку «Вставить матрицу». На экране появится сетка с изображением маленьких квадратиков.

Перемещаем указатель на эту сетку. Настраиваем курсор на нужные габариты матрицы. Кликаем дважды ЛКМ.
На экране появляется новая матрица.

Матрица может быть переименована, после того, как пользователь дважды кликнет по левой скобке.

Чтобы быстро вставить или удалить строчки да столбцы, можно вызвать контекстное меню «Операторы с векторамиматрицами» на одноименной вкладке.

Работа с матрицами
Эффекты от матриц или вектором гораздо проще сообразить, пользуясь специально разработанными символами. Обратите внимание на скрин ниже.

Оператор транспортировки вызывается посредством выполнения операции Математика –> Операторы –> Векторы и матрицы:

Кликаем по правой стороне матрицы и применяем оператор. Он подходит как для символьных, так и численных матриц.

Операции в векторах часто выполняются по одному элементу. В этой ситуации можно воспользоваться очень удобным оператором, который отвечает за разработку вектора. Чтобы перемножить два вектора, понадобится выполнить простой пример.

Теперь нам нужно выбрать нужные параметры и активировать векторизацию.

Вычисляем заданные параметры и смотрим на результат. Первый элемент приумножился на второй, и так далее.

Еще примеры таких опций.

Операции поэлементного типа могут применяться исключительно к массивам одинакового размера.
Добавление и вычитание
Данные операции относятся к поэлементному типу.

Она также применяется к массивам одинакового размерного типа.
Пользуясь оператором, предназначенным для суммирования, можно отыскать сумму всех векторных частей.

Скалярное произведение работает по представленному ниже принципу.

При таком типе умножения матриц, программа занимается умножением данных элементов по столбцам. Данная операция может применяться исключительно к тем матрицам, которые характеризуются равным количеством строчек и столбцов.

Обратите внимание, что немалая роль отводится поочередности множителей.

Только в редких случаях скалярное произведение может стать коммутативным.

Скаляр двух векторов показывает результат как на фотографии ниже.

Данная опция может использоваться исключительно для двух векторных столбов из трех элементов.

Векторное произведение часто используется для механики, гидродинамики и огромного количества подобных сфер деятельности.
Обратная матрица может быть применима для квадратных матриц:

В результате у нас получится матрица единичного типа

Если произвести матрицу и единичную матрицу, мы получим первоначальный вариант.


Определитель может быть разработан исключительно для матрицы квадратного типа. Он может быть нулевым в любых условиях. Обратная матрица имеет в своей структуре дроби, в состав которых входит определитель.

В ситуациях, когда определитель установлен на ноль, к нему нереально подобрать обратную матрицу. Сама матрица автоматически становится сингулярной. О таких изменениях пользователь узнает из оповещения программы.

В ситуациях со скалярами, определитель соответствует их модулям

Команда «определитель» помогает отыскать длину вектора .

Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.

Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»

Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»

В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»

Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.

Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.
Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.
Векторы и матрицы в MathCAD
Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.
Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.
Поэлементный ввод массива Х
| Вводимые символы | Отображаемые символы |
| X [ 1 Shift+: 5 | X1:=5 |
| X [ 2 Shift+: 8 | X2:= 8 |
| X [ 3 Shift+: 10 | X3:= 10 |
Поэлементный ввод матрицы А
| Вводимые символы | Отображаемые символы |
| A [ 1,1 Shift+: 0.1 | A11 := 0.1 |
| A [ 1,2 Shift+: -2.5 | A12 := -2.5 |
| A [ 2,1 Shift+: -1.0 | A21 := -1.0 |
| A [ 2,2 Shift+: 5.2 | A22 := 5.2 |
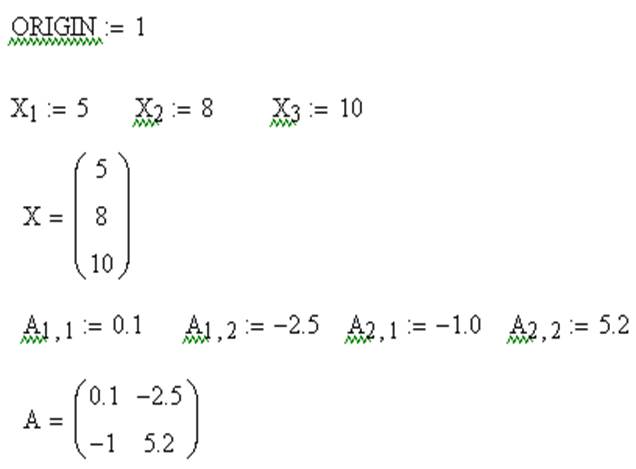
Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке  в панели математических инструментов.
в панели математических инструментов.

ПанельMatrix содержит следующие кнопки:
 – определение размеров матрицы;
– определение размеров матрицы;
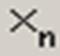 – ввод элемента массива
– ввод элемента массива 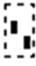 ;
;
 – вычисление матрицы, обратной к данной
– вычисление матрицы, обратной к данной 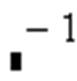 ;
;
 – вычисление определителя матрицы
– вычисление определителя матрицы 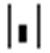 ;
;
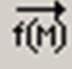 – оператор векторизации (поэлементные операции с векторами и матрицами)
– оператор векторизации (поэлементные операции с векторами и матрицами) 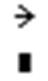 ;
;
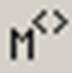 – определение столбца матрицы
– определение столбца матрицы 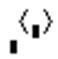 ;
;
 – транспонирование матрицы
– транспонирование матрицы 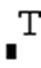 ;
;
 – определение ранжированной переменной;
– определение ранжированной переменной;
 – вычисление скалярного произведения векторов;
– вычисление скалярного произведения векторов;
 – вычисление векторного произведения векторов;
– вычисление векторного произведения векторов;
 – вычисление суммы компонент вектора.
– вычисление суммы компонент вектора.
 – визуализация цифровой информации.
– визуализация цифровой информации.
Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки  панели Matrix:
панели Matrix:
1. Ввести с клавиатуры имя матрицы и знак присваивания;
2. Щелчком по кнопке  открыть окно диалога:
открыть окно диалога:
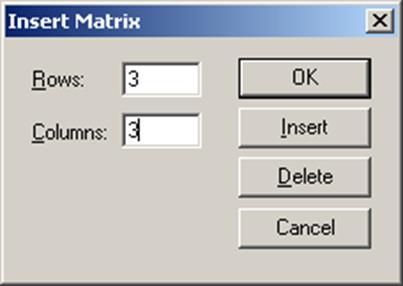
3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;
4. Закрыть окно диалога, щелкнув по кнопке OK;
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:
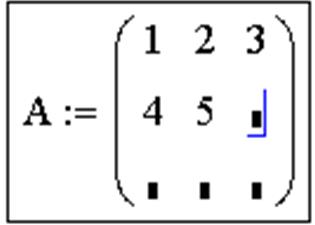

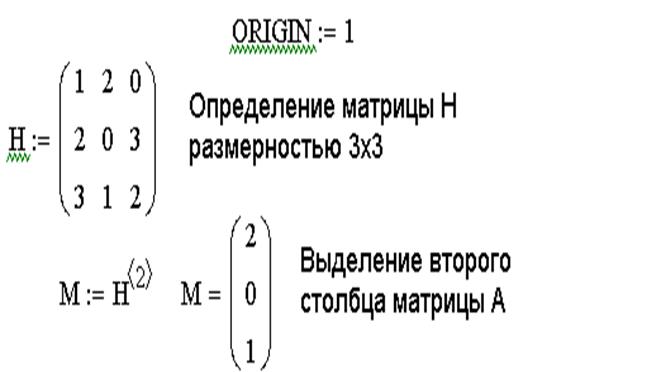
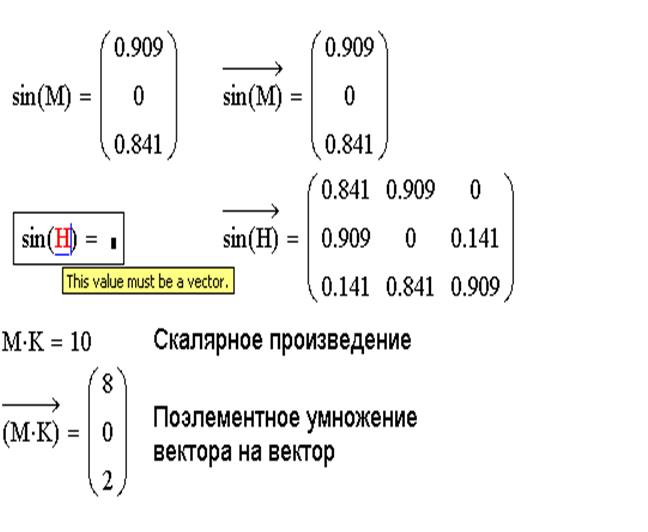
Функции определения матриц и операции с блоками матриц:
matrix(m,n,f) – создает и заполняет матрицу A=ij> размерности m на n, каждый элемент которой aij равен значению функции f(i,j);
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние – матрицу В (матрицы А и В должны иметь одинаковое число строк);
stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние – матрицу В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l
Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;
Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;
Функции вычисления различных числовых характеристик матриц:
last(v) – вычисление номера последнего элемента вектора v;
length(v) – вычисление количества элементов вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице (векторе) А;
min(A) – вычисление наименьшего элемента в матрице (векторе) А;
mean(A) – вычисление среднего значения матрицы (вектора) А;
tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;
ranc(A) – вычисление ранга матрицы А;
Функции, реализующие численные алгоритмы:
rref(A) – приведение матрицы А к ступенчатому виду;
geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;
lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.
lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;
qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;
cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙L T , где А – квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;
sort(v) – сортировка элементов вектора v в порядке возрастания их значений;
reverse(v) – перестановка элементов вектора v в обратном порядке;
csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;
rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.
ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.
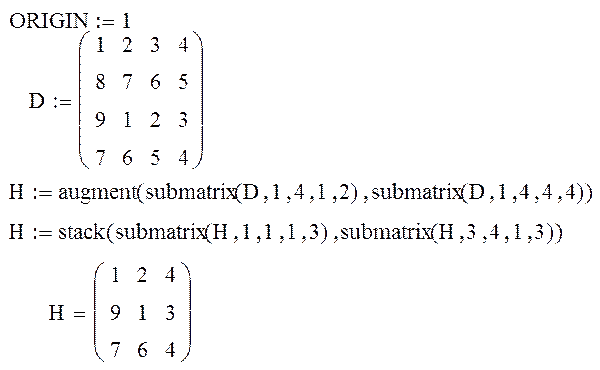
ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.
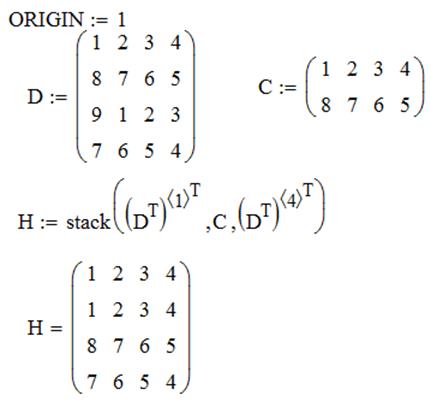
ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.
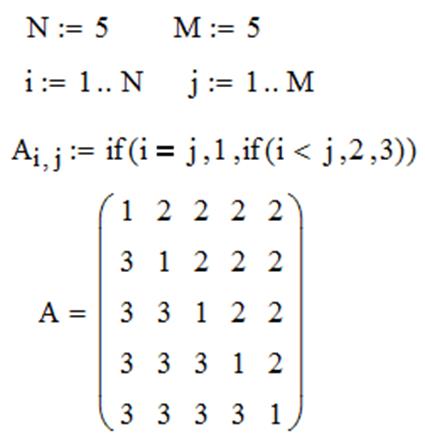
ЗАДАЧА 4. Элементы матрицы формируются по формуле 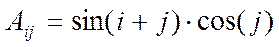 . Сформировать вектор из максимальных элементов столбцов матрицы А. Найти сумму элементов матрицы, расположенных в четных строках.
. Сформировать вектор из максимальных элементов столбцов матрицы А. Найти сумму элементов матрицы, расположенных в четных строках.

ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:
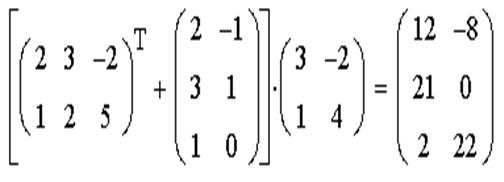
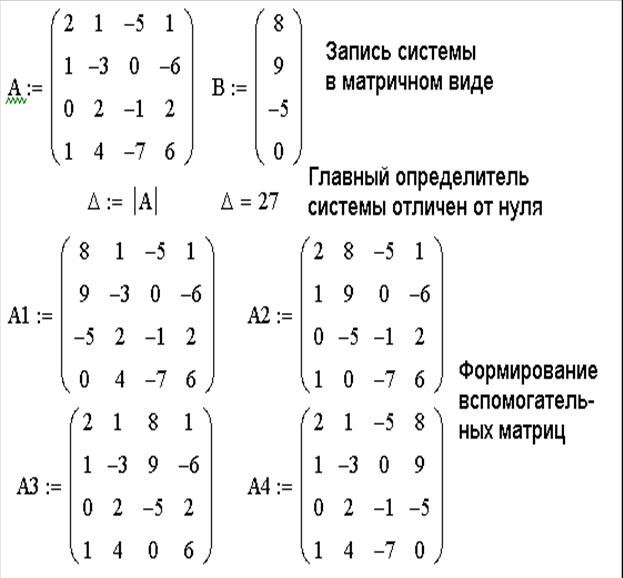
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:
Для решения поставленной задачи необходимо выполнить следующие действия:
1. Сформировать матрицу системы А и вектор правых частей b.
2. Вычислить главный определитель ∆.
3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆i;
4. Вычислить определители ∆i;
5. Найти решение системы по формуле xi=∆i/∆.

ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.
1. Сформировать матрицу коэффициентов и вектор свободных членов системы.
2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.

ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.
Порядок решения задачи:
1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.
2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);
3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.
4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.
5. Выполнить проверку Ax-B=0.
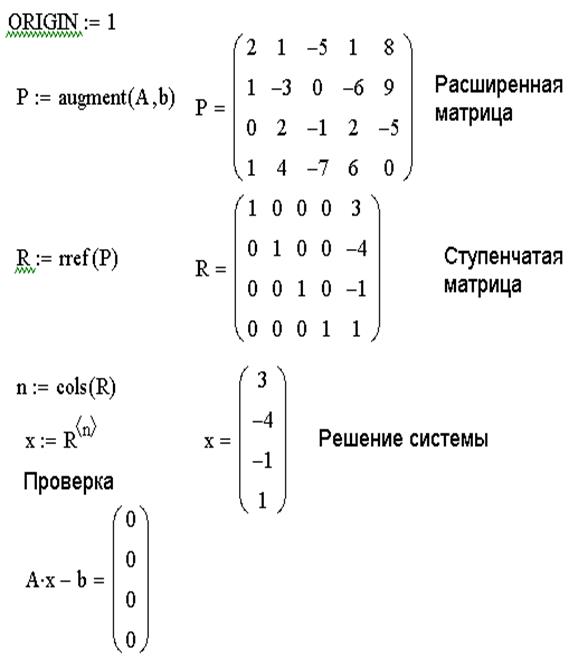
ЗАДАЧА 9. Решить систему при помощи функции lsolve:
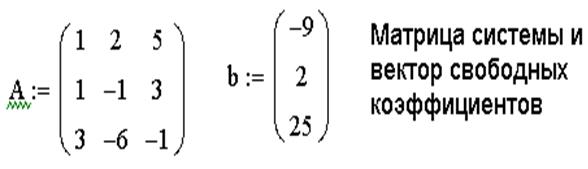

Пример системы, которая не имеет решений:
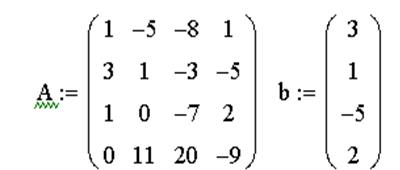
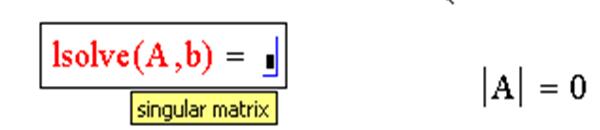
Пример системы, которая имеет бесконечное множество решений
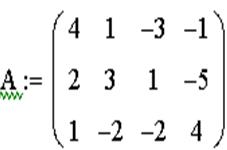
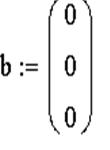

ЗАДАЧА 10. Решить систему при помощи решающего блока.
Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.
Правее и ниже ключевого слова записываются уравнения системы.
Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.
Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.
Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).
Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).
Лекція№9 – Операции с векторами и матрицами, матричные функции в математическом пакете MathCad
Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.
Понятие «вектор» обычно не отделяют от понятия «матриц». Векторы могут рассматриваться как матрицы, состоящие из одного столбца (или строки).
Матричные вычисления в MathCAD можно условно разделить на три основных типа.
К первому относятся такие элементарные действия над матрицами, как создание, извлечение из них данных, их умножение, сложение или скалярное произведение (в случае векторов). Для их реализации служат специальные операторы трех панелей семейства Math (Математические): Calculator (Калькулятор), Matrix (Матричные) иSymbolics (Символьные).
Ко второму типу можно отнести те матричные преобразования, которые требуют использования специальных функций и встроенных алгоритмов матричной алгебры, таких как, например, функции вычисления определителя, матричных норм или сортировки элементов векторов по возрастанию. Функции этой группы можно найти в категории Vector and Matrix (Векторные и матричные) у мастера функций.
И, наконец, к третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования MathCAD.
В языках программирования начальные индексы массивов обычно равняются 0. По умолчанию в MathCAD индексы строк и столбцов также отсчитываются с 0. В том случае, если такая система вам неудобна или непривычна, можно изменить точку отсчета индексов на 1, задав системную переменную ORIGIN: ORIGIN:= 1.
Доступ к элементам вектора или матрицы осуществляется с помощью индексированных переменных. Например, чтобы использовать пятый элемент вектора с именем А, нужно записать этот элемент в виде: . А для того, чтобы взять элемент матрицы В, расположенный на пересечении 3-ей строчки и 4-го столбца нужно записать: .
Для задания индексов на панели Matrix предусмотрена специальная кнопка Subscript (Индекс). Перейти к записи индекса можно также с помощью клавиши «[» ( левая квадратная скобка). Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором – столбца.
3.1. Создание векторов и матриц
В системе предусмотрены различные возможности задания векторов и матриц:
Определение матрицы последовательным заданием каждого элемента.
С помощью индексированных переменных.
С помощью использования команды Insert→Matrix, либо с помощью соответствующей кнопки панели Matrix.
Задание с помощью элементов программирования.
Применение встроенных функций.
Через связь с другим приложением, например Excel.
Создание таблицы данных.
Чтение из внешнего файла.
Рассмотрим некоторые из них. Определение матрицы последовательным заданием каждого элемента очевидно и не требует пояснений. При создании матрицы или вектора с помощью индексированной переменной следует исходить из того, что любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.
Пример 1. Требуется сформировать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.
Решение. Предоставим два варианта решения этой задачи:
с помощью индексированной переменной;
с помощью команды Insert→Matrix.
Вариант а
Для того, чтобы сформировать вектор, воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i), а затем будем использовать эту переменную для здания элементных значений вектора x. Формирование вектора представлено на рис. 3.1.
Рис. 3.1. Формирование вектора с использованием индексированной переменной
Вариант b
Формирование вектора х будем производить с помощью команды Matrix. Для этого сначала напишем оператор присваивания: «х:=» , а затем выполним команду Matrix. Эта команда открывает диалоговое окно«Insert Matrix», которое представлено на рис. 3.2, в котором необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1.
После нажатия кнопки «Ok» команда предоставит шаблон с шестью ячейками, в которые следует вписать значения элементов вектора.
Рис. 3.2. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»
Пример 2. В файле с именем «int(4_4).txt» записаны числа в виде матрицы четыре строчки по четыре элемента, разделенными пробелами. В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.
Решение. Для чтения данных из файла в матрицу/вектор можно воспользоваться функцией READPRN, которая имеет один параметр — имя файла. Фрагмент с решением представлен на рис. 3.3.
Рис. 3.3. Чтение данных из файлов
С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCAD обозначаются так, как это принято в математике: –, +, *, … .
На рис. 3.4 показано назначение некоторых специализированных команд, расположенных на панели инструментов Matrix.
Помимо этого, система MathCAD представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x).
Х -1 – получить обратную матрицу
|X| – вычислить детерминант
М Т – транспонировать
М – из матрицы взять вектор-столбец
v – получить сумму элементов
–скалярное произведение векторов
–векторное произведение векторов
Рис. 3.4. Назначение некоторых команд, расположенных на панели инструментов «Matrix»
На рис. 3.5 представлены вычисления с использованием операций над матрицами.
Рис. 3.5. Примеры матричных вычислений в MathCAD
Пример 3. Требуется сформировать диагональную квадратную матрицу с(6×6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.
Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начнем с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 3.6.
Рис. 3.6. Формирование диагональной матрицы
Пример 4. Даны две матрицы: А(4×3) и В(4×2). Требуется объединить эти матрицы в одну матрицу С(4×5), причем, первыми столбцами новой матрицы должны быть столбцы матрицы А, а справа от этих элементов следовать столбцы матрицы В (методом «дописывания справа»).
Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 7.7.
Рис. 3.7. Объединения двух матриц по правилу «дописывания справа»
Пример 5. Даны две матрицы: А(2×3) и В(3×3). Требуется объединить эти матрицы в одну матрицу С(5×3), причем, в новой матрицы в качестве первых строк должны быть строки матрицы А, а за ними должны следовать строки матрицы В.
Решение. Для соединения двух матриц в одну матрицу по правилу «друг под другом» можно использовать функцию stack, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 3.8.
Рис. 3.8. Объединения двух матриц по правилу «друг под другом»
Пример 6. Дана матрица А(6×6). Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2-го по номер 4-ый, и столбцах, начиная с номера 0-го по номер 5-ый.
Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет 5 параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 3.9.
Рис. 3.9. Выделение подматрицы из заданной матрицы
Пример 7. Дана матрица А(6×6). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 4–ым столбцом матрицы А, а второй – с 3-ей строкой матрицы А.
Решение. Для получения векторных значений можно воспользоваться командой М (из матрицы взять вектор-столбец), которая расположена на панели «Мatrix». Для получения первого вектора эту команду нужно применить непосредственно к матрице А, а для получения второго вектора нужно сначала получить из матрицы Атранспонированную матрицу, а только потом воспользоваться командой «взять столбец». Возможное решение представлено на рис. 3.10.
Рис. 3.10. Выделение векторных значений из заданной матрицы
Пример 8. Из матрицы А(6×6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.
Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 3.11.
Рис. 3.11. Выделение минора из заданной матрицы
3.2. Использование матриц специального вида для выполнения матричных операций в системе MathCad
Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i–ый элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i–ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементуi–ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.
Пример 9. Даны матрица: А(4×4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0–ым столбцом матрицы А, а второй — с 3-им столбцом матрицы А.
Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1 – с единичным значением в строке с номером 0, а второй вектор В4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 3.12.
Рис. 3.12. Выделение векторных значений из заданной матрицы
Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор – строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.
Пример 10. Дана матрица: А(4×4). Требуется выделить из матрицы первую строку по порядку (с номером 0).
Решение. Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В1.
Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.
Пример 11. Дана матрица: А(4×4). Требуется переставить в матрице строки с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц:
Пример 12. Дана матрица: А(4×4). Требуется переставить в матрице столбцы с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц:
Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).
Пример 13. Дана матрица: А(4×4). Требуется найти сумму элементов в столбце с номером 3.
Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
Пример 14. Дана матрица: А(4×4). Требуется получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.
Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
3.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований
Для простоты решения ограничимся случаем системы из трех линейных уравнений с тремя неизвестными. Рассуждения на случай большего числа уравнений можно провести аналогичным образом. Пусть требуется найти решение система линейных алгебраических уравнений (СЛАУ) вида:
(3.1)
Введем следующие обозначения:
, (3.2)
А – матрица коэффициентов;
В – вектор свободных членов;
х – вектор неизвестных.
В обозначениях (5.2) систему уравнений (5.1) можно записать в виде:
Из линейной алгебры известно, что система (3.3) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.
В разделе 6.4 мы уже рассматривали решение систем с использованием блока решения. Если применить к уравнению (3.3) аппарат матричных преобразований можно получить «матричную» формулу для вычисления x:
Помножим уравнение (3.3) слева на матрицу, обратную к матрице А:
. (3.4)
Воспользуемся свойством, что , гдеЕ – единичная матрица. Тогда уравнение (3.4) примет вид:
. (3.5)
Воспользуемся свойством, что Ex = x. Тогда уравнение (3.5) примет вид:
, (3.6)
где (3.6) – решение системы (3.3).
Пример 15. Требуется найти решение следующей системы линейных уравнений:
Решение. Решение СЛАУ матричным способом в системе MathCAD приведено на рис.3.13.
[spoiler title=”источники:”]
http://poisk-ru.ru/s7928t3.html
http://site-e1fab4c.1c-umi.ru/lekcii/lekciya_3_-_operacii_s_vektorami_i_matricami_matrichnye_funkcii_v_matematicheskom_pakete_mathcad/
[/spoiler]
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Сумма элементов матрицы
|
|||
|
Ребят, помогите правильно написать в маткаде…..а то как ни напишу все неправильно. [math][Q = left(!!begin{array}{*{20}{c}}{4.3 + x} & 4 & {7.2} \{0.5} & {14 – 2.3x} & 2 \{8.2} & {1.5} & {0.35 + sqrt x } end{array}!!right)][/math] По формуле [math]S=sum_{i=1}^3 sum_{j=1}^3 q_{i,j}[/math] х изменяется от 1 до 5 с шагом 2
|
||
| Вернуться к началу |
|
||
|
Andrei93 |
Заголовок сообщения: Re: Сумма элементов матрицы
|
|
VSIскажи пожалуйста может ты знаешь какой нормальный сайт ……на котором можно найти полезную информацию о Mathcad???
|
|
| Вернуться к началу |
|

 Сообщение было отмечено Rammil как решение
Сообщение было отмечено Rammil как решение





