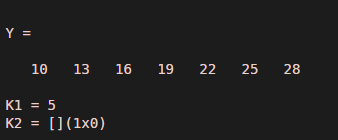Матлаб как найти индекс элемента массива - Сайт, где вы сможете решить свои вопросы

Find indices and values of nonzero elements

Syntax

Description

example

k = find(X)
returns a vector containing the linear indices of each nonzero element in array
X.

If X is a vector, then find
returns a vector with the same orientation as
X.
If X is a multidimensional array, then
find returns a column vector of the linear
indices of the result.

example

k = find(X,n) returns
the first n indices corresponding to the nonzero
elements in X.

example

k = find(X,n,direction),
where direction is 'last', finds
the last n indices corresponding to nonzero elements
in X. The default for direction is 'first',
which finds the first n indices corresponding to
nonzero elements.

example

[row,col] = find(___) returns the row and column subscripts
of each nonzero element in array X using any of
the input arguments in previous syntaxes.

example

[row,col,v] = find(___) also returns vector v,
which contains the nonzero elements of X.

Examples

collapse all

Zero and Nonzero Elements in Matrix

Find the nonzero elements in a 3-by-3 matrix.

X = [1 0 2; 0 1 1; 0 0 4]

X = 3×3

     1     0     2
     0     1     1
     0     0     4

Use the logical not operator on X to locate the zeros.

Elements Satisfying a Condition

Find the first five elements that are less than 10 in a 4-by-4 magic square matrix.

X = 4×4

    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

View the corresponding elements of X.

Elements Equal to Specific Values

To find a specific integer value, use the == operator. For instance, find the element equal to 13 in a 1-by-10 vector of odd integers.

x = 1×10

     1     3     5     7     9    11    13    15    17    19

To find a noninteger value, use a tolerance value based on your data. Otherwise, the result is sometimes an empty matrix due to floating-point roundoff error.

y = 1×11

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000    1.0000

k =

  1x0 empty double row vector

k = find(abs(y-0.3) < 0.001)

Last Several Nonzero Elements

Create a 6-by-6 magic square matrix with all of the odd-indexed elements equal to zero.

X = magic(6);
X(1:2:end) = 0

X = 6×6

     0     0     0     0     0     0
     3    32     7    21    23    25
     0     0     0     0     0     0
     8    28    33    17    10    15
     0     0     0     0     0     0
     4    36    29    13    18    11

Locate the last four nonzeros.

Elements Satisfying Multiple Conditions

Find the first three elements in a 4-by-4 matrix that are greater than 0 and less than 10. Specify two outputs to return the row and column subscripts to the elements.

X = [18 3 1 11; 8 10 11 3; 9 14 6 1; 4 3 15 21]

X = 4×4

    18     3     1    11
     8    10    11     3
     9    14     6     1
     4     3    15    21

[row,col] = find(X>0 & X<10,3)

The first instance is X(2,1), which is 8.

Subscripts and Values for Nonzero Elements

Find the nonzero elements in a 3-by-3 matrix. Specify three outputs to return the row subscripts, column subscripts, and element values.

X = [3 2 0; -5 0 7; 0 0 1]

X = 3×3

     3     2     0
    -5     0     7
     0     0     1

Subscripts of Multidimensional Array

Find the nonzero elements in a 4-by-2-by-3 array. Specify two outputs, row and col, to return the row and column subscripts of the nonzero elements. When the input is a multidimensional array (N > 2), find returns col as a linear index over the N-1 trailing dimensions of X.

X = zeros(4,2,3);
X([1 12 19 21]) = 1

Input Arguments

collapse all

`X` — Input array
scalar | vector | matrix | multidimensional array

Input array, specified as a scalar, vector, matrix, or multidimensional array.

`n` — Number of nonzeros to find
positive integer scalar

Number of nonzeros to find, specified as a positive integer
scalar. By default, find(X,n) looks for the first n nonzero
elements in X.

`direction` — Search direction
`'first'` (default) | `'last'`

Search direction, specified as the string 'first' or 'last'.
Look for the last n nonzero
elements in X using find(X,n,'last').

Output Arguments

collapse all

`k` — Indices to nonzero elements
vector

Indices to nonzero elements, returned as a vector.

If X is a row vector, then
k is also a row vector. Otherwise,
k is a column vector.
k is an empty row vector or empty column
vector when X is an empty array or has no
nonzero elements.
find uses the convention that
k is an empty matrix
[] when X is an empty
matrix [].

You can return the nonzero values in X using X(k).

`row` — Row subscripts
vector

Row subscripts, returned as a vector. Together, row and col specify
the X(row,col) subscripts corresponding to the
nonzero elements in X.

`col` — Column subscripts
vector

Column subscripts, returned as a vector. Together, row and col specify
the X(row,col) subscripts corresponding to the
nonzero elements in X.

If X is a multidimensional array with N > 2, then col is a linear index over
the N-1 trailing dimensions of X.
This preserves the relation X(row(i),col(i)) == v(i).

`v` — Nonzero elements of `X`
vector

Nonzero elements of X, returned as a vector.

More About

collapse all

Linear Indices

A linear index allows use of a single subscript
to index into an array, such as A(k). MATLAB^® treats
the array as a single column vector with each column appended to the
bottom of the previous column. Thus, linear indexing numbers the elements
in the columns from top to bottom, left to right.

For example, consider a 3-by-3 matrix. You can reference the A(2,2) element
with A(5), and the A(2,3) element
with A(8). The linear index changes depending on
the size of the array; A(5) returns a differently
located element for a 3-by-3 matrix than it does for a 4-by-4 matrix.

The sub2ind and ind2sub functions
are useful in converting between subscripts and linear indices.

Tips

To find array elements that meet a condition, use find in
conjunction with a relational expression. For example, find(X<5) returns
the linear indices to the elements in X that are
less than 5.
To directly find the elements in X that
satisfy the condition X<5, use X(X<5).
Avoid function calls like X(find(X<5)), which
unnecessarily use find on a logical matrix.
When you execute find with a relational
operation like X>1, it is important to remember
that the result of the relational operation is a logical matrix of
ones and zeros. For example, the command [row,col,v] = find(X>1) returns
a column vector of logical 1 (true)
values for v.
The row and column subscripts, row and col,
are related to the linear indices in k by k = sub2ind(size(X),row,col).

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

Usage notes and limitations:

X must be a tall column vector.

For more information,
see Tall Arrays.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

If a variable-size input becomes a row vector at run
time, then code generation ends with an error. This limitation does
not apply when the input is scalar or is a variable-length row vector.
For variable-size inputs, the shape of empty outputs
(0-by-0, 0-by-1, or 1-by-0) depends on the upper bounds of the size
of the input. When the input array is a scalar or [] at run time,
the output might not match MATLAB. If the input is a variable-length
row vector, then the size of an empty output is 1-by-0. Otherwise,
the size is 0-by-1.
The generated code always returns a variable-length
vector. Even when you provide the output vector k,
the output is not fixed-size because the output can contain fewer
than k elements. For example, find(x,1) returns
a variable-length vector with one or zero elements.

Thread-Based Environment
Run code in the background using MATLAB® `backgroundPool` or accelerate code with Parallel Computing Toolbox™ `ThreadPool`.

This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

In MATLAB, the arrays are used to represent the information and data. You can use indexing to access the elements of the array. In MATLAB the array indexing starts from 1. To find the index of the element in the array, you can use the find() function. Using the find() function you can find the indices and the element from the array. The find() function returns a vector containing the data.

Syntax:

find(X) : Return a vector containing the indices of elements
find(X,n): Return first n indices of the elements in X
find(X,n, Direction): find n indices in X according to the Direction where Direction – ‘first‘ or ‘last‘
[row,col] = find(): It returns the row and column subscript of element in array
[row,col,V] = find(): returns vector V containing non-zero elements

Now let’s see how to find an index of any element in an array using the find() function with the help of examples.

find(x)

find(X) returns a vector containing the linear indices of each nonzero element in array X.

Example 1:

Matlab

array = [1 2 3 4 5 6]

index = find(array==3)

Output:

Note: If the array contains duplicates then find(X) function will return all the indices of that integer.

Example 2:

Matlab

array = [1 2 3 4 5 6 2 4 2]

index = find(array==2)

Output:

When the array contains duplicate values the find() function will print all the indices of that corresponding element. So if you don’t want all the indices of that element you can use the find(X,n) function.

find(X,n)

Return first n indices of the elements in X.

Example:

Matlab

array = [1 2 3 4 5 6 2 4 2]

index = find(array==2,1)

Output:

find(X,n,Direction)

You can also find the index of the elements from both directions in the array. Both directions mean from starting and from last by using find(X,n,Direction). This function find n indices in X according to the Direction. The Direction parameter accepts either ‘first’ or ‘last’. If the direction is first it will return first n indices of that corresponding element or if the direction is last it will return the indices by traversing from the end of the array. By default, the Direction parameter is ‘first’.

Example 1:

Matlab

array = [1 2 3 4 5 6 2 4 2]

index = find(array==2,2,'first')

Output:

Example 2:

Matlab

array = [1 2 3 4 5 6 2 4 2]

index = find(array==2,2,'last')

Output:

[row,col] = find(x)

For finding the index of an element in a 3-Dimensional array you can use the syntax [row,col] = find(x) this will give you the row and the column in which the element is present.

Example:

Matlab

array = [1 2 3; 4 5 6; 7 8 9]

[row,col] = find(array==5)

Output:

[row,col,v] = find(X)

If you want to find the indices of all the non-zero elements present in the 3-dimensional array you can use [row,col,v] = find(X) where X is our array. This will find all indices of all non-zero elements present in the array and store them into the vector v.

Example:

Matlab

x = [1 9 0; 3 -1 0; 0 0 7]

[row,col,v] = find(x)

Output:

Last Updated :
04 Jul, 2021

Like Article

Save Article

Источник

find

Найдите индексы и значения ненулевых элементов

Синтаксис

Описание

пример

k = find(X) возвращает вектор, содержащий линейные индексы каждого ненулевого элемента в массиве X.

Если X вектор, затем find возвращает вектор с той же ориентацией как X.
Если X многомерный массив, затем find возвращает вектор-столбец линейных индексов результата.

пример

k = find(X,n) возвращает первый n индексы, соответствующие ненулевым элементам в X.

пример

k = find(X,n,direction), где direction 'last', находит последний n индексы, соответствующие ненулевым элементам в X. Значение по умолчанию для direction 'first', который находит первый n индексы, соответствующие ненулевым элементам.

пример

[row,col] = find(___) возвращает индексы строки и столбца каждого ненулевого элемента в массиве X использование любого из входных параметров в предыдущих синтаксисах.

пример

[row,col,v] = find(___) также возвращает векторный v, который содержит ненулевые элементы X.

Примеры

свернуть все

Нулевые и ненулевые элементы в матрице

Найдите ненулевые элементы в 3х3 матрице.

X = [1 0 2; 0 1 1; 0 0 4]

X = 3×3

     1     0     2
     0     1     1
     0     0     4

Используйте логический not оператор на X определять местоположение нулей.

Элементы, удовлетворяющие условие

Найдите первые пять элементов, которые меньше 10 в матрице магического квадрата 4 на 4.

X = 4×4

    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

Просмотрите соответствующие элементы X.

Элементы, равные определенным значениям

Чтобы найти определенное целочисленное значение, используйте == оператор. Например, найдите элемент равным 13 в 1 10 векторе из нечетных целых чисел.

x = 1×10

     1     3     5     7     9    11    13    15    17    19

Чтобы найти значение нецелого числа, используйте значение допуска на основе своих данных. В противном случае результатом иногда является пустая матрица из-за ошибки округления с плавающей точкой.

y = 1×11

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000    1.0000

k =

  1x0 empty double row vector

k = find(abs(y-0.3) < 0.001)

В последний раз несколько ненулевых элементов

Создайте 6 6 матрицу магического квадрата со всеми нечетно индексированными равными нулю элементами.

X = magic(6);
X(1:2:end) = 0

X = 6×6

     0     0     0     0     0     0
     3    32     7    21    23    25
     0     0     0     0     0     0
     8    28    33    17    10    15
     0     0     0     0     0     0
     4    36    29    13    18    11

Найдите последние четыре ненуля.

Элементы, удовлетворяющие несколько условий

Найдите первые три элемента в матрице 4 на 4, которые больше 0 и меньше, чем 10. Задайте два выходных параметров, чтобы возвратить индексы строки и столбца в элементы.

X = [18 3 1 11; 8 10 11 3; 9 14 6 1; 4 3 15 21]

X = 4×4

    18     3     1    11
     8    10    11     3
     9    14     6     1
     4     3    15    21

[row,col] = find(X>0 & X<10,3)

Первой инстанцией является X(2,1), который является 8.

Индексы и значения для ненулевых элементов

Найдите ненулевые элементы в 3х3 матрице. Задайте три выходных параметров, чтобы возвратить индексы строки, индексы столбца и значения элемента.

X = [3 2 0; -5 0 7; 0 0 1]

X = 3×3

     3     2     0
    -5     0     7
     0     0     1

Индексы многомерного массива

Найдите ненулевые элементы в 4 2 3 массивами. Задайте два выходных параметров, row и col, возвратить индексы строки и столбца ненулевых элементов. Когда вход является многомерным массивом (N > 2Поиск возвращает col как линейный индекс по N-1 последующие измерения X.

X = zeros(4,2,3);
X([1 12 19 21]) = 1

Входные параметры

свернуть все

`X` — Входной массив
скаляр | вектор | матрица | многомерный массив

Входной массив, заданный как скалярный, векторный, матричный или многомерный массив.

`n` — Количество ненулей, чтобы найти
положительный целочисленный скаляр

Количество ненулей, чтобы найти в виде положительного целочисленного скаляра. По умолчанию, find(X,n) ищет первый n ненулевые элементы в X.

`direction` — Поисковое направление
`'first'` (значение по умолчанию) | `'last'`

Поисковое направление в виде строки 'first' или 'last'. Ищите последний n ненулевые элементы в X использование find(X,n,'last').

Выходные аргументы

свернуть все

`k` — Индексы к ненулевым элементам
вектор

Индексы к ненулевым элементам, возвращенным как вектор.

Если X вектор-строка, затем k также вектор-строка. В противном случае, k вектор-столбец.
k вектор пустой строки или вектор пустого столбца когда X пустой массив или не имеет никаких ненулевых элементов.
find использует соглашение что k пустой матричный [] когда X пустой матричный [].

Можно возвратить ненулевые значения в X использование X(k).

`row` — Индексы строки
вектор

Индексы строки, возвращенные как вектор. Вместе, row и col задайте X(row,col) индексы, соответствующие ненулевым элементам в X.

`col` — Индексы столбца
вектор

Индексы столбца, возвращенные как вектор. Вместе, row и col задайте X(row,col) индексы, соответствующие ненулевым элементам в X.

Если X многомерный массив с N > 2, затем col линейный индекс по N-1 последующие измерения X. Это сохраняет отношение X(row(i),col(i)) == v(i).

`v` — Ненулевые элементы `X`
вектор

Ненулевые элементы X, возвращенный как вектор.

Больше о

свернуть все

Линейные индексы

Линейный индекс позволяет использованию одного индекса индексировать в массив, такой как A(k)MATLAB^® обрабатывает массив как вектор отдельного столбца с каждым столбцом, добавленным к нижней части предыдущего столбца. Таким образом, линейные порядковые номера элементы в столбцах сверху донизу, слева направо.

Например, рассмотрите 3х3 матрицу. Можно сослаться на A(2,2) элемент с A(5), и A(2,3) элемент с A(8). Линейный индекс изменяется в зависимости от размера массива; A(5) возвращает по-другому расположенный элемент для 3х3 матрицы, чем это делает для матрицы 4 на 4.

sub2ind и ind2sub функции полезны в преобразовании между индексами и линейными индексами.

Советы

Чтобы найти элементы массива, которые удовлетворяют условию, используйте find в сочетании с выражением отношения. Например, find(X<5) возвращает линейные индексы в элементы в X это меньше 5.
Непосредственно найти элементы в X это удовлетворяет условию X<5, используйте X(X<5). Избегайте вызовов функции как X(find(X<5)), которые излишне используют find на логической матрице.
Когда вы выполняете find с реляционной операцией как X>1, важно помнить, что результатом реляционной операции является логическая матрица единиц и нулей. Например, команда [row,col,v] = find(X>1) возвращает вектор-столбец логического 1 TRUE) значения для v.
Индексы строки и столбца, row и col, связаны с линейными индексами в k k = sub2ind(size(X),row,col).

Расширенные возможности

“Высокие” массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Указания и ограничения по применению:

X должен быть высокий вектор-столбец.

Для получения дополнительной информации см. Раздел “Высокие массивы”.

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Указания и ограничения по применению:

Если вход переменного размера становится вектором-строкой во время выполнения, то концы генерации кода с ошибкой. Это ограничение не применяется, когда вход является скаляром или является вектором-строкой переменной длины.
Для входных параметров переменного размера форма пустых выходных параметров (0 на 0, 0 1, или 1 на 0) зависит от верхних границ размера входа. Когда входной массив является скаляром или [] во время выполнения, выход не может совпадать с MATLAB. Если вход является вектором-строкой переменной длины, то размер пустого выхода 1 на 0. В противном случае размер 0 1.
Сгенерированный код всегда возвращает вектор переменной длины. Даже когда вы предоставляете выходному вектору k, выход не является фиксированным размером, потому что выход может содержать меньше, чем k элементы. Например, find(x,1) возвращает вектор переменной длины с элементами единицы или нули.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® `backgroundPool` или ускорьте код с Parallel Computing Toolbox™ `ThreadPool`.

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает распределенные массивы. Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).

Представлено до R2006a

Источник

Introduction to Matlab find Index

Matlab finds the index function used to remit a vector containing the linear indices of each nonzero element in the array. For Matlab find the index “Find” statement is used. For example, D = find(Y) remits a vector containing the linear indices of each nonzero element in array Y. If Y is a vector, then find returns a vector with the same orientation as Y. If Y is a multidimensional array, then find returns a column vector of the linear indices of the result. If Y contains no nonzero elements or is empty, then find returns an empty array.

Syntax

D = find(Y)
D = find(Y,n)
D = find(Y, n, direction )
[row, col] = find (___)
[row, col, v] = find (___)

How to Do Matlab Fscanf?

Find the function used to find indices and values of nonzero value. For finding indices and values of nonzero elements, we need to take all elements into a variable and use proper syntax.

The steps to find indices and values of nonzero value using find the statement:-

Step 1: We need to take all elements into a variable

Step 2: Then, we use a find statement with proper syntax to find indices and values of the nonzero element.

Examples of Matlab find Index

Given below are the examples of Matlab find Index:

Example #1

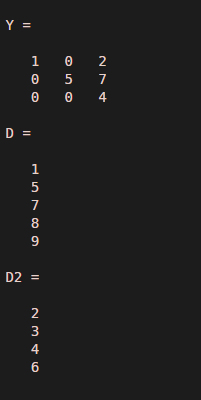
Let us see an example related to find function, find function used to find indices and values of nonzero value. So in this example, we take a 3-by-3 matrix, and this matrix takes into a variable ‘Y’. So index 1 starts with row 1 and column one, and the next index value is 2 corresponds to row 2 and column one, then the same sequence will continue till the last index value; in our example, the last index value is 9 because we take 3-by-3 matrix. So now we use a find function; we take to find(Y); this command displays the indices of nonzero values like in our examples non zero values are 1, 2, 5, 7 and 4 the find displays the indices values of these numbers, and then we take a complement of 1st command that is found (~Y), this command is used to display the indices value of zero values present in the matrix so that indices are stored in d2 variable.

Code:

clc; close all; Y = [1 0 2; 0 5 7; 0 0 4] D = find(Y) D2 = find(~Y)

Output:

As we saw the result, the Y variable shows the 3 by 3 matrix, then the D stores the indices values of nonzero values present at the Y matrix and the D2 stores the value of indices of a zero present in the matrix. The result of D and D2 shows in n*1 format, where n is the number of rows.

Example #2

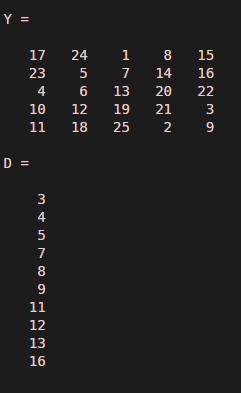
In this example, we take a 5 by 5 matrix using a magic function; magic creates a matrix; if we take magic(n), it creates a by n matrix; the matrix number is 1 to n^2 with equal rows and columns. So in our example, we take magic(5) which means it creates a 5 by 5 matrix; the numbers are 1 to 25 because 5^2. This matrix we assign to the Y variable. Then now, we use a find function, find(Y<15,10); it is used to find the first 10 elements that are less than 15 in a 5 by 5 magic square matrix, and the indices values of that 10 numbers are stored in D variable and display it.

Code:

clc; clear all; close all; Y = magic(5) D = find(Y<15,10)

Output:

Example #3

Let us see another example related to find function, as we know to find function used to find indices and values of nonzero value. So in this example, we take a number in the range of 10 to 30 with the difference of 3, and these elements take into a variable ‘Y’ the numbers are 13, 16, 19, 22, and 25. Now we find a specific integer value for that we use a == operator, so we write command as find(Y==22) then it displays the index value where 22 is present. If that number is not present in that row, then it returns an empty.

Code:

clc; clear all; close all; Y = 10:3:30 K1 = find(Y==22) K2 = find(Y==20)

Output:

Example #4

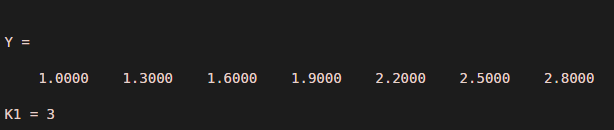
Let us see an example for find function, as we know to find function used to find indices and values of nonzero value. So in this example, we take a number in the range of 1 to 3 with the difference of 0.3, and these elements take into a variable ‘Y’ the numbers are 1.3, 1.6, 1.9, 2.2, 2.5, and 28. Now we find a specific value for that we use a == operator, so we write command as find(Y==1.6) then it displays the index value where 1.6 is present. If that number is not present in that row, then it returns an empty.

Code:

clc; clear all; close all; Y = 1:0.3:3 K1 = find(Y== 1.6)

Output:

Conclusion

In this article, we saw the concept of Matlab find the index. Basically, Matlab finds index is used for indicating values of the nonzero element. Then saw syntax related to Matlab find index statements and how it’s used in Matlab code. Also, we saw some examples related to Matlab’s find index statement.

Find Index of Value in Array Using `find()` Function in MATLAB

In an array, elements are placed on certain indexes starting from 1 and so on. To find the index of a value in a given array, we can use the find() function. The find() function is used to find indices and values of elements in an array or matrix. To find indices of elements, we need to define a condition inside the find() function. For example, if we want to find the index of a single element, we can use the equal operator inside the find() function. If the same element is present at different indices, the find() function will return all the indices where the element is present. We can use all kinds of conditional statements inside this function. For example, suppose we want to find indices of all the elements greater than a certain number. In that case, we can use the greater-than operator, and it will return the indices of all the elements greater than that specific number. For example, let’s find the index of a single element present inside a given array. See the code below.

mat = [2 3 1 2];
indices = find(mat==2)

Output:

The variable indices contain two values in the above output, which means the element is present at index 1 and 4 inside the array or vector. Now let’s consider, we want to find the indices of elements that are greater than 1. We need to change the condition inside the find() function. Instead of using the equal operator, we will use the greater-than operator. See the code below.

mat = [2 3 1 2];
indices = find(mat>1)

Output:

In the above output, the variable indices contain three values, and as you can see, three elements are greater than one inside the given array or vector. If we have a matrix and want to find an element’s position inside the vector, we can use the find() function. We know that the element inside a matrix is placed on a certain row and column, and to find that specific row and column, we can use the find() function. If the element is present at multiple positions, the find() function will return multiple values for row and column. See the code below.

mat = [2 3 ; 2 1]
[row, col] = find(mat==2)

Output:

In the above output, the matrix has two rows and two columns, the first value of the row and column vector is the first position of the element, which is 1st row and 1st column, and the second value of the row and column is the second position of the element which is 2nd row and 1st column. If you want to find the indices of element 2 in the given matrix, the find() function will return 1 and 2 because the values are placed column-wise in the case of the matrix. That means the value 2 is at index 1 and 2 and value 3 is at index 3, and value 1 is at index 4. So if instead of two output variables, you only pass one variable, the find() function will return the indices column-wise. For example, let’s find the indices of the element and replace them with another value. See the code below.

mat = [2 3 ; 2 1]
indices = find(mat==2)
mat(indices) = 5

Output:

In the above code, first, we find the indices of element two and then replace the value with 5 using the indices, and as you can see, the matrix values have been changed. If you don’t want to use the find() function for some reason, you can always make your function using a for loop and if statement. You need to traverse all the elements of the array or matrix, and using the if statement, you can check if the current value matches your desired value or not. If it is matched with your desired value, you can save its index and move on until you have checked all the elements present inside the array. For example, let’s use a for loop and an if statement to find the indices of a vector or array. See the code below.

mat = [2 3 2 1]
indices = [];
for i=1:length(mat)
    if(mat(i) == 2)
        indices = [indices i];
    end
end
indices

Output:

mat =

     2     3     2     1


indices =

     1     3

In the above code, we initialized the variable indices with an empty vector. When the value two matches with any element inside the array, we will save that index in the indices variable.

Источник

Syntax

Description

Examples

Zero and Nonzero Elements in Matrix

Elements Satisfying a Condition

Elements Equal to Specific Values

Last Several Nonzero Elements

Elements Satisfying Multiple Conditions

Subscripts and Values for Nonzero Elements

Subscripts of Multidimensional Array

Input Arguments

X — Input array scalar | vector | matrix | multidimensional array

n — Number of nonzeros to find positive integer scalar

direction — Search direction 'first' (default) | 'last'

Output Arguments

k — Indices to nonzero elements vector

row — Row subscripts vector

col — Column subscripts vector

v — Nonzero elements of X vector

More About

Linear Indices

Tips

Extended Capabilities

Tall Arrays Calculate with arrays that have more rows than fit in memory.

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

Thread-Based Environment Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Distributed Arrays Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

Version History

find(x)

Matlab

Matlab

find(X,n)

Matlab

find(X,n,Direction)

Matlab

Matlab

[row,col] = find(x)

Matlab

[row,col,v] = find(X)

Matlab

find

Синтаксис

Описание

Примеры

Нулевые и ненулевые элементы в матрице

Элементы, удовлетворяющие условие

Элементы, равные определенным значениям

В последний раз несколько ненулевых элементов

Элементы, удовлетворяющие несколько условий

Индексы и значения для ненулевых элементов

Индексы многомерного массива

Входные параметры

X — Входной массив скаляр | вектор | матрица | многомерный массив

n — Количество ненулей, чтобы найти положительный целочисленный скаляр

direction — Поисковое направление 'first' (значение по умолчанию) | 'last'

Выходные аргументы

k — Индексы к ненулевым элементам вектор

row — Индексы строки вектор

col — Индексы столбца вектор

v — Ненулевые элементы X вектор

Больше о

Линейные индексы

Советы

Расширенные возможности

“Высокие” массивы Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Генерация кода C/C++ Генерация кода C и C++ с помощью MATLAB® Coder™.

Основанная на потоке среда Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.

Массивы графического процессора Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Распределенные массивы Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Introduction to Matlab find Index

How to Do Matlab Fscanf?

Examples of Matlab find Index

Example #1

Example #2

Example #3

Example #4

Conclusion

Recommended Articles

Find Index of Value in Array Using find() Function in MATLAB

`X` — Input array
scalar | vector | matrix | multidimensional array

`n` — Number of nonzeros to find
positive integer scalar

`direction` — Search direction
`'first'` (default) | `'last'`

`k` — Indices to nonzero elements
vector

`row` — Row subscripts
vector

`col` — Column subscripts
vector

`v` — Nonzero elements of `X`
vector

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Thread-Based Environment
Run code in the background using MATLAB® `backgroundPool` or accelerate code with Parallel Computing Toolbox™ `ThreadPool`.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

`X` — Входной массив
скаляр | вектор | матрица | многомерный массив

`n` — Количество ненулей, чтобы найти
положительный целочисленный скаляр

`direction` — Поисковое направление
`'first'` (значение по умолчанию) | `'last'`

`k` — Индексы к ненулевым элементам
вектор

`row` — Индексы строки
вектор

`col` — Индексы столбца
вектор

`v` — Ненулевые элементы `X`
вектор

“Высокие” массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® `backgroundPool` или ускорьте код с Parallel Computing Toolbox™ `ThreadPool`.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Find Index of Value in Array Using `find()` Function in MATLAB