Матлаб как найти модуль вектора

Глава 3. Элементы программирования

1+mod(i,2),’Color’,colors(mod(i,3)+1)). Здесь дважды использована функция mod(), у которой два аргумента, а в качестве результата возвращается остаток от деления первого аргумента на второй. Поэтому результатом инструкции 1+mod(i,2) является значение 1 для четных значений переменной i и 2 для нечетных. В результате графики по очереди отображаются тонкой и толстой кривыми. Значением выражения mod(i,3)+1 являются числа 1, 2 и 3, поэтому инструкцией colors(mod(i,3)+1) осуществляется циклический перебор элементов массива colors. Наконец, после создания всех графиков инструкцией hold off отменяется режим отображения графиков в одном окне. На рис. 3.36 показано окно редактора m-файлов с кодом рассмотренной выше функции.

Рис. 3.36. Код функции с переменным числом аргументов в окне редактора m-файлов

Пример вызова созданной функции представлен в командном окне на рис. 3.37.

Сначала создается базовый массив со значениями аргумента, а затем еще четыре массива со значениями различных функций в этих точках. Следующие три команды представляют собой вызов функции с одним, пятью и тремя аргументами (жирным шрифтом выделены команды, вводимые пользователем):

>>x=-2*pi:0.01:2*pi;

>>y1=sin(x);

>>y2=cos(x);

>>y3=sin(x)./x;

Самоучитель Matlab

Рис. 3.37. Вызов функции с разным количеством аргументов в командном окне

>>y4=(1-cos(x))./x;

>>MyPlots(x)

Недостаточное количество аргументов!

>>MyPlots(x,y1,y2,y3,y4)

>>MyPlots(x,y1,y2)

При вызове функции с одним аргументом появляется сообщение о недостаточном количестве аргументов. Результат вызова функции с пятью аргументами показан на рис. 3.38.

Рис. 3.38. Результат вызова функции с пятью аргументами

Глава 3. Элементы программирования

Если вызвать функцию с тремя аргументами, получим результат, как на рис. 3.39.

Рис. 3.39. Результат вызова функции с тремя аргументами

На заметку

Отметим, что если вызвать функцию MyPlots() с двумя аргументами, будет построен лишь один график, поскольку в теле оператора цикла нижняя граница диапазона изменения индексной переменной превышает верхнюю, и поэтому оператор цикла не выполняется.

Точно так же, как функция может иметь произвольное количество аргументов, она может возвращать и произвольное количество значений в качестве результата. В этом случае в качестве результата функции указывается переменная varargout. Как и переменная varargin, переменная varargout является массивом ячеек, каждая из которых содержит возвращаемый функцией результат. Ниже приведен пример функции, которая называется moments() и может возвращать произвольное количество значений в качестве результата:

function [varargout] = moments(x) for k=1:nargout

y=x.^k;

varargout{k}=sum(y)/length(x); end

end

Самоучитель Matlab

Предполагается, что функции аргументом передается массив числовых значений. В качестве значений функцией возвращаются статистические (или выборочные) моменты. Здесь имеет смысл отметить, что статистическим

порядка представляет собой среднее арифметическое. В данном случае количество вычисляемых моментов определяется тем, сколько переменных содержит массив результата. На рис. 3.40 показан редактор m-файлов с кодом функции.

Рис. 3.40. Программный код функции в окне редактора m-файлов

На рис. 3.41 показано командное окно с примером использования функции moments().

Рис. 3.41. Пример использования функции moments()

Глава 3. Элементы программирования

Здесь с помощью команд (жирным шрифтом выделен ввод пользователя)

>>x=[1,2,5,-3,-2,0,2,1,-1,3];

>>[m1,m2,m3]=moments(x)

m1 =

0.8000

m2 =

5.8000

m3 =

13.4000

сначала создается числовой массив x, а затем на его основе вычисляются моменты от первого до третьего порядка включительно. Результат записывается соответственно в переменные m1, m2 и m3.

Функции eval () и feval ()

Софистика, пастор, софистика!

К/ф “Семнадцать мгновений весны”

Полезными при составлении программных кодов в Matlab могут оказаться системные функции eval() и feval(). У функций есть несколько вариантов использования. Здесь рассмотрим самый распространенный. Начнем с функции eval(). Функции передается текстовый аргумент, представляющий собой команду, которую необходимо выполнить. Обратимся к документу на рис. 3.42.

Рис. 3.42. Использование функции eval()

Фрагмент кода следующий:

>> eval(‘x=[1,2,3,4,5]’) x =

Самоучитель Matlab

>> eval(‘y=sin(pi./x)’) y =

При выполнении команды eval(‘x=[1,2,3,4,5]’) результат такой же, как если бы выполнялась команда x=[1,2,3,4,5]. А при выполнении команды eval(‘y=sin(pi./x)’), как если бы выполнялась команда y=sin(pi./x). В качестве иллюстрации полезности функции eval() рассмотрим следующий пример (жирным шрифтом выделен ввод пользователя):

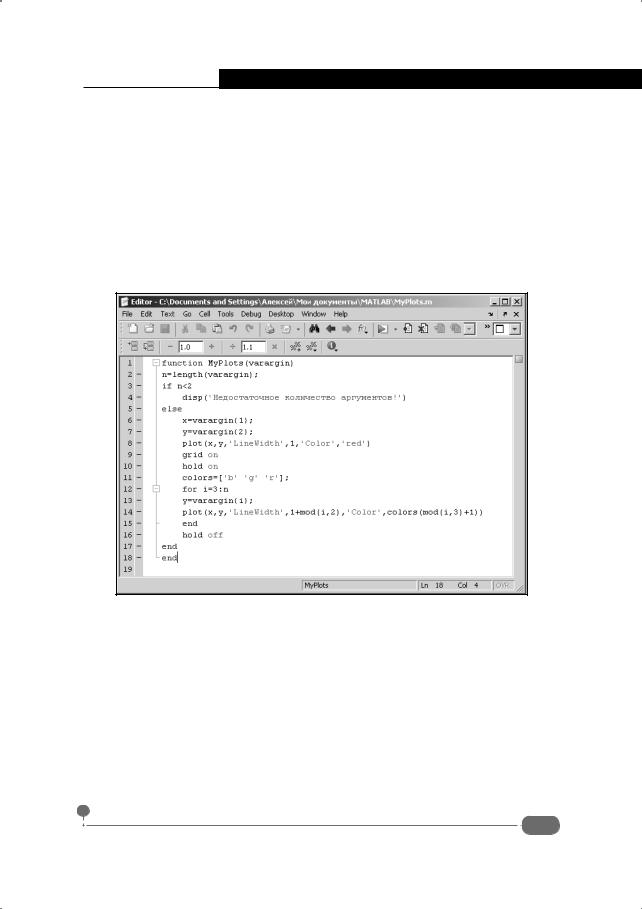
>>A=[1,2,3;4,5,6;7,8,9];

>>for i=1:3

for j=1:3 str=[‘a’,int2str(i),int2str(j),’=A(i,j);’]; eval(str);

end

end

>> [a11,a12,a13;a21,a22,a23;a31,a32,a33] ans =

1 2 3

4 5 6

7 8 9

Командой A=[1,2,3;4,5,6;7,8,9] создается матрица A размерами 3×3, заполненная натуральными числами от 1 до 9 включительно. Затем выполняется двойной оператор цикла, в котором индексные переменные i и j пробегают значения от 1 до 3 каждая. Внутри тела циклов выполняется по две команды. Командой str=[‘a’,int2str(i),int2str(j), ‘=A(i,j);’] формируется текстовая строка str, которая получается объединением нескольких фрагментов. Первый фрагмент – буква ‘a’. Два других фрагмента получаются преобразованием индексных переменных к текстовому формату. Для преобразования числа в текст используем встроенную функцию int2str(). Еще один фрагмент – текст ‘=A(i,j);’. Обращаем внимание, что в конце текстового фрагмента находится точка с запятой. Это сделано для того, чтобы при выполнении соответствующей команды результат не отображался. Таким образом, переменная str содержит текст, который получается объединением буквы a, текущих значений индексов, оператора присваивания, элемента матрицы A с соответствующими индексами и точки с запятой. Для выполнения команды, представленной этой текстовой строкой, используем инструкцию eval(str). В результате элементы матрицы A записываются в переменные a11, a12 и так далее до a33. То есть фактически здесь с помощью функции eval() мы автоматизировали процедуру присваивания значений этим переменным вместо того, чтобы выполнять каждую команду

Глава 3. Элементы программирования

присваивания в явном виде. На рис. 3.43 показан документ с описанным выше кодом.

Рис. 3.43. Еще один пример использования функции eval()

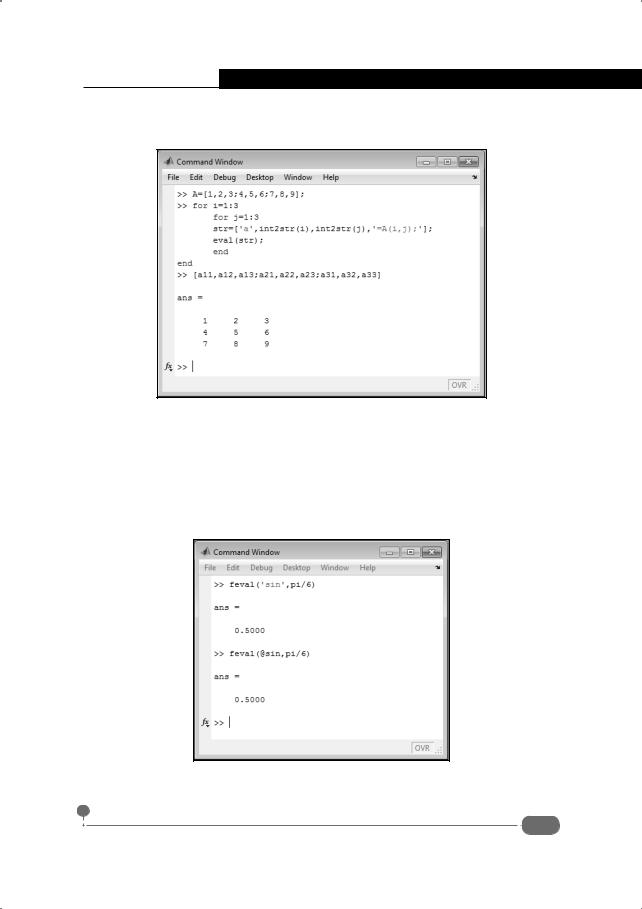
Функция feval() используется для непрямого вызова других функций. Первым аргументом функции feval() передается указатель вызываемой функции или ее текстовое имя, а прочие аргументы функции feval() – это те аргументы, которые передаются неявно вызываемой функции. Примеры использования этой функции приведены в документе на рис. 3.44.

Рис. 3.44. Примеры использования функции feval()

Самоучитель Matlab

Здесь мы последовательно использовали команды feval(‘sin’,pi/6) и feval(@sin,pi/6), которыми вычисляется один и тот же результат. В последнем случае для получения указателя на функцию вычисления синуса задействован оператор @ перед именем функции (вся инструкция для указателя на функцию вычисления синуса имеет вид @sin).

На заметку

Здесь мы воспользовались общим правилом получения указателя на функцию. Для этого перед именем функции указывают оператор @. Результатом такой инструкции является указатель на соответствующую функцию.

Глава 4 Элементы матричной алгебры

Мы столкнулись с трудной задачей… Надо придумать что-то необычное.

К/ф “Клуб самоубийц, или Приключения титулованной особы”

В этой главе мы рассмотрим основные приемы, методы, функции, которые полезны при решении задач линейной алгебры. Интриги прибавляет то обстоятельство, что данные в Matlab, так сказать, по умолчанию, реализуются в виде матриц, что дает небезосновательные надежды на эффективное применение Matlab в данном случае.

Векторы и операции с ними

Никто нам не мешает перевыполнить наши законы.

В. Черномырдин

С точки зрения технической реализации вектор в Matlab – это матрица, состоящая из одной строки (вектор-строка) или одного столбца (векторстолбец). Здесь мы рассмотрим методы выполнения некоторых базовых операций с векторами – например, вычисление скалярного и векторного произведений (разумеется, с использованием средств Matlab). Для соответствующих операций в Matlab предусмотрены специальные функции, хотя при желании можно обойтись и без них.

На заметку

Следует понимать, что обсуждаемые далее функции описаны в контексте тех задач, для решения которых они применяются. В общем случае функции, как правило, имеют более широкое применение.

С практической точки зрения наибольший интерес представляют векторы в двумерном (на плоскости) и трехмерном (в объеме) пространстве. Именно последним случаем и ограничимся. Другими словами, здесь и далее будем

числить такое значение, нет. Но в Matlab для этих целей имеется специальная функция norm(). Аргументом функции указывается вектор, для которого вычисляется модуль. Результатом функции, как несложно догадаться, является модуль вектора. Пример вычисления модулей для векторов-строк и векторов-столбцов приведен в документе на рис. 4.1.

Самоучитель Matlab

Рис. 4.1. Вычисление модуля вектора

В командном окне вводится и выполняется следующий код (жирным шрифтом выделен ввод пользователя):

>> a=[1 3 5] a =

1 3 5

>>norm(a) ans =

5.9161

>>b=[1;3;5]

b =

1

3

5

>>norm(b) ans =

5.9161

Видим, что результат одинаково хорош как для вектора-строки, так и для вектора-столбца.