Матрица Кирхгофа — одно из представлений конечного графа с помощью матрицы. Матрица Кирхгофа представляет дискретный оператор Лапласа для графа. Она используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.
Определение[править | править код]
Дан простой граф 


Также матрицу Кирхгофа можно определить как разность матриц
где 

Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы весов рёбер, инцидентных соответствующей вершине. Для смежных (связанных) вершин 


Для взвешенного графа матрица смежности 

Пример[править | править код]
Пример матрицы Кирхгофа простого графа.
| Помеченный граф | Матрица Кирхгофа |
|---|---|
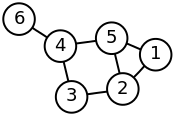
|

|
Свойства[править | править код]
- Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:
.
- Определитель матрицы Кирхгофа равен нулю:
- Матрица Кирхгофа простого графа симметрична:
.
- Все алгебраические дополнения
симметричной матрицы Кирхгофа равны между собой — постоянная матрицы Кирхгофа. Для простого графа значение данной постоянной совпадает с числом всех возможных остовов графа (см. Матричная теорема о деревьях).
- Существует алгоритм восстановления матрицы Кирхгофа по матрице сопротивлений
.
- 0 является собственным значением матрицы (соответствующий собственный вектор — все единицы), кратность его равна числу связных компонент графа.
- Остальные собственные значения положительны. Второе по малости значение Фидлер назвал индексом связности графа, соответствующий собственный вектор — вектор Фидлера (не путать с индексом связности графа Рандича).
См. также[править | править код]
- Матричная теорема о деревьях
- Оператор Лапласа
| Определение: |
| Матрицей Кирхгофа простого графа называется матрица , элементы которой определяются равенством: |
Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении -й строки и -го столбца () стоит , если вершины с номерами и смежны, и в противном случае.
Пример матрицы Кирхгофа
| Граф | Матрица Кирхгофа |
|---|---|
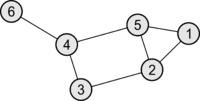
|
Некоторые свойства
| Утверждение: |
|
Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:
|
| Утверждение: |
|
Определитель матрицы Кирхгофа равен нулю: |
|
Прибавим к первой строке все остальные строки (это не изменит значение определителя): Так как сумма элементов каждого столбца равна , получим: |
| Утверждение: |
|
Матрица Кирхгофа простого графа симметрична:
|
| Утверждение: |
|
Собственным значением матрицы называют значения , которые удовлетворяют уравнению: Прибавим к первой строке все остальные строки (это не изменит значение определителя): Так как сумма элементов каждого столбца равна , получим: Следовательно, является собственным значением. Доказательство кратности: Пусть дан граф c компонентами связности. Перенумеруем его вершины так, чтобы сначала шли вершины первой компоненты связности, затем второй и т.д. Тогда матрица Кирхгофа примет блочно-диагональный вид, и -тый блок этой матрицы будет являтся матрицей Кирхгофа для -той компоненты связности. Из свойства блочно-диагональной матрицы , где — матрица Кирхгофа для -той компоненты связности, и свойства, доказанного выше, |
См. также
- Связь матрицы Кирхгофа и матрицы инцидентности
- Подсчет числа остовных деревьев с помощью матрицы Кирхгофа
Источники информации
- Асанов М., Баранский В., Расин В.: Дискретная математика: Графы, матроиды, алгоритмы. стр. 18
- Википедия — Матрица Кирхгофа
Определение 1. Пусть G – неориентированный граф. Пусть Mc – квадратная матрица, строки и столбцы которой обозначены вершинами неориентированного графа G. Элемент i-ой строки и j-гo столбца матрицы Mc, обозначаемый cij, равен единице, если имеется ребро из i-ой вершины в j-ую вершину, и равен нулю в противном случае. Матрица Mc называется матрицей смежности графа G.
Заметим, что для сокращения записи обозначения строк и столбцов в матрицах смежности можно опускать, но рекомендуется их оставлять особенно в матрицах больших размерностей.
Говоря о свойствах матрицы смежности неориентированного графа, необходимо отметить, что она не только квадратная, но и всегда симметрична относительно главной диагонали.
Для демонстрации примеров введём следующие графы (см. два рис. ниже).
Этот неориентированный граф G1 состоит из множества вершин V(G1), содержащего 6 элементов, и множества рёбер E(G1), содержащего 6 элементов: V(G1) = {a, b, c, d, e, f}, E(G1) = {{a, b}, {a, c}, {b, d}, {c, d}, {с, e}, {d, f}}.
Неориентированный граф G2 состоит из множества вершин V(G2), содержащего 6 элементов, и множества рёбер E(G2), содержащего 5 элементов: V(G2) = {a, b, c, d, e, f}, E(G2) = {{a, c}, {b, e}, {c, d}, {d, e}, {d, f}}.
Пример 1. Для неориентированных графов G1 и G2, показанных на рис. выше, определим матрицы смежности.
Неориентированный граф G1 состоит из 6 вершин, поэтому его матрица смежности имеет размерность 6 на 6:
Неориентированный граф G2 также состоит из 6 вершин, поэтому его матрица смежности также имеет размерность 6 на 6:
Определение 2. Пусть G – неориентированный граф. Списком вершин (списком смежности) неориентированного графа называется таблица, в первом столбце которой указаны вершины графа, во втором столбце – соответствующие им смежные вершины. Таким образом, можно считать, что список вершин получен из матрицы смежности неориентированного графа путём замены единиц в каждой строке (столбце) на обозначение соответствующей строки (столбца), а нули отброшены.
Пример 2. Для неориентированных графов G1 и G2, показанных на рис. выше, определим списки вершин. Неориентированный граф G1 состоит из 6 вершин, поэтому список вершин будет состоять из 6 строк (см. табл. далее).
Неориентированный граф G2 также состоит из 6 вершин, поэтому его список вершин также будет состоять из 6 строк (табл. ниже).
Определение 3. Пусть G – неориентированный граф. Списочной структурой (списком смежности) неориентированного графа называется массив указателей на списки смежных вершин, другими словами, каждый элемент списка смежности представляется структурой с двумя полями: номером вершины и указателем на смежные вершины.
Пример 3. Для неориентированных графов G1и G2, показанных на рис. выше, изобразим списочную структуру. Неориентированный граф G1 состоит из 6 вершин, поэтому списочная структура (см. рис. далее) будет состоять из 6 строк. Введём обозначение вершин графа G1 таким образом, чтобы каждой вершине присвоить номер: вершине a присвоим номер 1, вершине b – 2, вершине с – 3, вершине d – 4, вершине e – 5, вершине f – 6.
Неориентированный граф G2 также состоит из 6 вершин, поэтому его списочная структура (см. рис. ниже) также будет состоять из 6 строк (более того, также введём номерное обозначение: вершине a присвоим номер 1, вершине b – 2, вершине с – 3, вершине d – 4, вершине e – 5, вершине f – 6).
Определение 4. Пусть G – неориентированный граф. Пусть Mи − матрица, строки которой обозначены вершинами графа, а столбцы – рёбрами графа. Будем считать, что вершины и рёбра неориентированного графа пронумерованы. Элемент i-ой строки и j-гo столбца матрицы Mи, обозначаемый Mij, равен единице, если i-ая вершина инцидентна j-ому ребру, и равен нулю в противном случае. Построенная таким образом матрица Mи называется матрицей инцидентности графа G.
Замечание. Поскольку каждая единица в строке матрицы инцидентности представляет инцидентность этой вершины соответствующему ребру, то степень каждой вершины графа равна сумме элементов строки матрицы инцидентности, а в каждом столбце имеются две единицы, так как каждое ребро инцидентно двум вершинам.
Заметим также, что если имеется неориентированный граф с петлями, то это сразу можно определить по виду матрицы инцидентности: соответствующий столбец содержит только одну единицу. При этом заметим, что в матрице инцидентности для неориентированного графа с петлями сумма элементов строки, соответствующей некоторой вершине, не представляет собой степень вершины, если в ней имеются петли.
Пример 4. Для неориентированных графов G1 и G2, показанных на рис. выше, определим матрицы инцидентности. Неориентированный граф G1 состоит из 6 вершин и 6 рёбер, поэтому его матрица инцидентности имеет размерность 6 на 6:
Неориентированный граф G2 состоит из 6 вершин и 5 рёбер, поэтому его матрица инцидентности имеет размерность 6 на 5:
Определение 5. Пусть G – неориентированный граф. Списком рёбер (списком инцидентности) неориентированного графа называется таблица, в первой строке которой указаны рёбра графа, во второй строке – инцидентные этим рёбрам вершины. Таким образом, можно считать, что список рёбер получен из матрицы инцидентности путём замены единиц в каждом столбце на обозначение соответствующих вершин, а нули отброшены.
Пример 5. Для неориентированных графов G1 и G2 , показанных на рис. выше, определим списки рёбер.
Неориентированный граф G1 состоит из шести рёбер, поэтому список рёбер будет состоять из шести столбцов (см. табл. далее).
Неориентированный граф G2 состоит из пяти рёбер, поэтому его список рёбер будет состоять из пяти столбцов (см. табл. далее).
Определение 6. Пусть G – неориентированный граф. Пусть MK– квадратная матрица, строки и столбцы которой обозначены вершинами неориентированного графа G. Элементы матрицы MK, обозначаемые kij, расположенные на главной диагонали, т.е. элементы i-ой строки и i-гo столбца, равны степени i-ой вершины, элементы i-ой строки и j-гo столбца (при i не равном j) равны -1, если имеется ребро из i-ой вершины в j-ую вершину, и равен нулю в противном случае. Матрица MK называется матрицей Кирхгофа неориентированного графа G.
Замечание. Матрица Кирхгофа неориентированного графа G связана с его матрицей смежности следующей зависимостью: MK = D – Mс, где D представляет собой матрицу, диагональные элементы которой равны степеням соответствующих вершин, остальные элементы нулевые.
Пример 6. Для неориентированных графов G1и G2, показанных на рис. выше, определим матрицы Кирхгофа.
Неориентированный граф G1 состоит из шести вершин, поэтому его матрица Кирхгофа имеет размерность 6 на 6.
На диагонали матрицы Кирхгофа располагаем числа, соответствующие степеням вершин графа: вершине a инцидентно 2 ребра, вершине b – 2 ребра, c – 3, d – 3, e – 1, f – 1.
Далее матрица заполняется в соответствии со смежностью вершин: вершины a и c – смежные – в соответствующие клетки матрицы ставим «-1», смежные вершины в графе a и b, c и d, d и f, b и d, e и c.
Матрица Кирхгофа неориентированного графа G1 имеет вид:
Проверим выполнимость замечания о связи матрицы Кирхгофа и матрицы смежности следующими вычислениями:
Как видно из выражений выше, левая и правая часть совпадают, следовательно, показана связь между матрицами смежности и Кирхгофа.
Неориентированный граф G2 также состоит из шести вершин, поэтому его матрица Кирхгофа также имеет размерность 6 на 6.
На диагонали матрицы Кирхгофа располагаем числа, соответствующие степеням вершин графа: вершине a инцидентно 1 ребро, вершине b – 1 ребро, c – 2, d – 3, e – 2, f – 1.
Далее матрица заполняется в соответствии со смежностью вершин: вершины a и c – смежные – в соответствующие клетки матрицы ставим «-1», смежные вершины в графе c и d, d и e, b и e, d и f.
Матрица Кирхгофа неориентированного графа G2 имеет следующий вид:
В качестве Упражнения предлагается записать все выше определённые способы задания неориентированных графов для следующих вариантов графов.
Как
уже отмечалось, в каждом графе имеется
остов. В
общем случае остов определен неоднозначно.
Естественно
возникает вопрос: как много остовов в
графе? Очевидно, что при ответе на
этот вопрос достаточно ограничиться
случаем связного графа. В связном графе
остовом служит
любое остовное дерево, т. е. остовный
подграф, являющийся
деревом. Число остовов в связном графе
определяется
в неявной форме следующей теоремой.
Теорема
Кирхгофа (1847 г.).
Число остовных деревьев
в связном графе G
порядка
n
2
равно алгебраическому
дополнению любого элемента матрицы
Кирхгофа
В (G].
Доказательство
опирается на следующую лемму.
Лемма
14.1.
Пусть H
— (m+l,
m)-граф,
I
— матрица
инцидентности какой-либо его ориентации,
М — произвольный
минор порядка m
матрицы I.
Тогда:
-
если
Н — дерево, то М = ± 1; -
если
Н не является деревом, то М = 0.
Доказательство
леммы. Прежде всего заметим,
что можно произвольно менять нумерации
вершин и
ребер графа Н, от этого рассматриваемый
минор может лишь
изменить знак.
Пусть
а — вершина, соответствующая строке
матрицы
I,
не вошедшей в минор М. Если граф Н не
является деревом,
то он несвязен. Пусть К = {1, 2, …, k}
— его область
связности, не содержащая вершины а. С
помощью подходящей
перенумерации ребер графа Н матрицу I
приведем
к клеточно-диагональному виду I
= diag
[I1,
I2],
где
I1
— матрица инцидентности компоненты
Н(К). Минор
М содержит все первые k
строк матрицы I,
сумма которых
равна нулевой строке. Следовательно, М
= 0.
Пусть
теперь Н — дерево. Заново перенумеруем
вершины
и ребра графа Н следующим образом. Одной
из концевых
вершин v,
отличных от вершины а, а также ребру,
инцидентному вершине v,
присвоим номер 1. Далее рассмотрим
дерево Т1 = Н — v.
Если его порядок больше 1,
то
одной из его концевых вершин и, отличных
от а также
инцидентному ей ребру присвоим номер
2. Рассмотрим дерево Т2 = Т1 — и. Итерируя
этот процесс, по лучим
новые нумерации вершин и ребер дерева
Н, при чем
вершина а будет иметь номер т + 1. Матрица
I
npи
этом
примет вид
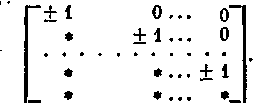
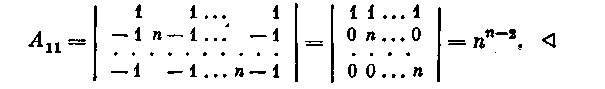
(Здесь и в дальнейшем
символом * будут обозначаться
элементы
или блоки матрицы, значения которых не
влияют
на ход рассуждений.) Минор М, остающийся
после
удаления
последней строки этой матрицы, равен
±1. Еще один факт, используемые при
доказательстве теоремы
Кирхгофа,— формула Бинэ — Коши, которую
мы приведем
без доказательства. Пусть А и В — n
x
m
и m
x
n-матрицы
соответственно, С = АВ и n т.
Минор
порядка
n матрицы В назовем соответствующим
минору
порядка
n матрицы А, если множества номеров строк
первые 70
из них и номеров столбцов второго
совпадают.
Формула
Бинэ — Коши. Определитель матрицы
С равен сумме произведений каждого
минора порядка
матрицы
А на соответствующий минор матрицы В.
Доказательство
теоремы Кирхгофа.
Пусть
I
— матрица инцидентности какой-либо
ориентации
(n,т)
-графа G.
Согласно утверждению 6.4 верно равенство
B(G)
= IIT. (1)
Поскольку
G
– связный граф, то т
n — 1. Если В — подматрица,
остающаяся после удаления из B(G)
последних
строки и столбца, а С — подматрица,
остающаяся после
удаления
из I
последней строки, то в силу (1) В =CСТ.
Алгебраическое дополнение Аnn
элемента, занимающего
в матрице B(G)
позицию (n,n),
равно detB.
Из формулы
Бинэ — Коши теперь следует, что Аnn
равно сумме
квадратов всех миноров порядка n — 1
матрицы С. Согласно
лемме 14.1 каждый такой минор М равен ±1,
и
остовный подграф графа G,
ребра которого соответствуют столбцам,
вошедшим в М, является деревом, и нет
в
противном случае. Следовательно, Аnn
равно числу остовных деревьев в графе
G.
Поскольку алгебраические долнения
всех элементов матрицы B(G)
равны (ут-верждение
6.2), то теорема доказана.
Следствие
14.2.
Для числа компонент n-вершинного
графа G
верно равенство
k(G)=n-rankB(G).
Если
граф G
связен, то в нем есть остовное дерево.
Согласно
предыдущей теореме rank
B
(G)
n — 1. С другой
стороны, всегда det
B(G)=0.
Следовательно, rankB(G)=n-1.
Пусть
теперь граф G
имеет ровно k
компонент. Тогда при
подходящей нумерации вершин матрицей
B(G)
служит
клеточно-диагональная матрица diag[B1,
B2,
…, Bk],
диагональные
клетки которой Вi
являются матрицами Кирхгофа
соответствующих компонент. Учитывая
уже доказанное,
имеем rank
В (G)
= n
— k.
.
С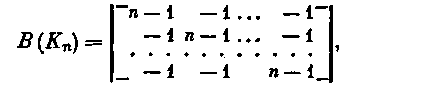
ледствие
14.3. При n > 1 число остовое в полном
графе Кn
равно nn-2.>
Рассмотрим алгебраическое дополнение
А11 элемента
матрицы
з
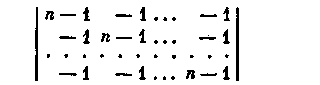
анимающего
позицию (1, 1). Оно равно определителю
порядка n-1.Далее
имеем
Очевидно,
что число остовов в Кn
равно числу помеченных
деревьев порядка n. Поэтому предыдущее
следствие
можно сформулировать в виде следующей
теоремы, впервые
полученной А. Кэли в 1897 году.
Теорема
Кэли.
Число помеченных деревьев порядка
n равно nn-2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In the mathematical field of graph theory, Kirchhoff’s theorem or Kirchhoff’s matrix tree theorem named after Gustav Kirchhoff is a theorem about the number of spanning trees in a graph, showing that this number can be computed in polynomial time from the determinant of a submatrix of the Laplacian matrix of the graph; specifically, the number is equal to any cofactor of the Laplacian matrix. Kirchhoff’s theorem is a generalization of Cayley’s formula which provides the number of spanning trees in a complete graph.
Kirchhoff’s theorem relies on the notion of the Laplacian matrix of a graph that is equal to the difference between the graph’s degree matrix (a diagonal matrix with vertex degrees on the diagonals) and its adjacency matrix (a (0,1)-matrix with 1’s at places corresponding to entries where the vertices are adjacent and 0’s otherwise).
For a given connected graph G with n labeled vertices, let λ1, λ2, …, λn−1 be the non-zero eigenvalues of its Laplacian matrix. Then the number of spanning trees of G is
An example using the matrix-tree theorem[edit]
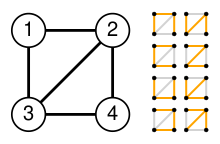
The Matrix-Tree Theorem can be used to compute the number of labeled spanning trees of this graph.
First, construct the Laplacian matrix Q for the example diamond graph G (see image on the right):
Next, construct a matrix Q* by deleting any row and any column from Q. For example, deleting row 1 and column 1 yields
Finally, take the determinant of Q* to obtain t(G), which is 8 for the diamond graph. (Notice t(G) is the (1,1)-cofactor of Q in this example.)
Proof outline[edit]
(The proof below is based on the Cauchy-Binet formula. An elementary induction argument for Kirchhoff’s theorem can be found on page 654 of Moore (2011).[1])
First notice that the Laplacian matrix has the property that the sum of its entries across any row and any column is 0. Thus we can transform any minor into any other minor by adding rows and columns, switching them, and multiplying a row or a column by −1. Thus the cofactors are the same up to sign, and it can be verified that, in fact, they have the same sign.
We proceed to show that the determinant of the minor M11 counts the number of spanning trees. Let n be the number of vertices of the graph, and m the number of its edges. The incidence matrix E is an n-by-m matrix, which may be defined as follows: suppose that (i, j) is the kth edge of the graph, and that i < j. Then Eik = 1, Ejk = −1, and all other entries in column k are 0 (see oriented incidence matrix for understanding this modified incidence matrix E). For the preceding example (with n = 4 and m = 5):
Recall that the Laplacian L can be factored into the product of the incidence matrix and its transpose, i.e., L = EET. Furthermore, let F be the matrix E with its first row deleted, so that FFT = M11.
Now the Cauchy-Binet formula allows us to write
where S ranges across subsets of [m] of size n − 1, and FS denotes the (n − 1)-by-(n − 1) matrix whose columns are those of F with index in S. Then every S specifies n − 1 edges of the original graph, and it can be shown that those edges induce a spanning tree if and only if the determinant of FS is +1 or −1, and that they do not induce a spanning tree if and only if the determinant is 0. This completes the proof.
Particular cases and generalizations[edit]
Cayley’s formula[edit]
Cayley’s formula follows from Kirchhoff’s theorem as a special case, since every vector with 1 in one place, −1 in another place, and 0 elsewhere is an eigenvector of the Laplacian matrix of the complete graph, with the corresponding eigenvalue being n. These vectors together span a space of dimension n − 1, so there are no other non-zero eigenvalues.
Alternatively, note that as Cayley’s formula counts the number of distinct labeled trees of a complete graph Kn we need to compute any cofactor of the Laplacian matrix of Kn. The Laplacian matrix in this case is
Any cofactor of the above matrix is nn−2, which is Cayley’s formula.
Kirchhoff’s theorem for multigraphs[edit]
Kirchhoff’s theorem holds for multigraphs as well; the matrix Q is modified as follows:
- The entry qi,j equals −m, where m is the number of edges between i and j;
- when counting the degree of a vertex, all loops are excluded.
Cayley’s formula for a complete multigraph is mn-1(nn-1-(n-1)nn-2) by same methods produced above, since a simple graph is a multigraph with m = 1.
Explicit enumeration of spanning trees[edit]
Kirchhoff’s theorem can be strengthened by altering the definition of the Laplacian matrix. Rather than merely counting edges emanating from each vertex or connecting a pair of vertices, label each edge with an indeterminate and let the (i, j)-th entry of the modified Laplacian matrix be the sum over the indeterminates corresponding to edges between the i-th and j-th vertices when i does not equal j, and the negative sum over all indeterminates corresponding to edges emanating from the i-th vertex when i equals j.
The determinant of the modified Laplacian matrix by deleting any row and column (similar to finding the number of spanning trees from the original Laplacian matrix), above is then a homogeneous polynomial (the Kirchhoff polynomial) in the indeterminates corresponding to the edges of the graph. After collecting terms and performing all possible cancellations, each monomial in the resulting expression represents a spanning tree consisting of the edges corresponding to the indeterminates appearing in that monomial. In this way, one can obtain explicit enumeration of all the spanning trees of the graph simply by computing the determinant.
Matroids[edit]
The spanning trees of a graph form the bases of a graphic matroid, so Kirchhoff’s theorem provides a formula to count the number of bases in a graphic matroid. The same method may also be used to count the number of bases in regular matroids, a generalization of the graphic matroids (Maurer 1976).
Kirchhoff’s theorem for directed multigraphs[edit]
Kirchhoff’s theorem can be modified to count the number of oriented spanning trees in directed multigraphs.
The matrix Q is constructed as follows:
- The entry qi,j for distinct i and j equals −m, where m is the number of edges from i to j;
- The entry qi,i equals the indegree of i minus the number of loops at i.
The number of oriented spanning trees rooted at a vertex i is the determinant of the matrix gotten by removing the ith row and column of Q
Counting spanning k-component forests[edit]
Kirchhoff’s theorem can be generalized to count k-component spanning forests in an unweighted graph.[2] A k-component spanning forest is a subgraph with k connected components that contains all vertices and is cycle-free, i.e., there is at most one path between each pair of vertices. Given such a forest F with connected components 

where the sum is over all k-component spanning forests and 

The last factor in the polynomial is due to the zero eigenvalue 

where the sum is over all n–k-element subsets of 

Since a spanning forest with n–1 components corresponds to a single edge, the k = n – 1 case states that the sum of the eigenvalues of Q is twice the number of edges. The k = 1 case corresponds to the original Kirchhoff theorem since the weight of every spanning tree is n.
The proof can be done analogously to the proof of Kirchhoff’s theorem. An invertible 
The coefficients 
See also[edit]
- List of topics related to trees
- Markov chain tree theorem
- Minimum spanning tree
- Prüfer sequence
References[edit]
- ^ Moore, Cristopher (2011). The nature of computation. Oxford England New York: Oxford University Press. ISBN 978-0-19-923321-2. OCLC 180753706.
- ^ Biggs, N. (1993). Algebraic Graph Theory. Cambridge University Press.
- Harris, John M.; Hirst, Jeffry L.; Mossinghoff, Michael J. (2008), Combinatorics and Graph Theory, Undergraduate Texts in Mathematics (2nd ed.), Springer.
- Maurer, Stephen B. (1976), “Matrix generalizations of some theorems on trees, cycles and cocycles in graphs”, SIAM Journal on Applied Mathematics, 30 (1): 143–148, doi:10.1137/0130017, MR 0392635.
- Tutte, W. T. (2001), Graph Theory, Cambridge University Press, p. 138, ISBN 978-0-521-79489-3.
- Chaiken, S.; Kleitman, D. (1978), “Matrix Tree Theorems”, Journal of Combinatorial Theory, Series A, 24 (3): 377–381, doi:10.1016/0097-3165(78)90067-5, ISSN 0097-3165
External links[edit]
- A proof of Kirchhoff’s theorem







![Q=left[{begin{array}{rrrr}2&-1&-1&0\-1&3&-1&-1\-1&-1&3&-1\0&-1&-1&2end{array}}right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/578516027c122e4b3fb198bc7cc830acc2d8342b)
![Q^{ast }=left[{begin{array}{rrr}3&-1&-1\-1&3&-1\-1&-1&2end{array}}right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4e0948fbaaf312ad9993e2a3054b9bb7d606ac)






