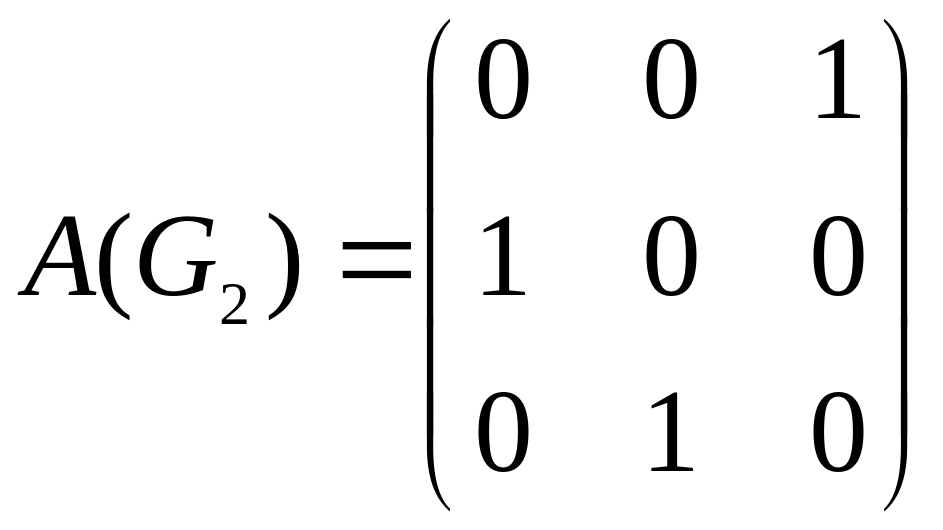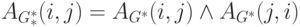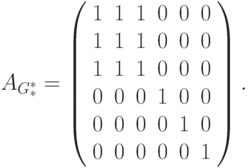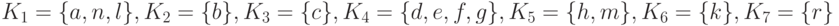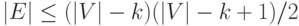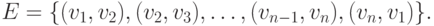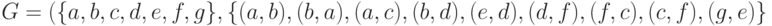Матрица сильной связности как найти - Сайт, где вы сможете решить свои вопросы

Неориентированный
граф называется связным,
если каждая пара различных вершин может
быть соединена, по крайней мере, одной
цепью.

Ориентированный
граф называется сильно
связным,
если для любых двух его вершин

существует
хотя бы один путь, соединяющий

.
Ориентированный граф называется
односторонне
связным,
если для любых двух его вершин, по крайней
мере, одна достижима из другой.

Компонентой
связности неориентированного графа
называется его связный подграф, не
являющийся собственным подграфом
никакого другого связного подграфа
данного графа (максимально связный
подграф).

Компонентой
сильной связности ориентированного
графа
называется его сильно связный подграф,
не являющийся собственным подграфом
никакого другого сильно связного
подграфа данного графа (максимально
сильно связный подграф).

Компонентой
односторонней связности ориентированного
графа называется
его односторонне связный подграф, не
являющийся собственным подграфом
никакого другого односторонне связного
подграфа данного графа (максимально
односторонне связный подграф).

Пусть

неориентированный граф с множеством
вершин

.
Квадратная матрица

порядка

,
у которой

называется
матрицей
связности графа

Для ориентированного
графа квадратная матрица

порядка

,
у которой

называется
матрицей
односторонней связности (достижимости).

Квадратная матрица

порядка

,
у которой

называется матрицей
сильной связности.

Пример. У
неориентированного графа, изображенного
на рис. 22 две компоненты связности.
Первая компонента связности включает
вершины

,
а вторая
состоит из одной вершины

Рис. 22. Компоненты
связанности неориентированного графа

Матрица связности
этого графа имеет вид:

.

Мы видим, что 1-ая,
2-ая, 4-ая и 5-ая строки матрицы

одинаковы.

Пример. У
ориентированного графа, изображенного
на рис. 23 две компоненты сильной связности.
Первая компонента связности включает
вершины

,
а вторая
состоит из одной вершины

.
Действительно, для любой пары вершин
из множества

существует
хотя бы один путь, соединяющий эти
вершины. Например, путь

соединяет все эти вершины. Из вершины

нет пути ни в одну вершину графа.

Рис. 23. Компоненты
сильной связанности ориентированного
графа

Матрица сильной
связности этого графа имеет вид:

Заметим, что 1-ая,
2-ая, 3-ая и 5-ая строки матрицы

одинаковы.

Для того, чтобы
выделить компоненты сильной связности,
необходимо сначала найти матрицу
достижимости

ориентированного графа, затем находим
матрицу сильной связности

ориентированного графа (она должна быть
симметрической).

Алгоритм выделения
компонента сильной связности:

1. Присваиваем

(

− количество компонент связности),

2. Включаем в
множество вершин

компоненты
сильной связности

вершины, соответствующие единицам
первой строки матрицы

.
В качестве матрицы смежности

возьмем подматрицу матрицы

,
состоящую из элементов матрицы

,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из

3. Вычеркиваем из

строки и столбцы, соответствующие
вершинам из

.
Если не остается ни одной строки (и
столбца), то


количество компонент сильной связности.
В противном случае обозначим оставшуюся
после вычеркивания срок и столбцов
матрицу как

,
присваиваем

и переходим к п. 2.

Пример. Выделим
компоненты связности ориентированного
графа, изображенного на рис. 25. Количество
вершин

.

Рис. 25.

Значит, для данного
ориентированного графа матрица смежности
будет иметь размерность

и будет выглядеть следующим образом

Найдем матрицу
достижимости и матрицу сильной связности
для данного ориентированного графа:

Присваиваем

и составляем множество вершин первой
компоненты сильной связности

:
это те вершины, которым соответствуют
единицы в первой строке матрицы

.
Таким образом, первая компонента сильной
связности состоит из одной вершины

.

Вычеркиваем из
матрицы

строку и столбец, соответствующие
вершине

,
чтобы получить матрицу

.

Присваиваем

.
Множество вершин второй компоненты
связности составят те вершины, которым
соответствуют единицы в первой строке
матрицы

,
то есть

.
Составляем матрицу смежности для
компоненты сильной связности

исходного графа

− в ее
качестве возьмем подматрицу матрицы

,
состоящую из элементов матрицы

,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из

Вычеркиваем из
матрицы

строки и столбцы, соответствующие
вершинам из

,чтобы
получить матрицу

,
которая состоит из одного элемента

,
присваиваем

.
Таким образом, третья компонента сильной
связности исходного графа, как и первая,
состоит из одной вершины

.

Таким образом,
выделены 3 компоненты сильной связности
ориентированного графа

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

Cоставляем матрицу смежности A(D) размерности (N− количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин, из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины Vi и входящая в Vj, то элемент матрицы смежности, стоящий на пересечении I-той строки и J-того столбца равен 1, иначе – 0.).

Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа по первой формуле утверждения 3, затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической) по второй формуле из того же утверждения.

Алгоритм выделения компонент сильной связности

1. Присваиваем P=1 (P − количество компонент связности), .

2. Включаем в множество вершин Vp Компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp. В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.

3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то P– количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp+1, присваиваем P=P+1 и переходим к п. 2.

Пример

Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин N=5.

Рис. 6.

Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом

Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:

, ,

Следовательно,

Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:

Присваиваем P=1 и составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины .

Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине V1, чтобы получить матрицу S2(D):

Присваиваем P=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S2(D), то есть . Составляем матрицу смежности для компоненты сильной связности исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:

Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3(D), которая состоит из одного элемента:

И присваиваем P=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины .

Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:

< Предыдущая		Следующая >

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 апреля 2020 года; проверки требуют 11 правок.

Матрица достижимости простого ориентированного графа — бинарная матрица замыкания по транзитивности отношения (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.

Способы построения матрицы достижимости[править | править код]

Перемножение матриц[править | править код]

Пусть дан простой граф , матрица смежности которого есть ${displaystyle mathbf {A} =(a_{ij})_{ntimes n}}$ , где ${displaystyle a_{ij}=1Leftrightarrow (i,j)in A}$ . Матрица смежности даёт информацию о всех путях длины 1 (то есть дугах) в орграфе. Для поиска путей длины 2 можно найти композицию отношения с самим собой:

По определению, матрица композиции отношений есть ${displaystyle mathbf {A^{2}} =({a^{2}}_{ij})_{ntimes n}={Bigl (}sum _{k}a_{ik}a_{kj}{Bigr )}={Bigl (}(a_{i1}land a_{1j})lor (a_{i2}land a_{2j})lor ldots lor (a_{in}land a_{nj}){Bigr )}}$ , где land — конъюнкция, а lor — дизъюнкция.

После нахождения матриц ${displaystyle mathbf {A} ^{k}}$ композиций ${displaystyle underbrace {Acirc ldots circ A} _{k}}$ для всех , будет получена информация о всех путях длины от до n-1 . Таким образом, матрица ${displaystyle mathbf {R(G)} =mathbf {E} lor mathbf {A} lor mathbf {A^{2}} lor ldots lor mathbf {A^{n-1}} =({a^{*}}_{ij})_{ntimes n}=({a}_{ij}lor {a^{2}}_{ij}lor ldots lor {a^{n-1}}_{ij})}$ есть искомая матрица достижимости, где — единичная матрица.

${displaystyle mathbf {E} ={begin{pmatrix}1&0&0&0\0&1&0&0\0&0&1&0\0&0&0&1end{pmatrix}}}$

Случай нескольких путей[править | править код]

Если булевы операции дизъюнкции и конъюнкции заменить обычными алгебраическими операциями +,times сложения и умножения соответственно, нахождение матрицы достижимости сведётся к обычному пошаговому перемножению матриц с последующим сложением результатов каждого шага. Тогда получившаяся матрица будет состоять не только из 0 и 1 и будет характеризовать не только наличие путей между вершинами, но уже и количество таких путей. В таком случае можно разрешить наличие кратных рёбер в графе.

Пример[править | править код]

Граф

Рассмотрим простой связный ориентированный граф .
Он имеет матрицу смежности вида:

${displaystyle mathbf {A} ={begin{pmatrix}0&1&1&0\0&0&0&0\0&1&0&1\0&0&1&0end{pmatrix}}}$

Найдём булевы степени этой матрицы ${displaystyle mathbf {A^{2}} }$ , ${displaystyle mathbf {A^{3}} }$ :

${displaystyle mathbf {A^{2}} ={begin{pmatrix}0&1&0&1\0&0&0&0\0&0&1&0\0&1&0&1end{pmatrix}}}$ ,
${displaystyle mathbf {A^{3}} ={begin{pmatrix}0&0&1&0\0&0&0&0\0&1&0&1\0&0&1&0end{pmatrix}}}$ ,

Получим матрицу достижимости

${displaystyle mathbf {R(G)} =mathbf {Elor Alor A^{2}lor A^{3}} ={begin{pmatrix}1&1&1&1\0&1&0&0\0&1&1&1\0&1&1&1end{pmatrix}}}$

Таким образом, из вершины можно добраться в любую другую.

При использовании же алгебраических операций получится матрица

${displaystyle mathbf {R(G)} =mathbf {E+A+A^{2}+A^{3}} ={begin{pmatrix}1&2&2&1\0&1&0&0\0&2&2&2\0&1&2&2end{pmatrix}}}$

Она показывает количество путей длины от 0 до 3 между вершинами орграфа.

Алгоритм Уоршелла[править | править код]

Существует другой алгоритм, позволяющий найти матрицу достижимости в точности за $2n^{3}$ шагов — алгоритм Уоршелла.

Связанные понятия[править | править код]

Матрица сильной связности[править | править код]

Матрица сильной связности простого орграфа — бинарная матрица, содержащая информацию обо всех сильно связанных вершинах в орграфе. Матрица сильной связности симметрична. У сильно связного графа такая матрица заполнена единицами.

Построение матрицы сильной связности[править | править код]

Матрица сильной связности может быть построена из матрицы достижимости. Пусть $mathbf {E} ^{*}$ — матрица достижимости орграфа G=(V,E) . Тогда матрица сильной связности состоит из элементов $(c_{ij})=left((e_{ij})land (e_{ji})right)$ .

Пример[править | править код]

Рассмотрим тот же граф, что и ранее.

Его матрица достижимости:

${displaystyle mathbf {E^{*}} ={begin{pmatrix}1&1&1&1\0&1&0&0\0&1&1&1\0&1&1&1end{pmatrix}}}$

Из неё получаем матрицу сильной связности:

${displaystyle mathbf {C} ={begin{pmatrix}1&0&0&0\0&1&0&0\0&0&1&1\0&0&1&1end{pmatrix}}}$

Вершины 3 и 4 сильно связаны друг с другом и сами с собой.

Матрица связности графа[править | править код]

Для обычного (не ориентированного) связного графа существует понятие матрицы связности, сходное с матрицей достижимости.

Матрица контрдостижимости[править | править код]

Матрица контрдостижимости Q графа G может быть найдена из матрицы достижимости путем ее транспонирования.

Примечания[править | править код]

Источник

Контрольная работа №1 – файл n12.doc

Контрольная работа №1
скачать (389.2 kb.)
Доступные файлы (12):

n1.doc	1050kb.	11.09.2007 13:06	скачать
n2.doc	32kb.	25.03.2005 13:56	скачать
n3.doc	31kb.	25.03.2005 13:56	скачать
n4.doc	32kb.	25.03.2005 13:56	скачать
n5.doc	32kb.	25.03.2005 13:57	скачать
n6.doc	32kb.	25.03.2005 13:57	скачать
n7.doc	31kb.	25.03.2005 13:57	скачать
n8.doc	32kb.	25.03.2005 13:57	скачать
n9.doc	32kb.	25.03.2005 13:58	скачать
n10.doc	32kb.	25.03.2005 13:48	скачать
n11.doc	33kb.	25.03.2005 13:58	скачать
n12.doc	996kb.	19.10.2005 13:21	скачать

n12.doc

Пусть A(D) – матрица смежности ориентированного псевдографа D=(V,X) (или псевдографа G=(V,X)), где V={v₁,…, v_n}. Обозначим через A^k=[a⁽^k⁾_ij] k-ю степень матрицы смежности A(D).

Элемент a⁽^k⁾_ij матрицы A^k ориентированного псевдографа D=(V,X) (псевдографа G=(V,X)) равен числу всех путей (маршрутов) длины k из v_i в v_j.

Матрица достижимости ориентированного графа D ? квадратная матрица T(D)=[t_ij] порядка n, элементы которой равны

Матрица сильной связности ориентированного графа D ? квадратная матрица S(D)=[s_ij] порядка n, элементы которой равны

Матрица связности графа G ? квадратная матрица S(G)=[s_ij] порядка n, элементы которой равны

Утверждение 3. Пусть D=(V,X) – ориентированный граф, V={v₁,…, v_n}, A(D) – его матрица смежности. Тогда

T(D)=sign[E+A+A²+A³+… A^n-1],
S(D)=T(D)T^T(D) (T^T-транспонированная матрица, - поэлементное умножение).

Пусть G=(V,X) – граф, V={v₁,…, v_n}, A(G) – его матрица смежности. Тогда

S(G)=sign[E+A+A²+A³+… A^n-1] (E– единичная матрица порядка n).
1.7. Расстояния в графе

Пусть – граф (или псевдограф). Расстоянием между вершинами называется минимальная длина пути между ними, при этом , , если не пути.

Расстояние в графе удовлетворяют аксиомам метрики

1) ,

2) (в неориентированном графе)

4) в связном неориентированном графе.

Пусть связный граф (или псевдограф).

Диаметром графа G называется величина .

Пусть .

Максимальным удалением (эксцентриситетом) в графе G от вершины называется величина .

Радиусом графа G называется величина

Центром графа G называется любая вершина такая, что .
1.8. Образ и прообраз вершины и множества вершин

Пусть ориентированный граф – некоторая вершина .
Обозначим – образ вершины ;

– прообраз вершины ;

– образ множества вершин V₁ ;

– прообраз множества вершин V₁.
1.9. Нагруженные графы

Нагруженный граф ? ориентированный граф D=(V,X), на множестве дуг которого определена некоторая функция , которую называют весовой функцией.

Цифра над дугой (см. рис. 5)? вес дуги (цена дуги).

Рис. 5.

Обозначения: для любого пути П нагруженного ориентированного графа D через l(П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П).

Величина l называется длиной пути.

Если выбрать веса равными 1, то придем к ненагруженному графу.

Путь в нагруженном ориентированном графе из вершины v в вершину w, где vw, называется минимальным, если он имеет наименьшую длину.

Аналогично определяется минимальный путь в нагруженном графе.

Введем матрицу длин дуг C(D)=[c_ij] порядка n, причем

Свойства минимальных путей в нагруженном ориентированном графе

1) Если для  дуги , то  минимальный путь (маршрут) является простой цепью;

2) если минимальный путь (маршрут) то для  i,j : путь (маршрут) тоже является минимальным;

3) если ? минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k+1 дуг (ребер), то ? минимальный путь (маршрут) из v в u среди путей (маршрутов), содержащих не более k дуг (ребер).
1.10. Деревья и циклы

Граф G называется деревом если он является связным и не имеет циклов.

Граф G называется лесом если все его компоненты связности – деревья.

Свойства деревьев:

Следующие утверждения эквивалентны:

1) Граф G есть дерево.

2) Граф G является связным и число его ребер ровно на 1 меньше числа вершин.

3)  две различные вершины графа G можно соединить единственной (и при этом простой) цепью.

4) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл

Утверждение 4. Если у дерева G имеется, по крайней мере, 1 ребро, то у него найдется висячая вершина.

Утверждение 5.Пусть G связный граф, а ? висячая вершина в G, граф получается из G в результате удаления вершины и инцидентного ей ребра. Тогда тоже является связным.

Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G – связный граф. Тогда остовное дерево графа G должно содержать n(G)-1 ребер. Значит, для получения остовного дерева из графа G нужно удалить ребер.

Число называется цикломатическим числом графа G.
2. Решение контрольных задач
2.1. Компоненты сильной связности ориентированного графа

С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

Cоставляем матрицу смежности A(D) размерности (n? количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин , из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины v_i и входящая в v_j, то элемент матрицы смежности, стоящий на пересечении i-той строки и j-того столбца равен 1, иначе – 0.).

Алгоритм выделения компонент сильной связности

1. Присваиваем p=1 (p ? количество компонент связности), .

2. Включаем в множество вершин V_p компоненты сильной связности D_p вершины, соответствующие единицам первой строки матрицы S_p. В качестве матрицы A(D_p) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V_p.

3. Вычеркиваем из S_p строки и столбцы, соответствующие вершинам из V_p. Если не остается ни одной строки (и столбца), то p– количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как S_p₊₁, присваиваем p=p+1 и переходим к п. 2.

Пример

Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин n=5.

Рис. 6.
Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5Ч5 и будет выглядеть следующим образом

Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:

, ,

Следовательно,

Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:

Присваиваем p=1 и составляем множество вершин первой компоненты сильной связности D₁: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины .

Вычеркиваем из матрицы S₁(D) строку и столбец, соответствующие вершине v₁, чтобы получить матрицу S₂(D):

Присваиваем p=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S₂(D), то есть . Составляем матрицу смежности для компоненты сильной связности исходного графа D ? в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V₂:

Вычеркиваем из матрицы S₂(D) строки и столбцы, соответствующие вершинам из V₂ ,чтобы получить матрицу S₃(D), которая состоит из одного элемента:

и присваиваем p=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины .

Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:

D₁:

D₂:

D₃:

2.2. Расстояния в ориентированном графе

С помощью алгоритма фронта волны найти расстояния в ориентированном графе D: диаметр, радиус и центры.

Пусть ориентированный граф с n2 вершинами и v,w (vw) – заданные вершины из V.

Алгоритм поиска минимального пути из в в ориентированном графе

(алгоритм фронта волны).

Помечаем вершину индексом 0, затем помечаем вершины  образу вершины индексом 1. Обозначаем их FW₁ (v). Полагаем k=1.
Если или k=n-1, и одновременно то вершина не достижима из . Работа алгоритма заканчивается.

В противном случае продолжаем:

Если , то переходим к шагу 4.

В противном случае мы нашли минимальный путь из в и его длина равна k. Последовательность вершин

есть этот минимальный путь. Работа завершается.

Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин c индексом k. Множество вершин с индексом k+1 обозначаем . Присваиваем k:=k+1 и переходим к 2).

Замечания

Чтобы найти расстояния в ориентированном графе, необходимо составить матрицу расстояний R(D) между его вершинами. Это квадратная матрица размерности , элементы главной диагонали которой равны нулю (, i=1,..,n).

Сначала составляем матрицу смежности. Затем переносим единицы из матрицы смежности в матрицу минимальных расстояний (, если ). Далее построчно заполняем матрицу следующим образом.

Рассматриваем первую строку, в которой есть единицы. Пусть это строка ? i-тая и на пересечении с j-тым столбцом стоит единица (то есть ). Это значит, что из вершины можно попасть в вершину за один шаг. Рассматриваем j-тую сроку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент . Тогда из вершины в вершину можно попасть за два шага. Таким образом, можно записать . Следует заметить, что если в рассматриваемых строках две или более единиц, то следует прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу длину наикратчайшего из них.

Примечание. Самый длинный путь найти при помощи алгоритма фронта волны.

Пример

Найдем расстояния в ориентированном графе D, изображенном на рис. 7. В данной задаче количество вершин n=7, следовательно, матрицы смежности и минимальных расстояний между вершинами ориентированного графа D будут иметь размерность 7Ч7.

Рис.7.
Матрица смежности:

Начинаем заполнять матрицу R(D) минимальных расстояний: сначала ставим нули по главной диагонали и r_ij=a_ij, если a_ij=1, (т.е. переносим единицы из матрицы смежности). Рассматриваем первую строку. Здесь есть две единицы, то есть из первой вершины за один шаг можно попасть во вторую и шестую. Из второй вершины можно попасть за один шаг в третью (путь в первую вершину нас не интересует), следовательно, можно записать . Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит, , . Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому . В итоге получаем следующую матрицу:

Таким образом, диаметром исследуемого ориентированного графа будет .

Для каждой вершины заданного ориентированного графа найдем максимальное удаление (эксцентриситет) в графе G от вершины нее по формуле, которая была приведена выше : r(v_i) ? максимальное из расстояний, стоящих в i-той строке. Таким образом,

r(v₁)=3, r(v₂)=3, r(v₃)=5, r(v₄)=4, r(v₅)=2, r(v₆)=2, r(v₇)=3.

Значит, радиусом графа G будет

Соответственно, центрами графа G будут вершины v₅ и v₆ , так как величины их эксцентриситетов совпадают с величиной радиуса.

Опишем теперь нахождение минимального пути из вершины v₃ в вершину v₆ по алгоритму фронта волны. Обозначим вершину v₃ как V₀, а вершину v₆  как W (см. рис. 8).

Рис.8.
Множество вершин, принадлежащих образу V₀, состоит из одного элемента  это вершина v₄, которую, согласно алгоритму, обозначаем как V₁: FW₁(v₃)={v₄}. Поскольку искомая вершина не принадлежит фронту волны первого уровня , продолжаем работу алгоритма. Строим фронт волны второго уровня  это множество вершин, принадлежащих образу вершины V₁: FW₂(v₃)={v₇}, обозначаем v₇?V₂. В образ вершины V₂ входят две вершины  v₅ и v₄, но, так как v₄ уже была помечена как V₀, то фронт волны третьего уровня состоит из одного элемента: FW₃(v₃)={v₅}, v₅?V₃. Из непомеченных вершин в образ вершины V₃ входят v₁ и v₂, соответственно, FW₄(v₃)={v₁, v₂}, v₁?V₄, v₂?V₄. Теперь помечены все вершины, кроме v₆, которая входит в образ вершины , то есть FW₅(v₃)={v₆?W}, работа алгоритма закончена. Минимальный путь (5 шагов) из вершины v₃ в вершину v₆: v₃ v₄ v₇ v₅ v₁ v₆.
2.3. Минимальный путь в нагруженном ориентированном графе

Найти минимальный путь в нагруженном ориентированном графе из вершины в вершину по методу Форда-Беллмана.

Рассмотрим сначала общую задачу – нахождения минимального пути из вершины v_нач в v_кон.

Пусть D=(V,X) – нагруженный ориентированный граф, V={v₁,…,v_n}, n>1. Введем величины , где i=1,…,n, k=0,1,2,…,n–1.

Для каждого фиксированного i и k величина равна длине минимального пути среди путей из v_нач в v_i содержащих не более k дуг. Если путей нет, то .

Положим также .

Составляем матрицу длин дуг C(D)=[c_ij] порядка n:

Утверждение. При i=2,…,n, k0 выполняется равенство

. (3.1)

Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе D из v_нач в v_кон.( v_нач ? v_кон)
записываем в виде матрицы, i– строка, k-столбец.

Составляем таблицу , i=1,…,n, k=0,…,n-1. Если , то пути из v_нач в v_кон нет. Конец алгоритма.
Если то это число выражает длину любого минимального пути из v_нач в v_кон. Найдем минимальное k₁1, при котором . По определению получим, что k₁– минимальное число дуг в пути среди всех минимальных путей из v_нач в v_кон.
Затем определяем номера i₂,…, такие, что

то есть, восстанавливаем по составленной таблице и матрице стоимости искомый минимальный путь из v_нач в v_кон.

Пример

Найдем минимальный путь из вершины v₂ в v₆ в ориентированном нагруженном графе D, изображенном на рис. 9. В рассматриваемом графе количество вершин n=7, следовательно, матрица длин дуг ориентированного графа D будет иметь размерность 7Ч7.

Рис. 9.
Матрица длин дуг для рассматриваемого графа будет выглядеть следующим образом:

Согласно алгоритму, составляем таблицу стоимости минимальных путей из вершины v₂ в вершину v_i не более, чем за k шагов, k=0,…n-1 (n=7, следовательно, k=0,…6). Как было определено выше, , и для всех остальных вершин v_i ? v₂, то есть первый столбец таблицы состоит из элементов, равных , кроме элемента . Второй столбец таблицы повторяет вторую строку матрицы стоимости, поскольку представляет собой стоимость возможных путей из вершины v₂ за один шаг. Далее по формуле (3.1) находим по столбцам все оставшиеся элементы таблицы. Например, чтобы найти элемент , складываем элементы столбца и первого столбца матрицы стоимости и выбираем минимальное из получившихся чисел:

В конечном итоге получаем следующую таблицу:

Теперь необходимо по построенной таблице и по матрице C(D) восстановить минимальный путь из вершины v₂ в v₆, который будет строиться с конца, то есть, начиная с вершины v6. Для этого выбираем минимальное из чисел, стоящих в строке, соответствующей v₆ в таблице. Это число – 21 – длина минимального искомого пути. В первый раз такая длина была получена при количестве шагов, равном 4. В вершину v₆ мы можем попасть за один шаг из вершин v₁ и v₇ (длина соответствующих дуг 8 и 5 соответственно – данные из матрицы C(D)). Выбираем минимальную по длине из этих дуг. Далее, в вершину v₇ можно попасть из v₄ и v₅ (длина соответствующих дуг 7 и 3 соответственно). Продолжая аналогичным образом, найдем искомый путь за 4 шага минимальной длины из вершины v₂ в v₆: v₂ v₃ v₅ v₇ v₆.
2.4. Эйлеровы циклы и цепи

Найти Эйлерову цепь в неориентированном псевдографе.

Исходя из утверждений 1 и 2, чтобы найти Эйлерову цепь, нужно соединить две вершины с нечетными степенями фиктивным ребром. Тогда задача сводится к нахождению Эйлерова цикла по приведенному ниже алгоритму. Из найденного цикла удаляется фиктивное ребро, тем самым находится искомая Эйлерова цепь.

Алгоритм выделения эйлерова цикла в связном мультиграфе с четными степенями вершин

Выделим из G цикл ₁. (так как степени вершин четны, то висячие вершины отсутствуют). Положим l=1, G=G.
Удаляем из G ребра, принадлежащие выделенному циклу ₁. Полученный псевдограф снова обозначаем как G. Если в G отсутствуют ребра, то переходим к шагу 4. Если ребра есть, то выделяем из G цикл _l₊₁ и переходим к шагу 3.
Присваиваем l:=l+1 и переходим к шагу 2.
По построению выделенные циклы содержат все ребра по одному разу. Если l:=1, то искомый Эйлеров цикл найден (конец работы алгоритма). В противном случае находим циклы, содержащие хотя бы по одной общей вершине (в силу связности графа это всегда можно сделать). Склеиваем эти циклы. Повторяем эти операции, пока не останется один цикл, который является искомым.

Пример.

Найдем Эйлерову цепь в неориентированном графе G, изображенном на рис. 10.

Прежде, чем приступать к нахождению Эйлеровой цепи, необходимо проверить степени вершин графа G ? согласно утверждению 2, для существования Эйлеровой цепи, необходимо и достаточно, чтобы в графе G ровно 2 вершины нечетной степени.

Рис. 10.
В рассматриваемом графе нечетные степени имеют вершины v₃ и v₁ (степень этих вершин равна 3). Соединяя эти вершины фиктивным ребром так, как показано на рис. 11, получаем граф G:

Рис. 11.
Поскольку в конечном итоге будет получена цепь, то очевидно, что началом и концом этой цепи будут вершины с нечетными степенями. Поэтому, следуя описанному выше алгоритму, будем циклы _i так, чтобы хотя бы один из них начинался или кончался на вершинах v₃ или v₁.

Пусть цикл ₁ составят ребра, проходящие через следующие вершины: v₃ v₄ v₇ v₆ v₁ v₂ v₃. Согласно алгоритму, удаляем из G все ребра, задействованные в цикле ₁. Теперь граф G’ будет таким, как показано на рис. 12.

Составляем следующий цикл ₂: v₄ v₅ v₆ v₂ v₅ v₇ v₄. Граф G после удаления ребер, составляющих цикл ₂, изображен на рис. 13.


Рис.12	Рис. 13

Очевидно, что последний цикл ₃ будет состоять из v₃ v₅ v₁|v₃, где последнее ребро, соединяющее вершины v₁ и v₃ – фиктивно. После удаления ребер, составляющих цикл ₃, в графе G не останется ни одного ребра.

Теперь по общим вершинам склеиваем полученные циклы. Поскольку ₁ и ₂ имеют общую вершину v₄, то, объединяя их, получим следующий цикл: v₃ v₄ v₅ v₆ v₂ v₅ v₇ v₄ v₇ v₆ v₁ v₂ v₃. Теперь склеим получившийся цикл с циклом ₃: v₃ v₄ v₅ v₆ v₂ v₅ v₇ v₄ v₇ v₆ v₁ v₂ v₃ v₅ v₁|v₃. Удаляя фиктивное ребро, получаем искомую Эйлерову цепь: v₃ v₄ v₅ v₆ v₂ v₅ v₇ v₄ v₇ v₆ v₁ v₂ v₃ v₅ v₁.

2.5. Минимальное остовное дерево

Найти минимальное остовное дерево в неориентированном нагруженном графе.

Алгоритм выделения минимального остовного дерева в неориентированном нагруженном графе G

Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G₂ графа G. Положим i:=2.
Если i=n(G), то задача решена и G_i – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3).
Строим граф G_i₊₁. Для этого добавим к графу G_i новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа G_i и одновременно вершине, не содержащейся в G_i. Вместе с этим ребром включаем в G_i₊₁ и эту инцидентную ему вершину. Присваиваем i:=i+1 и переходим к шагу 2).

Пример.

Найдем минимальное остовное дерево в неориентированном нагруженном графе, изображенном на рис.14.

Рис.14.
Обозначим ребро, соединяющее вершины v_i и v_j через x_ij.

Для удобства использования приведенного выше алгоритма решения поставленной задачи, составим матрицу длин ребер. В рассматриваемом графе количество вершин n=8, следовательно, матрица длин ребер графа G будет иметь размерность 8Ч8 и выглядеть следующим образом:

Согласно приведенному выше алгоритму, выбираем ребро минимальной длины (выбираем среди элементов матрицы C(G), минимальное ? это c₄₇=1) и вместе с инцидентными ему двумя вершинами относим к графу G₂. Таким образом, . Длина дерева G₂ будет равна l(G₂)=c₄₇=1. Поскольку , продолжаем работу алгоритма. По четвертой и седьмой строкам ищем минимальное число (за исключением использованной единицы) ? ребро минимальной длины, инцидентное либо вершине v₄, либо v₇. Выбираем ребро x₄₆ с длиной c₄₆=3 и вместе с вершиной v₆ добавляем к графу G₂, обозначая его теперь как G₃: , при этом l(G₃)=c₄₇+c₄₆=1+3=4. Аналогично находим графы:

, ;

;

Поскольку i=8=n(G), работа алгоритма заканчивается.

Таким образом, искомое минимальное остовное дерево графа G ? граф G₈, изображенный на рис. 15, длина которого равна 22.

Рис.15.
2.6. Задача о коммивояжёре

Найти в нагруженном неориентированном графе гамильтонов цикл минимального веса.

Эта задача имеет практическую интерпретацию, благодаря которой и получила своё название: коммивояжёр (бродячий торговец) должен выйти из первого города, посетить по разу в неизвестном порядке города 2,3..n и вернуться в первый город. Стоимости проезда между городами известны. В каком порядке следует объезжать города, чтобы замкнутый путь (тур) коммивояжера был наименее затратным?

Сформулируем задачу в терминах теории графов, введя следующие обозначения: пусть D=[V, X] – полный ориентированный граф и f: X – весовая функция, V={v₁, v₂,…, v_n} – множество вершин, X – множество дуг, C={c_ij}, i,j=1,2…n – весовая матрица данного ориентированного графа, то есть с_ij=f(v_i,v_j), причем для любого i справедливо c_ii=. Требуется найти простой остовной ориентированный цикл (или «цикл коммивояжёра») минимального веса.

Следует заметить, что требование полноты ориентированного графа (наличие дороги из любого города в любой) можно опустить. Однако в этом случае гамильтонов цикл может и не существовать (по теореме, для его существования достаточна полнота орграфа). Следовательно, описываемый метод ветвей и границ приведёт к полному перебору всех вариантов незаконченных циклов прежде, чем станет очевиден факт отсутствия решения.

Очевидно, c_ij следует трактовать как стоимость проезда из города i в город j. Допустим, что добрый мэр города j издал указ выплачивать каждому въехавшему в город коммивояжеру $5. Это означает, что любой тур подешевеет на $5, поскольку в любом туре нужно въехать в город j. Но поскольку все туры равномерно подешевели, то прежний минимальный тур будет и теперь стоить меньше всех. Добрый же поступок мэра можно представить как уменьшение всех чисел j-го столбца матрицы M на 5. Если бы мэр хотел спровадить коммивояжеров из j-го города и установил награду за выезд в размере $10, это можно было бы выразить вычитанием 10 из всех элементов j-й той строки. Это снова бы изменило стоимость каждого тура, но минимальный тур остался бы минимальным. Итак, доказана следующая лемма.

Вычитая любую константу из всех элементов любой строки или столбца матрицы C, мы оставляем минимальный тур минимальным.

В этой связи введем следующие термины. Пусть имеется некоторая числовая матрица. Привести строку этой матрицы означает выделить в строке минимальный элемент (его называют константой приведения) и вычесть его из всех элементов этой строки. Очевидно, в результате в этой строке на месте минимального элемента окажется нуль, а все остальные элементы будут неотрицательными. Аналогичный смысл имеют слова «привести столбец матрицы».

Привести матрицу по строкам означает, что все строки приводятся. Аналогичный смысл имеют слова «привести матрицу по столбцам». Приведение матрицы означает сначала приведение этой матрицы по строкам, а затем по столбцам.

Если с помощью приведённой матрицы удастся построить такую последовательность переходов по городам (по вершинам графа), которым соответствует последовательность нулевых элементов приведенной матрицы, то ясно, что для этой матрицы мы получим минимальный тур. Но он же будет минимальным и для исходной весовой матрицы С, только для того, чтобы получить правильную стоимость тура, нужно будет прибавить все константы приведения. Таким образом, сумма констант приведения играет роль оценки снизу для стоимости всех туров.

Весом элемента матрицы называют сумму констант приведения матрицы, которая получается из данной матрицы заменой обсуждаемого элемента на . Следовательно, слова «самый тяжёлый нуль в матрице» означают, что в матрице подсчитан вес каждого нулевого элемента, а затем фиксирован нуль с максимальным весом.

Продемонстрируем теперь метод ветвей и границ для решения задачи о коммивояжёре.

Пусть требуется найти легчайший простой остовной ориентированный цикл в полном взвешенном ориентированном графе на пяти вершинах, со следующей весовой матрицей C:

	1	2	3	4	5
1		9	8	4	10
2	6		4	5	7
3	5	3		6	2
4	1	7	2		8
5	2	4	5	2	

Верхняя строка и левый столбец, выделенные затемненным фоном, содержат номера вершин графа; символ , стоящий на главной диагонали означает отсутствие дуг-петель; кроме того, символ  здесь и всюду означает «компьютерную бесконечность», то есть самое большое из возможных в рассмотрении чисел; считается, что в сумме  с любым числом даёт .

Обозначим за Г множество всех обходов коммивояжера (т. е. всех простых ориентированных остовных циклов). Поскольку граф – полный, это множество заведомо не пусто. Сопоставим ему число (Г), которое будет играть роль значения на этом множестве оценочной функции: это число равно сумме констант приведения данной матрицы весов дуг графа и является оценкой снизу для стоимости минимального тура коммивояжёра. Приведённую матрицу весов данного графа следует запомнить, обозначим ее через С₁.

Подсчитаем (Г). Для этого выполним приведение матрицы весов.

Сначала – по строкам:

	1	2	3	4	5
1		5	4	0	6	4	 min в первой строке
2	2		0	1	3	4	 min во второй строке
3	3	1		4	0	2	 min в третьей строке
4	0	6	1		7	1	 min в четвёртой строке
5	0	2	3	0		2	 min в пятой строке

	1	2	3	4	5
1		5	4	0	6
2	2		0	1	3
3	3	1		4	0
4	0	6	1		7
5	0	2	3	0	

Теперь ? по столбцам:

	1	2	3	4	5
1		5	4	0	6
2	2		0	1	3
3	3	1		4	0
4	0	6	1		7
5	0	2	3	0	
	0	1	0	0	0
	?min в первом столбце	?min во втором столбце	?min в третьем столбце	?min в четвёртом столбце	?min в пятом столбце

	1	2	3	4	5
1		4	4	0	6
2	2		0	1	3
3	3	0		4	0
4	0	5	1		7
5	0	1	3	0	

1.6. Матрицы достижимости и связности

Источник

Взаимная достижимость, компоненты сильной связности и базы графа

По аналогии с графом достижимости определим граф сильной достижимости.

Определение 9.10. Пусть G=(V,E) – ориентированный граф. Граф сильной достижимости G_*^*=(V,E_*^*) для G имеет то же множество вершин V
и следующее множество ребер E_*^* ={ (u, v) | в графе G вершины v и u взаимно достижимы}.

По матрице графа достижимости 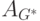$A_{G^*}$ легко построить матрицу $A_{G_*^*}$ графа
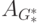
сильной достижимости.
Действительно из определений достижимости и сильной достижимости непосредственно
следует, то для всех пар (i,j), 1<= i,j <= n, значение элемента 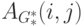$A_{G_*^*}(i,j)$ равно 1 тогда и только тогда,
когда оба элемента A_G*(i, j) и A_G*(j, i) равны 1, т.е.

$A_{G_*^*}(i,j) = A_{G^*}(i, j) wedge A_{G^*}( j, i)$

По матрице 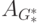$A_{G_*^*}$ можно выделить компоненты сильной связности графа G следующим образом.

Поместим в компоненту K₁ вершину v₁ и все такие вершины v_j, что A_{G_*^*}(1,j) = 1.
Пусть уже построены компоненты K₁, …, K_i и v_k – это вершина с минимальным номером, еще не попавшая в компоненты. Тогда поместим в компоненту K_{i+1} вершину v_k и все такие вершины v_j,
что A_{G_*^*}(k,j) = 1.

Повторяем шаг (2) до тех пор, пока все вершины не будут распределены по компонентам.

В нашем примере для графа G на рис.2 по матрице 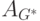$A_{G^*}$ получаем
следующую матрицу графа сильной достижимости

$A_{G_*^*}= left( begin{array}{cccccc} 1 & 1 & 1 & 0& 0& 0\ 1 & 1 & 1 & 0& 0& 0\ 1 &1 & 1 & 0& 0& 0\ 0 & 0 & 0 & 1& 0& 0\ 0 & 0 & 0 & 0& 1& 0\ 0 & 0 & 0 & 0& 0& 1 end{array}right).$

Используя описанную выше процедуру, находим, что вершины графа G разбиваются на 4 компоненты сильной связности: K₁= {v₁, v₂, v₃}, K₂ ={ v₄}, K₃ ={ v₅}, K₄ ={ v₆}.

На множестве компонент сильной связности также определим отношение достижимости.

Определение 9.11. Пусть K и K’ – компоненты сильной связности графа G.
Компонента K достижима из компоненты K^prime, если K= K’
или существуют такие две вершины u in K
и v in K' , что u достижима из v. K строго достижима из K^prime, если Kne K' и K достижима из K’.

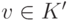
Компонента K называется минимальной, если она не является строго
достижимой ни из какой компоненты.

Так как все вершины в одной компоненте взаимно достижимы, то нетрудно понять,
что отношения достижимости и строгой достижимости на компонентах не зависят
от выбора вершин 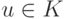u in K и v in K' .

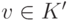
Из определения легко выводится следующая характеристика строгой достижимости.

Лемма 9.3.
Отношение строгой достижимости является отношением частичного порядка, т.е. оно
антирефлексивно, антисимметрично и транзитивно.

Это отношение можно представлять в виде ориентированного графа, вершинам и которого
являются компоненты, а ребро (K’, K) означает, что K строго достижима из K’.
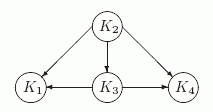
На рис. 9.4 показан этот граф компонент для рассматриваемого выше графа G.

Рис.
9.4.
Граф отношения достижимости на компонентах G

В данном случае имеется одна минимальная компонента K₂.

Во многих приложениях ориентированный граф представляет собой сеть распространения
некоторого ресурса: продукта, товара, информации и т.п. В таких случаях естественно возникает
задача поиска минимального числа таких точек (вершин),
из которых этот ресурс может быть доставлен в любую
точку сети.

Определение 9.12. Пусть G=(V,E) – ориентированный граф.
Подмножество вершин 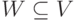называется порождающим,
если из вершин W
можно достичь любую вершину графа.
Подмножество вершин 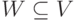называется базой графа,
если оно является порождающим,
но никакое его собственное подмножество порождающим не является.

Следующая теорема позволяет эффективно находить все базы графа.

Теорема 9.1.
Пусть G=(V,E) – ориентированный граф. Подмножество вершин
является базой G тогда и только тогда, когда содержит по одной вершине из каждой
минимальной компоненты сильной связности G и не содержит никаких других вершин.

Доказательство Заметим вначале, что каждая вершина графа достижима из вершины,
принадлежащей некоторой минимальной компоненте. Поэтому множество вершин W,
содержащих по одной вершине из каждой минимальной компоненты, является порождающим
а при удалении из него любой вершины перестает быть таковым, так как вершины из
соответствующей минимальной компоненты становятся недостижимы. Поэтому W является базой.

Обратно, если W является базой, то оно обязано включать хотя бы по одной вершине
из каждой минимальной компоненты, иначе вершины такой минимальной компоненты окажутся
недоступны. Никаких других вершин W содержать не может, так как каждая из них
достижима из уже включенных вершин.

Из этой теоремы вытекает следующая процедура построения одной или перечисления всех баз графа G.

Найти все компоненты сильной связности G.
Определить порядок на них и выделить минимальные относительно этого порядка компоненты.
Породить одну или все базы графа, выбирая по одной вершине из каждой минимальной компоненты.

Пример 9.5.
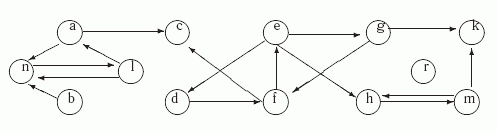
Определим все базы ориентированного графа G, показанного на рис.9.5.

Рис.
9.5.
Граф G

На первом этапе находим компоненты сильной связности G:

$K_1 ={ a, n, l }, K_2 = { b }, K_3 ={ c}, K_4 ={ d,e, f, g}, \ K_5={ h, m}, K_6 ={ k}, K_7= { r}$

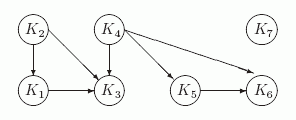
На втором этапе строим граф строгой достижимости на этих компонентах.

Рис.
9.6.
Граф отношения достижимости на компонентах G

Определяем минимальные компоненты: K₂ = { b }, K₄ ={ d,e, f, g} и K₇= { r}.

Наконец перечисляем все четыре базы G: B₁= { b, d, r}, B₂= { b, e, r}, B₃= { b, f, r} и B₁= { b, g, r}.

Задачи

Задача 9.1. Докажите, что сумма степеней всех вершин произвольного ориентированного графа четна.

У этой задачи имеется популярная интерпретация: доказать, что общее число
рукопожатий, которыми обменялись люди, пришедшие на вечеринку,
всегда четно.

Задача 9.2. Перечислите все неизоморфные неориентированные графы, у которых не
более четырех вершин.

Задача 9.3.
Докажите, что неориентированный связный граф остается связным после
удаления некоторого ребра это ребро принадлежит некоторому циклу.

Задача 9.4.
Докажите, что неориентированный связный граф с n вершинам и

содержит не менее n-1 ребер,
если содержит больше n-1 ребер, то имеет, по крайней мере, хотя бы один цикл.

Задача 9.5.
Докажите, что в любой группе из 6 человек есть трое попарно знакомых или
трое попарно незнакомых.

Задача 9.6.
Докажите, что неориентированный граф G=(V,E) связен
для каждого разбиения $V= V_{1}cup V_{2}$ с непустыми V₁ и V₂ существует ребро, соединяющее V₁ с V₂.

Задача 9.7.
Докажите, что, если в неориентированном графе имеется ровно две вершины нечетной
степени, то они связаны путем.

Задача 9.8.
Пусть G=(V,E) неориентированный граф с |E| < |V|-1. Докажите, что тогда G несвязный граф.

Задача 9.9. Докажите, что в связном неориентированном графе
любые два простых пути максимальной длины имеют общую вершину.

Задача 9.10.
Пусть неориентированный граф без петель G=(V,E) имеет k компонент связности. Доказать, что тогда

Задача 9.11. Определите, что представляет из себя граф достижимости для

графа с n вершинам и и пустым множеством ребер;
графа с n вершинам и: V= {v₁,… , v_n}, ребра которого образуют цикл:

$E ={(v_1,v_2), (v_2,v_3), ldots , (v_{n-1},v_n), (v_n,v_1) }.$

Задача 9.12. Вычислите матрицу графа достижимости 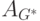$A_{G^*}$ для графа

$G=({a,b,c,d,e,f, g}, { (a,b), (b,a), (a,c), (b,d), (e,d), \(d, f), (f,c), (c,f), (g,e)}$

и постройте соответствующий ей граф достижимости. Найдите все базы графа G.

Задача 9.13.
Построить для заданного на рис. 9.7 ориентированного графа G₁=(V,E)
его матрицу смежности A_G1, матрицу инцидентности B_G1
и списки смежности. Вычислить матрицу достижимости A_G1*
и построить соответствующий граф достижимости G₁^*.

Рис.
9.7.

Источник

Способы построения матрицы достижимости[править | править код]

Перемножение матриц[править | править код]

Случай нескольких путей[править | править код]

Пример[править | править код]

Алгоритм Уоршелла[править | править код]

Связанные понятия[править | править код]

Матрица сильной связности[править | править код]

Построение матрицы сильной связности[править | править код]

Пример[править | править код]

Матрица связности графа[править | править код]

Матрица контрдостижимости[править | править код]

Примечания[править | править код]

Контрольная работа №1 – файл n12.doc

n12.doc

Взаимная достижимость, компоненты сильной связности и базы графа

Задачи

Вам также может понравиться

Как найти светило по координатам

Как найти тайник коллекционера на радаре

Как найти наименьшее общее кратное несколько чисел

Добавить комментарий Отменить ответ