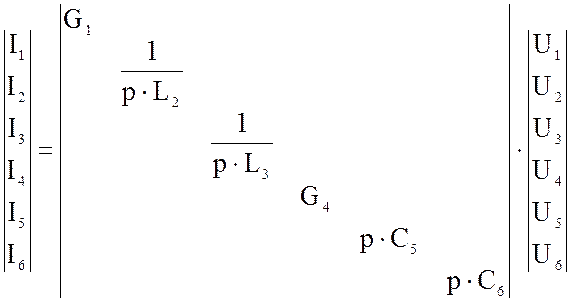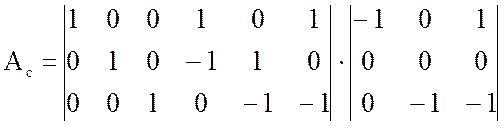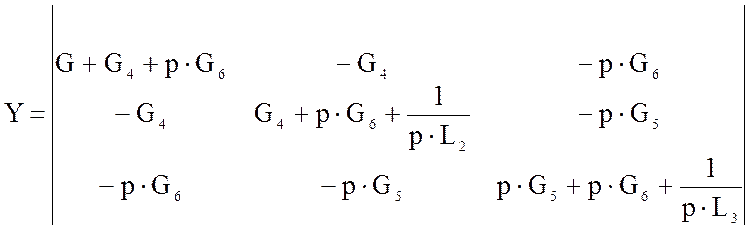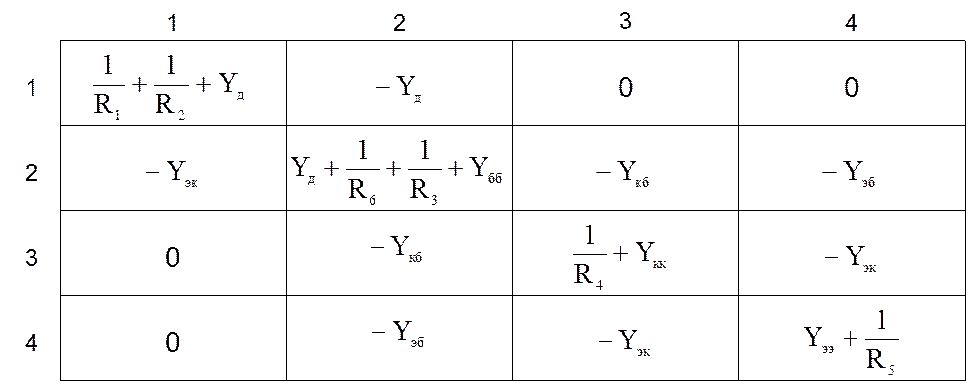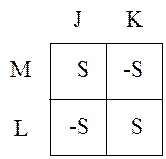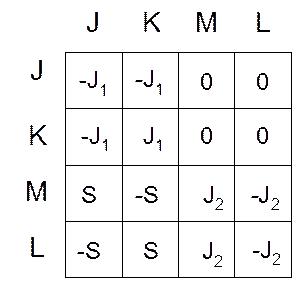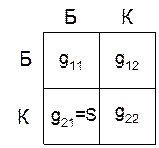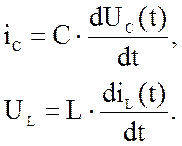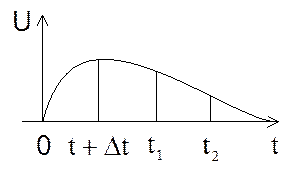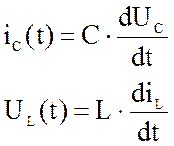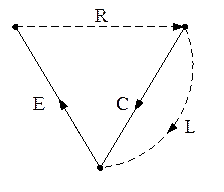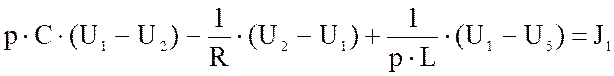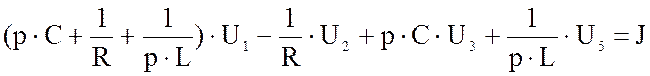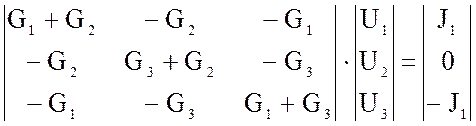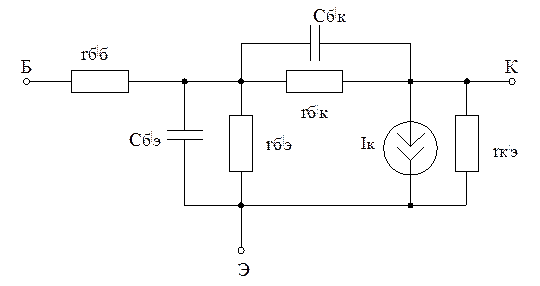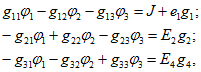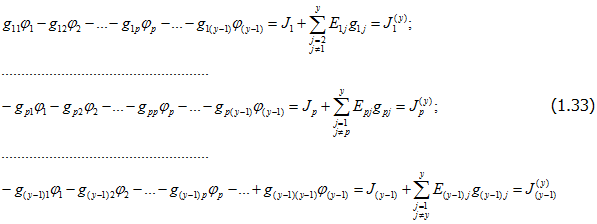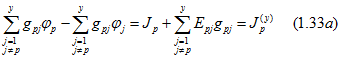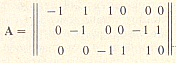Матрица узловых проводимостей как составить

Матрица коэффициентов
системы уравнений узловых напряжений
[Y] квадратная (в силу
способа ее получения) неособенная,
симметрическая,n-ого
порядка. Для схем переменного тока
матрица [Y] имеет комплексные
элементы или, что равносильно, распадается
на две вещественные матрицыY=Y’ -jY”. Для
реальных схем электрических сетей
матрица [Y] – слабозаполненная,
т.е. содержит много нулевых элементов.
Изn²ее возможных
элементов только 4nэлементов являются ненулевыми.
Действительно, принимая, что число
ветвей схемыm1,5n, получим:

– nдиагональных элементовy_ii;

– mпобочных элементовy_ij;

– mсимметричных побочных элементовy_ji.

При разработке
алгоритмов и промышленных программ
используют методы компактного хранения
этой симметрической слабозаполненной
матрицы, исключающие действия с ненулевыми
элементами. Это снижает требуемый объем
памяти ПЭВМ и повышает быстродействие
программ, что остается актуальным и до
настоящего времени, несмотря на большие
ресурсы и быстродействие современных
ПЭВМ.

Получим
матрицу узловых проводимостей для
конкретной схемы электрической сети.

2

3

II

2

1

1

4

БУ

I

М_бу

3

3

(40)

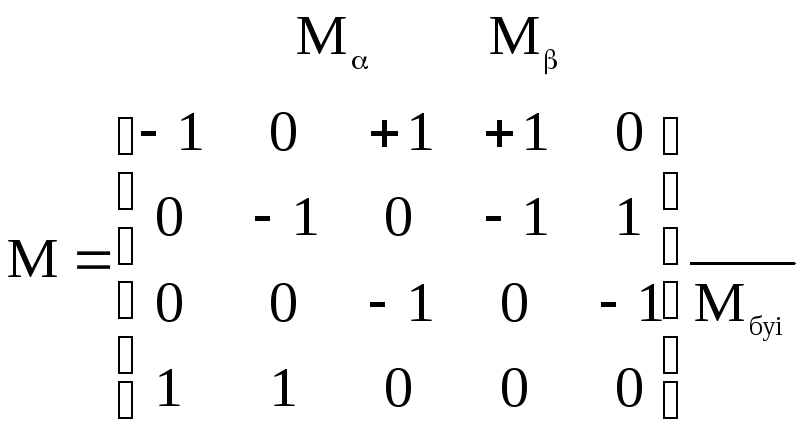
Рис. 1

(41)

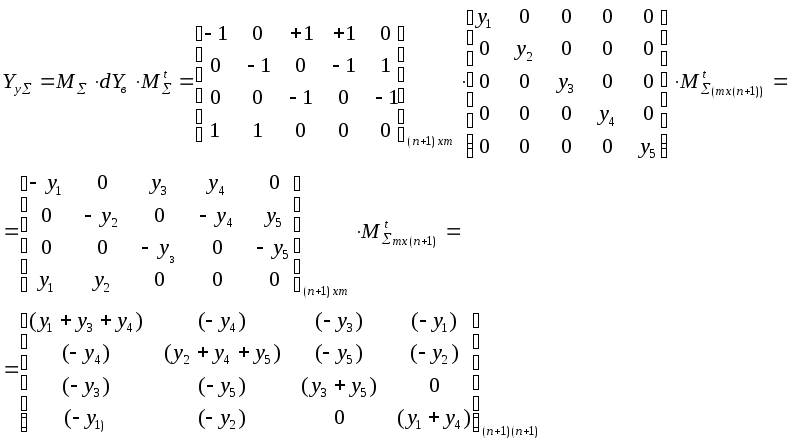
Как видим, матрица
узловых проводимостей квадратная,
симметричная. Ее диагональные элементы
y_iiпредставляют суммы побочных элементов
строки (или столбца)y_ij,
взятые с противоположным знаком, и
называютсясобственными проводимостями
узлов.Ее побочные элементыy_ijпредставляют проводимости ветвей между
узламиiиjи называютсявзаимными проводимостями
узлов; если между узламиiиjнепосредственная связь
отсутствует, тоy_ij= 0, поэтому матрица [Y] –
слабозаполненная (или разреженная).

Матрица узловых
проводимостей [Y_Σ]
для схемы электрической сети, включая
балансирующий узел, обязательно
вырожденнаяв силу способа
ее получения, и в этом легко убедиться
– сумма элементов строк или столбцовY_yравна 0. Поэтому, когда в схеме назначается
балансирующий узел, для которого не
составляется узловое уравнение, (т.е.
удаляется строка из матрицыY_y) то матрицаYобязательно
оказывается невырожденной

При удалении
строки, соответствующей балансирующему
узлу, порядок матрицы Yпонижается. Для большинства строк
матрицы имеет место

y_ii
=
y_{ij (42)}

и
только для узлов, имеющих связь с
балансирующим, имеет место соотношение

y_ii
=
y_ij
+ y_iб
> y_ij,

то
есть диагональный элемент оказывается
больше суммы побочных элементов. Это
обстоятельство имеет решающее значение
для сходимости итерационных методов
решения узловых уравнений. Здесь i,j– номера узлов,
ограничивающих ветви с проводимостямиy_ij

Можно ветви и
соответствующие им проводимости записать
с индексами ветвей в массиве ветвей.

Матрица узловых
проводимостей содержит полную информацию
о конфигурации и параметрах электрической
сети и может быть составлена непосредственно
по схеме сети, минуя процедуру перемножения
матриц.

В общем случае для
схемы переменного тока проводимости
ветвей носят комплексный характер, и
матрица Yсодержит
комплексные элементы.

Поэтому

(43)

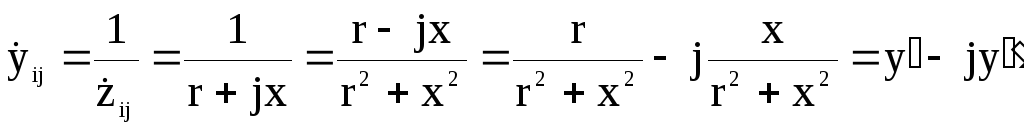
Для схемы n-ого
порядка в общем случае матрица узловых
проводимостей получится:

Вопросы
для самопроверки:

1. На основе каких
законов электротехники выводятся
узловые уравнения установившихся
режимов?

2. Что выражают
левая и правая части уравнений узловых
напряжений и система узловых уравнений
в целом?

3. Какая связь между
переменными U_
иUy?

4. Чем отличаются
системы узловых уравнений, составленные
относительно напряжений U_
иUy?

5. Как связаны
переменные U_
иU?

6. Как определяются
проводимости ветвей схемы замещения
электрической сети?

7. Как определяются
элементы матрицы узловых проводимостей?

8. Как соотносятся
знаки элементов матрицы Yy?

9. Каково соотношение
между диагональными и побочными
элементами матрицы Yy?

10. Сформулируйте
основные свойства матрицы узловых
проводимостей.

11. Задание:
Составьте матрицу узловых проводимостей
непосредственно по схеме сети, минуя
процедуру умножения по (29), опираясь на
свойства матрицы. Для этого составьте
самостоятельно схему из 4-5 узлов.

Соседние файлы в папке ШИМАНСКАЯ пособия

• #
• #
• #
• #
• #
• #
• #

2.5 Метод узловых потенциалов

За неизвестные аргументы принимаются потенциалы узлов N_УП = n − 1, т.к.
потенциал одного из узлов определён (его условно заземляют) и равен
нулю.

Исходным для обоснования метода является закон Ома.

С другой стороны, U^(В) = A^Tφ.

После обозначения Y^(У) = AY^(В)A^T, J^(У) = AJ^(В) − AY^(В)E^(В), получим
узловые уравнения:

где
Y^(У) – квадратная матрица узловых проводимостей размера (n − 1) � (n − 1);
J^(У) – столбцовая матрица узловых токов.

Пример.

n = 4
m = 6

Граф схемы

Принимаем, что φ₄ = 0.

Узловая матрица:

Матрица проводимостей ветвей:

где
g_k = 1∕R_k, k = 1,…, 6.

Матрица узловых проводимостей:

При умножении матрицы размера k � l на матрицу размером l � r
получается матрица размером k � r.

Матрица токов источников тока ветвей:

Матрица ЭДС источников ЭДС ветвей:

Матрица узловых токов:

Таким образом, узловые уравнения принимают вид:

Порядок составления матриц

1. Столбцовая матрица φ – матрица неизвестных потенциалов.
2. Матрица узловых
   проводимостей Y^(У) – квадратная. На главной диагонали записываются
   суммы проводимостей ветвей, присоединённых к соответствующему
   узлу – собственные узловые проводимости, Y _pp > 0.

   Остальные элементы матрицы Y _ij – общие узловые проводимости,
   которые равны сумме проводимостей ветвей, присоединённых между
   узлами i и j, Y _ij < 0.

   Матрица Y^(У) симметрична, т.е Y _ij = Y _ji и Y^(У) = ^T.

3. Столбцовая матрица узловых токов J^(У) состоит из элементов J_p^(У),
   равных сумме токов источников тока, присоединённых к p-му узлу,
   включая и токи источников тока, эквивалентных источникам ЭДС.

   J_p^(У) > 0, если ток направлен к узлу, в противном случае J_p^(У) < 0.

После нахождения неизвестных потенциалов по закону Ома определяются токи
ветвей

(знак «+» у слагаемых числителя используется в том случае, если направление
тока İ_i совпадает с направлением _i или Ė_k).

Частным случаем метода узловых потенциалов является метод двух узлов
для схем, имеющих лишь два узла. После заземления одного из узлов
определяется узловое напряжение:

Слагаемые E_kg_k и J_k суммируются с положительным знаком, если они
направлены к узлу 1.

С учётом данного метода можно привести следующие преобразования
схем.

1. Рассмотрим фрагмент схемы, состоящей из m параллельных ветвей.

Заземлим 2-ой узел. U = φ₁ − φ₂ = φ₁.

Уравнение по методу узловых потенциалов представляется в виде:

Вводя обозначения

получим U = E − RI.

Данному уравнению соответствует следующая схема:

Таким образом, ряд параллельных ветвей можно заменить эквивалентной
ветвью. При определении эквивалентной ЭДС, слагаемые E_kg_k и J_k суммируются
с положительным знаком, если они направлены к узлу 1.

2. Аналогичное преобразование можно осуществить для источников
тока.

Рассмотренные методы расчета электрических цепей – непосредственно по законам
Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально
рассчитать любую схему. Однако их применение без использования введенных ранее
топологических матриц рационально для относительно простых схем. Использование
матричных методов расчета позволяет формализовать процесс составления уравнений
электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно
существенно при расчете сложных разветвленных схем.

Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.

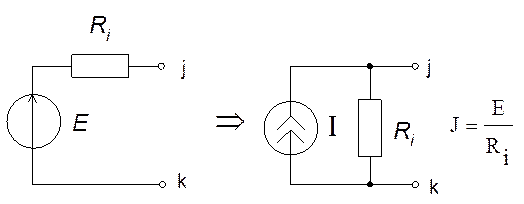
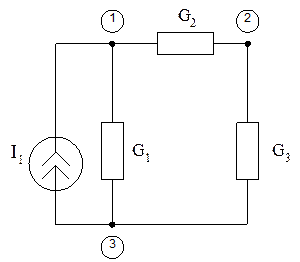
Пусть имеем схему по рис. 1, где – источник тока. В соответствии
с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы
можно записать:

.

(1)

Однако, для дальнейших выкладок будет удобнее представить ток
как сумму токов k-й
ветви и источника тока, т.е.:

.

(2)

Подставив (2) в (1), получим:

.

(3)

Формула (3) представляет собой аналитическое выражение закона Ома для участка
цепи с источниками ЭДС и тока (обобщенной ветви).

Соотношение (3) запишем для всех n ветвей схемы
в виде матричного равенства

или

,

(4)

где Z
– диагональная квадратная (размерностью n x n)
матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не
учитываем), за исключением элементов главной диагонали, равны нулю.

Соотношение (4) представляет собой матричную запись закона Ома.

Если обе части равенства (4) умножить слева на контурную матрицу В 
и учесть второй закон Кирхгофа, согласно которому

,

(5)

то

,

(6)

то есть получили новую запись в матричной форме второго закона Кирхгофа.

Метод контурных токов в матричной форме

В соответствии с введенным ранее понятием матрицы главных контуров
В, записываемой для
главных контуров, в качестве независимых переменных примем токи ветвей связи,
которые и будут равны искомым контурным токам.

Уравнения с контурными токами получаются на основании второго закона Кирхгофа;
их число равно числу независимых уравнений, составляемых для контуров, т.е.
числу ветвей связи c=n–m+1.
Выражение (6) запишем следующим образом:

.

(7)

В соответствии с методов контурных токов токи всех ветвей могут быть выражены
как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей
связи. Если элементы j–го столбца матрицы В
умножить соответствующим образом на контурные токи, то сумма таких произведений
и будет выражением тока j–й
ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано
в виде матричного соотношения

,

(8)

где – столбцовая матрица контурных
токов; – транспонированная контурная
матрица.

С учетом (8) соотношение (7) можно записать, как:

(9)

Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить

,

(10)

.

(11)

то получим матричную форму записи уравнений, составленных по методу контурных
токов:

,

(12)

где – матрица контурных сопротивлений;
– матрица контурных ЭДС.

В развернутой форме (12) можно записать, как:

,

(13)

то есть получили известный из
метода контурных токов результат.

Рассмотрим пример составления контурных уравнений.

Пусть имеем схему по рис. 2. Данная схема имеет четыре узла (m=4)
и шесть обобщенных ветвей (n=6). Число независимых контуров, равное числу ветвей связи,

c=n-m+1=6-4+1=3.

Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.

Запишем матрицу контуров, которая
будет являться матрицей главных контуров, поскольку каждая ветвь связи входит
только в один контур. Принимая за направление обхода контуров направления ветвей
связи, получим:

B

Диагональная матрица сопротивлений ветвей

Z

Матрица контурных сопротивлений

Z_k=BZB^T

.

Матрицы ЭДС и токов источников

Тогда матрица контурных ЭДС

.

Матрица контурных токов

Таким образом, окончательно получаем:

,

где ; ; ; ; ; ; ; ; .

Анализ результатов показывает, что полученные три уравнения идентичны тем,
которые можно записать непосредственно из рассмотрения схемы по известным правилам
составления уравнений по методу контурных токов.

Метод узловых потенциалов в матричной форме

На основании полученного выше соотношения (4), представляющего собой, как было
указано, матричную запись закона Ома, запишем матричное выражение:

,

(14)

где – диагональная матрица проводимостей
ветвей, все члены которой, за исключением элементов главной диагонали, равны
нулю.

Матрицы Z
и Y взаимно обратны.

Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа,
согласно которому

,

(15)

получим:

..

(16)

Выражение (16) перепишем, как:

.

(17)

Принимая потенциал узла, для которого отсутствует строка в матрице А, равным нулю, определим напряжения
на зажимах ветвей:

.

(18)

Тогда получаем матричное уравнение вида:

.

(19)

Данное уравнение представляет собой узловые уравнения в матричной форме. Если
обозначить

(20)

,

(21)

то получим матричную форму записи уравнений, составленных по методу узловых
потенциалов:

(22)

где – матрица узловых проводимостей;
– матрица узловых токов.

В развернутом виде соотношение (22) можно записать, как:

(23)

то есть получили известный из метода узловых потенциалов результат.

Рассмотрим составление узловых уравнений на примере схемы по рис. 4.

Данная схема имеет 3 узла (m=3)
и 5 ветвей (n=5). Граф схемы с выбранной ориентацией ветвей представлен
на рис. 5.

Узловая матрица (примем )

А

Диагональная матрица проводимостей ветвей:

Y

где .

Матрица узловых проводимостей

.

Матрицы токов и ЭДС источников

Следовательно, матрица узловых токов будет иметь вид:

Таким образом, окончательно получаем:

,

где ; ; ; ; .

Анализ результатов показывает, что полученные уравнения идентичны тем, которые
можно записать непосредственно из рассмотрения схемы по известным правилам составления
уравнений по методу узловых потенциалов.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
   С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические
   цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
   специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. В чем заключаются преимущества использования матричных методов
   расчета цепей?
2. Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
3. Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
4. Составить узловые уравнения для цепи на рис. 2.

Ответ:



5. Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано
   ветвями 3 и 4 (см. рис. 5).

Ответ:

руются с соответствующими элементами
вектора токов

Пример схемы. (см. 3).

 

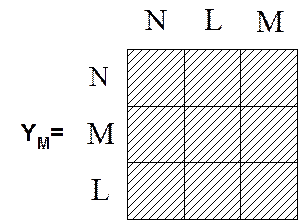
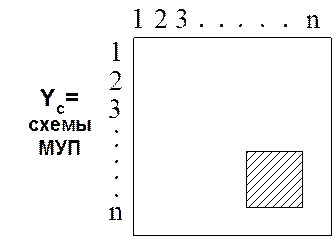
Y_M-матрица
многополюсника.

Правило формирования матрицы
узловых проводимостей и вектора источников тока.

Правило формирования матрицы
узловых проводимостей:

1. Диагональные элементы  матрицы узловых
проводимостей положительны и равны сумме проводимостей, подключенных к  j –узлу.

2. Не диагональные элементы  – отрицательны и равны сумме
проводимостей, включенных между j- иk- узлам.

Вектора источников тока.

1. Элементы  jj
– вектора токов равен сумме токов независимых источников, втекающих в j- узел.

2. Независимые источники
напряжения должны быть преобразованы в источники тока с помощью преобразования Нортока.

Все источники ЭДС необходимо
преобразовать в источники тока. В случае применения в схеме неудобных элементов
(направления идеальных источников напряжений), которые не позволяют перейти к
источникам тока необходимо ввести активное внутреннее сопротивление (исходя из
анализируемой схемы и параметров элементов).

  
Топологический метод составления уравнений по методу узловых потенциалов.

Для того чтобы разрабатывать
математическую модель схемы для ЭВМ, необходимо рассматривать алгоритмы,
которые легко формируются.

1. Все источники напряжения
преобразовать в источники тока.

В любой ветви ток равен: .

Для  цепи в целом : ,где –
диагональная матрица, где по диагонали расположены проводимости ветвей.

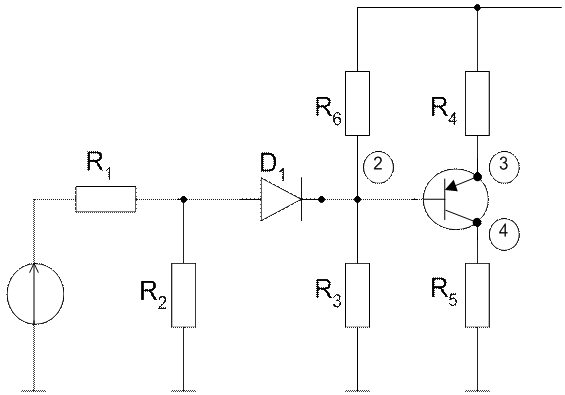
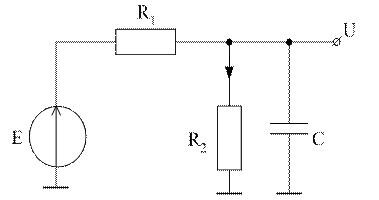
Рассмотрим схему:

 

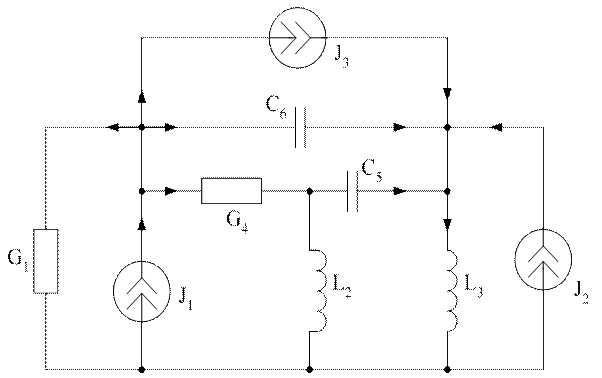Для схемы формируется структурная
матрица (матрица

инцеденций), причем источники
тока занимают в ней

последние столбцы и нумеруются
отдельно. Структур-

ная матрица разбивается на
подматрицы

 ,
где – подматрица источников тока.

Матрица проводимостей

,где
-подматрица из структурной,

                                – вектор источника тока в ветвях.

После вычисления получим матрицу
узловых проводимостей.

Вектор источников тока:

.

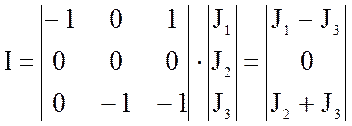
Пример:

Имеем два многополюсника – диод и
транзистор.

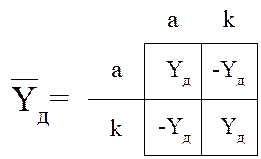
Матрица полюсных проводимостей:

                                                                       

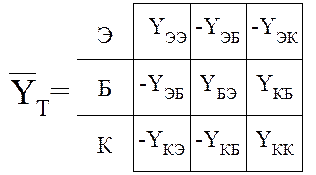
В связи с этим удобно
пользоваться библиотекой стандартных элементов.

Зависимые
источники (управляемые).

Наиболее часто используется
источник тока управляемый напряжением:

 

-крутизна

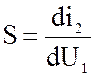
                источника.

Таблица для этого источника имеет
вид:

M, L- узел подключения управляемой ветви,

J, K- узлы подключения управляющей ветви,

причем L
и J начальные узлы, а M и K конечные узлы.

На пересечении начальных и
конечных узлов +S, если нет –S.

 В данном случае имеются в виду
идеальные источники.

Реальные  источники обладают
входной и выходной проводимостью.

С учётом этого таблица имеет вид:

 

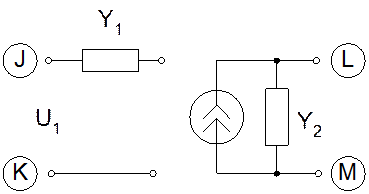Для примера рассмотрим низко
частотную модель транзистора (модель Логона).

Полярность дана для
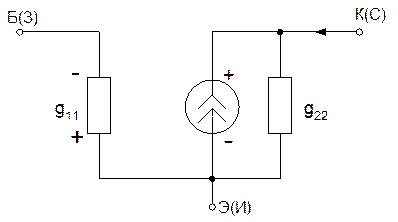
транзистора обратной проводимости.

Для схемы с общим эммитером ().

                                    
Динамический анализ цепей.

Динамический анализ цепей – это
анализ переходных процессов в схеме при некоторых воздействиях.

Отклик цепи описывается системой дифференциальных
уравнений n-порядка.

;

     

                                                     
                (1)

Из уравнения (1) можно найти U(t) в точке t.

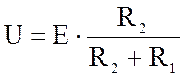
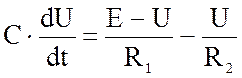
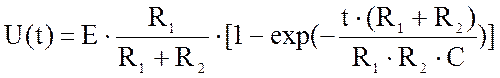
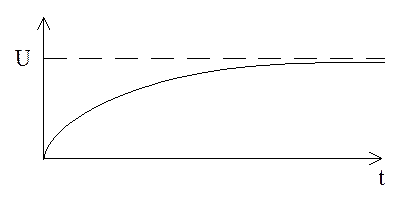
Уравнение (1) называется
аналитическим решением.

Для реальных цепей выражение
найти почти невозможно так

как: 1.схема
описывается, как правило, системой уравнений.

        2. напряжение, как
правило, имеют сложную форму воздейст-

вия.

        3.зависимости напряжений
от токов, как правило, нелинейны.

По этим причинам вместо
аналитических выражений применяются численные методы.

                                                   
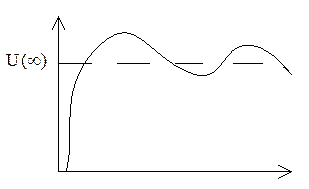
Временные характеристики.

                            1(t)=h(t)-переходная характеристика.

                             d(t)=g(t)-импульсная характеристика.

            срезает
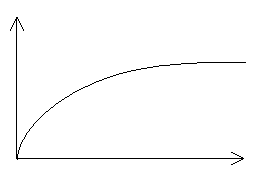
высокие частоты                                  передает высокие частоты

                         
           Явная форма математической модели схемы.

Существует две основных формы математической
модели схемы явная и неявная.

Алгоритм формирования явнойматематической модели схемы.

1. Для схемы составляется главное
дерево.

2. Составляется система уравнений
для контуров, образованных индуктивными хордами и сечений образованных
емкостными ветвями.

U_L=f₁(U),

i_C=f₂(i).                                                
(131)

3.
i_C и U_L заменяются производными :Остальные переменные в системе
выражаются через U_с(t) и
i_L(t)  c помощью
компонентных уравнений и законов Кирхгофа.

В результате получаем систему
уравнений вида:

                                                    
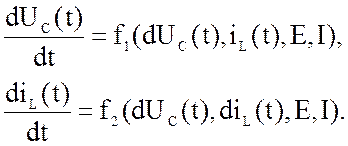
(132)

 Это система обыкновенных
дифференциальных уравнений.

Таким образом, метод переходных
состояний позволяет сформировать  систему уравнений математической модели схемы
в явном виде пригодную для математического анализа цепей.

Динамический анализ заключается в
периодическом решении уравнений (132).

1. Добавив в (132)  уравнение
токов резисторов: .

Производится статический расчет нахождения
начальных условий, и .
Подставляют эти условия в уравнения токов резисторов. Зачастую начальные
условия равны нулю.

2. Подставив эти данные в
уравнение состояний,  дав приращение для времени ∆t,
решают систему уравнений каким- либо численным методом (132)  то есть, находим  U_C(t+∆t) и  i_L(t+∆t).

3. Подставив найденные значения
вектора  X(t₁) в
уравнения токов резисторов, находим
значения вектора токов резисторов .

                               

4. Со значениями  X(t₁) и переходим к пункту 2.

Пример реализации алгоритма.

1) Строим
дерево (главное)

2) U_L = U_C

   
i_C = i_R-i_L

Формирование
математической модели схемы методом узловых потенциалов.

,где
– операторная проводимость.

,а
,где –
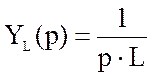
ном. частота.

Закон Кирхгофа: сумма токов,
вытекающих из узла через пассивные компоненты, равна сумме токов, вытекающих  через
независимые источники.

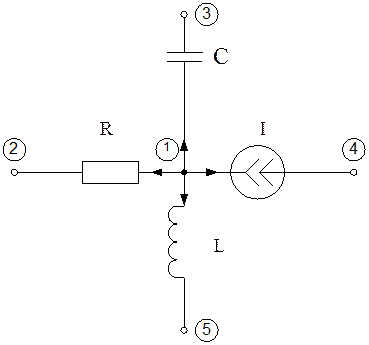
Схема:

Представим токи в ветвях через их
проводимости и узловые потенциалы, измеренные относительно нулевого узла.

 

раскрываем скобки и преобразуем:

 

раскрываем скобки и преобразуем:

Получим уравнение по методу
узловых потенциалов.

Пример

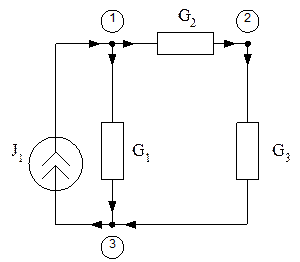
1)

2)

3)

Разрешим эти уравнения
относительно потенциалов (U).

1)      

2)    

3)  

Математическая модель схемы
сформированная по методу узловых потенциалов.

В матричной форме запишем
уравнения:

Сокращенная запись: ,где  –
матрица узловых проводимостей размером ,а 

                                                                
– это  количество узлов в
схеме,             

                                                               
– вектор узловых потенциалов,

                                                                
– вектор источников тока.

                           
Статический анализ схемы.

Находим все узловые напряжения и
токи в ветвях, в том числе при синусоидальных воздействиях. –

Система уравнений для всех узлов
и опорного () имеет
ряд свойств:

 1) Алгебраическая сумма
элементов неопределённой матрицы узловых проводимостей по
строкам                                                 

     и столбцам вектора
источников токов равны нулю.

2) Электрическая цепь с n-
узлами может быть описана системой уравнений n- порядка. Однако в неопределённой системе одно уравнение  
линейно зависимо и может быть вычеркнуто. После  вычеркивания переходим к
определённой системе уравнений. Вычеркивается то уравнение, которое соответствует
заземлённому или общему узлу. Если не определён общий узел общий узел, то общим
объявляется тот узел, к которому подключено большее  количество источников
напряжения.

Для примера:

– общий ;

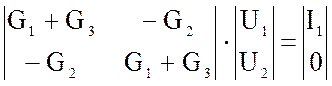
– общий ;

                             
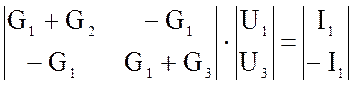
         Эквивалентная схема транзистора.

В этих уравнениях — суммы проводимостей ветвей, присоединенных соответственно к узлам 1 и 2; — сумма проводимостей ветвей, соединяющих эти узлы.
Правая часть каждого из уравнений (1.30) равна алгебраической сумме произведений ЭДС в каждой ветви на проводимость ветви, присоединенной к рассматриваемому узлу. Произведение вида Eg записывается с положительным знаком в том случае, если ЭДС направлена к узлу, для которого записывается уравнение, и с отрицательным, если ЭДС направлена от узла.
Уравнения (1.30) не зависят от выбранных положительных направлений токов в ветвях.
Чтобы подтвердить это положение, рассмотрим опять схему, показанную на рис. 1.16, и для каждого узла примем положительные направления токов от узла.
Для узлов 1 и 2 справедливы уравнения

Принимая, как и раньше, φ₃ = 0 напишем выражения для токов ветвей:
для узла 1

для узла 2

После подстановки (1.32) в (1.31) и группировки слагаемых получаются уравнения, совпадающие с (1.30).
Таким образом, можно написать уравнения для определения потенциалов узлов произвольной электрической цепи, не задаваясь положительными направлениями токов в ветвях, при этом потенциал одного из узлов надо принять равным нулю.
Если электрическая схема содержит не только источники ЭДС, но и источники тока, то в уравнения, составленные по первому закону Кирхгофа, войдут и токи источников тока. При составлении уравнений вида (1.30) токи заданных источников тока учитываются для каждого узла в виде слагаемых в правой части, причем, как было отмечено выше, с положительными знаками должны быть взяты токи источников тока, направленные к узлу, с отрицательными — от узла.
Например, для узлов 1, 2 и 3 схемы, показанной на рис. 1.17, при φ₄ = 0 получим соответственно следующие уравнения:

где

Если электрическая схема имеет в своем составе У узлов (У — любое целое число), а потенциал, например, У-го узла принят равным нулю, то для определения У — 1 потенциалов остальных узлов получается У — 1 уравнений:

или в более общей форме для любого узла р при φ_у = О

В этих уравнениях, так же как и в уравнениях (1.30), проводимость g_pp (с двумя одинаковыми индексами) представляет собой суммарную проводимость ветвей, присоединенных к узлу р, и называется собственной узловой проводимостью этого узла; проводимость g_jp = g_pj с двумя различными индексами равна сумме проводимостей ветвей, соединяющих между собой рассматриваемые узлы j и р, и называется общей узловой проводимостью этих узлов. Правая часть каждого из уравнений содержит алгебраические суммы произведений ЭДС на соответствующие проводимости для всех ветвей, присоединенных к узлу р, ток J_p равен алгебраической сумме токов всех источников тока, присоединенных к тому же узлу. В свою очередь, ток — узловой ток — равен алгебраической сумме J_p и токов, определяемых источниками ЭДС, которые присоединены к узлу р, при этом следует иметь в виду, что для замкнутых поверхностей сумма всех узловых токов, как это вытекает из первого закона Кирхгофа, равна нулю. К узловым токам можно отнести и уже известные в каких-либо ветвях токи. Проводимости таких ветвей в выражения вида g_pp и g_jp не входят.
Решив уравнения (1.33), можно определить потенциалы узлов, а зная потенциалы, найти токи во всех ветвях по закону Ома (1.12а).
Если в цепи имеются ветви с идеальными источниками ЭДС и сопротивлениями этих ветвей можно пренебречь, то при составлении уравнений (1.33) получается неопределенность, поскольку проводимости таких ветвей бесконечно большие. Такое затруднение преодолевается путем переноса заданной ЭДС из ветви с нулевым сопротивлением через соответствующий узел в другие ветви, присоединенные к тому же узлу и имеющие конечные значения сопротивлений. В результате такого преобразования токи во всех ветвях заданной схемы не изменяются.
Для иллюстрации рассмотрим схему (рис. 1.18, а), у которой сопротивление ветви 2-4 равно нулю, а ЭДС равна Е. Если в каждую ветвь, присоединенную, например, к узлу 2, включить источник напряжения с ЭДС, равной Е и направленной от узла 2 (на рис. 1.18, а эти ЭДС изображены штриховой линией), то токи во всех ветвях останутся без изменения, поскольку разности потенциалов между точками 1‘, 3′, 4’ будут, так же как и в заданной схеме, равны нулю. Теперь потенциалы узлов 2 и 4, очевидно, одинаковы и их можно объединить в одну точку (рис. 1.18,6). Для полученной схемы с тремя узлами (вместо четырех) можно составить два независимых уравнения вида (1.33), из которых определяются искомые потенциалы двух узлов, а затем по закону Ома токи во всех ветвях схемы (рис. 1.18,6), после чего легко найти ток в ветви с сопротивлением r = 0 (рис. 1.18, а) по первому закону Кирхгофа.

Рассмотренную и аналогичные ей задачи можно решить и без предварительного переноса ЭДС через узел в другие ветви. Действительно, если принять в заданной схеме (рис. 1.18, а) φ₄ = 0, то потенциал φ₂ узла 2, очевидно, будет равен Е. Для определения двух неизвестных потенциалов φ₁ и φ₃ нужно составить уравнения (1.33), которые полностью совпадут с уравнениями, составленными для тех же узлов эквивалентной схемы (рис. 1.18,6).
Полезно еще рассмотреть применение уравнений (1.33) для частного случая схемы с двумя узлами и произвольным числом ветвей, все или часть которых содержат источники ЭДС. Требуется определить напряжение между этими узлами.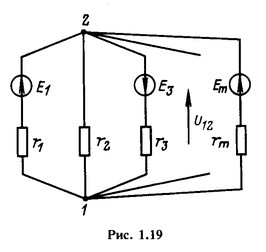
Пусть между узлами 1 и 2 включено m ветвей (рис. 1.19). Найдем напряжение U₁₂, записав уравнение (1.33) для первого узла

откуда

где числитель представляет собой алгебраическую сумму произведений ЭДС на проводимость для всех ветвей, содержащих ЭДС (с положительным знаком записываются ЭДС, направленные к узлу 1), а знаменатель — арифметическую сумму проводимостей всех ветвей, включенных между узлами.
Если между узлами 1 и 2 включены еще источники тока, то их значения следует добавить в числитель (1.34), причем со знаком плюс записываются токи, направленные к узлу 1.

Пример 1.3.
На рис. 1.20, к изображена электрическая схема с шестью неизвестными токами; ЭДС источников: Е₁ = 6 В, Е₂ = 12 В, Е₃ = 18 В; сопротивления ветвей: r₁ = r₂ = r₃ = 2 Ом и r₄ = r₅ = r₆ = 6 Ом. Пользуясь методом узловых потенциалов, определить токи во всех ветвях.
Решение.
Пусть потенциал точки 0 равен нулю. Запишем уравнения для узлов с потенциалами φ₁, φ₂ и φ₃:



или после подстановки численных значений проводимостей и ЭДС



Решив совместно эти уравнения, найдем искомые потенциалы: φ₁ = -9 В; φ₂ = 3 В; φ₃ = 6 В. Для определения токов в ветвях следует задаться их положительными направлениями. При выбранных положительных направлениях токов (рис. 1.20, а)



Матричные уравнения узловых потенциалов.
Уравнения узловых потенциалов (1.33) можно записать в матричной форме:

где

— квадратная матрица узловых проводимостей схемы;

— матрица-столбец потенциалов узлов и матрица-столбец узловых токов, причем по (1.33а) , при этом алгебраическое суммирование, выполняемое с учетом знаков, распространяется на все ветви с источниками токов и с источниками напряжений, присоединенные к i-му узлу.
Умножив слева уравнение (1.35) на получим уравнение для определения потенциалов узлов схемы в виде

где — матрица, обратная матрице .
Ниже показано, что матрицу узловых проводимостей можно составить непосредственно по соответствующей схеме цепи по формуле

где А — матрица соединений (узловых проводимостей ветвей схемы) или ее направленного графа; g — диагональная матрица проводимостей ветвей; — транспонированная матрица соединений.
Для иллюстрации применения формулы (1.39) рассмотрим схему рис. 1.20, а, для которой на рис. 1.20,6 построен направленный граф. Поскольку у заданной схемы четыре узла, то для нее можно составить три независимых уравнения, чему и соответствует матрица соединения узловых проводимостей ветвей из трех строк и шести столбцов (для узлов 1, 2, 3):

Диагональная матрица проводимостей ветвей

Произведение матриц А и g

Матрица узловых проводимостей цепи (1.39) получается после перемножения матриц Ag и :

Матрица-столбец потенциалов узлов

Матрица-столбец узловых токов

Пользуясь выражением (1.35), легко получить систему уравнений, приведенную в примере 1.3.
Если матрицу А дополнить четвертой строкой, соответствующей узлу О, то по (1.39) получится неопределенная матрица узловых проводимостей цепи, для которой сумма элементов по всем четырем строкам и четырем столбцам равна нулю; определитель такой матрицы также равен нулю. После вычеркивания любой строки и соответствующего этой строке столбца, например четвертой строки и четвертого столбца, получается определенная квадратная матрица третьего порядка.
Определитель неопределенной матрицы симметричен относительно главной диагонали. Если вычеркнутая строка не соответствует вычеркнутому столбцу, то и в этом случае получается определенная квадратная матрица, соответствующая независимой системе уравнений. Однако определитель такой матрицы уже не имеет симметрии относительно главной диагонали.
Здесь следует особо подчеркнуть, что если принять равным нулю потенциал того же узла схемы, который соответствует вычеркнутой строке матрицы А, то напряжения на всех ветвях схемы определяются через потенциалы узлов по формуле

где положительное направление напряжения U_jp совпадает с положительным направлением тока в ветви. Это непосредственно получается из формул для напряжения на каждой ветви. Например, для схемы по рис. 1.20

Из этого выражения следует

как и должно быть.