Матрицы как найти значение матричного многочлена - Сайт, где вы сможете решить свои вопросы

Определение 14. Пусть дан многочлен

и пусть

– квадратная матрица, тогда значением
многочлена

от матрицы

называется матрица

,
где

– единичная матрица,

– матрица, получающаяся при умножении
матрицы

на себя

раз.

№ 827 (П).
Найти значение многочлена

от матрицы

Р е ш е н и е.

Найдем

.

;

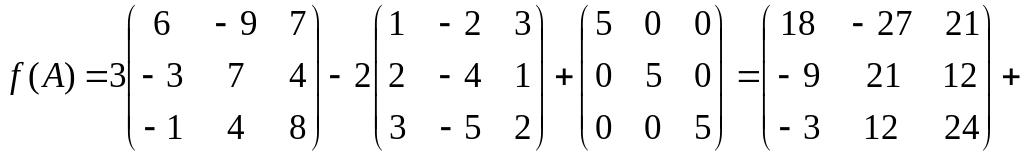
Ответ:

.

Обратная матрица

Определение 15. Матрица

называется обратной к квадратной
матрице

,
если

.

Определение 16. Квадратная матрица

называется невырожденной, если
она имеет единственную обратную матрицу

.
В противном случае

– вырожденная матрица.

Утверждение. Квадратная матрица

порядка

является невырож-денной в том и только
том случае, если определитель этой
матрицы отличен от нуля.

Для отыскания обратной матрицы
существуют два способа.

Припишем
к матрице

справа единичную матрицу и, применяя
метод Гаусса (см. §5), преобразуем
расширенную матрицу так, чтобы слева
стояла единичная матрица, тогда справа
будет находиться обратная матрица

:

Обоснование этого способа состоит в
следующем.

Пусть нам дана невырожденная квадратная
матрица. Задачу нахождения обратной
матрицы можно рассматривать как задачу
решения матричного уравнения

,
которое эквивалентно системе

уравнений с

неизвестными.

Эта система является объединением

систем уравнений, каждая из которых
содержит

неизвестных. Умножая поочередно строки
матрицы

на 1-й столбец матрицы

и приравнивая к 1-му столбцу матрицы

,
получим систему уравнений, матричная
форма записи которой имеет вид

(1.2.1)

С помощью элементарных операций над
строками матрицы систему уравнений
можно привести к виду

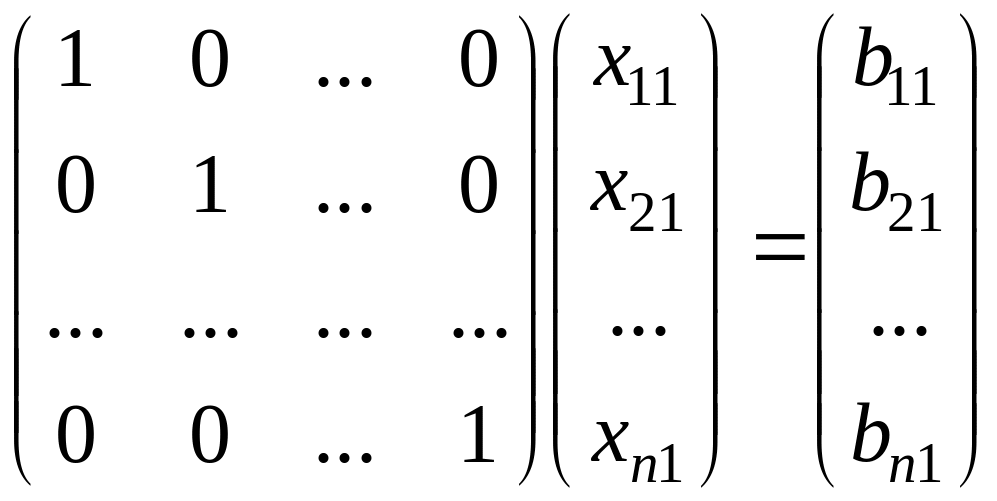
Умножая
поочередно строки матрицы

на второй столбец матрицы

и приравняв ко второму столбцу матрицы

,
получим систему уравнений

.
(1.2.2)

С помощью тех же элементарных операций,
что применялись для решения системы
(1.2.1), мы приведем систему (1.2.2) к виду

и т.д.

Поэтому
для нахождения обратной матрицы и был
предложен описанный выше способ.

,
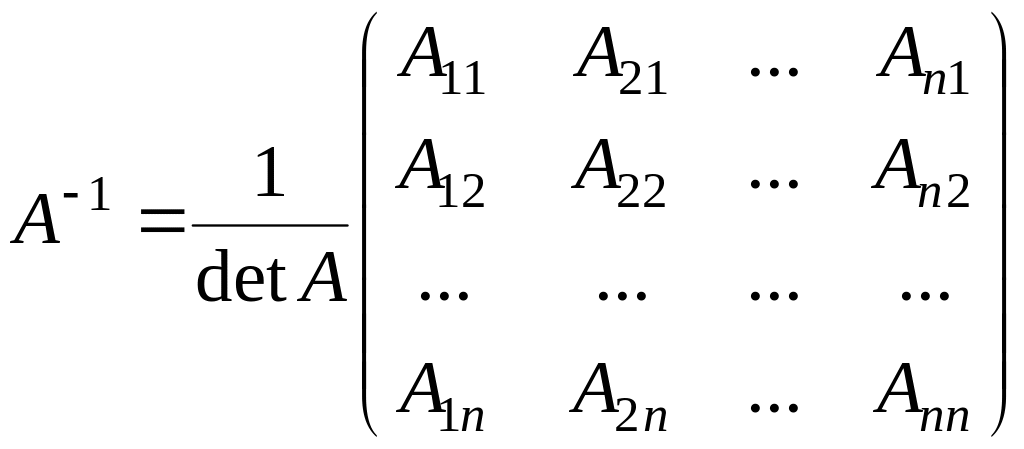
где

– алгебраические дополнения к элементу

,

– определитель матрицы

(см. §2).

№ 840 (П).
Найти обратную матрицу для матрицы

.

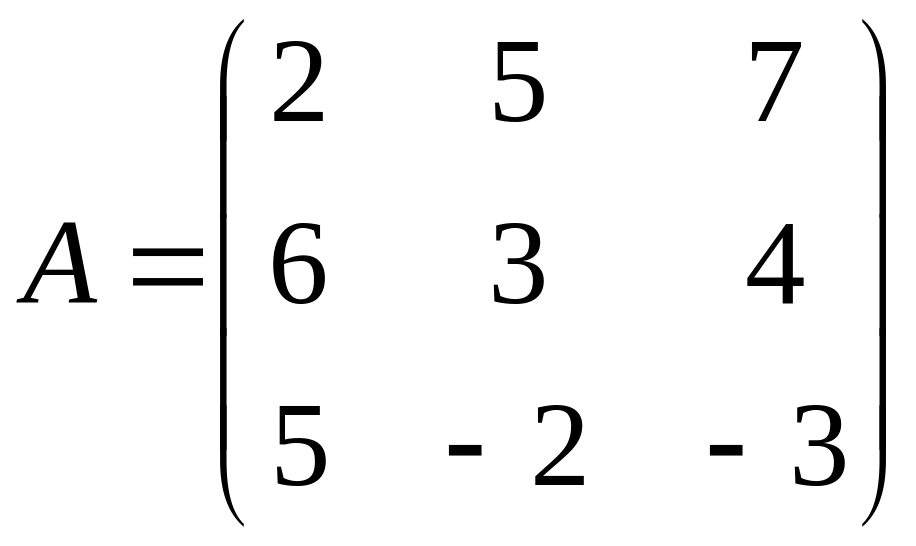
Р е ш е н и е.

I
способ.

Ответ:

.

II
способ.

;

;

;

;

Таким образом,

Ответ:

№ 861 (П).
Решить матричное уравнение

.

Р е ш е н и е.

1 вариант.

Пусть

,
тогда

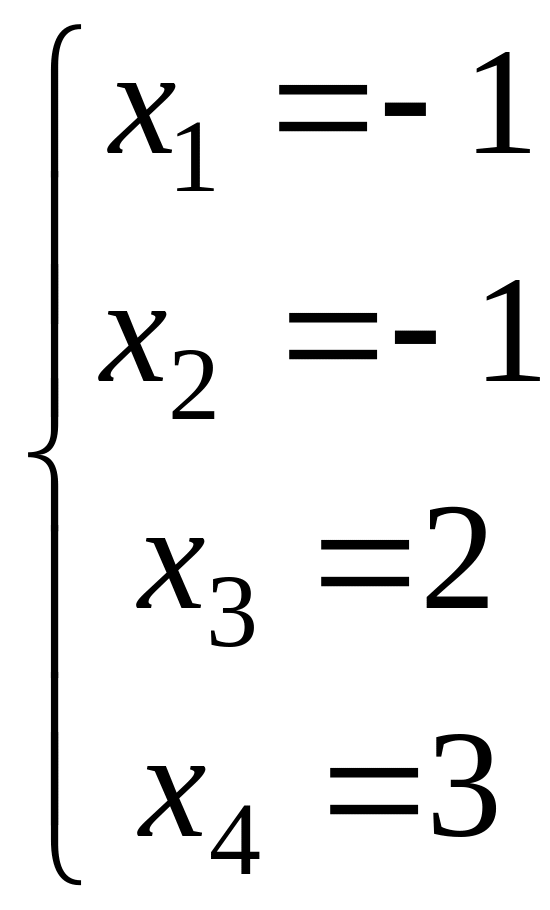
Ответ:

.

2 вариант.

Очевидно, что

.
Найдем матрицу, обратную к матрице

.

I
способ:

II
способ:

Таким образом,

Ответ:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Многочлены от матриц

Напомним определение многочлена от матрицы. Пусть заданы многочлен (степени ) переменной lambda:

$f(lambda)=a_mcdot lambda^m+a_{m-1}cdot lambda^{m-1}+ldots+a_1cdot lambda+a_0,$

(7.40)

где — квадратная матрица n-го порядка. Выражение вида

$f(A)=a_mcdot A^m+a_{m-1}cdot A^{m-1}+ldots+a_1cdot A+a_0cdot E,$

(7.41)

называется многочленом от матрицы .

При больших значениях и вычисление выражения (7.41) затруднительно из-за операции возведения матрицы в натуральную степень. Поэтому требуется найти другие, эквивалентные определению (7.41), формы записи и алгоритмы эффективного вычисления многочлена от матрицы. Для упрощения (7.41) имеются две возможности. Во-первых, можно упростить матрицу так, чтобы многочлен (7.40) от упрощенной матрицы уже вычислялся сравнительно просто. Например, выражение (7.41) легко вычисляется, если матрица диагональная. Во-вторых, можно понизить степень многочлена, тогда самая трудоемкая операция — возведение матрицы в степень — упрощается.

Использование жордановой формы для нахождения многочлена от матрицы

Использование жордановой формы матрицы для нахождения многочлена от матрицы основано на трех свойствах.

1. Многочлены от подобных матриц подобны.

Действительно, пусть при помощи преобразования подобия матрица приведена к жордановой форме $J_A=S^{-1}AS$ . Подставим $A=SJ_AS^{-1}$ в правую часть (7.41):

$f(A)=a_mcdot(SJ_AS^{-1})^m+ a_{m-1}cdot(SJ_AS^{-1})^{m-1}+ldots+ a_1cdot(SJ_AS^{-1})+a_0cdot E$

Учитывая, что $(SJ_AS^{-1})^k= underbrace{SJ_AS^{-1}cdot SJ_AS^{-1} cdotldotscdot SJ_AS^{-1}}_{k}= SJ_A^kS^{-1}$ для любого натурального , получаем

$f(A)=ScdotBigl(a_mJ_A^m+a_{m-1}J_A^{m-1}+ldots+a_1J_A+a_0EBigr)cdot S^{-1}=Scdot f(J_A)cdot S^{-1}.$

Таким образом, многочлены f(A) и f(J_A) подобны (с той же самой преобразующей матрицей ):

$A=Scdot J_Acdot S^{-1}qquad Rightarrowqquad f(A)=Scdot f(J_A)cdot S^{-1}.$

2. Многочлен от блочно-диагоналъной матрицы является блочно-диагоналъной матрицей.

Пусть $A=begin{pmatrix}A_1!!&vline!!&O\hline O!!&vline!!&A_2end{pmatrix}$ , где A_1 и A_2 — квадратные матрицы, а — нулевые матрицы соответствующих размеров. Для блочно-диагональных матриц справедливы равенства (они следуют из операций над блочными матрицами):

$A^k=begin{pmatrix} A_1!!&vline!!&O\hline O!!&vline!!&A_2end{pmatrix}^k= begin{pmatrix} A_1^k!!&vline!!&O\hline O!!&vline!!&A_2^kend{pmatrix}!,quad a_kcdot A_k=begin{pmatrix} a_kA_1!!&vline!!&O\hline O!!&vline!!&a_kA_2end{pmatrix}!,$ где kinmathbb{N}

Поэтому $f(A)=begin{pmatrix} f(A_1)!!&vline!!&O\hline O!!&vline!!& f(A_2) end{pmatrix}$ .Для большего числа блоков доказательство V. о 1Аг)) аналогичное.

3. Многочлен (7.41) от жордановой клетки J_r(lambda_0) имеет вид

$f(J_r(lambda_0))= begin{pmatrix}f(lambda_0)& dfrac{1}{1!}f'(lambda_0)& cdots& dfrac{1}{(r-1)!}f^{(r-1)}(lambda_0)\[8pt] 0&f(lambda_0)& cdots& dfrac{1}{(r-2)!}f^{(r-2)}(lambda_0)\ vdots&vdots&ddots&vdots\ 0&0&cdots&f(lambda_0) end{pmatrix}!.$

(7.42)

Это верхняя треугольная матрица r-го порядка, на главной диагонали которой стоят значения функции f(lambda) в точке lambda_0 , над диагональю — значения первой производной в этой же точке и т.д., т.е. коэффициенты ряда Тейлора для функции .

Действительно, разложим многочлен (7.40) по формуле Тейлора в окрестности точки lambda=lambda_0:

$f(lambda)= f(lambda_0)+ frac{1}{1!},f'(lambda_0)(lambda-lambda_0)+ frac{1}{2!}, f''(lambda_0)(lambda-lambda_0)^2+ldots+ frac{1}{m!},f^{(m)} (lambda_0)(lambda-lambda_0)^m.$

Остаточный член в данном случае равен нулю, так как все производные более высокого порядка, чем , тождественно равны нулю. При вычислении f(J_r(lambda_0)) линейный двучлен (lambda-lambda_0) заменяется матрицей

$I=Bigl(J_r(lambda_0)-lambda_0EBigr)= begin{pmatrix}lambda_0&1&cdots&0&0\ 0&lambda_0&ddots&0&0\ vdots&vdots&ddots&ddots&vdots\ 0&0&cdots&lambda_0&1\ 0& 0&cdots&0&lambda_0end{pmatrix}- begin{pmatrix}lambda_0&0&cdots&0&0\ 0&lambda_0 &ddots&0&0\ vdots&vdots&ddots&ddots&vdots\ 0&0&cdots&lambda_0&0\ 0&0&cdots& 0&lambda_0end{pmatrix}= begin{pmatrix}0&1&cdots&0&0\ 0&0&ddots&0&0\ vdots&vdots& ddots&ddots&vdots\ 0&0&cdots&0&1\ 0&0&cdots&0&0 end{pmatrix}!,$

у которой элементы над главной диагональю равны единице, а остальные элементы равны нулю, т.е. $I=begin{pmatrix}0&e_1&e_2&cdots&e_{r-1}end{pmatrix}$ , где e_i — i-й столбец единичной матрицы r-го порядка.

Можно показать, что при возведении в степень единичные элементы матрицы смещаются вверх:

$I^2=begin{pmatrix}0&0&e_1&e_2&cdots&e_{r-2}end{pmatrix},quad I^3=begin{pmatrix}0&0&0&e_1&cdots&e_{r-3}end{pmatrix}$ и т.д.

причем I^k — нулевая матрица при kgeqslant r . Подставляя эти матрицы в формулу Тейлора, получаем

$f(A)= f(lambda_0)cdot E+frac{1}{1!},f'(lambda_0)cdot I+ frac{1}{2!}, f''(lambda_0)cdot I^2+ frac{1}{m!},f'^{(m)}(lambda_0)cdot I^m,$

Складывая матрицы в правой части, получаем квадратную матрицу r-го порядка, у которой элементы главной диагонали равны f(lambda_0) , элементы над главной диагональю равны — $frac{1}{1!},f'(lambda_0)$ и т.д., т.е. матрицу вида (7.42).

Пример 7.16. Найти многочлен f(lambda)= lambda^2+ lambda+1 от матриц

$A=begin{pmatrix}2&1&0\0&2&1\0&0&2end{pmatrix}!,qquad B=begin{pmatrix} 2&1&0\ 0&2&0\ 0&0&2 end{pmatrix}!,qquad C=begin{pmatrix}2&1&0\ 0&2&0\ 0&0&3 end{pmatrix}!.$

Решение. а) Матрица – это жорданова клетка 3-го порядка, соответствующая собственному значению 2: A=J_3(2) . Находим значения функции и ее производных в точке lambda=2: f(2)=7, f'(2)=5, f''(2)=2 . Составляем матрицу вида (7.42), учитывая, что r=3:

$f(A)=f(J_3(2))= begin{pmatrix}f(2)&dfrac{1}{1!},f'(2)&dfrac{1}{2!},f''(2)\[8pt] 0&f(2)&dfrac{1}{1!},f'(2)\[4pt] 0&0&f(2) end{pmatrix}= begin{pmatrix}7&5&1\ 0&7&5\ 0&0&7 end{pmatrix}!.$

Матрица имеет жорданову форму $B=operatorname{diag} (J_2(2),,J_1(2))$ , т.е. является блочно-диагональной. По свойству 2 многочлен от матрицы является блочно-диагональной матрицей. Записываем многочлен f(lambda) от каждой жордановой клетки по формуле (7.42):

$f(J_2(2))=begin{pmatrix}7&5\0&7end{pmatrix}!,qquad f(J_1(2))=f(2)=7.$

Здесь число 7 рассматривается как квадратная матрица 1-го порядка. Составляем из этих квадратных матриц искомую блочно-диагональную матрицу

$f(B)= operatorname{diag}!left(begin{pmatrix}7&5\0&7end{pmatrix}!,,(7)right)= begin{pmatrix} 7&5!!&vline!!&0\ 0&7!!&vline!!&0\hline 0&0!!&vline!!&7 end{pmatrix}!.$

Матрица имеет жорданову форму $C=operatorname{diag} (J_2(2),J_1(3))$ , т.е. является блочно-диагональной. Записываем многочлен f(lambda) от каждой жордановой клетки по формуле (7.42):

$f(J_2(2))=begin{pmatrix}7&5\0&7end{pmatrix}!,qquad f(J_1(3))=f(3)=13.$

Составляем из этих квадратных матриц искомую блочно-диагональную матрицу

$f(C)= operatorname{diag}!left(begin{pmatrix}7&5\0&7end{pmatrix}!,,(13)right)= begin{pmatrix} 7&5!!&vline!!&0\ 0&7!!&vline!!&0\hline 0&0!!&vline!!&13 end{pmatrix}!.$

Первый способ нахождения многочлена от матрицы

1. Привести матрицу к жордановой форме $J_A=S^{-1}AS$ , т.е. определить жорданову форму J_A и преобразующую матрицу .

2. Составить блочно-диагональную матрицу f(J_A) , размещая на ее диагонали многочлены от жордановых клеток (7.42).

3. Найти многочлен от матрицы А по формуле $f(A)=Scdot f(J_A)cdot S^{-1}$ .

Пример 7.17. Найти многочлен f(lambda)=lambda^m (при m>1 ) от матриц:

$A=begin{pmatrix} 4&4\-1&0 end{pmatrix}!;quad B=begin{pmatrix} 1&0&1\ 0&1&-1\ -1&-1&1 end{pmatrix}!;quad C=begin{pmatrix} 1&1&1\ 1&1&1\ 1&1&1 end{pmatrix}!;quad D=begin{pmatrix} -2&5&-3\ -2&5&-3\ 1&-1&0end{pmatrix}!.$

Решение. Матрица . 1. Жорданова форма J_A и преобразующая матрица были найдены в примере 7.15:

$J_A=begin{pmatrix}2&1\0&2end{pmatrix}!,qquad S=begin{pmatrix}2&1\-1&0 end{pmatrix}!,qquad S^{-1}=begin{pmatrix}0&-1\1&2 end{pmatrix}!.$

2. Жорданова форма J_A состоит из одной жордановой клетки J_A=J_2(2) 2-го порядка, соответствующей собственному значению lambda=2 . Найдем значения функции f(lambda)=lambda^m и ее производной $f'(lambda)=m lambda^{m-1}$ при lambda=2: f(2)=2^m, $f'(2)=m2^{m-1}$ . Запишем многочлен от жордановой формы (блочно-диагональную матрицу с одним блоком): $f(J_A)= begin{pmatrix} 2^m&m2^{m-1}\ 0&2^mend{pmatrix}$ .

3. Найдем многочлен от матрицы

$begin{aligned}f(A)&= begin{pmatrix}2&1\-1&0end{pmatrix}!cdot! begin{pmatrix} 2^m&m2^{m-1}\ 0&2^m end{pmatrix}!cdot! begin{pmatrix}0&-1\1&2end{pmatrix}= begin{pmatrix} 2&1\-1&0 end{pmatrix}!cdot! begin{pmatrix}m2^{m-1}&(m-1)2^{m}\ 2^m&2^{m+1} end{pmatrix}=\[2pt] &= begin{pmatrix}(m+1)2^m&m2^{m+1}\ -m2^{m-1}&-(m-1)2^{m} end{pmatrix}!.end{aligned}$

Матрица В. 1. Жорданова форма J_B и преобразующая матрица были найдены в примере 7.15:

$J_B=begin{pmatrix}1&1&0\ 0&1&1\ 0&0&1end{pmatrix}!,qquad S=begin{pmatrix}-1&0&1\ 1&0&0\ 0&-1&0end{pmatrix}!,qquad S^{-1}= begin{pmatrix}0&1&1\ 0&0&-1\ 1&1&0 end{pmatrix}!.$

2. Жорданова форма J_B состоит из одной жордановой клетки J_B=J_3(1) 3-го порядка, соответствующей собственному значению lambda=1 . Найдем значения функции f(lambda) и ее производных f'(lambda),,f''(lambda) при lambda=1: f(1)=1, f'(1)=m, f''(1)=m(m-1) . Запишем многочлен от жордановой формы (r=3)colon

$f(J_B)= begin{pmatrix} 1&m&frac{m}{2}(m-1)\ 0&1&m\ 0&0&1 end{pmatrix}!.$

3. Найдем многочлен от матрицы

$f(b)= begin{pmatrix}-1&0&1\ 1&0&0\ 0&-1&0end{pmatrix}!cdot! begin{pmatrix} 1&m&frac{m}{2}(m-1)\ 0&1&m\ 0&0&1end{pmatrix}!cdot! begin{pmatrix} 0&1&0\ 0&0&-1\ 1&1&0 end{pmatrix}= begin{pmatrix} 1-dfrac{m}{2}(m-1)&-dfrac{m}{2}(m-1)&m\[9pt] dfrac{m}{2}(m-1)& 1+dfrac{m}{2}(m-1)&-m\[4pt] -m&-m&1 end{pmatrix}!.$

Матрица . 1. Жорданова форма J_C и преобразующая матрица были найдены в примере 7.15:

$J_C=begin{pmatrix}0&0&0\0&0&0\0&0&3end{pmatrix}!,qquad S=begin{pmatrix} 1&0&-1\ 1&1&-1\ -2&-1&-1 end{pmatrix}!,qquad S^{-1}=begin{pmatrix} 2/3&-1/3&-1/3\ -1&1&0\ -1/3&-1/3&-1/3end{pmatrix}!.$

2. Жорданова форма J_C состоит из трех жордановых клеток 1-го порядка $J_C= operatorname{diag}(J_1(0),,J_1(0),,J_1(3))$ , соответствующих собственным значениям lambda=0 и lambda=3 . Найдем значения функции f(lambda)=lambda^m при и lambda=3: f(0)=0, f(3)=3^m . Запишем многочлен от жордановой формы:

$f(J_C)= operatorname{diag}Bigl(f(J_1(0)),,f(J_1(0)),,f(J_1(3))Bigr)= begin{pmatrix}0&0&0\ 0&0&0\ 0&0&3^m end{pmatrix}!.$

3. Найдем многочлен от матрицы

$begin{aligned}f(C)&= begin{pmatrix} 1&0&-1\ 1&1&-1\ -2&-1&-1end{pmatrix}!cdot! begin{pmatrix} 0&0&0\ 0&0&0\ 0&0&3^m end{pmatrix}!cdot! begin{pmatrix} 2/3&-1/3&-1/3\ -1&1&0\ -1/3&-1/3&-1/3end{pmatrix}=\[2pt] &=begin{pmatrix} 3^{m-1}&3^{m-1}&3^{m-1}\3^{m-1}&3^{m-1}&3^{m-1}\3^{m-1}&3^{m-1}&3^{m-1}end{pmatrix}= 3^{m-1}cdot! begin{pmatrix}1&1&1\ 1&1&1\ 1&1&1 end{pmatrix}!.end{aligned}$

Результат совпадает с найденным в примерах 7.10, 7.12.

Матрица . 1. Жорданова форма J_D и преобразующая матрица были найдены в примере 7.15:

$J_D=begin{pmatrix}0&1&0\0&0&0\0&0&3end{pmatrix}!;qquad S= frac{1}{9}!begin{pmatrix} 3&5&9\3&2&9\3&-1&0end{pmatrix}!;qquad S^{-1}=begin{pmatrix} 1&-1&3\3&-3&0\ -1&2&-1end{pmatrix}!.$

2. Жорданова форма J_D состоит из двух жордановых клеток 2-го и 1-го порядков $J_D=operatorname{diag}(J_2(0),,J_1(3))$ . соответствующих собственным значениям lambda=0 и lambda=3 . Найдем значения функции f(0)=0, f(3)=3^m и производной f'(0)=0 (так как m>1 ). Запишем многочлен от жордановой формы

$f(J_D)= operatorname{diag}Bigl(f(J_2(0)),,f(J_1(3))Bigr)= begin{pmatrix}0&0&0\ 0&0&0\ 0&0&3^m end{pmatrix}!.$

3. Найдем многочлен от матрицы

$f(D)= frac{1}{9}!begin{pmatrix} 3&5&9\3&2&9\ 3&-1&0 end{pmatrix}!cdot! begin{pmatrix} 0&0&0\ 0&0&0\ 0&0&3^m end{pmatrix}! cdot! begin{pmatrix} 1&-1&3\ 3&-3&0\ -1&2&-1 end{pmatrix}= 3^m! begin{pmatrix}-1&2&-1\ -1&2&-1\ 0&0&0 end{pmatrix}!.$

Использование аннулирующих многочленов

Для понижения степени многочлена (7.41) можно использовать аннулирующие многочлены матрицы , например, ее характеристический Delta_A(lambda)=det(A-lambda E) или минимальный mu_A(lambda) многочлены.

Обозначим через степень минимального многочлена

$mu_A(lambda)= (lambda-lambda_1)^{m_1}cdot (lambda-lambda_2)^{m_2}cdot ldotscdot (lambda-lambda_k)^{m_k}.$

Заметим, что не превосходит порядка матрицы (или, что то же самое, степени характеристического многочлена Delta_A(lambda) ), т.е. nu=m_1+ldots+m_kleqslant n . Разделим заданный многочлен (7.40) на минимальный:

f(lambda)= q(lambda)cdot mu_A(lambda)+r(lambda).

(7.43)

Здесь q(lambda) — частное, а r(lambda) — остаток, степень которого меньше nu:

$r(lambda)= r_{nu-1}cdot lambda^{nu-1}+ r_{nu-2}cdot lambda^{nu-2}+ldots+ r_1cdot lambda+r_0.$

(7.44)

Подставив в (7.43) вместо переменной lambda матрицу , получим:

f(A)=r(A).

(7.45)

поскольку минимальный многочлен является аннулирующим (mu_A(lambda)=O) .

Таким образом, вместо вычисления многочлена (7.41) степени можно вычислить многочлен (7.44), степень которого меньше . Коэффициенты $r_0,r_1,ldots,r_{nu-1}$ многочлена (7.44) находятся следующим образом.

Если все корни минимального многочлена простые, то, подставляя корень lambda_j в (7.43), получаем f(lambda_j)=r(lambda_j) , так как mu_A(lambda_j)=0 , т.е.

$f(lambda_j)= r_{nu-1}lambda_j^{nu-1}+ r_{nu-2} lambda_j^{nu-2}+ldots+ r_1 lambda_j+r_0,quad j=1,2,ldots,nu.$

Если lambda_j — корень минимального многочлена кратности m_j , учитывая, что

$mu_A(lambda_j)=0,quad mu'_A(lambda_j)=0,quad ldots,quad mu_{A}^{(m_j-1)}(lambda_j)=0$

из (7.43), последовательно дифференцируя, получаем

$f(lambda_j)=r(lambda_j),quad left.{left(dfrac{d^i}{d lambda^i} f(lambda)right)}!right|_{lambda=lambda_j}= left.{left(dfrac{d^i}{d lambda^i} r(lambda)right)}!right|_{lambda=lambda_j},quad i=1,2,ldots,m_j-1.$

(7.46)

Записывая равенства (7.46) для каждого корня минимального многочлена, получим совместную систему линейных уравнений с неизвестными $r_0,r_1,ldots,r_{nu-1}$ .

Второй способ нахождения многочлена от матрицы

1. Найти минимальный многочлен mu_A(lambda) матрицы одним из способов, рассмотренных в разд.7.2.4. Определить его степень и записать многочлен (7.44) с неопределенными коэффициентами $r_0,r_1,ldots,r_{nu-1}:$

$r(lambda)= r_{nu-1}cdot lambda^{nu-1}+ r_{nu-2}cdot lambda^{nu-2}+ldots+ r_1cdot lambda+r_0.$

2. Для каждого корня lambda_j (кратности m_j ) минимального многочлена по формулам (7.46) составить m_j уравнений. Все уравнения объединить в одну систему.

3. Решить составленную систему, т.е. найти коэффициенты $r_0,r_1,ldots,r_{nu-1}$ многочлена r(lambda) .

4. По формуле (7.45) найти многочлен от матрицы:

$f(A)=r(A)= r_{nu-1}cdot A^{nu-1}+ r_{nu-2}cdot A^{nu-2}+ldots+r_1cdot A+r_0cdot E.$

Замечания 7.8.

1. Вместо минимального многочлена можно использовать характеристический многочлен матрицы, который также является аннулирующим (см. теорему Гамильтона-Кэли). При этом в пунктах 1,2 алгоритма минимальный многочлен заменяется характеристическим, степень которого равна .

2. В первом способе нахождения многочлена от матрицы используются все инвариантные множители, так как нужно получить жорданову форму. Во втором способе требуется только один последний инвариантный множитель, который совпадает с минимальным многочленом. Можно сказать, что жорданова форма матрицы излишне информативна для решения поставленной задачи.

Пример 7.18. Найти (вторым способом) многочлен f(lambda)= lambda^m (при m>1 ) от матриц:

$A=begin{pmatrix}4&4\-1&0end{pmatrix}!;quad B=begin{pmatrix}1&0&1\ 0&1&-1\ -1&-1&1 end{pmatrix}!;quad C=begin{pmatrix}1&1&1\ 1&1&1\ 1&1&1 end{pmatrix}!;quad D=begin{pmatrix}-2&5&-3\ -2&5&-3\ 1&-1&0 end{pmatrix}!.$

Решение. Матрица . 1. Для матрицы в примере 7.15 были найдены инвариантные множители. Минимальный многочлен совпадает с последним инвариантным множителем. Поэтому mu_A(lambda)=e_2(lambda)=(lambda-2)^2 . Степень минимального многочлена равна двум. Значит, многочлен (7.44) линейный: r(lambda)=r_1 lambda+r_0 .

2. Для двойного корня lambda=lambda_1=2~(m_1=2) составляем уравнения (7.46):

$begin{cases}f(2)=r(2),\ left.{dfrac{df(lambda )}{d lambda}}right|_{lambda=2}= left.{dfrac{dr(lambda )}{d lambda}}right|_{lambda=2},end{cases}Rightarrowquad begin{cases}2^m=r_1cdot2+r_0,\mcdot2^{m-1}=r_1.end{cases}$

3. Решая систему, получаем $r_1=m2^{m-1},~r_0=(1-m)2^m$ и $r(lambda)=m2^{m-1}cdot lambda+(1-m)2^m$ .

4. Находим многочлен от матрицы

$f(A)=r(A)= m2^{m-1}cdot! begin{pmatrix}4&4\-1&0end{pmatrix}+()2^mcdot! begin{pmatrix}1&0\0&1end{pmatrix}= begin{pmatrix}(m+1)2^m&m2^{m+1}\ -m2^{m-1}& -(m-1)2^mend{pmatrix}!.$

Матрица . 1. Инвариантные множители характеристической матрицы (B-lambda E) найдены в примере 7.15. Минимальный многочлен равен последнему инвариантному множителю: mu_B(lambda)=e_3(lambda)=(lambda-1)^3 . Степень минимального многочлена равна 3. Значит, многочлен (7.44) — это квадратный трехчлен: r(lambda)=r_2 lambda^2+r_1 lambda+r_0 .

2. Для тройного корня lambda=lambda_1=1~(m_1=3) составляем уравнения (7.46):

$begin{cases} f(1)=r(1),\[4pt] left.{dfrac{df(lambda )}{d lambda}}right|_{lambda=1}= left.{dfrac{dr(lambda )}{d lambda}}right|_{lambda=1},\[8pt] left.{dfrac{d^2f(lambda )}{d lambda^2}}right|_{lambda=1}= left.{dfrac{d^2r(lambda )}{d lambda^2}}right|_{lambda=1}, end{cases}Rightarrowquad begin{cases}1^m=r_2cdot1^2+r_1cdot1+r_0,\ mcdot1^{m-1}=2r_2cdot1+r_1,\ m(m-1)cdot1^{m-2}=2r_2. end{cases}$

3. Решая систему, получаем $r_2=frac{m(m-1)}{2},~~r_1=m(2-m),~~r_0=frac{(m-1)(m-2)}{2}$ и

$r(lambda)=frac{m(m-1)}{2}cdot lambda^2+ m(m-1)cdot lambda+frac{(m-1)(m-2)}{2}.$

4. Вычисляя $B^2=begin{pmatrix}0&-1&2\ 1&2&-2\ -2&-2&1 end{pmatrix}$ , записываем искомый многочлен:

$begin{aligned} f(B)=r(B)&= frac{m(m-1)}{2}cdot! begin{pmatrix}0&-1&2\ 1&2&-2\ -2&-2&1end{pmatrix}+ m(2-m)cdot! begin{pmatrix}1&0&1\ 0&1&-1\ -1&-1&1 end{pmatrix}+ frac{(m-1)(m-2)}{2}cdot! begin{pmatrix}1&0&0\ 0&1&0\ 0&0&1end{pmatrix}=\[2pt] &= begin{pmatrix}1- dfrac{m(m-1)}{2}&-dfrac{m(m-1)}{2}&m\[9pt] dfrac{m(m-1)}{2}& 1+dfrac{m(m-1)}{2}&-m\[4pt] -m&-m&1 end{pmatrix}!.end{aligned}$

Матрица . 1. Минимальный многочлен найден в примере7.15: mu_C(lambda)=lambda(lambda-3) . Степень многочлена равна 2. Следовательно, многочлен (7.44) имеет первую степень: r(lambda)=r_1 lambda+r_0 .

2. Для каждого простого корня lambda=lambda_0=0 и lambda= lambda_2=3 записываем пер вое равенство из (7.46):

$begin{cases}f(0)=r(0),\ f(3)=r(3),end{cases},Rightarrowquad begin{cases} 0^m=r_1cdot0+r_0,\ 3^m=r_1cdot3+r_0.end{cases}$

3. Решая систему, получаем $r_1=3^{m-1},~r_0=0$ и $r(lambda)=3^{m-1}lambda$ .

4. Находим многочлен от матрицы

$f(C)=r(C)=3^{m-1}C= 3^{m-1}cdot! begin{pmatrix}1&1&1\ 1&1&1\ 1&1&1 end{pmatrix}!.$

Найдем f(C) , используя характеристический многочлен вместо минимального. Согласно пункту 1 замечаний 7.8, выполняем все действия второго способа, заменяя минимальный многочлен характеристическим.

1. Найдем характеристический многочлен матрицы (см. при мер 7.11): Delta_C(lambda)=lambda^2(3-lambda) . Это многочлен 3-й степени. Поэтому многочлен (7.44) будет 2-ой степени: r(lambda)=r_2 lambda^2+r_1 lambda+r_0 .

2. Для двойного корня lambda=0 записываем два уравнения из (7.46), а для простого корня lambda=3 одно:

$begin{cases} f(0)=r(0),\ left.{dfrac{df(lambda)}{d lambda}}right|_{lambda=0}= left.{dfrac{dr(lambda)}{d lambda}} right|_{lambda=0},\ f(3)=r(3), end{cases},Rightarrowquad begin{cases} 0^m=r_2cdot 0^2+r_1cdot0+r_0,\ mcdot0^{m-1}=2r_2cdot0+r_1,\ 3^m=r_2cdot 3^2+r_1cdot3+r_0.end{cases}$

3. Решая систему, получаем $r_2=3^{m-2},~ r_1=r_0=0$ и $r(lambda)=3^{m-2}lambda^2$ .

4. Вычисляя $C^2=begin{pmatrix} 3&3&3\ 3&3&3\ 3&3&3 end{pmatrix}$ , записываем искомый многочлен:

$f(C)=r(C)=3^{m-2}cdot! begin{pmatrix}3&3&3\ 3&3&3\ 3&3&3end{pmatrix}= 3^{m-1}cdot! begin{pmatrix}1&1&1\ 1&1&1\ 1&1&1 end{pmatrix}!.$

Поскольку степень характеристического многочлена больше степени минимального многочлена (3>2) , его применение менее эффективно.

Матрица . 1. Инвариантные множители характеристической матрицы (D-lambda E) найдены в примере 7.15. Минимальный многочлен равен последнему инвариантному множителю: mu_D(lambda)=e_3(lambda)=lambda^2(lambda-3) . Степень минимального многочлена равна 3. Значит, многочлен (7.44) — это квадратный трехчлен: r(lambda)=r_2 lambda^2+r_1 lambda+r_0 .

2. Для двойного корня lambda=lambda_1=0~(m_1=2) записываем первые два равенства (7.46), а для простого корня lambda=lambda_2=3 (m_2=1) — первое равенство из (7.46). Получаем систему трех уравнений относительно коэффициентов квадратного трехчлена r(lambda):

$begin{cases} f(0)=r(0),\ left.{dfrac{df(lambda)}{d lambda}}right|_{lambda=0}= left.{dfrac{dr(lambda)}{d lambda}}right|_{lambda=0},\ f(3)=r(3), end{cases}Rightarrowquad begin{cases}0^m=r_2cdot0^2+r_1cdot0+r_0,\ mcdot0^{m-1}=2r_2cdot0+r_1,\ 3^m=r_2cdot3^2+r_1cdot3+r_0. end{cases}$

3. Решая систему, получаем $r_2=3^{m-2},~r_1=r_0=0$ и $r(lambda)=3^{m-2}lambda^2$ .

4. Находим многочлен от матрицы

$f(D)=r(D)=3^{m-2}D^2= 3^{m-2}cdot! begin{pmatrix}-2&5&-3\ -2&5&-3\ 1&-1&0 end{pmatrix}= 3^mcdot! begin{pmatrix}-1&2&-1\ -1&2&-1\ 0&0&0end{pmatrix}!.$

Эта формула справедлива при m>1 , так как при m=1 или m=0 в системе для нахождения коэффициентов многочлена r(lambda) появляются неопределенные выражения (0^0) . Впрочем, для этих показателей степени (m=1,~m=0) многочлен f(D) легко находится по определению D^1=D,~D^0=E .

Все результаты совпадают с полученными в примере 7.17.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Содержание

УСЛОВИЕ:
РЕШЕНИЕ:
ОТВЕТ:
Решения пользователей
Написать комментарий
Здравствуйте
Транскрипт
Вычисление суммы, разности, произведения матриц онлайн
Вычисление обратной матрицы онлайн
Вычисление определителя матрицы онлайн
Вычисление ранга матрицы онлайн
Вычисление псевдообратной матрицы онлайн
Удаление линейно зависимых строк или столбцов матрицы онлайн
Скелетное разложение матрицы онлайн
Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
LU-разложение или LUP-разложение матрицы онлайн
Построение ядра (нуль-пространства) матрицы онлайн
Сложение матриц
Вычитание матриц
Умножение матриц

УСЛОВИЕ:

Найдите значение матричного многочлена f(A):

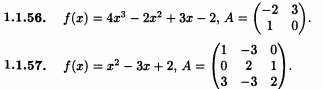
РЕШЕНИЕ:

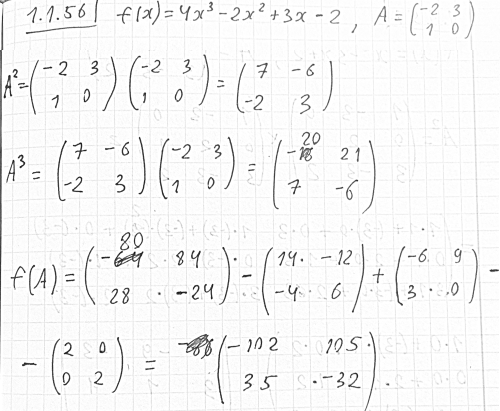
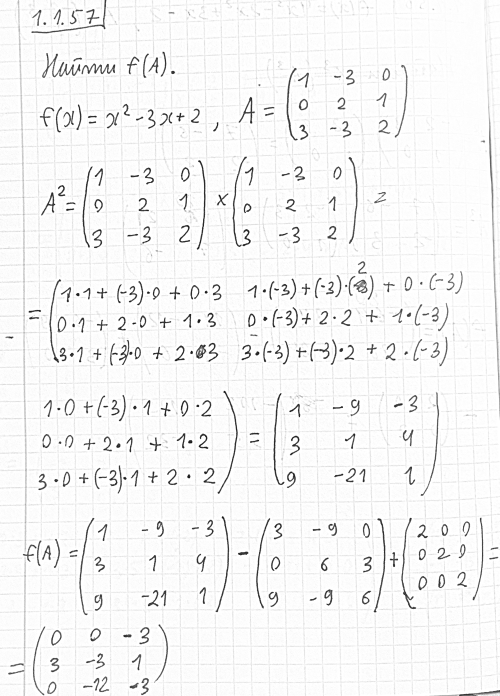
ОТВЕТ:

Добавил slava191 , просмотры: ☺ 13644 ⌚ 03.09.2017. математика 1k класс

Решения пользователей

Написать комментарий

1.
Нормальный вектор vector=(5;-4) прямой 5х-4у+3=0 является направляющим вектором искомой прямой.

Уравнение прямой, проходящей через точку (x_(o);y_(o)) c направляющим вектором vector~~=(p;q) имеет вид:~~

Геометрический смысл углового коэффициента:

угловой коэффициент равен тангенсу угла α , образованного прямой y=kx+b с положительным направлением оси Ох

По условию
α=60 градусов

k=tg α =tg60 ° =sqrt(3)

Уравнение прямой имеет вид:
y=sqrt(3)x+b

Подставляем координаты точки А(4;1) и находим b:
1=sqrt(3)*4+b
b=1-4sqrt(3)

О т в е т. [b]y=sqrt(3)*x+1-4sqrt(3)[/b]

3.
Запишем уравнение:
3x+4y+1=0
в виде:
4y=-3x-1
y=-0,75x-0,25

Угловой коэффициент k_(1)=-0,75

x-2y+3=0
2y=x+3
y=0,5x+1,5
Угловой коэффициент k_(2)=0,5

k_(1) ≠ k_(2) ⇒ Прямые не параллельны

k_(1) *k_(2)≠ -1 ⇒ Прямые не перпендикулярны

О т в е т. Прямые пересекаются.

4.
Составляем уравнение прямой МТ, как прямой, проходящей через две точки
М(2;4) и Т(-4;7)

О т в е т[b]х+2у-10=0[/b]

Высота СН проведена в стороне АВ

Составляем уравнение прямой АВ, как прямой, проходящей через две точки А(-1;2) и B(2;-3)

Если прямые y=k_(1)x+b_(1) и y=k_(2)x+b_(2) перпендикулярны, то произведение угловых коэффициентов равно (-1)
k_(1)*k_(2)=-1 ⇒

Уравнение имеет вид:

Чтобы найти b подставляем координаты точки С:

как правильно писать ответ в таком случае? извините за скриншоты, у меня плохо сайт работает, не могу формулы написать

задан 25 Мар ’16 14:40

s1mka
1.2k ● 7 ● 40
98&#037 принятых

У Вас ответ и записан как надо: f(A) равно найденной при вычислениях матрицы. Пример так был подобран составителями, что в ответе получилась матрица из нулей, но могла быть и какая-то другая.

В записи решения я бы лишние слова убрал, а написал в начале f(A)=A^2-2A+E, и далее по тексту.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Транскрипт

1 1. Найти значение матричного многочлена: f(a) = A + 5A E f(x) = x + 5x, A = () 5 1 A = () () = () () = (() 0 ()) = () 5 () = () = () A = () = () A = 5 () = () E = (0 1 0) = (0 0) f(a) = A + 5A E = = () + () (0 0) = = () = (). Вычислить определитель, используя элементарные преобразования:

2 Получим нули в первом столбце определителя: = = = Разложим определитель по первому столбцу: 4 7 = = 1 (1) = Получим нули в первом столбце определителя третьего порядка: = = Запишем разложение определителя по третьему столбцу: = 1 (1) = () = = () = (160) = 160. Для основной матрицы системы уравнений найти обратную матрицу методом присоединенной матрицы: x 1 + x 4x = 0 < 4x 1 x + x = 9 x 1 x x = 8 Основная матрица системы: 1 4 A = (4) 1 1 Найдем обратную матрицу методом присоединенной матрицы. Допишем справа единичную матрицу:

делаем нули в 1 столбце

делим строку на (15)

делаем нули во столбце

делим строку на (1)

делаем нули в столбце

(1) Тогда: 1 A 1 = 1 (Проверка: 1 A 1 A = 1 () (4) =)

5 1 0 4 = 4 9 = = = 4 9 = = Теперь найдем значения неизвестных: x 1 = 1 = = 1 x = = = x = = 0 15 = 5. Найти ранг матрицы методом окаймляющих миноров. Указать базисный минор: 1 () 8 Т.к. матрица содержит ненулевые элементы, то минимальный ранг матрицы равен 1. равен. Т.к. матрица состоит из трех строк, то максимальный ранг матрицы Определим ранг матрицы методом окаймляющих миноров: 1 A = (M 1 =) 8 Найдем минор первого порядка: Найдем минор второго порядка: M = 1 = = Найдем миноры третьего порядка:

6 1 M 1 = 5 4 = = M = 5 7 = = Значит ранг матрицы A равен. Базисный минор: 1 4 M = уравнений: виду: 6. Исследовать совместность и найти общее решение системы x 1 + x x + 5x 4 7x 5 = x < 1 + 5x 4x + 8x 4 11x 5 = x 1 x x 4 + x 5 = x 1 x + 7x x 4 + 5x 5 = Выпишем расширенную матрицу системы и приведем ее к ступенчатому 1 A = (

) () система совместна и имеет бесконечное множество решений 0 1)

8 X = (C 4 5 C C C C C 5 C 4 C 5) 7. Даны векторы: Найти: a = (7; ; 1), b = (1; 5;), c = (1; 4; 0) а) скалярное произведение векторов a и b ; б) векторное произведение векторов a и b ; с) смешанное произведение векторов a, b и c. а) скалярное произведение векторов a и b ; В декартовой системе координат скалярное произведение векторов: a = и b = находим по формуле: (a, b) = a x b x + a y b y + a z b z В нашем случае: (a, b) = = = 5 б) векторное произведение векторов a и b ; В декартовой системе координат векторное произведение векторов: a = и b = определяется формулой: i j k = a x a y a z b x b y b z

9 В нашем случае: = i j k 7 1 = i 1 5 j k = 1 5 = i (9 5) j (1 1) + k (5) = 4i 0j + k = (4; 0;) с) смешанное произведение векторов a, b и c. Смешанное произведение трех векторов: a = , b = и c = в декартовой системе координат находим по формуле: a x a y a z (a, b, c) = b x c x b y c y b z c z В нашем случае: 7 1 (a, b, c) = 1 5 = = Дана пирамида с вершинами: Найти: A 1 (; 1;), A (1; ; 1), A (; ; 1), A 4 (4; ; 5) а) длину ребер A 1 A, A 1 A, A 1 A 4 ; б) косинус угла между ребрами A 1 A и A 1 A 4 ; в) площадь грани A 1 A A ; г) объем пирамиды; д) проекцию вектора A 1 4 на направление вектора A. 1 а) длину ребер A 1 A, A 1 A, A 1 A 4 ; Длины ребер A 1 A, A 1 A, A 1 A 4 равны модулям векторов A, 1 A, 1 A. 1 4 Модуль вектора a = вычисляется по формуле:

10 a = a x + a y + a z A 1 = <1 ; + 1; 1 >= < 1; ; >A 1 = < ; + 1; 1 >= <1; ; 1>A 1 4 = < 4 ; + 1; 5 >= < 6; ; >Подставляя в эту формулу исходные данные, получим: A 1 = (1) + + () = = 19 (ед.) A 1 = (1) = = 11 (ед.) A 1 4 = (6) + + = = 54 (ед.) б) косинус угла между ребрами A 1 A и A 1 A 4 ; Угол между ребрами будем искать, используя формулу скалярного произведения векторов: cosα = a b a b, a b = a x b x + a y b y + a z b z, a = a x + a y + a z В нашем случае: a = A 1 = < 1; ; >b = A 1 4 = < 6; ; >cosα = A 1A A 1 4 A 1 A 1 4 = ,18 = 1 (6) = = в) площадь грани A 1 A A ; Площадь грани A 1 A A найдем как половину площади параллелограмма, построенного на векторах A 1 и A. 1 A 1 = < 1; ; >A 1 =

11 S A1 A A = 1 A 1A A 1 A 1 A 1 = i j k 1 = i (+ 9) j (1 +) + k () = 1 1 = 6i 4j 6k = <6; 4; 6>S A1 A A = 1 A 1A A 1 = (4) + (6) = = = ,69 (кв. ед.) г) объем пирамиды; Объем пирамиды A 1 A A A 4 вычислим с помощью смешанного произведения трех векторов, на которых построена пирамида: V = 1 6 (A 1A A 1 A) 1 4 A 1 = < 1; ; >A 1 = <1; ; 1>A 1 4 = < 6; ; >1 (A 1 A 1 A) 1 4 = 1 1 = = 66 6 V = = = 11 (куб. ед.) 6 6 д) проекцию вектора A 1 4 на направление вектора A. 1 пр A1 A 1 A 4 = A 1A 4 A 1 A 1 6 (1) + + () = 19 = = = Даны вершины треугольника:

12 точку A. Найти: A(;), B(4;), C(; 5) а) угол между медианой AD и высотой AH; б) уравнение прямой, параллельной стороне BC и проходящей через а) угол между медианой AD и высотой AH; Найдем уравнение медианы AD. Для определения уравнения медианы AD найдем координаты точки D, которая делит отрезок BC пополам: x D = x + x y D = y + y AD: = 4 = + 5 = = 1 = 7 Тогда координаты точки D (1; 7). Медиана AD проходит через точки A(;) и D (1; 7). x x 1 x E x 1 = y y 1 y E y 1 x = y x + 4 = y x + = 4y + 1 1x + 9 = 8y + 4 1x 8y + 15 = 0 Из уравнения медианы AD: 1x 8y + 15 = 0 k AD = 1 8 Найдем уравнение высоты AH. Для составления уравнения высоты AH, воспользуемся условием перпендикулярности прямых: l 1 l k 1 k = 1 Так как AH BC, то k AH k BC = 1 k AH = 1 Уравнение стороны BC найдем по формуле уравнения прямой, проходящей через две точки: k BC

13 BC: x x x x = y y y y x 4 4 = y 5 x 4 6 = y x 1 = 6y + 1 x + 6y 4 = 0 x + y 8 = 0 Из уравнения стороны BC: x + y 8 = 0 k BC = 1 Так как k BC = 1, то k AH = 1 = 1 Уравнение прямой с угловым коэффициентом k, проходящей через точку M 0 (x 0, y 0), имеет вид: y y 0 = k(x x 0) Тогда уравнение высоты AH с угловым коэффициентом k AH =, проходящей через точку A(;), имеет вид: y + = (x +) y + = x + 6 x y + = 0 формулу: Из уравнения высоты AH: x y + = 0 k AH = Для вычисления угла между медианой AD и высотой AH, используем tgα = k AH k AD = 1 + k AD k AH α = arctg(0,088) = = = 4 0,088 б) уравнение прямой, параллельной стороне BC и проходящей через точку A. Чтобы составить уравнение прямой AN, найдем угловой коэффициент этой прямой. Так как AN BC, то угловые коэффициенты этих прямых равны между собой, т.е. k AN = k BC. Из уравнения прямой BC: x + y 8 = 0 k BC = 1. Тогда k AN = 1. Составим уравнение прямой AN, зная угловой коэффициент k AN = 1 и

14 координаты точки A(;): y + = 1 (x +) y + 6 = x x + y + 9 = 0

Пример Вычислить определитель Решение типовых задач 5 5 7, разложив его по 9 9 элементам первой строки 7 5 7 5 5 6 9 9 9 9 Пример Вычислить определитель, приведя его к треугольному виду: 5 7 Обозначим

1. Найдите произведение матриц ABC: Решение типового варианта: Так как произведение матриц не перестановочно, то найти данное произведение можно двумя способами: Для определенности воспользуемся вторым

Задачи для отработки пропущенных занятий Оглавление Тема: Матрицы, действия над ними. Вычисление определителей. 2 Тема: Обратная матрица. Решение систем уравнений с помощью обратной матрицы. Формулы

Векторы Даны координаты векторов a b c в правом ортонормированном базисе i j k Показать что векторы a b c тоже образуют базис и найти координаты вектора в базисе a b c) () a () b () c ()) () a (

Министерство образования и науки Российской Федерации Казанский государственный архитектурно-строительный университет Кафедра высшей математики Элементы векторной и линейной алгебры. Аналитическая геометрия.

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИРОДООБУСТРОЙСТВА ЛИНЕЙНАЯ АЛГЕБРА МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ДЛЯ СТУДЕНТОВ — ЗАОЧНИКОВ МГУП

Фонд оценочных средств для проведения промежуточной аттестации обучающихся по дисциплине (модулю) Общие сведения 1 Кафедра Математики, физики и информационных технологий 2 Направление подготовки 010302

Примеры выполнения контрольных работ при заочном обучении Контрольная работа 1 (КР-1) Тема 1. Линейная алгебра Задача 1 Необходимо решить систему уравнений, представленную в задании в виде Постоянные параметры

8. Фонд оценочных средств для проведения промежуточной аттестации обучающихся по дисциплине (модулю): Общие сведения 1. Кафедра М и ММЭ 2. Направление подготовки 01.03.02 (010400.62) Прикладная математика

Примеры решений контрольных работ Л.И. Терехина, И.И. Фикс 1 Контрольная работа 2 Векторная алгебра 1. Даны три вектора a = <0; 1; 3>, b = <3; 2; 1>, c = <4; 0; 4>. Требуется найти: a) вектор d = 2 a b

Глава Элементы линейной алгебры Матрицы О п р е д е л е н и е Матрицей размерности m n называется прямоугольная таблица чисел, расставленных в m строк и n столбцов Обозначаются матрицы латинскими буквами,

Матрицы 1 Даны матрицы и Найти: а) А + В; б) 2В; в) В T ; г) AВ T ; д) В T A Решение а) По определению суммы матриц б) По определению произведения матрицы на число в) По определению транспонированной матрицы

Методические указания к контрольным работам Контрольная работа «Переаттестация» Тема. Элементы аналитической геометрии на плоскости. Прямая на плоскости Расстояние между двумя точками M () и () плоскости

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ ЗАНЯТИЕ МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ Дать определение матрицы Классификация матриц по размерам Что такое нулевая и единичная матрицы? При каких условиях матрицы считаются равными?

Ne Экзамен по ЛА для бакалавров экономики в 04-0 уч году, Найдите вектор Ne (6 4 ; 6 8) и Ne ДЕМОвариант 0 (x ; y)(у которого Ne и x возвести матрицу в степень , умножить матрицу на число , сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы , проводить исключение Гаусса , решить матричное уравнение AX=B , сделать LU разложение матрицы , вычислить ядро (нуль пространство) матрицы , сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта .

Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы и вводить числа в виде a или a /b , где a и b целые или десятичные числа (b положительное число). Например 12/67, -67.78/7.54, 327.6, -565.

Кнопка в верхем левом углу матрицы открывает меню (Рис.1) для преобразования исходной матрицы (создание единичной матрицы , нулевой матрицы или очищать содержимое ячеек ).

При вычислениях пустая ячейка воспринимается как нуль.

Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .

Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.

Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы и , а также преобразовать на месте элементы матрицы в обыкновенную дробь, смешанную дробь или в десятичное число.

Вычисление суммы, разности, произведения матриц онлайн

сумму , разность или произведение матриц . Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.

Для вычисления суммы, разности или произведения матриц:

Вычисление обратной матрицы онлайн

Матричным онлайн калькулятором можно вычислить обратную матрицу . Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.

Для вычисления обратной матрицы:

Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы . Теорию вычисления обратной матрицы смотрите .

Вычисление определителя матрицы онлайн

Матричным онлайн калькулятором можно вычислить определитель матрицы . Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.

Для вычисления определителя матрицы:

Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы . Теорию вычисления определителя матрицы смотрите .

Вычисление ранга матрицы онлайн

Матричным онлайн калькулятором можно вычислить ранг матрицы .

Для вычисления ранга матрицы:

Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы . Теорию вычисления ранга матрицы смотрите .

Вычисление псевдообратной матрицы онлайн

Матричным онлайн калькулятором можно вычислить псевдообратную матрицу . Псевдообратная к данной матрице всегда существует.

Для вычисления псевдообратной матрицы:

Удаление линейно зависимых строк или столбцов матрицы онлайн

Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.

Для удаления линейно зависимых строк или столбцов матрицы:

Скелетное разложение матрицы онлайн

Для проведения скелетного разложения матрицы онлайн

Решение матричного уравнения или системы линейных уравнений AX=B онлайн

Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.

Для решения матричного уравнения:

Учтите, что матрицы и должны иметь равное количество строк.

Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн

Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.

Для исключения Гаусса или приведения матрицы к треугольному виду

LU-разложение или LUP-разложение матрицы онлайн

Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU) , где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение, при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.

Построение ядра (нуль-пространства) матрицы онлайн

С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.

Для построения нуль-пространства (ядра) матрицы.

Назначение сервиса . Матричный калькулятор предназначен для решения матричных выражений, например, таких как, 3A-CB 2 или A -1 +B T .

Инструкция . Для онлайн решения необходимо задать матричное выражение. На втором этапе необходимо будет уточнить размерность матриц.

Допустимые операции: умножение (*), сложение (+), вычитание (-), обратная матрица A^(-1) , возведение в степень (A^2 , B^3), транспонирование матрицы (A^T).

Допустимые операции: умножение (*), сложение (+), вычитание (-), обратная матрица A^(-1) , возведение в степень (A^2 , B^3), транспонирование матрицы (A^T).
Для выполнения списка операций используйте разделитель точка с запятой (;). Например, для выполнения трех операций:
а) 3А+4В
б) АВ-ВА
в) (А-В) -1
необходимо будет записать так: 3*A+4*B;A*B-B*A;(A-B)^(-1)

Матрица — прямоугольная числовая таблица, имеющая m строк и n столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника.
Нулевой матрицей (нуль-матрицей) называют матрицу, все элементы которой равны нулю и обозначают 0.
Единичной матрицей называется квадратная матрица вида

Две матрицы A и B равны , если они одинакового размера и их соответствующие элементы равны.
Вырожденной матрицей называется матрица, определитель которой равен нулю (Δ = 0).

Определим основные операции над матрицами .

Сложение матриц

Пример 6 . .
Операция сложения матриц распространяется на случай любого числа слагаемых. Очевидно, что A+0=A .
Еще раз подчеркнем, что складывать можно только матрицы одинакового размера; для матриц разных размеров операция сложения не определена.

Вычитание матриц

Умножение матриц

Пример 7 . Даны матрицы и . Найти матрицы C = A·B и D = B·A.
Решение. Прежде всего заметим, что произведение A·B существует, так как число столбцов A равно числу строк B.

Заметим, что в общем случае A·B≠B·A , т.е. произведение матриц антикоммутативно.
Найдем B·A (умножение возможно).

Пример 8 . Дана матрица . Найти 3A 2 – 2A.
Решение.

.
; .
.
Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.

Источник

Содержание:

1 Использование жордановой формы для нахождения многочлена от матрицы
2 Первый способ нахождения многочлена от матрицы
3 Использование аннулирующих многочленов
4 Второй способ нахождения многочлена от матрицы
- 4.1 Здравствуйте

Напомним определение многочлена от матрицы. Пусть заданы многочлен (степени [math]m[/math] ) переменной [math]lambda:[/math]

где [math]A[/math] — квадратная матрица n-го порядка. Выражение вида

называется многочленом от матрицы [math]A[/math] .

При больших значениях [math]m[/math] и [math]n[/math] вычисление выражения (7.41) затруднительно из-за операции возведения матрицы в натуральную степень. Поэтому требуется найти другие, эквивалентные определению (7.41), формы записи и алгоритмы эффективного вычисления многочлена от матрицы. Для упрощения (7.41) имеются две возможности. Во-первых, можно упростить матрицу [math]A[/math] так, чтобы многочлен (7.40) от упрощенной матрицы уже вычислялся сравнительно просто. Например, выражение (7.41) легко вычисляется, если матрица [math]A[/math] диагональная. Во-вторых, можно понизить степень [math]m[/math] многочлена, тогда самая трудоемкая операция — возведение матрицы в степень — упрощается.

Использование жордановой формы для нахождения многочлена от матрицы

Использование жордановой формы матрицы для нахождения многочлена от матрицы основано на трех свойствах.

1. Многочлены от подобных матриц подобны.

Действительно, пусть при помощи преобразования подобия матрица [math]A[/math] приведена к жордановой форме [math]J_A=S^<-1>AS[/math] . Подставим [math]A=SJ_AS^<-1>[/math] в правую часть (7.41):

Учитывая, что [math](SJ_AS^<-1>)^k= underbracecdot SJ_AS^ <-1>cdotldotscdot SJ_AS^<-1>>_= SJ_A^kS^<-1>[/math] для любого натурального [math]k[/math] , получаем

Таким образом, многочлены [math]f(A)[/math] и [math]f(J_A)[/math] подобны (с той же самой преобразующей матрицей [math]S[/math] ):

2. Многочлен от блочно-диагоналъной матрицы является блочно-диагоналъной матрицей.

Пусть [math]A=eginA_1!!&vline!!&Ohline O!!&vline!!&A_2end[/math] , где [math]A_1[/math] и [math]A_2[/math] — квадратные матрицы, а [math]O[/math] — нулевые матрицы соответствующих размеров. Для блочно-диагональных матриц справедливы равенства (они следуют из операций над блочными матрицами):

Поэтому [math]f(A)=egin f(A_1)!!&vline!!&Ohline O!!&vline!!& f(A_2) end[/math] .Для большего числа блоков доказательство V. о 1Аг)) аналогичное.

3. Многочлен (7.41) от жордановой клетки [math]J_r(lambda_0)[/math] имеет вид

Это верхняя треугольная матрица r-го порядка, на главной диагонали которой стоят значения функции [math]f(lambda)[/math] в точке [math]lambda_0[/math] , над диагональю — значения первой производной в этой же точке и т.д., т.е. коэффициенты ряда Тейлора для функции [math]f(lambda)[/math] .

Действительно, разложим многочлен (7.40) по формуле Тейлора в окрестности точки [math]lambda=lambda_0:[/math]

Остаточный член в данном случае равен нулю, так как все производные более высокого порядка, чем [math]m[/math] , тождественно равны нулю. При вычислении [math]f(J_r(lambda_0))[/math] линейный двучлен [math](lambda-lambda_0)[/math] заменяется матрицей

у которой элементы над главной диагональю равны единице, а остальные элементы равны нулю, т.е. [math]I=egin0&e_1&e_2&cdots&e_end[/math] , где [math]e_i[/math] — i-й столбец единичной матрицы r-го порядка.

Можно показать, что при возведении в степень единичные элементы матрицы [math]I[/math] смещаются вверх:

причем [math]I^k[/math] — нулевая матрица при [math]kgeqslant r[/math] . Подставляя эти матрицы в формулу Тейлора, получаем

Складывая матрицы в правой части, получаем квадратную матрицу r-го порядка, у которой элементы главной диагонали равны [math]f(lambda_0)[/math] , элементы над главной диагональю равны — [math]frac<1><1!>,f'(lambda_0)[/math] и т.д., т.е. матрицу вида (7.42).

Пример 7.16. Найти многочлен [math]f(lambda)= lambda^2+ lambda+1[/math] от матриц

Решение. а) Матрица [math]A[/math] — это жорданова клетка 3-го порядка, соответствующая собственному значению 2: [math]A=J_3(2)[/math] . Находим значения функции и ее производных в точке [math]lambda=2:[/math] [math]f(2)=7,[/math] [math]f'(2)=5,[/math] [math]f»(2)=2[/math] . Составляем матрицу вида (7.42), учитывая, что [math]r=3:[/math]

Матрица [math]B[/math] имеет жорданову форму [math]B=operatorname (J_2(2),,J_1(2))[/math] , т.е. является блочно-диагональной. По свойству 2 многочлен от матрицы [math]B[/math] является блочно-диагональной матрицей. Записываем многочлен [math]f(lambda)[/math] от каждой жордановой клетки по формуле (7.42):

Матрица [math]C[/math] имеет жорданову форму [math]C=operatorname (J_2(2),J_1(3))[/math] , т.е. является блочно-диагональной. Записываем многочлен [math]f(lambda)[/math] от каждой жордановой клетки по формуле (7.42):

Составляем из этих квадратных матриц искомую блочно-диагональную матрицу

Первый способ нахождения многочлена от матрицы

1. Привести матрицу [math]A[/math] к жордановой форме [math]J_A=S^<-1>AS[/math] , т.е. определить жорданову форму [math]J_A[/math] и преобразующую матрицу [math]S[/math] .

2. Составить блочно-диагональную матрицу [math]f(J_A)[/math] , размещая на ее диагонали многочлены от жордановых клеток (7.42).

3. Найти многочлен от матрицы А по формуле [math]f(A)=Scdot f(J_A)cdot S^<-1>[/math] .

Пример 7.17. Найти многочлен [math]f(lambda)=lambda^m[/math] (при 1″>[math]m>1[/math] ) от матриц:

Решение. Матрица [math]A[/math] . 1. Жорданова форма [math]J_A[/math] и преобразующая матрица [math]S[/math] были найдены в примере 7.15:

2. Жорданова форма [math]J_A[/math] состоит из одной жордановой клетки [math]J_A=J_2(2)[/math] 2-го порядка, соответствующей собственному значению [math]lambda=2[/math] . Найдем значения функции [math]f(lambda)=lambda^m[/math] и ее производной [math]f'(lambda)=m lambda^[/math] при [math]lambda=2:[/math] [math]f(2)=2^m,[/math] [math]f'(2)=m2^[/math] . Запишем многочлен от жордановой формы (блочно-диагональную матрицу с одним блоком): [math]f(J_A)= egin 2^m&m2^ 0&2^mend[/math] .

3. Найдем многочлен от матрицы [math]A:[/math]

Матрица В. 1. Жорданова форма [math]J_B[/math] и преобразующая матрица [math]S[/math] были найдены в примере 7.15:

2. Жорданова форма [math]J_B[/math] состоит из одной жордановой клетки [math]J_B=J_3(1)[/math] 3-го порядка, соответствующей собственному значению [math]lambda=1[/math] . Найдем значения функции [math]f(lambda)[/math] и ее производных [math]f'(lambda),,f»(lambda)[/math] при [math]lambda=1:[/math] [math]f(1)=1,[/math] [math]f'(1)=m,[/math] [math]f»(1)=m(m-1)[/math] . Запишем многочлен от жордановой формы [math](r=3)colon[/math]

3. Найдем многочлен от матрицы [math]B:[/math]

Матрица [math]C[/math] . 1. Жорданова форма [math]J_C[/math] и преобразующая матрица [math]S[/math] были найдены в примере 7.15:

2. Жорданова форма [math]J_C[/math] состоит из трех жордановых клеток 1-го порядка [math]J_C= operatorname(J_1(0),,J_1(0),,J_1(3))[/math] , соответствующих собственным значениям [math]lambda=0[/math] и [math]lambda=3[/math] . Найдем значения функции [math]f(lambda)=lambda^m[/math] при [math]lambda=0[/math] и [math]lambda=3:[/math] [math]f(0)=0,[/math] [math]f(3)=3^m[/math] . Запишем многочлен от жордановой формы:

3. Найдем многочлен от матрицы [math]C:[/math]

Результат совпадает с найденным в примерах 7.10, 7.12.

Матрица [math]D[/math] . 1. Жорданова форма [math]J_D[/math] и преобразующая матрица [math]S[/math] были найдены в примере 7.15:

2. Жорданова форма [math]J_D[/math] состоит из двух жордановых клеток 2-го и 1-го порядков [math]J_D=operatorname(J_2(0),,J_1(3))[/math] . соответствующих собственным значениям [math]lambda=0[/math] и [math]lambda=3[/math] . Найдем значения функции [math]f(0)=0,[/math] [math]f(3)=3^m[/math] и производной [math]f'(0)=0[/math] (так как 1″>[math]m>1[/math] ). Запишем многочлен от жордановой формы

3. Найдем многочлен от матрицы [math]D:[/math]

Использование аннулирующих многочленов

Для понижения степени многочлена (7.41) можно использовать аннулирующие многочлены матрицы [math]A[/math] , например, ее характеристический [math]Delta_A(lambda)=det(A-lambda E)[/math] или минимальный [math]mu_A(lambda)[/math] многочлены.

Обозначим через [math]
u[/math] степень минимального многочлена

Заметим, что [math]
u[/math] не превосходит порядка [math]n[/math] матрицы [math]A[/math] (или, что то же самое, степени [math]n[/math] характеристического многочлена [math]Delta_A(lambda)[/math] ), т.е. [math]
u=m_1+ldots+m_kleqslant n[/math] . Разделим заданный многочлен (7.40) на минимальный:

Здесь [math]q(lambda)[/math] — частное, а [math]r(lambda)[/math] — остаток, степень которого меньше [math]
u:[/math]

Подставив в (7.43) вместо переменной [math]lambda[/math] матрицу [math]A[/math] , получим:

поскольку минимальный многочлен является аннулирующим [math](mu_A(lambda)=O)[/math] .

Таким образом, вместо вычисления многочлена (7.41) степени [math]m[/math] можно вычислить многочлен (7.44), степень которого меньше [math]
u[/math] . Коэффициенты [math]r_0,r_1,ldots,r_<
u-1>[/math] многочлена (7.44) находятся следующим образом.

Если все корни минимального многочлена простые, то, подставляя корень [math]lambda_j[/math] в (7.43), получаем [math]f(lambda_j)=r(lambda_j)[/math] , так как [math]mu_A(lambda_j)=0[/math] , т.е.

Если [math]lambda_j[/math] — корень минимального многочлена кратности [math]m_j[/math] , учитывая, что

из (7.43), последовательно дифференцируя, получаем

Записывая равенства (7.46) для каждого корня минимального многочлена, получим совместную систему [math]
u[/math] линейных уравнений с [math]
u[/math] неизвестными [math]r_0,r_1,ldots,r_<
u-1>[/math] .

Второй способ нахождения многочлена от матрицы

1. Найти минимальный многочлен [math]mu_A(lambda)[/math] матрицы [math]A[/math] одним из способов, рассмотренных в разд.7.2.4. Определить его степень [math]mu[/math] и записать многочлен (7.44) с неопределенными коэффициентами [math]r_0,r_1,ldots,r_<
u-1>:[/math]

2. Для каждого корня [math]lambda_j[/math] (кратности [math]m_j[/math] ) минимального многочлена по формулам (7.46) составить [math]m_j[/math] уравнений. Все уравнения объединить в одну систему.

3. Решить составленную систему, т.е. найти коэффициенты [math]r_0,r_1,ldots,r_<
u-1>[/math] многочлена [math]r(lambda)[/math] .

4. По формуле (7.45) найти многочлен от матрицы:

Пример 7.18. Найти (вторым способом) многочлен [math]f(lambda)= lambda^m[/math] (при 1″>[math]m>1[/math] ) от матриц:

Решение. Матрица [math]A[/math] . 1. Для матрицы [math]A[/math] в примере 7.15 были найдены инвариантные множители. Минимальный многочлен совпадает с последним инвариантным множителем. Поэтому [math]mu_A(lambda)=e_2(lambda)=(lambda-2)^2[/math] . Степень [math]
u[/math] минимального многочлена равна двум. Значит, многочлен (7.44) линейный: [math]r(lambda)=r_1 lambda+r_0[/math] .

2. Для двойного корня [math]lambda=lambda_1=2

(m_1=2)[/math] составляем уравнения (7.46):

3. Решая систему, получаем [math]r_1=m2^,

r_0=(1-m)2^m[/math] и [math]r(lambda)=m2^cdot lambda+(1-m)2^m[/math] .

4. Находим многочлен от матрицы [math]A:[/math]

Матрица [math]B[/math] . 1. Инвариантные множители характеристической матрицы [math](B-lambda E)[/math] найдены в примере 7.15. Минимальный многочлен равен последнему инвариантному множителю: [math]mu_B(lambda)=e_3(lambda)=(lambda-1)^3[/math] . Степень [math]
u[/math] минимального многочлена равна 3. Значит, многочлен (7.44) — это квадратный трехчлен: [math]r(lambda)=r_2 lambda^2+r_1 lambda+r_0[/math] .

2. Для тройного корня [math]lambda=lambda_1=1

(m_1=3)[/math] составляем уравнения (7.46):

3. Решая систему, получаем [math]r_2=frac<2>,

4. Вычисляя [math]B^2=egin0&-1&2 1&2&-2 -2&-2&1 end[/math] , записываем искомый многочлен:

Матрица [math]C[/math] . 1. Минимальный многочлен найден в примере7.15: [math]mu_C(lambda)=lambda(lambda-3)[/math] . Степень [math]
u[/math] многочлена равна 2. Следовательно, многочлен (7.44) имеет первую степень: [math]r(lambda)=r_1 lambda+r_0[/math] .

2. Для каждого простого корня [math]lambda=lambda_0=0[/math] и [math]lambda= lambda_2=3[/math] записываем пер вое равенство из (7.46):

3. Решая систему, получаем [math]r_1=3^,

r_0=0[/math] и [math]r(lambda)=3^lambda[/math] .

4. Находим многочлен от матрицы [math]C:[/math]

Найдем [math]f(C)[/math] , используя характеристический многочлен вместо минимального. Согласно пункту 1 замечаний 7.8, выполняем все действия второго способа, заменяя минимальный многочлен характеристическим.

1. Найдем характеристический многочлен матрицы [math]C[/math] (см. при мер 7.11): [math]Delta_C(lambda)=lambda^2(3-lambda)[/math] . Это многочлен 3-й степени. Поэтому многочлен (7.44) будет 2-ой степени: [math]r(lambda)=r_2 lambda^2+r_1 lambda+r_0[/math] .

2. Для двойного корня [math]lambda=0[/math] записываем два уравнения из (7.46), а для простого корня [math]lambda=3[/math] одно:

3. Решая систему, получаем [math]r_2=3^,

r_1=r_0=0[/math] и [math]r(lambda)=3^lambda^2[/math] .

4. Вычисляя [math]C^2=egin 3&3&3 3&3&3 3&3&3 end[/math] , записываем искомый многочлен:

Поскольку степень характеристического многочлена больше степени минимального многочлена 2)”>[math](3>2)[/math] , его применение менее эффективно.

Матрица [math]D[/math] . 1. Инвариантные множители характеристической матрицы [math](D-lambda E)[/math] найдены в примере 7.15. Минимальный многочлен равен последнему инвариантному множителю: [math]mu_D(lambda)=e_3(lambda)=lambda^2(lambda-3)[/math] . Степень [math]
u[/math] минимального многочлена равна 3. Значит, многочлен (7.44) — это квадратный трехчлен: [math]r(lambda)=r_2 lambda^2+r_1 lambda+r_0[/math] .

2. Для двойного корня [math]lambda=lambda_1=0

(m_1=2)[/math] записываем первые два равенства (7.46), а для простого корня [math]lambda=lambda_2=3[/math] [math](m_2=1)[/math] — первое равенство из (7.46). Получаем систему трех уравнений относительно коэффициентов квадратного трехчлена [math]r(lambda):[/math]

3. Решая систему, получаем [math]r_2=3^,

r_1=r_0=0[/math] и [math]r(lambda)=3^lambda^2[/math] .

4. Находим многочлен от матрицы [math]D:[/math]

Эта формула справедлива при 1″>[math]m>1[/math] , так как при [math]m=1[/math] или [math]m=0[/math] в системе для нахождения коэффициентов многочлена [math]r(lambda)[/math] появляются неопределенные выражения [math](0^0)[/math] . Впрочем, для этих показателей степени [math](m=1,

m=0)[/math] многочлен [math]f(D)[/math] легко находится по определению [math]D^1=D,

Все результаты совпадают с полученными в примере 7.17.

Примерный вариант и образец выполнения контрольной работы №2

Задача 1. Даны многочлен f(x) и матрица А:

Требуется найти значение матричного многочлена f (A).

Задача 2. Дана система трех линейных алгебраических уравнений с тремя неизвестными:

1) записать систему в матричном виде;

2) найти решение системы с помощью формул Крамера;

3) решить систему при помощи обратной матрицы.

Задача 3. Даны координаты трех векторов: и вектор :

вычислить модуль вектора ;

найти координаты вектора ;

найти угол φ между векторами и ;

вычислить проекцию вектора на направление вектора ;

вычислить площадь треугольника, построенного на векторах и ;

вычислить объем параллелепипеда, построенного на векторах .

Задача 4. Даны координаты точек – вершин пирамиды ABCD:

1) вычислить длину ребра AB;

2) найти уравнение плоскости грани ABC;

3) найти угол между гранями ABC и BCD;

4) составить параметрические уравнения прямой AB;

5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;

6) найти координаты точки пересечения DK и грани ABC;

7) найти угол между ребрами AB и BC;

8) найти угол между ребром AD и гранью ABC;

9) сделать чертеж пирамиды в системе координат.

Решение задачи 1.

Записываем матричный многочлен: Здесь Е – единичная матрица той же размерности, что и А, т.е. 3-го порядка.

Найдем матрицу A2. При умножении матрицы A на себя используем правило «строка на столбец» (формула (23)):

Найдем матрицу 2Е, используя правило умножения матрицы на число (формула (21)):

Теперь найдем значение матричного многочлена f(A), используя правило умножения матрицы на число и правило сложения матриц (формула (22)):

Решение задачи 2.

Запишем систему в матричном виде:

(Во втором уравнении системы отсутствует неизвестная х3, т.е. а23 = 0).

2) Решим систему с помощью формул Крамера. Для этого по формулам (29) составляем главный определитель системы из коэффициентов при неизвестных в левых частях уравнений и три вспомогательных определителя:

Вычислим эти определители, используя формулу (25):

Так как ∆ ≠ 0, то данная система имеет единственное решение.

Найдем решение системы по формулам Крамера (30):

3) Решим систему при помощи обратной матрицы.

Определитель следовательно, обратная матрица существует.

б) Чтобы найти союзную матрицу А* к матрице А, необходимо вычислить по формулам (26) алгебраические дополнения всех ее элементов:

Здесь определители 2-го порядка вычислены по формуле (24).

Тогда союзная матрица (см. формулу (31)):

в) Найдем обратную матрицу по формуле (32):

г) Получим решение системы при помощи обратной матрицы по формуле (33) (правило «строка на столбец»):

Решение, полученное матричным способом, совпадает с тем, которое получено по формулам Крамера, что подтверждает правильность этого решения.

1) система в матричном виде: AX = B, где ;

2) решение системы, полученное с помощью формул Крамера:

3) решение системы, полученное при помощи обратной матрицы:

Решение задачи 3.

Модуль вектора вычисляется по формуле (35):

Чтобы найти координаты вектора , используем формулы (38) и (39):

Косинус угла между векторами и найдем по формуле (41):

Для этого вычислим скалярное произведение и по формуле (40): = –2∙0 + 2∙(–3) + (–1)∙4 = –10, затем модуль вектора : , тогда и

Проекцию вектора на направление вычислим по формуле (42):

Площадь треугольника, построенного на векторах и найдем по

формуле (44). Для этого сначала находим векторное произведение этих векторов по формуле (43):

Следовательно, площадь треугольника, построенного на векторах и :

Для вычисления объема параллелепипеда, построенного на векторах

находим смешанное произведение векторов по формуле (45):

тогда объема параллелепипеда по формуле (47): .

угол между векторами и :

проекция вектора на направление вектора :

площадь треугольника, построенного на векторах и : (кв.ед.);

объем параллелепипеда, построенного на векторах : (куб.ед.).

Решение задачи 4.

Длину ребра найдем по формуле (36):

Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т.е. вектор, перпендикулярный векторам и . Одним из таких векторов является векторное произведение на . Для того, чтобы найти его, сначала вычислим координаты векторов по формуле (37):

Векторное произведение и найдем по формуле (43):

В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например, = <9; 17; 4>. Используем уравнение плоскости, проходящей через точку перпендикулярно вектору (формула (48):

– уравнение плоскости грани ABC.

Прежде, чем найти угол между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки (формула (49):

– уравнение грани BCD.

Из уравнения плоскости BCD возьмем координаты вектора нормали , перпендикулярного этой плоскости: =<3; 7; –4>.

Косинус угла между плоскостями (гранями) ABC и BCD найдем по формуле(50):

Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A(–2;1;1) и имеющей направляющий вектор = <–1; 1; –2>(формулы (51)):

– параметрические уравнения AB.

Другой способ: можно использовать уравнения прямой, проходящей через две точки (формулы (53)):

откуда, обозначив каждую из дробей буквой t, получаем:

– параметрические уравнения AB.

Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор , коллинеарный вектору нормали плоскости ABC. Можно взять, например, = = <9; 17; 4>. Запишем канонические уравнения высоты DK, используя точку D(–1; 0; –3) и вектор = <9; 17; 4>(формулы (52)):

– канонические уравнения DK.

Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK. Обозначив каждую из дробей в канонических уравнениях буквой t, получаем:

– параметрические уравнения DK.

Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты , и принадлежит плоскости, т.е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:

Решим последнее уравнение относительно t:

Вычислим координаты точки K, подставив найденное значение параметра t в первые три уравнения системы:

Итак, точка пересечения DK и грани ABC: .

Угол между ребрами AB и BC найдем, как угол между направляющими векторами прямых AB и BC: = <–1; 1; –2>и =<8; –4; –1>. Вычислим косинус угла по формуле (54):

Тогда угол между ребрами AB и BC:

Чтобы определить угол между ребром AD и гранью ABC, найдем направляющий вектор прямой: =<1; –1; –4>. Плоскость ABC имеет вектор нормали = <9; 17; 4>. Синус угла между прямой и плоскостью ABC можно вычислить по формуле (55):

Тогда угол между ребром AD и гранью ABC:

9) Выполним чертеж пирамиды в системе координат (рис. 19).

9) чертеж пирамиды на рис. 19.

задан 25 Мар ’16 14:40

s1mka
1.2k ● 7 ● 40
98&#037 принятых

В записи решения я бы лишние слова убрал, а написал в начале f(A)=A^2-2A+E, и далее по тексту.

Здравствуйте

Источник

Многочлен и матрица как аргумент

Исходный полином f(x) (его коэффициенты)

Аргумент является квадратной матрицей с элементами

Многочлен

Переменная x=

Результат вычислений

Расссмотрим в данном материале одну из трудоёмких задач в высшей математике, которая звучит так: Найти чему задан многочлен

если аргумент есть квадратная матрица, то есть $x=begin{pmatrix}x_{00} & x_{10} &...&x_{i0}\ x_{01} & x_{11}&...&x_{i1}\ ... & ...&...&... \ x_0j} & x_{1j}&...&x_{ij}end{pmatrix}$

И если сам принцип вычисления понятен, особенно если вы в совершенстве поняли как умножать матрицы, то непосредственное вычисление, для меня лично считается рутиной, которую по возможности нужно избежать.

Сразу хотелось бы сказать, где этот калькулятор пригодится. Для учителей, преподавателей, для создателей учебников, для тех, кому необходимо создавать оригинальные задачи по данной теме.

Также пригодится для студентов или аспирантов которые пишут рефераты, курсовые, дипломы.

Для всех остальных, это легкий способ проверить ошибку в заданном примере, решить, без долгих промежуточных вычислений, поставленную задачу.

Когда калькулятор был написан, оказалось что сайты, которые были посвещенны этой теме, содержали ошибки в промежуточных вычислениях и как как результат были неверные.

Данный калькулятор, я надеюсь избавлен от ошибок и Вы сможете безопасно решать любые примеры.

Как и подавляющее большинство калькуляторов на этом сайте, значениями как коэффициентов полинома, так и элементов матрицы, могут быть комплексные значения.

Такого на конец 2017 года, больше нигде не найдете, не считая конечно специальных созданных математических программ.

Приступим к примерам?

Найти значение полинома от матрицы $x=begin{pmatrix}-1 &2 &0\2 & 1&3 & -1&2end{pmatrix}$

Еще один пример

Чему равен полином если $x=begin{pmatrix}2 &2-i &3\-7 & 0&i\1+i &2&0end{pmatrix}$

Найти значение многочлена от комплексной матрицы

$x=begin{pmatrix}-1%20&%200%20&%200%20&%20-1%20&%200%20&%200%20\%200%20&%20-1%20&%201%20&%200%20&%20-1%20&%201%20\%20-1%20&%200%20&%20i%20&%20i%20&%20i%20&%20-1%20\%20-1%20&%20-1%20&%20i%20&%20-1%20&%20-1%20&%20i%20\%200%20&%201%20&%20-1%20&%200%20&%20-1%20&%20i%20\%201%20&%200%20&%200%20&%200%20&%20i%20&%200%20\%20end{pmatrix}$

Удачный расчетов !

Источник

Обратная матрица

Многочлены от матриц

Использование жордановой формы для нахождения многочлена от матрицы

Первый способ нахождения многочлена от матрицы

Использование аннулирующих многочленов

Второй способ нахождения многочлена от матрицы

УСЛОВИЕ:

РЕШЕНИЕ:

ОТВЕТ:

Решения пользователей

Написать комментарий

Здравствуйте

Транскрипт

Вычисление суммы, разности, произведения матриц онлайн

Вычисление обратной матрицы онлайн

Вычисление определителя матрицы онлайн

Вычисление ранга матрицы онлайн

Вычисление псевдообратной матрицы онлайн

Удаление линейно зависимых строк или столбцов матрицы онлайн

Скелетное разложение матрицы онлайн

Решение матричного уравнения или системы линейных уравнений AX=B онлайн

Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн

LU-разложение или LUP-разложение матрицы онлайн

Построение ядра (нуль-пространства) матрицы онлайн

Сложение матриц

Вычитание матриц

Умножение матриц

Использование жордановой формы для нахождения многочлена от матрицы

Первый способ нахождения многочлена от матрицы

Использование аннулирующих многочленов

Второй способ нахождения многочлена от матрицы

Здравствуйте

Многочлен и матрица как аргумент

Вам также может понравиться

Как исправить проблемы в сексе

Как составить расчет командировочных расходов

Как найти работу латвия

Добавить комментарий Отменить ответ