Мажоранта (от фр. majorer — повышать) — термин, который используется в математике для обозначения нескольких понятий, обобщающих понятие супремума или точной верхней грани.
Наиболее часто применяется при доказательстве сходимости интегралов и рядов.
Мажоранта упорядоченного множества[править | править код]
Понятие мажоранты упорядоченного множества вводится для определения супремума множества. Пусть M подмножество упорядоченного множества. Тогда мажорантой множества M называется элемент не меньший любого элемента M. Супремум множества М — это минимум всех мажорант множества М.[1]
Мажоранта функции[править | править код]
Мажоранта функции — функция, значения которой не меньше соответствующих значений данной функции на рассматриваемом интервале независимого переменного. Интегрируемость мажоранты последовательности интегрируемых функций является достаточным условием существования интеграла от предела последовательности.[2]
Пример[править | править код]
Пусть интегрируемые функции 


Мажоранта ряда[править | править код]
Мажоранта ряда — числовой ряд, все члены которого, начиная с некоторого номера, не меньше абсолютной величины соответствующих членов данного ряда. Если исходный ряд зависит от аргумента, например, является степенным или тригонометрическим, то указывают интервал, на котором выполняется неравенство. Для построения мажорант матричных рядов используют норму матрицы.
В качестве мажорант обычно используют простые хорошо сходящиеся ряды — одномерную и многомерную геометрическую прогрессию и ряды с факториалом в знаменателе членов. Из сходимости мажоранты вытекает сходимость исходного ряда. Для рядов, которые являются функциями, построение мажорант – основной инструмент доказательства сходимости.
Примерами являются доказательства теоремы Адамара о числовом ряде, леммы Абеля для рядов нескольких комплексных переменных и доказательство поточечной сходимости тригонометрического ряда.[4][5]
Мажоранта класса[править | править код]
Понятие мажоранты можно ввести на любом множестве, если на нём задана числовая функция. Мажорантой класса или подмножества является элемент, значение функции на котором является супремумом значений функции на этом классе или подмножестве. Подобные определения вводятся для упрощения изложения. [6]
Примечания[править | править код]
- ↑ Ограниченные множества. Мажоранты и миноранты. Дата обращения: 3 июня 2019. Архивировано 3 июня 2019 года.
- ↑ Математический энциклопедический словарь. — М.: «Сов. энциклопедия », 1988. — С. 847.
- ↑ МАЖОРА́НТА И МИНОРА́НТА : [арх. 3 июня 2019] // Ломоносов — Манизер. — М. : Большая российская энциклопедия, 2011. — С. 440. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 18). — ISBN 978-5-85270-351-4.
- ↑ Конспект установочных лекций к государственному экзамену по математике по направлению «Прикладные математика и физика» (СПбГУ). Дата обращения: 3 июня 2019. Архивировано 3 июня 2019 года.
- ↑ Комплексный анализ. Дата обращения: 3 июня 2019. Архивировано 23 ноября 2018 года.
- ↑ МАЖОРАНТЫ И МИНОРАНТЫ КЛАССА ГРАФОВ С ФИКСИРОВАННЫМИ ДИАМЕТРОМ И ЧИСЛОМ ВЕРШИН. Т. И. Федоряева. Дата обращения: 3 июня 2019. Архивировано 3 июня 2019 года.
Мажорируемые ряды
Опр. Функциональный ряд
называется мажорируемым в
области Х, если
такой сходящийся знакоположительный
числовой ряд
,
что выполняются в каждой точке Х
соотношения
.Соответствующий
числовой ряд называется
мажорантным.
Замечание. Мажорируемый ряд –
абсолютно сходящийся ряд.
Понятие о равномерной сходимости функционального ряда
Вопрос о том, при каких условиях сумма
ряда – функция непрерывная, когда
функциональный ряд можно почленно
дифференцировать и интегрировать
решается с помощью понятия равномерной
сходимости ряда.
Опр. Функциональный ряд называется
равномерно сходящимся на множестве
Х, если для
.
Замечание. Геометрическая иллюстрация:
у = S(х), у = S(х)
– ε, у = S(х) + ε.
Для
лежит в этой полосе.
Теорема. (Достаточный прзнак равномерной
сходимости ряда, признак Вейерштрасса).
Мажорируемый ряд является
рядом равномерно сходящимся.
Пример. Доказать, что ряд
сходится равномерно на всей числовой
оси.
ряд сходится равномерно на всей числовой
оси.
Свойства равномерно сходящихся рядов
Теорема 1. Если ряд
сходится равномерно на Х, на котором
его члены
непрерывны, то сумма ряда
S(x)
непрерывна на этом множестве.
Теорема 2. Если функции
непрерывны на Х и ряд сходится равномерно
на Х, то ряд,
полученный интегрированием
членов данного ряда также сходится
равномерно
на Х, причем
или
,
где
.
Теорема 3. Пусть функции
определены на множестве Х и имеют на
нем непрерывные производные
.
Если на этом множестве сходится ряд
и равномерно сходится ряд, составленный
из производных
,
то сумма S(x)
ряда
имеет производную, равную сумме ряда
,
т.е.
или
.
Степенные ряды
Степенные ряды – это простейшие
функциональные ряды.
Опр. Степенным рядом называется ряд
вида
(1) – степенной ряд
по степеням (х –с) . аn
– числа, коэффициенты ряда,с– число.
В простейшем случае с = 0, тогда ряд
(1) приобретает вид
(2) – степенной ряд по степеням х.
Очевидно, что путем подстановки
от первого ряда можно перейти ко второму,
поэтому теорию степенных рядов
рассматривают для ряда(2).
Теорема Абеля. Если степенной ряд
(2) сходится при
,
то он абсолютно
сходится для любого х,
удовлетворяющего условию
.
Если при
,
ряд (2) расходится, то он расходится для
любого х,
удовлетворяющего условию
.
Следствие. Для каждого степенного
ряда (2) существует число R
> 0, называемое
радиусом сходимости этого
ряда и обладающее следующими свойствами:
при
ряд (2) сходится абсолютно,
при
ряд (2) расходится .
Промежуток (-R,R)
называется интервалом сходимости
степенного ряда(2). На
концах интервала вопрос о
сходимости ряда решается индивидуально
для
каждого конкретного ряда.
Способы определения радиуса сходимости:
1) по признаку Даламбера, 2) по радикальному
признаку Коши.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
Теоретический минимум
В связи с функциональными рядами часто возникает вопрос о качестве их сходимости. Функциональные ряды помимо быстроты сходимости обладают
ещё одной важной характеристикой. Чтобы продемонстрировать её наглядно, обратимся сначала к функциональным последовательностям. Это
необходимо, так как сходимость ряда определяется сходимостью последовательности его частичных сумм.Итак, рассмотрим на отрезке
две последовательности
и
. На данном отрезке они
сходятся:.
На графиках ниже приведены первые двадцать функций обеих последовательностей (график первой функции отмечен красным цветом).
Как видно, сходимость последовательностей разная. Количественно это отличие можно описать следующим образом. Посмотрим, как сильно отклоняется
каждая следующая функция последовательности от предельной функции. В данном случае сравнивать нужно с тождественно равной нулю функцией.
Конечно, при разных значениях аргументаотклонения функций последовательности от нуля различны. Однако можно заметить, что
у функцийс ростом
максимальное отклонение функции от нуля постепенно уменьшается, чего не наблюдается
у функций. Это отличие и фиксируется с помощью понятия равномерной сходимости.
Дадим определение сходимости функциональной последовательности.
Последовательностьсходится на множестве
к функции
, если
.
Это определение мало отличается от определения сходящейся числовой последовательности. Подробный комментарий к этому определению
можно прочитать в теме “МА. Предел последовательности. Определение на языке “эпсилон-дельта”.Теперь обратим внимание на одну деталь: номер
, начиная с которого элемент последовательности начинает отличаться от предельной
функции не более чем на, зависит не только от
, но и от точки
. Иными словами, в определении
сходимости сказано, что рано или поздно для каждой точки множестванайдётся такой номер
. Другое дело, что для одних
точек он найдётся раньше, а для других – позже. Для “простой” сходимости это неважно.Последовательность
равномерно сходится на множестве
к функции
, если
Главное здесь в том, что фрагментпереместился внутрь утверждения, а номер
перестал зависеть от точки
. Т.е.
половина определения сохранилась: по-прежнему требуется, чтобы, начиная с некоторого номера, элементы последовательности отличались от
предельной функции не более чем на. Только теперь утверждается, что при заданном
это условие
выполнится для всех значенийсразу.
Вернёмся к двум первым графикам. Проведём горизонтальную линию. Она будет соответствовать некоторому значению
из определения
сходимости. Видно, что в случае функцийсколь бы велик ни был номер
, графики элементов последовательности
будут пересекать синюю прямую, т.е. не будет выполнено неравенствосразу для всех значений
–
равномерной сходимости нет. В случае функцийдля любого положения горизонтальной прямой найдётся элемент последовательности,
график которого находится целиком ниже этой прямой. Это и говорит о равномерной сходимости последовательности.
Критерий равномерной сходимости прост и в свете проведённых выше рассуждений понятен. Последовательность
равномерно сходится
на множествек функции
тогда и только тогда, когда
.
Продемонстрируем этот критерий на нескольких примерах.Пример 1.
И начнём с двух последовательностей, которые сразу были приведены в пример.Сразу отметим, что при
обе последовательности сходятся к тождественно равной нулю функции (убедитесь в этом!).
Рассмотрим функцию, где
– предельная функция. Выражение под модулем на рассматриваемом
отрезке неотрицательно, поэтому модуль можно снять. Чтобы найти, где эта разность достигает максимума, вычислим производную и приравняем
её к нулю:
.
Точкане соответствует максимуму в отличие от точки
. Таким образом,
.
Следовательно,
.
Это значит, что последовательность не является равномерно сходящейся. Это было видно и по графикам. Кстати, получившаяся
аналитически четверть как верхняя грань всех функций последовательности тоже прекрасно видна.Переходим к функции
, где
– предельная функция. Снова модуль можно снять. Ищем точку максимума:
,
точкаснова не соответствует максимуму.
.
В пределе припервая скобка стремится к
, а вторая – к нулю, следовательно,
.
Таким образом, последовательность сходится равномерно.Пример 2.
Исследовать на равномерную сходимость последовательностии
на интервале
.
Предельная функция в обоих случаях одна и та же – тождественно равная нулю
. Рассмотрим функцию
:
.
Очевидно, что.
Следовательно, последовательность не является равномерно сходящейся.Теперь рассмотрим функцию
:
.
Таким образом, последовательность сходится равномерно.Проиллюстрируем эти два примера графически. Изображены первые семь функций обеих последовательностей.
Пример 3.
Исследовать на равномерную сходимость последовательностьна интервале
.
Предельная функция здесь
. Рассмотрим функцию
:
.
Таким образом, последовательность сходится равномерно. Здесь тоже возможна графическая интерпретация, только строить нужно
графики функций.
-
Теоретический минимум (окончание)
Продолжим с функциональными рядами. Функциональный ряд сходится, если сходится последовательность его частичных сумм. Если эта сходимость
равномерная, то и ряд называется равномерно сходящимся. Следовательно, непосредственный способ установить, сходится ли ряд равномерно –
исследовать функциональную последовательность его частичных сумм, как показано выше. Однако этот способ может быть тяжело реализуемым.
Фактически он предполагает суммирование функционального ряда – а это более сложная задача. Поэтому существует набор теорем, позволяющих
ответить на вопрос о равномерной сходимости ряда без проведения его суммирования. Перед тем как обратиться к этим теоремам, укажем, что не может
равномерно сходиться ряд, последовательность членов которого не сходится равномерно к нулю. Обратное неверно: из того, что последовательность
общих членов ряда равномерно сходится к нулю, не следует равномерная сходимость ряда.Одна из часто используемых теорем – мажорантный признак Вейерштрасса. Рассмотрим ряд
. Если
,
а рядсходится, то ряд
равномерно сходится на множестве
.
Этот признак очень удобен в использовании.Приведём ещё два признака равномерной сходимости: Абеля и Дирихле.
Признак Абеля заключается в следующем. Если общий член ряда можно представить в виде, причём
последовательность
монотонна и ограничена:
, а ряд
равномерно сходится на множестве
, то ряд
равномерно сходится на множестве
.
Признак Дирихле основан тоже на представлении общего члена ряда в виде произведения
.
Теперь последовательностьпредполагается монотонной и равномерно сходящейся к тождественно равной нулю функции.
Частичные суммы рядапредполагаются равномерно ограниченными, т.е. любая частичная сумма для любого значения
по модулю
не превышает одного и того же числа. В этом случае рядравномерно сходится на множестве
.
Наконец, существует ещё критерий Коши равномерной сходимости ряда. Этот признак формализован несколько сложнее, так как формулируется
на языке эпсилон-дельта. Рядравномерно сходится на множестве
тогда и только тогда, когда
.
Почему так интересна равномерная сходимость ряда? Ответ заключается в том, что качество сходимости ряда лучше, если он сходится равномерно.
Этот ответ, конечно, ни на какую строгость не претендует, но отражает общую идею, чему способствуют и графические интерпретации. Вернитесь
ещё раз к самому первому графику темы и сравните, как сходятся две функциональные последовательности. Особенно обратите внимание на поведение
в окрестности правого конца отрезка элементов последовательности с ростом их номера. Несложно видеть, что в пределе поведение функции в этой
области становится “плохим”: резкий скачок вверх, а потом вниз. Другое дело, что в пределе этот скачок исчезает. Однако представьте себе, что
это последовательность частичных сумм некоторого функционального ряда. Такое поведение частичных сумм не может не сказаться на аналитических
свойствах. В первую очередь речь идёт о предельном переходе и дифференцировании ряда.На почленном дифференцировании ряда хотелось бы остановиться немного подробнее. Интересно то, что для того чтобы ряд можно было почленно
дифференцировать не требуется его равномерная сходимость. Требуется, однако, равномерная сходимость ряда, составленного из производных
от членов исходного ряда. В этом случае если сам ряд сходится к некоторой функции, то ряд производных сходится к функции
.
Строго говоря, ещё требуется непрерывная дифференцируемость членов исходного ряда.Примеры
Пример 1. Исследование на основе определения равномерной сходимости.
Исследовать на равномерную сходимость на отрезкеряд
.
В данном случае можно не прибегать к специальным признакам равномерной сходимости, так как легко найти частичные суммы ряда:
.
Следовательно,
Применим критерий равномерной сходимости функциональной последовательности:
.
Значит, последовательность не является равномерно сходящейся. Поэтому и ряд не сходится равномерно.
Ниже изображены графики нескольких первых частичных сумм (первая отмечена красным цветом). Отсутствие равномерной сходимости можно
увидеть непосредственно.
Пример 2. Использование критерия Коши.
Исследовать на равномерную сходимость на отрезкеряд
.
Здесь применим критерий Коши, для чего оценим сумму членов ряда, начиная с
-го, заканчивая
-м:
.
Таким образом, при выборекритерий Коши будет выполнен. Ряд сходится равномерно.
На графике ниже изображены кривые
для нескольких первых значений
(первая кривая красная, последняя –
зелёная). Видно, что последовательность частичных сумм сходится равномерно.
Пример 3. Использование признака Вейерштрасса.
Исследовать на равномерную сходимость на интервалеряд
.
Здесь удобно применить признак Вейерштрасса, так как несложно подобрать мажоранту для ряда. Найдём максимум общего члена ряда:
.
Следовательно,
.
Мажорирующий рядсходится. Поэтому исходный ряд сходится равномерно.
Пример 4. Использование признака Дирихле.
Исследовать на равномерную сходимость на интервалеряд
.
Применим признак Дирихле. Представим общий член ряда в виде произведения
.
Последовательность, монотонно убывая, стремится к нулю. Рассмотрим далее частичные суммы
:
.
Следовательно,
.
Здесь сыграло свою роль то обстоятельство, что концы заданного в условии промежутка не входят в рассмотрение, а потому знаменатель
последней дроби в нуль не обращается. Итак, исходный ряд сходится равномерно по признаку Дирихле.Пример 5. Использование критерия Коши.
Исследовать на равномерную сходимость на отрезкеряд
.
Как должно быть уже понятно, на данном отрезке исследовать ряд тем же методом, что и в предыдущем примере, не получится:
частичные суммы вспомогательного ряда не будут ограничены. Более того, мы сейчас с помощью критерия Коши покажем, что ряд на данном
промежутке не сходится равномерно. Для этого сначала запишем отрицание критерия Коши:
.
Выберем, тогда
.
Итак, для ряда выполнилось отрицание критерия Коши, следовательно, он не сходится равномерно.Пример 6. Почленное дифференцирование ряда.
Докажем, что рядможно почленно дифференцировать.
Непрерывная дифференцируемость членов ряда очевидна. Составим ряд производных:
.
Оценим общий член этого ряда:
.
Таким образом, подобран мажорирующий ряд, который сходится. Поэтому по признаку
Вейерштрасса ряд производных сходится равномерно. Следовательно, исходный ряд можно почленно дифференцировать.
Поделиться этой страницей


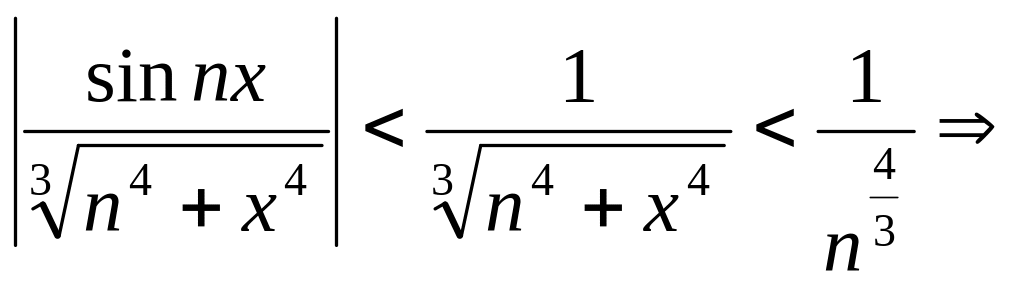
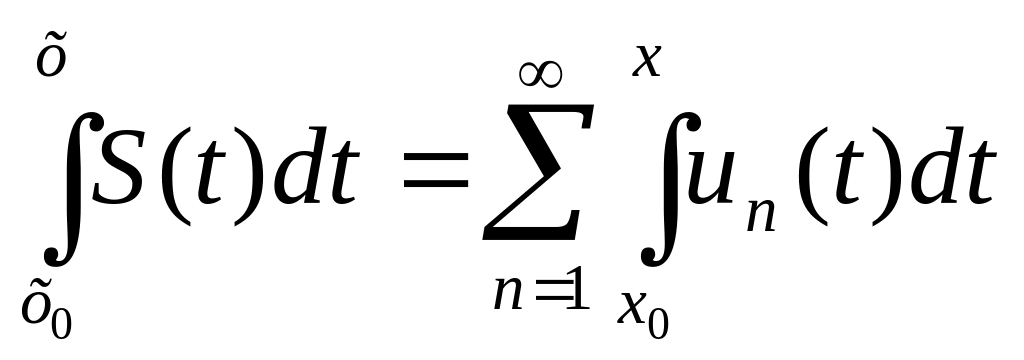
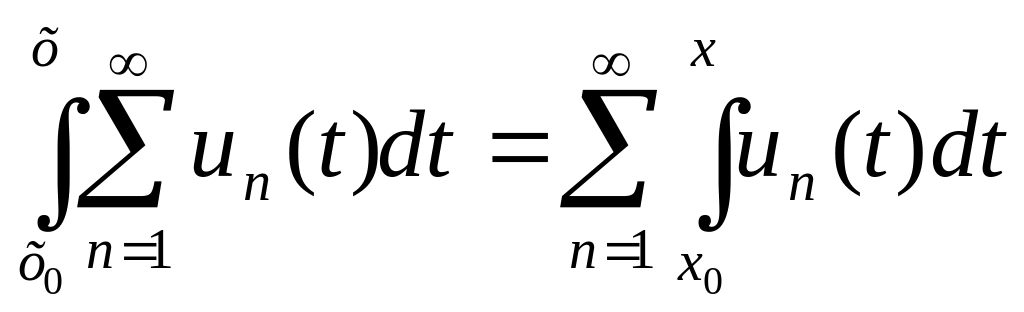
![[IMG]](http://corum.mephist.ru/tex/images/e6d5b5dafb82c2bf8b920a812188ac06.gif) две последовательности
две последовательности ![[IMG]](http://corum.mephist.ru/tex/images/60baf8688a8761e0887ed56b8d3b052b.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/557196d5c4a14eb07b4cf941ee4e7cea.gif) . На данном отрезке они
. На данном отрезке они ![[IMG]](http://corum.mephist.ru/tex/images/01973c4fcf99f9392ac204335b66827f.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_22354.png)
![[IMG]](http://corum.mephist.ru/tex/images/8725029ea89712eed8670bae64d30e47.gif) отклонения функций последовательности от нуля различны. Однако можно заметить, что
отклонения функций последовательности от нуля различны. Однако можно заметить, что![[IMG]](http://corum.mephist.ru/tex/images/2720faf89c8c7afaa601b654d5dfc6ca.gif) с ростом
с ростом ![[IMG]](http://corum.mephist.ru/tex/images/e4a3f5f7a18b1ed0ee22a93864ad15d8.gif) максимальное отклонение функции от нуля постепенно уменьшается, чего не наблюдается
максимальное отклонение функции от нуля постепенно уменьшается, чего не наблюдается![[IMG]](http://corum.mephist.ru/tex/images/cceba7796dff6e1337471f17dfa58e62.gif) . Это отличие и фиксируется с помощью понятия равномерной сходимости.
. Это отличие и фиксируется с помощью понятия равномерной сходимости.![[IMG]](http://corum.mephist.ru/tex/images/d3d7ca1e49b90a4f207622239e7e5d30.gif) сходится на множестве
сходится на множестве ![[IMG]](http://corum.mephist.ru/tex/images/474e6c59d39ab2b9f9eb79ab75b9da90.gif) к функции
к функции ![[IMG]](http://corum.mephist.ru/tex/images/465a703f084c610f250f9ab50ff3f895.gif) , если
, если![[IMG]](http://corum.mephist.ru/tex/images/0dfbb1f1952277d3351c7a74dd488828.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/e25ec8b0af895735d0fe10be2ae08fc9.gif) , начиная с которого элемент последовательности начинает отличаться от предельной
, начиная с которого элемент последовательности начинает отличаться от предельной![[IMG]](http://corum.mephist.ru/tex/images/80143d6aee9baf966ffc50105bdb03ad.gif) , зависит не только от
, зависит не только от ![[IMG]](http://corum.mephist.ru/tex/images/2cf4da0f3488b5e72afcf208a366d8d3.gif)
![[IMG]](http://corum.mephist.ru/tex/images/6242484dc53670f0bc666777edd72881.gif) переместился внутрь утверждения, а номер
переместился внутрь утверждения, а номер ![[IMG]](http://corum.mephist.ru/tex/images/473d3c0db88d8462d2683dcf8d5af2de.gif) сразу для всех значений
сразу для всех значений ![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_30235.png)
![[IMG]](http://corum.mephist.ru/tex/images/d9d0cca0719e945b6bd324f9397e95dc.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/3d336db67f13077e91bf3f036f10c170.gif) обе последовательности сходятся к тождественно равной нулю функции (убедитесь в этом!).
обе последовательности сходятся к тождественно равной нулю функции (убедитесь в этом!).![[IMG]](http://corum.mephist.ru/tex/images/7b9543087dab055e4ddec530dbf75f5f.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/aa3b8398382b2fa8b7907fabe565247c.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/1567ccbc3aa038b2ecac14e445922a7d.gif) не соответствует максимуму в отличие от точки
не соответствует максимуму в отличие от точки ![[IMG]](http://corum.mephist.ru/tex/images/4a6fba6d01a041214d350132610b2e67.gif) . Таким образом,
. Таким образом,![[IMG]](http://corum.mephist.ru/tex/images/ab75bc630356a8ee2ff62d35a19c974d.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/3b81b7b335827f0fdb2dd6246535e75b.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/e949c6b4203e11cd9b46c1faafdf196f.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/f821ff24d1597320831f8d6d9f1bf25a.gif) – предельная функция. Снова модуль можно снять. Ищем точку максимума:
– предельная функция. Снова модуль можно снять. Ищем точку максимума:![[IMG]](http://corum.mephist.ru/tex/images/74521daa542599c4d5bdbc84d9ea146e.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/279675419f7382391983f405a510bbef.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/5abcac1b9582ead544e656697991138c.gif) первая скобка стремится к
первая скобка стремится к ![[IMG]](http://corum.mephist.ru/tex/images/f9e39e0b67e2d96891d0b3fe60901ddd.gif) , а вторая – к нулю, следовательно,
, а вторая – к нулю, следовательно,![[IMG]](http://corum.mephist.ru/tex/images/8ab4c9e3061874827e4c5b013368b440.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/0372881fecd4e91ea9748d5acfa57732.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/249063194afccc93cffa9aeaaa7adb9d.gif) на интервале
на интервале ![[IMG]](http://corum.mephist.ru/tex/images/eddfb6b6092ae01853d619174220e3e1.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/cd7ff144f932551f18f3e59e6add1a6b.gif) . Рассмотрим функцию
. Рассмотрим функцию ![[IMG]](http://corum.mephist.ru/tex/images/2b3e5e1f038aacfa689e3a4b927c50f8.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/24a50a0a09e5b4c980b372312aced039.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/1525e0c62e27044dd5fd28650613cb07.gif) :
:![[IMG]](http://corum.mephist.ru/tex/images/18933002b98277e4e830d701073f43a1.gif)
![[IMG]](http://corum.mephist.ru/tex/images/9207f0e3189467c95bbf0cb1c5469907.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_32835.png)
![[IMG]](http://corum.mephist.ru/tex/images/1450c3155a2d2fa8f981b42cc456a4b9.gif) на интервале
на интервале ![[IMG]](http://corum.mephist.ru/tex/images/2788b81fd6e236ef370dc1e1e419a7d3.gif) . Рассмотрим функцию
. Рассмотрим функцию ![[IMG]](http://corum.mephist.ru/tex/images/c3e953c139ba3277cde1281416c94017.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/633f9240cee1b7cb1373701fe5b720a5.gif)
![[IMG]](http://corum.mephist.ru/tex/images/acc2dcf7df6bbf36a27a56e5da59d25a.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_7386.png)
![[IMG]](http://corum.mephist.ru/tex/images/657036f942343f4f352801ec9fe1df65.gif) . Если
. Если ![[IMG]](http://corum.mephist.ru/tex/images/a1c1f77d9cdeb05f30c1f993d9bbaecc.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/9731543076abca4e525c1af92a88b348.gif) сходится, то ряд
сходится, то ряд ![[IMG]](http://corum.mephist.ru/tex/images/50b0a06dc9d52baeb54bc066a2960ec3.gif) , причём
, причём ![[IMG]](http://corum.mephist.ru/tex/images/9db01290ce6c24a7198f1d4797a22b40.gif) монотонна и ограничена:
монотонна и ограничена:![[IMG]](http://corum.mephist.ru/tex/images/2ffcc7a0bbac8d02eaefc518d990fbde.gif) , а ряд
, а ряд ![[IMG]](http://corum.mephist.ru/tex/images/ecb9aac53a18de93faa8040f8c7b43f1.gif) равномерно сходится на множестве
равномерно сходится на множестве ![[IMG]](http://corum.mephist.ru/tex/images/104ab1ed99d11a33007bc334575e5b75.gif) по модулю
по модулю ![[IMG]](http://corum.mephist.ru/tex/images/38672be0d3fb4d5cbe87c4eaf296d55f.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/d39100c8d71f9470466150d363e30395.gif) , то ряд производных сходится к функции
, то ряд производных сходится к функции ![[IMG]](http://corum.mephist.ru/tex/images/e2d706e22ff108b7366e3873cf9f4c78.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/9e22a4b4cac8d6c4dfa5c999247620a8.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/83aa550f5fd1b6b7fa7a7773c9244004.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/d9fa0e4d255794716ce31adca827033a.gif)
![[IMG]](http://corum.mephist.ru/tex/images/b703b7d495321d088d997113ded2bd33.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_1227.png)
![[IMG]](http://corum.mephist.ru/tex/images/4d26c010df5b87dc823161955cda07a6.gif) ряд
ряд ![[IMG]](http://corum.mephist.ru/tex/images/cb2ee526fdf9d69698d592651e798818.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/f52ba22baf75438bb1b02f476954c023.gif) -м:
-м:![[IMG]](http://corum.mephist.ru/tex/images/31f02cc9f9940830f4a9c5d6a0e1db26.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/f87f263e9b9a573b12f3722238064a5f.gif) критерий Коши будет выполнен. Ряд сходится равномерно.
критерий Коши будет выполнен. Ряд сходится равномерно.![[IMG]](http://corum.mephist.ru/tex/images/c39429b54e60ea37e3e459583733baa3.gif) для нескольких первых значений
для нескольких первых значений ![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_5155.png)
![[IMG]](http://corum.mephist.ru/tex/images/a0fb72f51317109ae2e3eb9ed6bb48ee.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/c03180d4b670a3d2949a12e9910c85d7.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/8997719742f59ef545c9f754f871ac0e.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/13b82d505ae0a508c91fe55d74f96781.gif) сходится. Поэтому исходный ряд сходится равномерно.
сходится. Поэтому исходный ряд сходится равномерно.![[IMG]](http://corum.mephist.ru/tex/images/5f4c9e635964c96f74abd23780dbbbfa.gif) ряд
ряд ![[IMG]](http://corum.mephist.ru/tex/images/793b0b07baeda90e26fe3f50c56e4edb.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/1be8b7779d5869869d544d9edd7ca6ed.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/e785a7d7342a4a5d2ceff4727cec0857.gif) , монотонно убывая, стремится к нулю. Рассмотрим далее частичные суммы
, монотонно убывая, стремится к нулю. Рассмотрим далее частичные суммы ![[IMG]](http://corum.mephist.ru/tex/images/9fe90220cb8564f83ef3ab730e2ea37c.gif) :
:![[IMG]](http://corum.mephist.ru/tex/images/93f1930ab8bf72c3c172859a9a51c660.gif)
![[IMG]](http://corum.mephist.ru/tex/images/86bf0d7c7d60d7f5a61be31d5eaa8a10.gif)
![[IMG]](http://corum.mephist.ru/tex/images/28bb68b0f4ee0141dd4a9945ee206c14.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/fc0d1e85731519ec4bceb827f16d1204.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/0fdad617b5f6227e089bf336792a4827.gif) ряд
ряд ![[IMG]](http://corum.mephist.ru/tex/images/3a6f523cf05dce34bed746fe92b6c5e2.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/94210f4de5e2aa3c7e6a4c71851405ea.gif) , тогда
, тогда![[IMG]](http://corum.mephist.ru/tex/images/c799327e92ec9dfd324460000389a023.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/aab2094d918b5c31e212c51471ff513b.gif) можно почленно дифференцировать.
можно почленно дифференцировать.![[IMG]](http://corum.mephist.ru/tex/images/3884d60476e728e423dc2b78b0195c4a.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/608cd39a3bacf54747200a37a7200171.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/5e1507573b64f1632232b1996dab9b16.gif) , который сходится. Поэтому по признаку
, который сходится. Поэтому по признаку