Медиана равна половине гипотенузы прямоугольного треугольника!
Почему??? При чём тут прямой угол?
Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник.
Ты заметил, что наш треугольник ( displaystyle ABC) – ровно половина этого прямоугольника?
Проведём диагональ ( displaystyle BD):
Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам?
Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, ромб…»
Но одна из диагоналей – ( displaystyle AC) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы ( displaystyle Delta ABC).
Она называлась у нас ( displaystyle M).
Значит, половина второй диагонали – наша медиана ( displaystyle BM). Диагонали равны, их половинки, конечно же, тоже. Вот и получим ( displaystyle BM=MA=MC)
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника?
Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.
Решение задач на свойства медианы в прямоугольном треугольнике
Давай посмотрим, как это свойство помогает решать задачи.
Задача №1:
В ( displaystyle Delta ABC) стороны ( displaystyle AC=5); ( displaystyle BC=12). Из вершины ( displaystyle C) проведена медиана ( displaystyle CN).
Найти ( displaystyle AB), если ( displaystyle AB=2CN).
Рисуем:
Сразу вспоминаем, это если ( displaystyle CN=frac{AB}{2}), то ( displaystyle angle ACB=90{}^circ )!
Ура! Можно применить теорему Пифагора!
Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})
( A{{B}^{2}}={{5}^{2}}+{{12}^{2}}=169)
Ответ: ( AB=13)
А в следующей задаче пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?
Запомни очень важный факт:
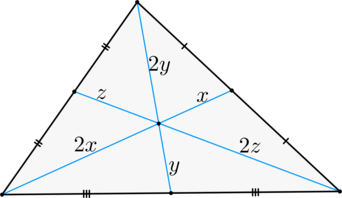
Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении ( 2:1), считая от вершины.
Сложно? Смотри на рисунок:
Медианы ( displaystyle AM), ( displaystyle BN) и ( displaystyle CK) пересекаются в одной точке.
Запомни:
- ( displaystyle AO) – вдвое больше, чем ( displaystyle OM);
- ( displaystyle BO) – вдвое больше, чем ( displaystyle ON);
- ( displaystyle CO) – вдвое больше, чем ( displaystyle OK).
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении ( displaystyle 2:1 ), считая от вершины.
Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?
1. Медианы треугольника пересекаются в одной точке.
2. Точкой пересечения медианы делятся в отношении ( displaystyle 2:1 ), считая от вершины.
Давай попробуем разгадать секрет этой теоремы, то есть доказать ее.
Доказательство теоремы о трех медианах треугольника
Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой ( displaystyle E).
Соединим точки ( displaystyle N) и ( displaystyle K). Что получилось?
Конечно, ( displaystyle NK) – средняя линяя ( displaystyle triangle ABC). Ты помнишь, что это значит?
- ( displaystyle NK) параллельна ( displaystyle AC);
- ( displaystyle NK=frac{AC}{2}).
А теперь проведем ещё одну среднюю линию: отметим середину ( displaystyle AE) – поставим точку ( displaystyle F), отметим середину ( displaystyle EC) — поставим точку ( displaystyle G).
Теперь ( displaystyle FG) – средняя линия ( displaystyle triangle AEC). То есть:
- ( displaystyle FG) параллельна ( displaystyle AC);
- ( displaystyle FG=frac{AC}{2}).
Заметил совпадения? И ( displaystyle NK) , и ( displaystyle FG) – параллельны ( displaystyle AC). И ( displaystyle NK=frac{AC}{2}), и ( displaystyle FG=frac{AC}{2}).
Что из этого следует?
- ( displaystyle NK) параллельна ( displaystyle FG);
- ( displaystyle NK=FG)
Посмотри теперь на четырехугольник ( displaystyle NKGF). У какого четырехугольника противоположные стороны (( displaystyle NK) и ( displaystyle FG)) параллельны и равны?
Конечно же, только у параллелограмма!
Значит, ( displaystyle NKGF) – параллелограмм. Ну и что?
А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.
Снова смотрим на рисунок.
Получилось что:
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике по треугольникам
Лучше всего смотреть это видео с ручкой и тетрадкой в руках. То есть ставьте видео на паузу и решайте задачи самостоятельно.
Помните, понимать и уметь решать — это два, совершенно разных навыка. Очень часто вы понимаете как решить задачу, но не можете это сделать. Или допускаете ошибки, или просто теряетесь и не можете найти ход решения.
Как с этим справиться?
Нужно решать много задач. Другого способа нет. Вы должны совершить свои ошибки, чтобы научиться их не допускать.
ЕГЭ №6 Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и «обычные» треугольники.
ЕГЭ №6 Прямоугольный треугольник, теорема Пифагора, тригонометрия
Большинство задач в планиметрии решается через прямоугольные треугольники. Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Но на уроках этой темы мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше.
И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ №16. Подобие треугольников. Задачи н доказательство
Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Пусть дан треугольник ![]() , длины сторон которого соответсвенно равны
, длины сторон которого соответсвенно равны ![]() :
:
Докажем, что длину медианы ![]() , проведенной из вершины
, проведенной из вершины ![]() можно выразить через длины сторон треугольника с помощью такой формулы:
можно выразить через длины сторон треугольника с помощью такой формулы:
![]()

1. Достроим данный треугольник до параллелограмма.

2. Из треугольника ![]() найдем косинус угла
найдем косинус угла ![]() с помощью теоремы косинусов.
с помощью теоремы косинусов.
![]()
![]()
Отсюда ![]() (1)
(1)
3. Так как ![]() (по свойству односторонних углов),
(по свойству односторонних углов), ![]()
4. Из треугольника ![]() выразим сторону
выразим сторону ![]() :
:
![]()
![]() (по свойству параллелограмма)
(по свойству параллелограмма)
![]()
Подставим выражение (1) для ![]()
![]()
![]()
![]()
Утверждение доказано.
И. В. Фельдман, репетитор по математике.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение высоты, биссектрисы и медианы треугольника
(blacktriangleright) Высота треугольника может упасть как на сторону, так и на ее продолжение. Второй случай возможен только если треугольник тупоугольный и высота проведена из вершины острого угла.
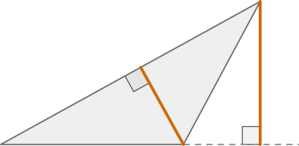
(blacktriangleright) Все медианы треугольника пересекаются в одной точке.
Все высоты (или их продолжения) пересекаются в одной точке.
Все биссектрисы пересекаются в одной точке.
(blacktriangleright) В равнобедренном треугольнике биссектриса, высота и медиана, проведенные к основанию, совпадают (отрезок (BO,)).
Обратно: если в треугольнике совпадают биссектриса и медиана (биссектриса и высота, высота и медиана), проведенные к одной стороне, то этот треугольник равнобедренный.
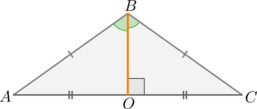
(blacktriangleright) В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Обратно: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.

(blacktriangleright) Медианы треугольника своей точкой пересечения делятся в отношении (2:1), считая от вершины.
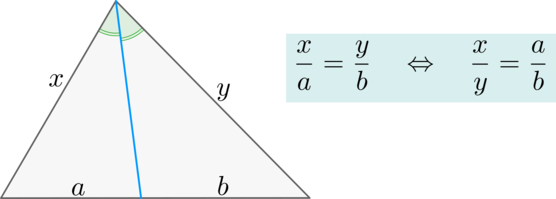
(blacktriangleright) Биссектриса треугольника делит сторону, к которой она проведена, на отрезки, пропорциональные прилежащим сторонам.
Обратно: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
(blacktriangleright) Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Обратно: каждая точка биссектрисы угла равноудалена от его сторон.
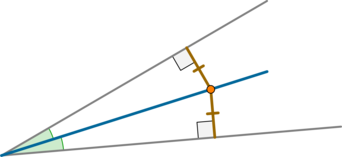
Задание
1
#234
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): (AB = BC), (BM) – биссектриса, (AC = 5). Найдите (AM).
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой, тогда (BM) – медиана и (AM = MC). Таким образом, (5 = AC = AM + MC = 2cdot AM), откуда находим (AM = 2,5).
Ответ: 2,5
Задание
2
#235
Уровень задания: Равен ЕГЭ
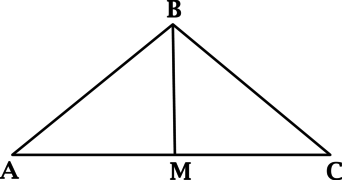
В треугольнике (ABC): (BM) – высота, причем (AM = MC), (angle ABM = 28^{circ}). Найдите (angle ABC). Ответ дайте в градусах.
в треугольниках (ABM) и (BMC):
(AM = MC),
(angle AMB = angle BMC),
(MB) – общая,
тогда треугольники (ABM) и (BMC) равны по двум сторонам и углу между ними и, значит, (AB = BC), то есть треугольник (ABC) – равнобедренный. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой, значит (angle MBC = angle ABM = 28^{circ}), тогда (angle ABC = 2cdot angle ABM = 56^{circ}).
Ответ: 56
Задание
3
#236
Уровень задания: Равен ЕГЭ
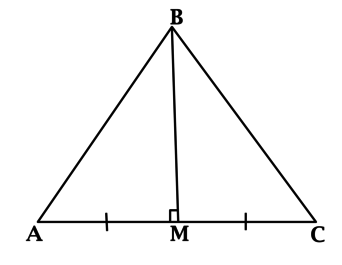
В треугольнике (ABC): (angle C = 90^{circ}), (CE) – медиана, (angle ACE = 50^{circ}). Найдите (angle B). Ответ дайте в градусах.
(angle ECB = angle ACB – angle ACE = 40^{circ}). В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда (CE = BE), значит треугольник (CEB) – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда (angle B = angle ECB = 40^{circ}).
Ответ: 40
Задание
4
#237
Уровень задания: Равен ЕГЭ
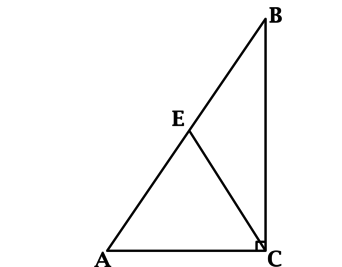
В треугольнике (ABC): (angle B = 90^{circ}), (BE) – медиана, (angle CBE = 25^{circ}). Найдите (angle AEB). Ответ дайте в градусах.
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда (CE = BE), значит треугольник (CEB) – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда (angle C = angle CBE = 25^{circ}).
Так как внешний угол треугольника равен сумме двух углов треугольника не смежных с ним, то (angle AEB = angle C + angle CBE = 50^{circ}).
Ответ: 50
Задание
5
#1766
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): (angle B = 90^{circ}), (BE) – медиана, (angle CBE = 22^{circ}). Найдите (angle BAC). Ответ дайте в градусах.

В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда (AE = BE), значит треугольник (AEB) – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle ABE).
Так как (angle B = 90^{circ}), (angle CBE = 22^{circ}), то (angle ABE = 90^{circ} – 22^{circ} = 68^{circ}), откуда (angle
BAC = 68^{circ}).
Ответ: 68
Задание
6
#239
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): (AD) и (BE) – высоты, пересекающиеся в точке (F), (angle EFD = 104^{circ}). Найдите (angle C). Ответ дайте в градусах.
(angle AFE = 180^{circ} – angle EFD = 76^{circ}), тогда (angle FAE = 90^{circ} – angle AFE = 14^{circ}) (так как (angle FEA = 90^{circ})). Треугольник (ADC) – прямоугольный. (angle C = 90^{circ} – angle FAE = 76^{circ}).
Ответ: 76
Задание
7
#240
Уровень задания: Равен ЕГЭ
В треугольнике (ABC): (CE) и (BF) – высоты, пересекающиеся в точке (T), (angle CTB = 152^{circ}). Найдите (angle A). Ответ дайте в градусах.
(angle FTC = 180^{circ} – angle CTB = 28^{circ}), тогда (angle TCF = 90^{circ} – angle FTC = 62^{circ}) (так как (angle TFC = 90^{circ})). Треугольник (AEC) – прямоугольный. (angle A = 90^{circ} – angle TCF = 28^{circ}).
Ответ: 28
Если выпускник планирует сдавать ЕГЭ по математике базового уровня и при этом стремится получить конкурентные баллы, ему непременно следует научиться решать задачи, в которых требуется найти высоту треугольника. Подобные планиметрические задания из года в год встречаются в аттестационном испытании. Это означает, что справляться с задачами ЕГЭ, в которых искомой величиной является высота треугольника, должны школьники с любым уровнем подготовки.
Полезная информация
Задачи ЕГЭ, требующие найти угол между высотой и медианой или другую величину треугольника, зачастую можно решить, вспомнив основные понятия из базового школьного курса. При этом рекомендуется следовать определенному алгоритму. Вначале сделайте чертеж. Затем нанесите на него все известные данные согласно условию. После этого стоит определить все геометрические понятия (биссектриса, медиана треугольника и т. д.), которые известны и которые необходимо найти в задании ЕГЭ. Выполнив это, вспомните относящиеся к ним теоремы и отразите на чертеже все соотношения между элементами, которые из них следуют логически. Приведем пример. Если в задаче ЕГЭ встречается понятие «биссектриса угла треугольника», стоит вспомнить его определение и основные свойства, после чего найти и отразить на сделанном чертеже равные или пропорциональные отрезки и углы.
Как подготовиться к экзамену?
Задания в ЕГЭ на нахождение угла между биссектрисами треугольника, а также на вычисление отношения подобных треугольников вызывают у вас затруднения? Образовательный портал «Школково» поможет вам в решении этой проблемы. С нами вы сможете повторить материал по темам, которые являются для вас сложными. Наши специалисты собрали и изложили всю теоретическую информацию в максимально доступной и понятной форме.
Для каждого задания на портале вы найдете правильный ответ и описание алгоритма решения. Практиковаться можно как с простыми упражнениями, так и с более сложными. Тренироваться в решении задач на нахождение угла между биссектрисой и медианой треугольника, которые встречаются в ЕГЭ, выпускники могут в режиме онлайн, находясь в любом регионе России. Справившись в заданием, учащиеся имеют возможность сохранить его в разделе «Избранное», а затем при необходимости обсудить его с преподавателем в школе или репетитором.

УСТАЛ? Просто отдохни
Треугольник как основа стереометрии
Помимо этого, в 10 и 11 классах в учебную программу добавляется так называемая стереометрия. Данный раздел геометрии отвечает за различные предметы в трехмерном пространстве. Если в классической планиметрии основой для всего является точка, то в стереометрии на первый план выходит ребро. Именно с его помощью и происходит построение большинства геометрических объектов в стереометрии. Но есть 1 тема, которая объединяет 2 разные раздела геометрии – треугольник и все, что с ним связано. Большинство объектов в стереометрии состоят из множества небольших плоскостей с тремя или четырьмя углами, которые и являются основным объектом построения на ряду с ребром. Соответственно – для нахождения площади объемных шестиугольников, в первую очередь, необходимо знать все необходимые формулы и термины. Так, всего из одной вершины этой сложной геометрической фигуры можно прочертить сразу 4 различных прямых:
- Биссектрису;
- Перпендикуляр;
- Высоту;
- Медиану.
И если первая – просто делит угол пополам, а срединный перпендикуляр и высота зачастую являются одним понятием, медиана имеет множество своих индивидуальных и необычных признаков.
Медианой называют прямую, проведенную от угла до середины стороны, находящейся напротив выбранной вершины. Так, в зависимости от длины сторон, данный луч может соответствовать остальным отрезкам.
Важно! Также необходимо понимать, что, в отличие от перпендикуляра, прямая необязательно будет проведена к стороне под прямым углом. Благодаря этому, такой вид отрезков имеет несколько характерных только для него необычных свойств.
На плоскости медиана изображается как обычная линия, проведенная от вершины до противоположного угла. Причем на стороне, которую прямая делит пополам, обычно слева и справа ставятся 2 маленькие черточки. С их помощью как раз и показывается, что получившиеся отрезки являются равными (рис.1).
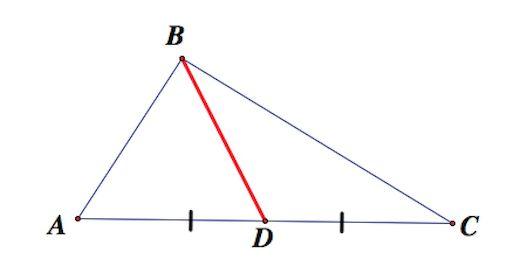
Рис. 1. Медиана
Свойства
Медиана, независимо от типа треугольника, имеет 5 характерных черт:
- Если нарисовать из каждой вершины по одной прямой, то можно найти центр тяжести. Именно место пересечения всех 3 лучей и будет точкой равновесия.
- Также, переплетаясь, они рассекают объект на 6 одинаковых по площади сегментов.
- Исходя из этого, можно сделать вывод, что 1 луч рассекает треугольник на 2 куска с равной площадью. В случае равнобедренных треугольников и с равными сторонами получившиеся сегменты даже являются симметричными.
- Самой большей стороне соответствует самая маленькая прямая. В случае равносторонней фигуры, соответственно, все 3 будут иметь одну и ту же длину.
- Соединяясь, лучи делят друг друга в соотношении 1 к 2.
Специфические свойства
Как ни странно, благодаря наличию одинаковых по длине сторон, равнобедренные и равносторонние треугольники имеют некоторые необычные признаки:
- Во-первых, в равностороннем – медианы, пересекаясь, создают 6 не только равных по площади, но и идеально симметричных треугольника.
- Помимо этого, в случае объектов с равными сторонами, начерченная прямая является одновременно и высотой, и биссектрисой.
- В равнобедренных – линия, нарисованная к основанию, также одновременно является перпендикуляром, остальные же 2 – просто равны между собой.
Первоначально тема дается на изучение в 7 классе. Позже встретить ее можно как на ОГЭ, так и в ЕГЭ. Именно из-за присутствия в экзаменах сразу двух заданий, связанных с темой, так важно ее регулярное повторение. Смотрите также наглядный разбор всех свойств медианы в предложенном видео.
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Определение
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Определение
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Определение
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Определение
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Задание 25OM21R
В треугольнике АВС известны длины сторон АВ=36, АС=54, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите СD.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 900.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
AEAB=ABAF откуда по свойству пропорции АВ2=АЕ∙АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
AEAD=ACAF ; откуда выразим AD=AE∙AFАC=AE∙AFAC
Теперь рассмотрим наши два полученных равенства: АВ2=АЕ∙АF и AD=AE∙AFAC
Видим, что 362=АЕ∙АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD=AE∙AFAC=36254=24
Теперь найдем CD=AC-AD=54-24=30
Ответ: 30
pазбирался: Даниил Романович | обсудить разбор
Задание 18OM21R
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор
Задание 15OM21R
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 7.7k
