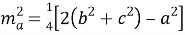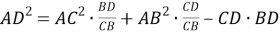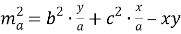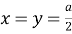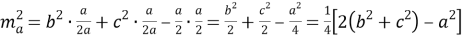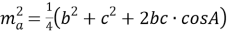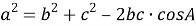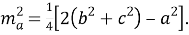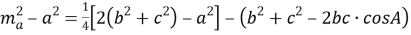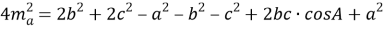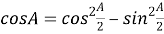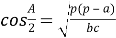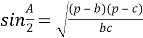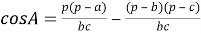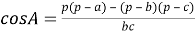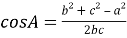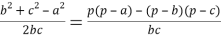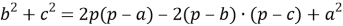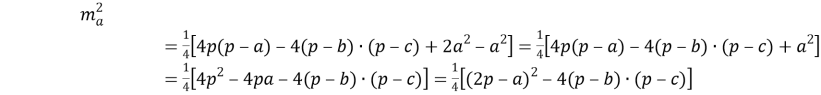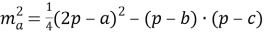Медиана в квадрате как найти

Медиана бывает, например, в треугольнике.

Медианой треугольника в геометрии называется отрезок, соединяющий какую-либо вершину этого треугольника с серединой противолежащей стороны.

В произвольном треугольнике ABC длины медиан, проведённых к сторонам a, b, c, можно найти по следующим формулам:

ma = [sqrt (2*b^2 + 2*c^2 – a^2)]/2

mb = [sqrt (2*a^2 + 2*c^2 – b^2)]/2

mc = [sqrt (2*a^2 + 2*b^2 – c^2)]/2

ma, mb, mc — длины медиан треугольника (соответственно: медиана к стороне a; медиана к стороне b; медиана к стороне c);

a, b, c — длины сторон треугольника;

^ — знак степени;

sqrt — обозначение квадратного корня.

Подробная информация о медианах треугольника, в том числе и том, как их найти (в смысле рассчитать их длины), находится здесь.

Если же Вас, допустим, интересует медиана в статистике, то я не прочь рассказать и о ней.

Медиана — это одна из характеристик статистического ряда.

Она вычисляется по двум простым правилам:

1) Если количество членов в ряду нечётное, то медиана равна среднему члену ряда;

2) Если количество членов в ряду чётное, то медиана равна полусумме двух центральных членов (тех, которые стоЯт в центре ряда).

Допустим, имеем ряд: 7, 2, 3, 9, 6.

Количество членов здесь нечётное. Медианой здесь будет число 3.

Если же убрать последний член нашего исходного ряда, то получится ряд: 7, 2, 3, 9.

Здесь ужЕ чётное количество членов, а значит, медиана будет равна (2 + 3)/2 = 2,5 (две целых пять десятых).

О медиане в статистике читайте здесь.

Библиографическое описание:

Магомедов, С. А. Квадрат длины медианы в произвольном треугольнике / С. А. Магомедов, В. В. Акопов. — Текст : непосредственный // Юный ученый. — 2022. — № 5 (57). — С. 66-68. — URL: https://moluch.ru/young/archive/57/3057/ (дата обращения: 18.05.2023).



В






данной статье рассматривается вывод формулы длины медианы в произвольном треугольнике. Вывод формулы разными способами даёт возможность учащимся повторить широкий спектр геометрических фактов, совершенствовать навыки применения разных методов и приёмов решения задач, способствует более глубокому и прочному пониманию и запоминанию материала.

Ключевые слова:



медиана, длина, полупериметр, произвольный треугольник.

Математика — это искусство называть разные вещи одним и тем же именем.

А. Пуанкаре

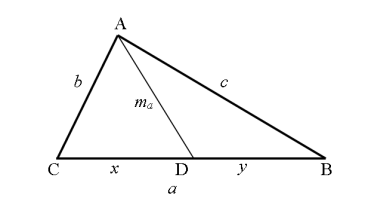
Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны (рис. 1). Медиана, соединяющая вершину

A

треугольника с серединой стороны

a

, обозначается

m

_a


.

Рис. 1

На сегодня известны две формулы квадрата длины медианы в произвольном треугольнике:

1. Через стороны треугольника:

, (1).

где

a, b, c

— стороны треугольника,

x

,

y

— отрезки основания медианы,

A, B, C

— углы треугольника.

Докажем эту формулу, для чего воспользуемся теоремой Стюарта: Если точка

D

лежит на стороне BC треугольника

АВС

(рис.1), то имеет место следующее равенство:

или

, тогда, учитывая, что

, будем иметь:

, что и требовалось доказать.

Задача. В треугольнике

АВС

(рис.1) проведена медиана

АD

. Известно, что

b=8

,

c=10

и

m

_a


=7. Найти

a

.

1. Через две стороны и угол:

   

   , (2).

Докажем эту формулу, для чего рассмотрим треугольник

АВС

(рис.1) со сторонами

a, b

и

c

. Из вершины

А

на сторону

СВ=a

опустим медиану

АD=m

_a


. Из треугольника

АВС

по теореме косинусов, имеем:

. С другой стороны воспользуемся выражением (1):

Используя эти два выражения, получим:

, отсюда

или

, что и требовалось доказать.

Задача. В треугольнике

АВС

(рис.1) проведена медиана

АD

. Известно, что

b=8

,

c=10

и

m

_a


=7. Найти угол

А

.

Рассмотрим зависимость квадрата длины медианы в произвольном треугольнике через полупериметр и стороны.

Используя формулу двойного угла

с учётом, что

и

, будем иметь:

, отсюда

, (3). Из треугольника

АВС

по теореме косинусов имеем:

, отсюда

, (4). Используя выражения (3) и (4), получим:

, отсюда

, (5). Используя выражения (1) и (5), будем иметь:

, отсюда

, (6).

Таким образом, квадрат длины медианы произвольного треугольника равен одной четвёртой квадрата разности периметра и одной из сторон треугольника без произведения разностей полупериметра и каждой из двух других его сторон.

Задача. В треугольнике

АВС

(рис.1) с полупериметром

21см

и сторонами

b=14см

и

c=12см

из вершины

А

проведена медиана

m

_a


. Найти квадрат медианы.

Литература:

1. Выгодский М. Я. Справочник по элементарной математике. Москва. «Наука». 1986.
2. Некрасов В. Б. Школьная математика. Санкт-Петербург. «Авалон». 2006.

Есть, но её обычно изучают в виде задачи о поиске медианы треугольника через три стороны. Но её можно представить и в виде теоремы, которую можно сформулировать так:

Теорема о медиане. Квадрат медианы треугольника равен полусумме квадратов прилежащих сторон (между которыми проведена медиана) минус четверть квадрата противолежащей стороны (к которой проведена медиана).

С помощью формулы это записывается так. Если есть треугольник со сторонами a, b и c, и к стороне c проведена медиана m, то справедливо равенство:

m² = a²/2 + b²/2 – c²/4

Доказать теорему можно, рассмотрев один из треугольников, на которые данный треугольник делит эта медиана: в нём известны две стороны (одна – это сторона исходного треугольника, другая – половина другой стороны исходного треугольника), а косинус угла между ними (это угол в исходном треугольнике) можно найти из теоремы косинусов через три стороны. Сторона против этого угла – данная медиана.

Или же достроив треугольник до параллелограмма, удвоив медиану и воспользовавшись теоремой, утверждающей, что сумма квадратов диагоналей параллелограмма равен сумме квадратов всех его сторон. Две стороны параллелограмма – это стороны треугольника, одна диагональ – третья сторона, а вторая – удвоенная медиана. Отсюда с² + (2m)² = a² + b² + a² + b², откуда следует утверждение теоремы.

В частном случае, если треугольник прямоугольный, а медиана проведена из вершины прямого угла, то a² + b² = c². Подставляя это в формулу, получаем m² = c²/2 – c²/4, откуда m² = с²/4 и m = c/2, и мы получаем всем известное утверждение о медиане прямоугольного треугольника, равной половине гипотенузы.

Все формулы медианы треугольника

Определение и свойства медианы прямоугольного треугольника

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми ( Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.

• BC = 2AD
• AD = BD = DC

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b 2 = с 2 – a 2 = 20 2 – 12 2 = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.

Все формулы медианы прямоугольного треугольника

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.

Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).

M – медиана

R – радиус описанной окружности

O – центр описанной окружности

с – гипотенуза

a, b – катеты

α – острый угол CAB

Медиана равна радиусу и половине гипотенузы, ( M ):

Формула длины через катеты, ( M ):

Формула длины через катет и острый угол, ( M ):

Медиана в прямоугольном треугольнике

Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы.

Все медианы прямоугольного треугольника пересекаются в одной точке и делятся этой точкой в отношении два к одному, считая от вершины:

Из всех медиан прямоугольного треугольника в задачах чаще всего речь идет о медиане, проведенной к гипотенузе. Это связано с ее свойствами.

Свойства медианы, проведенной к гипотенузе:

1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

(в следующий раз рассмотрим доказательство этого свойства)

2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

Пользуясь свойствами прямоугольного треугольника, длины медиан прямоугольного треугольника можно выразить через катеты и острые углы.

Например:

12 Comments

Информация очень хорошая. Правда не помогла мне решить задачу, которую мой сын не решил на контрольной. приведу условие:
Из прямого угла треугольника проведена медиана на гипотенузу. Длина медианы 6см. Определить катеты.

Петр, данных для определения катетов недостаточно. Длина гипотенузы в 2 раза больше длины медианы — 12 см. Это всё, что можно сказать по данным условия.

не правда надо провести высоту из прямого угла дальше все получится. один катет равен 6 а второй 2 корня из 22

Сумма квадратов катетов равна квадрату гипотенузы. Проверим 6^2+(2*корень из 22)^2
=36+4*22=36+88=124. Квадрат гипотенузы 12^2=144

попробуйте составить уравнение,обозначив 1 из катетов через х а 2-ой катет обозначьте буквами…x^2+BC^2=12^2…да числа не очень,но это 1 способ..решаю дальше:BC^2=12^2-x^2
BC^2=11x
X^2+11X=144
X^2=12
x(1 катет)=корню из 12,а «-ой катет=11 корней из 12….решал на основе теоремы пифагора

задача имеет бесконечное кол-во решений. решение возможно только в виде формулы или графика, где описана зависимость между катетами и гипотенузой

Да просто треугольник медианой делится на два треугольника с одинаковыми катетами, а дальше как уже предлагалось выше Пифагор во спасение))

А кто вам сказал, что медиана в прямоугольном треугольнике является еще и высотой? Откуда у вас два треугольника с одинаковыми катетами?

Спасибо за понятное объяснение, но у нас задача немного другая.
В прямоугольном треугольнике АВС угол С= 90 градусов,медиана ВВ1 равна 10 см.Найдите медианы АА1 СС1, если известно, что АС=12 см.( используя т.Пифагора.

1) Рассмотрим треугольник BB1C. В нём угол С равен 90 градусов, BB1=10 см, B1C=6 см (так как BB1 — медиана). По теореме Пифагора находим BC: BC=8 см. 2) Рассмотрим треугольник AA1C. В нём угол С равен 90 градусов, AC=12 см, AA1=4 см (так как BB1 — медиана). По теореме Пифагора находим AA1: AA1=4√10 см.3) Из треугольника ABC по теореме Пифагора найдём AB: AB=4√13 см. 4) CC1=1/2 AB (как медиана, проведённая к гипотенузе), CC1=2√13 см.
Где-то так.

[spoiler title=”источники:”]

http://www-formula.ru/medianrectangulartriangle

[/spoiler]