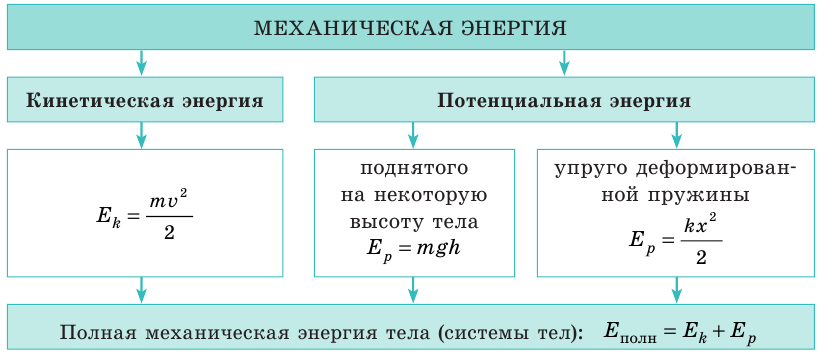
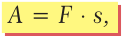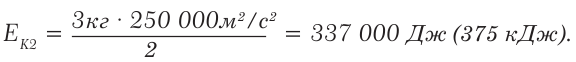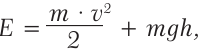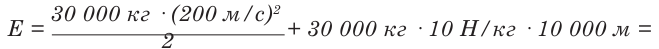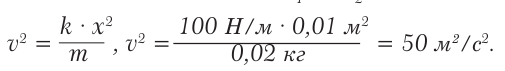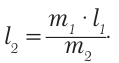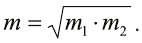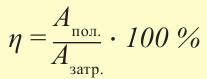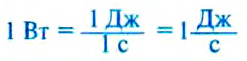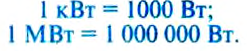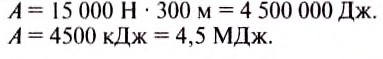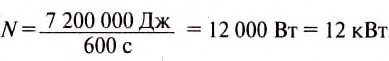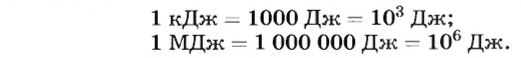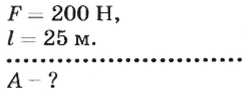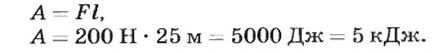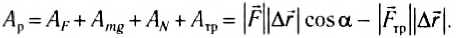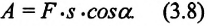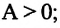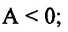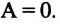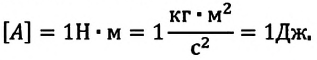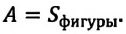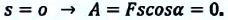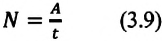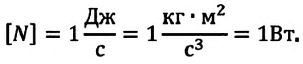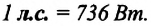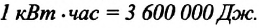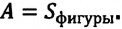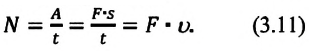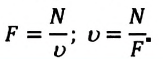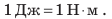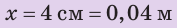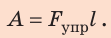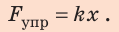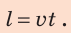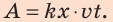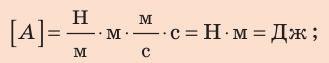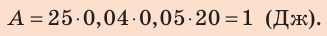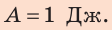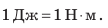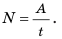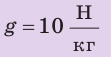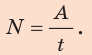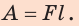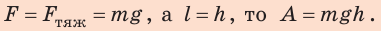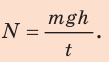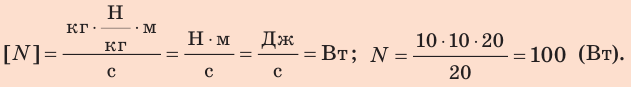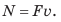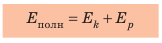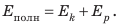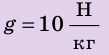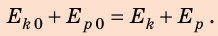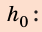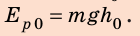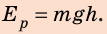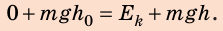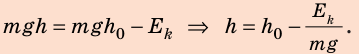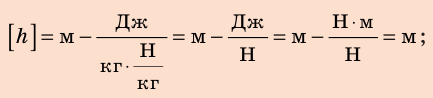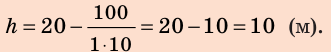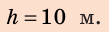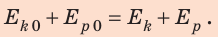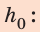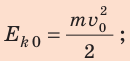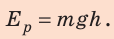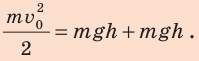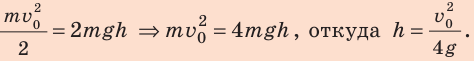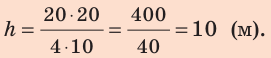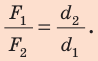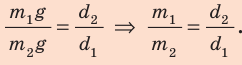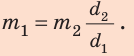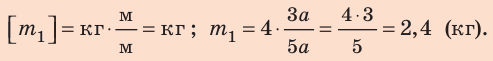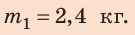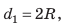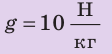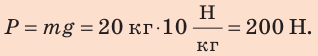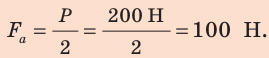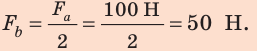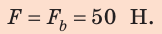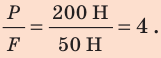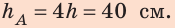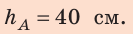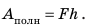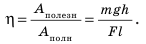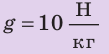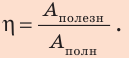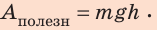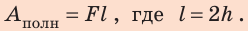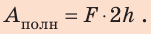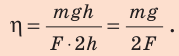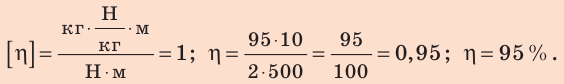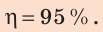Полная механическая энергия тела равна сумме его кинетической и потенциальной энергии.
Полную механическую энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остаётся постоянной.
Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движению, тогда полная механическая энергия тела остаётся неизменной во времени.
Eпот+Eкин=const
Разумеется, что в повседневной жизни не существует идеальной ситуации, в которой тело полностью сохраняло бы свою энергию, так как любое тело вокруг нас взаимодействует хотя бы с молекулами воздуха и сталкивается с сопротивлением воздуха. Но, если сила сопротивления очень мала и движение рассматривается в относительно коротком промежутке времени, тогда такую ситуацию можно приближённо считать теоретически идеальной.
Закон сохранения полной механической энергии обычно применяют при рассмотрении свободного падения тела, при его вертикальном подбрасывании или в случае колебаний тела.
Пример:
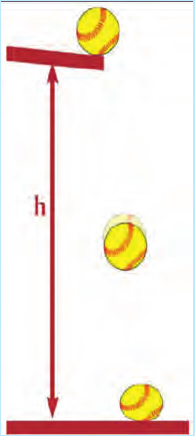
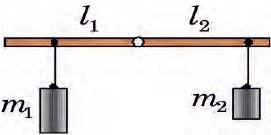
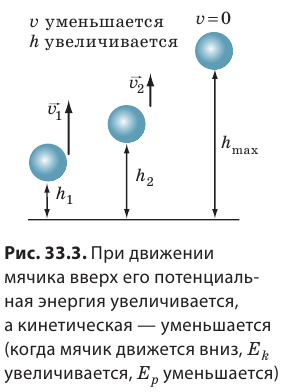
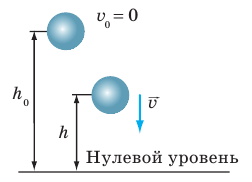
При вертикальном подбрасывании тела его полная механическая энергия не меняется, а кинетическая энергия тела переходит в потенциальную и наоборот.
Преобразование энергии отображено на рисунке и в таблице.
|
Точка нахождения тела |
Потенциальная энергия |
Кинетическая энергия |
Полная механическая энергия |
|
3) Самая верхняя (h = max) |
Eпот
= m⋅g⋅h (max) |
Eкин
= 0 |
Eполная
= m⋅g⋅h |
|
2) Средняя (h = средняя) |
Eпот
= m⋅g⋅h |
Eкин
= m⋅v22 |
Eполная
= m⋅v22 + m⋅g⋅h |
|
1) Самая нижняя (h = 0) |
Eпот
= 0 |
Eкин
= m⋅v22 (max) |
Eполная
= m⋅v22 |
Исходя из того, что в начале движения величина кинетической энергии тела одинакова с величиной его потенциальной энергии в верхней точке траектории движения, для расчётов могут быть использованы ещё две формулы.
Если известна максимальная высота, на которую поднимается тело, тогда можно определить максимальную скорость движения по формуле:
Если известна максимальная скорость движения тела, тогда можно определить максимальную высоту, на которую поднимается тело, брошенное вверх, по такой формуле:
Чтобы отобразить преобразование энергии графически, можно использовать имитацию «Энергия в скейт-парке», в которой человек, катающийся на роликовой доске (скейтер) перемещается по рампе. Чтобы изобразить идеальный случай, предполагается, что не происходит потерь энергии в связи с трением. На рисунке показана рампа со скейтером, и далее на графике показана зависимость механической энергии от места положения скейтера на траектории.
На графике синей пунктирной линией показано изменение потенциальной энергии. В средней точке рампы потенциальная энергия равна (нулю). Зелёной пунктирной линией показано изменение кинетической энергии. В верхних точках рампы кинетическая энергия равна (нулю). Жёлто-зелёная линия изображает полную механическую энергию — сумму потенциальной и кинетической — в каждый момент движения и в каждой точке траектории. Как видно, она остаётся (неизменной) во всё время движения. Частота точек характеризует скорость движения — чем дальше точки расположены друг от друга, тем больше скорость движения.
На графике видно, что значение потенциальной энергии в начальной точке совпадает со значением кинетической энергии в середине рампы.
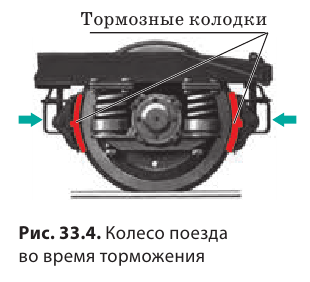
В реальной ситуации всегда происходят потери энергии, так как часть энергии выделяется в виде тепла под влиянием сил трения и сопротивления.
Поэтому для того, чтобы автомобиль двигался с равномерной и неизменной скоростью, необходимо постоянно подводить дополнительную энергию, которая компенсировала бы энергетические потери.
Айгулик
Ученик
(120),
закрыт
10 лет назад
Лучший ответ
дэв
Просветленный
(28590)
10 лет назад
ты совсем тупая или как? высота тебе известна, сила притяжения земли тоже, остаётся только взвесить падающий предмет
Остальные ответы
Валентина Вавилова(Серкова)
Гений
(62183)
10 лет назад
По закону сохранения энергии: потенциальная энергия в верхней точке = кинетической энергии в точке падения.
Еп=Ек.
Еп=m*g*h .
Ек=m*v^2 / 2. приравняем.
m*g*h = m*v^2 / 2. сократим на массу.
g*h = v^2 / 2. выразим скорость
v=корень квадратный из 2*g*h.
v=кор. кв. из 2*10*20=20м/c.
Похожие вопросы
Содержание:
Механическая энергия и работа:
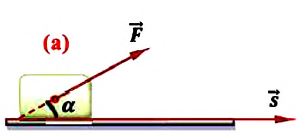
Если на тело действует сила F и тело под действием этой силы осуществляет перемещение s в направлении действия силы, то при этом выполняется работа A, которую вычисляют по формуле:
где A – работа, а F – сила, направленная параллельно вектору перемещения (рис. 30.1). Формула дает правильный результат лишь при условии, что сила остается постоянной в течение всего процесса перемещения.
Таким образом, работа равняется произведению силы на величину перемещения.
В СИ работа измеряется в джоулях (Дж). Единица названа в честь английского физика Джеймса Джоуля, который впервые доказал, что теплота – это разновидность энергии. Согласно формуле (30.1) Дж = Н · м: работа величиной в один джоуль (Дж) выполняется силой один ньютон (Н), которая перемещает тело в направлении действия силы на один метр (м).
Если на тело действует несколько сил, то работа каждой силы вычисляется отдельно. Когда сила действует в противоположном перемещению направлении, то ее работа считается отрицательной. Такой может быть, например, работа силы трения: Aтр = –Fтр · s.
Если сила направлена перпендикулярно перемещению, то ее работа равна нулю. Мы, например, не указали на рис. 30.1 силу реакции опоры N и силу тя-жести mg, поскольку работу эти силы не выполняют.
Пример:
Тело переместили на расстояние s = 2 м, двигая его равномерно в горизонтальном направлении под действием силы F = 3Н. Вычислите работу силы F и силы трения Fтр.
| Дано: m = 10 кг s = 2 м F = 3 H |
Решение. Работу силы F вычислим по формуле AF = F · s = 3H · 2м = 6 Дж. Поскольку тело движется равномерно, то сила F компенсирует действие силы Fтр, то есть равна ей по величине (и противоположна по направлению): Fтр = F = 3H Работа силы трения равна: Атр = –Fтр · s = –3H · 2м = –6 Дж. |
| AF – ? Aтр – ? |
Ответ: Работа силы F равна 6 Дж, работа силы трения равна – 6 Дж.
Работа в поле тяжести:
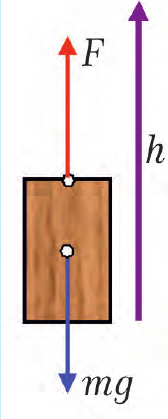
Если тело равномерно поднимают вверх, преодолевая силу тяжести «mg», или опускают вниз под действием силы тяжести (рис. 30.2), то работа вычисляется по той же формуле (31.1), но перемещение обозначают буквой h:
A = mg · h. (30.1)
При подъеме работа силы тяжести отрицательна, а работа поднимающей силы – положительна.
Рис. 30.2. К формуле 30.1
Пример:
Какая работа была выполнена краном, поднявшим бетонную плиту массой 400 кг на высоту 5 м? 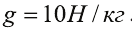
| Дано: m = 400 кг h = 2 м g = 10 H/кг |
Решение. Очевидно, что кран должен действовать на плиту вверх с силой F, не меньшей, чем mg. Работу силы F, которая приложена к плите со стороны крана, вычислим по формуле: AF = F · h = mg · h = 20 000 Дж. |
| Aтяж – ? |
Ответ: Кран выполнил работу 20 000 Дж (20 кДж).
График силы:
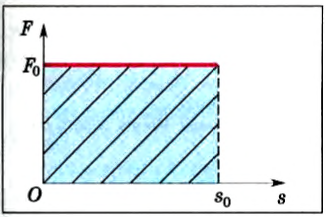
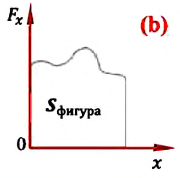
Начертим график зависимости величины силы «F» от перемещения «s» для случая, когда величина силы не изменяется, а направление силы совпадает с направлением перемещения (рис. 30.3). Легко заметить, что произведение F · s совпадает по численному значению с площадью прямоугольника abcd, то есть работа может быть вычислена как площадь фигуры на графике зависимости силы от перемещения F (s).
Этот новый способ вычисления работы может пригодиться в случае, когда сила изменяется в процессе перемещения. Если мы растягиваем пружину с некоторой силой F, то величина этой силы увеличивается по мере увеличения удлинения пружины согласно закону Гука. Следовательно, вычислять работу по формуле (30.1) уже нельзя.
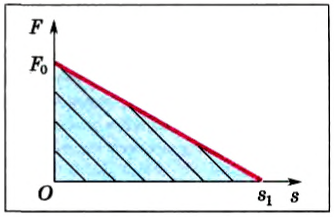
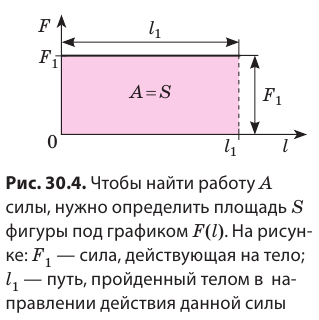
Начертим график силы для случая удлинения пружины (рис. 30.4). Работа численно равняется площади треугольника abc, где ab = x – удлинение, а отрезок bc = F – максимальная сила, которая удерживает пружину в удлиненном состоянии.
Таким образом, работа по удлинению пружины равняется:
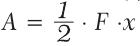
Учитывая, что F = k · x, формулу (31.2) можно записать и так:
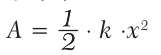
Мощность:
Скорость выполнения работы называют мощностью и обозначают буквой P. Мощность равняется отношению работы ко времени, в течение которого эта работа была выполнена:
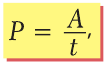
где A – работа, выполненная за время t.
В СИ мощность измеряется в ваттах (Вт) в честь английского ученого и инженера Джеймса Ватта, который построил первую паровую машину. Согласно (30.4) Вт = Дж/с: при мощности один ватт за одну секунду выполняется работа один джоуль.
На практике часто используются большие единицы мощности – киловатт (кВт) и мегаватт (МВт): 1кВт = 1 000 Вт, 1 МВт = 1 000 000 Вт.
Если в формуле (31.4) «A» заменить на F · s и учесть, что 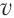
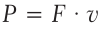
По формуле (30.5) можно вычислить мощность машины в данный момент времени. Более мощные машины выполняют работу быстрее. Например, мощный двигатель дает возможность автомобилю двигаться с большим ускорением, что улучшает возможности маневрирования.
По формуле (30.4) можно получить новое выражение для вычисления работы:
A = P · t, (30.6)
которое справедливо, если мощность машины постоянна на протяжении времени t.
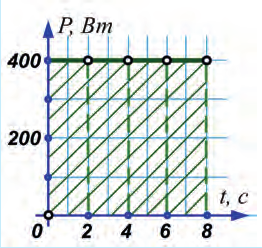
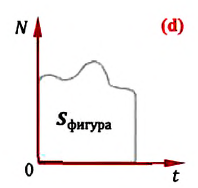
Если построить график зависимости мощности от времени (при постоянной мощности), то станет очевидно, что на графике зависимости мощности от времени площадь фигуры, ограниченной графиком и осью абсцисс, равняется работе (рис. 30.5).
Рис. 30.5. Площадь под графиком P (t) численно равняется работе
Пример:
Электросчетчик (рис. 30.6) определяет потребленную энергию в кВт·ч. Что это за физическая величина?
Решение: Согласно формуле (30.6), это – работа. Виразим кВт-ч в Дж:
1 кВт-ч = 1000 Вт · 3600 с = 3 600 000 Дж.
Ответ: 1 кВт-ч. равен работе 3 600 000 Дж, або 3,6 МДж.
Рис. 30.6. Электросчетчик
Итоги:
- Механическая работа равняется произведению силы на величину перемещения: A = F · s.
- Когда сила действует в противоположном перемещению направлении, то ее работа считается отрицательной.
- Если сила направлена перпендикулярно к перемещению, то ее работа равняется нулю.
- Мощность равняется отношению работы ко времени, в течении которого эта работа была выполнена: P = A / t.
- Работа переменной силы может быть вычислена по площади под графиком F(s).
Механическая энергия и ее виды
Понятие энергии – одно из важнейших не только в физике. От количества выработанной энергии и способа ее получения зависит качество нашей жизни. Вспомним такие выражения, как тепловая энергия, энергетический кризис, оплата электроэнергии, энергичный человек, объединенные энергетические системы.
Мы привыкли, что энергия – это определенный ресурс, позволяющий улучшить быт. Производство и распределение энергии всесторонне касается жизни человека. Поэтому надо знать, как она производится, передается и хранится. Вот некоторые свойства энергии:
- Тело может иметь, получать и отдавать энергию.
- Существует множество видов энергии (механическая, тепловая, электрическая…), и она может переходить из одного вида в другой.
- При определенных условиях энергия может сохранятся.
Механическая энергия
Если тело может выполнить работу, то оно имеет энергию. Чтобы иметь энергию, нет необходимости выполнять работу, достаточно иметь такую возможность.
Величина энергии равняется максимальной работе, которую тело при определенных обстоятельствах может выполнить. Как и работа, энергия из-меряется в Дж.
Есть два вида механической энергии: потенциальная и кинетическая. Обозначим энергию буквой E. Нижний индекс (значок) в выражениях для энергии около буквы E будет означать: «K» – кинетическая, «P» – потенциальная.
Кинетическая энергия
Кинетическая энергия (EK) – это энергия движущихся тел («кинема» по-гречески означает «движение»). Это может быть энергия ветра, потока воды, вращательная энергия массивного маховика. Вы-числить кинетическую энергию можно по формуле:
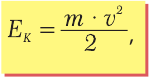
где «m» – масса тела, а «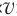
Тело, которое участвует одновременно в двух движениях – поступательном и вращательном – имеет две кинетических энергии, как, например, колесо автомобиля (рис. 31.2). Поступательное движение центра колеса происходит со скоростью автомобиля, а вращательная скорость увеличивается от нуля (центр) до скорости автомобиля (на уровне протектора шин). Возможно, вы видели в фильмах, как продолжают вертеться колеса у перевернувшегося автомобиля – поступательной энергии уже нет, а вращательная еще есть.
Пример №1
Сравните кинетические энергии: а) легкового автомобиля массой 1 500 кг, который движется со скоростью 72 км/ч; б) снаряда массой 3 кг, летящего со скоростью 500 м/с.
Решение:
а) Скорость автомобиля 72 км/год = 20 м/с. Кинетическая энергия автомобиля: 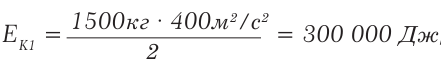
Объясним, как получили Дж: кг · м2/с2 = (кг · м/с2)м = Н·м = Дж.
б) Кинетическая энергия снаряда:
Замечание. Обратите внимание, что масса снаряда в 500 раз меньше массы автомобиля, в то время как его скорость больше лишь в 25 раз. Одна-ко кинетическая энергия снаряда оказалась больше, поскольку выражение зависит 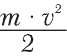
Кинетическую энергию ветра используют очень давно. В наше время модернизированные ветряные мельницы вырабатывают значительное количество электричества (рис. 31.3). Электротранспорт преобразует часть своей энергии движения в электрическую энергию, когда уменьшает скорость перед остановкой.
Потенциальная энергия
Потенциальная энергия тела (EP) – это энергия возможности (от англ. potential – потенциал, возможность). Такую энергию имеют неподвижные тела вследствие взаимодействия и взаимного расположения.
Рис. 31.3. Кинетическую энергию ветра ветросиловые установки преобразуют в электрическую энергию
Потенциальная энергия тяжести. Рассмотрим неподвижное тело массой m, которое находится на высоте h (рис. 31.4). На это тело действует сила тяжести mg, и если дать телу возможность упасть, то эта сила выполнит роботу A = mgh. Поскольку запас энергии равняется наибольшей работе, которую тело может выполнить при дан-ных условиях, то энергия тела, находящегося на некоторой высоте над землей, составляет:
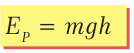
Тело, находясь на некоторой высоте «h», имеет энергию уже только потому, что оно притягивается Землей и может упасть. Тело, лежащее на полу, не имеет потенциальной энергии относительно пола, хотя на него действует сила тяжести. Заметим, что начало отсчета высоты «h» может быть разным, поэтому о потенциальной энергии тяжести можно говорить лишь по от-ношению к выбранному начальному (нулевому) уровню.
Если тело находится ниже нулевого уровня, например, в яме, то его потенциальная энергия отрицательна. Это значит, что за счет этой энергии тело не может выполнить работу при перемещении на нулевой уровень. Более того, чтобы поднять тело на этот уровень, придется кому-то выполнять положительную работу, которая по величине равняется потенциальной энергии тела.
Потенциальную энергию люди также используют издавна. Вспомните водяные мельницы или старинные часы с гирями. Когда строят гидроэлектростанцию (ГЭС), то реку перекрывают плотиной, чтобы поднять уровень воды (рис. 31.5). Падая вниз, вода вращает турбины генераторов и выполняет работу. Чем выше плотина и чем больше воды несет река, тем больше электроэнергии производит ГЭС.
Пример №2
Какова масса тела, поднятого на высоту 20 м, если его потенциальная энергия составляет 300 кДж?
Решение. Очевидно, что речь идет о потенциальной энергии тяжести, поэтому EP = mgh.
Отсюда m = EP/(gh) = 300 000 Дж/(10Н/кг · 20м) = 1500 кг.
Ответ: масса тела равна 1 500 кг или 1,5 т.
Замечание. 300 кДж – это кинетическая энергия автомобиля из примера 30.1. Интересно, что если бы автомобиль на каком-либо трамплине подпрыгнул вертикально вверх, а его кинетическая энергия полностью пере-шла в потенциальную, то он смог бы подняться на высоту 20 м.
Потенциальная энергия упруго деформированного тела
Если удлинение пружины жесткости «k» составляет «x», то она может выполнить работу 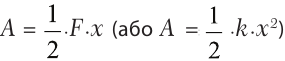
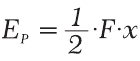
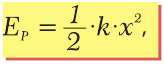
где «F» – сила, которая удерживает пружину в удлиненном на «x» состоянии.
Накручивая пружину механических часов, мы сообщаем ей запас потенциальной энергии, которая затем будет затрачена на приведение в движение механизма и стрелок. Часы остановятся после того, как пружина опять распрямится и истратит свою энергию.
Полная механическая энергия
Тело может одновременно иметь несколько видов механической энергии: как потенциальной, так и кинетической. Полная механическая энергия «Е» тела равняется сумме поступательной и вращательной кинетических энергий, а также потенциальных энергий упругой деформации и тяжести:
E = EКпост. + EКвращ. + EРтяж. + EРупруг. (31.4)
Пример №3
Самолет массой 30 т летит на высоте 10 000 м со скоростью 720 км/ч. Вы-числите его полную механическую энергию (g=10H/кг).
| Дано: h = 10 000 м 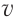 = 720 км/ч = 720 км/чg = 10 H/кг |
Решение. |
| Е – ? |
= 600 000 000 Дж + 3 000 000 000 Дж = 3 600 МДж
Ответ: полная механическая энергия самолета равна 3600 МДж.
Итоги:
Закон сохранения механической энергии
Преобразование энергии:
В природе и технике постоянно происходят преобразования энергии из одного вида в другой. Перекрывая реку плотиной гидроэлектростанции, добиваются того, что вода поднимается на значительную высоту и приобретает огромную потенциальную энергию. Падая вниз, вода увеличивает свою кинетическую энергию, за счет которой она вращает лопасти гидротурбин. Те, в свою очередь, вращают электрогенераторы, которые производят электрическую энергию.
Рассмотрим для примера падение мячика с определенной высоты (рис. 32.1). Когда мячик опускается, его потенциальная энергия уменьшается, скорость растет, а с ней растет и кинетическая энергия. Около самой земли потенциальная энергия уменьшится до нуля и полностью перейдет в кинетическую энергию, которая достигнет своего наибольшего значения. Далее кинетическая энергия начнет переходить в энергию упругой деформации мячика, который сжимается.
Рис. 32.1. Переход потенциальной энергии мяча в кинетическую энергию
Закон сохранения энергии
Многочисленные и достаточно точные опыты показали, что кинетическая энергия увеличивается ровно настолько, насколько уменьшается потенциальная, если только можно пренебречь работой силы трения, то есть сумма потенциальной и кинетической энергии остается постоянной (сохраняется) при отсутствии силы трения. Другими словами, полная механическая энергия тела сохраняется, если на тело не действуют силы трения, или если они малы и ими можно пренебречь.
Рис. 32.2. Потенциальная энергия деформированного лука перешла в кинетическую энергию стрелы, которая в свою очередь перешла в потенциальную энергию тяжести
Если E1 = EK1 + EP1 – полная механическая энергия тела в одном состоянии, а E2 = EK2 + EP2 – в другом состоянии, то E1 = E2, то есть энергия сохраняется при условии отсутствия действия сил трения.
Примеры решения задач на применение закона сохранения энергии
Пример:
Скорость стрелы во время выстрела из лука (рис. 32.2) составляет 20 м/с. На какую наибольшую высоту она может подняться? 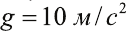
Ответ: При условии отсутствия трения стрела может подняться на высоту 20 м.
Обсуждение результатов:
- а) Высота 20 м была достигнута при условии отсутствия трения (то есть потерь энергии). Реальная высота подъема будет несколько меньшей.
- б) Масса тела в процессе расчета сократилась. Это значит, что тело произвольной массы, которому придали скорость 20 м/с, достигнет высоты 20 м. Если этот факт вас удивляет, то попробуйте решить этот парадокс.
Пример:
Тело массой 3 кг падает с высоты 8 м. Какова будет его скорость в момент
касания поверхности? g = 10 м/с2.
Решение. Подобно предыдущей задаче,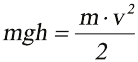
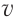
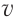
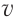
Ответ: тело достигнет скорости 16 м/с.
Пример:
Игрушечный пружинный пистолет, жесткость пружины которого 1 Н/см, зарядили шариком массой 20 г и сжали пружину на 10 см. С какой скоростью вылетит шарик при выстреле?
Решение. Прежде чем решать задачу, надо перевести единицы измерения в систему СИ:
1 Н/см = 100 Н/м, 20 г = 0,02 кг, 10 см = 0,1 м.
Энергия сжатой пружины составляет 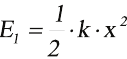
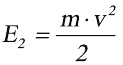
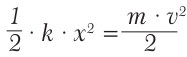
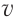
Ответ: шарик будет иметь скорость приблизительно 7 м/с.
Энергия и работа
Напомним, что работу можно вычислить:
- По формуле A = F · s, если сила постоянна.
- По графику силы – как площадь под графиком.
- Через мощность, как A = P · t. Исходя из определения энергии, можно еще одним способом вычислять работу:
- Работа силы равняется изменению энергии тела в результате действия этой силы.
Если полная энергия тела увеличивается, то это значит, что какая-то сила выполняет положительную работу. Тогда увеличение полной энергии тела равняется работе этой силы: A = E2 – E1. Если полная энергия тела уменьшается, то это значит, что некая сила выполняет отрицательную работу. Сила трения скольжения, например, выполняет отрицательную работу, и потому в равенстве Aтр = E2 – E1, Aтр < 0, поскольку E2 < E1.
Таким образом, изменение механической энергии является следствием выполнения работы, а выполнение работы приводит к изменению энергии.
Итоги:
- Энергия не возникает из ничего и не исчезает бесследно. Она лишь переходит из одного вида в другой.
- Закон сохранения механической энергии: полная механическая энергия тела не изменяется, если нет потерь на трение.
- Механическая работа может быть вычислена как изменение полной механической энергии.
Момент силы
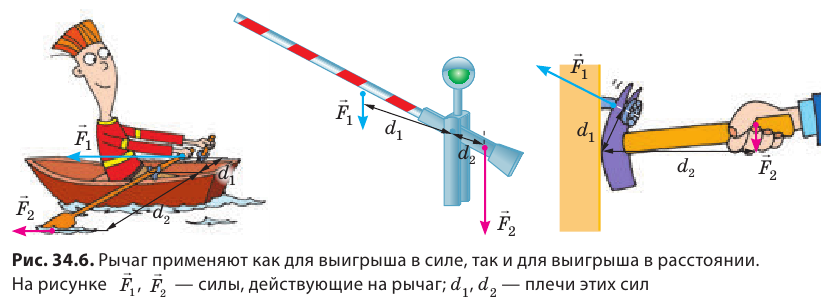
Рычаг – простейший и едва ли не самый древний механизм, используемый человеком. Ножницы, кусачки, лопата, двери, весло, руль и рычаг переключения передач в автомобиле – все они действуют по принципу рычага. Уже при строительстве египетских пирамид рычагами поднимали камни массой свыше 10 тонн.
Правило рычага
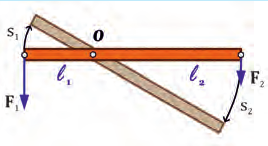
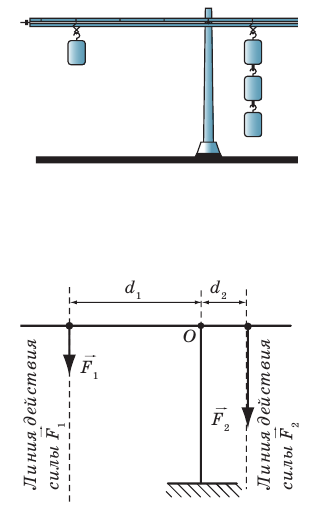
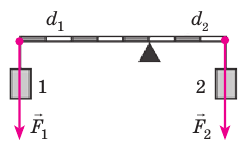
Рычагом называют стержень, который может вращаться вокруг некоторой неподвижной оси. Ось О перпендикулярна к плоскости рисунка 33.1. На правое плечо рычага длиной l2 действует сила F2, а на левое плечо рычага длиной l1 действует сила F1. Длину плеч рычага l1 и l2 измеряют от оси вращения О до соответствующих линий действия сил F1 і F2.
Пусть силы F1 и F2 таковы, что рычаг не вращается. Опыты показывают, что в этом случае выполняется условие
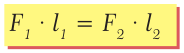
Перепишем это равенство по-другому:
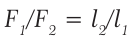
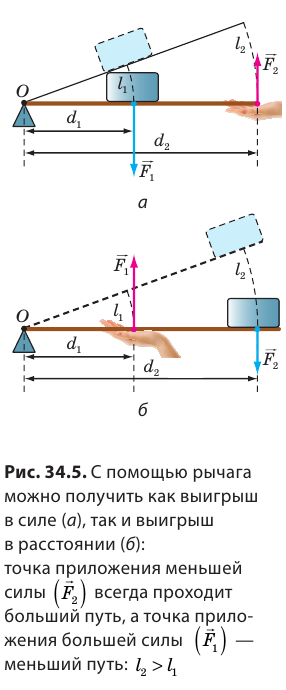
Смысл выражения (33.2) таков: во сколько раз плечо l2 длиннее плеча l1, во столько же раз величина силы F1 больше величины силы F2. Это утверждение называют правилом рычага, а соотношение F1 / F2 – выигрышем в силе.
Получая выигрыш в силе, мы проигрываем в расстоянии, поскольку нужно сильно опустить правое плечо, чтобы немного поднять левый конец плеча рычага.
Зато весла лодки закреплены в уключинах так, что мы тянем за короткое плечо рычага, прикладывая значительную силу, но зато получаем выигрыш в скорости на конце длинного плеча (рис. 33.2).
Если силы F1 и F2 равны по величине и направлению, то рычаг будет пребывать в равновесии при условии, что l1 = l2, то есть ось вращения, находится посредине. Конечно, никакого выигрыша в силе в этом случае мы не получим. Руль автомобиля устроен еще интереснее (рис. 33. 3).
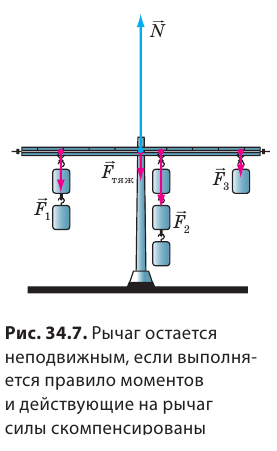
Условие равновесия рычага
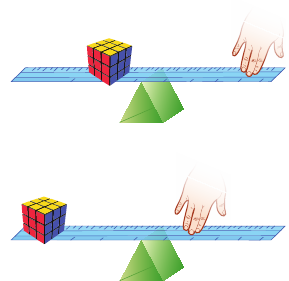
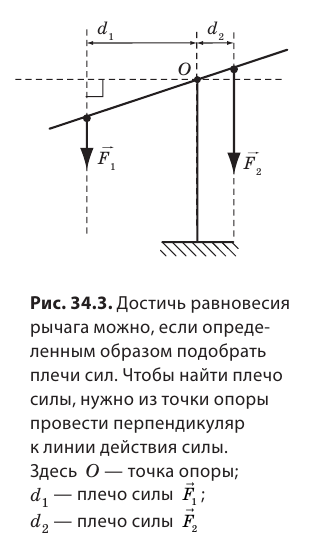
Плечом силы l называют кратчайшее расстояние от оси вращения до линии действия силы. В случае на рис. 33.4, когда линия действия силы F образует острый угол с гаечным ключом, плечо силы l1 меньше плеча l2 в случае на рис. 33.5, где сила действует перпендикулярно ключу.
Произведение силы F на длину плеча l называют моментом силы и обозначают буквой M:
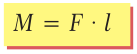
Момент силы измеряется в Н·м. В случае на рис. 33.5 гайку повернуть легче, потому что момент силы, с которой мы действуем на ключ, больше.
Из соотношения (33.1) следует, что в случае, когда на рычаг действуют две силы (рис. 33.1), условие отсутствия вращения рычага заключается в том, что момент силы, которая пытается его вращать по часовой стрелке (F2 · l2), должен равняться моменту силы, которая пытается вращать рычаг против часовой стрелки (F1 · l1).
Если на рычаг действует более двух сил, правило равновесия рычага зву-чит так: рычаг не вращается вокруг неподвижной оси, если сумма моментов всех сил, которые вращают тело по часовой стрелке, равняется сумме моментов всех сил, которые вращают его против часовой стрелки.
Если моменты сил не уравновешены, рычаг вращается в ту сторону, куда его вращает больший по сумме момент.
Пример №4
К левому плечу рычага длиной 15 см под-весили груз массой 200 г. На каком расстоянии от оси вращения нужно подвесить груз массой 150 г, чтобы рычаг находился в равновесии?
| Дано: m1 = 200 г m2 = 150 г 11 = 15 см |
Решение. |
| l2 – ? |
Вычисление: 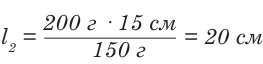
Ответ: длина правого плеча рычага в положении равновесия составляет 20 см.
Рис. 33.6
Опыт:
Оборудование: легкий и достаточно крепкий провод длиной приблизительно 15 см, скрепки, линейка, нить.
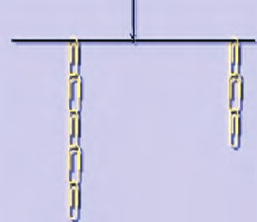
Ход работы. Наденьте на провод нитяную петлю. Примерно посредине провода туго ее затяните. Затем подвесьте провод на нити (прикрепив нить, скажем, к настольной лампе). Установите провод в равновесии, передвигая петлю. Нагрузите рычаг с двух сторон от центра цепочками из разного количества скрепок и добейтесь равновесия (рис. 33.7).
Рис. 33.7. Исследования равновесия рычага
Измерьте длины плеч l1 и l2 с точностью до 0,1 см. Силу будем измерять в «скрепках». Запишите результаты в таблицу.
| N1 –скрепок слева | l1,см | N2–скрепок слева | l2,см | A = N1 · l1, скр. · см | A = N2 · l2, скр. · см |
Сравните величины А и В. Сделайте выводы.
Проблемы точного взвешивания
Рычаг используют в весах, и от того, насколько точно совпадает длина плеч, зависит точность взвешивания.
Современные аналитические весы могут взвешивать с точностью до одной десятимиллионной части грамма, то есть до 0,1 мкг (рис. 33.8). Причем есть две разновидности таких весов: одни для взвешивания легких грузов, другие – тяжелых. Первую разновидность вы можете увидеть в аптеке, ювелирной мастерской или химической лаборатории.
На весах для взвешивания больших грузов можно взвешивать грузы весом до тонны, но при этом они остаются очень чувствительными. Если ступить на такие весы, после чего выдохнуть воздух из легких, то весы среагируют.
Рис. 33.8. Современные аналитические весы
Ультрамикровесы измеряют массу с точностью до 5·10–11 г (пять стомиллиардных долей грамма!).
При взвешивании на очень точных весах возникает много проблем:
- а) как ни старайся, плечи коромысла все равно не одинаковы.
- б) чаши весов хотя и мало, но отличаются по массе.
- в) начиная с определенного порога точности, весы начинают реагировать навыталкивающую силу воздуха, которая для тел обычных размеров очень мала.
- г) при размещении весов в вакууме от этого недостатка можно избавиться, но при взвешивании очень маленьких масс начинают чувствоваться удары молекул воздуха, откачать который полностью невозможно никаким насосом.
Два способа повысить точность неравноплечных весов
- Метод тарирования. Уравновесим груз с помощью сыпучего вещества, например, песка. Потом снимем груз и разновесами уравновесим песок. Очевидно, что масса разновесов равняется истинной массе груза.
- Метод поочередного взвешивания. Взвешиваем груз на чаше весов, которая находится, например, на плече длиной l1. Пусть масса разновесов, которая приводит к уравновешиванию весов, равняется m2. Потом взвесим этот же груз в другой чаше, которая находится на плече длиной l2. Получим не-сколько иную массу разновесов m1. Но в обоих случаях настоящая масса груза равняется m. При обоих взвешиваниях выполнялись условия: m·l1 = m2·l2 и m·l2 = m1·l1. Решая систему этих уравнений, получим:
Итоги:
- Плечом силы l называют кратчайшее расстояние от оси вращения до линии действия силы.
- Моментом силы называют произведение силы на плечо: M = F · l.
- Рычаг не вращается, если сумма моментов всех сил, которые вращают тело по часовой стрелке, равняется сумме моментов всех сил, которые вращают его против часовой стрелки.
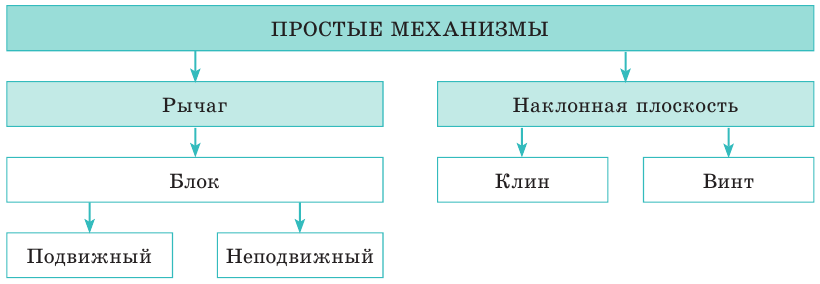
Простые механизмы
Машина – это устройство, которое осуществляет механическое движение для преобразования энергии. Термин «машина» (лат. machina) означает механизм, устройство, конструкция. Термин «механизм», в свою очередь, про-исходит от греческого «механе» – двигать.
Простая машина – это механизм, который изменяет направление или величину силы без потребления энергии.
Сложные машины, которыми сейчас пользуются, содержат так называемые простые механизмы. Простые механизмы можно разделить на две группы:
- Рычаг, блок, ворот, лебедкa, кабестан, полиспаст: их работа сводится к принципу действия рычага.
- Наклонная плоскость, винт и клин, работу которых можно свести к принципу наклонной плоскости.
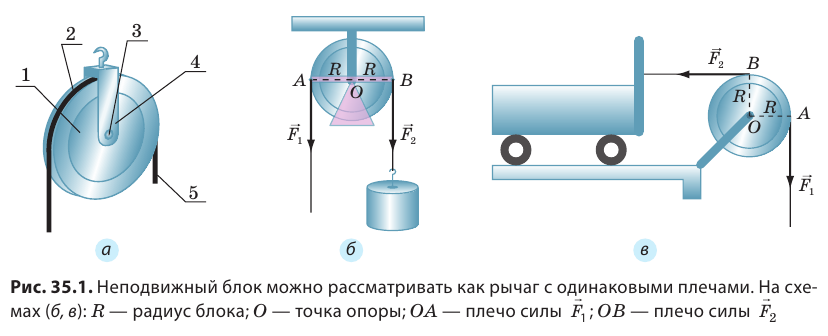
Блок как рычаг
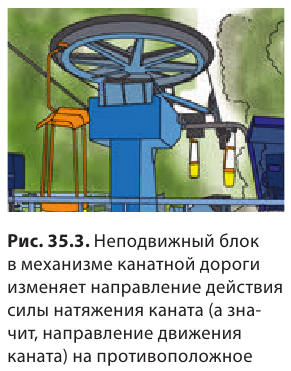
Блок – колесо с желобом и осью вращения – используется в кранах (рис. 34.1), экскаваторах, подвесных дорогах и т. п. По желобу двигается трос, который тянет или поддерживает грузы. Если ось блока закреплена, то он называется неподвижным (рис. 34.2) и используется для изменения направления действия силы.
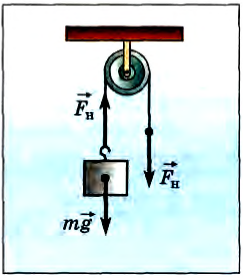
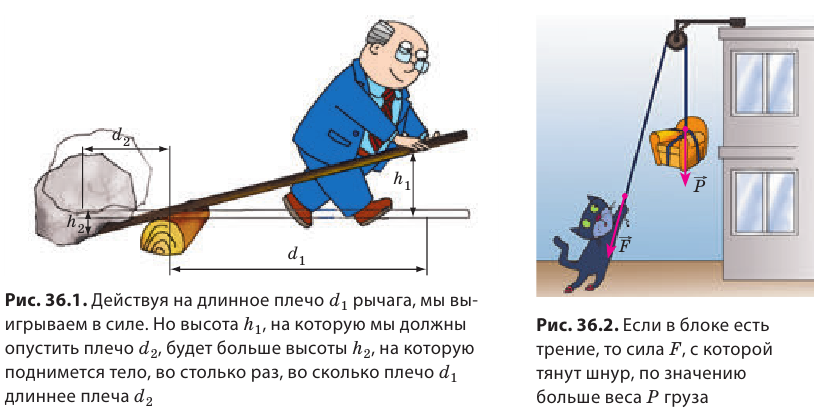
У рычага есть недостаток – он имеет ограниченное пространство действия. Повернув плечо рычага на некоторый небольшой угол, нужно вернуть его в предыдущее положение и начинать все сначала. Блок позволяет сделать процесс выполнения роботы непрерывным. Рассмотрим принцип действия неподвижного блока с помощью рис. 34.3. Сила F, с которой мы действуем на правый конец троса вниз, позволяет поднимать груз вверх, и это удобнее, чем непосредственно поднимать груз.
Сила тяжести mg уравновешена направленной вверх силой натяжения левого конца троса T. Такие же по величине силы натяжения T действуют со стороны троса вниз на блок. Плечи этих сил (они указаны оранжевыми стрелками) одинаковы – следовательно, выигрыша в силе мы не получили. Правый конец троса можно тянуть также в сторону или горизонтально, в таком случае блок называют направляющим.
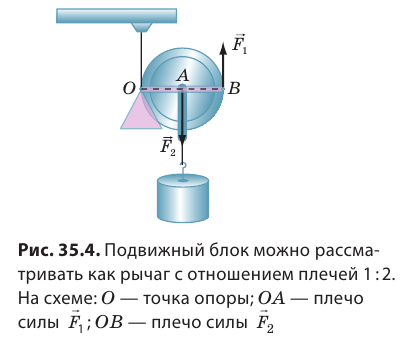
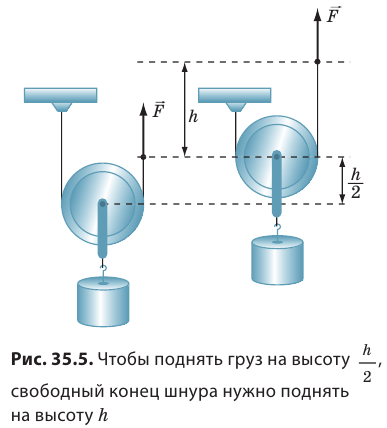
Подвижный блок
Рассмотрим рис. 34.4. Направленная вверх сила F, которая действует на правый конец троса, уравновешена силой натяжения троса T, направленной вниз. Величина сил натяжения в любой точке троса одинакова. Две направленные вверх силы натяжения T, действующие на блок, уравновешивают силу тяжести mg, которая действует на груз вниз. Следовательно, величина силы натяжения в тросе вдвое меньше веса груза. Прикладывая силу F, мы получаем выигрыш в силе в два раза.
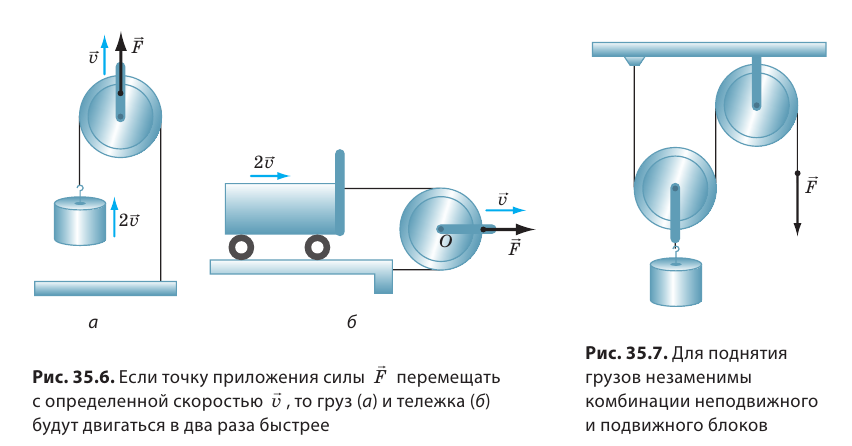
Если тянуть за ось блока вниз с некоторой скоростью, то правый конец троса будет двигаться со вдвое большей скоростью, то есть подвижный блок можно использовать и для выигрыша в скорости.
Можно объяснить выигрыш в силе, который дает подвижный блок и по-другому: плечо силы F относительно точки О вдвое больше плеча силы mg.
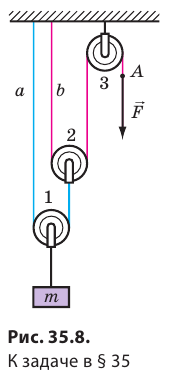
Если применить много подвижных блоков, соединив их в две группы, то получим полиспаст (рис. 34.5). Полиспаст дает многократный выигрыш в силе.
Наклонная плоскость
Вы, наверное, видели, как массивный предмет, который тяжело поднять (например, шкаф) грузят в машину. Груз поднимают по крепкой доске, один конец которой находится на земле, а другой – опирается на край кузова. Ленточные транспортеры, эскалаторы – примеры наклон-ной плоскости.
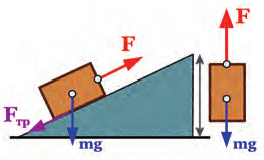
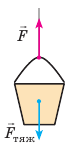
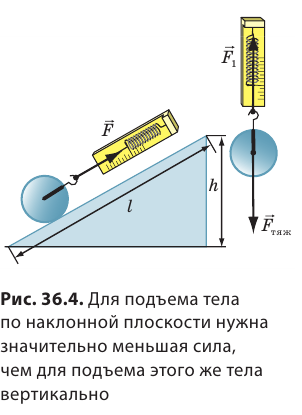
Сила, которую нужно приложить к телу, чтобы двигать его вверх по наклонной плоскости (рис. 34.6), тем меньше, чем меньший угол наклона плоскости к горизонту, и она всег-да меньше силы тяжести Fтяж = mg, которая действует на тело. Тяжелые каменные блоки, из которых строили египетские пирамиды, тянули вверх по наклонной насыпи. Чем выше становилась пирамида, тем более длинной приходилось делать насыпь.
Разновидностями наклонной плоскости являются клин, винт, лемех плуга, шнек мясорубки (дальний потомок винта Архимеда).
Рис. 34.6. Перемещать тело по наклонной плоскости легче, чем поднять вертикально вверх
Клин
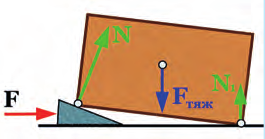
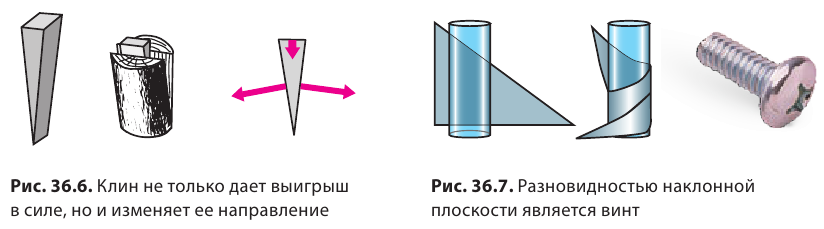
Вместо того, чтобы тянуть тело по наклонной плоскости, можно наклонную плоскость двигать под телом. Так делают, когда нужно приподнять очень тяжелый предмет (рис. 34.7). Чем более острый клин, тем с меньшей силой его надо под-бивать (но и тем меньший эффект подъема).
Клин под действием не слишком большой силы удара молотка распирает половинки колоды, действуя на них со значительно большей силой. Подобным образом топор или колун расщепляют полено. Нож также является разновидностью клина, и чем острее он будет, тем легче им резать.
Рис. 34.7. Сила N, которая поднимает ящик, больше силы F, с которой мы подбиваем клин
Винт
Следующей модификацией наклонной плоскости является винт. Резьба винта является наклонной плоскостью, обвивающей цилиндр. Наклон такой плоскости можно сделать очень маленьким (за счет малого шага винта), а саму плоскость – очень длинной.
Опыт:
Начертите на листе бумаги для чертежей наклоненную прямую АВ, оставив полосу для склеивания шириной 0,5 см, как указано на рис. 34.8. Сверните лист в цилиндр и склейте его так, чтобы точка В оказалась в точности над точкой А. Вы убедитесь, что прямая АВ превратилась в спираль.
Шаг спирали (расстояние АВ на поверхности цилиндра) будет тем меньшим, чем меньше угол, под которым вы провели линию АВ на листе.
Гайка, двигаясь по винту болта, может поднимать груз, вес которого значительно больше усилия, которое прикладывают, чтобы поворачивать винт или гайку.
Винтовые подъемники вы можете увидеть в автомастерских, небольшие винтовые домкраты есть в каждом автомобиле. С помощью винтовых устройств зажимают детали в тисках и двигают суппорты токарных и фрезерных станков. На рис. 34.9 приведены фотографии шнека домашней ручной мясорубки и струбцины (разновидность тисков).
Итоги:
- Неподвижный блок позволяет изменить направление действия силы.
- Подвижный блок дает выигрыш в силе.
- Чем меньше угол наклона наклонной плоскости – тем больше выигрыш в силе.
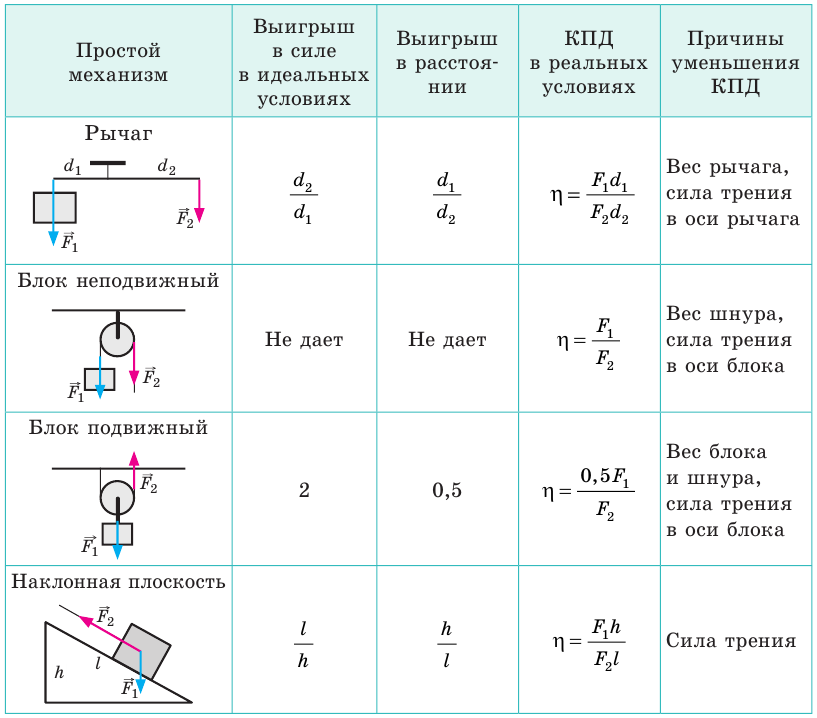
Коэффициент полезного действия механизмов (КПД)
В большинстве устройств, машин и механизмов происходит передача и преобразование энергии. Для характеристики этих машин с точки зрения их полезности вводится коэффициент полезного действия.
Коэффициентом полезного действия машины или механизма (сокращенно – КПД) называют умноженное на 100% отношение полезной работы Aпол., которую выполняет машина, ко всей энергии, затраченной на выполнение этой работы Aзатр:
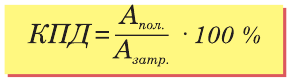
Пример №5
Максимальный коэффициент полезного действия лампы накаливания составляет 5%. Это значит, что из 100% потребляемой электроэнергии в свет преобразуется 5%, а остальные преобразуются в тепло.
Пусть с помощью наклонной плоскости мы подняли определенный груз массы «m» на высоту «h». Полезная работа заключается в поднятии груза на определенную высоту h и составляет: Aпол. = mgh. Но была выполнена работа не только по поднятию груза, но и по преодолению силы трения скольжения при движении по плоскости. Следовательно, затраченная работа равняется: Aзатр. = Aпол. + |Aтр.|. Работа силы трения взята по модулю, поскольку она отрицательна.
Затраченная работа всегда больше полезной, поэтому КПД реальной машины не может достичь 100%, а тем более превысить его. Желательно, и это задача огромной экономической важности, добиться того, чтобы затраты на выполненную работу ненамного превышали полезную работу, то есть что-бы КПД машин был как можно более высоким. В таблице 35.1 приведены данные о КПД некоторых машин и устройств.
Таблица 35.1 Коэффициент полезного действия некоторых машин и механизмов, %
| Солнечная батарея | до 6 – 40 | Топливный элемент | до 85 |
| Мускулы | 14 – 27 | Гидротурбина | до 90 |
| Холодильник | 40 – 50 | Электродвигатель | до 99 |
| Газовая турбина | до 40 | ||
| Дизельный двигатель | до 50 | Лампа накаливания | 0,7 – 5 |
| Паровая турбина | до 60 | Лампа дневного света | до 15 |
| Ветрогенератор | до 60 | Светодиоды | до 35 |
Пример №6
Используя рис. 34.6, получите формулу для расчета КПД наклонной плоскости.
Решение. Полезная работа при применении наклонной плоскости заключается в том, чтобы поднять тело на высоту h. Следовательно, Aпол. = mgh. Затраченная работа равна: Азатр. = F · L. Таким образом, 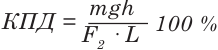
Золотое правило механики
Пусть рычаг под действием сил F1 и F2 находится в равновесии. Это значит, что:
F1 · l1 = F2 · l2. (35.2)
Медленно повернем рычаг в направлении действия силы F2 на некоторый небольшой угол. Конец рычага при этом опишет дугу длиной s2. Другой конец рычага при этом опишет дугу длиной s1 (рис. 34.3). При этом силы F1 и F2 должны постоянно действовать перпендикулярно рычагу.
Рис. 35.3. Плечо, на которое действует большая сила, описывает при вращении рычага более короткую дугу, поэтому выполняется равенство F1 · s1 = F2 · s2
Поскольку обе части рычага повернулись на один и тот же угол, а концы описали дуги радиусами l1 и l2, то выполняется равенство:
l1/l2 = s1/s2 (35.3)
Это значит, что более длинное плечо описывает и более длинную дугу. Из равенств (35.2) и (35.3) следует, что:
F1 ∙ s1 = F2 ∙ s2 (35.4)
Равенство (35.4) значит, что работа силы F1 равняется работе силы F2. Следовательно, рычаг дает выигрыш в силе, но не дает выигрыша в работе.
«Золотое правило» механики: выигрывая с помощью некоторого механизма в силе, мы обязательно проигрываем в расстоянии (и наоборот).
Вечный двигатель – «PERPETUUM MOBILE»
Perpetuum mobile (лат.) – вечное движение. Столетиями изобретатели пытались придумать конструкцию машины, которая бы работала вечно (рис. 35.4), но ни одна из них не функционировала.
Иногда даже довольно сложно разобраться, в чем же ошибался творец того или иного проекта вечного двигателя. Как только стало понятно, что закон сохранения энергии является универсальным законом природы, научные учреждения перестали принимать к рассмотрению проекты таких машин. Впервые так поступила французская Академия наук в 1848 году.
Вечный двигатель первого рода – это машина, выполняющая работу, большую затраченной на выполнение этой работы энергии.
Но ни один из известных на сегодняшний день механизм или машина не дают выигрыша в работе.
Итоги:
- Коэффициентом полезного действия машины или механизма называют отношение полезной работы, которую выполняет машина, ко всей энергии, затраченной на выполнение этой работы.
- «Золотое правило» механики: выигрывая с помощью некоторого механизма в силе, мы обязательно проигрываем в расстоянии (и наоборот).
- По закону сохранения энергии невозможно создать вечный двигатель первого рода.
Развитие физической картины мира
Несколько лет тому назад австрийский парашютист совершил затяжной прыжок из стратосферы с высоты 39 км (рис. 36.1). Поскольку воздух на такой высоте сильно разрежен, то падение довольно долго было почти свободным.
Свободное падение – удивительное и не до конца изученное явление. Во-первых, свободно падающее тело ничего не весит – оно находится в состоянии невесомости. Во-вторых, и это самое удивительное, – все свободно падающие тела, независимо от массы, падают одинаково, то есть с одинаковым ускорением. Возможно, все эти мысли промелькнули в голове смельчака, который не побоялся прыгнуть вниз почти из космоса, чтобы почувствовать радость свободного полета.
Рис. 36.1. Затяжной прыжок
Гипотезы нужно проверять
В воздухе более тяжелые тела опережают легкие, и об этом свидетельствует наш повседневный опыт. Выдающийся ученый древнего мира Аристотель в свое время изложил гипотезу о том, что более тяжелые тела и в вакууме будут падать быстрее. Лишь через 2000 лет итальянский физик Галилео Галилей осмелился проверить гипотезу Аристотеля. Он стал первым в истории ученым, который попробовал подтвердить свое предположение о независимости ускорения свободного падения от массы тела при помощи опыта. Бросая тела различной массы с наклонной Пизанской башни (рис. 36.2), Галилей заметил, что при условии малого сопротивления воздуха тела разной массы па-дают практически с одинаковым ускорением.
Рис. 36.2. Пизанскую башню Галилей использовал для проверки гипотезы Аристотеля
Отличие античного мышления от современного
Оказывается, люди не всегда исследовали физические явления одинаково. В античном мире не было принято проверять гипотезы опытным путем, а толь-ко теоретическими рассуждениями.
Еще одно отличие – во времена Древней Греции не было места для вакуума. Ум тогдашних ученых не принимал пустого пространства. Аристотель считал, что вода следует за поршнем насоса потому, что природа «боится» пустоты.
Такая теория не давала возможности строить систему водопровода в сегодняшнем понимании этого слова. В знаменитых римских акведуках (рис. 36.3) вода текла ручейком по наклонному желобу. То, что вода может опускаться в трубе, а потом опять подниматься – не приходило людям в голову.
Только опыты Торричелли (рис. 36.4) показа-ли, что существует атмосферное давление, и что оно очень большое. На каждый квадратный метр поверхности действует сила, которую создавал бы груз весом в 10 тонн. Обратите внимание, что мир меняют не только новые знания и факты, но и новый способ мышления.
Исследование свободного падения с помощью вакуумного насоса
То, что нам сегодня кажется привычным, когда-то было удивительным. Мы уже говорили о том, какие интересные опыты показывал своим соотечественникам бургомистр города Магдебурга Отто фон Герике. Он смог это сделать, пользуясь изобретенным им вакуумным насосом.
Около поверхности земли наблюдать свободное падение сложно – мешает воздух. Но выдающийся английский физик Исаак Ньютон использовал вакуумный насос, чтобы выкачать воздух из стеклянной трубы, и наблюдал, как свинцовая дробинка и перышко падали вместе. Таким образом Ньютон подтвердил наблюдения Галилея: тела разной массы в состоянии свободного падения падают одинаково.
Казалось бы, что со свободным падением уже все ясно, но еще Ньютона, а впоследствии и Эйнштейна беспокоила загадка массы.
Загадка двух масс
Если мы не можем мгновенно ускорить или остановить тело, то это потому, что при изменении скорости начинает проявлять себя инертная масса. Когда тяжелый чемодан оттягивает нам руку вниз, сигнализирует о себе гравитационная, то есть «тяжелая» масса. Причем обе массы у каждого тела одинаковы. А вот этот факт как раз и не очевиден!
В городе Бремене есть лаборатория, в которой исследуют свободное падение в вакуумной трубе высотой 140 м (рис. 36.5). Это гигантский вариант трубки Ньютона. Ее еще называют пятисекундной тру-бой, потому что время падения в этой трубе длится приблизительно 5 с.
На что надеются исследователи? Они надеются, что, увеличив точность измерения, удастся заметить хоть и малое, но различие между инертной и гравитационной массами тела. Пока что их усилия безуспешны.
Тёмная масса
Ученые еще не успели до конца разобраться со свободным падением, а от астрофизиков и исследователей в области ядерной физики одновременно пришли данные о возможности существования третьей разновидности массы, которую пока что называют темной, и которую имеющиеся приборы неспособны воспринимать.
Каждый шаг вперед в науке дает новые факты и загадки, которые начинают изучать уже другие поколения исследователей. Два нанограмма протонов в такой супермашине как коллайдер удалось за десять часов разогнать почти до скорости света. Но, если подумать, то один грамм протонов нужно будет разгонять в течение миллионов лет – таково нынешнее состояние нашей науки с точки зрения будущего!
Происхождение вселенной
Астрофизики установили, что Вселенная расширяется, большинство галактик отдаляются от нас и друг от друга, а скорость самых отдаленных объектов достигает 240 000 км/с. Это при-вело ученых к мысли о том, что наша Вселенная появилась около 15 млрд. лет назад в результате гигантского взрыва. Отголосок этого взрыва «звучит» до сих пор, а «услышать» его можно с помощью очень чувствительных антенн радио-телескопов (рис. 36.6), которые постоянно прослушивают космическое пространство.
В разных отдаленных уголках Вселенной можно наблюдать рождение и гибель звезд, а также катастрофы чрезвычайного масштаба – взрывы сверхновых звезд и столкновения целых галактик (рис. 36.7).
Последние достижения астрофизики
Сила тяжести действует на расстоянии, но как она передается от тела к телу – не совсем понят-но. Гравитационная сила вызывает только притяжение, и еще никогда не наблюдалось отталкивания. Сейчас, благодаря эффекту гравитационного линзирования (рис. 36.8), появились данные, свидетельствующие об ускоренном расширении Вселенной, а это можно объяснить разве что наличием антигравитации и «темной энергии».
Рис. 36.8. Гравитационные линзы, образованные притяжением отдаленных галактик, свидетельствуют о новом виде энергии
Вращение края нашей Галактики происходит значительно быстрее, чем это рассчитано по имеющимся в настоящее время формулам, что свидетельствует о существовании скрытой («темной»)
массы, которую современные приборы даже не способны воспринять.
Звезды бывают намного больше и горячее Солнца, а бывают и совсем маленькими и сравнительно холодными. Некоторые из них сжимаются силами притяжения до такой степени, что один кубический сантиметр вещества так называемой нейтронной звезды весит сто миллионов тонн. Другие сжимаются еще больше и исчезают из поля зрения, превращаясь в «черную дыру», которая не выпускает из своей сферы действия даже свет. Все эти чрезвычайно интересные данные получены с помощью спектрометров и цифровых фото-камер. Приборы эти работают круглосуточно – как на Земле, так и в космосе.
Космические телескопы
Современные системы связи дают возможность получать информацию от разнообразных устройств, даже не выходя из дома – через систему Интернет. Именно так с американского космического телескопа «Хаббл» (рис. 36.9) получена фотография галактики М 30.
На орбите находится и украинский теле-скоп «Астрон-1», а космический аппарат «СИЧ-1М» (рис. 36.10) исследует Мировой океан. Эти сложные приборы и аппараты спроектировали украинские физики. Полученная информация обрабатывается и анализируется. Вот так и появляются малые и большие открытия.
Что движет исследователями
В наш век воздушных лайнеров и космических ракет людей трудно чем-либо удивить. Но всегда достойна удивления человеческая любознательность. Вспомним еще раз о том, что первыми оторвались от земли воздушные шары, которые построили братья Монгольфье, потому что очень хотели летать.
Внизу, около открытого отверстия шара, они разожгли огонь из соломы и шерсти. Когда воздух внутри разогрелся, шар взлетел и поднялся на высоту 1 000 м, пробыв в воздухе 10 минут. Он приземлился за полторы мили (2,4 км) от места старта.
В сентябре 1782 года в Версале состоялся полет подобного шара в присутствии короля и королевы Франции, придворных и послов разных стран. Первыми пассажирами были овца, петух и утка. Полет длился 23 минуты, а шар пролетел 9 км. Посол России во Франции Барятинский писал «о поднятии на воздух великой тягости посредством дыма»: «Величие сего зрелища и чувствование, какое происходило в нескольких ста тысячах народа, описать никак не-возможно, ибо радость, страх, ужас и восторг видимы были на всех лицах».
Исаак Ньютон (Isaac Newton, 1643–1727) – английский физик и математик. Открыл закон всемирного тяготения, разложил белый свет на цвета и сформулировал три основных закона механики. Его научный труд «Основы натуральной философии» – один из наиболее выдающихся в истории науки.
Ньютон родился в 1643 г. в небольшой английской деревне Вулсторп. В детстве любил мастерить различные механические устройства, самостоятельно построил маленькую мельницу. В 12 лет его отдали на обучение в городскую школу близлежащего городка Грэнтем. Сначала он учился посредственно, но в старших классах начал упорно работать и стал лучшим учеником.
Затем Ньютон учился в Тринити-колледже. И по сегодняшний день у входа в ворота колледжа растет яблоня в память о яблоке, которое «повлекло» открытие закона тяготения. В возрасте 27 лет Ньютон стал профессором Кембриджского университета. Этот университет славится физической и математической школой и поныне. В 1668 г. Ньютон сконструировал первый зеркальный телескоп (рис. 37.10), который затем усовершенствовал. За это изобретение его избрали членом Лондонского королевского общества (Английская академия наук). На основании убедительных экспериментов по разложению белого света на семь составных цветов он разработал теорию света.
В 1688 г. Ньютона избрали членом английского парламента, и он два года провел в Лондоне. Позже Ньютона назначили директором Монетного двора Англии (в наше время это должность министра финансов). Он провел очень важную для страны денежную реформу и довольно жестко боролся с казнокрадами.
В 1703 г. его избрали президентом Лондонского королевского общества, а в 1705 г. королева Анна впервые в истории Англии присвоила ему титул дворянина и подарила имение.
Ньютон был оригинальным человеком, и о нем рассказывают много интересных историй. Друзья, которые посещали Ньютона, заметили, что калитка около его дома довольно трудно открывается. Оказалось, что Ньютон присоединил к ней водяную помпу, и каждый посетитель накачивал немного воды в резервуар на чердаке.
Ньютон не любил отвлекаться от работы, и, чтобы кошка ему не докучала, просясь в дом, сделал в дверях небольшое отверстие. Когда появились котята, он сделал еще семь меньших отверстий, потому что котята поднимали страшный шум, когда кошка пролезала в свое отверстие без них.
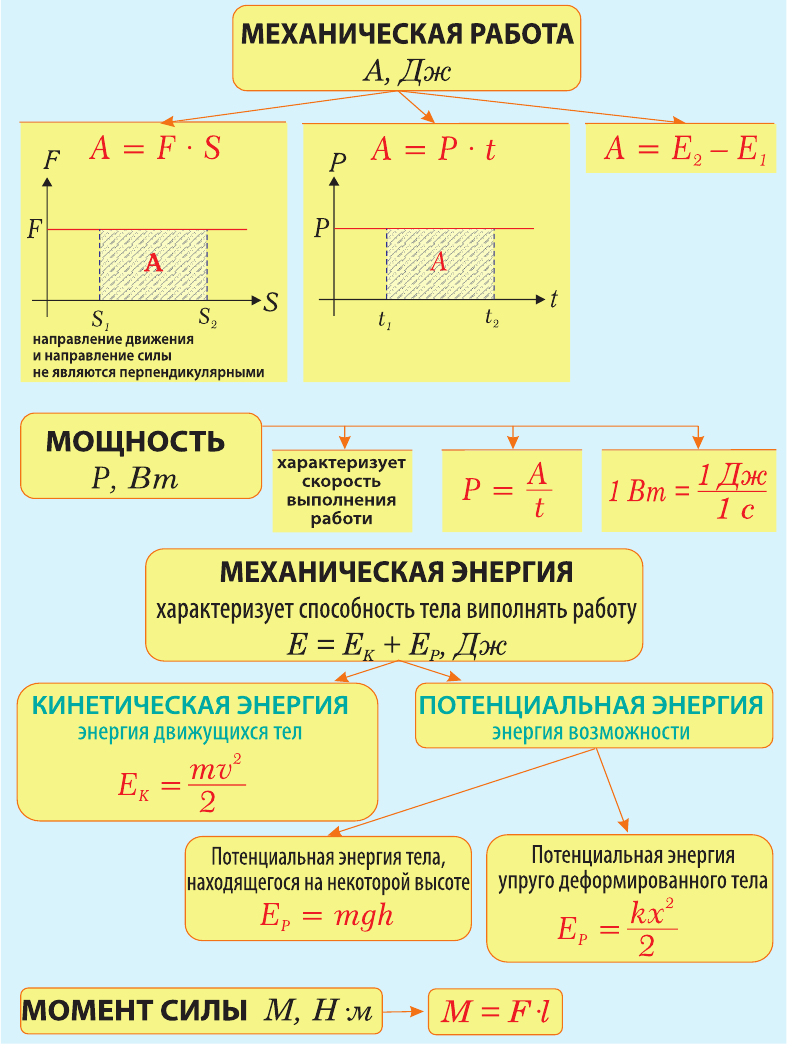
Карта механической работы и энергии
| ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ | |
| Энергия не возникает из ничего и не исчезает бесследно. Количество ее остается постоянным. Она только переходит из одного вида в другой, или от одного тела к другому |
Полная механическая энергия тела (системы) не изменяется, если нет потерь на трение |
| ПРОСТЫЕ МЕХАНИЗМЫ | |||
РЫЧАГ |
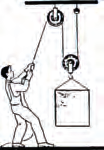 БЛОК БЛОК |
НАКЛОННАЯ ПЛОСКОСТЬ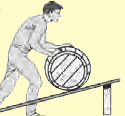 |
|
Выигрыш в силе зависит от соотношения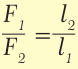 |
НЕПОДВИЖНЫЙ Выигрыша в силе не дает |
ПОДВИЖНЫЙ Выигрыш в силе |
Выигрыш в силе определяется высотой h и длиной l наклонной плоскости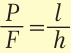 |
ЗОЛОТОЕ ПРАВИЛО МЕХАНИКИ: Выигрывая с помощью некоторого механизма в силе, мы обязательно проигрываем в расстоянии (и наоборот)
Коэффициент полезного действия механизмов (КПД)
Механическая работа и единицы работы
В повседневной жизни слово «работа» употребляется очень часто. Работой называют любую полезную работу рабочего, учёного, ученика.
В физике понятия работы значительно уже. Прежде всего рассматривают механическую работу.
Механическая работа выполняется при перемещении тела под действием приложенной к нему силы.
Рассмотрим примеры механической работы. Автомобиль тянет с определённой силой прицеп и перемещает его на некоторое расстояние, при этом выполняется механическая работа. Рабочий поднимает пакеты (рис. 168) и складывает их. Он выполняет механическую работу.
Шайба движется по льду, под действием силы трения она через некоторое время останавливается. В этом случае также выполняется механическая работа.
Рассмотрим, отчего зависит значение механической работы.
Для того чтобы поднять груз массой 1 кг на высоту 1 м, нужно приложить силу 9,8 Н. При этом выполняется механическая работа. А для того чтобы поднять тело массой 10 кг на такую же высоту, нужно приложить силу, в 10 раз большую. Выполненная работа в этом случае будет в 10 раз больше. Если поднимать тело массой 1 кг не на 1 м, а, например, на 10 м, то работа, выполненная при подъёме груза на 10 м, будет в 10 раз больше работы, выполненной при подъёме тела на 1 м.
Следовательно, механическая работа прямо пропорциональна приложенной к телу силе и расстоянию, на которое это тело перемещается.
Чтобы определить выполненную механическую работу, нужно значение силы умножить на путь, пройденный телом в направлении действия силы, т. е.

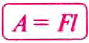
где А — механическая работа; 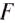
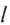
Единицей работы в СИ является один джоуль (1Дж).
1 джоуль – это работа, которую выполняет сила 1 Н, перемещая тело на 1 м в направлении действия силы: 1 Дж =1 Н х 1 м = 1 Нм.
Эта единица названа в честь английского физика Джеймса Джоуля. Единицами механической работы являются также килоджоуль и мегаджоуль:
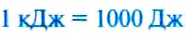
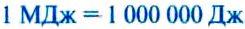
Рассмотрим случаи, когда механическая работа не выполняется. Мы хотим передвинуть тяжёлый шкаф, действуем на него с силой, но не можем сдвинуть его с места (т. е. 
Если тело движется по инерции (т. е. 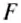
Мощность. единицы мощности
Рассмотрим следующие примеры выполнения механической работы.
Двум ученикам одинаковой массы нужно подняться по канату вверх на одну и ту же высоту (рис. 169), т. е. выполнить одинаковую механическую работу. Один из них может выполнить это быстрее.
Подъёмный кран на строительстве за несколько минут поднимает на заданную высоту, например, 400 кирпичей. Если бы эту работу выполнял рабочий, перенося кирпич вручную, то он затратил бы на это весь рабочий день.
Гектар земли сильная лошадь может вспахать за 10—12 ч, а трактор с многолемеховым плугом эту работу выполняет за 40—50 мин.
В этих примерах один из учеников выполняет одну и ту же работу быстрее, чем другой, подъёмный кран — быстрее, чем рабочий, а трактор – быстрее, чем лошадь. Скорость выполнения работы характеризуют физической величиной, которую называют мощностью.
Мощность – это физическая величина, которая определяется Г отношением выполненной работы к затраченному времени.
Чтобы определить мощность, нужно работу разделить на время её выполнения:
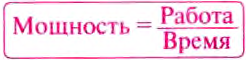
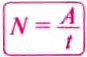
где N — мощность; А — механическая работа; t — время.
Единицей мощности в СИ является один ватт (1 Вт). Она названа в честь английского изобретателя паровой машины Джеймса Уатта.
1 ватт – это мощность, при которой за 1 с выполняется работа 1 Дж:

Используют также другие единицы мощности: киловатт и мегаватт:
Зная мощность двигателя N, можно определить работу А, которую выполняет этот двигатель на протяжении определённого интервала времени t, по формуле:
Кстати:
Мощность сердца в покое у разных людей лежит в пределах 0, 7-1,8 Вт, т. е. она соизмерима с мощностью электрического звонка. При нагрузке она может возрастать в 2-6 раз, у тренированных людей – даже в 10 раз. Длительное время человек способен работать со средней мощностью 75 Вт, а кратковременно, например во время бега, – до 600 Вт.
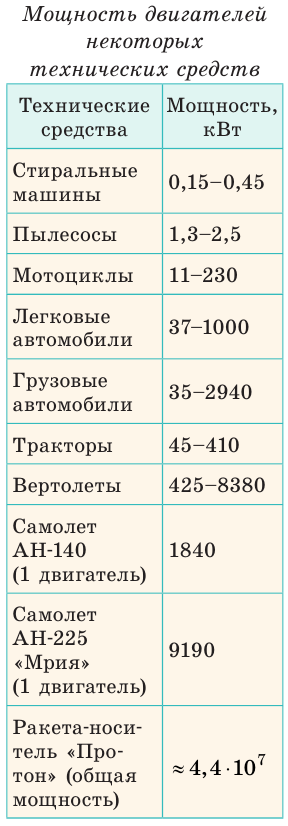
Хвост голубого кита имеет горизонтальные лопасти. Он развивает мощность 368 кВт. Эта мощность только в 2 раза меньше мощности двигателя самолёта Ан-2 и в 7 раз больше мощности двигателя трактора ДТ-75.
Тепловоз имеет мощность 4400 кВт, а ракета-носитель «Протон» – свыше 44 000 Мвт.
Пример №7
Какую работу выполняет трактор, тянущий прицеп с силой 15 000 Н на расстояние 300 м?
Дано:
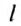
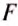
А = ?
Решение:
По формуле 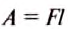
Ответ: трактор выполняет работу, равную 4500 кДж или 4,5 МДж.
Пример №8
Какую работу нужно выполнить, чтобы поднять мешок сахара массой 50 кг на второй этаж высотой 3 м?
Дано:
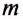
Н = 3 м
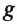
А = ?
Решение:
Работу для подъёма тела на некоторую высоту определяем по формуле:
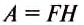
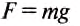
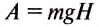
А = 50кг • 10 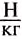
А = 1500Дж
Ответ: чтобы поднять мешок сахара на второй этаж, нужно выполнить работу, равную 1500Дж.
Пример №9
Определить мощность двигателя, если он за 10 мин выполнил работу 7200 кДж.
Дано:
А = 7200 кДж = 7200 000Дж
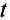
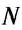
Решение:
По формуле 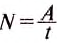
Ответ: мощность двигателя равна 12 кВт.
Работа и энергия
Усвоив материал этого раздела, вы будете знать:
- какие существуют виды механической энергии, единицы измерения работы, мощности;
- что такое простые механизмы, использование машин и простых механизмов.
Вы сможете объяснить:
- закон сохранения и превращения энергии, «золотое правило» механики;
- превращение энергии в механических процессах.
Вы будете уметь:
- измерять мощность и КПД механизмов;
- пользоваться простыми механизмами.
Механическая работа
Слово работа мы слышим очень часто: и когда говорим о действии каких-либо машин или механизмов, и когда описываем какие-либо события будничной жизни. Так, характеризуя деятельность грузчика, который переносит мешки с мукой, мы говорим, что он выполняет работу. Слово работа мы употребляем и тогда, когда объясняем принцип действия двигателя внутреннего сгорания, в котором горячий газ, образовавшийся при сгорании топливно-воздушной смеси, передвигает поршни в цилиндрах. Во всех упомянутых случаях слово работа используют тогда, когда тела изменяют свое состояние.
Что такое механическая работа
В физике используют понятие — механическая работа. Она выполняется всегда, когда тело перемещается под действием определенной силы. Так, под действием силы тяжести шарик падает на поверхность Земли. Говорят, что сила тяжести выполняет работу по перемещению шарика.
Пуля в стволе ружья перемещается в результате действия пороховых газов, вследствие чего летит на значительное расстояние.
Под действием силы упругости, которая возникает при растяжении тетивы лука, стрела приобретает значительную скорость и отлетает от лука. Но никто не скажет, что сила притяжения, которая действует на неподвижный камень, выполняет работу. Так как камень не изменяет своего состояния.
Поэтому считают, что работа выполняется только тогда, когда на тело действует сила и оно при этом осуществляет перемещение.
Механическая работа является физической величиной и ее можно рассчитать.
Как рассчитывают механическую работу
Представим, что на высоту 2 м нужно поднять сначала груз массой 5 кг, а затем – массой 10 кг. Очевидно, что во втором случае должна быть выполнена большая работа, чем в первом, поскольку к телу нужно приложить большую силу.
Большая работа будет выполнена и тогда, когда один и тот же груз нужно поднять на большую высоту, например, не на 2 м, а на 4 м.
Значение работы зависит от значения силы и пути, на кото-]28 Р°м действует эта сила. Это простая зависимость, и ее можно записать в виде формулы.
Если работу обозначить буквой 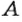
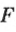
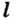
Единицы работы
Соответственно определению установлена единица работы. Если действующая сила равна 1 Н и тело перемещается на 1 м, то при этом выполняется работа 1 Дж (джоуль).
1 джоуль = 1 ньютон • 1 метр,
или
Единица работы так названа в честь выдающегося физика, исследователя в области механики и теплоты Дж. Джоуля.

Для удобства записей и расчетов используют такие кратные единицы работы, как килоджоуль (кДж) и мегаджоуль (МДж):
Рассмотрим пример расчета выполненной работы как физическую задачу.
Пример №10
Рабочий перевез тележку на расстояние 25 м. Прикрепленный к ручке тележки динамометр показал, что рабочий прикладывал к тележке силу 200 Н. Какая работа выполнена?
Дано:
Решение
Ответ. Выполненная работа равна 5 кДж.
Используя определение работы и соответствующую формулу, можно рассчитывать величины, от которых зависит работа.
Так, если известны работа и путь, на котором эта работа выполнена, можно определить силу:
Аналогично можно определить путь, на котором выполнена работа:
Вычисление механической работы
C понятием «механическая работа» или просто «работа» мы уже встречались в курсе физики. Механическая работа — это процесс передачи движения от одного тела (системы тел) к другому телу (или системе тел); физическая скалярная величина, являющаяся количественной мерой этого процесса, называется работой. Она определяется следующим образом. Когда на тело действует постоянная сила и тело, двигаясь прямолинейно в направлении действия силы, совершает перемещение 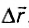
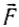
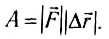
Из определения следует, что работа — скалярная величина, а также то, что в метрической системе единиц (СИ) единица измерения работы 1H-1 м=1 Дж (джоуль). Эта единица названа в честь английского ученого Д. Джоуля, впервые экспериментально обосновавшего эквивалентность работы и теплоты.
Мы рассмотрели самый простой случай, когда перемещение тела и сила, действующая на него, совпадают по направлению. А как нужно вычислять работу силы, если ее направление не совпадает с перемещением?
Для выяснения этого вопроса рассмотрим следующий опыт (рис. 123). Через блок перекинута нить, на которой висит брусок некоторой массы. На брусок действуют две силы — сила натяжения нити 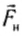
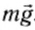
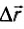
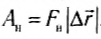
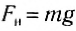
Рис. 123
Если вектор силы и перемещения составляют между собой угол а, то работа этой силы определяется по формуле
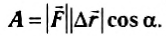
Это и есть общее выражение для работы постоянной силы. Действительно, если векторы 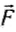
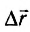
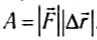
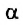
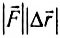
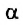
Для примера найдем работу каждой из всех сил, действующих на движущиеся санки.
Па рисунке 124 показаны все силы, действующие на тело. Это сила натяжения веревки 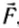
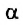
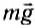
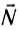
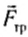
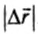
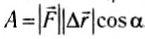
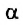
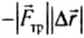
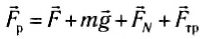
то работу результирующей силы можно найти как сумму работ всех действующих на санки сил:
Очевидно, что значение работы результирующей силы может быть положительным, отрицательным или равным нулю.
Рис. 124
При прямолинейном движении тела в одну сторону модуль перемещения 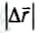
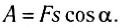
На рисунке 125 представлен график зависимости силы, приложенной к телу, совпадающей по направлению с перемещением, от пройденного пути s. В соответствии с формулой (1) работа этой силы численно равна площади прямоугольника (заштриховано).
Рис. 125
Если же сила изменяется в процессе движения, то работа этой силы тоже будет численно равна площади под кривой. В частности, на рисунке 126 представлен график силы, которая линейно уменьшается с пройденным расстоянием до нуля. Очевидно, что работа этой силы на пути s∣ численно равна площади треугольника, т. е.:
Рис. 126
Главные выводы:
- Механическая работа характеризует процесс передачи движения от одного тела (системы тел) к другому телу (или системе тел).
- Работа силы — это физическая скалярная величина, равная произведению модулей силы, перемещения и косинуса угла между направлениями силы и перемещения, если сила не изменяется в процессе движения.
- При движении тела все действующие на него силы совершают работу.
- Работа результирующей силы равна алгебраической сумме работ всех сил, действующих на тело.
Механическая работа и мощность
Механическая работа – физическая величина, характеризующая изменение состояния тела и зависящая от числового значения и направления равнодействующей силы и перемещения точки приложения этой силы.
Механическая работа равна произведению модуля силы, действующей на тело, модуля его перемещения и косинуса угла между векторами силы и перемещения:
Работа – скалярная физическая величина, которая, в отличие от других скалярных величин (например, путь, масса, площадь и другие), может быть равна нулю, принимать положительные или отрицательные числовые значение. Знак работы зависит от направления приложенной к телу силы и направления перемещения тела (а):
a) если угол между векторами силы, действующей на тело, и его перемещением равен нулю или острый 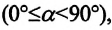
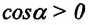
b) если угол между векторами силы, действующей на тело и его перемещением равен нулю или тупой 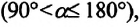
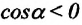
c) если сила, действующая на тело, перпендикулярна перемещению 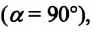
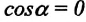
Единица измерения работы в СИ – джоуль (Дж):
- 1 джоуль (1 Дж) — это работа, которую совершает сила 1Н, перемещая тело на 1 м в направлении действия силы:
Частный случай:
Если тело движется вдоль оси 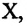
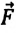
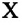
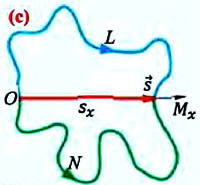
Работа постоянной по значению и направлению равнодействующей силы обладает двумя важными свойствами: (с)
1. Работа, постоянной равнодействующей силы по произвольной замкнутой траектории равна нулю. Потому, что модуль перемещения тела по замкнутой траектории равен нулю:
2. Работа, совершаемая постоянной равнодействующей силой во время движения тела между двумя данными точками, не зависит от формы траектории, соединяющей эти точки.
Например, так как перемещения тела, движущегося по траекториям OLM и ONM, соединяющим точки О и М, одинаковы, то и работы постоянной равнодействующей силы по этим траекториям одинакова (с):
Мощность:
Быстрота совершаемой работы характеризируется физической величиной, называемой мощностью.
- Мощностью называется отношение совершенной работы ко времени, затраченному на выполнение этой работы.
Единица измерения мощности в СИ — ватт (Вт):
- 1 Ватт определяется как мощность, при которой за 1с совершается работа в 1 Дж. Первую единицу измерения мощности предложил в 1789 году английский физик и изобретатель Джеймс Уатт – она называлась лошадиной силой (л.с.). Иногда и сегодня пользуются этой единицей:
Работа, совершаемая постоянной силой за промежуток времени 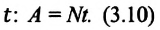
На основании этой формулы получена другая единица работы – киловатт-час:
Если мощность с течением времени меняется, то числовое значения работы можно определить как площадь фигуры, лежащей под графиком мощность -время (d):
При прямолинейном равномерном движении тела его мощность можно выразить через скорость движения тела. Например, мощность двигателя автомобиля, движущегося прямолинейно равномерно (при постоянном значении силы трения), равна:
Из этого выражения получается, что при постоянной мощности двигателя автомобиля при малых значениях скорости имеем выигрыш в силе тяги (в случае I передачи скорости), а при малых значениях силы тяги имеем выигрыш в скорости (в случае IV и V передач скорости автомобиля):
Физический смысл механической работы и энергия
На первый взгляд, привести примеры ситуаций, когда выполняется работа, очень легко. Работу выполняют вода и воздух, машины и механизмы, строители и грузчики. А выполняет ли работу учащийся, который неподвижно держит в руках тяжелый портфель? программист, который выполняет задание сидя за компьютером? И вообще, что имеют в виду физики, когда говорят о механической работе?
О механической работе говорят тогда, когда тело изменяет свое положение в пространстве в результате действия силы. Рассмотрим движение баржи, которую тянет буксир (рис.30.1). Буксир действует на баржу с некоторой силой — силой тяги 
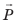
Чем больший путь пройдет баржа под действием силы тяги, тем большую механическую работу выполнит эта сила. Механическая работа увеличится и при возрастании силы тяги — если, например, заставить буксир с баржей двигаться с большей скоростью. В общем случае механическая работа, выполняемая некоторой силой, зависит от значения силы и пути, пройденного телом в результате действия этой силы.
Механическая работа — это физическая величина, которая характеризует изменение положения тела под действием силы и равна произведению силы на путь, пройденный телом в направлении этой силы: 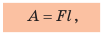
Единица работы в СИ — джоуль (Дж); названа так в честь английского ученого Джеймса Джоуля (рис. 30.2): 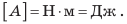
Обратите внимание! Поскольку сила действует на тело со стороны другого тела (буксир тянет баржу), не будет ошибкой говорить не о работе силы (работе силы натяжения троса), а о работе тела (работе буксира).
Какие значения может иметь механическая работа
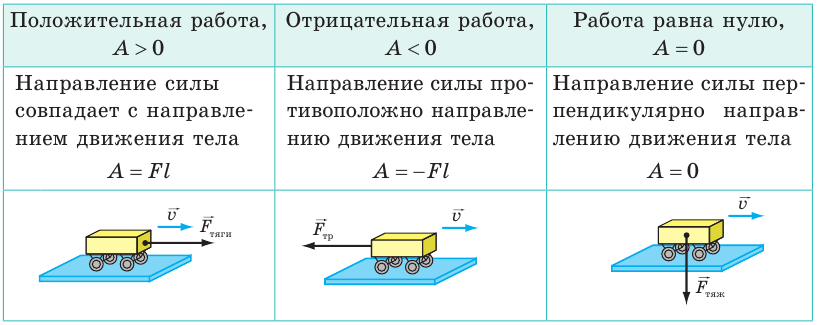
Вы уже знаете, что сила имеет направление, то есть сила — это векторная величина. А вот работа силы не имеет направления, то есть работа — скалярная величина. При этом работа может быть положительной, отрицательной или равной нулю — в зависимости от того, куда направлена сила относительно направления движения тела:
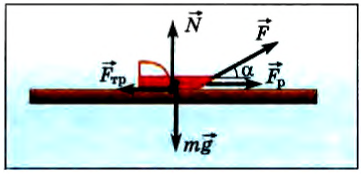
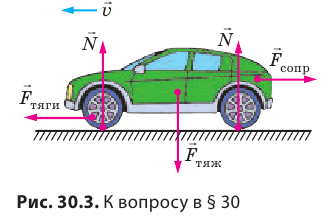
На рис. 30.3 показаны силы, которые действуют на автомобиль, движущийся по горизонтальному участку дороги: сила тяги, сила сопротивления движению, силы нормальной реакции опоры, сила тяжести. Какая сила, по вашему мнению, выполняет положительную работу? отрицательную работу? Работа каких сил равна нулю?
- Заказать решение задач по физике
Геометрический смысл механической работы
Пусть тело движется под действием постоянной силы 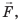
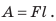
Из рисунка видим, что произведение 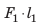
Пример №11
С помощью пружины жесткостью 25 Н/м брусок передвигают по столу с постоянной скоростью 5 см/с. Какую работу выполнит сила упругости за 20 с, если удлинение пружины равно 4 см? Анализ физической проблемы. Работа силы упругости положительна, поскольку брусок движется в направлении действия силы. Для определения работы нужно найти значение силы упругости 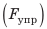
Дано:
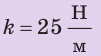
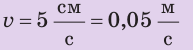

Найти:
Решение:
По определению работы:
По закону Гука:
Путь, пройденный бруском, равен:
Подставив выражения для 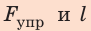
Проверим единицу, найдем значение искомой величины:
Ответ:
Итоги:
Механическая работа — это физическая величина, которая характеризует изменение положения тела под действием силы. Если сила постоянна и действует в направлении движения тела, механическую работу находят по формуле: 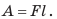
В зависимости от направления силы и направления движения тела механическая работа может быть положительной, отрицательной или равной нулю.
Мощность и энергия
Возможно, важнейшим в развитии человеческой цивилизации стало время, когда человек начал изготовлять простые орудия труда, строить примитивное жилье, пахать землю. сначала люди использовали для выполнения работы только мышечную силу своих рук, затем — силу домашних животных: лошадей, быков, ослов, верблюдов. это позволило за меньшее время выполнять ту же работу. однако настоящий прорыв произошел благодаря использованию машин и механизмов — автомобилей, судов, поездов, кранов, экскаваторов и т. п. современные машины могут выполнять работу в тысячи раз быстрее человека. Какая же характеристика машин является показателем их эффективности?
Разным исполнителям для выполнения одной и той же работы требуется разное время. Так, если экскаватор и землекоп одновременно начнут копать траншеи (рис. 31.1), то понятно, что экскаватор выполнит работу значительно быстрее, чем землекоп. Кран быстрее, чем грузчик, перенесет нужное количество кирпичей; трактор быстрее лошади вспашет поле.
Приведите еще несколько подобных примеров. Для характеристики скорости выполнения работы используют физическую величину мощность.
Мощность — это физическая величина, характеризующая скорость выполнения работы и равная отношению выполненной работы ко времени, за которое эта работа была выполнена: 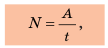
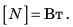
1 Вт равен мощности, при которой в течение 1 с выполняется работа 1 Дж: 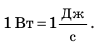
Как мощность зависит от силы тяги и скорости движения
Предположим, необходимо вычислить мощность движущегося с постоянной скоростью v транспортного средства, двигатель которого создает силу тяги F. Для определения мощности воспользуемся формулой:
В качестве единицы мощности Джеймс Ватт ввел лошадиную силу. Эту единицу и сейчас используют в технике: 1 л. с. ~ 735,5 Вт. Общая мощность двигателей самолета АН-225 (имеющего 6 двигателей) превышает общую мощность двигателей самолета АН-140 (имеющего 2 двигателя) в 15 раз.
Вспомним формулу для расчета работы: 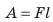
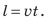
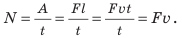
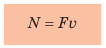
Пример №12
Человек равномерно поднимает ведро с водой на высоту 20 м за 20 с. Какую мощность развивает человек, если масса ведра с водой равна 10 кг?
Анализ физической проблемы. Чтобы определить мощность, нужно рассчитать работу, которую выполнил человек, поднимая ведро на определенную высоту. Для этого нужно найти значение силы 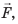
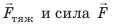
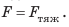
Дано:


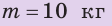
Найти:
Решение:
По определению мощности:
Работа, выполненная человеком:
Поскольку
Подставим выражение для работы в формулу мощности:
Проверим единицу, найдем значение искомой величины:
Ответ:
Итоги:
Мощность — это физическая величина, характеризующая скорость выполнения работы и равная отношению выполненной работы ко времени, за которое данная работа была выполнена: 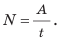
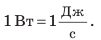
Потенциальная и кинетическая энергии тела
Слово «энергия» мы слышим в телевизионных репортажах, видим на страницах газет, книг и т. д. Им пользуются для характеристики людей (энергичный человек), природных явлений (энергия землетрясения или урагана), машин и механизмов (потребляемая ими электроэнергия). А что такое энергия с точки зрения физики?
Что такое энергия и как она связана с механической работой
Энергия (в переводе с греческого это слово означает «деятельность») — одна из важнейших физических величин. Из курса природоведения вам известны такие понятия, как «электрическая энергия», «атомная энергия», «механическая энергия», — все это разные виды энергии. В механике мы имеем дело с механической энергией и будем пользоваться таким определением:
Энергия — это физическая величина, которая характеризует способность тела (системы тел) выполнять работу. Энергию обозначают символом E (или W). Единица энергии в СИ, как и работы, — джоуль: [E]=Дж. Продемонстрируем способность тела выполнять механическую работу. Расположим маленький шарик на краю стола, а на полу поставим сосуд с водой. Если столкнуть шарик, он полетит вниз, упадет в воду и расплещет жидкость (рис. 32.1). Появление брызг означает, что шарик выполнил некоторую работу. Если же к шарику не прикасаться, он останется лежать на столе. Таким образом, энергия шарика может быть реализована выполнением работы во время падения или сохранится «до лучших времен». На рис. 32.2 крепкая веревка удерживает деформированную балку катапульты. Балка работу не выполняет, но может выполнить, если веревку отпустить: распрямляясь, балка придаст скорость метательному снаряду. При этом деформация балки уменьшится. Многим из вас, наверное, приходилось видеть, как играют в боулинг. Шар запускают по горизонтальной гладкой дорожке. От момента броска до попадания в кегли шар движется практически по инерции и работу не выполняет. Но затем, когда шар разбрасывает кегли, он выполняет работу (рис. 32.3) и уменьшает скорость своего движения.
Приведите еще несколько примеров тел, способных выполнить работу, то есть обладающих определенной механической энергией. Чем большую работу может выполнить тело, тем большей энергией это тело обладает. При выполнении механической работы энергия тела изменяется. Следовательно, механическая работа является мерой изменения энергии тела. Так, когда грузчик поднимает кирпичи, энергия кирпичей увеличивается на значение выполненной грузчиком работы (рис. 32.4). Энергия шарика, падающего со стола, уменьшается на значение выполненной этим шариком работы. То же можно сказать о работе, которую выполнила балка катапульты, о работе шара для боулинга и т. д.
Расчёт и вычисление потенциальной энергии, которую «запасает» поднятое тело
Тело, поднятое над поверхностью Земли, обладает энергией, что обусловлено притяжением тела к Земле. Такую энергию называют потенциальной.
Потенциальная энергия 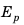
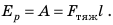
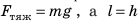
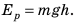
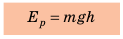
Доказываем, что упруго деформированные тела обладают потенциальной энергией:
В упруго деформированном теле части тела взаимодействуют силами упругости. Если тело «освободить», то силы упругости вернут его в недеформированное состояние, выполнив механическую работу. Следовательно, упруго деформированное тело тоже обладает потенциальной энергией (рис. 32.7). Потенциальная энергия упруго деформированной (растянутой или сжатой) пружины определяется по формуле: 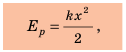
Кинетическая энергия тела
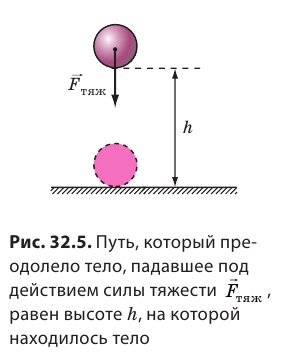
Вспомним пример с шаром для боулинга: он катится, разбрасывает кегли и уменьшает скорость своего движения. Шар выполнил работу, поэтому его механическая энергия уменьшилась. Вместе с тем потенциальная энергия шара не изменилась, ведь шар все время находился на одной и той же высоте, — изменилась только скорость его движения. Следовательно, энергия, позволившая шару выполнить работу, была обусловлена движением шара. В физике эту энергию называют кинетической. Кинетическая энергия зависит от массы тела и скорости его движения (см. рис. 32.8, 32.9). Так, из двух шаров, движущихся с одинаковой скоростью, шар большей массы отодвинет один и тот же брусок на большее расстояние, то есть выполнит большую работу. Это значит, что при одинаковой скорости движения шар большей массы обладает большей кинетической энергией (рис. 32.8).
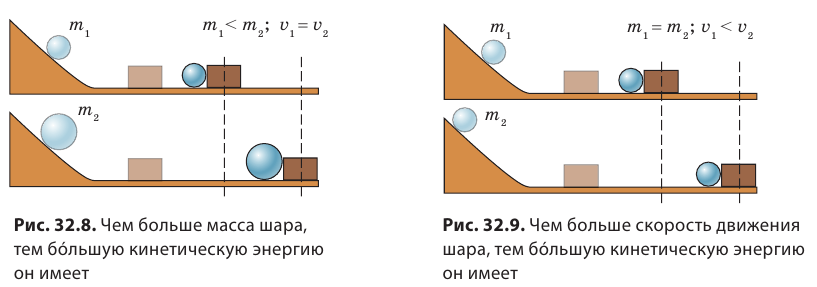
Если масса шаров одинакова, то большую работу выполнит тот шар, который движется с большей скоростью, то есть именно этот шар обладает большей кинетической энергией (рис. 32.9). В физике определена зависимость кинетической энергии от массы и скорости движения тела.
Кинетическая энергия — это энергия, которая обусловлена движением тела и равна половине произведения массы тела на квадрат скорости его движения: 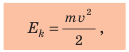
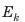
Определение полной механической энергии тела
Достаточно часто тело имеет и потенциальную энергию, и кинетическую. Например, самолет, который летит над землей на некоторой высоте, имеет и потенциальную энергию (поскольку взаимодействует с землей), и кинетическую энергию (поскольку движется).сумму кинетической и потенциальной энергий тела называют полной механической энергией тела:
Итоги:
Если тело (или система тел) может выполнить механическую работу, то говорят, что оно (она) имеет энергию. Энергию обозначают символом E или W.
Единица энергии в СИ — джоуль (Дж). Энергию, обусловленную взаимодействием тел или частей одного тела, называют потенциальной энергией. Потенциальной энергией обладают упруго деформированные тела и тела, поднятые на некоторую высоту.
Потенциальную энергию поднятого на некоторую высоту тела можно вычислить по формуле: 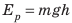
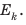
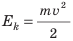
Закон сохранения и превращения механической энергии
Наверное, каждый из вас играл с мячиком-попрыгунчиком. Вспомните: мячик взлетает вверх, падает на пол, отскакивает от него, снова взлетает и снова падает… Когда мячик летит вверх, скорость его движения уменьшается, затем мячик на миг останавливается на некоторой высоте, а после этого начинает движение вниз. При движении вверх кинетическая энергия мячика уменьшается. А может ли исчезнуть энергия мячика совсем?
Превращение потенциальной энергии в кинетическую, и наоборот
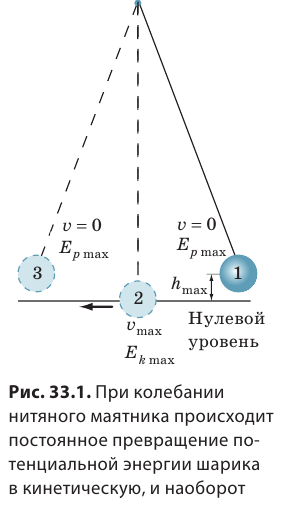
Одним из фундаментальных законов природы является закон сохранения и превращения энергии: энергия никуда не исчезает и ниоткуда не возникает, она лишь превращается из одного вида в другой, передается от одного тела к другому. Для примера рассмотрим превращение потенциальной энергии в кинетическую и наоборот во время свободных колебаний шарика на нити (маятника) (рис. 33.1). Будем считать, что трением можно пренебречь. За нулевой уровень примем самое нижнее положение шарика — положение равновесия (на рис. 33.1 — положение 2).
Отклоним шарик до положения 1. В данном опыте в положении 1 шарик будет находиться на максимальной высоте и, следовательно, будет обладать максимальной потенциальной энергией 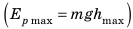
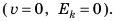
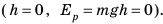
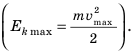
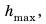
Таким образом, во время колебаний маятника один вид механической энергии переходит в другой: потенциальная энергия превращается в кинетическую, и наоборот. Попробуйте объяснить превращение энергии во время колебаний пружинного маятника (рис. 33.2).
Закон сохранения и превращения механической энергии
Вернемся к примеру с мячиком попрыгунчиком. Когда мячик летит вверх (рис. 33.3), высота, на которой он находится, увеличивается, а значит, возрастает его потенциальная энергия. Скорость движения мячика уменьшается, соответственно уменьшается его кинетическая энергия. При отсутствии силы сопротивления воздуха кинетическая энергия мячика уменьшается на столько, на сколько увеличивается его потенциальная энергия. Таким образом, полная механическая энергия системы мячик—Земля не изменяется. То же самое можно сказать о колеблющихся маятниках: при отсутствии сил трения полная механическая энергия маятников остается неизменной. Теоретические и экспериментальные исследования позволили сформулировать закон сохранения и превращения механической энергии:
В системе тел, взаимодействующих друг с другом только силами упругости и силами тяжести, полная механическая энергия не изменяется: 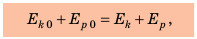
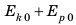
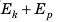
Что происходит с энергией, если в системе существуют силы трения
Еще раз подчеркнем: закон сохранения и превращения механической энергии* выполняется только в случаях, когда нет потерь механической энергии, в частности при отсутствии трения. Если в системе присутствует трение, то механическая энергия (или ее часть) превращается во внутреннюю энергию**. В качестве примера рассмотрим преобразование механической энергии во внутреннюю при торможении поезда. Когда машинист нажимает на тормоз, тормозные колодки прижимаются к колесам (рис. 33.4).
В результате действия силы трения скольжения скорость вращения колеса, а следовательно, скорость движения поезда уменьшаются, то есть уменьшается его механическая энергия. При этом, если прикоснуться к тормозным колодкам или колесу сразу после торможения, то можно обжечься — настолько сильно они нагреваются. Нагревание свидетельствует о том, что внутренняя энергия этих тел увеличилась. Следовательно, кинетическая энергия поезда превратилась во внутреннюю энергию тормозных колодок, колеса и окружающей среды.
Далее для краткости данный закон будем, как правило, называть «закон сохранения механической энергии».
Внутренняя энергия тела — это энергия движения и взаимодействия молекул (атомов, ионов), из которых состоит тело. С увеличением температуры тела его внутренняя энергия увеличивается.
Пример №13
Тело массой 1 кг начинает падать с высоты 20 м. На какой высоте кинетическая энергия тела будет равна 100 Дж? Сопротивлением воздуха пренебречь.
Анализ физической проблемы. При отсутствии сопротивления воздуха полная механическая энергия системы тело—Земля не изменяется, поэтому для решения задачи можем воспользоваться законом сохранения механической энергии. Тело начинает движение, поэтому его начальная скорость равна нулю: v0 = 0. Выполним пояснительный рисунок, на котором укажем положение тела в начале и в конце наблюдения. За нулевой уровень примем поверхность Земли. Задачу будем решать в единицах СИ.
Дано:
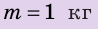
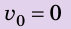
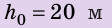
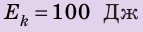
Найти:
Решение:
По закону сохранения механической энергии:
На начальной высоте
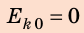
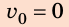
На искомой высоте h:
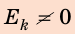
Следовательно:
Отсюда имеем:
Проверим единицы, найдем значение искомой величины:
Ответ:
Пример №14
Тело бросают вертикально вверх со скоростью 20 м/с. На какой высоте потенциальная энергия тела будет равна его кинетической энергии? Сопротивлением воздуха пренебречь. Анализ физической проблемы. Поскольку сопротивлением воздуха следует пренебречь, то полная механическая энергия системы тело—Земля не изменяется, поэтому для решения задачи можем воспользоваться законом сохранения механической энергии. Уровень, с которого бросают тело, примем за нулевой. Задачу будем решать в единицах СИ.
Дано:
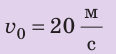
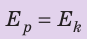
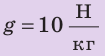
Найти:
Решение:
По закону сохранения механической энергии:
На начальной высоте
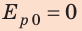
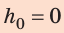
На искомой высоте h:
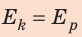
Следовательно:
Из полученного уравнения найдем искомую высоту:
Найдем значение искомой величины:
Ответ: h =10 м.
Итоги:
Потенциальная энергия тела (системы тел) может превращаться в кинетическую энергию, и наоборот. Закон сохранения и превращения механической энергии: в системе тел, взаимодействующих друг с другом только силами упругости и силами тяжести, полная механическая энергия не изменяется: 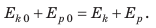
Момент силы и условие равновесия рычага
Проведите опыт. Возьмите длинную линейку и разместите ее на опоре так, как показано на рисунке. ближе к опоре положите (или подвесьте) любой груз, а рукой нажмите на другой конец линейки (подальше от опоры), — вы легко удержите груз. а теперь передвиньте груз дальше от опоры, а руку положите ближе к ней. Почему в этом случае вам приходится прилагать больше усилий, ведь груз остался тем же?
Давно известно, что тяжелое тело поднять значительно легче, если просунуть под него крепкий стержень — лом. В данном случае лом играет роль простого механизма — рычага. Рычаг — это твердое тело, которое может вращаться вокруг неподвижной оси — оси вращения. Лом, лопата (рис. 34.1), линейка, которой мы удерживали груз во время опыта, — все это примеры рычагов.
Рычаг — простейший механизм, которой люди пользуются тысячи лет. Изображение рычага можно найти на скалах и в пещерах, на стенах древних храмов и в папирусах. И сегодня применение рычага мы наблюдаем повсюду (рис. 34.2). Чаще всего в качестве рычага используют длинный стрежень с закрепленной осью вращения.
Условие равновесия рычага
Выясним, при каком условии рычаг находится в равновесии. Для этого воспользуемся лабораторным рычагом. С помощью проволочных крючков будем подвешивать к рычагу грузы. Передвигая крючки, будем изменять плечи сил, действующих на рычаг (рис. 34.3).
Плечо силы — это наименьшее расстояние от оси вращения рычага до линии, вдоль которой сила действует на рычаг. Например, подвесим слева от оси вращения на расстоянии 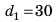
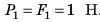
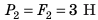
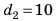
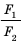
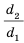
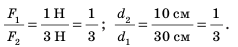
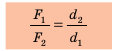
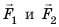
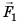
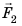
Всегда ли рычаг применяют для получения выигрыша в силе
Обычно говорят, что с помощью рычага можно получить выигрыш в силе. Например, прикладывая достаточно малую силу 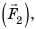
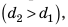
Момент силы
Для характеристики способности силы вращать твердое тело введена физическая величина момент силы.
Момент силы — физическая величина, равная произведению силы, действующей на тело, на плечо этой силы: 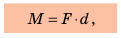
Правило моментов
Воспользуемся свойством пропорции и запишем правило рычага 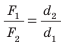
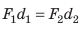
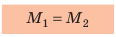
Рычаг находится в равновесии, если сумма моментов сил, вращающих рычаг против хода часовой стрелки, равен сумме моментов сил, вращающих рычаг по ходу часовой стрелки.
Например, когда на плечи рычага действуют три силы (рис. 34.7), условие его равновесия будет выглядеть так: 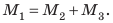
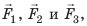

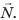
2. Рычаг неподвижен. Это означает, что силы, действующие на рычаг, скомпенсированы: 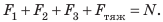
Пример №15
Определите массу груза 1 (см. рисунок), если масса груза 2 равна 4 кг. Массой рычага пренебречь.
Анализ физической проблемы. На плечи изображенного на рисунке рычага действуют две силы: вес груза 1 (сила 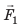
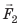
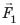
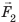
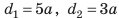
Дано:
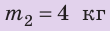
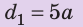
Найти:
Решение:
По правилу рычага:
Поскольку 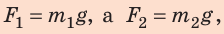
Следовательно
Проверим единицу, найдем значение искомой величины:
Анализ результата: к меньшему плечу рычага подвешен груз массой 4 кг, к большему — груз массой 2,4 кг. Результат правдоподобен.
Ответ:
Итоги:
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной оси. Плечо силы — кратчайшее расстояние от оси вращения рычага до линии действия силы.
Момент силы — физическая величина, характеризующая вращающее действие силы и равная произведению силы F, вращающей тело, на плечо d этой силы: M= Fd. Рычаг находится в равновесии, если сумма моментов сил, вращающих рычаг против хода часовой стрелки, равна сумме моментов сил, вращающих рычаг по ходу часовой стрелки.
Подвижный и неподвижный блоки
Первый блок был изобретен, когда через колесо, вращающееся вокруг своей оси, неизвестный механик древности перебросил веревку и с помощью этого устройства стал поднимать грузы. По легенде, Архимед с помощью нескольких блоков смог спустить на воду тяжелое судно, которое не могли сдвинуть с места десятки лошадей. сейчас блоки используют во многих машинах и механизмах. Чем объясняется их широкое применение?
Связь неподвижного блока и рычага
На рис. 35.1, а изображено колесо (1) с желобом (2). Колесо может вращаться вокруг своей оси (3), неподвижно закрепленнной в обойме (4). Через желоб переброшен шнур (5). Перед вами простой механизм — неподвижный блок. блок — это простой механизм, имеющий форму колеса с желобом по ободу, через который переброшен шнур (канат, веревка).
На первый взгляд, рычаг и неподвижный блок — абсолютно разные механизмы. На самом деле неподвижный блок — это рычаг с одинаковыми плечами. Действительно, приложим к концам шнура, переброшенного через блок, силы 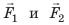
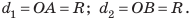
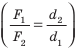
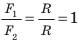
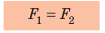
Исследуем подвижный блок:
С помощью обоймы прикрепим груз к оси блока. Сам блок подвесим на шнуре, один конец которого закреплен (рис. 35.4). Если поднимать свободный конец шнура, то за шнуром будет подниматься и блок с грузом. Полученный простой механизм — это подвижный блок. Подвижный блок можно рассматривать как рычаг, который вращается вокруг оси, проходящей через точку опоры O (см. рис. 35.4). Из рисунка видно, что плечо силы 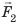
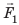
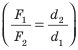
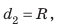
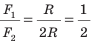
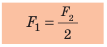
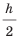
Как и рычаг, подвижный блок можно также использовать для получения выигрыша в расстоянии (либо выигрыша в скорости движения). Для этого груз прикрепляют к свободному концу шнура, а тянут за обойму, к которой прикреплена ось блока (рис. 35.6). Неподвижные и подвижные блоки, как правило, используются одновременно — в виде системы блоков (рис. 35.7). Как вы считаете, позволяет ли система блоков на рис. 35.7 изменить направление действия силы? получить выигрыш в силе?
Пример №16
На рис. 35.8 представлена система блоков. Определите силы натяжения шнуров a и b, если масса груза равна 20 кг. Какой выигрыш в силе дает данная система блоков? На какое расстояние 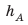
Анализ физической проблемы. Система блоков состоит из двух подвижных блоков (1 и 2) и одного неподвижного блока (3). По условию массой блоков следует пренебречь, значит, натяжение шнура вызвано только весом груза. Для определения выигрыша в силе сравним вес P груза и силу F, которая приложена к свободному концу шнура и под действием которой поднимается груз. Следует учесть, что, выиграв в силе, мы во столько же раз проигрываем в расстоянии, на которое перемещается груз.
Дано:

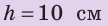
Найти:
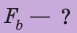
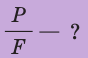
Решение:
Найдем вес груза:
Подвижный блок 1, к обойме которого подвешен груз, дает выигрыш в силе в 2 раза, следовательно, сила натяжения шнура a в 2 раза меньше, чем вес груза:
Подвижный блок 2, к обойме которого подвешен шнур a, тоже дает выигрыш в силе в 2 раза, следовательно, сила натяжения шнура b равна:
Сила F — сила натяжения шнура b:
Поэтому выигрыш в силе составляет:
Во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии:
Анализ результата: в системе два подвижных блока, оба используются для выигрыша в силе. Каждый подвижный блок дает выигрыш в силе в 2 раза, поэтому общий выигрыш в силе равен 4. Таким образом, получен реальный результат.
Ответ: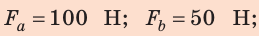
Итоги:
Блок — это простой механизм, имеющий форму колеса с желобом по ободу, через который переброшен шнур (канат, веревка). Различают подвижный и неподвижный блоки. Неподвижный блок похож на рычаг с одинаковыми плечами, поэтому он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок похож на рычаг с отношением плеч 1 : 2, поэтому он дает выигрыш в силе в 2 раза. Однако это сопровождается проигрышем в расстоянии в 2 раза. Подвижный блок также применяют для получения выигрыша в расстоянии (выигрыша в скорости движения). Для большей эффективности обычно используют комбинации подвижных и неподвижных блоков.
Простые механизмы и коэффициент полезного действия механизмов
Простые механизмы — это «труженики» со стажем работы более 40 веков, однако они ничуть не «состарились»: в каждом современном техническом устройстве обязательно найдется простой механизм, и не один. эти устройства позволяют изменить направление действия силы, получить выигрыш в силе или расстоянии. А дают ли они выигрыш в работе?
Характеристика простых механизмов
Вы уже знаете, что рычаги с разными плечами и подвижные блоки позволяют получить выигрыш в силе, но такой выигрыш дается не «даром», ведь, получив преимущество в силе, мы обязательно проиграем в расстоянии (рис. 36.1). Древнее так называемое «золотое правило» механики гласит: «Во сколько раз мы выиграем в силе, во столько же раз проиграем в расстоянии». А действительно ли это так? Допустим, что нужно поднять груз на определенную высоту. Воспользуемся неподвижным блоком: следует перебросить через блок шнур, привязать к шнуру груз и, взявшись за свободный конец шнура, равномерно тянуть его вниз (рис. 36.2). Неподвижный блок можно представить как равноплечий рычаг, поэтому сила, с которой тянут шнур, должна быть равна весу груза: F= P. Однако на практике вращению блока всегда мешает сила трения, поэтому, чтобы поднять груз, к свободному концу шнура следует приложить большую, чем вес груза, силу: 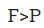
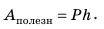
Поскольку 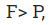
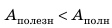
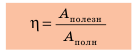
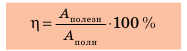
Наклонная плоскость
Кроме рычага и блока люди с античных времен используют еще один простой механизм — наклонную плоскость (рис. 36.3). С помощью наклонной плоскости можно поднимать тяжелые предметы, прикладывая к ним относительно небольшую силу.
Выведем формулу для определения КПД наклонной плоскости. Пусть требуется поднять тело массой m на высоту h по наклонной плоскости длиной l (рис. 36.4). Чтобы поднять тело вертикально (без наклонной плоскости), нужно приложить к нему силу 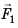
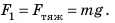
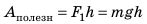
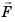
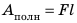
Подумайте, как можно увеличить КПД наклонной плоскости. Движению тела по наклонной плоскости препятствует сила трения. При отсутствии трения между телом и наклонной плоскостью полезная работа была бы равна полной работе: 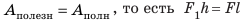
В таком случае мы получили бы наибольший выигрыш в силе: 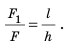
Разновидности наклонной плоскости
Одна из разновидностей наклонной плоскости — клин. Чтобы облегчить рубку дров, в трещину бревна вставляют клин и бьют по нему обухом топора (рис. 36.6). На клин во время удара действуют три тела: сверху — обух топора, по бокам — две части бревна. Соответственно клин действует на обух топора вверх, а на древесину бревна — в стороны, то есть раздвигает части бревна. Таким образом, клин изменяет направление силы удара топора. Кроме того, каждая из двух сил, с которыми клин раздвигает части бревна, намного больше силы, с которой топор ударяет по клину. Еще одна разновидность наклонной плоскости — винт. Возьмем треугольник, вырезанный из тонкого картона, и расположим его рядом с цилиндром (рис. 36.7). Наклонной плоскостью будет служить ребро картона. Обернув картонный треугольник вокруг цилиндра, получим винтовую наклонную плоскость. Собственно нарезка винта — это наклонная плоскость, многократно обернутая вокруг цилиндра. Подобно клину винт может изменять направление и значение приложенной силы.
Принцип действия винта используют во многих механизмах и устройствах: механических домкратах и подъемниках, мясорубке, тисках, струбцинах, сверлах, шурупах, резьбовых креплениях и т. п. Какие свойства винтовой наклонной плоскости мы используем, поднимаясь по горным «серпантинам»? винтовым лестницам?
Если в задаче дан КПД или предлагается его найти, решение лучше начинать с записи формулы для расчета КПД. В условии значение КПД удобнее выражать в частях и далее пользоваться формулой 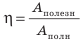
Пример №17
Груз массой 95 кг равномерно поднимают на третий этаж дома с помощью подвижного и неподвижного блоков (см. рисунок). Определите КПД данной системы, если к свободному концу шнура прикладывают силу 500 Н. Анализ физической проблемы. Для определения КПД системы нужно найти: работу, которую следует выполнить, чтобы поднять груз на высоту h, то есть полезную работу 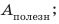
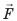

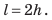
Дано:


Найти:
Решение:
По определению КПД:
Что делают? Поднимают груз на высоту h, поэтому полезная работа равна увеличению потенциальной энергии груза:
Как это делают? Тянут за шнур, прикладывая силу 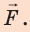
Подставив выражения для 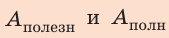
Проверим единицу, найдем значение искомой величины:
Анализ результата: КПД механизма меньше 100 % — это правдоподобный результат.
Ответ:
Итоги:
Для облегчения труда люди с древних времен использовали простые механизмы — устройства для преобразования силы. Простые механизмы — неотъемлемые составляющие и современных машин. К простым механизмам относят рычаг и его разновидности (подвижный и неподвижный блоки, коловорот); наклонная плоскость и ее разновидности (клин, винт). На практике полезная работа, выполняемая с помощью любого механизма, всегда меньше полной работы: 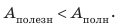
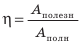
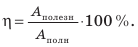
Итоги:
Вы узнали о механической работе, механической энергии и мощности.
Вы научились различать кинетическую и потенциальную энергии и узнали о полной механической энергии.
Вы ознакомились с законом сохранения и превращения механической энергии и узнали, как изменяется механическая энергия, если существует трение:
Вы ознакомились с простыми механизмами.
Вы узнали, что ни один простой механизм не дает выигрыша в работе, ознакомились с физической величиной — коэффициентом полезного действия механизма. Использование простых механизмов для поднятия тел.
- Золотое правило механики
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
- Инерциальные системы отсчета
- Энергия в физике
- Мощность в физике
- Взаимодействие тел
На прошлых уроках мы с вами
видели, какое важное значение имеет импульс тела, для которого существует закон
сохранения. Столь же большую играет и другая величина, которая для замкнутой
системы тоже остаётся постоянной. Эта величина — энергия, с которой приходится
иметь дело не только в механике, но и в других разделах физики, во всех науках
о природе, во всех отраслях техники, да и в повседневной жизни. Подобно тому,
как одна величина — импульс тела, связана с другой величиной — импульсом силы,
энергия тоже связана с другой величиной — работой силы, или механической
работой.
С понятиями механическая работа
и энергия мы с вами знакомились в седьмом классе. Давайте вспомним, работой
называется скалярная физическая величина, численно равная произведению модуля
силы на модуль перемещения тела.
А механическая энергия
— это физическая величина, характеризующая способность системы совершать
работу.
В механике принято различать
два вида механической энергии: кинетическую и потенциальную.
В седьмом классе мы говорили о
том, что кинетической энергией обладает любое движущееся тело, и она
равна работе, которую нужно совершить, чтобы разогнать тело из состояния покоя
до данной скорости.
Также мы с вами говорили о
том, что кинетическую энергию можно найти, как половину произведения массы тела
на квадрат его скорости.
Потенциальная энергия — это энергия взаимодействия тел или частей одного и
того же тела. Потенциальная энергия тела, поднятого над землёй, равна работе,
которую совершает сила тяжести при перемещении тела на нулевой уровень, который
мы вправе выбирать совершенно произвольно.
Конечно же любое тело может
обладать как кинетической, так и потенциальной энергией одновременно. Примером может
служить летящий самолёт, в системе отсчёта, связанной с Землёй.
Вспомним, что сумма
кинетической и потенциальной энергий тела (или системы тел) называется полной
механической энергией или просто, механической энергией
При этом, если система тел
является замкнутой, а между телами системы действуют только силы тяготения и
силы упругости и отсутствуют силы сопротивления, то её механическая энергия
остаётся неизменной.
Иными словами, потенциальная и
кинетическая энергия системы могут меняться, превращаясь в друг друга. Но при
уменьшении одного вида энергии, на столько же увеличивается энергия другого
вида, благодаря чему их сумма и не меняется.
Давайте подтвердим
справедливость закона сохранения энергии. Для этого рассмотрим превращения
энергии в механической системе на примере свободного падения тела.
Допустим, шарик известной
массы падает с некоторой высоты, над поверхностью Земли.
Из полученного равенства
видно, при свободном падении шарика его потенциальная энергия уменьшалась ровно
на столько, на сколько увеличивалась энергия кинетическая.
Сгруппируем члены уравнения
так, чтобы между знаком равенства стояла сумма кинетической и потенциальной
энергий в начальном и конечном состояниях:
Формула, записанная в таком
виде, показывает, что действительно полная механическая энергия шарика при его
свободном падении остаётся неизменной.
Это уравнение выражает математическую
запись закона сохранения механической энергии.
Таким образом, мы смогли теоретически
доказать, что в случае замкнутой системы тел, её полная механическая энергия не
меняется с течением времени.
Рассмотрим применение закона
сохранения механической энергии для решения задач.
В заключении отметим, что
закон сохранения механической энергии является частным случаем всеобщего закона
превращения и сохранения энергии.
Энергия не создаётся и не
уничтожается, а только превращается из одного вида в другой.
В работе «О сохранении силы»
Герман фон Гельмгольц впервые сформулировал и обосновал закон сохранения
энергии, отметив его всеобщий характер. Основные свои идеи учёный доложил на
заседании Физического общества в 1847 году. Называя кинетическую энергию «живой
силой», а потенциальную — «напряжённой силой», Гельмгольц доказывает, что
«когда тела природы действуют друг на друга с силами притяжения или
отталкивания, независимыми от времени и скорости, то сумма живых и напряжённых
сил остаётся постоянной». Так был впервые сформулирован один из самых
фундаментальных законов природы — закон сохранения энергии.
Отрицать связь кинетической и потенциальной энергий на данном этапе просто невозможно. Складывается ощущение, что одно словно превращается в другое и наоборот. Но насколько это все-таки соответствует действительности? Сегодня в программе — закон сохранения энергии, понятными словами. Даже по пути обсудим нечто необычное под названием консервативные силы!
Закон сохранения энергии: предисловие о котиках
Чтобы понять, почему превращение энергии имеет место быть, обратимся к пикантному вычислительному эксперименту.
Скажем, что к вертолетной площадке, расположенной на крыше дома, подлетает воздушное кототакси. Пилот тем временем зависает на расстоянии $10~м$ от вертолета до платформы. Усатый пассажир готовится к выходу. Не переживайте: наш котик может беспрепятственно и безопасно спрыгнуть хоть с высоты двадцатого этажа. На то он и клиент кототакси.
Масса котика — $4~$ кг. Условимся, что его начальная скорость $upsilon_0$ составляет ноль. Котик не прыгал, а просто, так сказать, вышел из транспортного средства без прыжка. Чему же будет равна его кинетическая энергия в момент приземления?
По формуле кинетическая энергия равна:
$E_к=frac{m upsilon^2}{2}$.
Чтобы посчитать значение энергии, необходимо найти скорость в последний момент перед самим приземлением. Котик двигается равноускорено, с ускорением свободного падения $g$. Поэтому его скорость определяется следующей формулой:
$upsilon = upsilon_0 + gt$.
Поскольку начальная скорость $upsilon_0$ равна нулю, нам остается только найти время, за которое котик достигнет земли с высоты $10~м$. Путь при равноускоренном движении вычисляется по формуле:
$s=upsilon_0 t+frac{gt^2}{2}$.
У нас есть значение пути, но нет значения времени. Значит, мы можем через формулу пути выразить время, подставить его в формулу скорости, а после уже рассчитать значение энергии. Выполним подстановки:
$t=sqrt{frac{2s}{g}}\upsilon=gsqrt{frac{2s}{g}}$.
Возводим скорость в квадрат, умножаем на массу и делим полученное значение на два (ускорение свободного падения $g$ для удобства примем за $10~м/с$):
$E_к=frac{m(gsqrt{frac{2s}{g}})^2}{2}=400~Дж$.
Интересно, а чему же тогда равняется потенциальная энергия в точке выхода из вертолета? Давайте воспользуется формулой с прошлого урока и вычислим:
$E_п=mgh=4~кгcdot10~м/сcdot 10~м=400~Дж$.
Выходит, $E_п$ в начале спуска равняется $E_к$ в момент приземления на вертолетную площадку. Значения совершенно идентичные, ровно по четыреста джоулей.
Ну, определенно точно нужно во всем разбираться!..
Превращение энергии
Вызвать кототакси возможным не представляется, поэтому обратимся к опыту. Возьмем простой баскетбольный мяч и выйдем с ним на игровую площадку. Поднимем мяч на некоторую отметку и зафиксируем высоту у стены. Мяч, ударившись о поверхность, отскачет вверх. И если внимательно присмотреться к тому, на какую отметку вновь он поднимется, наш энергический пазл сложится воедино.
1. Пусть мяч начинает движение с отметки $1~м$. Постепенно разгоняясь, тело развивает максимальную скорость в точке соприкосновения с поверхностью. Очевидно, конечная скорость зависит от выбранной нами высоты. Чем выше было поднято тело, тем больше пути оно сможет пройти. Как следствие — развить большую скорость.
2. Мяч ударяется о поверхность. Он начинает движение в противоположную сторону — вверх. Сообщив мячу потенциальную энергию, мы приводим его тем самым в движение. Это значение постепенно уменьшается, с пройденным путем. Наверх поднимается тело за счет того, что в конечной точке потенциальная энергия $mgh$ полностью переходит в кинетическую $frac{m upsilon^2}{2}$.
Высота превратилась в скорость.
3. Движение вверх также представляет собой «обмен» энергиями. Когда потенциальная энергия полностью переходит в кинетическую, мяч опять придет в движение. Просто в противоположную сторону. И заметить мы можем, что он остановится как раз напротив зафиксированной отметки $1~м$.
Ну, практически напротив. Кинетическая энергия $frac{m upsilon^2}{2}$ опять перешла в потенциальную $mgh$. Скорость превратилась в высоту.
Самое главное: сколько потенциальной энергии мы сообщили телу, столько же кинетической получили в конце падения, ведь только при условии, что энергии равнозначны, мяч бы смог вновь подняться, отскакивая от площадки, на отметку $1~м$.
«Со звездочкой»: превращение энергии и математическое доказательство
Для интереса рассмотрим изменение кинетической и потенциальной энергии системы, где тело имеет некую начальную скорость $upsilon_0$.
Тогда вместо того, чтобы тело сбрасывать, подбросим его вверх. При подъеме, так как тело двигается только под ускорением свободного падения, его скорость убывает по закону $upsilon= upsilon_0-gt$. Мы сообщаем телу некоторое значение кинетической энергии и это значение так же, как скорость, убывает, изменяясь по закону:
$E_к=frac{m upsilon^2}{2}= frac{m(upsilon_0-gt)^2}{2}=frac{m(upsilon_0^2-2 upsilon_0gt+g^2t^2)}{2}$.
Мы воспользовались формулой квадрата разницы
$(a-b)^2=a^2-2ab+b^2$.
Раскроем скобки:
$E_к=frac{m upsilon_0^2}{2}-m upsilon_0gt+frac{mg^2t^2}{2}$.
Сканируем полученную формулу и видим, что $frac{m upsilon_0^2}{2}$ — это начальная кинетическая энергия нашего тела, $E_{к_0}$. $E_к$ — это значение кинетической энергии в момент времени $t$. Перенесем $E_{к_0}$ в левую часть уравнения и умножим обе части на $-1$:
$E_к- E_{к_0}=-Delta{E_к}=m upsilon_0gt-frac{mg^2t^2}{2}$.
Примечание: мы умножили обе части уравнения на $-1$, чтобы выразить убывание кинетической энергии.
Итого, под $-Delta{E_к}$ мы получили убыль кинетической энергии за время $t$ при подъеме тела наверх. К вопросу о подъемах, то есть о высоте, на которую поднимется тело, это — пройденный путь, определяемый формулой:
$h=s=upsilon_0t-frac{gt^2}{2}$.
Прирост потенциальной энергии, как следствие, определяется следующим образом (пользуемся подстановкой $h$ в формулу потенциальной энергии $mgh$):
$Delta{E_п}=mgh=m upsilon_0gt-frac{mg^2t^2}{2}$.
Полная энергия и промежуточные выводы
Если сопоставить выведенные соотношения для $Delta{E_п}$ и $Delta{E_к}$, то видим, что прирост потенциальной энергии за время $t$ всегда равняется убыли потенциальной энергии за то же время $t$.
Следовательно, делаем вывод, что, двигаясь, тело «расходует» свою потенциальную энергию на приращение кинетической энергии. Либо наоборот: при подъеме, кинетическая энергия превращается в потенциальную. Энергия движения «расходуется» на подъем.
Пояснение: сколько кинетической энергии убавилось, столько приросло потенциальной. Обратная зависимость убытка потенциальной энергии и прироста кинетической энергии работает аналогично.
Полная механическая энергия системы
Раз убыток или прирост одного вида энергии равен приросту или убытку другого вида энергии, в зависимости от вида движения, говорить можно о том, что сумма энергий механической системы остается величиной постоянной в любой точке. Энергии обмениваются между собой, меняя характер движения тела.
Математически подобное свойство записывается так:
$$E_{мех}=E_к+E_п=const,$$
где $E_{мех}$ — полная механическая энергия.
Так, накопив определенный запас потенциальной энергии, мы видим, как постепенно мяч падает, развивает скорость, то есть превращает запас в скорость. Скорость вновь переходит в запас, когда при взаимодействии с землей изменяется вектор движения — тело поднимается за счет перехода кинетической энергии обратно в потенциальную.
А если выбрать любую точку и сложить значения энергий, они будут оставаться постоянными, даже когда мы выберем еще одну произвольную точку. Все равно получим то же значение.
Полная энергия: определение
Иными словами:
| Движение вниз с отметки $h$, при $upsilon_0=0$ | Движение вверх с отметки $h=0$, при некоей начальной $upsilon_0>0$ |
|---|---|
| Тело приходит в движение под действием силы тяжести. Стартовая энергия механической системы равняется потенциальной энергии на высоте h. Тело падает, высота уменьшается, потенциальная энергия снижается, но она никуда не девается. Она превращается в скорость, в кинетическую энергию. Ровно сколько убыло потенциальной энергии, столько прибыло кинетической. Сумма энергий постоянна. | Тело приходит в движение под действием сторонней силы, сообщающей ему стартовую кинетическую энергию. Тело двигается, начинает постепенно набирать высоту, кинетическая энергия уменьшается, но вместе с тем увеличивается потенциальная энергия. Ровно сколько убыло кинетической энергии, столько прибыло потенциальной. Вновь: сумма энергий в любой точке постоянна. |
Подняться выше возможного тело не может, только если мы не сообщим дополнительную энергию. Поэтому сумма значений всегда находится в пределе стартовой энергии.
Теперь мы готовы дать определение:
Полная механическая энергия тела — сумма потенциальной и кинетической энергии, которая остается постоянной при условии, что система замкнута.
Звучит, как нечто похожее на именитый закон сохранения энергии, верно?
Закон сохранения в замкнутой системе
Однако подождите. Интересен прежде пункт про замкнутость системы.
Хм. В наших абстрактных примерах и размышлениях мы все время представляли, что тело возвращается в точку старта. Но вот если бы в реальности энергия никуда не «выливалась» из системы, баскетбольный мяч бы бесконечно прыгал туда-сюда. А он явно прыгает не до бесконечности, постепенно уменьшая размах прыжка. Начал с $1~м$, отскочил и вернулся на отметку чуть пониже метра, через круг — еще чуть ниже. И так до полной остановки.
Выходит, что полная механическая энергия постоянной быть не может — она понемногу убывает. И причина кроется в том, что не всякая сила, возникающая внутри системы, говоря условно, благотворно влияет на движение. Взять, к примеру, силу тяжести. Или силу упругости. Они «помогают» телу двигаться. Даже если их вектор направлен против вектора движения, обязательно приходит момент, когда кинетическая энергия полностью переходит в потенциальную. Тогда эти силы «возвращают» то, что взяли, в том же объеме.
Закон сохранения энергии: консервативные силы и диссипативные силы
Такие силы называются консервативными. К сожалению, мы пока не готовы дать им строгое определение, поэтому выразимся понятными нам терминами:
Консервативные силы (от лат. ‘conservare’ — «сохранять») — силы, работа против которых не изменяет количество полной механической энергии тела.
Разумеется, природа синоним гармонии, и консервативные силы — это не финиш. Всегда есть антитеза. Между телами непременно возникает сила трения, на работу против которой всегда приходится тратить какое-то количество энергии.
Такие силы называются диссипативными:
Диссипативные силы (от лат. ‘dissipare’ — «рассеиваться») — силы, работа против которых изменяет количество полной механической энергии тела.
Уменьшение размаха прыжка мяча происходит из-за того, что его окружает воздух, и молекулы воздуха так или иначе постоянно «трутся» о поверхность мяча, что замедляет его движение. Силы упругости, при столкновении с поверхностью, заставляют молекулы внутри мяча двигаться. Температура тела растет. А нагрев в том числе расходует механическую энергию.
Это интересно: вечный двигатель
Ах, если бы!
Если бы в этом мире была возможность создать систему, внутри которой действуют исключительно консервативные силы, то у человечества бы существовал вечный двигатель. Вообще, вечный двигатель — это воображаемое устройство, что единожды запущенное, не прекращает совершать полезную работу. Он, соответственно, умеет в полном объеме сохранять изначально переданную ему энергию и не расходует ее на работу против диссипативных сил. Потому что они там попросту не возникают.
Закон сохранения энергии в его идеальном воплощении… Однако для этого нужно соблюсти три нереальных условия:
- Никаких шероховатостей, даже микроскопических! Сила трения между деталями приводит к потере энергии. Значит, нужны идеально гладкие поверхности.
- Долой воздух! Сила трения также возникает при взаимодействии молекул воздуха с поверхностью деталей. Хоть и работа против воздуха крайне мала, энергия, как бы оно ни было, убывает.
- Полная тишина! Устройство не должно воспроизводить вообще никаких звуков, ибо звук — одна из форм передачи энергии. Но новости тут хорошие: проблема эта решается вакуумом, так как в нем звук не распространяется.
Жаль, что идеального вакуума, ровно как идеально гладких поверхностей, не существует. От диссипативных сил не спрятаться и не скрыться. Они есть причина, почему вечный двигатель в условиях физики Земли невозможен.

Закон сохранения энергии
В школьном курсе теоретической физики по большей части диссипативными силами пренебрегают. Только консервативные силы, только хардкор. А раз мы можем позволить себе представить, что их нет, то есть представить замкнутость механической системы, то, возвращаясь к пункту о полной энергии системы, мы можем словесно переиграть частный случай о постоянстве суммы энергий.
Есть система, внутрь которой сообщается некоторое количество энергии. Эта энергия начинает в границах системы циркулировать, закольцованно преобразовываясь из одного вида в другой. Работа против диссипативных сил не совершается — да, у нас все идеальное: ни воздуха, ни трения. Следовательно, энергия сохраняется в том числовом значении, в котором она впервые была передана системе.
Фактически, полная механическая энергия системы $E_к+E_п$ непостоянна. Но если списать со счетов потери на трение, эта сумма действительно является константой.
Так что выражение $E_{мех}=E_к+E_п=const$ — это частный случай полной механической энергии, который называется принцип сохранения энергии. Иногда его называют закон сохранения энергии. И гласит он следующее:
В замкнутой системе, то есть той, где действуют только консервативные силы, суммарная величина энергии всегда остается постоянной.
Тот самый закон сохранения энергии. Ничто из ниоткуда не берется и в никуда не уходит. Визитная карточка физики, знакомая хоть библиотекарю, ничего тяжелее арифметики в руках не державшему, хоть восьмилетнему ребенку. И получается, что каждый рассмотренный нами на уроке пример все время касался этого принципа.
Можете прямо сейчас все перечитать с нуля и проверить. Мы прошли по кольцу и вернулись в точку старта.
Ха, даже повествование урока своеобразно соблюдает закон сохранения энергии!
Задача на принцип сохранения энергии
Знакомство наше с законом, конечно, шапочное. Насколько позволяет математическая база и смежные темы физики. Однако знакомство достаточное, чтобы вы, уже далее перейдя к программе восьмого класса, могли смотреть на ряд вещей под другим углом. А дабы закрепить, попробуйте решить простенькую задачу.
Условие. Полная механическая энергия тела равна $0.8 space кДж$. Чему равна его кинетическая энергия, когда потенциальная составляет $250 space Дж$? Принять, что система изолирована.
Показать решение
Скрыть решение
Если система изолирована, то сумма кинетической и потенциальной энергии остается на любом отрезке пути постоянной. Значит, когда потенциальная энергия равняется $250~Дж$, можно говорить о том, что кинетическая равна полной сумме энергий, за вычетом потенциальной.
Полная механическая энергия равняется:
$E_{мех}=E_к+E_п=0,8~кДж$.
Не забываем про стандартизацию единиц измерения. В СИ $0,8~кДж$ — это $800~Дж$. Остается выразить из уравнения выше потенциальную энергию и подставить имеющиеся в условии значения.
Считаем:
$E_к=E_{мех}-E_п=800-250=550~Дж$.
Выводы
Надеемся, миссия «закон сохранения энергии понятными словами» удалась.
В целом, энергия не стоит на месте. Она переходит из одной формы в другую. За живым примером можете как-нибудь выбраться на гидроэлектростанцию и посмотреть, как все это происходит в режиме реального времени, а не на абстрактных мячах.
Безусловно, принцип сохранения энергии и реальная жизнь не совместимы. Но это не мешает человечеству конструировать системы, в которых энергии видоизменяются. Так, поднятая над нулевым уровнем вода обладает запасом потенциальной энергии, которая при падении дает достаточную кинетическую энергию, чтобы вращать турбину и вырабатывать электричество.
А вы задумайтесь: потенциальная энергия переходит в кинетическую; та в свою очередь переходит в энергию вращения; энергия вращения переходит в электроэнергию. Дома мы превращаем электроэнергию, к примеру, в хорошо проведенное время за компьютером.
Жаль, что цикл жизни энергии так или иначе заканчивается. Ведь существуют не только консервативные силы. Энергия превращается в конечном итоге в тепло, которое рассеивается в атмосфере. Ну, шуточно заметить, энергия не заканчивается только в теоретических задачах по физике.
Но нет, убывая, она не исчезает в никуда.
Она просто обретает формы, что мы более не можем уловить.
Упражнения
Упражнение №1
Какие превращения одного вида энергии в другой происходят: а) при падении воды водопада; б) при бросании мяча вертикально вверх; в) при закручивании пружины механических часов; г) на примере дверной пружины?
Посмотреть ответ
Скрыть
Ответ:
- При падении воды с водопада потенциальная энергия превращается в кинетическую
(при падении увеличивается скорость и уменьшается высота нахождения некоторого объема воды. Значит, идет увеличение кинетической энергии и уменьшение потенциальной); - При бросании мяча вертикально вверх кинетическая энергия превращается в потенциальную
(увеличивается высота и уменьшается скорость); - При закручивании пружины часов потенциальная энергия превращается в кинетическую
(а точнее: потенциальная энергия закрученной пружины превращается в кинетическую энергию движущихся стрелок); - На примере дверной пружины мы наблюдает превращение потенциальной энергии в кинетическую
(потенциальная энергия растянутой пружины превращается в кинетическую энергию движущейся двери).
Упражнение №2
Массы падающих тел одинаковы. Одинаковы ли значения потенциальной энергии тел на одной и той же высоте и одинаковы ли значения кинетической энергии на этой высоте?
Посмотреть ответ
Скрыть
Ответ:
Потенциальная энергия определяется по формуле: $E_п = gmh$.
Значит, если массы тел и их высота одинаковы, то их потенциальные энергии будут равны друг другу.
Кинетическая энергия падающих тел будет зависеть не только от их масс, но и от их скоростей: $E_к = frac{m upsilon^2}{2}$.
Если скорости этих тел будут равны (при падении с одинаковой высоты), то будут равны их кинетические энергии. Если их скорости будут отличаться друг от друга (при падении с разных высот), то эти тела будут обладать разными кинетическими энергиями.
Упражнение №3
Приведите примеры тел, обладающих одновременно кинетической и потенциальной энергией.
Посмотреть ответ
Скрыть
Ответ:
- Летящий самолет;
- Спускающийся парашютист;
- Скатывающийся с горки ребенок на санках;
- Механические часы;
- Маятник;
- Вода, падающая с плотины;
- Падающая с неба капля дождя.