
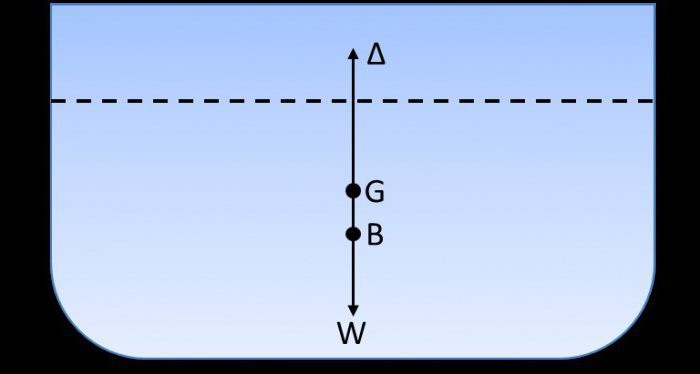
Ship stability diagram showing centre of gravity (G), centre of buoyancy (B), and metacentre (M) with ship upright and heeled over to one side.
As long as the load of a ship remains stable, G is fixed (relative to the ship). For small angles, M can also be considered to be fixed, while B moves as the ship heels.
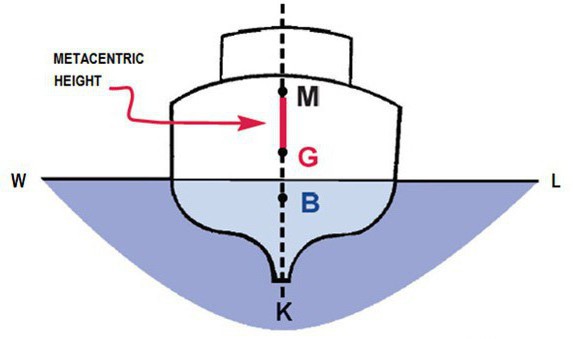
The metacentric height (GM) is a measurement of the initial static stability of a floating body. It is calculated as the distance between the centre of gravity of a ship and its metacentre. A larger metacentric height implies greater initial stability against overturning. The metacentric height also influences the natural period of rolling of a hull, with very large metacentric heights being associated with shorter periods of roll which are uncomfortable for passengers. Hence, a sufficiently, but not excessively, high metacentric height is considered ideal for passenger ships.
Metacentre[edit]
When a ship heels (rolls sideways), the centre of buoyancy of the ship moves laterally. It might also move up or down with respect to the water line. The point at which a vertical line through the heeled centre of buoyancy crosses the line through the original, vertical centre of buoyancy is the metacentre. The metacentre remains directly above the centre of buoyancy by definition.
In the diagram above, the two Bs show the centres of buoyancy of a ship in the upright and heeled conditions. The metacentre, M, is considered to be fixed relative to the ship for small angles of heel; however, at larger angles the metacentre can no longer be considered fixed, and its actual location must be found to calculate the ship’s stability.
It can be calculated using the formulae:
Where KB is the centre of buoyancy (height above the keel), I is the second moment of area of the waterplane around the rotation axis in metres4, and V is the volume of displacement in metres3. KM is the distance from the keel to the metacentre.[1]
Stable floating objects have a natural rolling frequency, just like a weight on a spring, where the frequency is increased as the spring gets stiffer. In a boat, the equivalent of the spring stiffness is the distance called “GM” or “metacentric height”, being the distance between two points: “G” the centre of gravity of the boat and “M”, which is a point called the metacentre.
Metacentre is determined by the ratio between the inertia resistance of the boat and the volume of the boat. (The inertia resistance is a quantified description of how the waterline width of the boat resists overturning.) Wide and shallow or narrow and deep hulls have high transverse metacenters (relative to the keel), and the opposite have low metacenters; the extreme opposite is shaped like a log or round bottomed boat.
Ignoring the ballast, wide and shallow or narrow and deep means that the ship is very quick to roll and very hard to overturn and is stiff. A log shaped round bottom makes it slow to roll and easy to overturn and tender.
“G”, is the center of gravity. “GM”, the stiffness parameter of a boat, can be lengthened by lowering the center of gravity or changing the hull form (and thus changing the volume displaced and second moment of area of the waterplane) or both.
An ideal boat strikes a balance. Very tender boats with very slow roll periods are at risk of overturning, but are comfortable for passengers. However, vessels with a higher metacentric height are “excessively stable” with a short roll period resulting in high accelerations at the deck level.
Sailing yachts, especially racing yachts, are designed to be stiff, meaning the distance between the centre of mass and the metacentre is very large in order to resist the heeling effect of the wind on the sails. In such vessels, the rolling motion is not uncomfortable because of the moment of inertia of the tall mast and the aerodynamic damping of the sails.
Different centres[edit]
Initially the second moment of area increases as the surface area increases, increasing BM, so Mφ moves to the opposite side, thus increasing the stability arm. When the deck is flooded, the stability arm rapidly decreases.
The centre of buoyancy is at the centre of mass of the volume of water that the hull displaces. This point is referred to as B in naval architecture.
The centre of gravity of the ship is commonly denoted as point G or CG. When a ship is at equilibrium, the centre of buoyancy is vertically in line with the centre of gravity of the ship.[2]
The metacentre is the point where the lines intersect (at angle φ) of the upward force of buoyancy of φ ± dφ. When the ship is vertical, the metacentre lies above the centre of gravity and so moves in the opposite direction of heel as the ship rolls. This distance is also abbreviated as GM. As the ship heels over, the centre of gravity generally remains fixed with respect to the ship because it just depends on the position of the ship’s weight and cargo, but the surface area increases, increasing BMφ. Work must be done to roll a stable hull. This is converted to potential energy by raising the centre of mass of the hull with respect to the water level or by lowering the centre of buoyancy or both. This potential energy will be released in order to right the hull and the stable attitude will be where it has the least magnitude. It is the interplay of potential and kinetic energy that results in the ship having a natural rolling frequency. For small angles, the metacentre, Mφ, moves with a lateral component so it is no longer directly over the centre of mass.[3]
The righting couple on the ship is proportional to the horizontal distance between two equal forces. These are gravity acting downwards at the centre of mass and the same magnitude force acting upwards through the centre of buoyancy, and through the metacentre above it. The righting couple is proportional to the metacentric height multiplied by the sine of the angle of heel, hence the importance of metacentric height to stability. As the hull rights, work is done either by its centre of mass falling, or by water falling to accommodate a rising centre of buoyancy, or both.
For example, when a perfectly cylindrical hull rolls, the centre of buoyancy stays on the axis of the cylinder at the same depth. However, if the centre of mass is below the axis, it will move to one side and rise, creating potential energy. Conversely if a hull having a perfectly rectangular cross section has its centre of mass at the water line, the centre of mass stays at the same height, but the centre of buoyancy goes down as the hull heels, again storing potential energy.
When setting a common reference for the centres, the molded (within the plate or planking) line of the keel (K) is generally chosen; thus, the reference heights are:
- KB – to Centre of Buoyancy
- KG – to Centre of Gravity
- KMT – to Transverse Metacentre
Righting arm[edit]

Distance GZ is the righting arm: a notional lever through which the force of buoyancy acts
The metacentric height is an approximation for the vessel stability at a small angle (0-15 degrees) of heel. Beyond that range, the stability of the vessel is dominated by what is known as a righting moment. Depending on the geometry of the hull, naval architects must iteratively calculate the center of buoyancy at increasing angles of heel. They then calculate the righting moment at this angle, which is determined using the equation:
Where RM is the righting moment, GZ is the righting arm and Δ is the displacement. Because the vessel displacement is constant, common practice is to simply graph the righting arm vs the angle of heel. The righting arm (known also as GZ — see diagram): the horizontal distance between the lines of buoyancy and gravity.[3]
[2] at small angles of heel
There are several important factors that must be determined with regards to righting arm/moment. These are known as the maximum righting arm/moment, the point of deck immersion, the downflooding angle, and the point of vanishing stability. The maximum righting moment is the maximum moment that could be applied to the vessel without causing it to capsize. The point of deck immersion is the angle at which the main deck will first encounter the sea. Similarly, the downflooding angle is the angle at which water will be able to flood deeper into the vessel. Finally, the point of vanishing stability is a point of unstable equilibrium. Any heel lesser than this angle will allow the vessel to right itself, while any heel greater than this angle will cause a negative righting moment (or heeling moment) and force the vessel to continue to roll over. When a vessel reaches a heel equal to its point of vanishing stability, any external force will cause the vessel to capsize.
Sailing vessels are designed to operate with a higher degree of heel than motorized vessels and the righting moment at extreme angles is of high importance.
Monohulled sailing vessels should be designed to have a positive righting arm (the limit of positive stability) to at least 120° of heel,[4] although many sailing yachts have stability limits down to 90° (mast parallel to the water surface). As the displacement of the hull at any particular degree of list is not proportional, calculations can be difficult, and the concept was not introduced formally into naval architecture until about 1970.[5]
Stability[edit]
GM and rolling period[edit]
The metacentre has a direct relationship with a ship’s rolling period. A ship with a small GM will be “tender” – have a long roll period. An excessively low or negative GM increases the risk of a ship capsizing in rough weather, for example HMS Captain or the Vasa. It also puts the vessel at risk of potential for large angles of heel if the cargo or ballast shifts, such as with the Cougar Ace. A ship with low GM is less safe if damaged and partially flooded because the lower metacentric height leaves less safety margin. For this reason, maritime regulatory agencies such as the International Maritime Organization specify minimum safety margins for seagoing vessels. A larger metacentric height on the other hand can cause a vessel to be too “stiff”; excessive stability is uncomfortable for passengers and crew. This is because the stiff vessel quickly responds to the sea as it attempts to assume the slope of the wave. An overly stiff vessel rolls with a short period and high amplitude which results in high angular acceleration. This increases the risk of damage to the ship and to cargo and may cause excessive roll in special circumstances where eigenperiod of wave coincide with eigenperiod of ship roll. Roll damping by bilge keels of sufficient size will reduce the hazard. Criteria for this dynamic stability effect remain to be developed. In contrast, a “tender” ship lags behind the motion of the waves and tends to roll at lesser amplitudes. A passenger ship will typically have a long rolling period for comfort, perhaps 12 seconds while a tanker or freighter might have a rolling period of 6 to 8 seconds.
The period of roll can be estimated from the following equation:[2]
where g is the gravitational acceleration, a44 is the added radius of gyration and k is the radius of gyration about the longitudinal axis through the centre of gravity and 
Damaged stability[edit]
If a ship floods, the loss of stability is caused by the increase in KB, the centre of buoyancy, and the loss of waterplane area – thus a loss of the waterplane moment of inertia – which decreases the metacentric height.[2] This additional mass will also reduce freeboard (distance from water to the deck) and the ship’s downflooding angle (minimum angle of heel at which water will be able to flow into the hull). The range of positive stability will be reduced to the angle of down flooding resulting in a reduced righting lever. When the vessel is inclined, the fluid in the flooded volume will move to the lower side, shifting its centre of gravity toward the list, further extending the heeling force. This is known as the free surface effect.
Free surface effect[edit]
In tanks or spaces that are partially filled with a fluid or semi-fluid (fish, ice, or grain for example) as the tank is inclined the surface of the liquid, or semi-fluid, stays level. This results in a displacement of the centre of gravity of the tank or space relative to the overall centre of gravity. The effect is similar to that of carrying a large flat tray of water. When an edge is tipped, the water rushes to that side, which exacerbates the tip even further.
The significance of this effect is proportional to the cube of the width of the tank or compartment, so two baffles separating the area into thirds will reduce the displacement of the centre of gravity of the fluid by a factor of 9. This is of significance in ship fuel tanks or ballast tanks, tanker cargo tanks, and in flooded or partially flooded compartments of damaged ships. Another worrying feature of free surface effect is that a positive feedback loop can be established, in which the period of the roll is equal or almost equal to the period of the motion of the centre of gravity in the fluid, resulting in each roll increasing in magnitude until the loop is broken or the ship capsizes.
This has been significant in historic capsizes, most notably the MS Herald of Free Enterprise and the MS Estonia.
Transverse and longitudinal metacentric heights[edit]
There is also a similar consideration in the movement of the metacentre forward and aft as a ship pitches. Metacentres are usually separately calculated for transverse (side to side) rolling motion and for lengthwise longitudinal pitching motion. These are variously known as 

Technically, there are different metacentric heights for any combination of pitch and roll motion, depending on the moment of inertia of the waterplane area of the ship around the axis of rotation under consideration, but they are normally only calculated and stated as specific values for the limiting pure pitch and roll motion.
Measurement[edit]
The metacentric height is normally estimated during the design of a ship but can be determined by an inclining test once it has been built. This can also be done when a ship or offshore floating platform is in service. It can be calculated by theoretical formulas based on the shape of the structure.
The angle(s) obtained during the inclining experiment are directly related to GM. By means of the inclining experiment, the ‘as-built’ centre of gravity can be found; obtaining GM and KM by experiment measurement (by means of pendulum swing measurements and draft readings), the centre of gravity KG can be found. So KM and GM become the known variables during inclining and KG is the wanted calculated variable (KG = KM-GM)
See also[edit]
- Kayak roll
- Turtling
- Angle of loll
- Limit of positive stability
- Weight distribution
References[edit]
- ^ Ship Stability. Kemp & Young. ISBN 0-85309-042-4
- ^ a b c d Comstock, John (1967). Principles of Naval Architecture. New York: Society of Naval Architects and Marine Engineers. p. 827. ISBN 9997462556.
- ^ a b Harland, John (1984). Seamanship in the age of sail. London: Conway Maritime Press. pp. 43. ISBN 0-85177-179-3.
- ^ Rousmaniere, John, ed. (1987). Desirable and Undesirable Characteristics of Offshore Yachts. New York, London: W.W.Norton. pp. 310. ISBN 0-393-03311-2.
- ^ U.S. Coast Guard Technical computer program support accessed 20 December 2006.
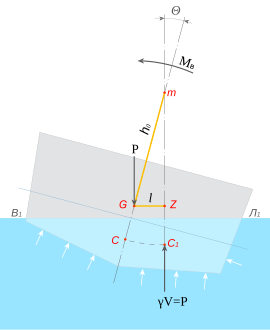
Отрезок mG — метацентрическая высота.
Метацентрическая высота — критерий остойчивости судна. Представляет собой возвышение метацентра над центром тяжести плавающего тела. Чем больше этот параметр, тем выше начальная остойчивость судна. При приобретении отрицательного значения метацентрической высоты судно утрачивает способность плавать без крена.
Ответить на вопрос «перевернется ли судно, имеющее отрицательную метацентрическую высоту» не представляется возможным, так как метацентрическая теория остойчивости верна лишь при наклонениях судна, не превышающих 10 градусов.
Тем не менее, в Правилах классификационных обществ, осуществляющих надзор за технической эксплуатацией судов (Российский речной регистр, Российский морской регистр судоходства и др.), запрещена эксплуатация судов, имеющих метацентрическую высоту менее 0,15 м[источник не указан 332 дня].
Характерным примером тела, имеющего нулевую метацентрическую высоту, является симметричный плавающий бочонок. При нахождении в спокойной воде такой бочонок будет совершать вращение вдоль продольной оси под воздействием любых внешних сил (например ветра).
Ссылки[править | править код]
- Метацентрическая высота. Дата обращения: 19 июля 2011.
Литература[править | править код]
- Справочник по теории корабля: В трёх томах. Том 2. Статика судов. Качка судов / под ред. Я. И. Войткунского. — Л.: Судостроение, 1985. — 440 с.
- Семёнов-Тян-Шанский В. В. Статика и динамика корабля. — Л.: Судостроение, 1973.
- Наставление по борьбе за живучесть судна (НБЖС), РД 31.60.14-81. С приложениями и дополнениями. СПб, ЦНИИМФ, 2004
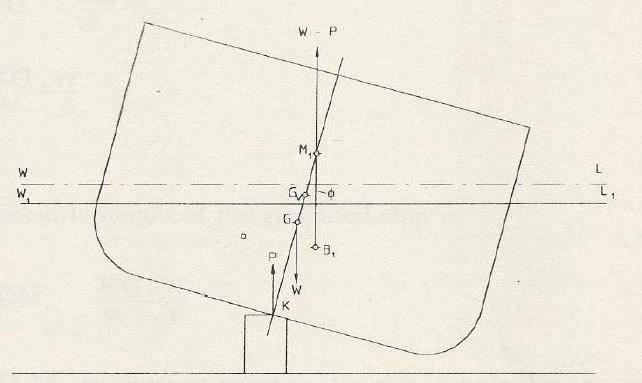
При
наклонной ватерлинии В1Л1
равнодействующая сил тяжести
–Р- и равнодействующая сил
поддержания –Q–
образуют пару сил с плечом –l–
(рис.15). Величина плеча –l–
зависит от возвышения метацентра
–m-над центром
тяжести –G– .
Возвышение
метацентра над центром тяжести называется
метацентрической высотой (поперечной
или продольной в зависимости от
поперечного или продольного наклонения).
Как
видно из треугольника GmA
(рис.15), катет GA=Gm*sin(гдеGm
-гипотенуза,
противолежащий угол).
Таким образом, GA=l=h*sin.
Как
видно из рис.16, поперечная метацентрическая
высота h=zm–zg или h=zc+r
–zg
Продольная метацентрическая
высотаH=z![]()
–zgилиH=zc+R–zg.
Так как
величина (zc–zg)
сравнительно мала по отношению кR
,то часто принимаютH~R.
После
составления грузового плана и определения
D=![]() ,
,
Mz=![]() *ziрассчитываютzg=Mz
*ziрассчитываютzg=Mz
/Dпо грузовой шкале в зависимости отDи![]() осадкуТ .Затем с помощью кривых
осадкуТ .Затем с помощью кривых
элементов теоретического чертежа или
таблиц в зависимости от Топределяют zm
, z![]()
zc
,r , R
.
После
этого по приведенным выше формулам
определяют h
и H.
-
16.Метацентрические формулы остойчивости. Условие остойчивости.
Восстанавливающий
момент равен Mв=g*D*l
. При малых
углах крена и дифферента l=h*sin
и ![]() =
=
H
* sin![]() .
.
Тогда при
малых углах крена:
Mв=g*D*h*sin
. (17).
-
При дифференте
 <100
<100
всегда, поэтому: -
M
 =g*D*H*sin
=g*D*H*sin ~g*D*R*
~g*D*R* рад
рад
(18).
Формулы
(17) и (18) называются метацентрическими
формулами остойчивости.
Из этих
формул следует, что восстанавливающий
момент положительный, если метацентрическая
высота положительна, то есть метацентр
возвышается над центром тяжести
Момент
дифферентующий на 1 см – Мо.может
быть получен, если в формулу (18) вместо
угла дифферента подставить его значение
при дифференте 1 см=0,01м.:
![]() =d/L=(0,01)/L
=d/L=(0,01)/L
, M![]() =
=
Мо.
Тогда
Mo=0,01*g*D*R/L
,а для момента массы, который дифферентует
на 1 см: M1=0,01*D*R/L.
-
17. Влияние горизонтального перемещения груза на остойчивость и посадку судна.
Перенос
груза можно рассматривать как снятие
груза с судна с последующим его приёмом
в заданную точку.
-
Поперечный
перенос груза.
Поперечный
горизонтальный перенос груза можно
рассматривать (рис.17) как его снятие
(приложение силы Р1
) и
приём груза в заданное положение
(приложение силы Р2
). Так
как I
Р1I=
I
P2I=
IP
I=m*g,
то перенос груза эквивалентен приложению
пары сил с кренящим моментом Mкр=b*m*g.
При действии кренящего момента судно
будет крениться до тех пор, пока
восстанавливающий момент (Мв)
не станет
равным кренящему Mв=Mкр.

Рис.17.
Перенос
груза.
Мв=g*D*h*sin
M
 кр=b*m*g
кр=b*m*g
D*h* sin
=b*m * sin=(b*m)/(D*h)
(19)
При горизонтальном
переносе груза не изменяются:
D
так как не изменяются ![]()
![]() ;
;
zm
так как
не изменяются
D
и
T;
zg=![]()
![]()
так как не изменяются mi
zi
h=zm–zg
так как
не изменяются
zm
и
zg.
17.2.Продольный перенос груза.
Рассуждая
аналогично, приходим к выводу, что при
продольном переносе груза создаётся
дифферентующий момент Мдиф=m*g*l
, где l
плечо
переноса груза.
Угол дифферента:
![]() рад=m*l
рад=m*l
/ (D*H)m*l
/(D*R)
(20).
Дифферент
d=![]() рад*L.(21).
рад*L.(21).
Изменение
осадок носом и кормой можно рассчитать,
учитывая, что судно наклоняется вокруг
оси, проходящей через Ц.Т. площади
ватерлинии с абсциссой xf
(рис.13).
Т н=
н=![]() рад*(L/2-xf
рад*(L/2-xf
)
.
T к=-(L/2+xf
к=-(L/2+xf
)*![]() рад
рад
(22)
-
 Тм=-
Тм=- рад*xf
рад*xf
.
При
продольном переносе D,H,R
не изменяются аналогично тому, как было
показано в п. 17.1.
Соседние файлы в предмете Теория и устройство судна
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение метацентрической высоты можно сформулировать следующим образом. Что это? Это – расстояние между центром тяжести и метацентром корабля. Само по себе определение не очень понятное, а потому стоит добавить, что очень часто эту высоту выражают через остойчивость судна. Это происходит потому, что метацентр является основным критерием определения этой самой остойчивости.
Общие понятия
Как ранее было сказано, метацентрическая высота – это возвышение центра тяжести над метацентром самого корабля. Тут важно знать о том, что чем больше значение данной характеристики, тем большей будет изначальная остойчивость судна. Если же по каким-либо причинам эта высота отклоняется в сторону отрицательного значения, это говорит о том, что судно не сможет плавать без крена. Что это значит? Допускать отрицательных значений метацентрической высоты ни в коем случае нельзя. Хотя… Получить точный ответ на вопрос о том, перевернется ли судно, имеющее отрицательное значение этой высоты, точно нельзя. Так как теория остойчивости распространяется лишь на наклонения кораблей, которые не превышают 10 градусов.
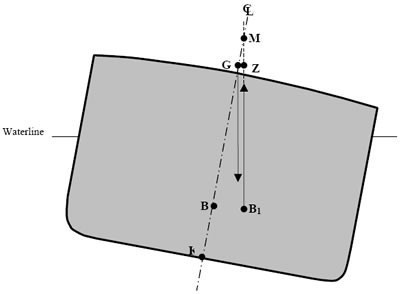
Правила и силы
Важно отметить, что существуют правила Классификационных Сообществ, которые следят за технической эксплуатацией судов. В данных документах описано, что эксплуатировать можно лишь те корабли, метацентрическая высота которых составляет не менее 0,2 метра. Чтобы понять, как будет вести себя тело с нулевой высотой, можно представить себе бочонок, плавающий в воде. Этот параметр данного тела будет равен 0, а его передвижение будет происходить вдоль продольной оси каждый раз, когда на него будет воздействовать любая внешняя сила, к примеру, волна или ветер.
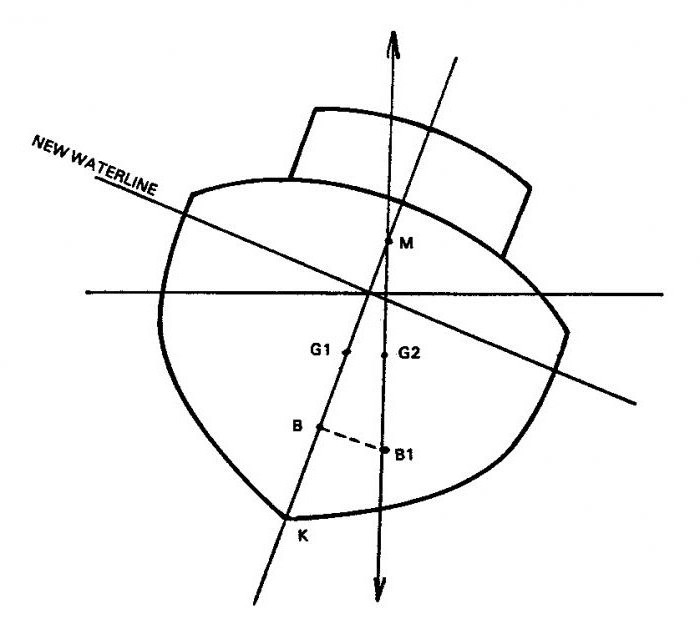
Еще одна основа, которая позволяет кораблю плавать, – это сила тяжести. А также Архимедова сила. Естественно, сила тяжести будет тянуть корабль вниз, то есть на дно. Числовое значение этой характеристики равняется его весу, а прикладывается она к центру тяжести корабля. Архимедова сила, или, как ее еще называют, сила плавучести, выталкивает морское судно из воды. Сила воздействия этого эффекта равняется водоизмещению корабля, которое приложено в центре подводного объема.
Работа сил
При “прямом” положении судна получается так, что эти две силы уравновешивают друг друга и находятся в одной вертикальной плоскости. Из-за этого корабль и способен перемещаться по воде. В том случае, если возникает крен судна, центр подводного объема ЦВ смещается в сторону наклона корабля. Смещение происходит из-за того, что меняется форма подводной части корпуса. Кроме того, при смещении ЦВ в одну из сторон возникает восстанавливающий момент, который будет противодействовать крену морского судна. При возникновении наклона ЦВ как бы начинает осуществлять поворот вокруг точки, которую условно называют метацентром m.

Расстояние от этой условной точки метоцентра m до центра тяжести судна ЦТ и будет являться его высотой. К примеру, для обычной гребной шлюпки числовое значение метацентрической высоты, которое будет являться достаточным для того, чтобы люди могли безопасно сесть и встать, равняется 0,3 м. В принципе, ничего сложного.
Как обеспечить остойчивость
Зная все то, что было описано выше, возникает явный вопрос о том, как же оценить безопасность лодки, парусной яхты, корабля и т. д.? Как понять, насколько велики шансы у корабля вернуться из положения “килем вверх” в нормальное, прямое состояние?
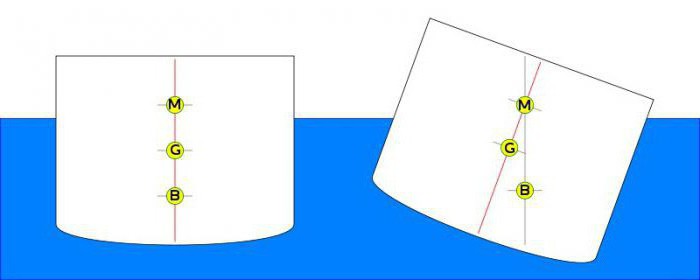
Для того чтобы добиться этого, необходимо улучшать остойчивость судна. Для этого существует несколько проверенных методов. Достаточно высокую остойчивость можно обеспечить за счет того, что на борту корабля будет размещен неподвижный балласт. Однако здесь нужно учитывать, что центр тяжести судна будет понижаться при дополнительной нагрузке. У кораблестроителей, моряков и всех, кто знаком с морским делом, есть такое правило: каждый килограмм груза, расположенный под ватерлинией, будет повышать остойчивость корабля, а вот каждый килограмм над этой линией будет ухудшать положение судна.
Восстановление судна
Для того чтобы увеличить вес, к примеру, яхты, ее оборудуют такой вещью, как неподвижный балластный киль. Но, здесь важно отметить, что он может быть размещен лишь на классическом типе яхты. Любой другой вид с таким килем окажется слишком тяжелым. Классические яхты – это абсолютная остойчивость речного судна, как ее называют. Все дело в том, что эта категория кораблей может выпрямиться практически после любого крена. Угол крена, который необходим для того, чтобы судно не восстановилось, – 155 градусов. Это параметр такой яхты, как Contessa 32. Если говорить другими словами, речное судно этого класса сможет восстановиться в прямое положение даже после того, как опрокинется килем вверх.
Тут важно понимать, что крупные суда имеют большую остойчивость формы изначально из-за своих габаритов. Еще один важнейший момент – это то, что забортная вода не должна попасть вовнутрь корабля при крене через какие-либо люки или отверстия. Если это случится, жидкость, оказавшаяся на борту, способна свести на нет всю остойчивость. Это произойдет из-за того, что вес попавшей воды сделает корабль тяжелее. Метацентрическая высота будет нарушена из-за смещения центра тяжести. И судно начнет тонуть.
Суда с надстройкой
Есть такой тип кораблей, которые обладают водонепроницаемой надстройкой. Естественно, вода не сможет попасть внутрь такого корабля, а это значит, что остойчивость останется на том же уровне даже при большом крене. Этот принцип стал основополагающим при изобретении спасательных шлюпок-неваляшек. Существуют спасательные плоты и шлюпки, которые считаются практически неопрокидываемыми из-за их конструкции. Такие категории кораблей способны восстановиться даже после того, как они полностью перевернулись.
Можно взять, к примеру, парусную яхту, которая обладает одним хитрым способом повышения остойчивости судна. Метод называется открениванием. А его суть заключается в том, что при наклоне будет перемещаться вес экипажа, балласта или качающегося киля по всей ширине судна. На сегодняшний день используется много различных типов перемещаемого балласта. А также существует один новейший, который заключается в наличии подводных управляемых крыльев.
Экспериментальная высота
Далее. Для того чтобы экспериментально вычислить метацентрическую высоту судна, можно перемещать большой груз по кораблю. Перемещение груза должно происходить на определенное расстояние Q от того места, где оно находилось изначально. Также при передвижении объекта нужно измерять малый угол вращения, который обозначается, как af. Числовое значение этой характеристики будет соответствовать углу наклона корабля.
Вот так будет выглядеть поперечная метацентрическая высота в формуле:
h0 =0,525(В/Т)2, м
В – это ширина судна, которая должна измеряться в метрах, а Т – это период качки, определяющийся в секундах.
Именно такой способ вычислений, а также экспериментальный способ определения стали основными положениями, которые позволили принять высоту метацентра корабля за основной критерий его остойчивости.
Парусные суда
В настоящее время парусные суда являются одними из самых опасных в плане эксплуатации, а также самыми требовательными к остойчивости. Все дело в том, что при ветре парус такого судна будет постоянно подвергаться сильному воздействию воздуха, что в таких условиях будет являться основным моментом, создающим возможность для крена. Именно из-за наличия паруса суда с большими и длинными мачтами и, как следствие, большими парусами, нуждаются в наличии дополнительного тяжелого неподвижного балласта, который сильно снизит центр тяжести судна, создавая тем самым большее значение метацентрической высоты.
Очень важно отметить: довольно часто допускают такую ошибку, как оценка остойчивости корабля только по его метацентру. Конечно, эта высота будет являться основным критерием. Однако нельзя игнорировать те преимущества, которые имеются на всей диаграмме статической остойчивости. Туда входит не только высота метацентра.
Случаи неостойчивости
Существует три случая неостойчивости судна. Рассмотрим их подробнее.
Первый случай возникает в той ситуации, если высота h>0. Это возникает по причине того, что центр тяжести располагается выше, чем центр величины. При соблюдении этих условий и наклоне корабля в любую из сторон линия действия силы поддержания будет пересекать диаметральную плоскость выше, чем находится центр тяжести.
Второй случай неостойчивости произойдет тогда, когда метацентрическая высота будет равна нулю. В этом случае, практически, как и в предыдущем, центр тяжести окажется выше, чем центр величины. А при наклоне корабля случится так, что линия ЦТ будет проходить вдоль линии величины. В таком случае центр величины всегда будет расположен в одной вертикали с центром тяжести. При таком расположении сил восстанавливающая пара, которая выравнивает корабль, будет просто отсутствовать. Без воздействия каких-либо внешних сил судно не сможет вернуться в свое исходное, прямое положение.
Третий случай возникает, если h<0. В данном случае ЦТ будет находиться выше, чем центр величины, а в наклонном положении линия действия силы поддержания будет пресекать след диаметральной плоскости ниже ЦТ. В таком случае при малейшем наклоне будет образовываться отрицательная пара сил, воздействующая на судно и приводящая к его опрокидыванию.
Для понимания остойчивости судна необходимо вначале ввести понятие метацентра, а затем — метацентрической высоты.
Метацентр
Если мы начнем наклонять судно, добавив внешнее воздействие, или перемещая внутри него какой-либо груз (например, переходить с одного борта на другой), у судна будет изменяться положение центра величины, из-за того, что один борт будет погружен в воду больше, чем другой. По сути, центр величины будет перемещаться по некоторой кривой траектории, при небольших кренах (до примерно 12º) похожей на дугу окружности.
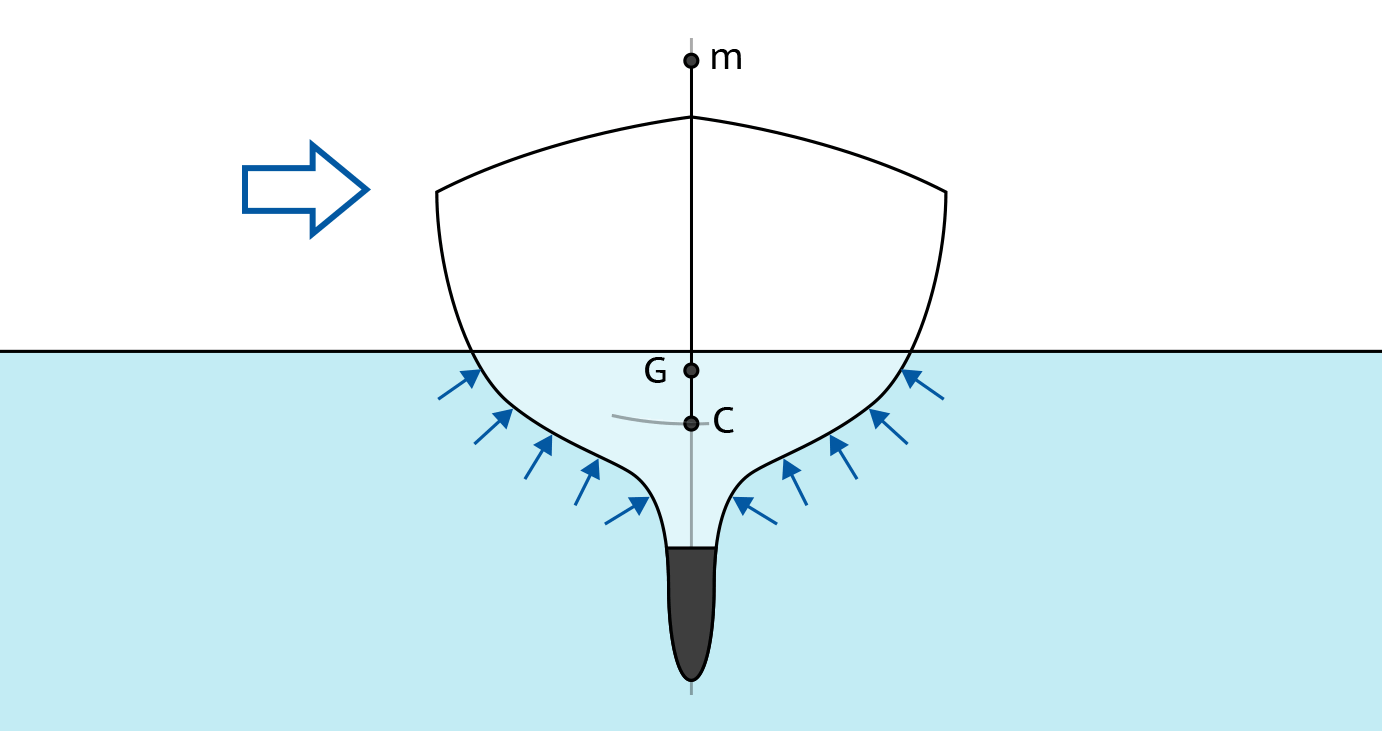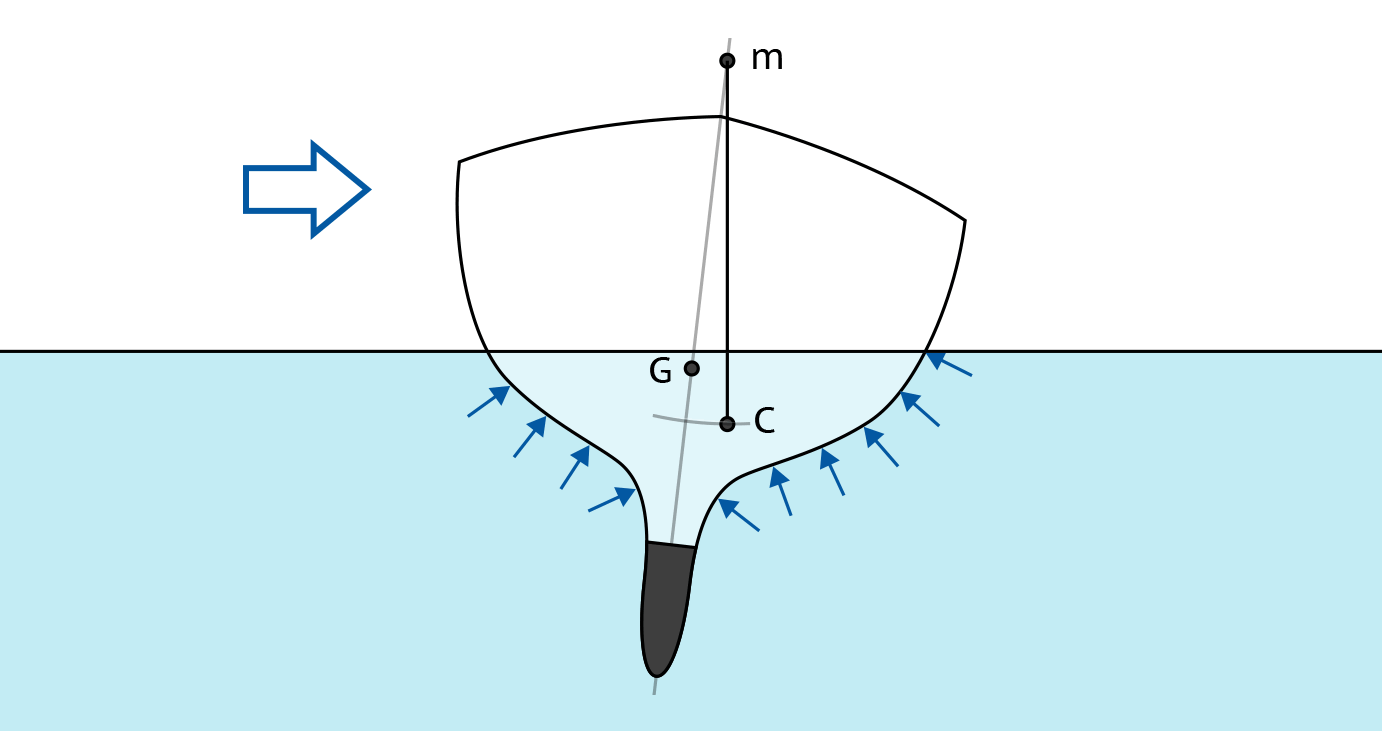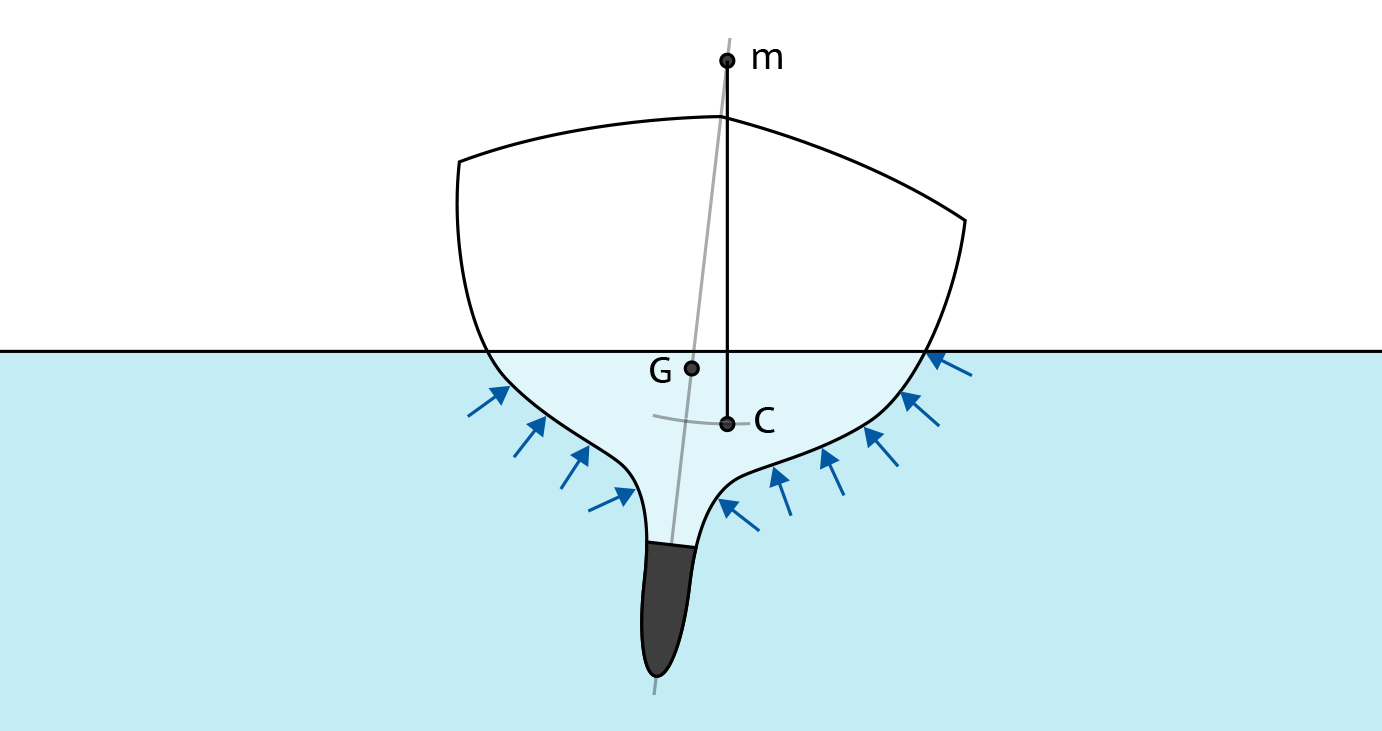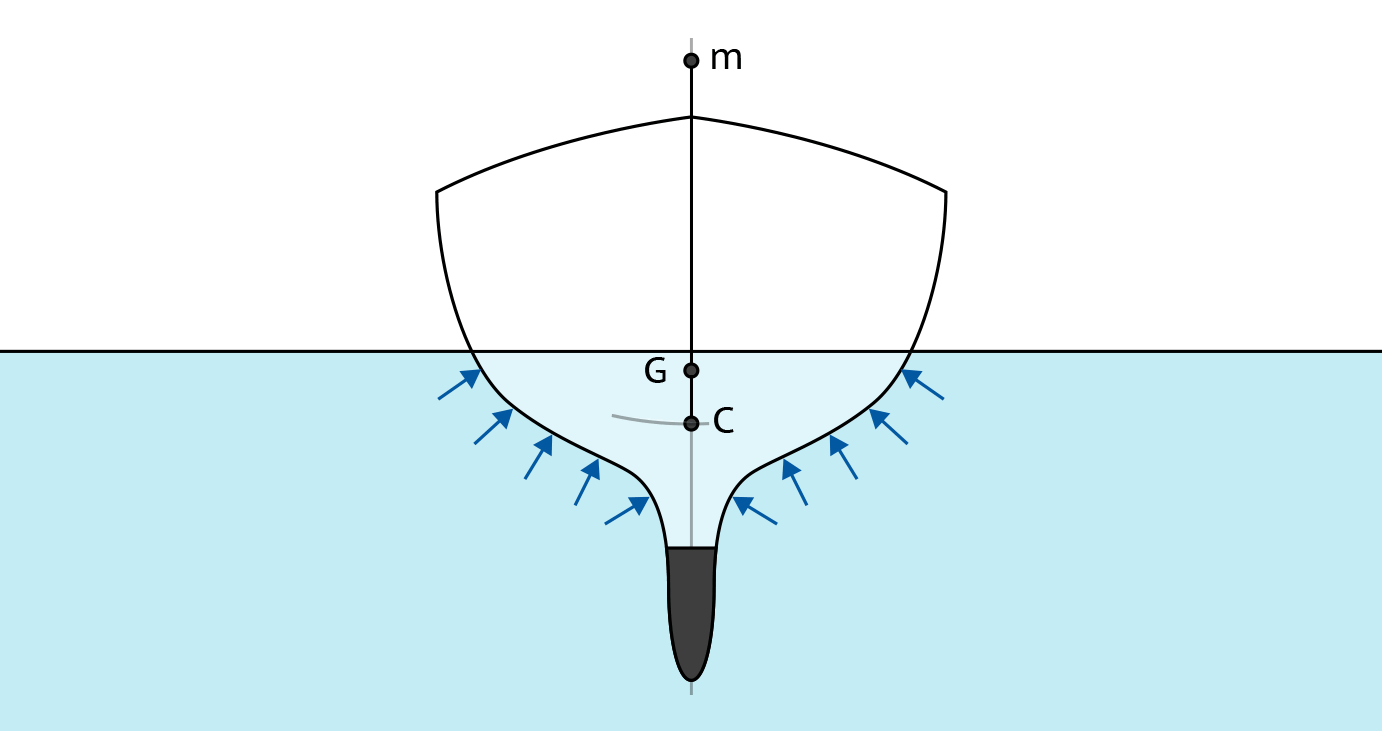
Центр кривизны этой дуги — то есть центр окружности, часть которой является описываемая дуга — будет называться метацентром. На чертежах он обозначается прописной латинской буквой m.
Причем поскольку при небольших кренах траектория действительно похожа на дугу, этот метацентр будет неподвижной точкой, а при больших углах крена — то есть когда центр величины будет меняться сильнее, поскольку вода будет уже касаться бортов и палубы судна — метацентр будет менять свое положение.
Метацентрическая высота
Если соединить метацентр m с центром тяжести судна G отрезком, то его длина будет называться метацентрической высотой. При этом если метацентр располагается выше центра тяжести, говорят о положительной метацентрической высоте, а если ниже (а такое бывает) – об отрицательной.
Метацентрическая высота при нормальном положении судна с нулевым креном – важный критерий остойчивости судна. Чем она выше, тем больше начальная остойчивость судна, то есть способность его держаться устойчиво прямо и сопротивляться внешним воздействиям.
Если метацентрическая высота равна нулю или отрицательна, то судно находится в неустойчивом состоянии — при любом малейшем воздействии оно приобретает крен и даже если это воздействие пропадет, судно не вернется в прямое положение.





