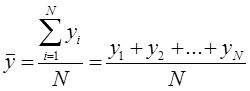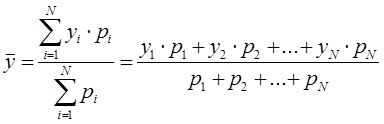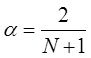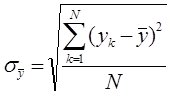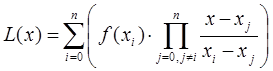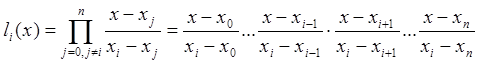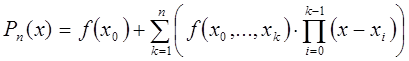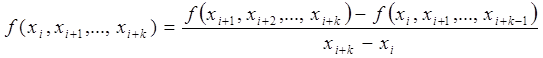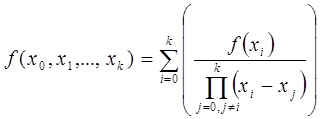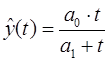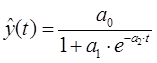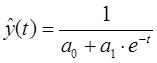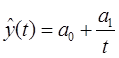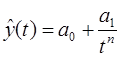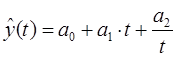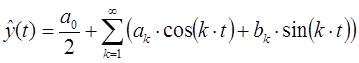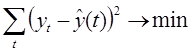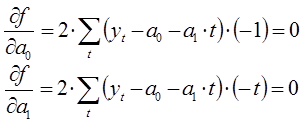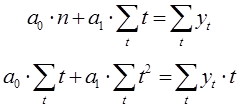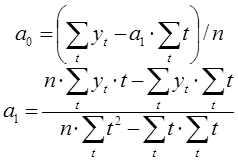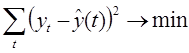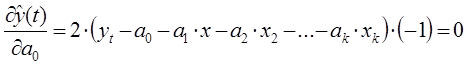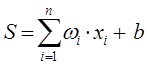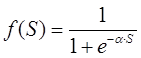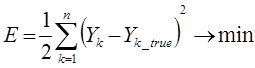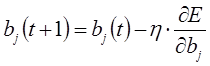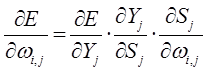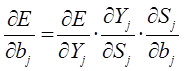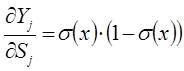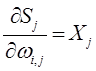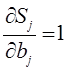Метод экстраполяции как найти

Содержание

• Использование экстраполяции
  • Способ 1: экстраполяция для табличных данных
  • Способ 2: экстраполяция для графика
• Вопросы и ответы

Существуют случаи, когда требуется узнать результаты вычисления функции за пределами известной области. Особенно актуален данный вопрос для процедуры прогнозирования. В Экселе есть несколько способов, с помощью которых можно совершить данную операцию. Давайте рассмотрим их на конкретных примерах.

Использование экстраполяции

В отличие от интерполяции, задачей которой является нахождения значения функции между двумя известными аргументами, экстраполяция подразумевает поиск решения за пределами известной области. Именно поэтому данный метод столь востребован для прогнозирования.

В Экселе можно применять экстраполяцию, как для табличных значений, так и для графиков.

Способ 1: экстраполяция для табличных данных

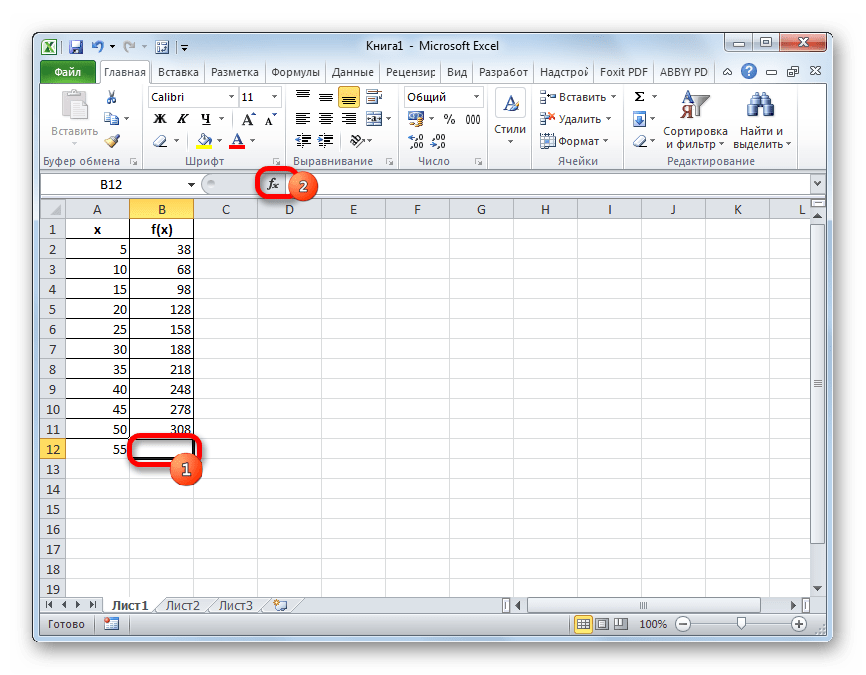
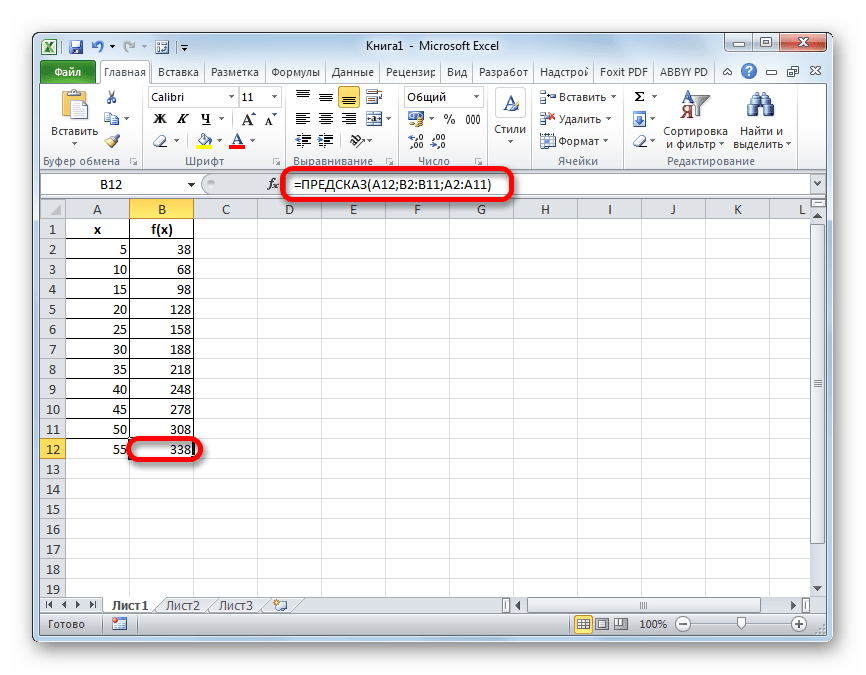
Прежде всего, применим метод экстраполяции к содержимому табличного диапазона. Для примера возьмем таблицу, в которой имеется ряд аргументов (X) от 5 до 50 и ряд соответствующих им значений функции (f(x)). Нам нужно найти значение функции для аргумента 55, который находится за пределом указанного массива данных. Для этих целей используем функцию ПРЕДСКАЗ.

1. Выделяем ячейку, в которой будет отображаться результат проведенных вычислений. Кликаем по значку «Вставить функцию», который размещен у строки формул.



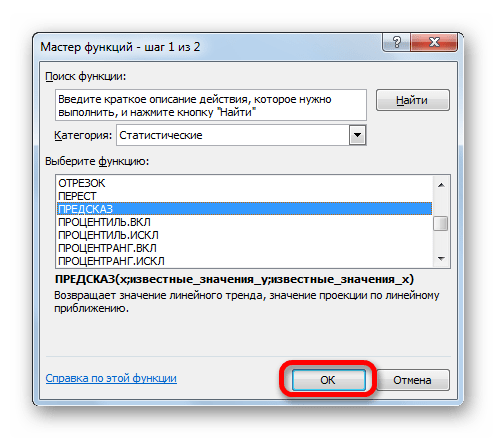
2. Запускается окно Мастера функций. Выполняем переход в категорию «Статистические» или «Полный алфавитный перечень». В открывшемся списке производим поиск наименования «ПРЕДСКАЗ». Найдя его, выделяем, а затем щелкаем по кнопке «OK» в нижней части окна.



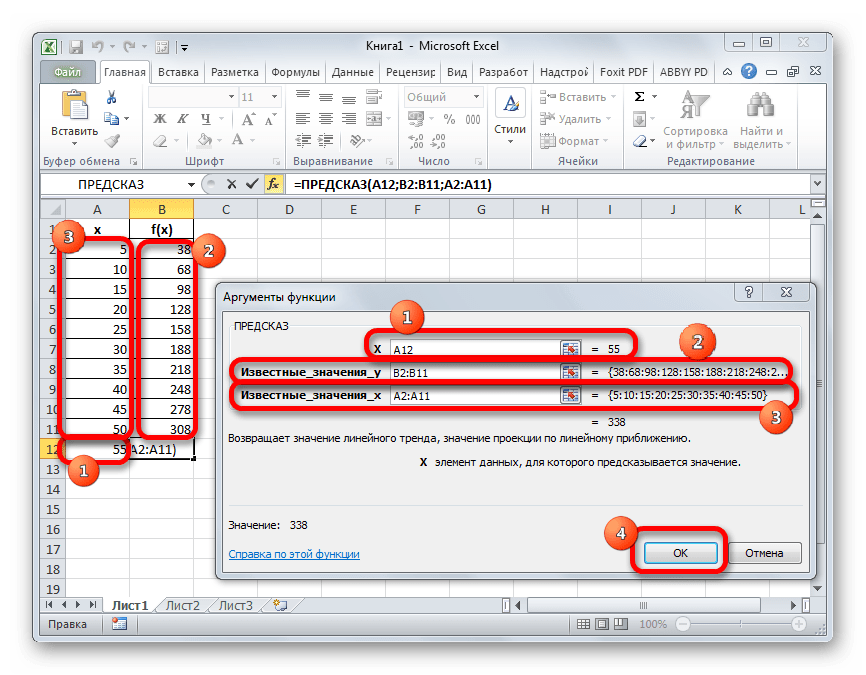
3. Мы перемещаемся к окну аргументов вышеуказанной функции. Она имеет всего три аргумента и соответствующее количество полей для их внесения.

   В поле «X» следует указать значение аргумента, функцию от которого нам следует вычислить. Можно просто вбить с клавиатуры нужное число, а можно указать координаты ячейки, если аргумент записан на листе. Второй вариант даже предпочтительнее. Если мы произведем внесение именно таким способом, то для того, чтобы просмотреть значение функции для другого аргумента нам не придется менять формулу, а достаточно будет изменить вводную в соответствующей ячейке. Для того, чтобы указать координаты этой ячейки, если был выбран все-таки второй вариант, достаточно установить курсор в соответствующее поле и выделить эту ячейку. Её адрес тут же отобразится в окне аргументов.

   В поле «Известные значения y» следует указать весь имеющийся у нас диапазон значений функции. Он отображается в колонке «f(x)». Следовательно, устанавливаем курсор в соответствующее поле и выделяем всю эту колонку без её наименования.

   В поле «Известные значения x» следует указать все значения аргумента, которым соответствуют внесенные нами выше значения функции. Эти данные находятся в столбце «x». Точно так же, как и в предыдущий раз выделяем нужную нам колонку, предварительно установив курсор в поле окна аргументов.

   После того, как все данные внесены, жмем на кнопку «OK».



4. После этих действий результат вычисления путем экстраполяции будет выведен в ячейку, которая была выделена в первом пункте данной инструкции перед запуском Мастера функций. В данном случае значение функции для аргумента 55 равно 338.



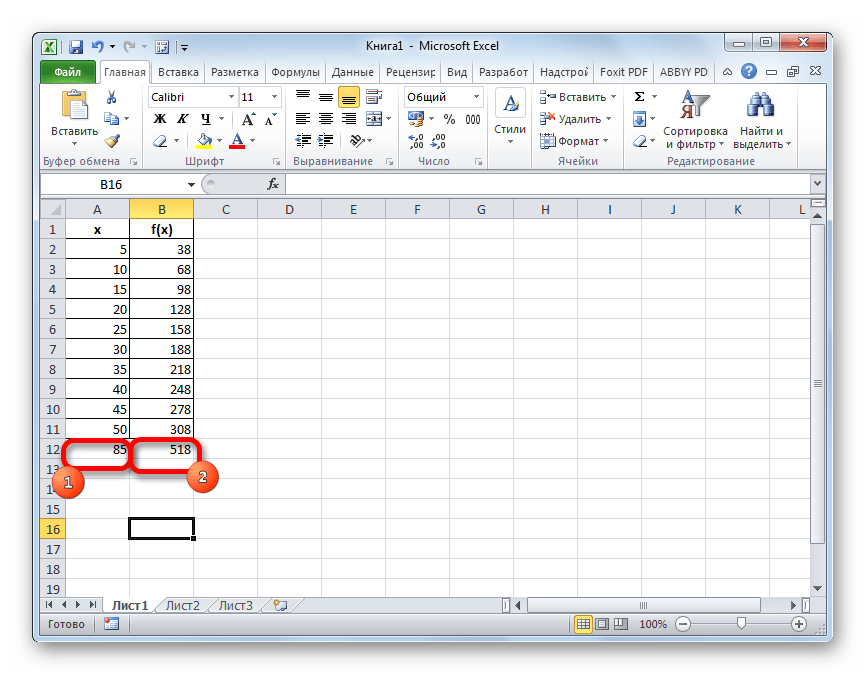
5. Если все-таки был выбран вариант с добавлением ссылки на ячейку, в которой содержится искомый аргумент, то мы легко сможем его поменять и просмотреть значение функции для любого другого числа. Например, искомое значение для аргумента 85 буде равно 518.

Урок: Мастер функций в Excel

Способ 2: экстраполяция для графика

Выполнить процедуру экстраполяции для графика можно путем построения линии тренда.

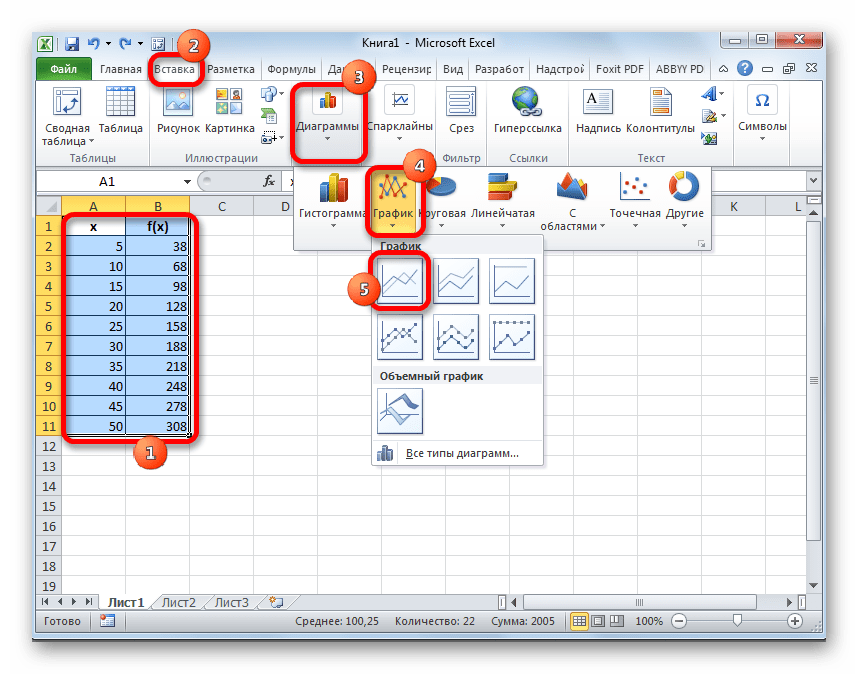
1. Прежде всего, строим сам график. Для этого курсором при зажатой левой кнопке мыши выделяем всю область таблицы, включая аргументы и соответствующие значения функции. Затем, переместившись во вкладку «Вставка», кликаем по кнопке «График». Этот значок расположен в блоке «Диаграммы» на ленте инструментов. Появляется перечень доступных вариантов графиков. Выбираем наиболее подходящий из них на свое усмотрение.



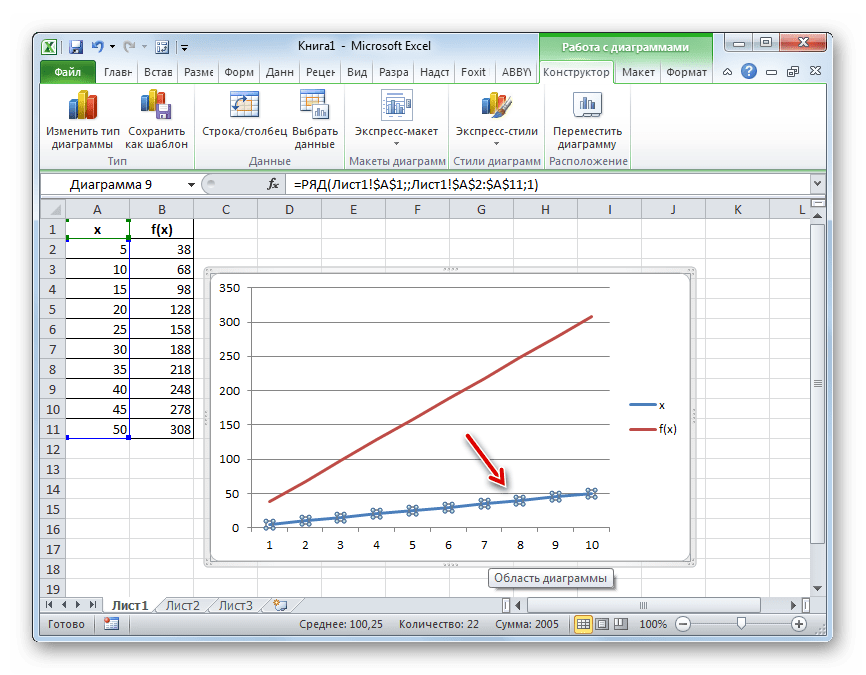
2. После того, как график построен, удаляем из него дополнительную линию аргумента, выделив её и нажав на кнопку Delete на клавиатуре компьютера.



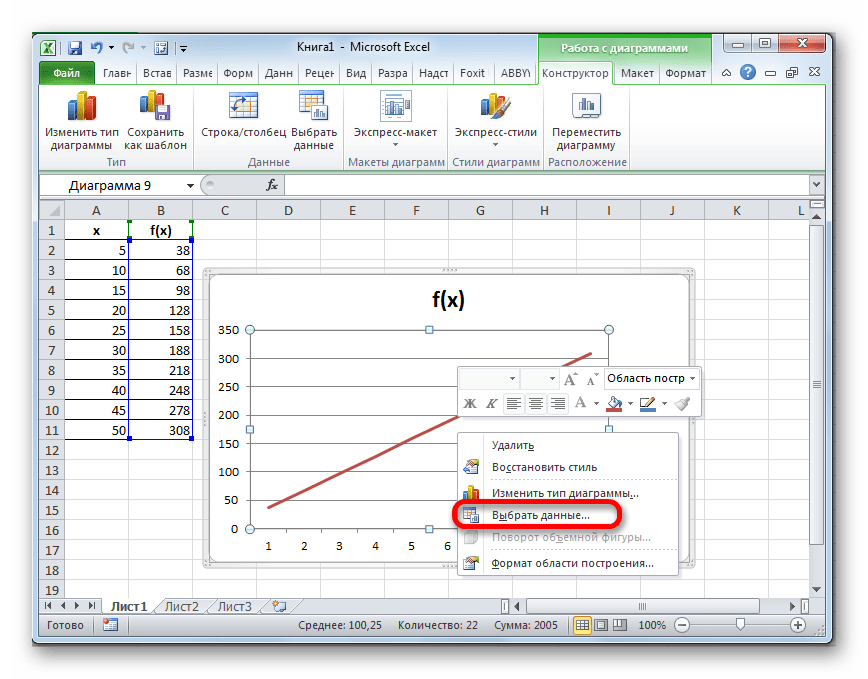
3. Далее нам нужно поменять деления горизонтальной шкалы, так как в ней отображаются не значения аргументов, как нам того нужно. Для этого, кликаем правой кнопкой мыши по диаграмме и в появившемся списке останавливаемся на значении «Выбрать данные».



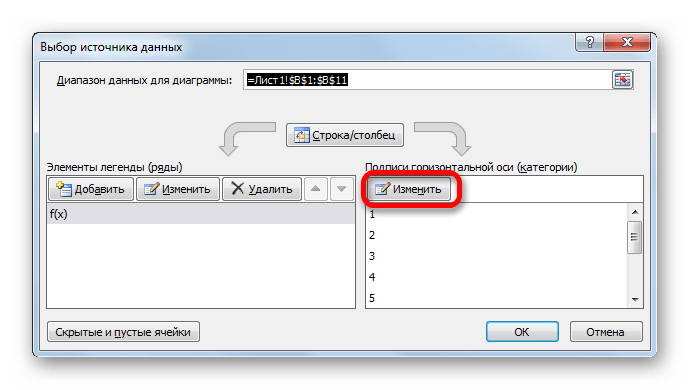
4. В запустившемся окне выбора источника данных кликаем по кнопке «Изменить» в блоке редактирования подписи горизонтальной оси.



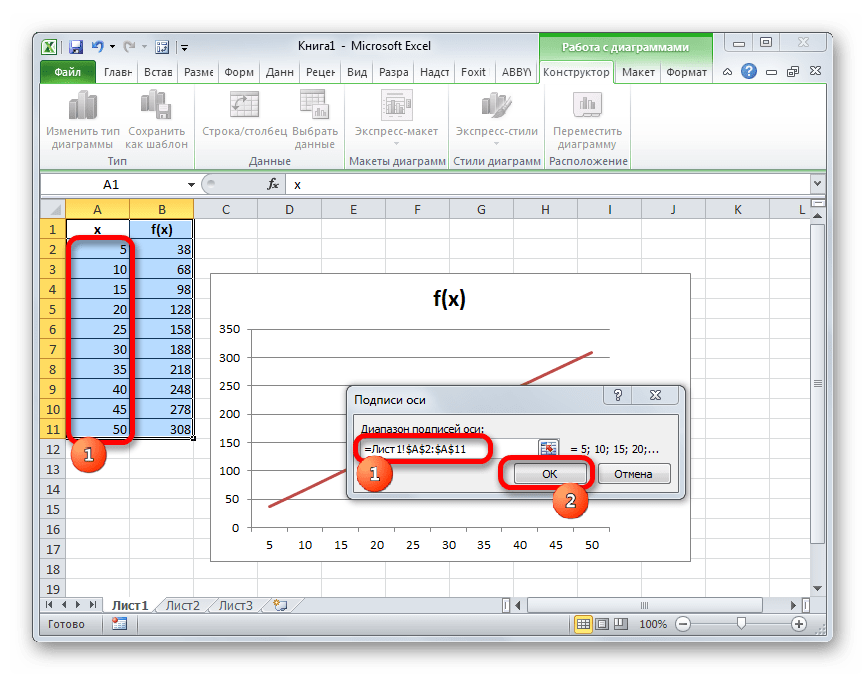
5. Открывается окно установки подписи оси. Ставим курсор в поле данного окна, а затем выделяем все данные столбца «X» без его наименования. Затем жмем на кнопку «OK».



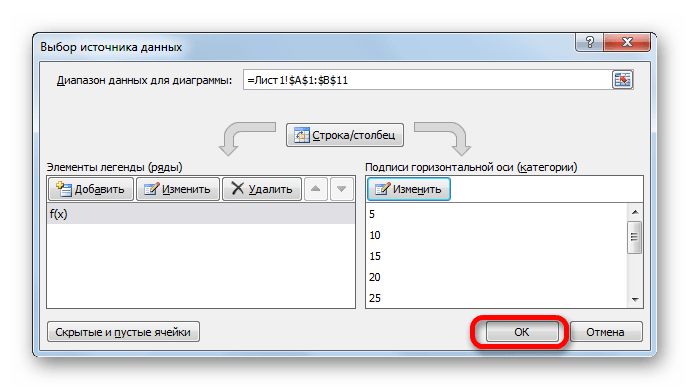
6. После возврата к окну выбора источника данных повторяем ту же процедуру, то есть, жмем на кнопку «OK».



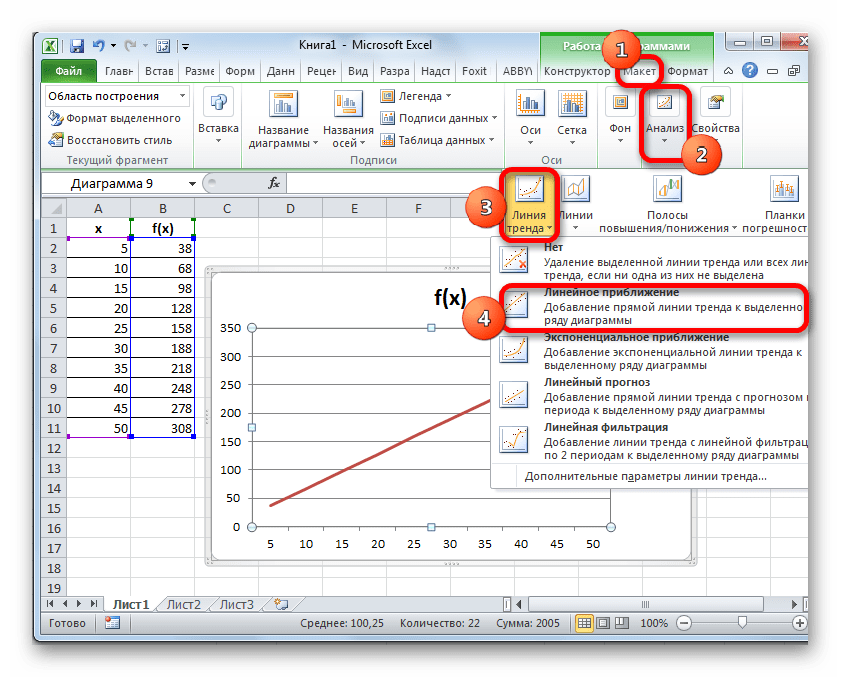
7. Теперь наш график подготовлен и можно, непосредственно, приступать к построению линии тренда. Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами». Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ». Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение».



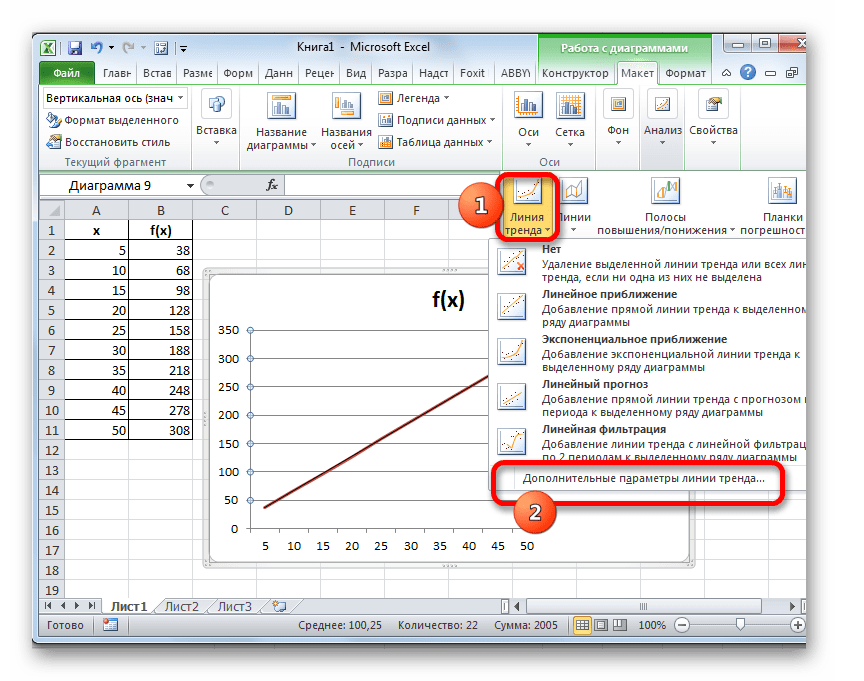
8. Линия тренда добавлена, но она полностью находится под линией самого графика, так как мы не указали значение аргумента, к которому она должна стремиться. Чтобы это сделать опять последовательно кликаем по кнопке «Линия тренда», но теперь выбираем пункт «Дополнительные параметры линии тренда».



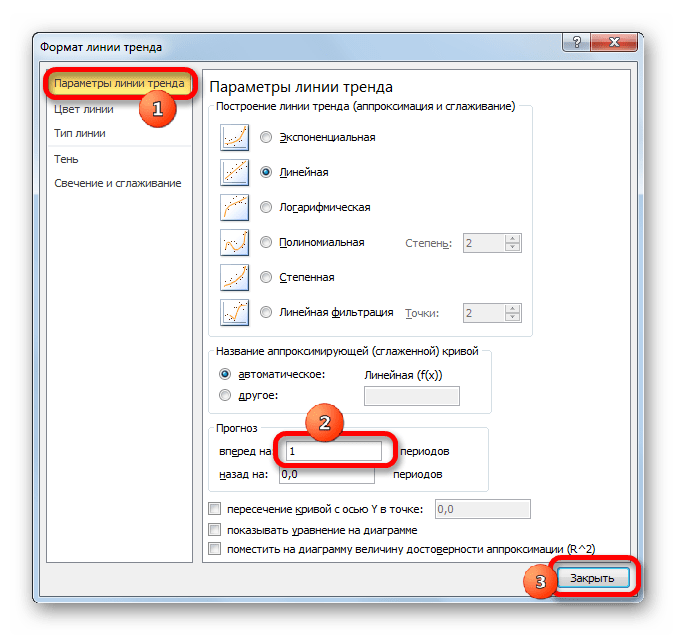
9. Запускается окно формата линии тренда. В разделе «Параметры линии тренда» есть блок настроек «Прогноз». Как и в предыдущем способе, давайте для экстраполяции возьмем аргумент 55. Как видим, пока что график имеет длину до аргумента 50 включительно. Получается, нам нужно будет его продлить ещё на 5 единиц. На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. В поле «Вперед на» вписываем значение «1». Жмем на кнопку «Закрыть» в нижнем правом углу окна.



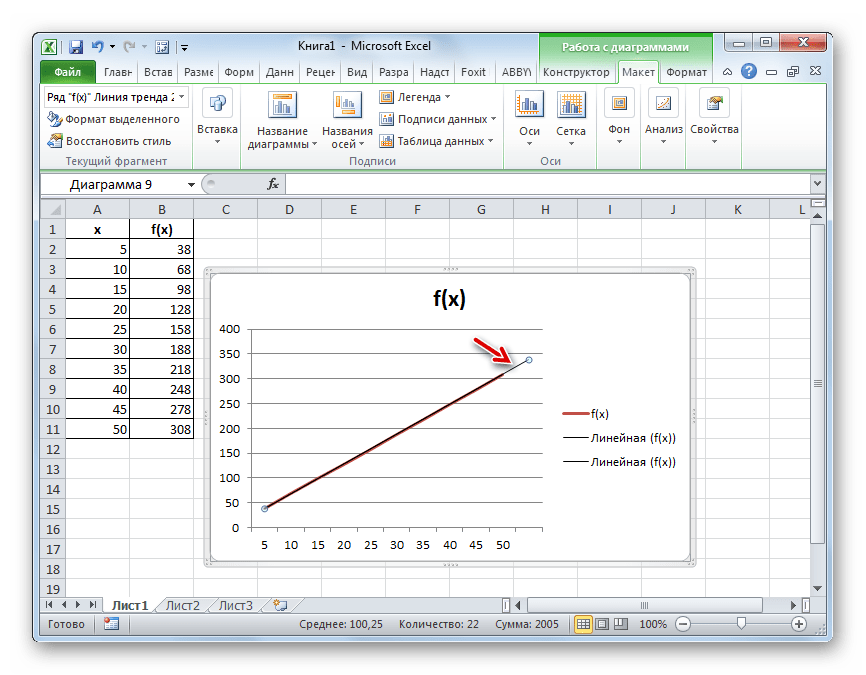
10. Как видим, график был продлен на указанную длину с помощью линии тренда.

Урок: Как построить линию тренда в Excel

Итак, мы рассмотрели простейшие примеры экстраполяции для таблиц и для графиков. В первом случае используется функция ПРЕДСКАЗ, а во втором – линия тренда. Но на основе этих примеров можно решать и гораздо более сложные задачи прогнозирования.

Еще статьи по данной теме:

Помогла ли Вам статья?

Экстраполяцияпредставляет
метод прогнозирования, заключающийся
в изучении сложившихся в прошлом и
настоящем устойчивых тенденций развития
процессов и явлений и переносе их на
будущее. Метод экстраполяции применим,
если используются следующиедопущения:
а) период времени, для которого построена
функция, должен быть достаточным для
выявлении тенденции развития; б)
анализируемый процесс является устойчиво
динамическим и обладает инерционностью,
т.е. для значительных изменений
характеристик процесса требуется время;
в) не ожидается сильных внешних воздействий
на изучаемый процесс, которые могут
серьезно повлиять на тенденцию развития.
Прогнозирование с помощью метода
экстраполяции – один из простейших
методов статистического прогнозирования.
Его использование оправдано при
недостаточном знании о природе изучаемого
явления или отсутствии данных, необходимых
для применения более совершенных методов
прогнозирования.

Различают а) простую экстраполяцию,
которая предполагает, что все действовавшие
в прошлом и настоящем тенденции сохранятся
в полном объеме, так как все действовавшие
факторы останутся неизменными; б)прогнозную экстраполяцию, которая
базируется на предположении об изменении
факторов, определяющих динамику
изучаемого процесса или явления.

Основу экстраполяции составляет изучение
динамических рядов, представляющих
собой упорядоченные во времени наборы
измерений тех или иных показателей
исследуемого объекта. В основе
динамического анализа лежит понятие
траектории, которая описывает состояние
изучаемого процесса как функцию от
времени:Q=Q(t),t[0,T],
[0,T] – отрезок времени.

При этом время может учитываться как
по интервалам, так и непрерывно. В первом
случае функция называется динамическим
рядом.

Использование экстраполяции имеет в
своей основе предположение о том, что
рассматриваемый процесс представляет
собой сочетание двух составляющих:
регулярной составляющей (Х_t)
и случайной переменной ().
Временной ряд может условно представлен
в виде:Y_t=X_t+
_t.

Регулярная составляющаяназывается
трендом, тенденцией и характеризует
существующую динамику развития процесса
в целом.Случайная составляющаяотражает случайные колебания (шумы
процесса).

Показателями развития процессаявляются абсолютный прирост, темп роста,
темп прироста. Показатели изменения
динамического ряда могут вычисляться
на постоянной и переменой базе. Для
обобщающей оценки скорости и интенсивности
изменения динамического ряда используются
различные средние характеристики, среди
которых являются средний темп роста и
средний темп прироста. Средний темп
роста рассчитывают как среднее
геометрическое и как среднее параболическое.Среднее геометрическоерассчитывается
из последовательных цепных темпов
роста:;среднее параболическоеориентировано
на сумму динамического ряда и определяется
из уравнения:

Задача ППЭсостоит в определении
вида экстраполирующих функций Х_tи
_tна основе исходных эмпирических данных
и параметров выбранной функции.

Методика построениятрендовых
моделей представляет сочетание
качественного экономического анализа
и формальных математико-статистических
методов и включает несколько этапов:
1)Выбор класса функции тренда.Существует более 40 временных функций,
отличающихся своими свойствами. Надо
выбрать ту, которая отражает главные
особенности динамики исследуемого
показателя, прежде всего тип развития.
Можно выделить 4 типа экономического
роста: постоянный, увеличивающийся,
уменьшающийся и рост с качественными
изменениями характеристик на протяжении
рассматриваемого периода. 2)Оценка
параметров функции. Он проводится
методами регрессионного анализа. 3)Расчет значений формальных критериев
аппроксимации. Для характеристики
близости тренда к аппроксимируемому
динамическому ряду применяют несколько
формальных критериев: сумма квадратов
отклонений значений тренда от фактических
значений, значение коэффициента
детерминации и т.д. 4)Анализ остаточной
компоненты динамического ряда.5)Выбор функции тренда. Результатом
предшествующих этапов является построение
нескольких функций тренда для одного
показателя. Выбор лучшей осуществляется
путем сопоставления значений, возможностей
экономической интерпретации и
использования в прогнозировании.

МЕТОД ЛИНЕЙНОЙ экстраполяции.
Сущность метода заключается в том,
что прогнозные величины определяются
на основе среднего прироста (снижения)
исследуемого показателя за определенный
период времени.

Пример. Предположим, у нас имеются
данные об объеме ВНП страны за ряд лет:

Таблица – Объем
ВНП страны

Год	Объем ВНП	Прирост ВНП
1995	16,0	–
1996	21,8	5,8
1997	27,0	5,2
1998	32,0	5,0
1999	36,8	4,8

Рассчитаем средний темп прироста за
четыре года: (5,8 + 5,2 + 5,0 + 4,8)/4 = 5,2

Определив средний темп прироста,
рассчитаем прогнозное значение ВНП
страны на 2000 год: Y₂₀₀₀=Y₁₉₉₉+Y= 36,8 + 5,2 = 42,0

В тех случаях, когда показатели базисного
и конечного прогнозного периода известны
и следует определить годовые промежуточные
показатели, используют метод линейной
интерполяции, рассчитывая средний
прирост за данный период времени:

Пример:Y₂₀₀₀=
205,Y₂₀₀₅ = 240.
Y= (240 – 205)/5 = 7.

Y₂₀₀₂ =Y₂₀₀₀+ 2*Y= 205 + 2*7 = 219.

МЕТОД ПРОСТОЙ СРЕДНЕЙ. Применяется в
тех случаях, когда в уравнении линейной
зависимости Y=a+bx, коэффициентb= 0. При таком условии график будет
представлен прямой параллельной
горизонтальной оси графика, а прогноз
будет состоять в расчете простой средней
из всех имеющихся данных:Y=Y/N.

Расчеты простой средней часто связывают
с сезонными колебаниями, происходящими
внутри общего тренда.

Пример.Имеются данные об объеме
ВНП за ряд лет по кварталам:

Год	1 квартал	2 квартал	3 квартал		В целом за год
1995	190	370	300	220	1080
1996	280	420	310	180	1190
1997	270	360	280	190	1100
1998	300	430	290	200	1220
1999	320	440	320	220	1300
Итого	1360	2020	1500	1010	5890
Средний объем	272	404	300	203	294,5

Рассчитываем квартальный индекс: 1
квартал = 272:294,5 = 0,92; 2 квартал = 404:294,5 =
1,37;

3 квартал
= 300:294,5 = 1,02; 4 квартал = 203:294,5 = 0,69.

Для того, чтобы составить прогноз
объема ВНП по кварталам на 2000 год,надо прогнозное значение ВНП за данный
год разделить на 4(количество кварталов)
и умножить на соответствующий квартальный
индекс. Предположим, что в 2000 году ВНП
будет равен 1450. Тогда в 1 квартале будет
произведено: (1450:4)*0,92= 333,5; 2 квартал =
(1450:4)*1,37 = 496,625 и т.д.

МЕТОД наименьших
квадратов. Позволяет подогнать
функцию под некоторый набор численных
значений и построить график функции по
некоторой совокупности точек. Выбор
этой функции считается наилучшим, если
стандартное отклонение определяемое
формулой:

E=
(d_t–d’_t)²
minоказывается сведено
к минимальному значению.

d_t–
фактические данные,

d`_t
– данные рассчитанной функции.

Как правило, используется линейная
функция Y
= a + bx.

Задача состоит в том, чтобы определить
значения а и b, где

а – значение Yв базисном периоде,

b– угол наклона прямой.

Чтобы определить значения aиbиспользуется система
уравнений:

Y=Na+b

Y=ax+bx², гдеN- число периодов

х – номер
периода.

Пример. Имеются данные об
объеме ВНП.

Год	Y(ВНП)	x	x2	xY	Yсглаженный
1995	108	0	0	0	108,4
1996	119	1	1	119	108,4 + 4,7 = 113,1
1997	110	2	4	220	108,4 + 2* 4,7 = 117,8
1998	122	3	9	366	108,4 + 3* 4,7 = 122,5
1999	130	4	16	520	108,4 + 4* 4,7 = 127,2
	589	10	30	1225

Система уравнений выглядит следующим
образом: 589 = 5а + 10b

1225 = 10ф + 30b.

Решая их, находим а = 108,4, b= 4,7.

Можно рассчитать ВНП 2000 года : Y₂₀₀₀=Y₁₉₉₅+ 5b= 108,4 + 5*4,7 = 131,9.

В отдельных случаях лучшего соответствия
теоретических данных эмпирическим
можно достигнуть вычерчивая по точкам
кривой сглаживания вида Y=ab^x,
т.е. используяпоказательную функцию.

Если показательное уравнение
логарифмировать, то значения коэффициентов
а и можно определить методом наименьших
квадратов:

log Y = log a + x* log b.

logaиlogbнаходят, решая нормальные
уравнения:
logY=Nloga+
xlogb.

x log Y =
x log a +x²
log b.

Если определить х таким образом, что

x= 0, то

log a =
log Y/ N, log b =x log Y/x².

МЕТОД СКОЛЬЗЯЩЕЙ СРЕДНЕЙ. При подготовке
прогноза методом скользящей привязки
число периодов, по которым производится
суммирование фактических данных,
несколько больше того числа, которое
было установлено и которое желательно
иметь для проведения необходимых
расчетов. Необходимость выравнивания
сезонных колебаний требует, чтобы
суммарная продолжительность всех
периодов была равна 1 году. Выравнивание
сезонных колебаний происходит в силу
того, что крайние значения тренда имеют
тенденцию к взаимному погашению.
Вовлечение в расчет скользящей средней
большего числа временных периодов
увеличивает эффект сглаживания и
одновременно уменьшает чувствительность
прогноза к данным последних периодов.

Движение скользящей средней во времени
дает возможность учесть самую последнюю
информацию и отказаться от использования
более старых данных. Использование
скользящей средней позволит подготовить
качественный прогноз только тогда,
когда данные будут относительно
стабильны.

Индекс сезонных колебаний, вычисленный
на основе скользящей средней, дает
возможность улучшить качество прогноза.
Индекс получают путем деления объема
фактического производства в соответствующем
периоде на величину центрированной
скользящей средней за тот же период.
Повысить надежность можно за счет
усреднения значения нескольких индексов
общих временных периодов.

Пример. Для разработки прогноза на
2000 год используем данные о квартальных
объемах производства. Скользящие средние
определяются исходя из разбивки года
на кварталы. Можно рассчитать скользящую
среднюю только за 2 квартал 1995 года путем
деления суммы данных за четыре квартала
данного года на 4: (190+370+300+220)/4= 270.

Для расчета следующей скользящей средней
берут данные за 2-4 кварталы 1995 года и 1
квартал 1996 года. Аналогично поступают
в дальнейшем.

Центрированная скользящая средняя
находится только для третьего квартала
путем деления суммы данных скользящей
средней за 2 и 3 кварталы 1995 года:
(270+292)/2 = 281.

Дальнейшие расчеты делаются аналогично,
заменяя одно значение другим.

Индекс сезонных колебаний получают
путем деления фактического объема
производства на величину центрированной
скользящей средней за тот же период.
Для 3 квартала 1995 года: 300:281 = 1,07.

Таблица. Расчет значений скользящей
средней и индексов сезонных колебаний

Год	Квартал	Объем производства	Скользящая средняя	Центрированная скользящая средняя	Индекс сезонных колебаний
1995	1	190
	2	370	(190+370+300+220):4=270
	3	300	(370+300+220+280):4=292	(270+292):2 = 281	1.07
	4	220	(300+220+280+420):4=305	(292+305):2= 298,5	0,74
1996	1	280	(220+280+420+310):4=307	(305+307):2= 306	0,91
	2	420	(280+420+310+180):4=297	(307+297):2= 302	1,39
	3	310	295	296	1,04
	4	180	280	287,5	0,63
1997	1	270	273	276,5	0,98
	2	360	275	274	1,32
	3	280	283	279	1,00
	4	190	300	286,5	0,66
1998	1	300	303	301,5	1,00
	2	430	305	304	1,42
	3	290	310	307,5	0,94
	4	200	312	311	0,64
1999	1	320	320	316	1,01
	2	440	325	322,5	1,37
	3	320
	4	220

На основе рассчитанных данных индекса
сезонных колебаний заполняем таблицу
2 и делаем расчет скорректированного
индекса.

Таблица 2 Расчет скорректированного
индекса сезонных колебаний

Год	1 квартал	2 квартал	3 квартал	4 квартал
1995			1.07	0,74
1996	0,91	1,39	1,04	0,63
1997	0,98	1,32	1,00	0,66
1998	1,00	1,42	0,94	0,64
1999	1,01	1,37
Итого	3,90	5,50	4,05	2,67
Средний индекс сезонных колебаний	0.975	1,375	1,0125	0,6675
Скорректированный индекс сезонных колебаний	0,97	1,37	1,00	0,66

Средний индекс сезонных колебаний
рассчитываем путем деления суммы
индексов за данный квартал на количество
данных: для 1 квартала: 3,90:4 = 0,975 и т.д.

Полученные средние индексы сезонных
колебаний проверяют на точность расчета.
Среднее значение всех квартальных
индексов не должна превышать 1. В нашем
случае:

(0.975 + 1,375 + 1,0125 + 0,6675): 4 = 1,0075

Так как индекс больше 1, его следует
скорректировать, уменьшив на 0.0075.

Завершающая стадия – составление
прогноза. Для этого берут центрированную
скользящую среднюю за определенный
период и умножают на скорректированный
индекс сезонных колебаний. Для 2000 года
мы должны взять центрированную скользящую
среднюю за 1 квартал 1999 года (316) и умножить
на скорректированный индекс сезонных
колебаний за 1 квартал (0,97):

1 квартал 2000 года = 316*0,97 = 307.

И т.д.

ЭКСПОНЕНЦИАЛЬНОЕ СГЛАЖИВАНИЕ. При
экспоненциальном сглаживании в равенство
вводится постоянный коэффициент
сглаживания
,
придающий больший вес последним данным.
Уравнение прогноза, учитывающее
экспоненциальное сглаживание, записывается
в виде:

F_n=Y_n-1+ (1 –)F_n-1,

где F_n
– прогноз предстоящего периода

F_n-1–
прогноз на текущий год

– коэффициент сглаживания

Y_n-1–
фактический объем прогнозируемого
показателя в текущем году.

Коэффициент
находится в интервале от 0 до
1.Чувствительность к происходящим
изменениям повышается с увеличением
коэффициента сглаживания и уменьшением
числа рассматриваемых периодов (N).
Связь междуиNописывается отношением=.

Поэтому, если нас не устраивает найденное
количество периодов N, то
мы легко можем найти значение,
которое нас устроит.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Добавлено в закладки: 0

Что такое метод экстраполяции? Описание и определение понятия.

Метод экстраполяции – это один из главных способов прогноза, который основывается на прогнозировании событий, учитывая анализ показателей, которые имели место в прошлые годы (при этом, не меньше чем за 5 – 8 лет). В данный момент есть приблизительно триста уравнений, которые дают возможность определить тенденции процессов и позволяют оценить  линейную простую зависимость явления и квадратичную зависимость.

Экстраполи́рование, экстраполя́ция, (от лат. extrā — снаружи, вне, кроме, за и лат. polire — выправляю, приглаживаю, меняю, изменяю) — это особенный вид аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не меж фиксированными значениями.

Другими словами, экстраполяция — это приближённое определение значений функции в точках, которые лежат вне отрезка, по её значениям в точках.

Методы

Во многих случаях методы экстраполяции похожи с методами интерполяции.

Самый распространённый способ экстраполяции — это параболическая экстраполяция, при которой в точке берётся значение многочлена степени, которая принимает в точке заданные значения. Для параболической экстраполяции применяют интерполяционные формулы.

Применение

Общее значение — это распространение выводов, которые получены из наблюдения над одной частью явления, на его другую часть.

В маркетинге — это распространение выявленных закономерностей развития изучаемого предмета на будущее.

В статистике — это распространение тенденций, установленных в прошлом, на будущий период (экстраполяция во времени используется для перспективных расчетов населения); распространение выборочных данных на прочую часть совокупности, которая не подвергнута наблюдению (экстраполяция в пространстве).

Одним из более распространенных способов краткосрочного прогнозирования экономических явлений — это экстраполяция

Термин “экстраполяция” имеет немного толкований в широком смысле экстраполяция – это способ научного исследования, который заключается в распространении выводов, которые получены из наблюдений за одной частью явления, на а другую его часть В узком смысле – это определение по нескольким данным функции прочих ее значений вне данного ряда за этим рядом.

Прогноз экстраполяции

Экстраполяция заключена в изучении сложившихся в настоящем и прошлом устойчивых тенденций экономического развития и их перенос на будущее

Цель данного прогноза — это показать, к каким итогам можно сделать в будущем, когда передвигаться к нему с аналогичной ускорением или скоростью, что и в прошлом

Прогноз определяет ожидаемые варианты данного экономического развития исходя из гипотезы, что главные факторы и тенденции прошлого периода сберегается на период прогноза или что возможно обосновать и учесть направление их изменений в рассматриваемой перспективе. Такую гипотезу выдвигают, учитывая инертность экономических процессов и явлений.

В прогнозировании экстраполяция используется при изучении временных рядов экстраполяции в общем типе можно представить, как определенное значение функции зависимо от особенностей изменения уровней в рядах динамики способы экстраполяции могут быть сложными и простыми.

Простые способы экстраполяции базируются на предположении относительной устойчивости в будущем абсолютных значений уровней, среднего абсолютного прироста, среднего уровня ряда, среднего темпа роста.

Различные способы экстраполяции

Рассмотрим дет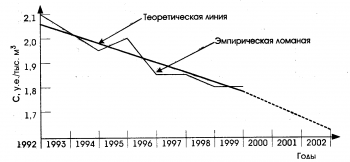альнее названные способы экстраполяции.

При экстраполяции на основании среднего уровня ряда применяется принцип, при котором прогнозируемый уровень равняется среднему значению в прошлом уровней ряда.

В данной ситуации экстраполяция дает точечную прогностическую оценку. Точное совпадение данных оценок с фактическими данными — маловероятное явление. Таким образом, прогноз обязан быть в виде интервала значений.

Полученный доверительный интервал учитывает неопределенность, которая связана с оценкой средней величины, и его использование для прогнозирования увеличивает степень надежности прогноза. Однако недостаток рассматриваемого подходов периода — это то, что доверительный интервал не связывается с периодом предупреждения.

Экстраполяцию по среднему абсолютному приросту можно провести тогда, когда линейной считать общую тенденцию развития явления.

Чтобы рассчитать прогнозное значение, уровень необходимо определить абсолютный средний прирост. Затем, зная уровень ряда динамики, который принимают за основу экстраполяции.

Экстраполяцию по среднему темпу роста можно осуществить, когда есть основания полагать, что суммарная тенденция ряда динамики характеризуется показательной кривой.

Доверительный интервал прогноза по средним темпом роста можно определить лишь в том случае, когда средний темп роста рассчитывают при помощи статистического оценивания параметров экспоненциальной кривой.

Все три рассмотренные способа экстраполяции тренда простейшие, но вместе и самые приближенные.

Сложные способы экстраполяции предусматривают выявление главной тенденции, то есть использование статистических формул, которые описывают тренд.

Способы данной группы возможно разделить на два главных вида: адаптивные и аналитические (кривые роста).

Аналитические способы прогнозирования

В основание аналитических способов прогнозирования (кривых роста) лежит принцип получения при помощи метода самых малых квадратов оценки детерминированной компоненты, которая характеризует главную тенденцию

Адаптивные способы прогнозирования основываются на том, что процесс реализации их заключен в вычислении последовательных во времени значений прогнозируемого показателя, учитывая степень влияния прошлых уровней. К ним относят способы экспоненциальной и текучей средних, способ гармонических весов, способ авторегрессииї.

Способ аналитического выравнивания тренда (способ наименьших квадратов) может быть использован лишь тогда, когда развитие явления довольно хорошо описывают построенную модель и условия, которые определяют тенденцию развития в прошлом, не изменятся существенно в будущем. При выполнении данных требований прогнозирование производится при помощи подстановки в уравнение тренда значений независимой переменной знает величине периода предупреждения.

Процедура создания прогноза по применению аналитического выравнивания тренда включает в себя такие этапы:

1) выбор формы кривой, которая отображает тенденцию;

2) определение показателей, характеризующие количественно тенденции изменений;

3) оценка вероятности прогнозных расчетов

Подбор формы кривой возможно осуществлять на основании построения графика, суммарный тип которого обычно дает возможность установить:

а) имеет динамический ряд показателя выраженную четко тенденцию;

б) если так, то данная тенденция плавная;

в) каков характер тенденции

Отвечая на данные вопросы, нужно помнить, что наружная простота графика ложная. Каждая динамическая задача намного сложнее от статического и каждая точка кривой — это результат изменения явления во времени и пространстве.

Ввиду этого для увеличения достоверности и обоснованности выравнивания для более точного выявления тенденции, которая есть, нужно провести вариантный расчет по некоторым аналитическими функциями и на основании статистических и экспертных оценок определить лучшую форму связей.

На втором этапе нужно определить параметры уравнения связи. Для того, чтобы их найти, применяют способ малых квадратов. В данной ситуации выравнивающая функция будет занимать данное положение среди факт политических значений показателей, при котором общее отклонение точек от функции будет наименьшим.

Обоснованную и достоверную оценку имеющимся результатам можно дать, применяя статистические показатели: средний коэффициент увеличения, коэффициент корреляции, остаточная и общая дисперсия, другой индекс корреляции, коэффициент корреляции ряда отклонений и исходного ряда, определенного по разнице выровненных и фактических по любой аналитической функции.

Для того, чтобы проверить гипотезу об отсутствии или наличии автокорреляции применяют таблицы с критическими значениями коэффициента автокорреляции при разных уровнях значимости. Когда табличное значение коефициэнта автокорреляции больше фактического, то возможно утверждать, что автокорреляция устраняется или отсутствует, а означает, возможно применять формулы для возиожностной оценки значений, которые прогнозируются по этому и точками.

Для прогноза были выбраны такие функции, как логарифмическая, линейная, ступенчатая, полиномиальная и экспоненциальная.

Не все выбранные аналитические функции выравнивают хорошо динамический выходной ряд. Об этом говорит значение индекса (коэффициента) корреляции Для того, чтобы прогнозировать, то есть продолжать сформированные тенденции на ближайшую перспективу, можно использовать лишь те функции, для которых индекс (коэффициент) корреляции больше 0,7 К таковым относят линейную, экспоненциальную и полиномиальную функцию. Последняя имеет самый большой коэффициент корреляции, равен 0,847, и самую малую величину остаточной дисперсией.

Порой, самой приемлемой формой аналитической функции для прогнозирования является полиномиальная функция, которая представлена уравнением:

Подставив в полученное уравнение значения периодов предубеждения, определяем прогнозное значение объема товарооборота на такие три месяца: у25 = 654,83; у = 655,93; у ”- 657,07 тыс грн 26 27

Возможность того, что экономический прогнозируемый показатель в заданный момент времени будет равняться значению, которое отвечает точечной прогноза, почти равняться нулю. Потому к точечному прогнозу границы вероятного изменения прогнозируемого значения показателя.

Заметим, что в полученных при прогнозировании оценок доверительных интервалов необходимо отнестись с осторожностью Это связывается со спецификой динамических рядов Их специфичность заключена в том, что увеличение количества наблюдений в статической совокупности дает возможность получить точные характеристики данной совокупности, в то время как аналогичное удлинение ряда динамики приводит не всегда к похожим результатам, особенно в тех ситуациях, когда ряды динамик применяются для прогнозирования. Данное обстоятельство связывается с тем, что информационная ценность уровней потеряется по мере их удаления от периода предубеждение, то есть означает уровни ряда динамики при прогнозировании неравноценно. Потому параметры уравнений аппроксимирующих кривых роста могут обладать погрешности и изменять собственные оценки при исключении части членов ряда или Анне добавил новых членов ряда динамики, что отображается на точности расчетных значений уровней ряда динамики. Помимо этого, параметры моделей тренда, которые получены способом самых малых квадратов, остаются неизменным и в течение рассматриваемого периода. На практике зачастую встречаются случаи, когда параметры моделей изменяются, а процедуры, которые сглаживают при помощи способа самых малых квадратов не могут определить такие изменения.

Поэтому наиболее эффективными являются адаптивные способы, в которых значимость уровней ряда динамики снижается по мере их удаления от прогнозируемого периода. К ним относят: способ текучих средних, способ экспоненциального сглаживания, способ гармонических весов и прочие, включаются в класс адаптивных способов.

Зачастую несколько динамики характеризуются резкими колебаниями показателей по годам. Данные ряды обычно, имеют слабую связь со временем и не проявляют четкой тенденции к изменению. В данной ситуации способы аналитического выравнивания малоэффективен, потому что возможность расчетов резко уменьшается. Доверительные границы прогноза порой оказываются шире, чем колебания показателя в некоторых динамиках.

При прогнозировании на основании временных рядов, которые весьма колеблются, можно применять способ текучих средних, при помощи которого возможно исключить случайные колебания временного ряда.

Интервал, величина которого все еще постоянная, постепенно помещается на одно наблюдение. Когда наблюдается определенная цикличность изменений показателей, интервал текучести равняется длительности циклу. В ситуации отсутствия цикличности в изменении показателей советуется исполнять различный расчет при параметре сглаживания. Лучший вариант определяется на основании дальнейшей оценки и выровненных рядов.

По данным выровненных значений ряда динамики производится подбор формы кривой, которая отражает тенденции развития явления. Полученное уравнение регрессии применяется для определения прогнозного значения исследуемого показатель.

На основании выровненных значений товарных запасов предприятия имеются такие значения коэффициента корреляции. Приведенные данные говорят, что наилучшие итоги должны по данным, которые выровнены на основании уровней исследуемого ряда динамики

Метод экспоненциального сглаживания

Экспоненциальное сглаживание – это выравнивание динамических рядов, весьма колеблются, цели стабильного прогнозирования По данному способу возможно дать обоснованные прогнозы на основе рядов динамики, имеют умеренный связь во времени, и обеспечить больше учета показателей, которые достигнуты за последние годы. Сущность метода оформляется в сглаживании временного ряда при помощи взвешенной текучей средней, в которые и веса подчиняются экспоненциальному закону.

Всякое сглажено значение рассчитано при помощи объединения прошлого текущего значения сглаженного значения и временного ряда. В данной ситуации текущие значения временного ряда разрешаются, учитывая константы, сглаживает.

Мы коротко рассмотрели метод экстраполяции: методы, применение. Оставляйте свои комментарии или дополнения к материалу.

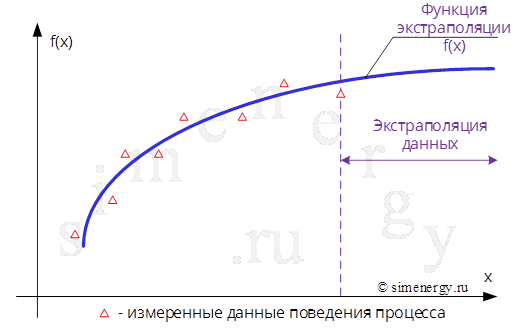
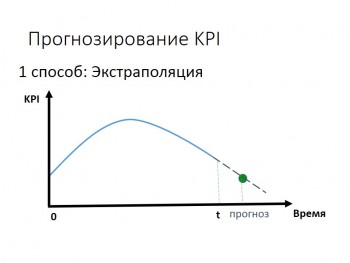
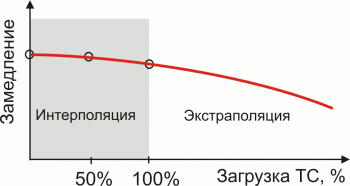
Экстраполяция – это способ предсказания поведения процесса (зависимость изменения данных) в будущем используя известные данные из прошлого. Другими словами, с помощью экстраполяции обобщают заведомо известные данные из прошлого и делают вывод об изменении этих данных в будущем.

Рис.1. Экстраполяция по данным измерений

Экстраполяция – это операция построения функции за пределами интервалов, на которых эта функция определена.

При использовании метода экстраполяции учитываются следующие допущения:

.- период времени, для которого построена функция, должен быть достаточным для выявлении тенденции развития;

.- анализируемый процесс является устойчиво динамическим и обладает инерционностью, т.е. для значительных изменений характеристик процесса требуется время;

.- не ожидается сильных внешних воздействий на изучаемый процесс, которые могут серьезно повлиять на тенденцию развития.

Методы экстраполяции являются одними из самых распространенных методов прогно­зирования. С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результа­тивности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др. Следует заметить, что метод экстраполяции позволяет предсказать поведение процесса в будущем, но степень истинности такого прогноза в значительной мере обусловливается аргументированностью выбора пределов экстраполяции и стабиль­ностью измерений. Так же следует обратить внимание на то, что слож­ные объекты, как правило, не могут быть охарактеризованы одним параметром.

Основные этапы действий при статистическом анализе тенден­ций и экстраполяции:

.- во-первых, сбор и систематизация данных. Сбор исходной информации о значении исследуемой характеристики. Проверка однородности дан­ных и их сопоставимость. При необходимости предварительная обработка исходной информации: усреднение значений временного ряда (сглаживание данных). Построение временной характеристики;

.- во-вторых, выбор функции экстраполяции и расчет параметров выбранной функции. В зависимости от того, какая функция будет выбрана, будет зависеть точность выполненного прогноза.

.- в-третьих, расчет границ доверительного интервала прогноза.

Использование экстраполяции имеет в своей основе предположение о том, что рассматриваемый процесс  представляет собой сочетание двух составляющих: регулярной составляющей  и случайной переменной . Временной ряд может условно представлен в виде:

Регулярная составляющая называется трендом (или тенденцией) и характеризует существующую динамику развития процесса в целом. Случайная составляющая отражает случайные колебания (шумы процесса).

При разработке моделей прогнозирования тренд является основной составляющей прогнозируемого времен­ного ряда, на которую уже накладываются другие составляющие. Ре­зультат при этом связывается исключительно с ходом времени. Пред­полагается, что через время можно выразить влияние всех основ­ных факторов.

Выделение тенденции в массиве данных сводится к определению среднего значения за выбранный период. При этом среднее значение может определяться в виде:

– Среднее арифметическое значение

– Взвешенное среднее арифметическое значение

– Среднее экспоненциальное значение

Средние скользящие значения обычно используются для сглаживания краткосрочных колебаний и выделения основных тенденций или циклов, тем самым позволяя увидеть скрытые тренды в рассматриваемых данных. Тренд характеризует процесс изменения показателя за длительное время, исключая случайные колебания.

Среднее арифметическое значение (Simple Moving Average, SMA) определяется как сумма чисел за рассматриваемый период, которую разделили на количество этих чисел за период.

 – значение функции (значение случайной величины) в i-точке;

– период расчета (целое положительное число);

– среднее арифметическое значение за рассматриваемый период N.

Взвешенное среднее арифметическое значение (Weighted Moving Average, WMA) применяется, когда к каждому известному значению  можно присвоить отдельные значения веса .

 – значение функции (значение случайной величины) в i-точке;

 – вес известного значения;

– период расчета (целое положительное число);

– взвешенное среднее арифметическое значение за рассматриваемый период N.

Экспоненциальное среднее значение (Exponential Moving Average, EMA) является частным случаем взвешенного скользящего среднего, когда значение веса  убывает экспоненциально и никогда не равно нулю. Среднее экспоненциальное значение определяется следующей формулой:

– среднее экспоненциальное значение в i-точке

–   значение функции (значение случайной величины) в i-точке

– сглаживающая константа, коэффициент характеризующий скорость уменьшения весов, принимает значение от 0 и до 1, чем меньше его значение тем больше влияние предыдущих значений на текущую величину среднего.

При этом, в качестве первого значения берется простое скользящее среднее (Simple Moving Average) с тем же самым интервалом сглаживания. экспоненциального скользящего среднего.

Коэффициент , может быть выбран произвольным образом, в пределах от 0 до 1. Однако в практике технического анализа на реальном рынке такой подход не применим, поскольку статистический ряд постоянно дополняется новыми значениями цен. Это делает невозможным одновременно зафиксировать α коэффициент и соблюсти критерий минимизации среднеквадратической ошибки. С этой целью для расчета α коэффициента используется следующая формула:

– период расчета (целое положительное число) или интервал сглаживания.

Измеренные значения  находятся в диапазоне (интервале) относительно рассчитанного среднего значения. Диапазон измерений обозначается буквой греческого алфавита – сигма .

– среднее значение за рассматриваемый период N;

– отклонение от среднего значения.

Аналитический расчет диапазона (интервала) измерений может быть выполнен по формуле определения среднеквадратичного отклонения.

Среднеквадратичное (стандартное) отклонение – показывает среднее значение разброса измеренной величины относительно среднего значения. Оценка среднеквадратичного (стандартного) отклонения может быть выполнена по формуле:

– период расчета (целое положительное число);

– среднее арифметическое значение за рассматриваемый период N;

Cреднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения. Следует заметить, что с вероятностью 0,9973 (99,73%) значение нормально распределённой случайной величины лежит в интервале ., другими словами значения распределённой случайной величины лежат в диапазоне:

Методы экстраполяции

Далее в статье рассмотрены основные методы экстраполяции данных. Следует отметить, что ни один из существующих методов не может обеспечить достаточной точности прогнозов. Применяе­мый в прогнозировании метод экстраполяции не дает точных резуль­татов на длительный срок прогноза, потому что данный метод исхо­дит из прошлого и настоящего, и тем самым погрешность накапли­вается. Этот метод дает положительные результаты на ближайшую (краткосрочную) перспективу прогнозирования тех или иных объектов.

Ниже представленные методы экстраполяции, которые позволяют определить параметры функции на основе ранее полученных данных (точки из заданной выборки). Вначале рассматривается способ построения интерполяционного полинома через (непосредственно) точки заданной выборки. В последствии в статье рассматривается способ построения интерполяционного полинома (однофакторные и многофакторные функции) в непосредственной близости от точек из заданной выборки.

П1. Экстраполяция на основе интерполяционного полиномома n-степени.

Интерполяционный полином n-степени – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.

В общем виде интерполяционный многочлен записывается следующим образом:

Для получения интерполяционного многочлена, который будет соединять все заданные точки из набора значений, используют либо построение через форму Лагранжа, либо  построение через форму Ньютона.

Интерполяционный многочлен в форме Лагранжа – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.

В общем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде:

где  ˗ степень полинома ;

 ˗  значение значения интерполирующей функции  в точке ;

 ˗  базисные полиномы (множитель Лагранжа), которые определяются по формуле:

Интерполяционный многочлен в форме Ньютона – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки с постоянным временным шагом измерений.

В общем виде интерполяционный многочлен в форме Ньютона записывается в следующем виде:

где n – вещественное число, которое указывает степень полинома;

 –  переменная, которая представляет собой разделенную разность k-го порядка, которая вычисляется по следующей формуле:

Разделённая разность является симметричной функцией своих аргументов, то есть при любой их перестановке её значение не меняется. Следует отметить, что для разделённой разности k-го порядка справедлива следующая формула:

Недостатки метода интерполяции данных на основе интерполяционного полиномома n-степени:

П1. С ростом числа точек порядок многочлена возрастает, а вместе с ним возрастает число операций, которое нужно выполнить для вычисления точки на кривой.

П2. С ростом числа точек у интерполяционной кривой могут возникнуть осцилляции, когда построенный интерполяционный многочлен в промежуточных точках кривой будет очень сильно (нехарактерно) раскачиваться и далеко уходить от заданных точек.

П3. С ростом числа точек плохо подходит для экстраполяции, так как значение многочлена степени n>0 вне отрезка интерполяции всегда расходится к бесконечности (тем быстрее, чем больше n) вне зависимости от сходимости экстраполируемой функции.

П2. Экстраполяция на основе однофакторной функции

Однофакторные функции – это такие функции, в которых прогнозируемый показатель зависит только от одной переменной (одного признака). В научно-техническом и экономическом прогнозировании в качестве главного фактора аргумента обычно используют время. Однако вполне очевидно, что не ход времени определяет величины прогнозируемого показателя, а действие многочисленных влияющих на него факторов, которые сложно выделить и определить.

В качестве однофакторных функций используются следующие функции, в которых временная переменная обозначена символом t (фактор-аргумент).

П.1. Степенной полином

Степенной полином может описать любые процессы изменения показателя в зависимости от значений времени. Корреляционное отношение для степенного полинома, служащее мерой тесноты корреляционной связи в нелинейных моделях, приближается к единице по мере увеличения числа степеней полинома до числа уровней временного ряда. Одновременно линия регрессии приближается к фактическим уровням показателя за прошедшее время, что не позволяет установить его тренд и экстраполировать его на перспективу. Поэтому для прогнозирования обычно не применяют полином выше третьей степени. Таким образом, в качестве прогнозирующей функции целесообразно использовать лишь три частных случая степенного полинома: линейную модель, параболу и полином третьего порядка.

П.1.1. Линейная функция (частный случай полинома)

Однофакторная линейная модель отражает постоянный ежегодный абсолютный прирост, т.е. арифметическую прогрессию.

П.1.2. Парабола (частный случай полинома)

Парабола (степенной полином) второго порядка описывает случаи увеличения абсолютного ежегодного прироста на постоянную величину, а третьего порядка – кривую с двумя точками изгибов.

П.2. Экспоненциальная (показательная) функция

Экспонента первого порядка (показательная функция) предусматривает постоянный ежегодный темп роста, равный  процентов (т.е. геометрическую прогрессию), а второго порядка – постоянное увеличение ежегодных темпов роста враз.

П.3. Степенная функция

Степенная функция соответствует случаю ускоряющегося при а1>1 или замедляющегося при а1<1 роста абсолютного ежегодного прироста.

П.4. Логарифмическая функция

Логарифмическая функция выражает случай сокращения абсолютного ежегодного прироста, а функции Торнквиста и Конюса, комбинация линейной функции с логарифмической – затухающий рост абсолютного ежегодного прироста. Логистическая (сигмоидальная) кривая представляет собой модифицированную геометрическую прогрессию, в которой возрастание затухает по мере приближения к определенному пределу.

П.4.1. Комбинация линейной и логарифмической функций

П.4.2. Функция Конюса

П.4.3. Функция Торнквиста

П.4.4. Функция логистическая (сигмоидальная)

П.5. Гиперболическая функция (Гипербола)

Гиперболическая функция характерна для тех случаев, когда в начальной стадии абсолютные уровни показателя резко сокращаются, а на последующих этапах этот процесс сокращения постепенно затухает

П.5.1. Комбинация линейной функции и гиперболы

П.6. При прогнозировании колебательных (циклических) процессов применяют тригонометрические функции, ряды Фурье.

k – количество учитываемых гармоник в сигнале.

Прогнозирование данных в будущем обеспечивают с помощью выбора функции, которая наилучшем образом описывает изменение наблюдаемой величины в прошлом. Для выбранной функции определяют значения коэффициентов выбранной функции. Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпиричес­ким значениям применяется метод наименьших квадратов. Его сущ­ность состоит в минимизации суммы квадратов отклонений меж­ду наблюдаемыми (фактическими) величинами и соответствующими оценками (расчет­ными величинами), вычисленными по подобранному уравнению связи.

где  – значение выбранной однофакторной функции в заданной точке, – исследуемый временной ряд в заданной точке

Полученное выражение носит название целевой функции. Целевая функция – эта функция нескольких переменных, подлежащая оптимизации (минимизации или максимизации) в целях решения некоторой оптимизационной задачи.

С помощью метода наименьших квадратов могут быть определены неизвестные коэффициенты во всех однофакторных прогнозирующих функциях.

В качестве примера, рассмотрим однофакторную функцию вида «линейная функция», с помощью которой будем моделировать заданный временной ряд.

Поиск неизвестных коэффициентов  осуществляется с помощью метода наименьших квадратов. В соответствии с методом наименьших квадратов запишем целевую функцию:

 

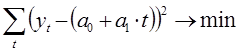
Целевая функция имеет минимум там, где частная производная по неизвестным коэффициентам равна нулю.  В результате у нас выражение перепишется в следующую систему уравнений:

Преобразуем полученную систему уравнений: для системы уравнений проведены сокращения, раскрытие скобок, перенос известных величин вправо, а неизвестных влево. В результате получим следующую систему уравнений:

n – количество используемых измерений в заданном временном ряду.

Из полученной системы уравнений определим неизвестные коэффициенты  следующим образом:

Таким образом, определив неизвестные коэффициенты  можно построить однофакторную функцию на заданном отрезке времени и сделать прогноз изменения функции в будущем.

П3. Экстраполяция на основе многофакторных прогнозирующих функций

Многофакторные зависимости определяются поведением не одного параметра, а многих факторов одновременно. Чтобы построить такую модель, вначале необходимо определить факторы, которые оказывают наибольшее влияние на исходные данные.

Многофакторные модели могут быть как линейными, так и нелинейными. 

П.1. в виде линейной многофакторной модели:

где – неизвестные коэффициенты модели,

– аргументы, влияющие на прогнозируемый показатель

П.2. в виде нелинейной многофакторной модели (степенного типа), которая может быть преобразована в линейную модель с помощью логарифмирования:

Более сложные виды нелинейных многофакторных моделей редко используются в практике прогнозирования и планирования.

Неизвестные коэффициенты выражений  определяются с помощью метода наименьших квадратов из системы нормальных уравнений. Его сущ­ность состоит в минимизации суммы квадратов отклонений меж­ду наблюдаемыми (фактическими) величинами и соответствующими оценками (расчет­ными величинами), вычисленными по подобранному уравнению связи.

Целевая функция имеет минимум там, где частная производная по неизвестным коэффициентам   равна нулю.  В результате у нас выражение перепишется в следующую систему уравнений:

В результате решения данной системы уравнений определяются неизвестные коэффициентам   при которых полученная система уравнений стремится к нулю.

Факторы-аргументы должны отвечать следующим условиям:

во-первых, иметь количественное измерение и отражаться в отчетах или, по крайней мере, определяться на основе специального анализа отчетных данных;

во-вторых, иметь перспективные оценки значений на прогнозируемый период;

в-третьих, число включаемых в модель факторов должно быть меньше числа данных ряда в три раза;

в-четвертых, быть линейно независимыми.

 П4. Экстраполяция на основе нейронной сети

Искусственные нейронные сети широко используются в задачах экстраполяции данных, когда неизвестен точный вид связи (функции) между входными и выходными значениями. Нейронная сеть является сложной нелинейной системой с огромным числом степеней свободы, что позволяет ей подстраивается под любые начальные данные.

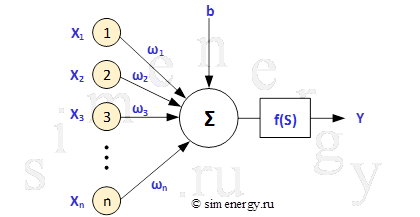
Искусственная нейронная сеть состоит из искусственных нейронов. Структурная схема искусственного нейрона приведена ниже.

Рис.2. Структурная схема искусственного нейрона

Искусственный нейрон имеет несколько входных сигналов (несколько входов) и только один выходной (единственный выход). Каждый вход имеет некоторый вес, на который умножается значение, поступившее по данному входу. В теле (ячейке) нейрона происходит суммирование взвешенных входов в соответствии с формулой:

 n — размерность входного вектора

— вес i-го входа нейрон

 — значение, поступающее на i-й вход нейрона

Как уже было написано, в теле нейрона происходит суммирование взвешенных входов, а полученная сумма преобразуется с помощью активационной (передаточной) функции нейрона (обычно нелинейной) в выходное значение нейрона.  Полученная сумма поступает в качестве аргумента S на функцию активации , результат которой является выходным значением нейрона.

Активационная функция (передаточная функция) может иметь различный вид: бинарный, пороговый, линейный, сигмоидальный. Одной из наиболее распространенных видов активационной функции является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):

При уменьшении α сигмоид становится более пологим, в пределе при α=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении α сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. 

Нейроны соединены между собой с помощью синапсов – упрощенных аналогов синаптических контактов нервных клеток, обладающих способностью изменять и сохранять свой вес (величину). Целенаправленная перестройка весов синапсов (т.е. коэффициентов, на которые умножаются входные сигналы, или подстроечных параметров) позволяет нейрону избирательно реагировать на сигналы других нейронов, обеспечивая на выходе наиболее “полезные” сигналы.

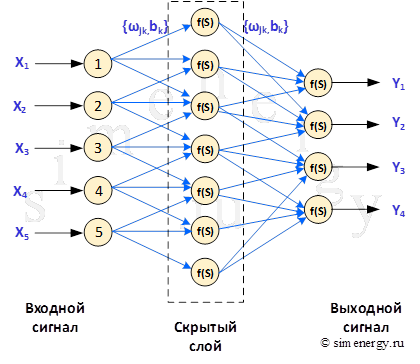
Если нейронная сеть имеет дополнительные слои между входным и выходным слоем, то они называются скрытыми, а обучение такой сети – глубоким. Дополнительные скрытые слои могут помочь нейросети определить более сложные закономерности между входными и желаемыми выходными данными.

Рис.3. Структурная схема нейронной сети

После создания структуры нейронной сети выполняется процесс обучения нейронной сети. В процессе обучения происходит подбор коэффициентов нейронной сети  тем самым выстраивается зависимость между заранее известными входными и выходными данными. Обучение нейронной сети означает, что для заданного набора заранее известных входных и выходных данных, необходимо подобрать оптимальные коэффициенты  нейросети так, что квадратичная ошибка между точным выходным значением и выходным значением, полученным посредством распространения входных значений через нейронную сеть, стремилась к минимуму:

Поиск оптимальных коэффициентов производится методом градиентного спуска с использованием метода обратного распространения ошибки.

 

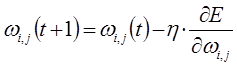
Производные функции минимизации определяются по следующим формулам:

В представленной системе уравнений частные производные имеют следующий вид:

 

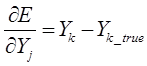
В настоящее время для создания и обучения нейронных сетей используют программные комплексы с готовыми библиотеками, например, на базе языка программирования Python.

Таким образом, экстраполяцию можно использовать в качестве средства для определения будущих, ожидаемых значений величин, на основе имеющихся данных о тенденциях их изменений в прошлые периоды. С оптимальным выбором метода экстраполяции возможно получить максимально точный результат, который будет правильно отражать будущие значения.