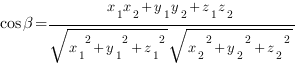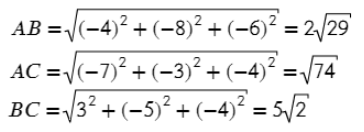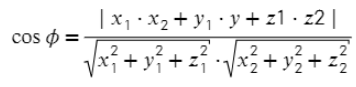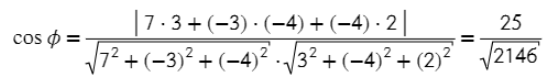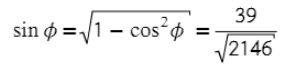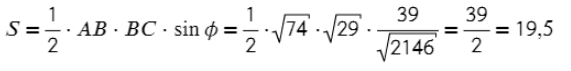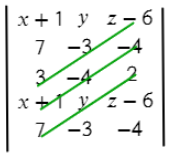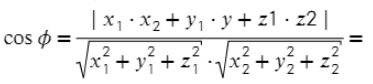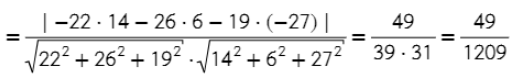({color{red}{textbf{Факт 1. Про векторы}}})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), то вектор (overrightarrow{AB}) имеет координаты [overrightarrow{AB} = {x_2-x_1;y_2-y_1;z_2-z_1}]
(bullet) Если в пространстве заданы два вектора (vec{a}
={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}), то:
(qquad blacktriangleright) сумма этих векторов (vec{a}+vec{b}={x_1+x_2;y_1+y_2;z_1+z_2})
(qquad blacktriangleright) разность этих векторов (vec{a}-vec{b}={x_1-x_2;y_1-y_2;z_1-z_2})
(qquad blacktriangleright) произведение вектора на число (lambda
vec{a}={lambda x_1;lambda
y_1;lambda z_1})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), а точка (O) — середина отрезка (AB), то (O) имеет координаты [Oleft(dfrac{x_1+x_2}2;dfrac{y_1+y_2}2;dfrac{z_1+z_2}2right)]
(bullet) Длина вектора (vec{a}={x;y;z}) обозначается (|vec{a}|) и вычисляется по формуле [|vec{a}|=sqrt{x^2+y^2+z^2}]
(bullet) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.
({color{red}{textbf{Факт 2. Про скалярное произведение}}})
(bullet) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: [{large{(vec{a},
vec{b})=|vec{a}|cdot|vec{b}|cdotcos angle (vec{a},
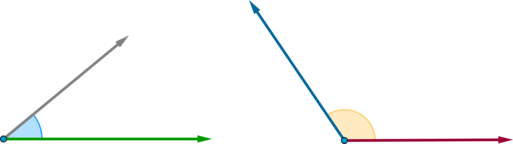
vec{b})}}] На рисунке показано, что такое угол между векторами:
(bullet) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: [(vec{a}, vec{b})=0 quadLeftrightarrowquad
vec{a}perp vec{b}]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: [|vec{a}|=sqrt{(vec{a},
vec{a})}]
III. Переместительный закон: [(vec{a}, vec{b})=(vec{b},
vec{a})]
IV. Распределительный закон: [(vec{a}+vec{b},
vec{c})=(vec{a}, vec{c})+(vec{b}, vec{c})]
V. Сочетательный закон ((lambda) – число): [lambda(vec{a}, vec{b})=(lambda
vec{a}, vec{b})]
(bullet) Скалярное произведение двух векторов (vec{a}
={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) можно вычислить с помощью координат этих векторов: [{large{(vec{a},
vec{b})=x_1x_2+y_1y_2+z_1z_2}}]
(bullet) Косинус угла между векторами (vec{a} ={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) вычисляется по формуле: [{large{cosangle(vec{a}, vec{b})=dfrac{x_1x_2+y_1y_2+z_1z_2}
{sqrt{x^2_1+y^2_1+z^2_1}cdot
sqrt{x^2_2+y^2_2+z^2_2}}}}]
({color{red}{textbf{Факт 3. Про уравнение плоскости}}})
(bullet) Если (vec{n}={a;b;c}) – нормаль к плоскости, то уравнение плоскости имеет вид [ax+by+cz+d=0] Для того, чтобы найти (d), нужно подставить в уравнение плоскости вместо (x, y, z) координаты любой точки, лежащей в этой плоскости.
Пример: если (vec{n}={1;2;3}) – нормаль к плоскости, (O(4;5;6)) – точка из плоскости, то справедливо: (1cdot 4+2cdot 5+3cdot
6+d=0), откуда (d=-32), следовательно, уравнение плоскости имеет вид (x+2y+3z-32=0).
(bullet) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть (A(1;0;0),
B(0;3;4), C(2;0;5)) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: [begin{cases}
1cdot a+0cdot b+0cdot c+d=0\
0cdot a+3cdot b+4cdot c+d=0\
2cdot a+0cdot b+5cdot c+d=0end{cases} quadRightarrowquad
begin{cases}
d=-a\
3b+4c-a=0\
a+5c=0end{cases}quadRightarrowquad begin{cases} d=-a\
a=-5c\
b=-3cend{cases}quadRightarrowquadbegin{cases}a=-5c\
b=-3c\
d=5cend{cases}] Следовательно, уравнение плоскости имеет вид: [-5ccdot x-3ccdot y+ccdot z+5c=0] Можно разделить обе части на (c), так как (cne 0) (иначе (a=b=c=d=0)), следовательно, уравнение плоскости имеет вид [-5x-3y+z+5=0]
({color{red}{textbf{Факт 4. Про углы между прямыми, плоскостями}}})
(bullet) Если векторы (vec{a} ={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}) являются направляющими прямых (p) и (q), то косинус угла между этими прямыми равен: [cos phi=dfrac{|x_1x_2+y_1y_2+z_1z_2|}
{sqrt{x^2_1+y^2_1+z^2_1}cdot sqrt{x^2_2+y^2_2+z^2_2}}]
(bullet) Если (vec{a}) — направляющий вектор прямой (p), а (vec{n}) — нормаль к плоскости (phi) (перпендикуляр к плоскости), то синус угла между прямой (p) и плоскостью (phi) равен модулю косинуса угла между векторами (vec{a}) и (vec{n}): [sin
angle(p, phi)=|cos angle(vec{a}, vec{n})|]
(bullet) Если две плоскости заданы уравнениями (a_1x+b_1y+c_1z+d_1=0) и (a_2x+b_2y+c_2z+d_2=0), то косинус угла между плоскостями ищется по формуле: [{large{cos phi=left| dfrac{a_1a_2+b_1b_2+c_1c_2}
{sqrt{a^2_1+b^2_1+c^2_1}cdot
sqrt{a^2_2+b^2_2+c^2_2}}right|}}]
({color{red}{textbf{Факт 5. Про расстояния от точки до плоскости,
между скрещивающимися прямыми}}})
(bullet) Если (M(x_0;y_0;z_0)) — некоторая точка вне плоскости (phi), (ax+by+cz+d=0) — уравнение плоскости (phi), то расстояние от точки (M) до плоскости (phi) ищется по формуле: [rho(M, phi)=dfrac{|ax_0+by_0+cz_0+d|}{sqrt{a^2+b^2+c^2}}]
(bullet) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.
25
Апр 2012
13 Задание (2022) (C2)

Если мы решили использовать этот метод, то будем придерживаться такого алгоритма:
1. Вводим систему координат.
2. Находим координаты направляющих векторов данных прямых.
3. По формуле косинуса угла между векторами находим косинус угла между направляющими векторами.
Косинус угла между векторами 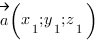
Вот, собствено, и все.
Важное уточнение: за угол между прямыми принимают меньший из двух углов, образованный этими прямыми, поэтому косинус угла между прямыми должен быть больше нуля, и он равен модулю косинуса угла между направляющими векторами.
Решим задачу.
В правильной шестиугольной призме 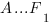
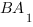
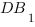



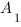
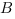
Длину отрезка 


Чтобы найти координаты вектора 
б) Найдем координаты направляющего вектора прямой 
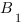
3. Найдем косинус угла 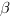


Ответ:
И.В. Фельдман, репетитор по математике.

|
Отзывов (9)
| Метки: решение задания С2
Координаты вектора
Вектор – отрезок, имеющий длину и указывающий направление.
На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.
Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$
Скрещивающиеся прямые
И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$
Уравнение плоскости
В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.
Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
Например, пусть даны три точки:
$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$
Подставим координаты точек в общее уравнение плоскости:
$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$
Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.
Теперь у нас есть три уравнения и три неизвестные – можем решить систему:
Пример 3
Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$
Расстояние от точки до плоскости
Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$
Пример 4
Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$
Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).
Пример 5
Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.
Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) – середина ребра (CE).
- Докажите, что прямые (AD) и (BG) перпендикулярны.
- Найдите расстояние между прямыми (AD) и (BG).
Решение:
Решим задачу полностью методом координат.
Нарисуем рисунок и выберем декартову систему координат. (Рис 5).
Сущность метода координат, как метода решения задач состоит в том, что задавая фигуры уравнениями и выражая в координатах различной геометрические соотношения мы можем решать геометрическую задачу средствами, алгебры метод координат – это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией которой дают богатые плоды. Какие они не могли бы дать, оставаясь разделёнными.
В некоторых случаях метод координат даёт возможность строить доказательства и решать многие задачи более рационально красиво, чем чисто геометрическими способами. Координатно- векторный способ позволяет без особого труда решить стереометрическую задачу из курса ЕГЭ профильной математики.
Вспомним теорию!
Интерактивное приложение
Алгоритм нахождения угла между скрещивающимися прямыми.
Видеоразбор задания
Решим задачу из открытого банка заданий ФИПИ.
Проверьте свои знания и пройдите веб-квест по этой теме:
Интерактивный формат заданий из открытого банка заданий ФИПИ:
Буду рада вам! Подписывайтесь на мои каналы!
https://www.youtube.com/channel/UCrrze24VyUrfKKfpoa9uL1Q
Метод координат (углы между векторами и плоскостями)
Нахождение координат и длин вектора.
Вычисление угла между векторами.
Составление уравнение плоскости по трем точкам.
Решение задач с доказательством.
Для того, чтобы успешно решать задачи методом координат, полезно помнить:
Чтобы задать вектор, проходящий черерз 2 точки, нужно из координат второй точки вычесть координаты первой точки.
Чтобы найти длину вектора, нужно извлечь корень квадратный из суммы квадратов его координат.
Задача. Найти координаты и длины векторов AB, BC, AC, если точки имееют координаты А = (5; 8; 3), B = (1; 0; −3), C = (−2; 5; −1).
AB = (1−5; 0-8; −3−3) = (−4; −8; −6)
AC = (−2−5; 5−8; −1−3) = (−7; −3; −4)
BC = (1−(−2); 0−5; −1−3) = (3; −5; −4)
Для нахождения угла между двумя векторами a = (x1; y1; z1) и b = (x2; y2; z2):
Задача. Найдите площадь треугольника, ограниченную точками A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
- Находим координаты векторов.
- Вычисляем косинус угла между векторами.
- Через основное тригометрическое тождество получаем синус.
- Подставляем в формулу площади.
AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)
AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)
Задача. Задайте уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
- Находим координаты векторов.
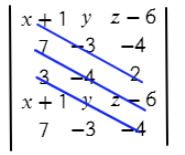
- Задаем матрицу плоскости.
- Вычисляем ее определитель, это и есть уравнение плоскости.
AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)
AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)
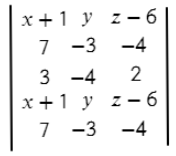
Вторая строчка – координаты первого вектора.
Третья строчка – координаты второго вектора (нет разницы какой из векторов задавать во второй строчке, а какой в третьей).
Четвертая заполняется аналогично первой.
Пятая – аналогично второй.
Теперь перемножаем все значения на одном синем отрезке и складываем с другими значениями на других отрезках:
(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4)
Аналогично делаем с зелеными отрезками:
(z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7
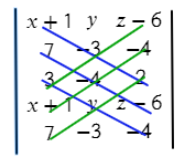
Осталось из значений синих отрезков вычесть значения зеленых отрезков:
(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4) − ((z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7) =
= −22х −26y −19z + 92
−22х −26y −19z + 92 – искомое уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
P.s. Если вам кажется, что это сложно, то огорчу вас. Одна из первых тем (самых простых), которые вы будите проходить на первом курсе любого университета – это матрицы, так что можно немного облегчить себе жизнь и разобраться заранее.
Задача. Найдите угол между плоскостью, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6), и плоскостью, заданную уравнением
14x + 6y −27z + 51 = 0.
- Задаем уравнение плоскости, проходящей через 3 точки ( нашли в предыдущей задаче).
- Находим косинус угла между плоскостями ( формула аналогична косинусу угла между прямыми).
Будь в курсе новых статеек, видео и легкого математического юмора.